0% found this document useful (0 votes)
12 views36 pagesLecture2 - Array, Pointers and Structures
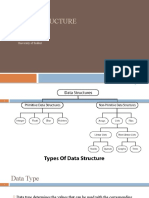
This document covers the fundamentals of Data Structures and Algorithms (DSAs), focusing on arrays, pointers, and structures. It explains array representation, operations such as insertion, deletion, search, and update, as well as the concept of pointers and their usage in programming. Additionally, it discusses structures and their initialization and assignment in programming languages like C.
Uploaded by
Polly Pius EmmanuelsCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PPTX, PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
12 views36 pagesLecture2 - Array, Pointers and Structures
This document covers the fundamentals of Data Structures and Algorithms (DSAs), focusing on arrays, pointers, and structures. It explains array representation, operations such as insertion, deletion, search, and update, as well as the concept of pointers and their usage in programming. Additionally, it discusses structures and their initialization and assignment in programming languages like C.
Uploaded by
Polly Pius EmmanuelsCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PPTX, PDF, TXT or read online on Scribd
/ 36