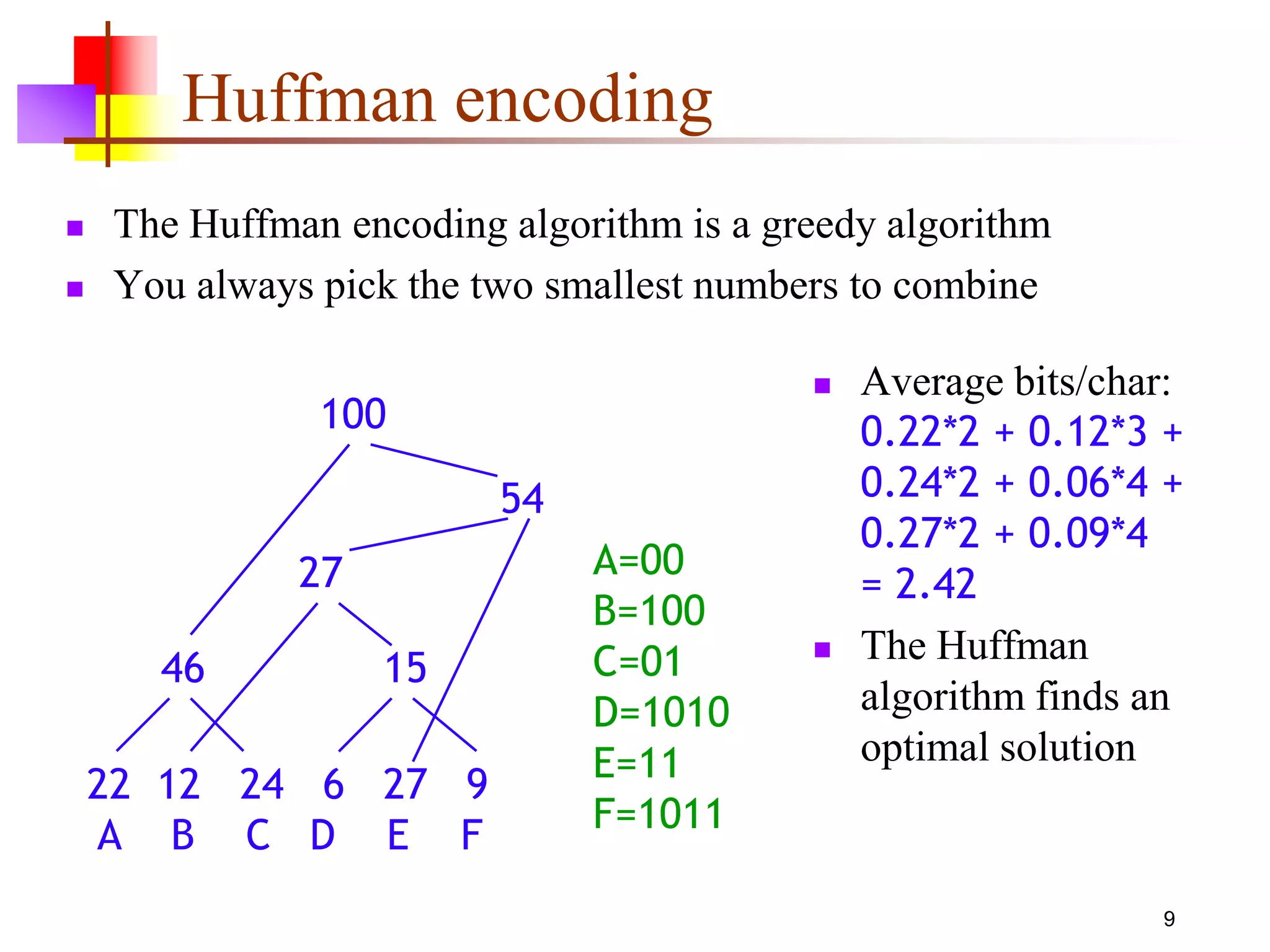
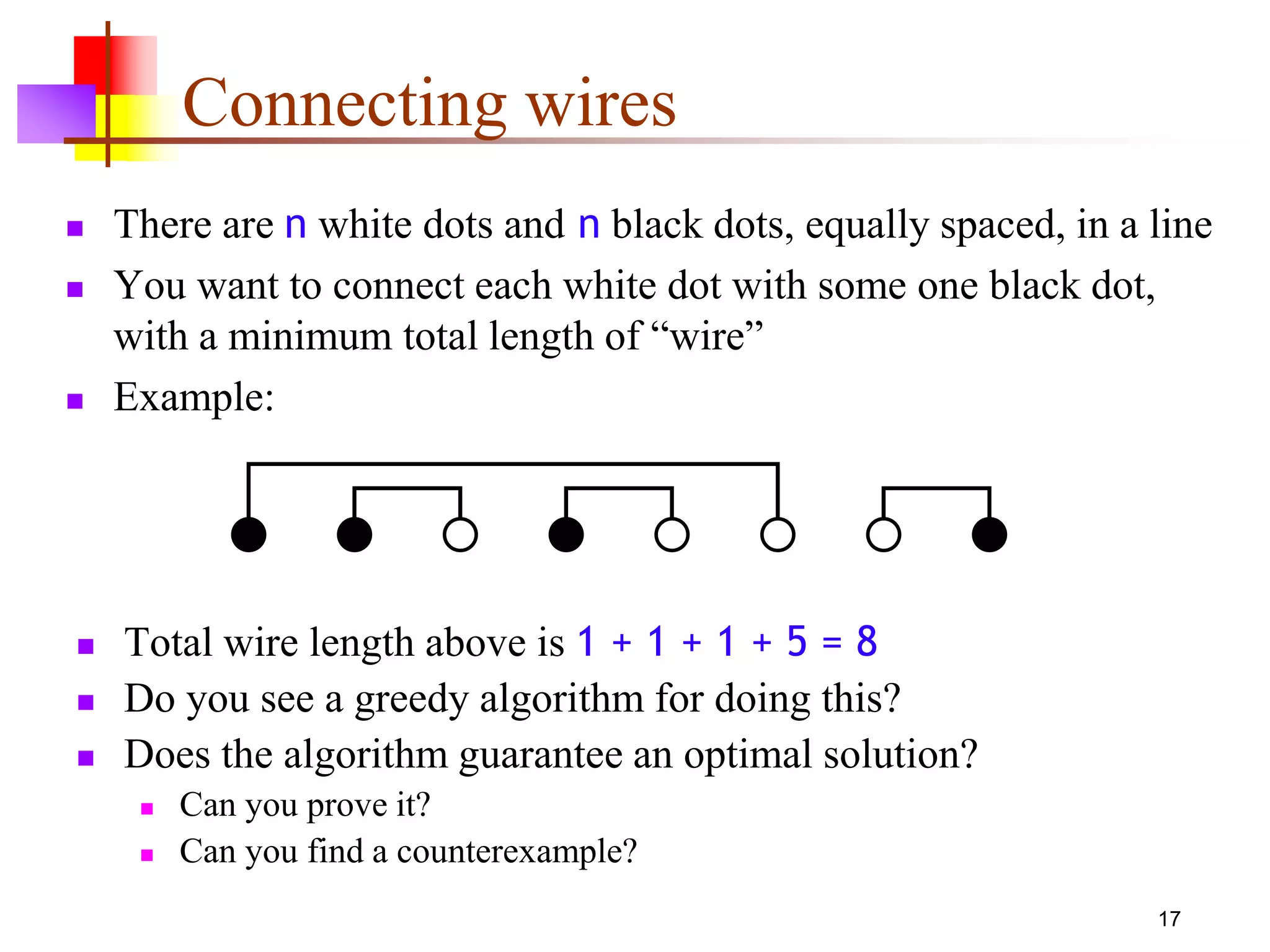
This document discusses greedy algorithms, which are algorithms that select locally optimal choices at each step in the hopes of finding a global optimum. It provides examples of problems that greedy algorithms can solve optimally, such as coin counting, and problems where greedy algorithms fail to find an optimal solution, such as scheduling jobs. It also analyzes the time complexity of various greedy algorithms, such as Dijkstra's algorithm for finding shortest paths.