Greedy algorithm activity selection fractional

Greedy Algorithms
Dr. AMIT KUMAR @JUET

Greedy algorithms
• A greedy algorithm always makes the choice that
looks best at the moment
– My everyday examples:
• Driving
• Playing cards
• Invest on stocks
• Choose a university
– The hope: a locally optimal choice will lead to a
globally optimal solution
– For some problems, it works
• greedy algorithms tend to be easier to code

An Activity Selection Problem
(Conference Scheduling Problem)
• Input: A set of activities S = {a1,…, an}
• Each activity has start time and a finish time
– ai=(si, fi)
• Two activities are compatible if and only if
their interval does not overlap
• Output: a maximum-size subset of
mutually compatible activities

The Activity Selection Problem
• Here are a set of start and finish times
• What is the maximum number of activities that can be
completed?
• {a3, a9, a11} can be completed
• But so can {a1, a4, a8’ a11} which is a larger set
• But it is not unique, consider {a2, a4, a9’ a11}

Interval Representation

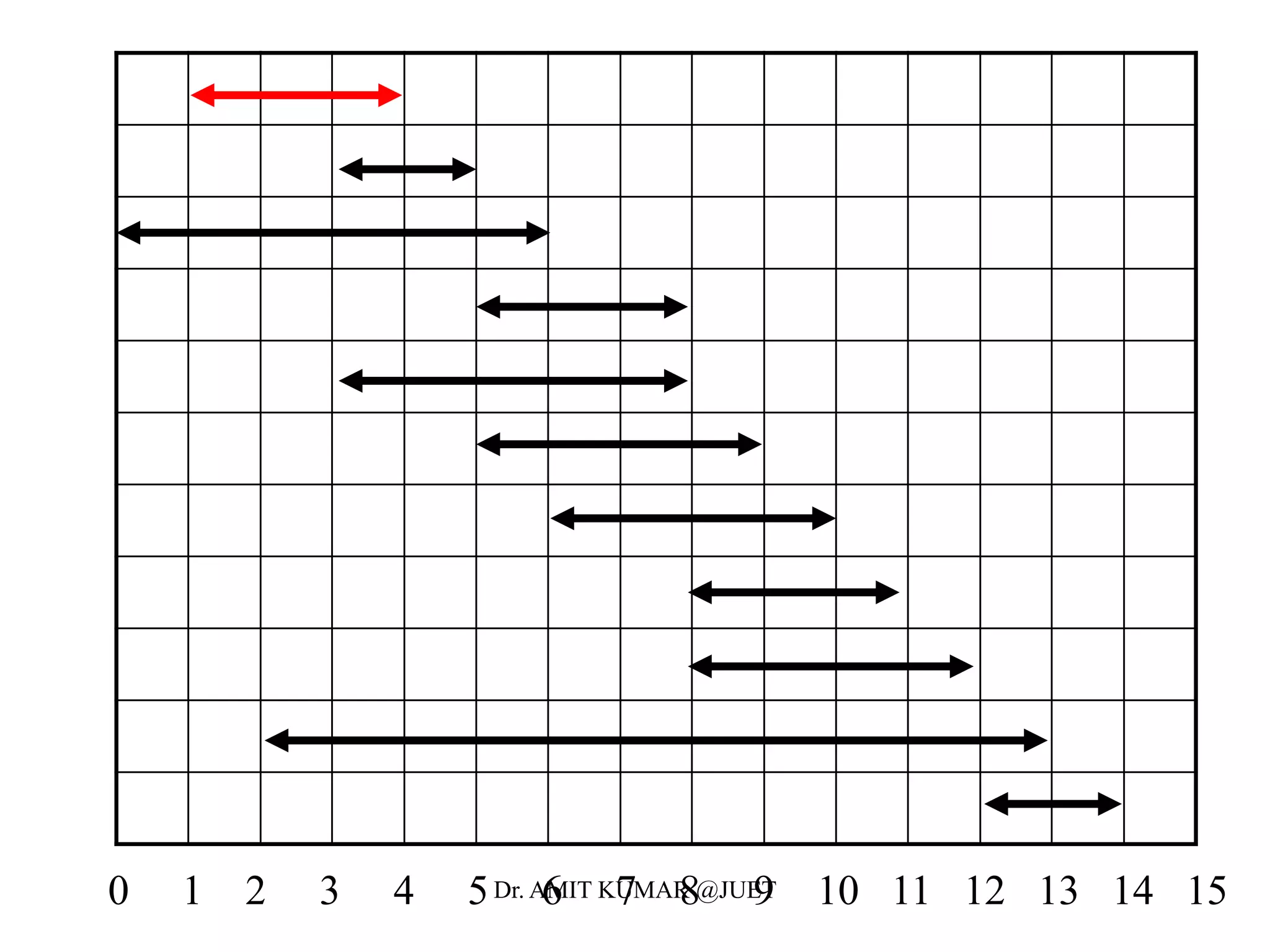
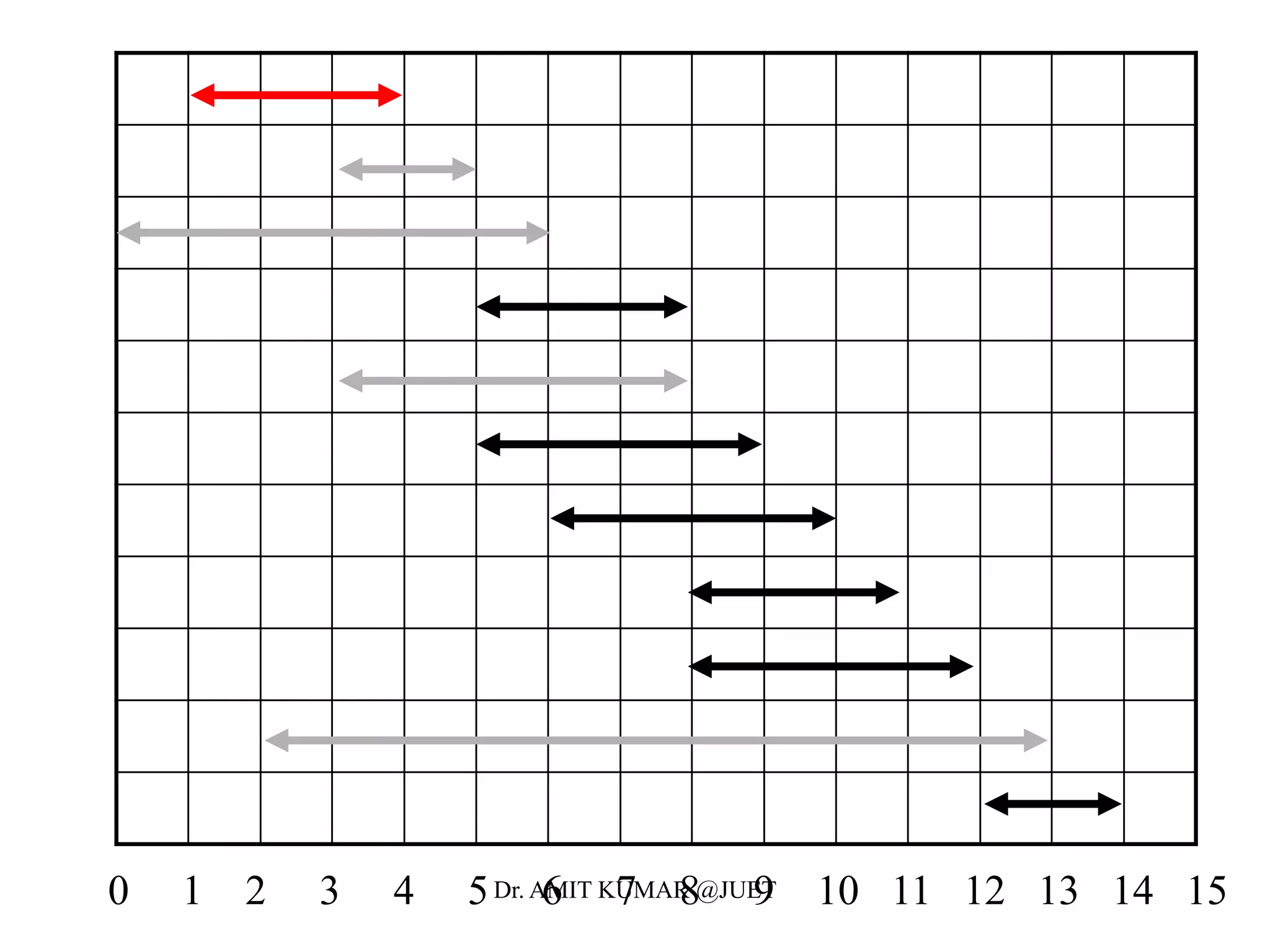
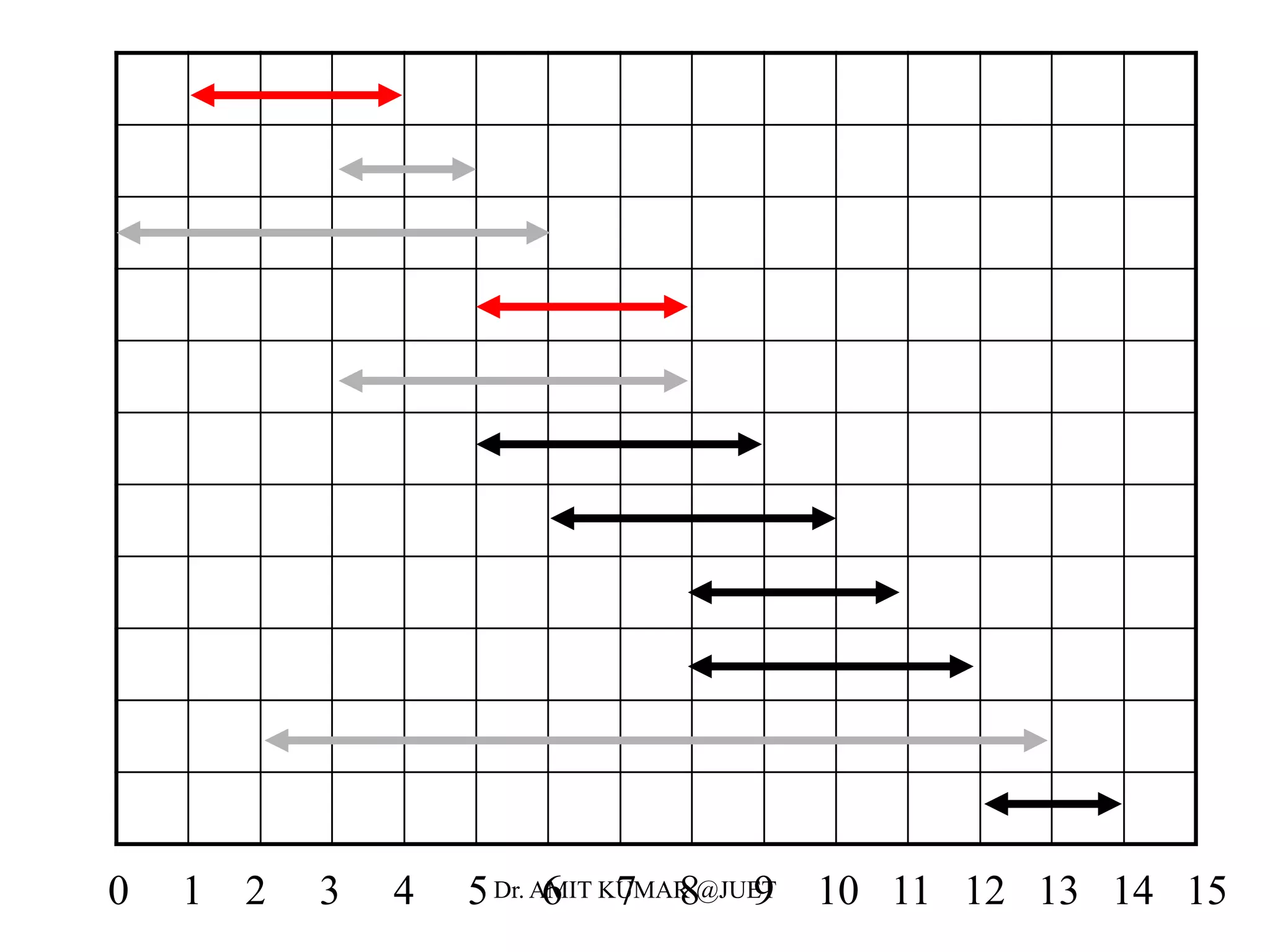
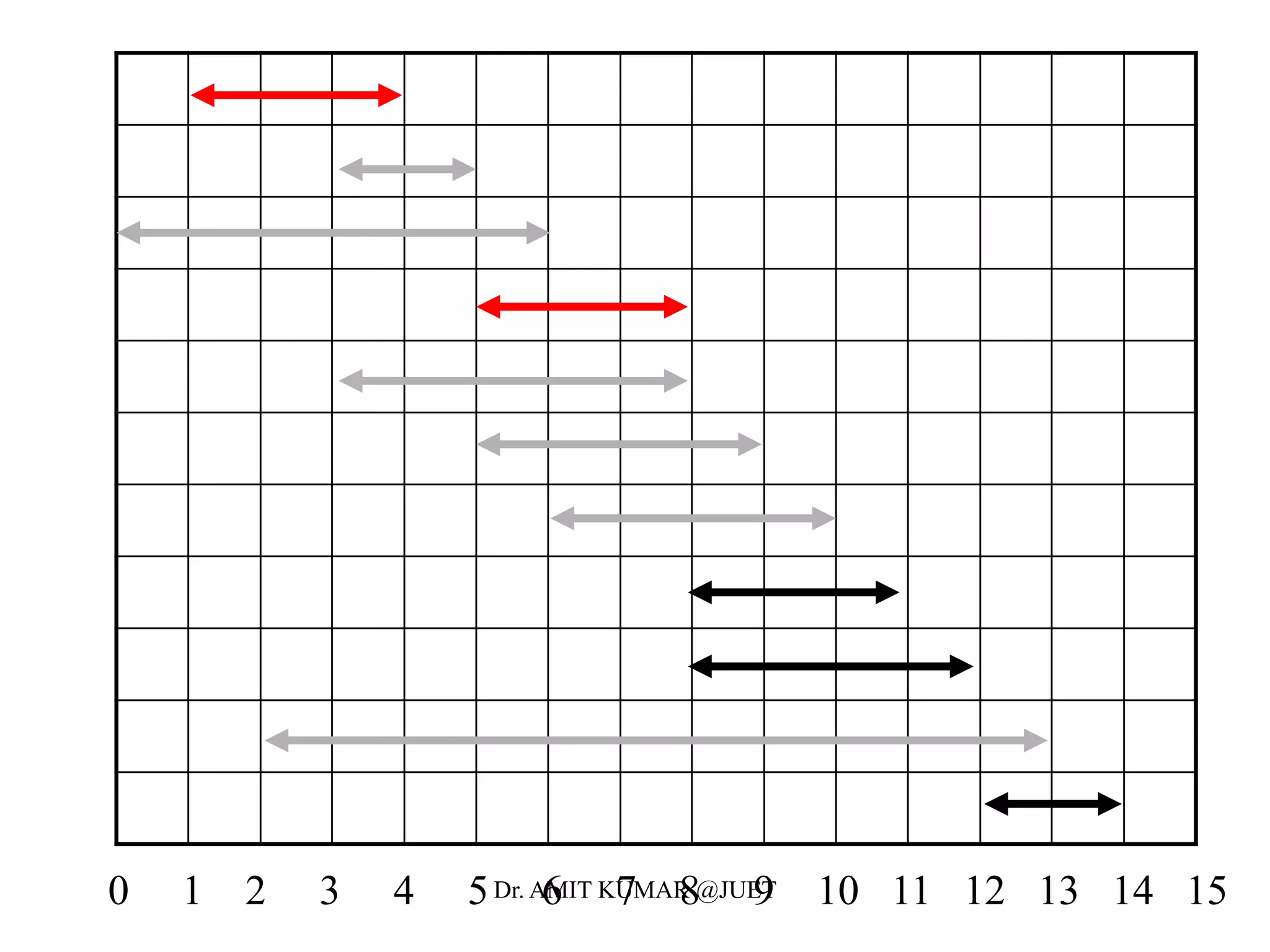
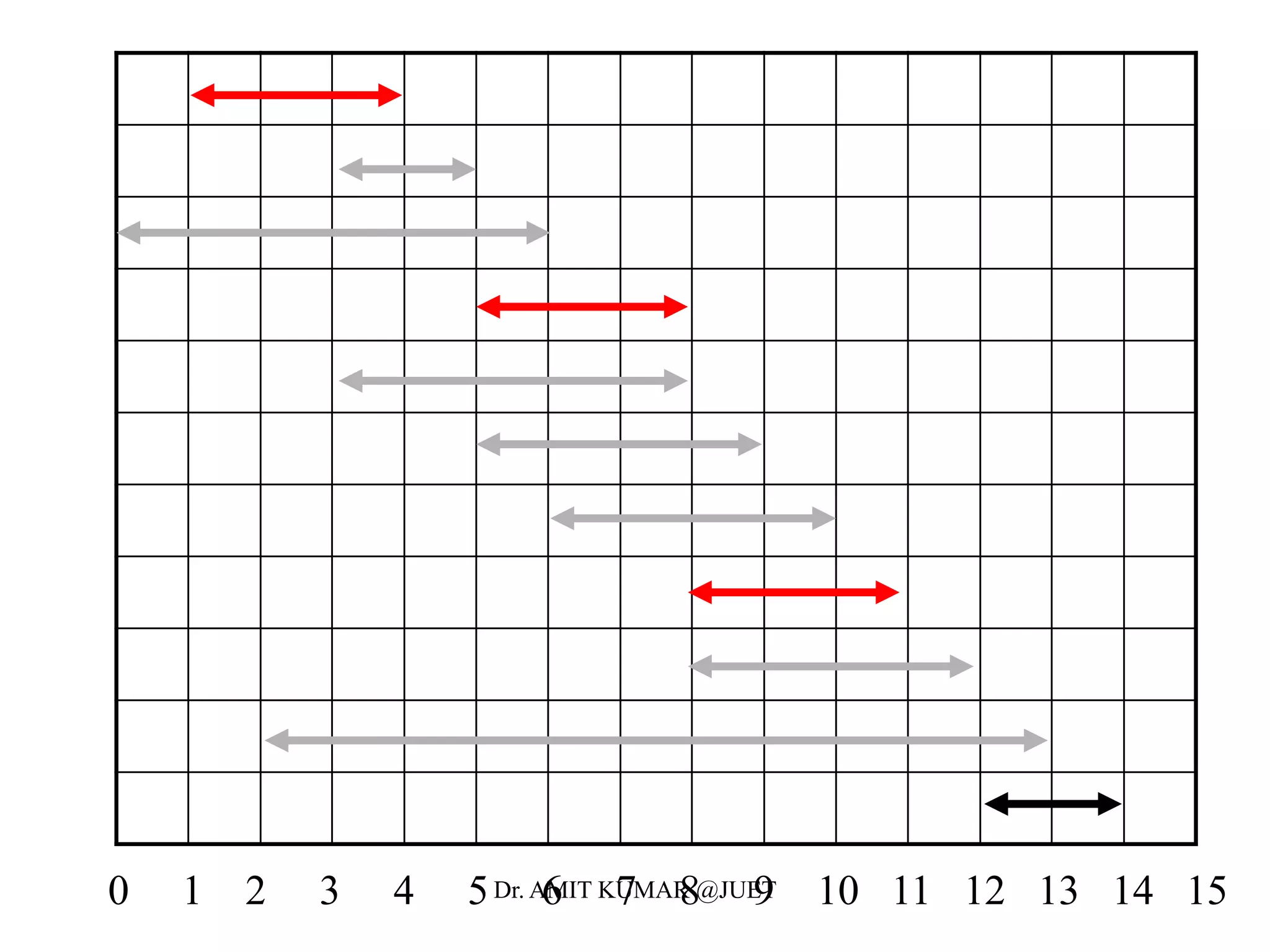
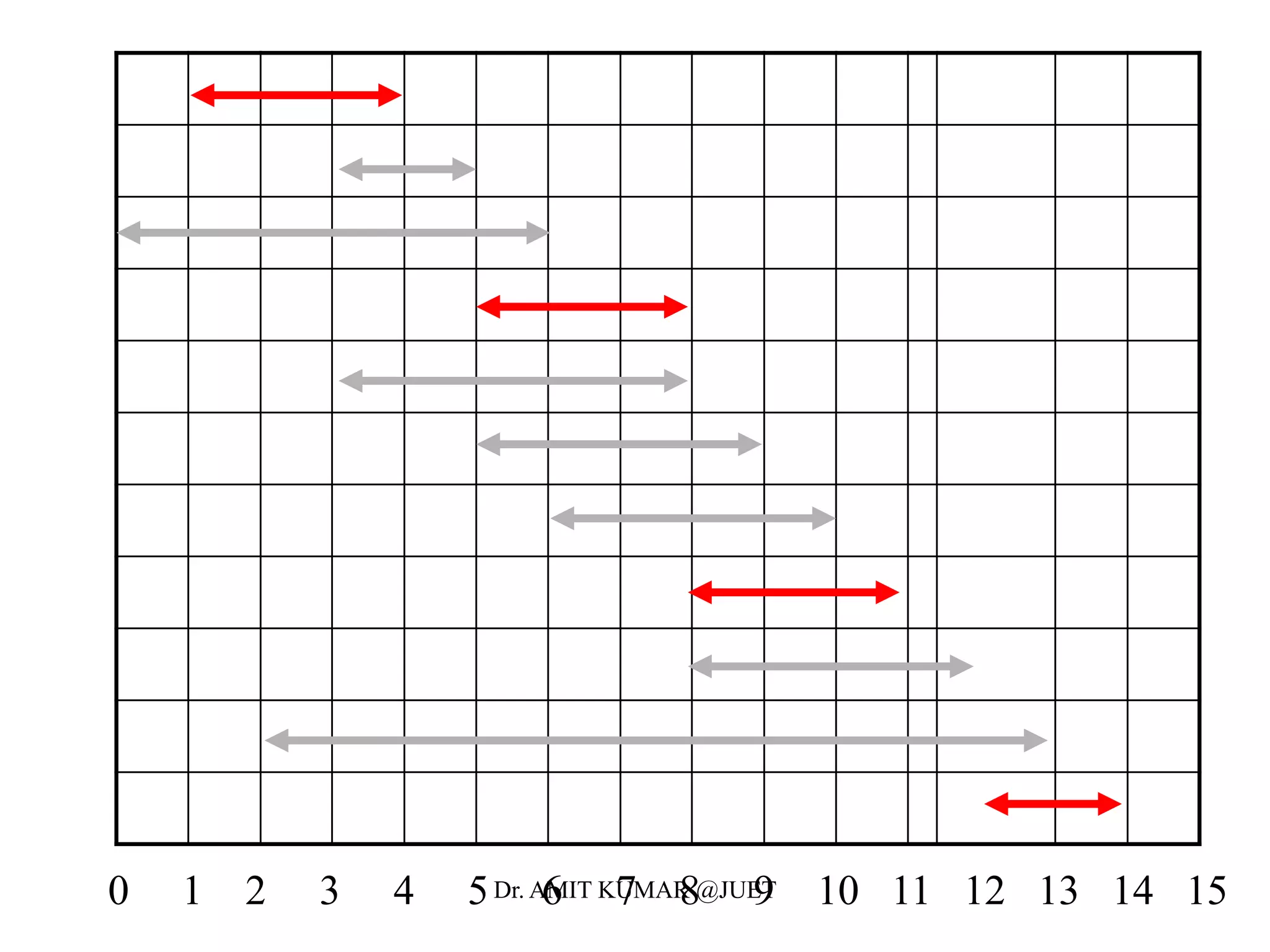
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15Dr. AMIT KUMAR @JUET

Early Finish Greedy
• Select the activity with the earliest finish
• Eliminate the activities that could not be
scheduled
• Repeat!

Example:
The solution set = {1, 4, 8, 11}
Algorithm:
Step 1: Sort fi into nondecreasing order. After sorting, f1
 f2  f3  …  fn.
Step 2: Add the next activity i to the solution set if i is
compatible with each in the solution set.
Step 3: Stop if all activities are examined. Otherwise, go
to step 2.
Time complexity: O(nlogn)
i 1 2 3 4 5 6 7 8 9 10 11
si 1 3 0 5 3 5 6 8 8 2 12
fi 4 5 6 7 8 9 10 11 12 13 14

Solution of the example:
Solution = {1, 4, 8, 11}
i si fi accept
1 1 4 Yes
2 3 5 No
3 0 6 No
4 5 7 Yes
5 3 8 No
7 6 10 No
8 8 11 Yes
9 8 12 No
10 2 13 No
11 12 14 Yes

Assuming activities are sorted by
finish time

Why it is Greedy?
• Greedy in the sense that it leaves as much
opportunity as possible for the remaining
activities to be scheduled
• The greedy choice is the one that maximizes
the amount of unscheduled time remaining

Why this Algorithm is Optimal?
• We will show that this algorithm uses the
following properties
• The problem has the optimal substructure
property
• The algorithm satisfies the greedy-choice
property
• Thus, it is Optimal

Elements of Greedy Strategy
• An greedy algorithm makes a sequence of choices, each
of the choices that seems best at the moment is chosen
– NOT always produce an optimal solution
• Two ingredients that are exhibited by most problems
that lend themselves to a greedy strategy
– Greedy-choice property
– Optimal substructure

Greedy-Choice Property
• A globally optimal solution can be arrived at by
making a locally optimal (greedy) choice
– Make whatever choice seems best at the moment and
then solve the sub-problem arising after the choice is
made
– The choice made by a greedy algorithm may depend on
choices so far, but it cannot depend on any future
choices or on the solutions to sub-problems
• Of course, we must prove that a greedy choice at
each step yields a globally optimal solution

Optimal Substructures
• A problem exhibits optimal substructure if an
optimal solution to the problem contains
within it optimal solutions to sub-problems
– If an optimal solution A to S begins with activity 1,
then A’ = A – {1} is optimal to S’={i S: si  f1}

Knapsack Problem
• One wants to pack n items in a luggage
– The ith item is worth vi dollars and weighs wi pounds
– Maximize the value but cannot exceed W pounds
– vi , wi, W are integers
• 0-1 knapsack  each item is taken or not taken
• Fractional knapsack  fractions of items can be taken
• Both exhibit the optimal-substructure property
– 0-1: If item j is removed from an optimal packing, the remaining
packing is an optimal packing with weight at most W-wj
– Fractional: If w pounds of item j is removed from an optimal
packing, the remaining packing is an optimal packing with weight
at most W-w that can be taken from other n-1 items plus wj – w of
item j Dr. AMIT KUMAR @JUET

Greedy Algorithm for Fractional
Knapsack problem
• Fractional knapsack can be solvable by the greedy
strategy
– Compute the value per pound vi/wi for each item
– Obeying a greedy strategy, take as much as possible of the
item with the greatest value per pound.
– If the supply of that item is exhausted and there is still more
room, take as much as possible of the item with the next value
per pound, and so forth until there is no more room
– O(n lg n) (we need to sort the items by value per pound)
– Greedy Algorithm?
– Correctness?

The Fractional knapsack problem
• n objects, each with a weight wi > 0
a profit pi > 0
capacity of knapsack: M
Maximize
Subject to
0  xi  1, 1  i  n
p xi i
i n1 

w x Mi i
i n1 
 

• The greedy algorithm:
Step 1: Sort pi/wi into nonincreasing order.
Step 2: Put the objects into the knapsack according
to the sorted sequence as possible as we can.
• e. g.
n = 3, M = 20, (p1, p2, p3) = (25, 24, 15)
(w1, w2, w3) = (18, 15, 10)
Sol: p1/w1 = 25/18 = 1.39
p2/w2 = 24/15 = 1.6
p3/w3 = 15/10 = 1.5
Optimal solution: x1 = 0, x2 = 1, x3 = 1/2
total profit = 24 + 7.5 = 31.5
The Fractional knapsack problem

Optimal substructures
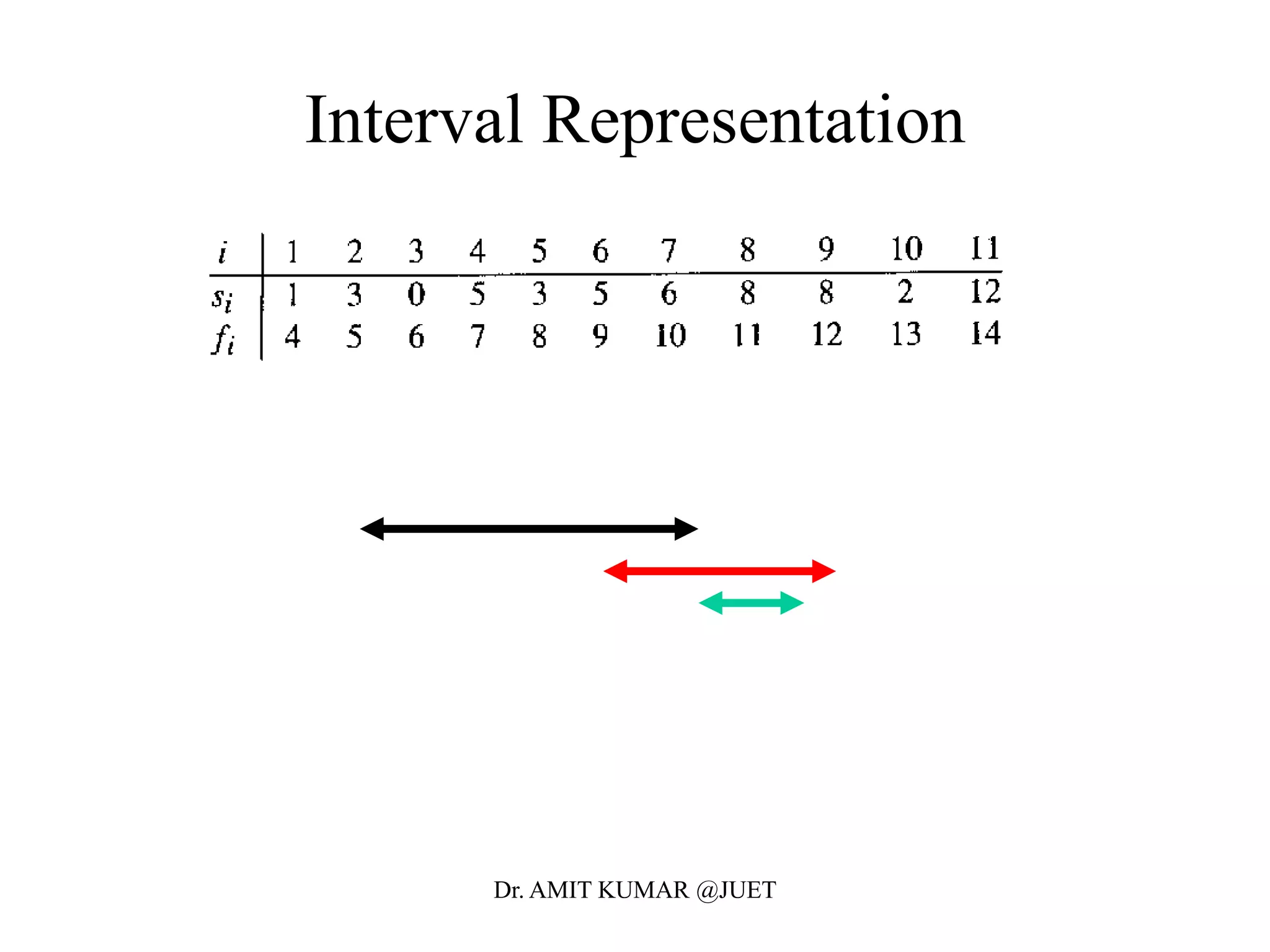
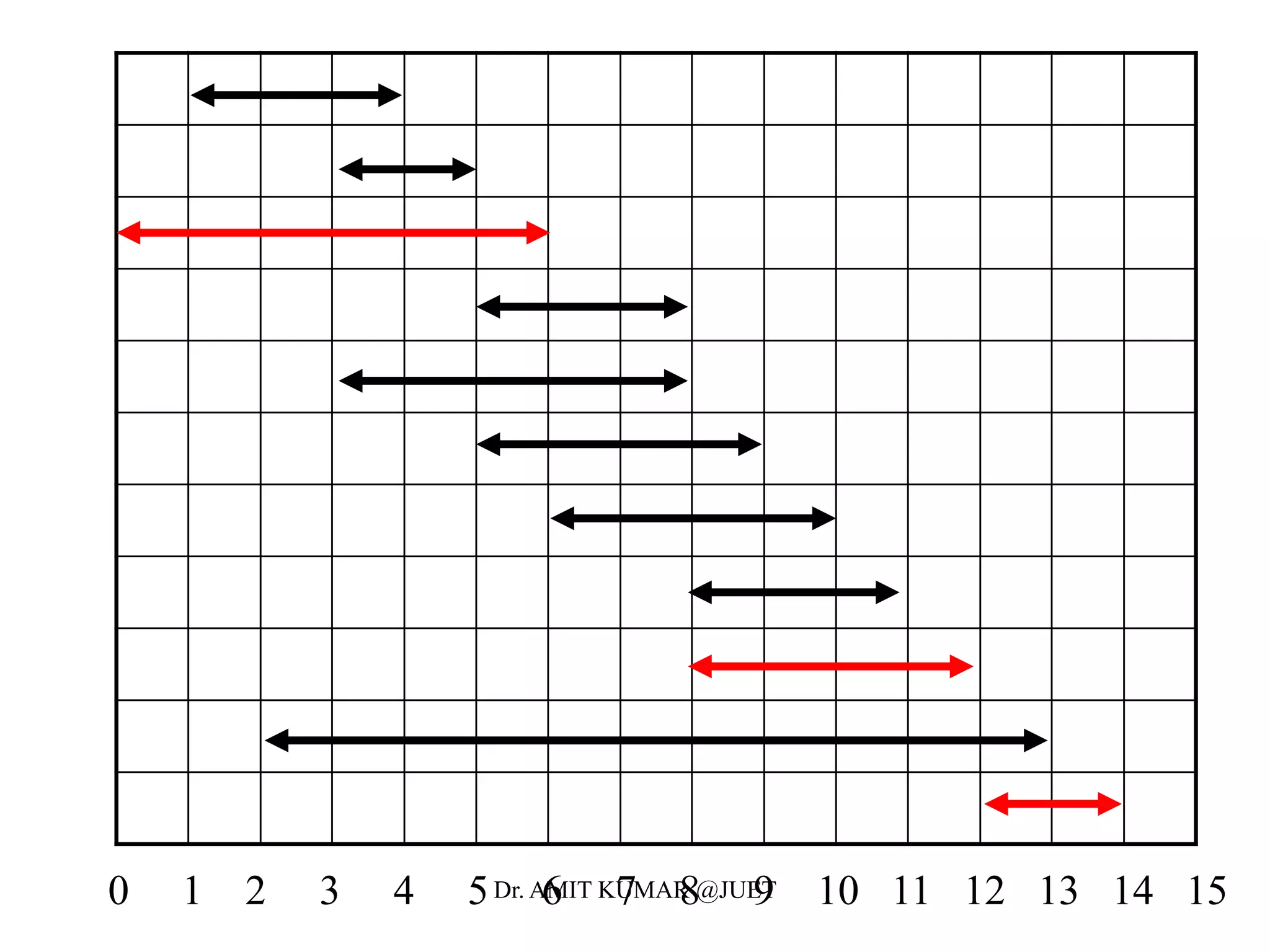
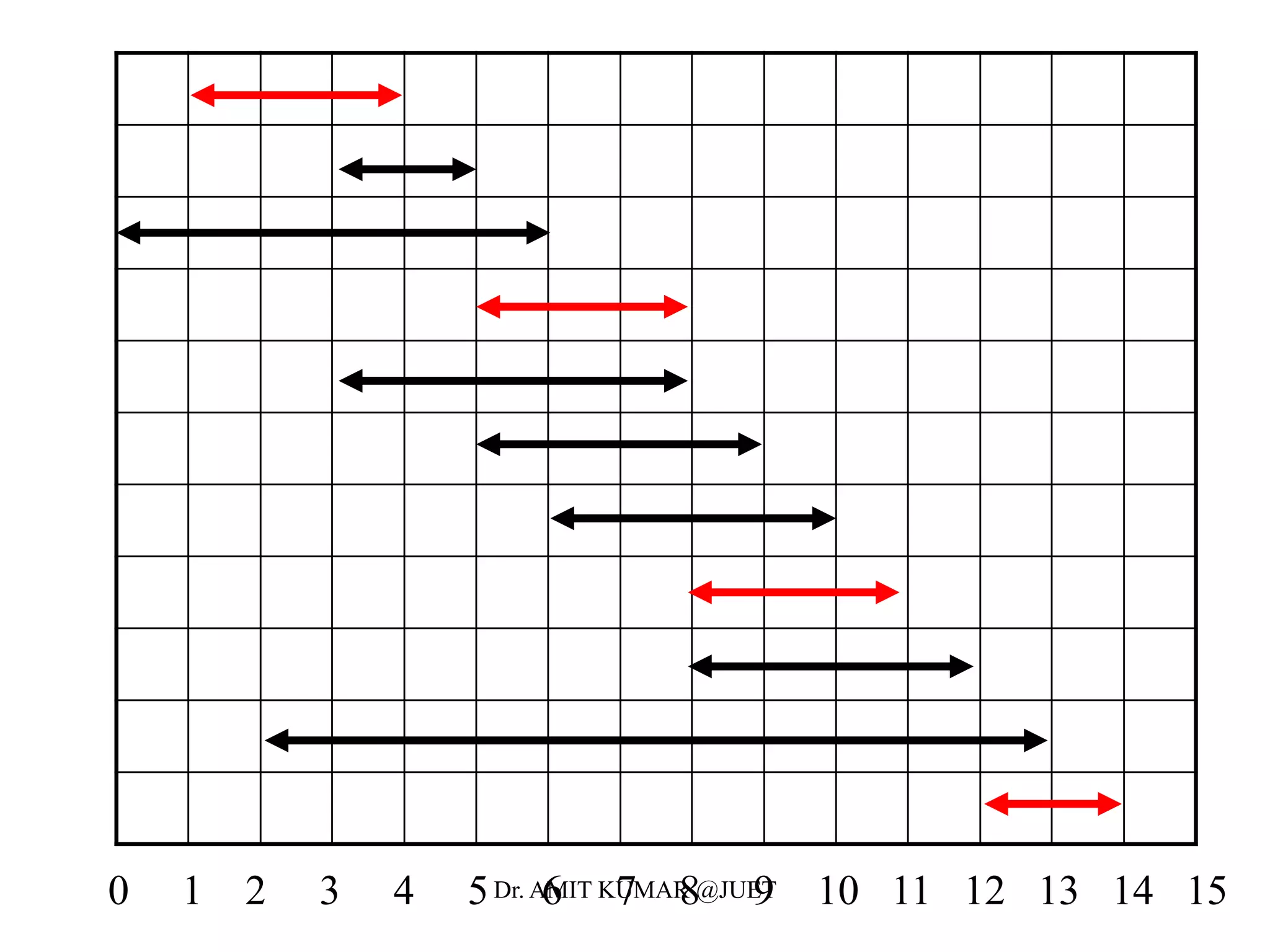
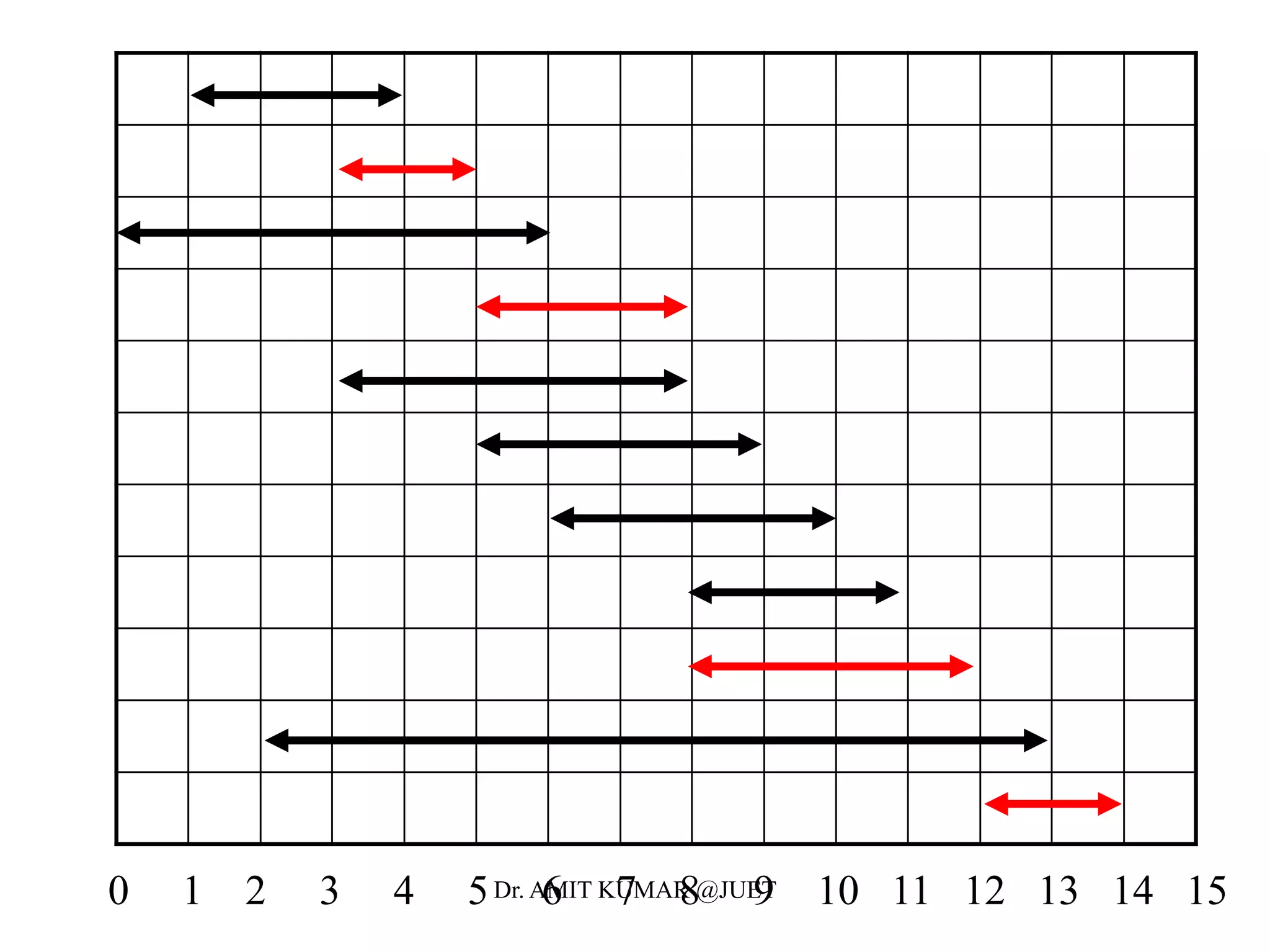
• Define the following subset of activities which are activities that
can start after ai finishes and finish before aj starts
• Sort the activities according to finish time
• We now define the the maximal set of activities from i to j as
• Let c[i,j] be the maximal number of activities
• We can solve this using dynamic programming, but a simpler
approach exists
• Our recurrence relation for finding c[i, j] becomes

Greedy algorithm activity selection fractional

More Related Content

What's hot

Similar to Greedy algorithm activity selection fractional

More from Amit Kumar Rathi

Recently uploaded

In this document

Greedy algorithm activity selection fractional