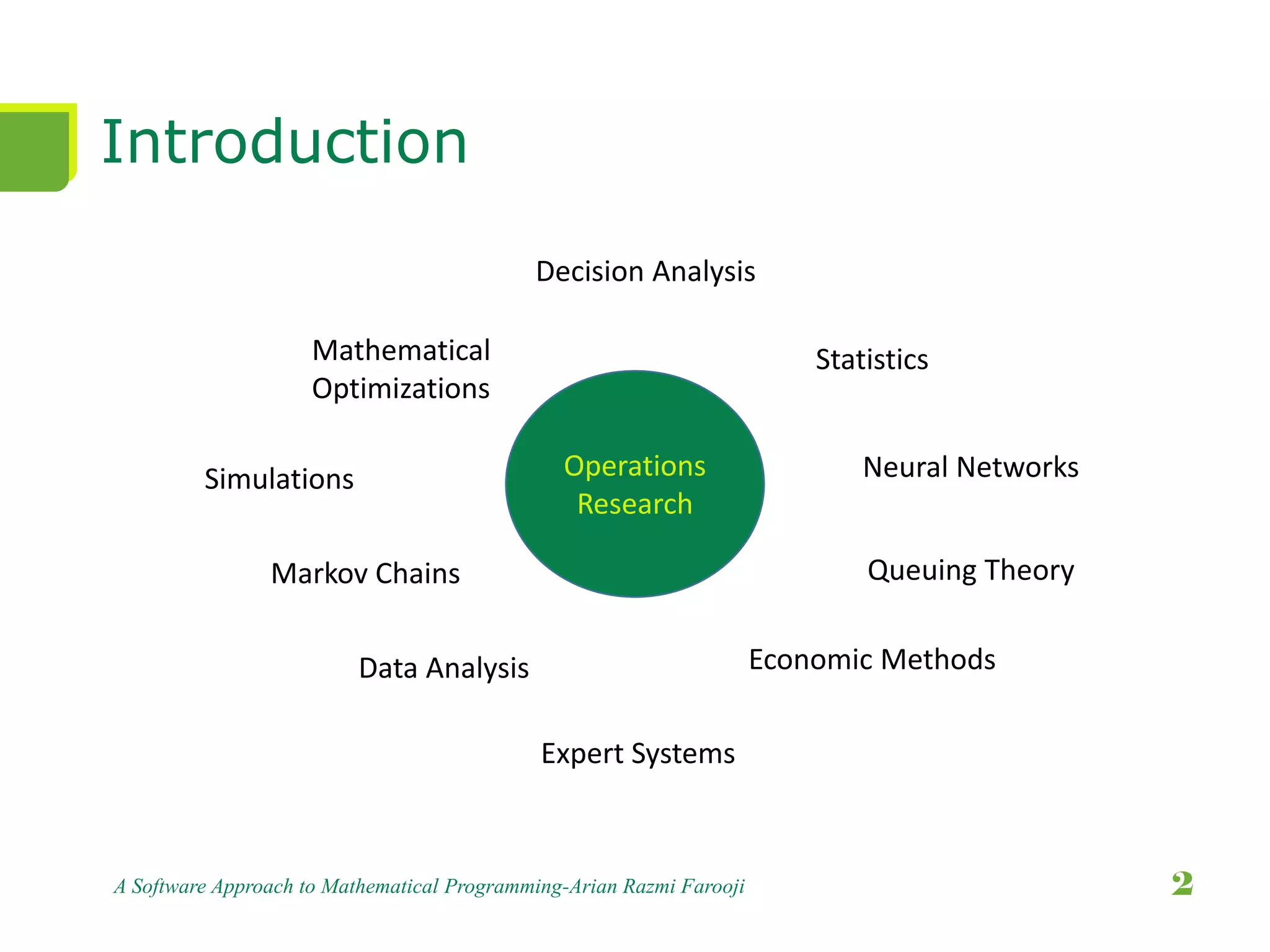
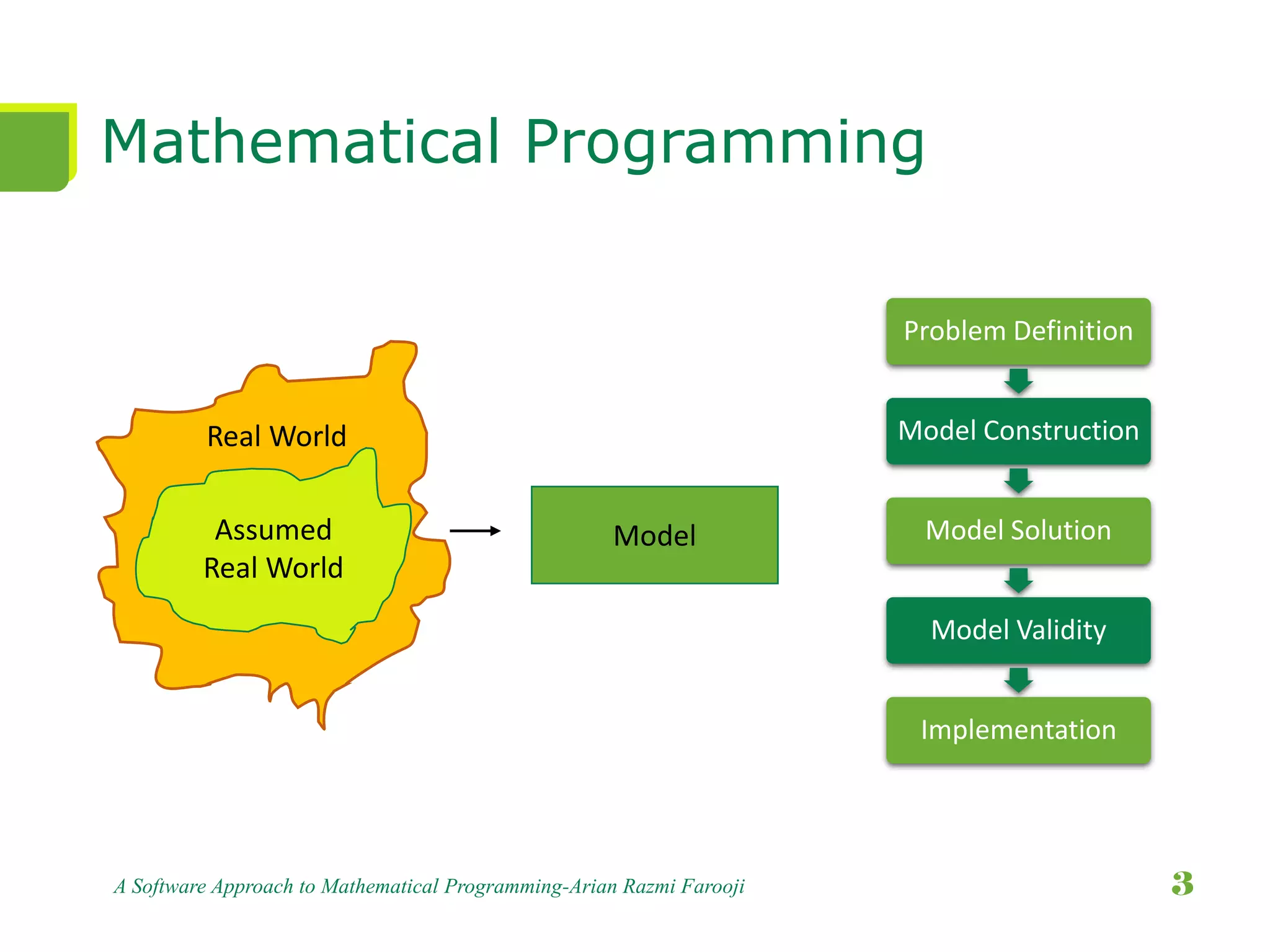
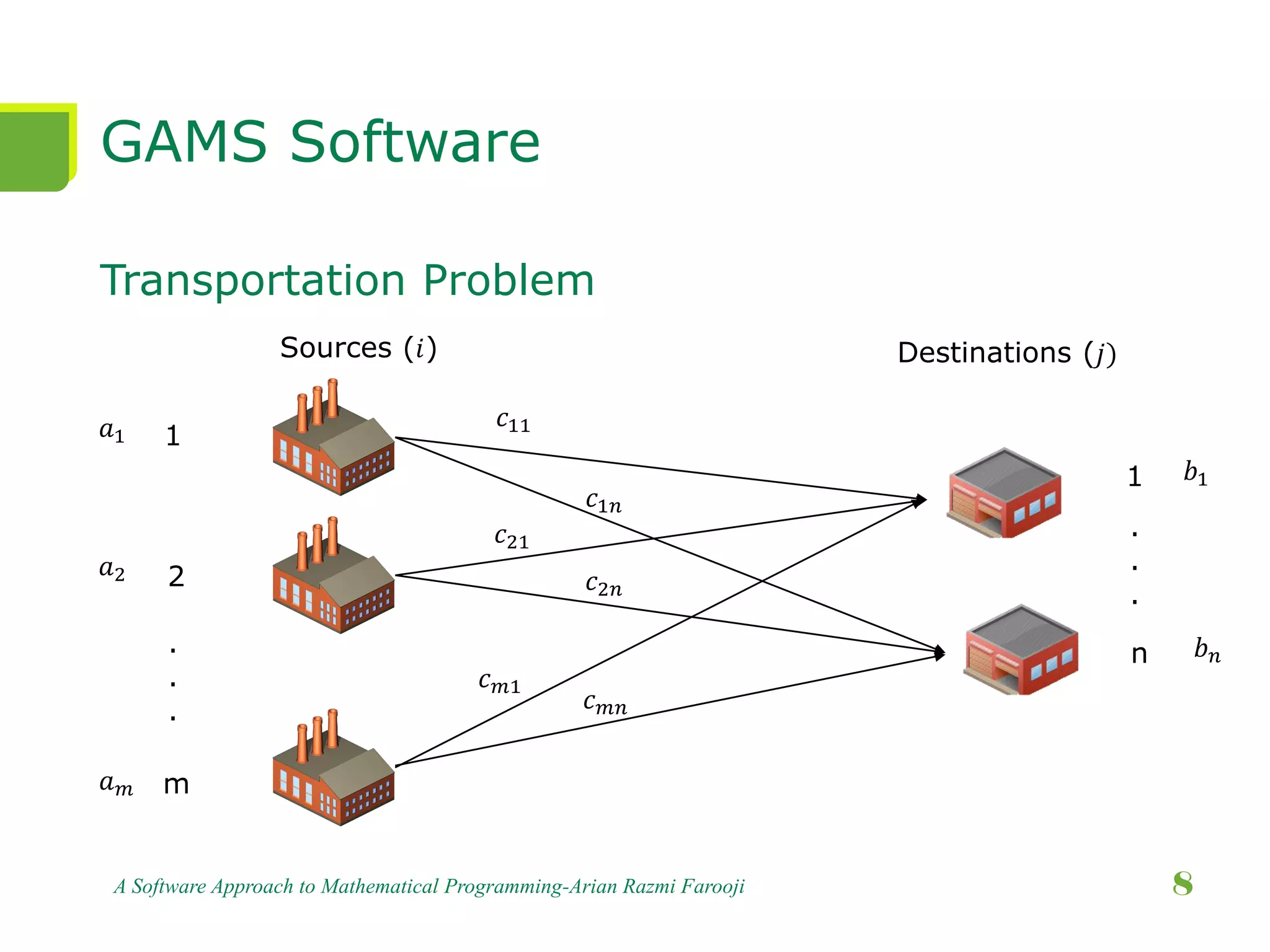
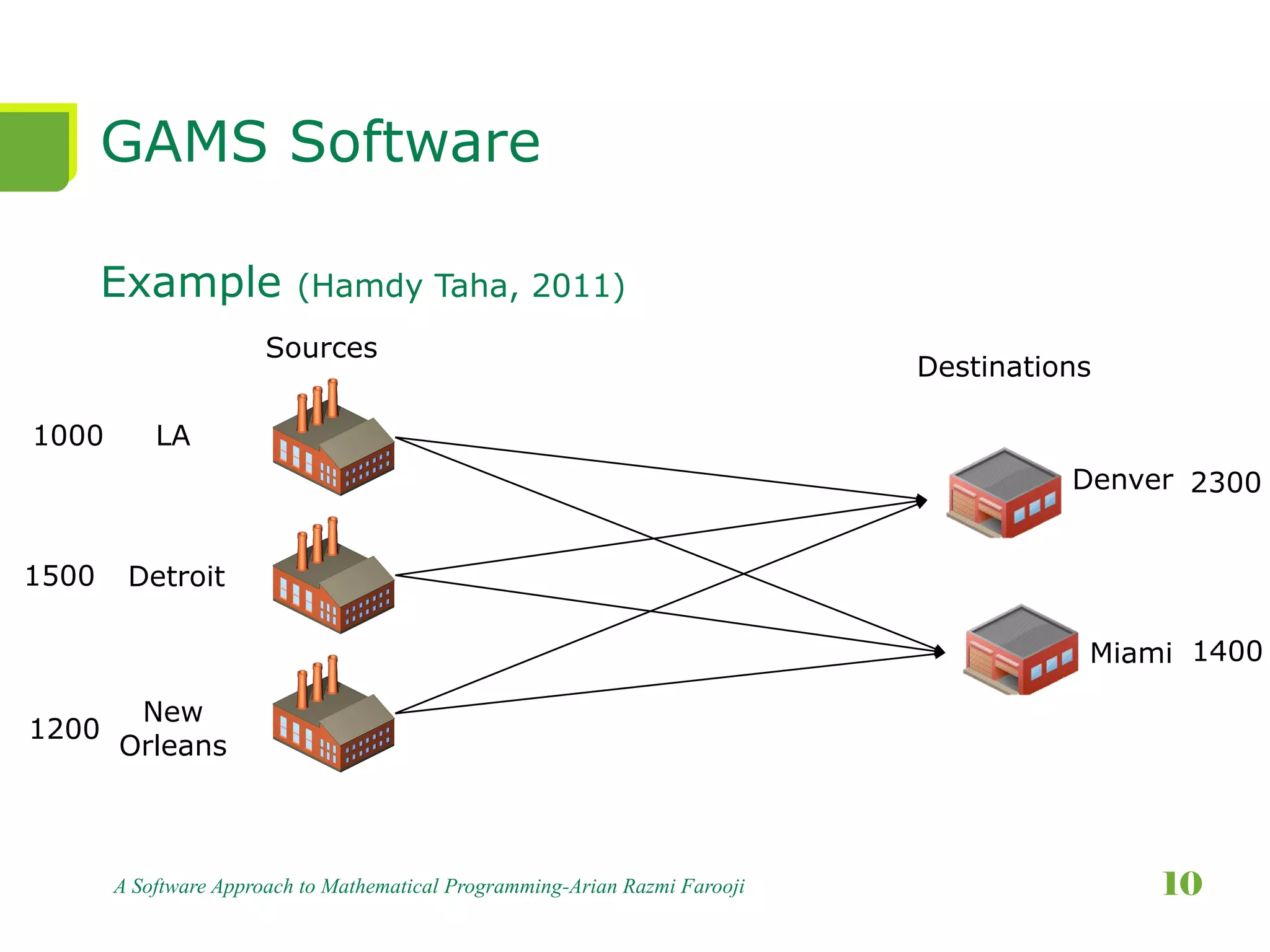
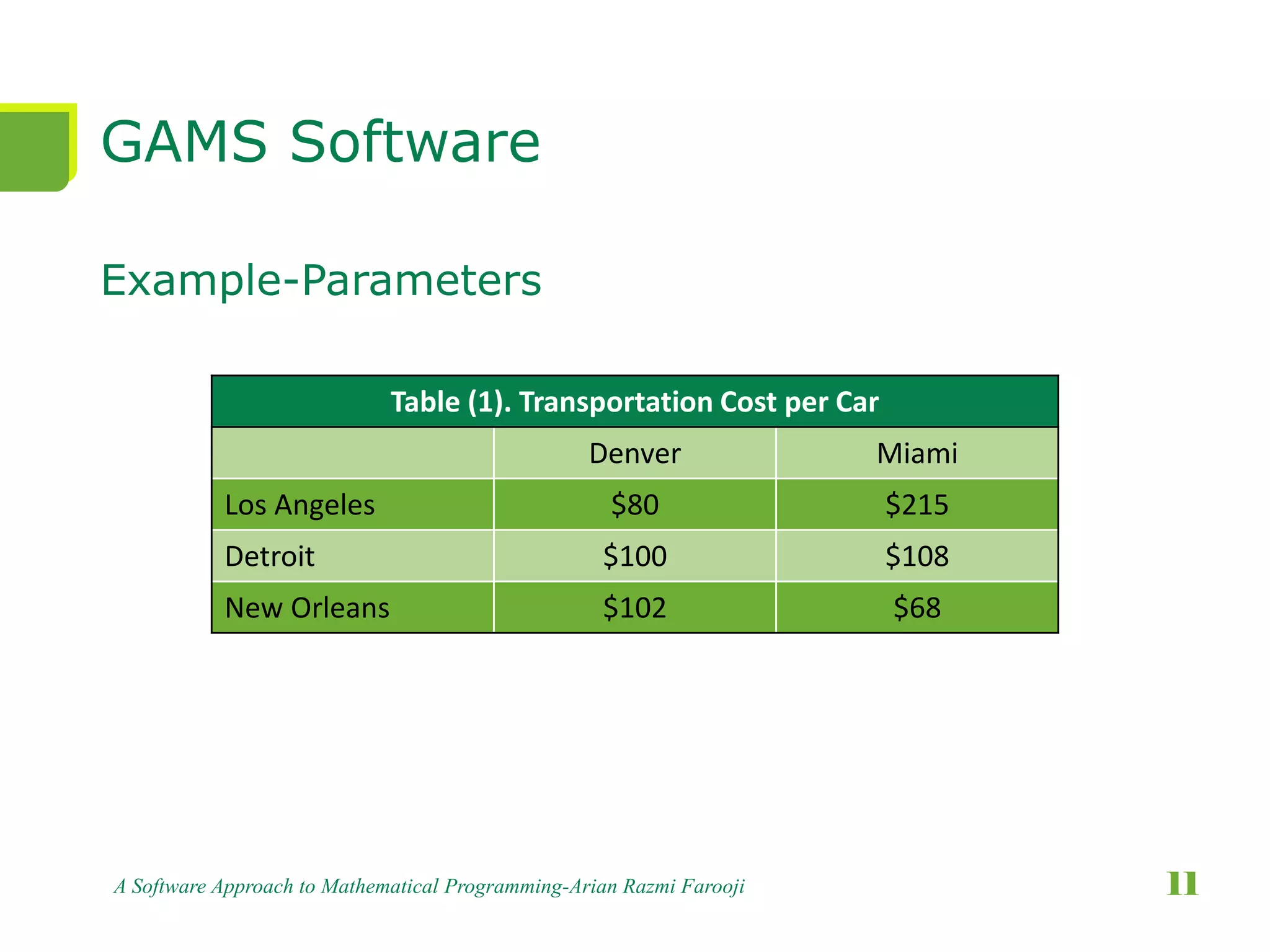
This document presents a comprehensive overview of mathematical programming, including techniques such as linear, integer, and dynamic programming. It highlights the GAMS software as a high-level modeling system for solving optimization problems and discusses the use of heuristics and metaheuristics for finding satisfactory solutions efficiently. The document emphasizes problem formulation, model construction, and provides examples, particularly focusing on transportation problems.