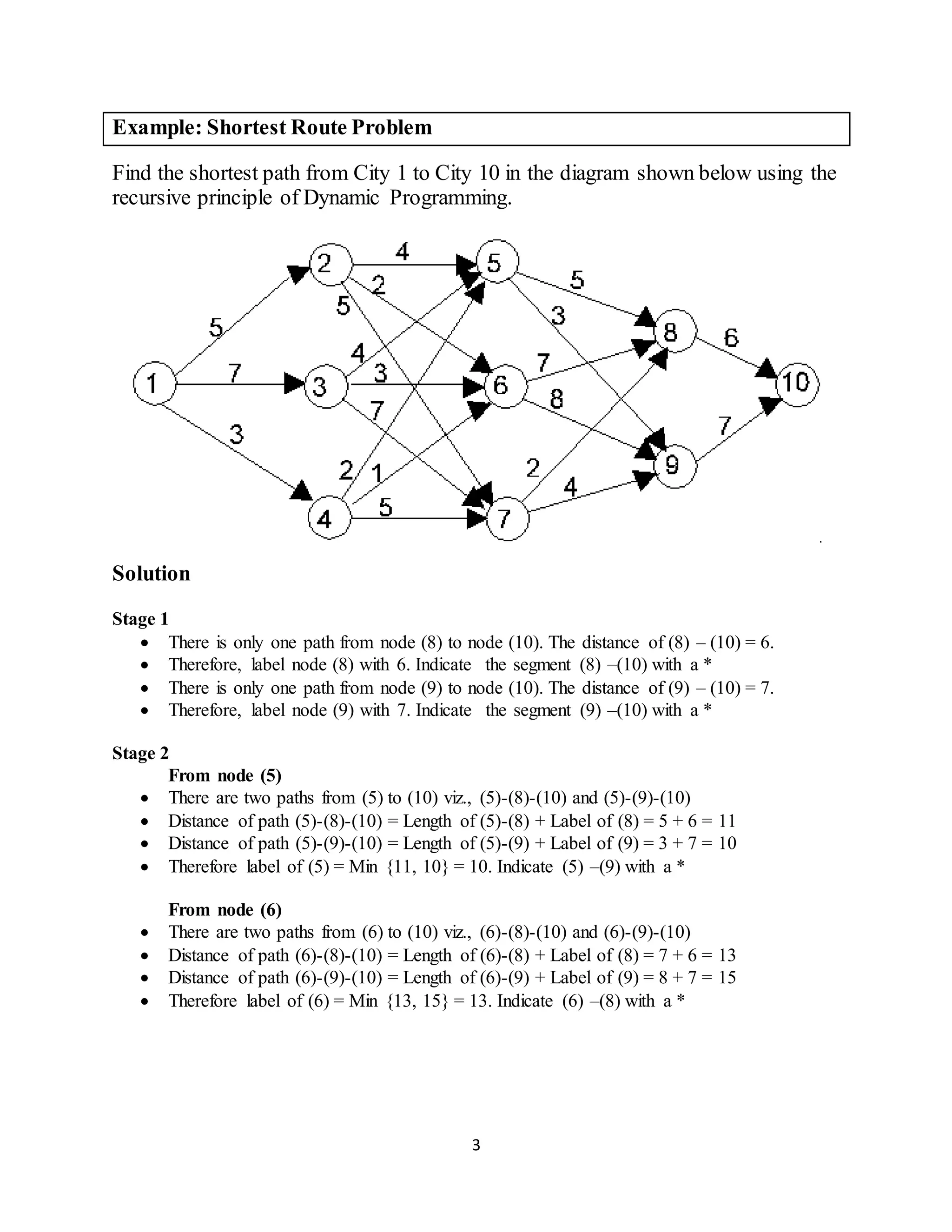
The document introduces dynamic programming as a technique for making optimal decisions over multiple time periods. It discusses how dynamic programming breaks large problems into smaller subproblems and solves each in order, working backwards from the last period. The document provides an example of using dynamic programming to find the shortest route between two cities by breaking the problem into stages and working backwards from the final destination.