Alignment scoring functions

Alignment scoring functions

• 1.
  Alignment Scoring Fuctions Dr Avril Coghlan alc@sanger.ac.uk Note: this talk contains animations which can only be seen by downloading and using ‘View Slide show’ in Powerpoint
• 2.
  Alignment scoring functions Letter b A R N D C Q E G H I L K M F P S T W Y V A 1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 • We define a scoring function σ(S1(i), S2(j)) R -1 1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 N -1 -1 1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 σ(S1(i), S2(j)) is the cost (score) of aligning symbols D -1 -1 -1 1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 S1(i) & S2(j)C -1 -1 -1 -1 1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 Letter a Q -1 -1 -1 -1 -1 1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 • 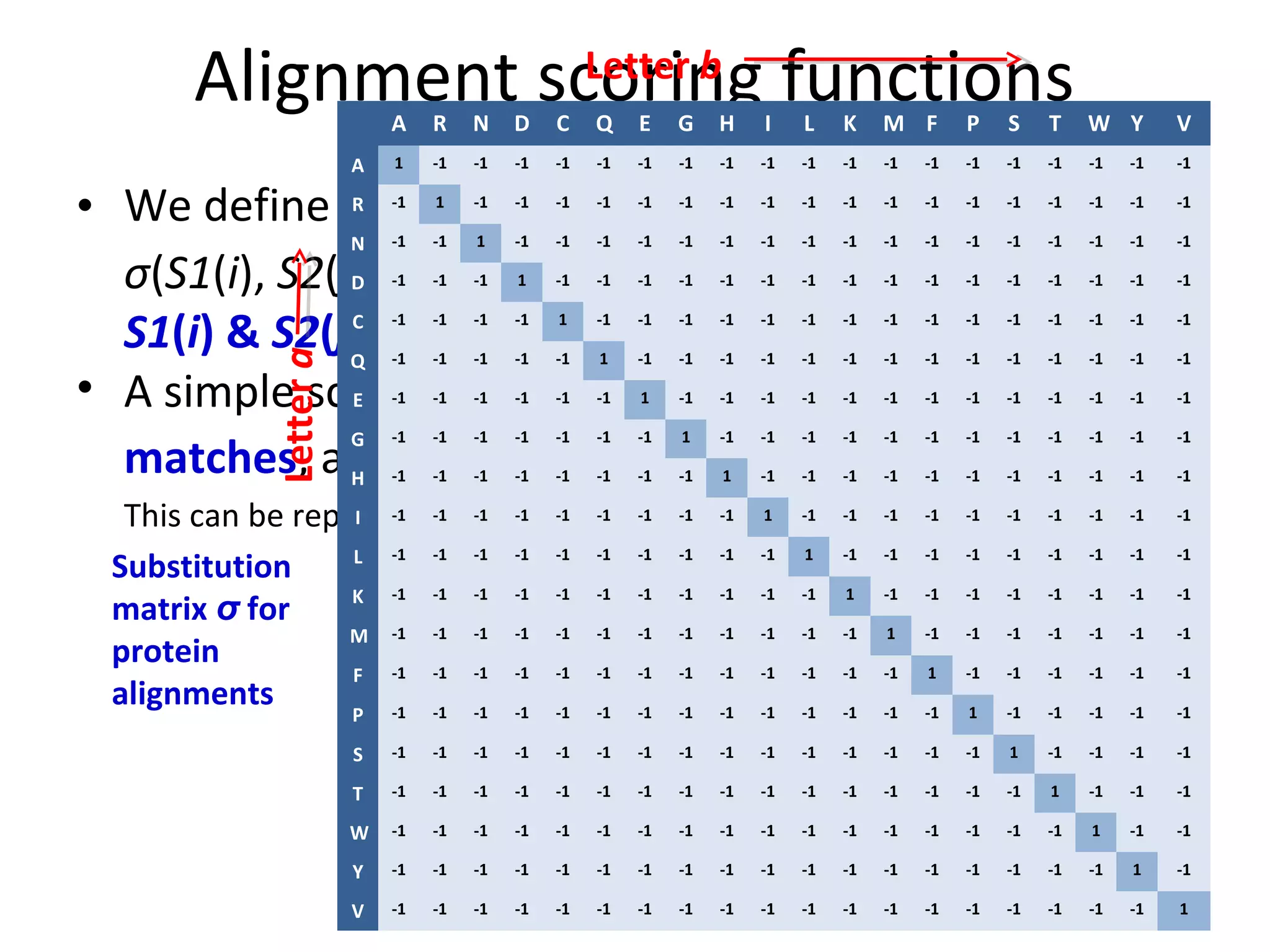A simple scoring function σ is a score of +1 for E -1 -1 -1 -1 -1 -1 1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 matches, and -1 for mismatches G -1 -1 -1 -1 -1 -1 -1 1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 H -1 -1 -1 -1 -1 -1 -1 -1 1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 I -1 -1 as -1 -1 -1 -1 -1 matrix This can be represented -1 a substitution -1 1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 L -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 1 -1 -1 -1 -1 -1 -1 -1 -1 -1 Substitution K -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 1 -1 -1 -1 -1 -1 -1 -1 -1 matrix σ for M -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 1 -1 -1 -1 -1 -1 -1 -1 protein F -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 1 -1 -1 -1 -1 -1 -1 alignments P -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 1 -1 -1 -1 -1 -1 S -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 1 -1 -1 -1 -1 T -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 1 -1 -1 -1 W -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 1 -1 -1 Y -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 1 -1 V -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 1
• 3.
  • The choiceof scoring function σ determines the A R N D C Q E G H I L K M F P S T W Y V score Aof the alignment 5 -2 -1 -2 -1 -1 -1 0 -2 -1 -1 -1 -1 -2 -1 1 0 -2 -2 0 σ determines the 0scores of1different0 possible 3alignments,-1so-1 R -2 7 -1 -3 0 -2 -3 -2 -1 -2 -2 -2 affects -1 -2 which alignment is ‘best’ (highest-scoring)-3 0 -2 -2 -2 1 0 N -1 0 6 2 -2 0 0 0 1 -2 one -4 -2 -3 D We need to-2be-1careful about which scoring function we use..-1 C 2 7 -3 0 2 -1 0 -4 -3 0 -3 -4 -1 0 . 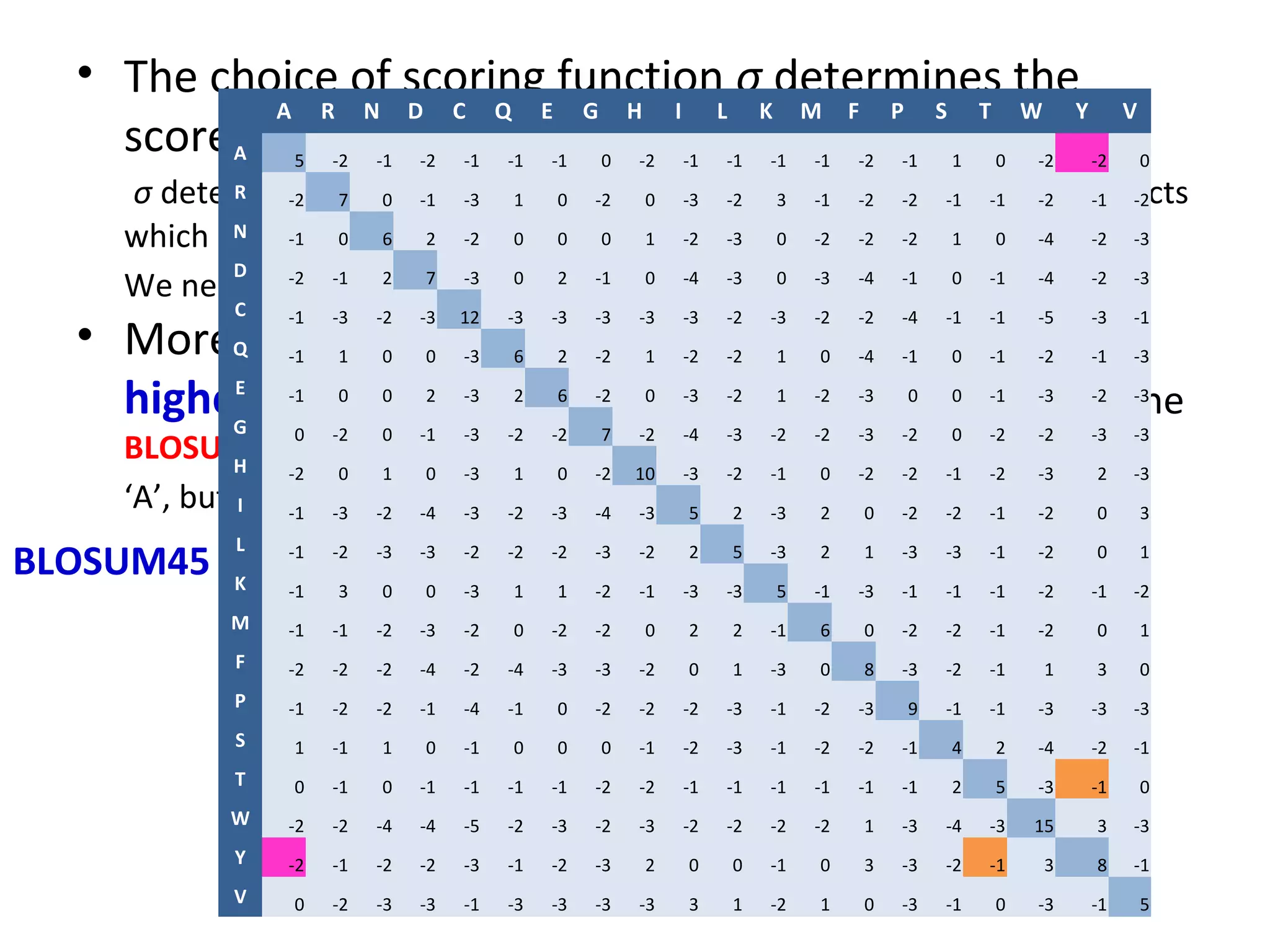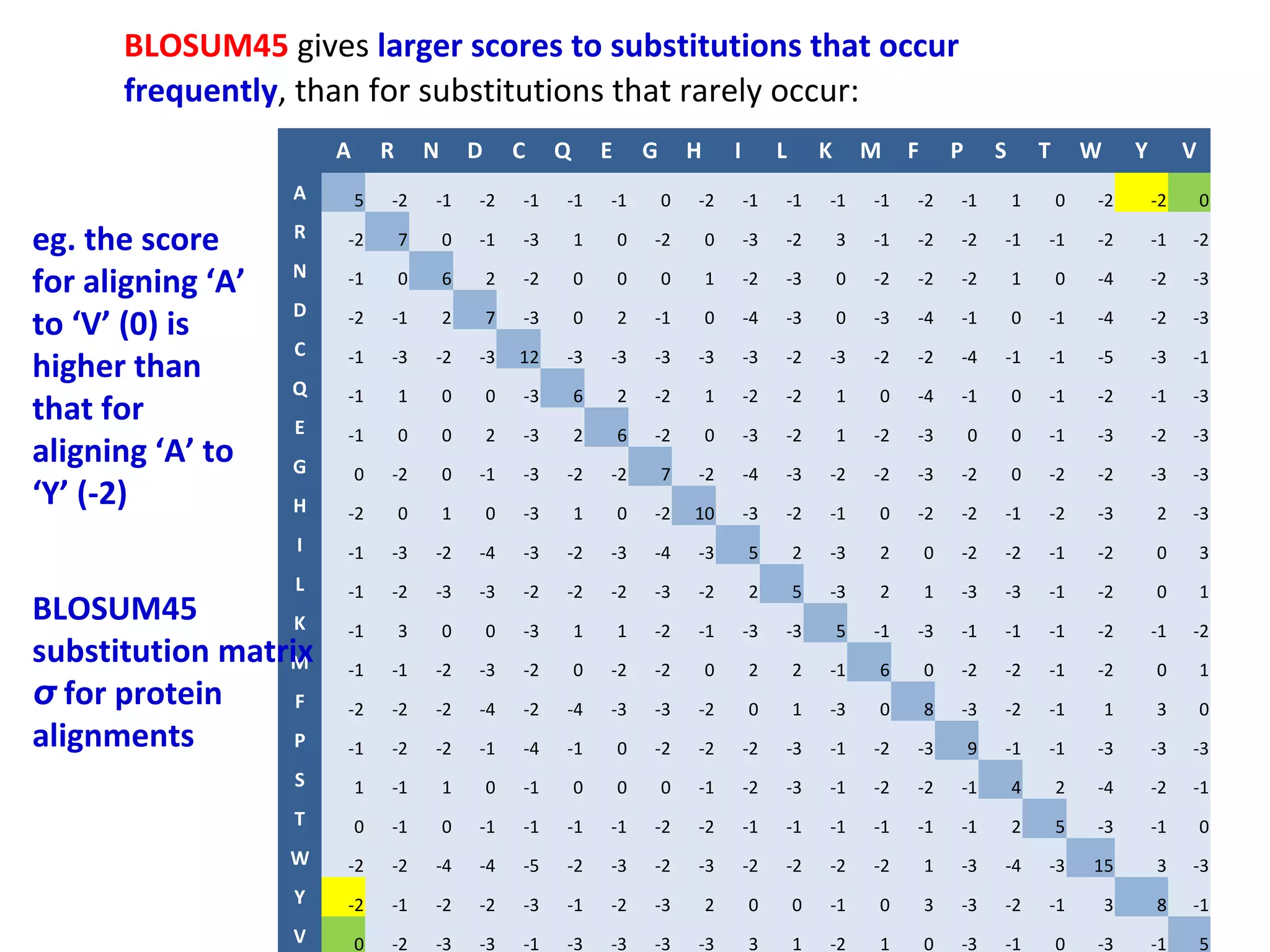-4 -2 -3 -1 -3 -2 -3 12 -3 -3 -3 -3 -3 -2 -3 -2 -2 -4 -1 -1 -5 -3 -1 • MoreQcomplex scoring functions exist that give -1 1 0 0 -3 6 2 -2 1 -2 -2 1 0 -4 -1 0 -1 -2 -1 -3 higher scores to certain matches/mismatches eg. the E G -1 0 0 2 -3 2 6 -2 0 -3 -2 1 -2 -3 0 0 -1 -3 -2 -3 0 -2 0 -1 -3 -2 -2 7 -2 -4 -3 -2 -2 -2 -2 -3 -3 BLOSUM45 0scoring function gives7 a -2 -4 of -2 for H -2 0 -1 -3 -2 -2 score -3 -2 -2 -3 -2 0 -2 -2 -3 -3 aligning ‘Y’ & -2 0 1 0 -3 1 0 -2 10 -3 -2 -1 0 -2 -2 -1 -2 -3 2 -3 ‘A’, but a score-3of-2 -4 -3 -2 -3 ‘Y’ -3 ‘T’ 2 -3 2 I -1 -1 for aligning -4 & 5 0 -2 -2 -1 -2 0 3 L BLOSUM45 K -1 -2 -3 -3 -2 -2 -2 -3 -2 2 5 -3 2 1 -3 -3 -1 -2 0 1 -1 3 0 0 -3 1 1 -2 -1 -3 -3 5 -1 -3 -1 -1 -1 -2 -1 -2 M -1 -1 -2 -3 -2 0 -2 -2 0 2 2 -1 6 0 -2 -2 -1 -2 0 1 F -2 -2 -2 -4 -2 -4 -3 -3 -2 0 1 -3 0 8 -3 -2 -1 1 3 0 P -1 -2 -2 -1 -4 -1 0 -2 -2 -2 -3 -1 -2 -3 9 -1 -1 -3 -3 -3 S 1 -1 1 0 -1 0 0 0 -1 -2 -3 -1 -2 -2 -1 4 2 -4 -2 -1 T 0 -1 0 -1 -1 -1 -1 -2 -2 -1 -1 -1 -1 -1 -1 2 5 -3 -1 0 W -2 -2 -4 -4 -5 -2 -3 -2 -3 -2 -2 -2 -2 1 -3 -4 -3 15 3 -3 Y -2 -1 -2 -2 -3 -1 -2 -3 2 0 0 -1 0 3 -3 -2 -1 3 8 -1 V 0 -2 -3 -3 -1 -3 -3 -3 -3 3 1 -2 1 0 -3 -1 0 -3 -1 5
• 4.
  Problem • Find thebest alignment between “WHAT” & “WHY” using the BLOSUM45 scoring function & -2 for a gap
• 5.
  Answer • Find thebest alignment between “WHAT” & “WHY” using the BLOSUM45 scoring function & -2 for a gap • Matrix T looks like this, giving 1 traceback: W H A T W H A T 0 -2 -4 -6 -8 0 -2 -4 -6 -8 W -2 15 13 11 9 W -2 15 13 11 9 H -4 13 25 23 21 H -4 13 25 23 21 Y -6 11 23 23 22 Y -6 11 23 23 22 • The traceback gives the following best alignment: W H A T | | W H - Y (Pink traceback)
• 6.
  • Using +1for a match, -1 for mismatch, & -2 for an insertion/deletion, the best alignment is: W H A T W H A T (Two equally highest- | | | | W H - Y W H Y - scoring solutions) • Using BLOSUM45, and -2 for an insertion/deletion, the best alignment is: W H A T | | (The highest- W H - Y scoring solution) • Should we use the simpler scoring scheme (match: +1,mismatch:-1) or BLOSUM45? BLOSUM45, because it takes into account that certain amino acids are more likely to substitute for each other during evolution than others
• 7.
  • Non-synonymous mutationschange the amino acid sequence eg. codon TTT encodes Phe (F), & TTA encodes Leu (L), so a TTT→TTA mutation causes a F→L mutation (substitution) • Certain amino acids are more likely to substitute for each other than others Because only organisms that carry mutations to similar amino acids tend to survive & reproduce Because a mutation to a dissimilar amino acid (eg. A→Y) is more likely to disrupt a protein’s function (& so kill the organism) than a mutation to a similar amino acid (eg. A→V) Alanine Valine Tyrosine (A) (V) (Y) A & V are small Y is much larger Image source: Wikimedia Commons
• 8.
  BLOSUM45 gives largerscores to substitutions that occur frequently, than for substitutions that rarely occur: A R N D C Q E G H I L K M F P S T W Y V A 5 -2 -1 -2 -1 -1 -1 0 -2 -1 -1 -1 -1 -2 -1 1 0 -2 -2 0 eg. the score R -2 7 0 -1 -3 1 0 -2 0 -3 -2 3 -1 -2 -2 -1 -1 -2 -1 -2 N for aligning ‘A’ -1 0 6 2 -2 0 0 0 1 -2 -3 0 -2 -2 -2 1 0 -4 -2 -3 D to ‘V’ (0) is -2 -1 2 7 -3 0 2 -1 0 -4 -3 0 -3 -4 -1 0 -1 -4 -2 -3 C higher than -1 -3 -2 -3 12 -3 -3 -3 -3 -3 -2 -3 -2 -2 -4 -1 -1 -5 -3 -1 Q -1 1 0 0 -3 6 2 -2 1 -2 -2 1 0 -4 -1 0 -1 -2 -1 -3 that for E -1 0 0 2 -3 2 6 -2 0 -3 -2 1 -2 -3 0 0 -1 -3 -2 -3 aligning ‘A’ to G 0 -2 0 -1 -3 -2 -2 7 -2 -4 -3 -2 -2 -3 -2 0 -2 -2 -3 -3 ‘Y’ (-2) H -2 0 1 0 -3 1 0 -2 10 -3 -2 -1 0 -2 -2 -1 -2 -3 2 -3 I -1 -3 -2 -4 -3 -2 -3 -4 -3 5 2 -3 2 0 -2 -2 -1 -2 0 3 L -1 -2 -3 -3 -2 -2 -2 -3 -2 2 5 -3 2 1 -3 -3 -1 -2 0 1 BLOSUM45 K -1 3 0 0 -3 1 1 -2 -1 -3 -3 5 -1 -3 -1 -1 -1 -2 -1 -2 substitution matrix M -1 -1 -2 -3 -2 0 -2 -2 0 2 2 -1 6 0 -2 -2 -1 -2 0 1 σ for protein F -2 -2 -2 -4 -2 -4 -3 -3 -2 0 1 -3 0 8 -3 -2 -1 1 3 0 alignments P -1 -2 -2 -1 -4 -1 0 -2 -2 -2 -3 -1 -2 -3 9 -1 -1 -3 -3 -3 S 1 -1 1 0 -1 0 0 0 -1 -2 -3 -1 -2 -2 -1 4 2 -4 -2 -1 T 0 -1 0 -1 -1 -1 -1 -2 -2 -1 -1 -1 -1 -1 -1 2 5 -3 -1 0 W -2 -2 -4 -4 -5 -2 -3 -2 -3 -2 -2 -2 -2 1 -3 -4 -3 15 3 -3 Y -2 -1 -2 -2 -3 -1 -2 -3 2 0 0 -1 0 3 -3 -2 -1 3 8 -1 V 0 -2 -3 -3 -1 -3 -3 -3 -3 3 1 -2 1 0 -3 -1 0 -3 -1 5
• 9.
  Further Reading • Chapter 3 in Introduction to Computational Genomics Cristianini & Hahn • Chapter 6 in Deonier et al Computational Genome Analysis • Practical on pairwise alignment in R in the Little Book of R for Bioinformatics: https://a-little-book-of-r-for- bioinformatics.readthedocs.org/en/latest/src/chapter4.html
• 10.
  Further Reading • Chapter 3 in Introduction to Computational Genomics Cristianini & Hahn • Chapter 6 in Deonier et al Computational Genome Analysis • Practical on pairwise alignment in R in the Little Book of R for Bioinformatics: https://a-little-book-of-r-for- bioinformatics.readthedocs.org/en/latest/src/chapter4.html