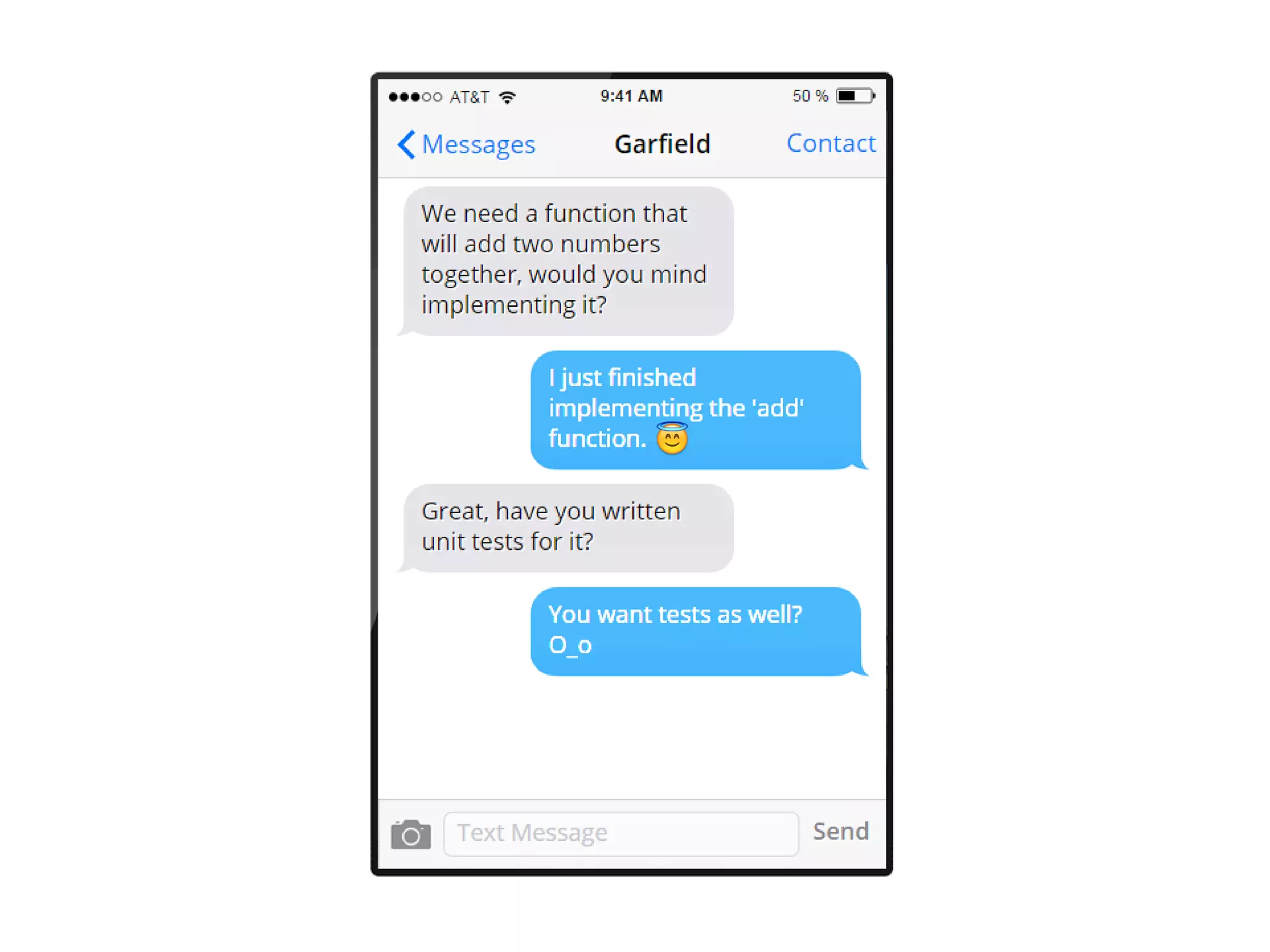
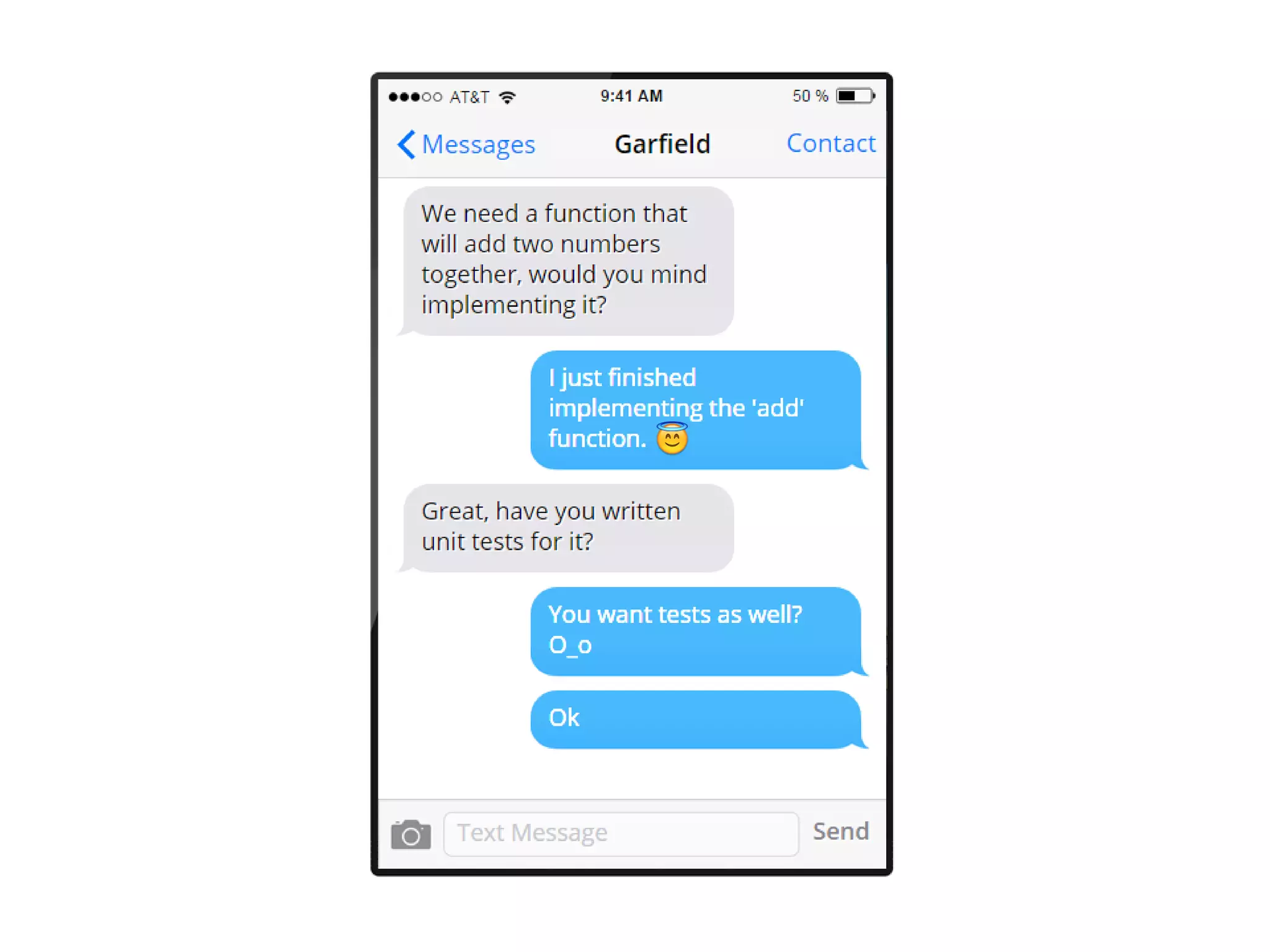
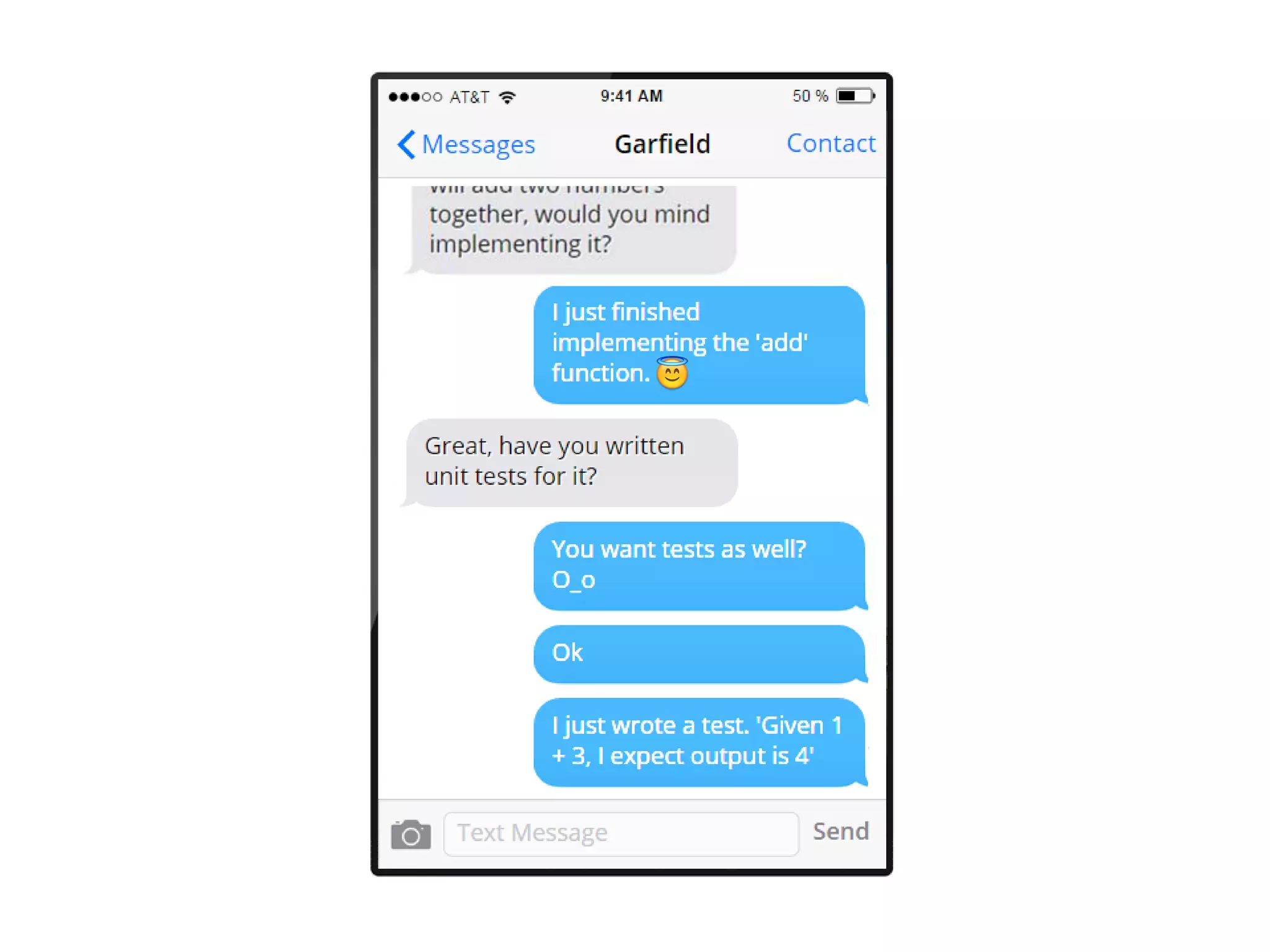
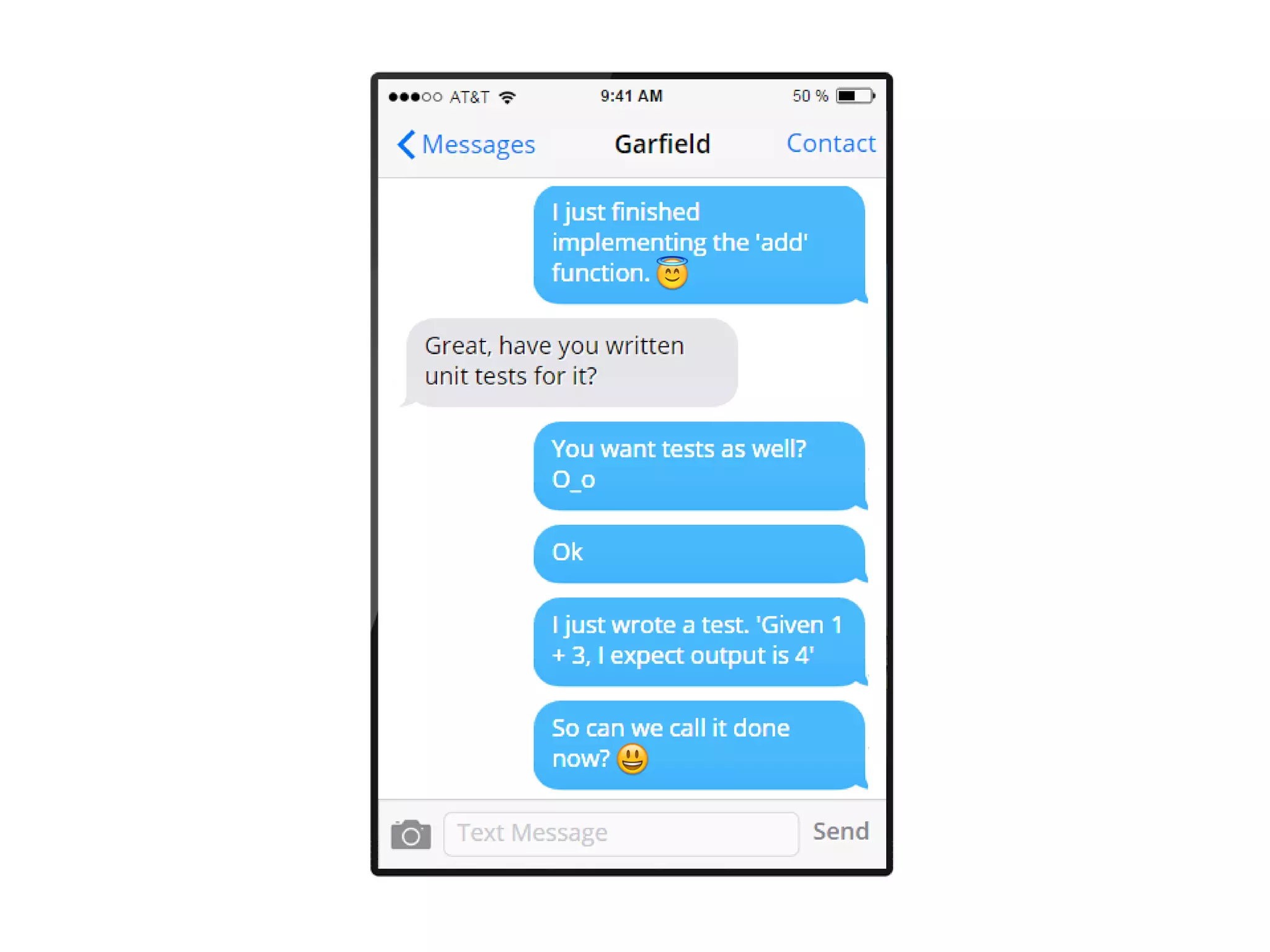
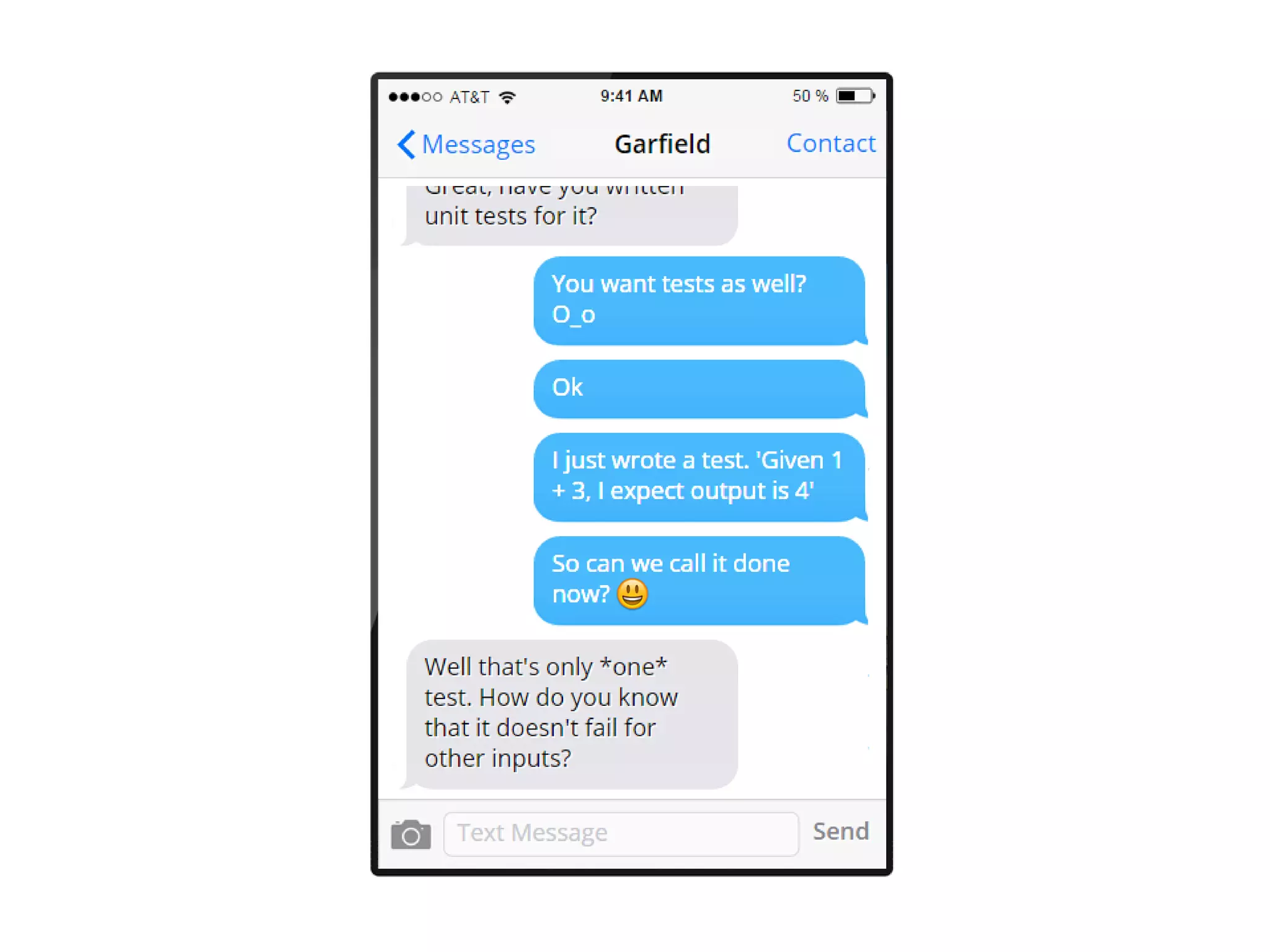
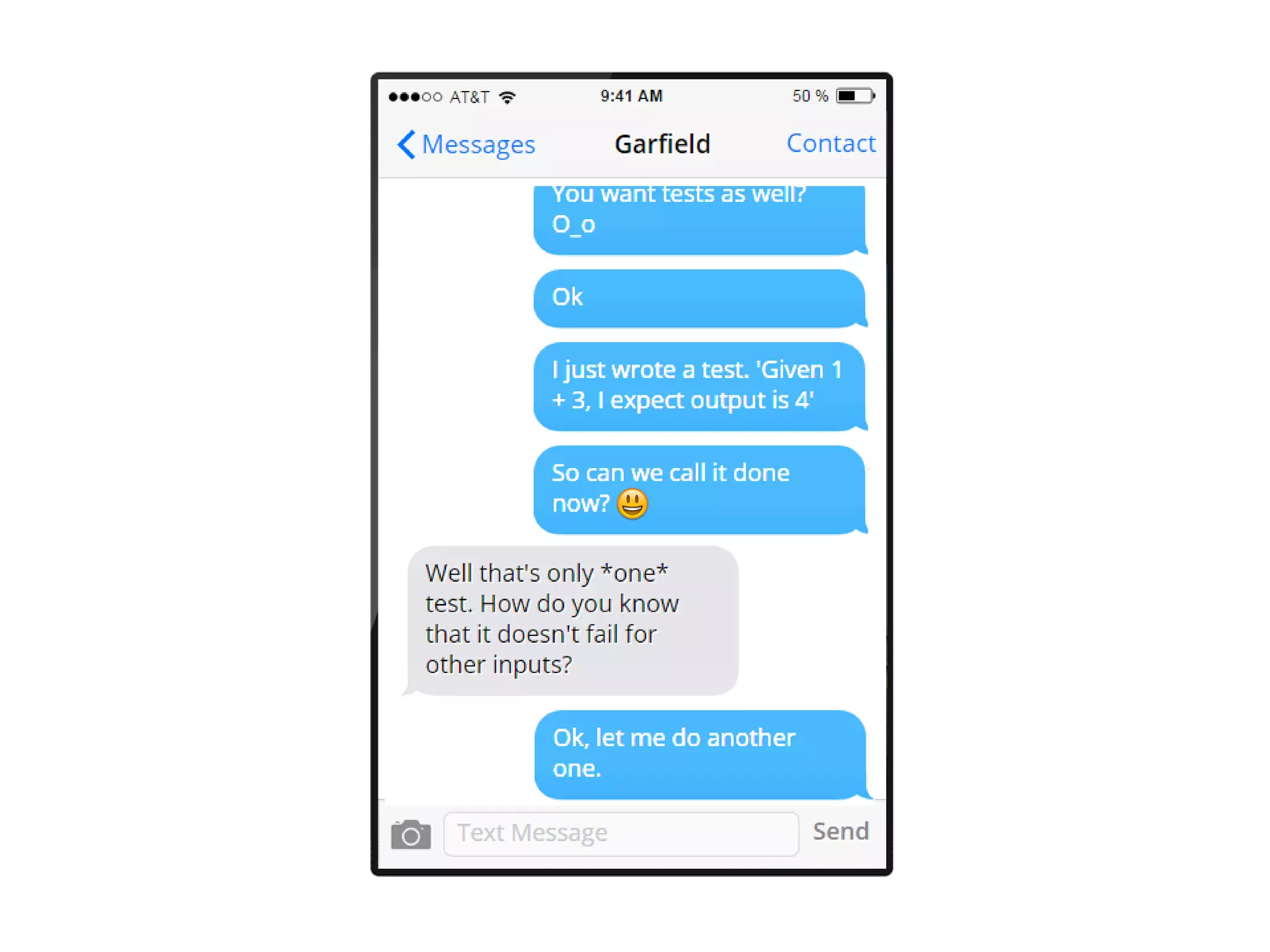
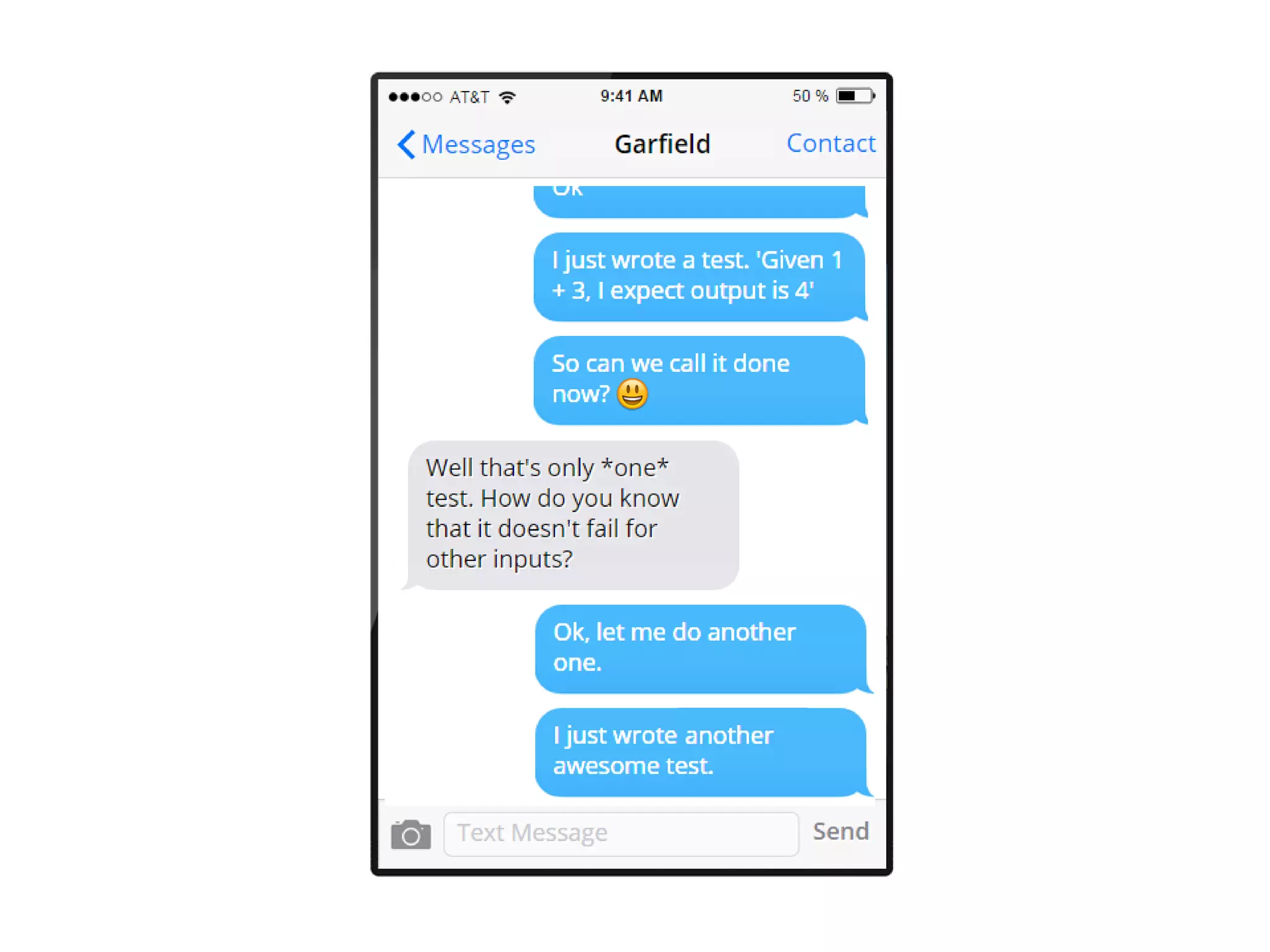
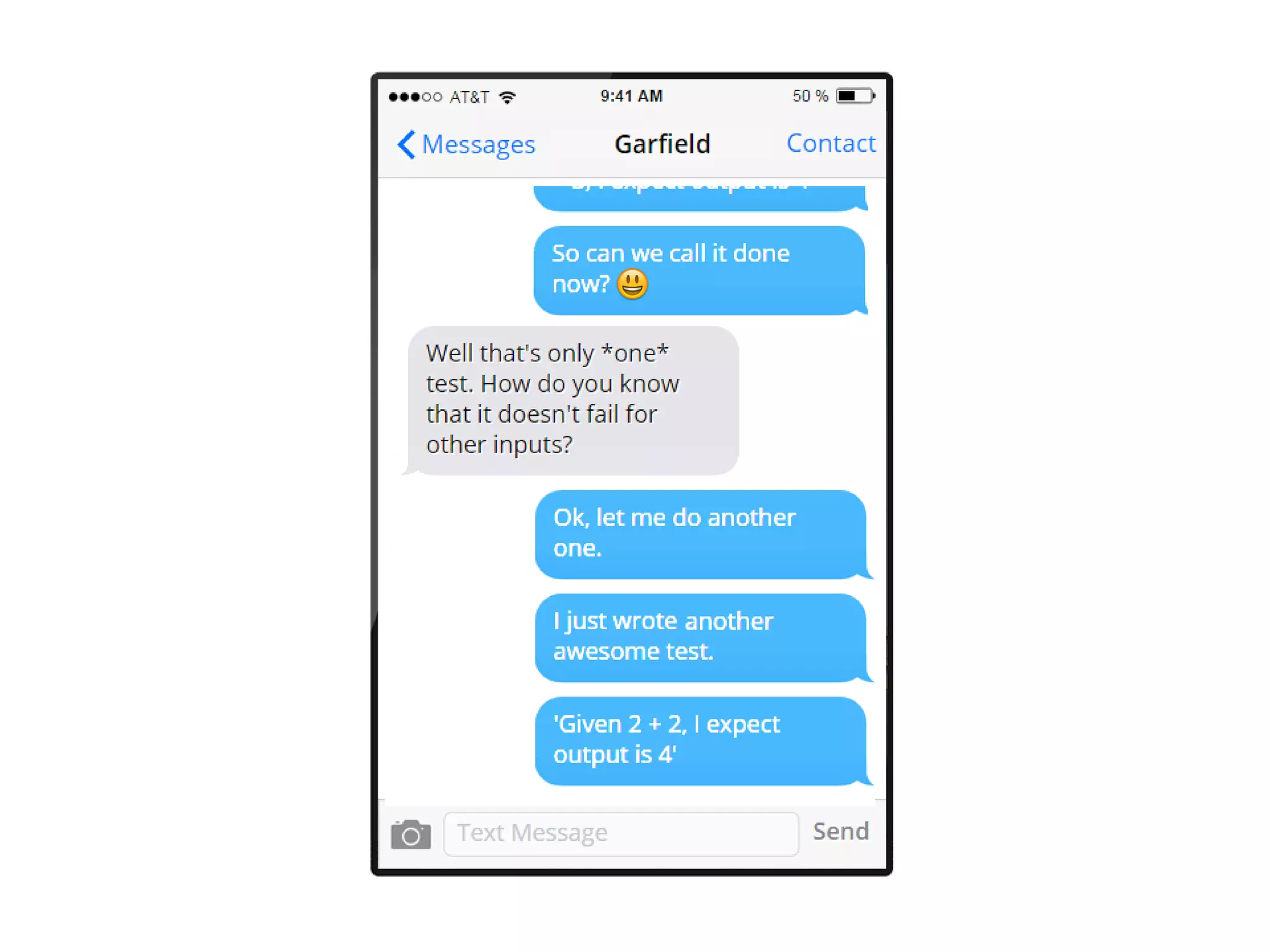
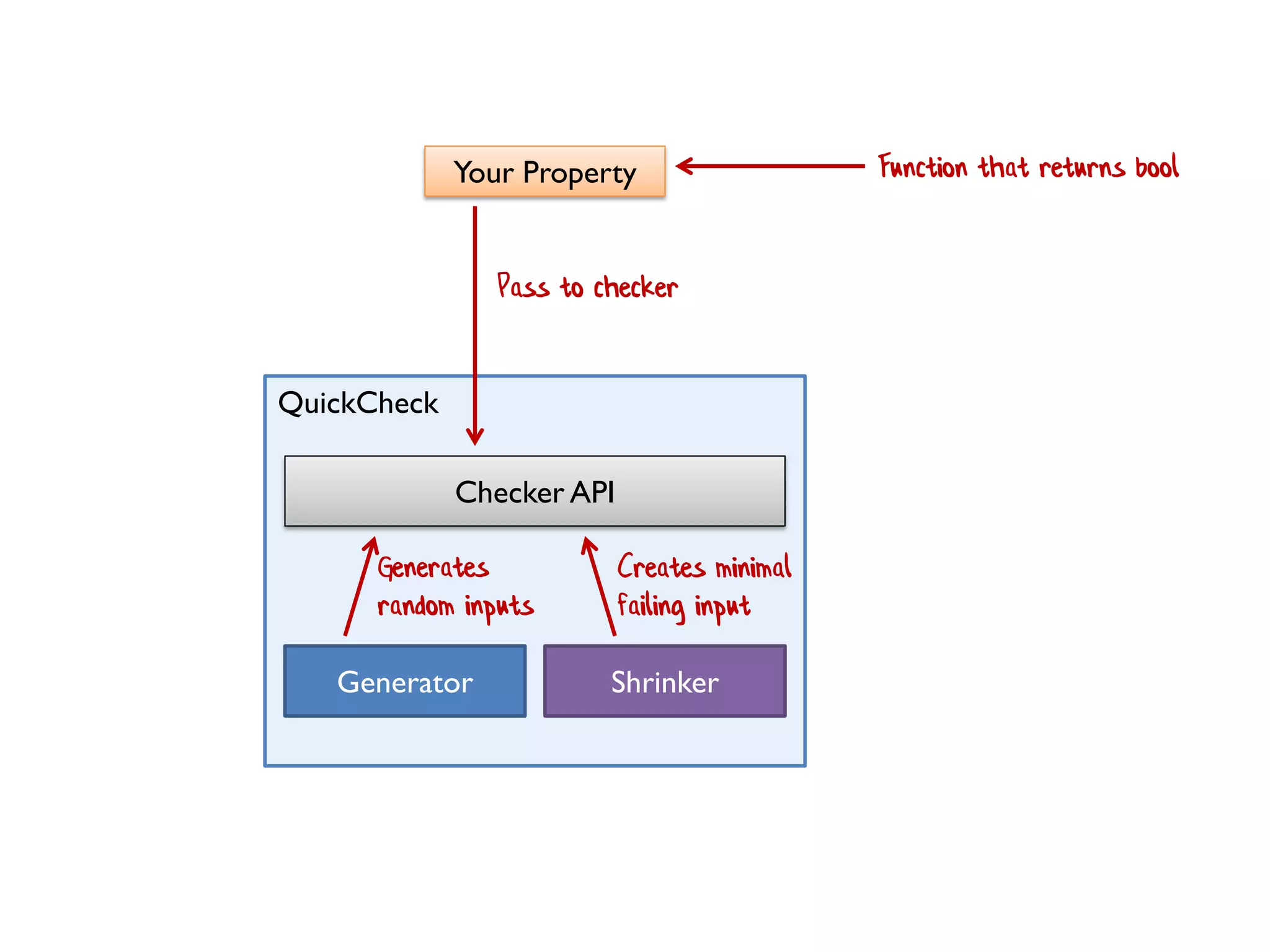
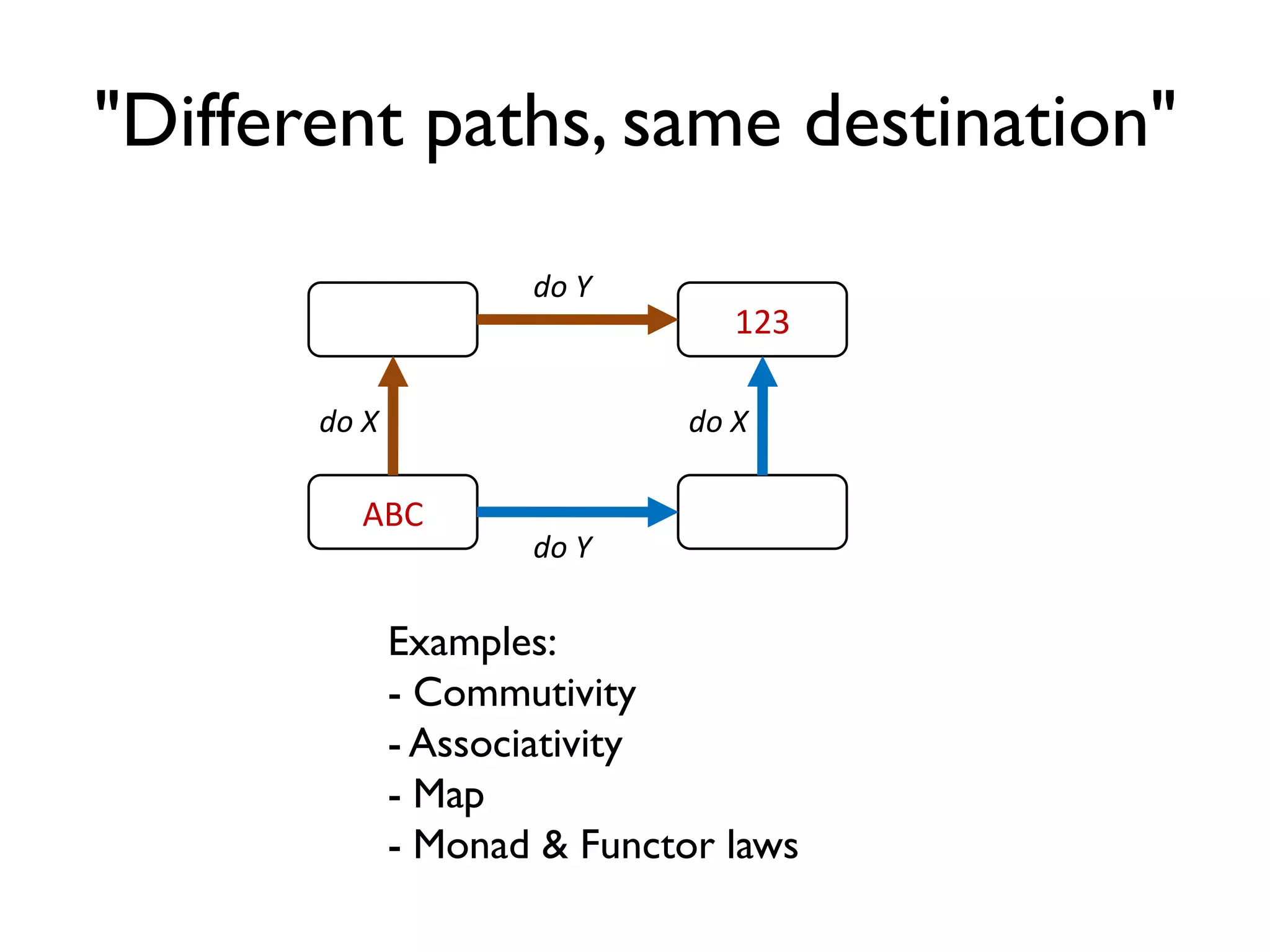
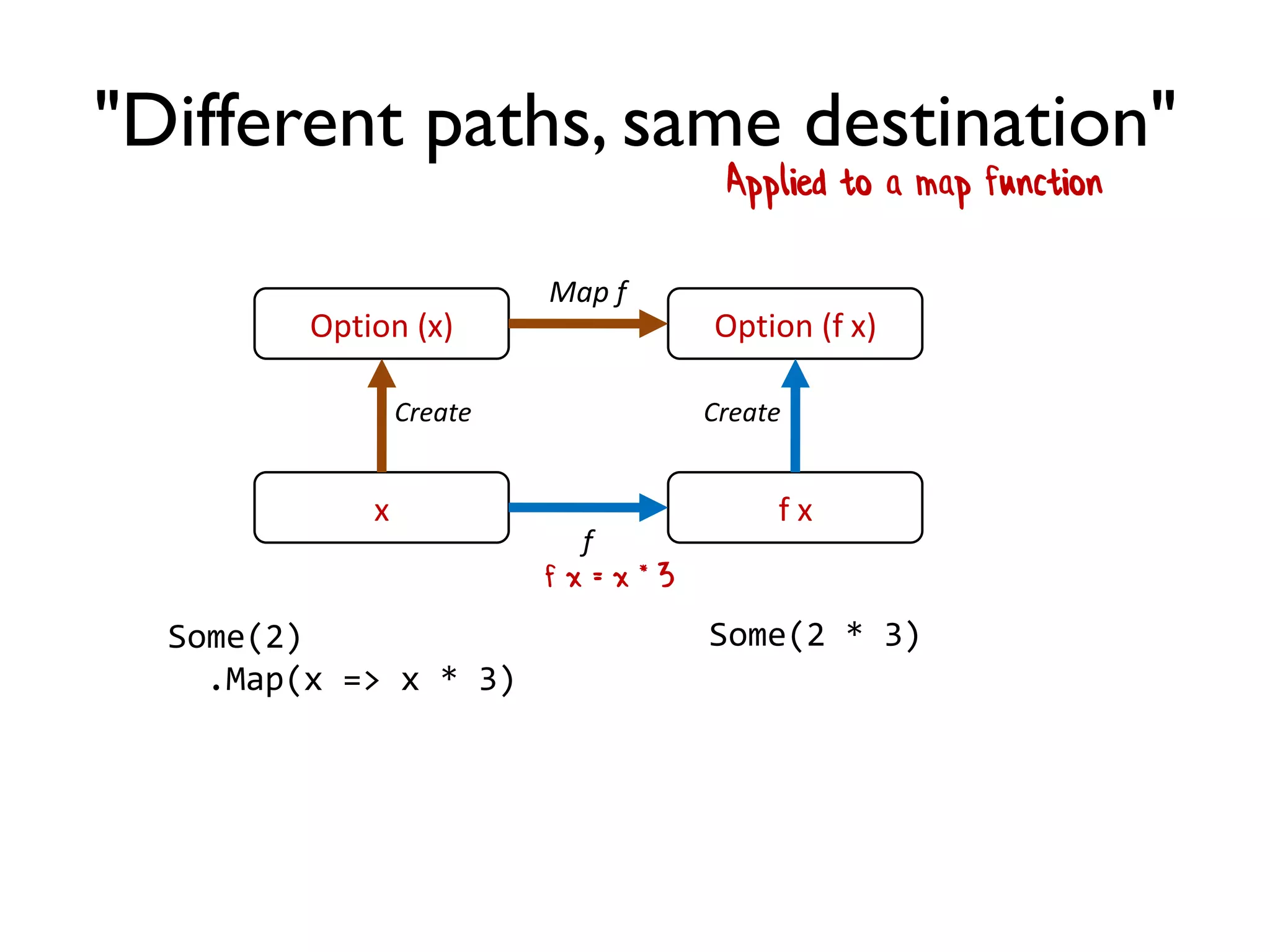
The document discusses the concept of property-based testing, illustrating how it can be applied to create robust unit tests for an 'add' function through usage of random inputs and defining properties like commutativity and identity. It emphasizes the importance of understanding the requirements of functions deeper than traditional example-based tests, enabling users to detect faulty implementations more effectively. Additionally, the text covers tools like 'quickcheck' that facilitate property-based testing in various programming environments.




![[<Test>]
let ``When I add 1 + 3, I expect 4``()=
let result = add 1 3
Assert.AreEqual(4,result)
[<Test>]
let ``When I add 2 + 2, I expect 4``()=
let result = add 2 2
Assert.AreEqual(4,result)
First, I had a look at the existing tests...](https://image.slidesharecdn.com/propbasedtesting-150610142543-lva1-app6892/75/An-introduction-to-property-based-testing-18-2048.jpg)
![[<Test>]
let ``When I add -1 + 3, I expect 2``()=
let result = add -1 3
Assert.AreEqual(2,result)
Ok, now for my first new test...](https://image.slidesharecdn.com/propbasedtesting-150610142543-lva1-app6892/75/An-introduction-to-property-based-testing-19-2048.jpg)

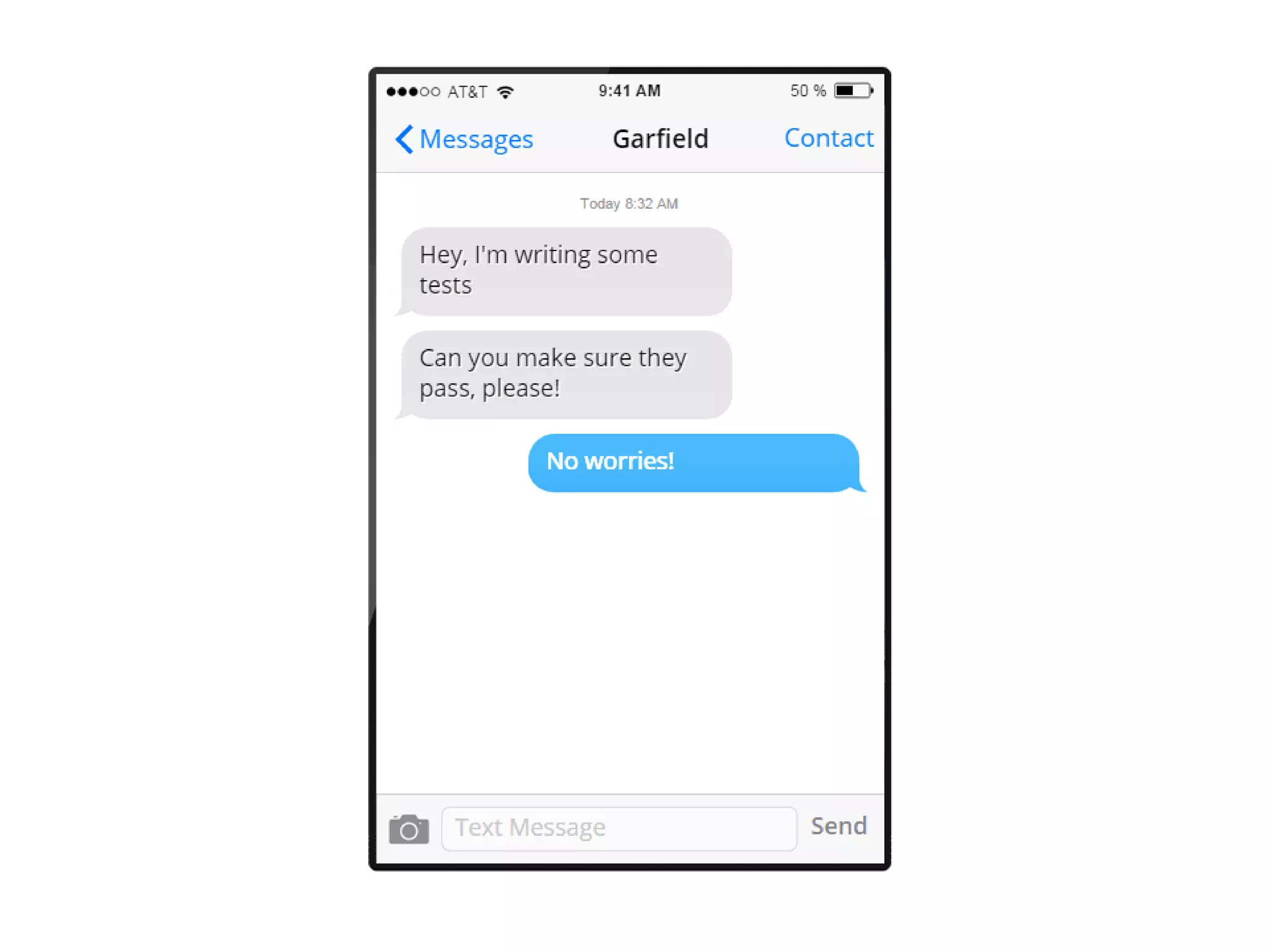
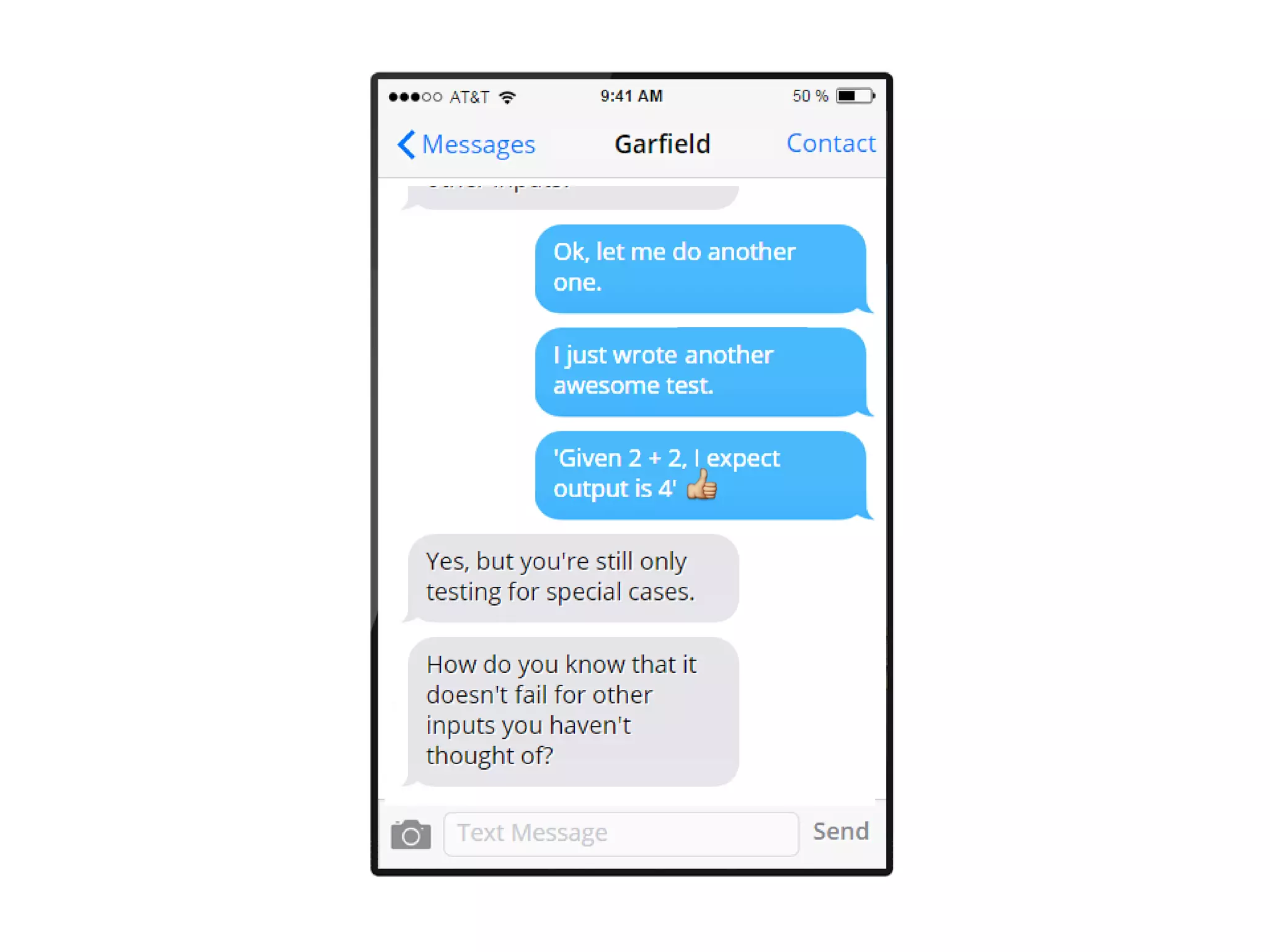
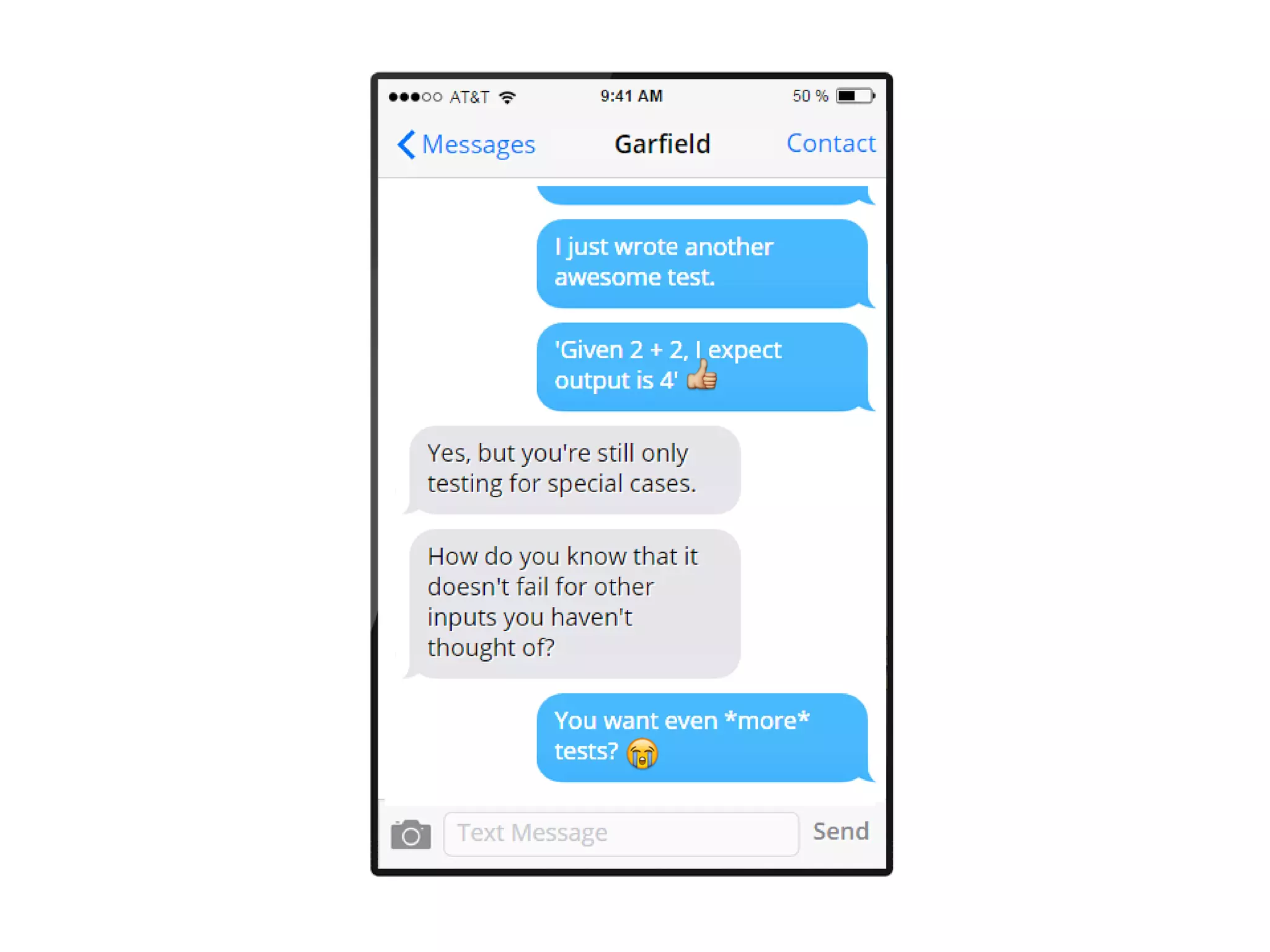
![[<Test>]
let ``When I add 2 + 3, I expect 5``()=
let result = add 2 3
Assert.AreEqual(5,result)
[<Test>]
let ``When I add 1 + 41, I expect 42``()=
let result = add 1 41
Assert.AreEqual(42,result)
Time for some more tests...](https://image.slidesharecdn.com/propbasedtesting-150610142543-lva1-app6892/75/An-introduction-to-property-based-testing-24-2048.jpg)



![[<Test>]
let ``When I add two numbers,
I expect to get their sum``()=
for (x,y,expected) in [
(1,2,3);
(2,2,4);
(3,5,8);
(27,15,42); ]
let actual = add x y
Assert.AreEqual(expected,actual)
Another attempt at a test
](https://image.slidesharecdn.com/propbasedtesting-150610142543-lva1-app6892/75/An-introduction-to-property-based-testing-30-2048.jpg)




![[<Test>]
let ``When I add two random numbers,
I expect their sum to be correct``()=
let x = randInt()
let y = randInt()
let expected = x + y
let actual = add x y
Assert.AreEqual(expected,actual)
Let's use random numbers instead...](https://image.slidesharecdn.com/propbasedtesting-150610142543-lva1-app6892/75/An-introduction-to-property-based-testing-35-2048.jpg)
![[<Test>]
let ``When I add two random numbers (100 times),
I expect their sum to be correct``()=
for _ in [1..100] do
let x = randInt()
let y = randInt()
let expected = x + y
let actual = add x y
Assert.AreEqual(expected,actual)
Yea! Problem solved!
And why not do it 100 times just to be sure...
The EDFH can't beat this!](https://image.slidesharecdn.com/propbasedtesting-150610142543-lva1-app6892/75/An-introduction-to-property-based-testing-36-2048.jpg)
![[<Test>]
let ``When I add two random numbers (100 times),
I expect their sum to be correct``()=
for _ in [1..100] do
let x = randInt()
let y = randInt()
let expected = x + y
let actual = add x y
Assert.AreEqual(expected,actual)
Uh-oh!
But if you can't test by using +, how CAN you test?
We can't test "add" using +!](https://image.slidesharecdn.com/propbasedtesting-150610142543-lva1-app6892/75/An-introduction-to-property-based-testing-37-2048.jpg)


![[<Test>]
let ``When I add two numbers, the result
should not depend on parameter order``()=
for _ in [1..100] do
let x = randInt()
let y = randInt()
let result1 = add x y
let result2 = add y x
Assert.AreEqual(result1,result2)
reversed params
So how does "add" differ from "subtract"?
For "subtract", the order of the parameters makes a
difference, while for "add" it doesn't.](https://image.slidesharecdn.com/propbasedtesting-150610142543-lva1-app6892/75/An-introduction-to-property-based-testing-40-2048.jpg)


![[<Test>]
let ``Adding 1 twice is the same as adding 2``()=
for _ in [1..100] do
let x = randInt()
let y = randInt()
let result1 = x |> add 1 |> add 1
let result2 = x |> add 2
Assert.AreEqual(result1,result2)
Test: two "add 1"s is the same as one "add 2".](https://image.slidesharecdn.com/propbasedtesting-150610142543-lva1-app6892/75/An-introduction-to-property-based-testing-43-2048.jpg)


![[<Test>]
let ``Adding zero is the same as doing nothing``()=
for _ in [1..100] do
let x = randInt()
let result1 = x |> add 0
let result2 = x
Assert.AreEqual(result1,result2)
Yes! Adding zero is the same as doing nothing
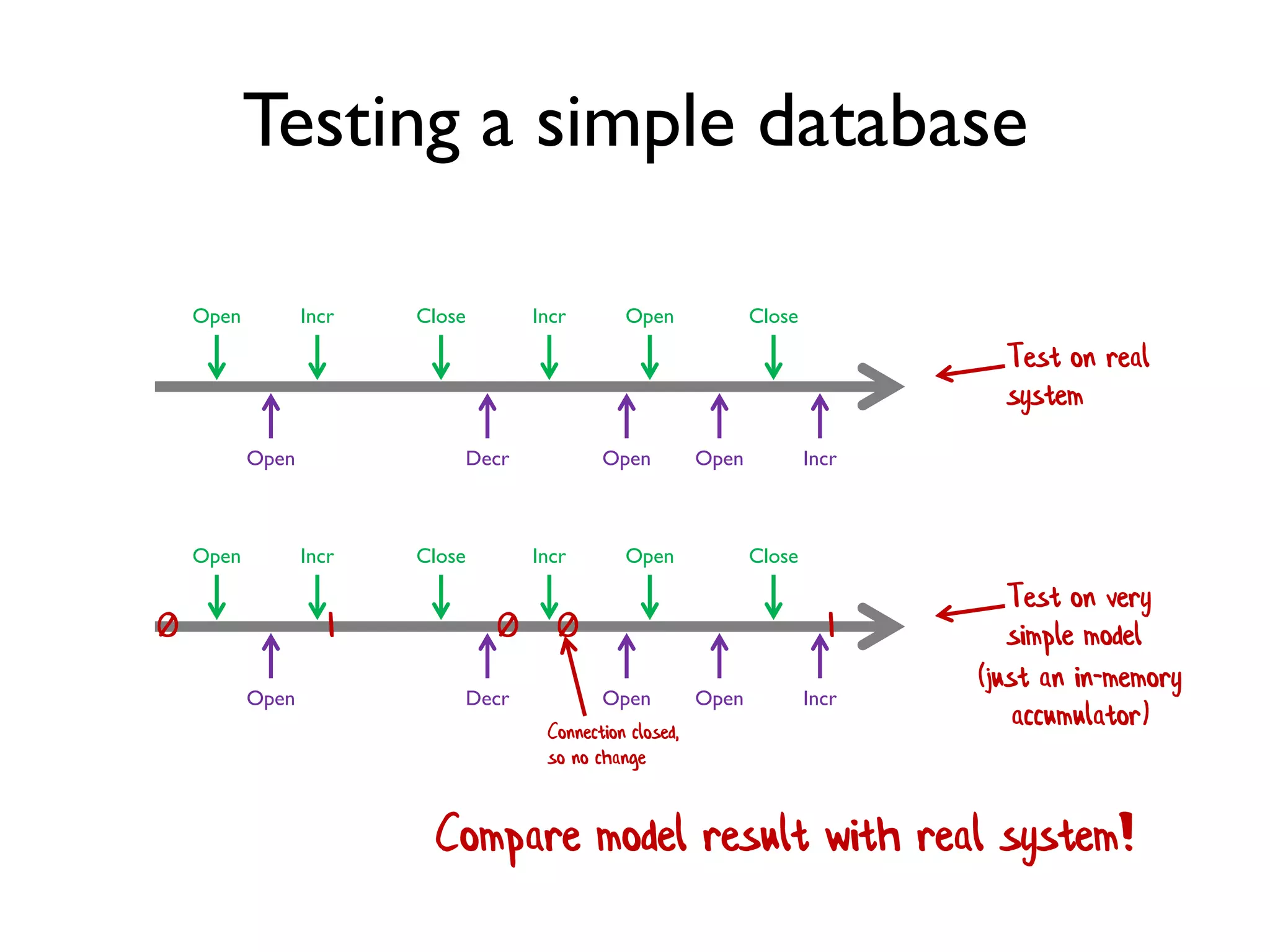
We have to check that the result is somehow connected to the input.
Is there a trivial property of add that we know the answer to
without reimplementing our own version?](https://image.slidesharecdn.com/propbasedtesting-150610142543-lva1-app6892/75/An-introduction-to-property-based-testing-46-2048.jpg)


![let propertyCheck property =
// property has type: int -> int -> bool
for _ in [1..100] do
let x = randInt()
let y = randInt()
let result = property x y
Assert.IsTrue(result)
Let's extract the shared code... Pass in a "property"
Check the property is
true for random inputs](https://image.slidesharecdn.com/propbasedtesting-150610142543-lva1-app6892/75/An-introduction-to-property-based-testing-49-2048.jpg)
![let commutativeProperty x y =
let result1 = add x y
let result2 = add y x
result1 = result2
And the tests now look like:
[<Test>]
let ``When I add two numbers, the result
should not depend on parameter order``()=
propertyCheck commutativeProperty](https://image.slidesharecdn.com/propbasedtesting-150610142543-lva1-app6892/75/An-introduction-to-property-based-testing-50-2048.jpg)
![let adding1TwiceIsAdding2OnceProperty x _ =
let result1 = x |> add 1 |> add 1
let result2 = x |> add 2
result1 = result2
And the second property
[<Test>]
let ``Adding 1 twice is the same as adding 2``()=
propertyCheck adding1TwiceIsAdding2OnceProperty](https://image.slidesharecdn.com/propbasedtesting-150610142543-lva1-app6892/75/An-introduction-to-property-based-testing-51-2048.jpg)
![let identityProperty x _ =
let result1 = x |> add 0
result1 = x
And the third property
[<Test>]
let ``Adding zero is the same as doing nothing``()=
propertyCheck identityProperty](https://image.slidesharecdn.com/propbasedtesting-150610142543-lva1-app6892/75/An-introduction-to-property-based-testing-52-2048.jpg)




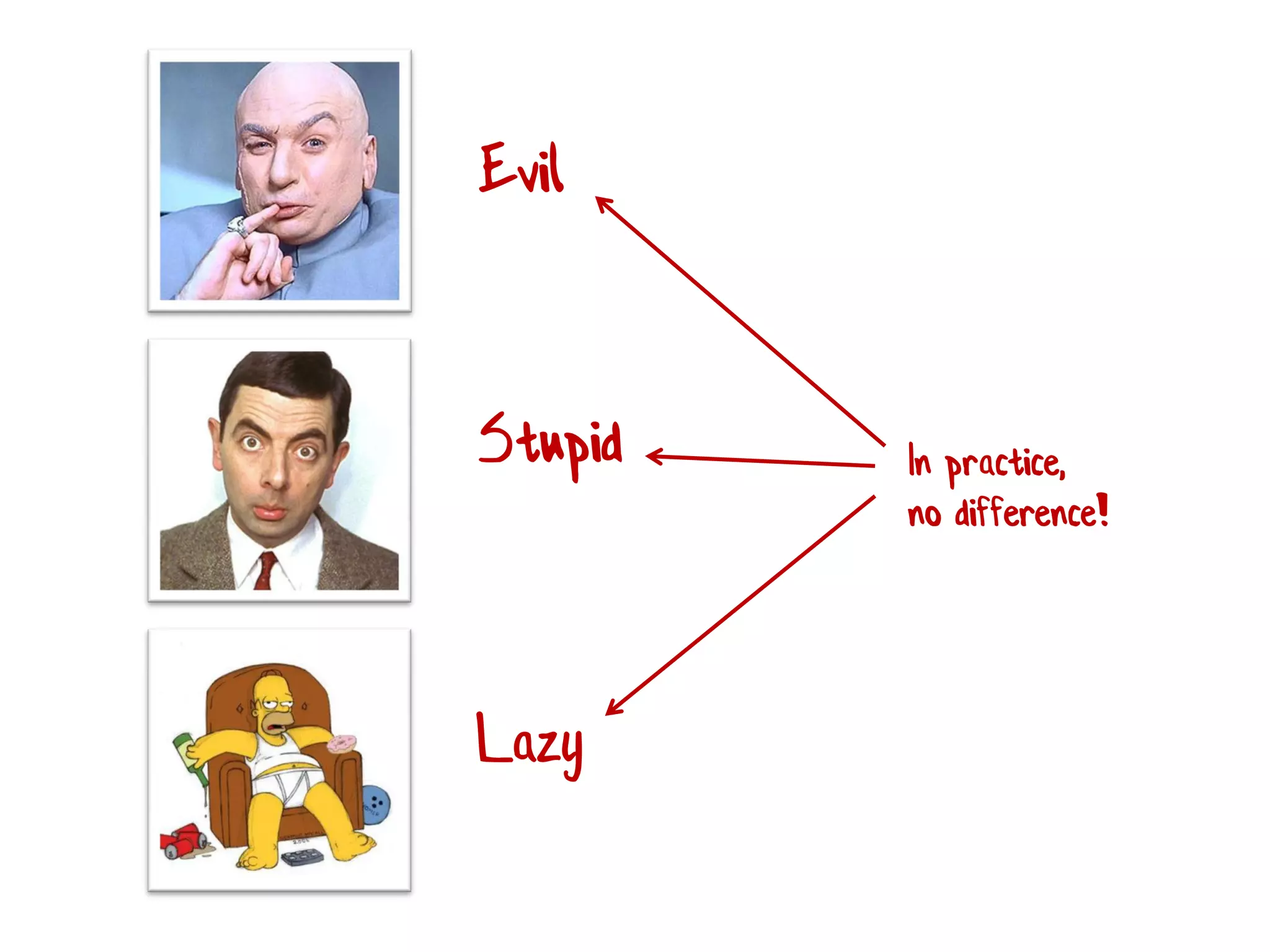















!["Different paths, same destination"
Applied to a sort function
[1;2;3]
?
do ? do ?
List.sort
List.sort](https://image.slidesharecdn.com/propbasedtesting-150610142543-lva1-app6892/75/An-introduction-to-property-based-testing-75-2048.jpg)
!["Different paths, same destination"
Applied to a sort function
[2;3;1]
[-2;-3;-1] [-3;-2;-1]
[1;2;3]
Negate
List.sort
List.sort
Negate
then reverse](https://image.slidesharecdn.com/propbasedtesting-150610142543-lva1-app6892/75/An-introduction-to-property-based-testing-76-2048.jpg)
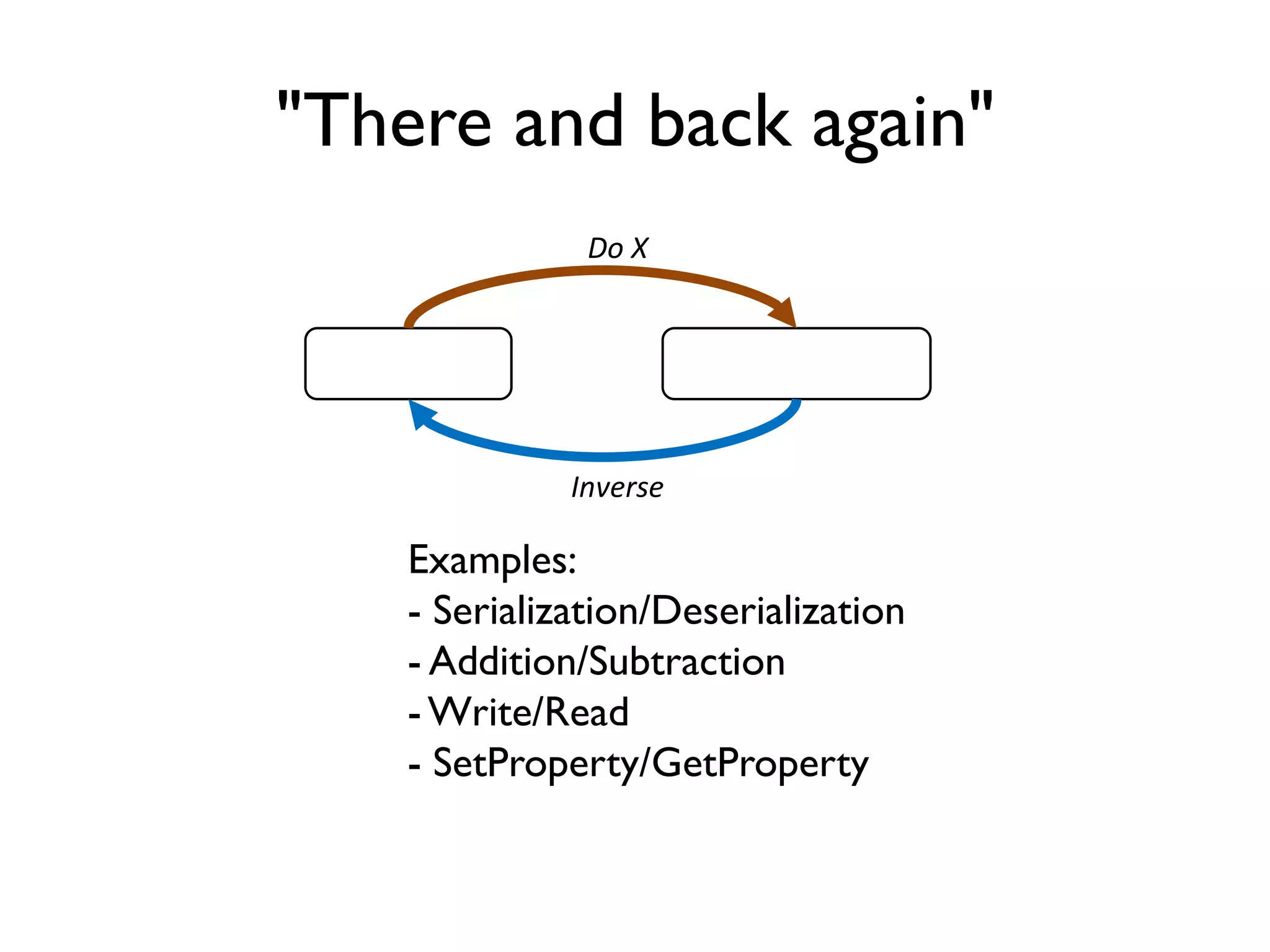
!["There and back again"
Applied to a list reverse function
[1;2;3] [3;2;1]
reverse
reverse](https://image.slidesharecdn.com/propbasedtesting-150610142543-lva1-app6892/75/An-introduction-to-property-based-testing-79-2048.jpg)

![[2;3;1]
[-2;-3;-1] [-3;-2;-1]
[1;2;3]
Negate
List.sort
List.sort
Negate
then reverse
The EDFH and List.Sort
The EDFH can beat this!](https://image.slidesharecdn.com/propbasedtesting-150610142543-lva1-app6892/75/An-introduction-to-property-based-testing-81-2048.jpg)
![The EDFH and List.Sort
[2;3;1]
[-2;-3;-1] [ ]
[ ]
Negate
List.evilSort
List.evilSort
Negate
then reverse
EvilSort just returns an empty list!
This passes the "commutivity" test!](https://image.slidesharecdn.com/propbasedtesting-150610142543-lva1-app6892/75/An-introduction-to-property-based-testing-82-2048.jpg)
!["Some things never change"
[2;3;1]
[1; 2; 3]; [2; 1; 3]; [2; 3; 1];
[1; 3; 2]; [3; 1; 2]; [3; 2; 1]
[1;2;3]
List.sort
Must be one of these
permutations
Used to ensure the sort function is good](https://image.slidesharecdn.com/propbasedtesting-150610142543-lva1-app6892/75/An-introduction-to-property-based-testing-83-2048.jpg)


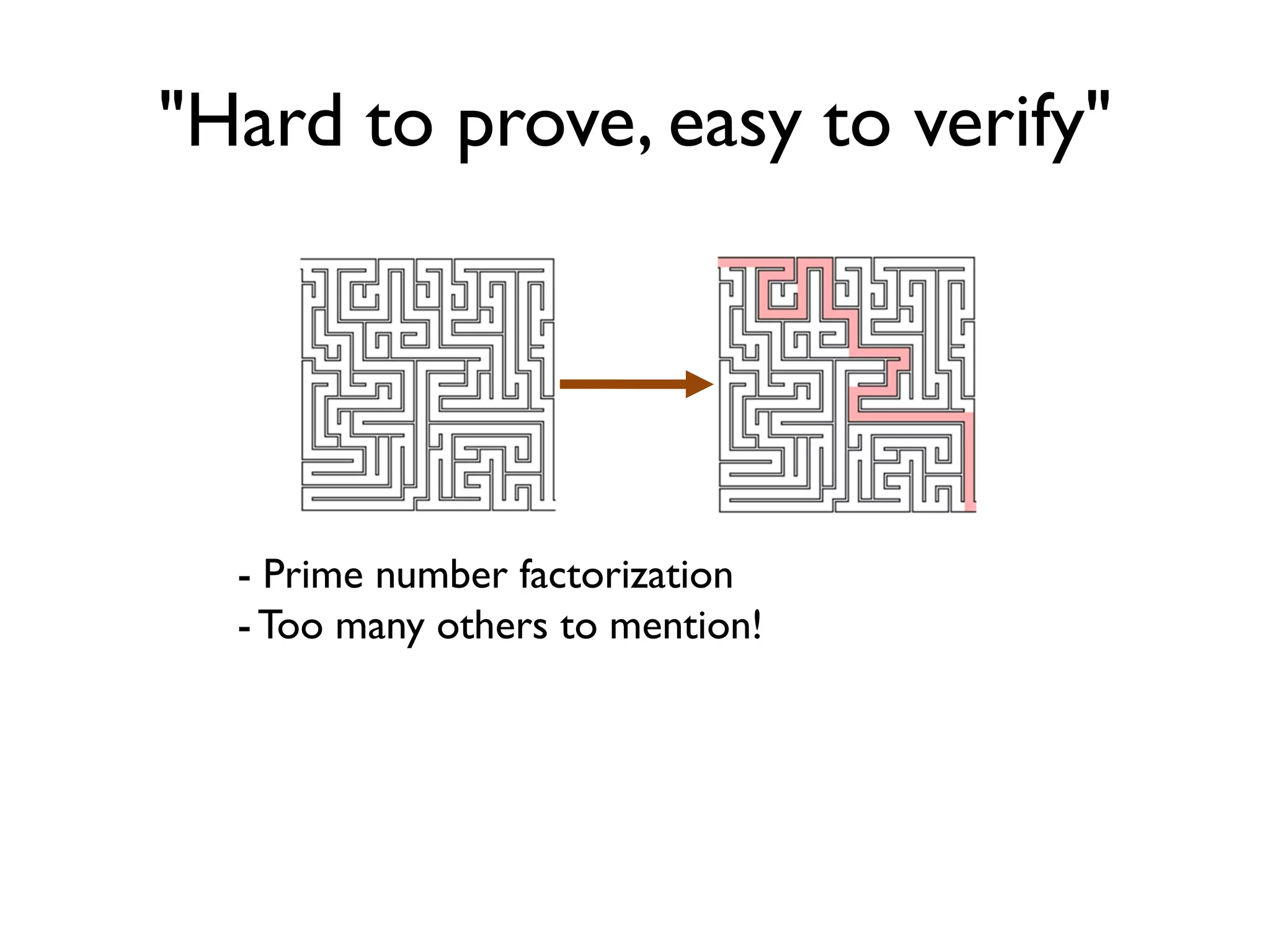
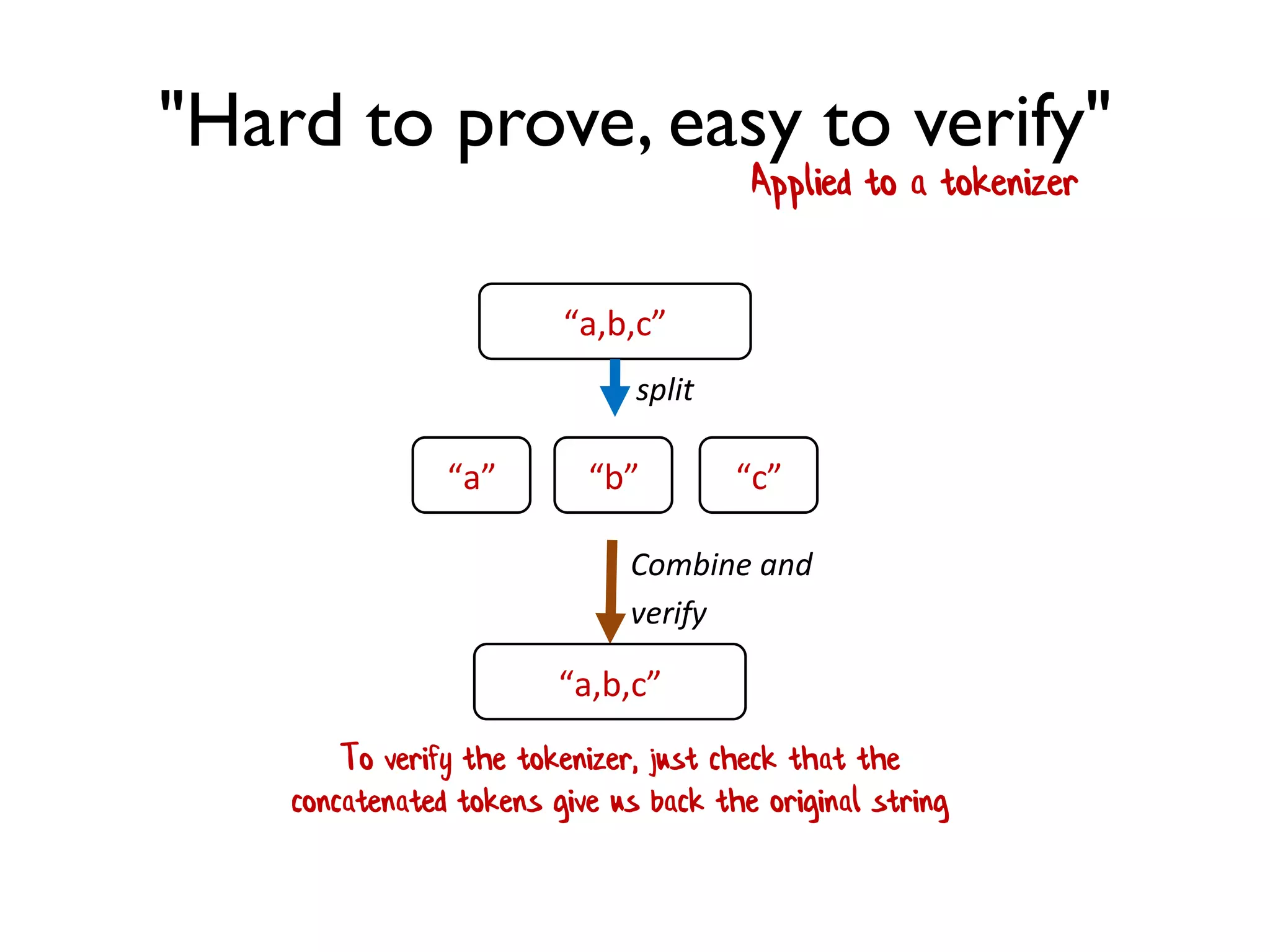
!["Hard to prove, easy to verify"
Applied to a sort
To verify the sort,
check that each pair is ordered
[2;3;1]
(1<=2) (2<=3)
[1;2;3]
List.sort](https://image.slidesharecdn.com/propbasedtesting-150610142543-lva1-app6892/75/An-introduction-to-property-based-testing-88-2048.jpg)