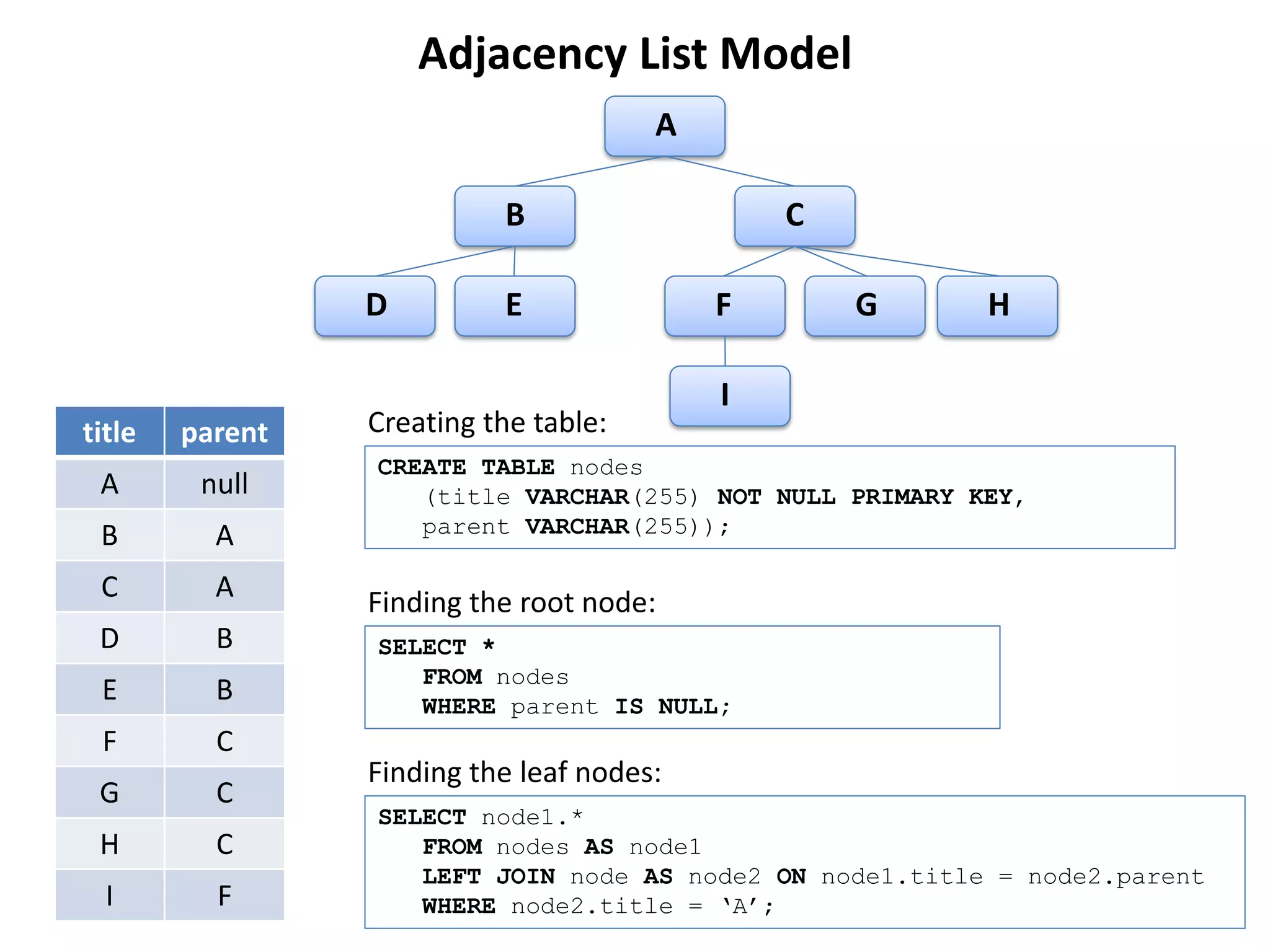
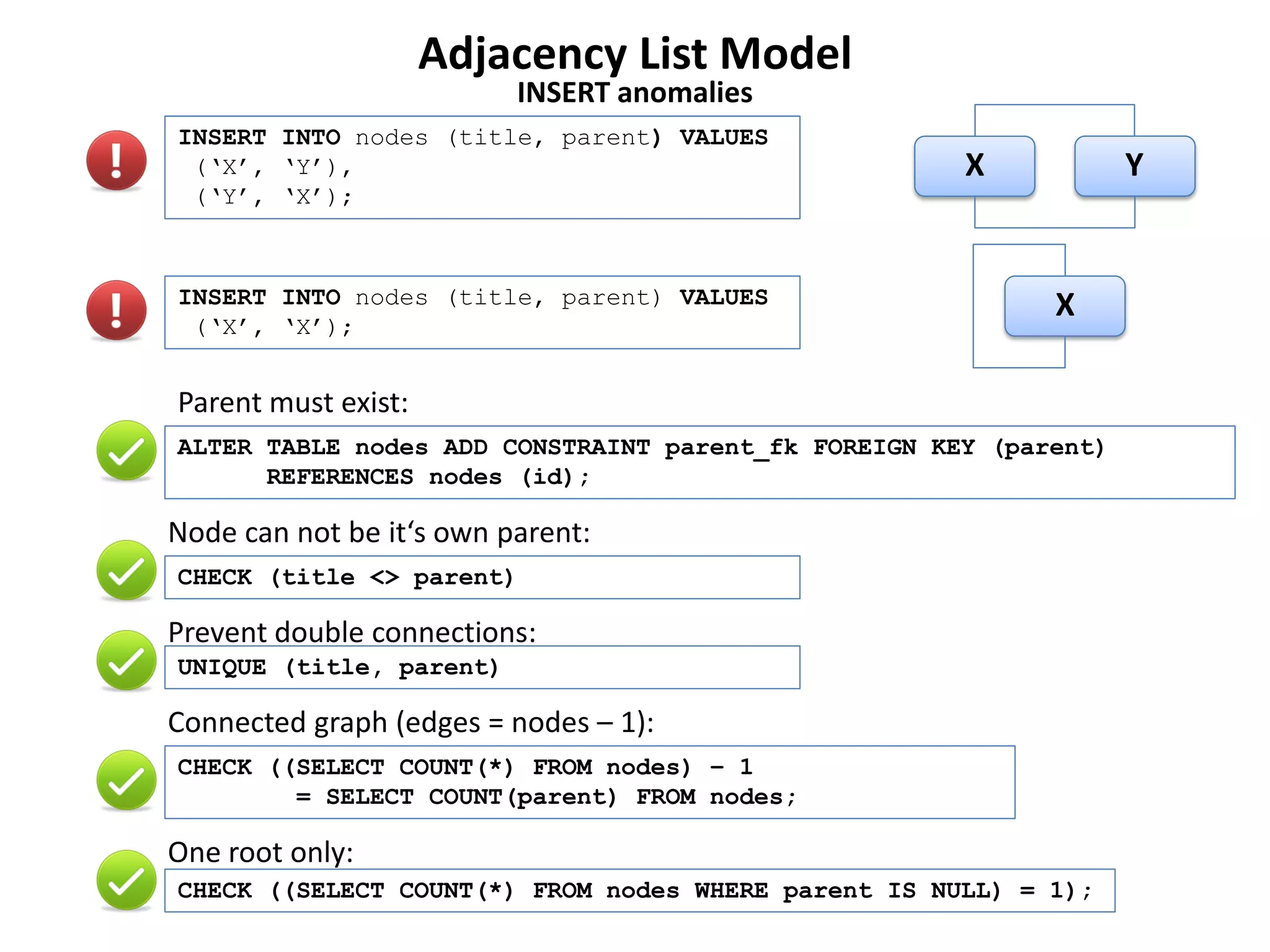
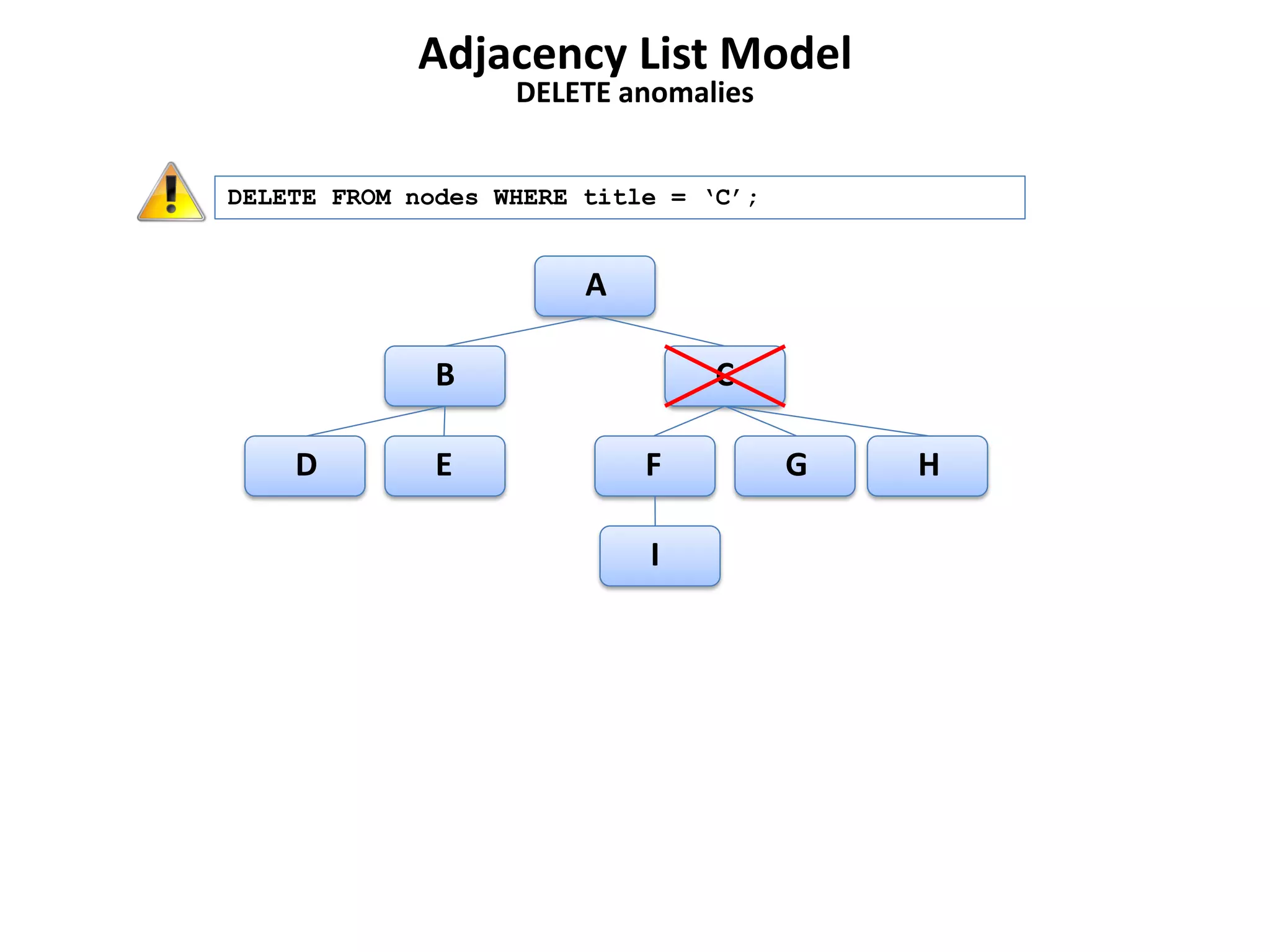
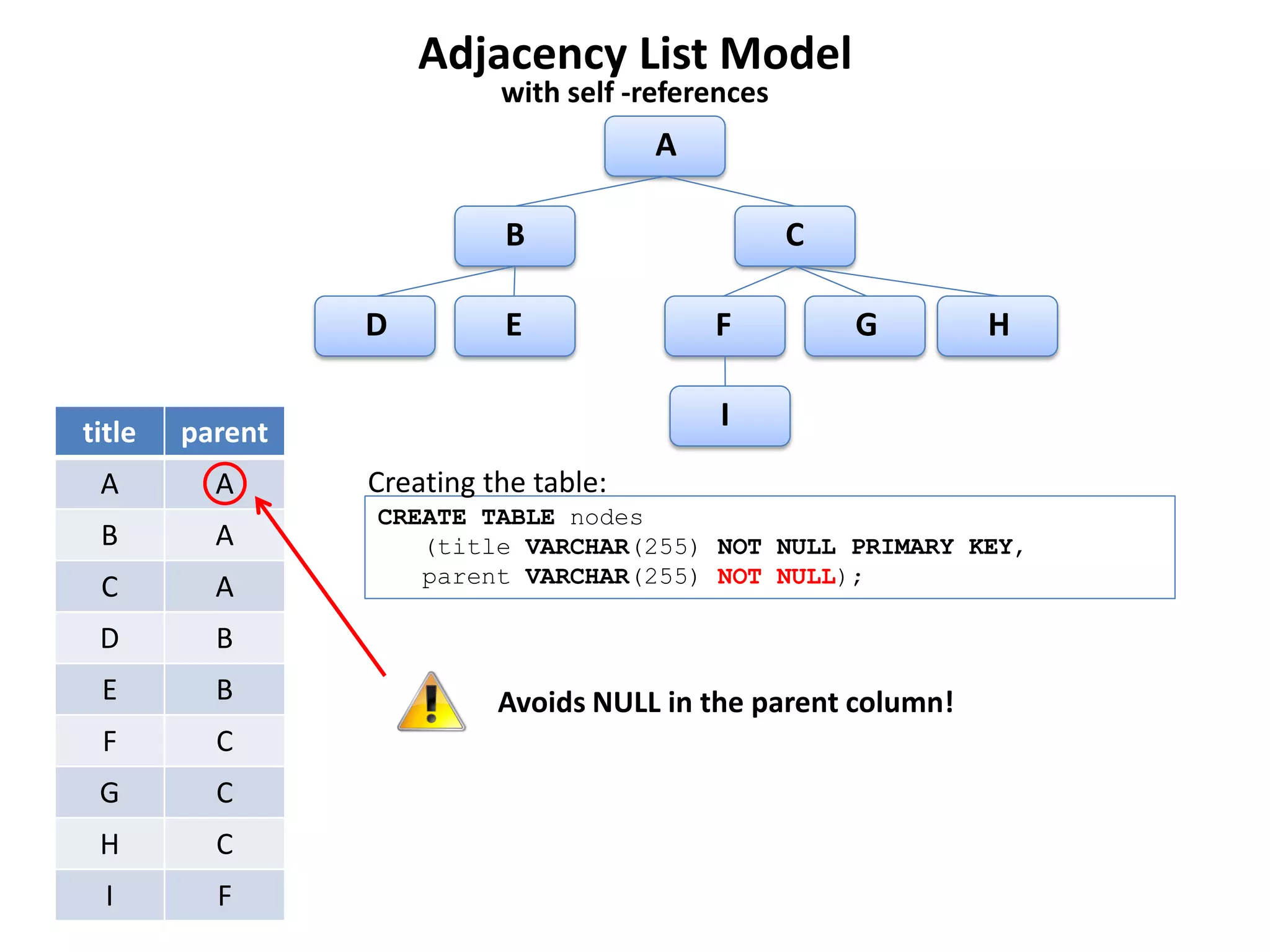
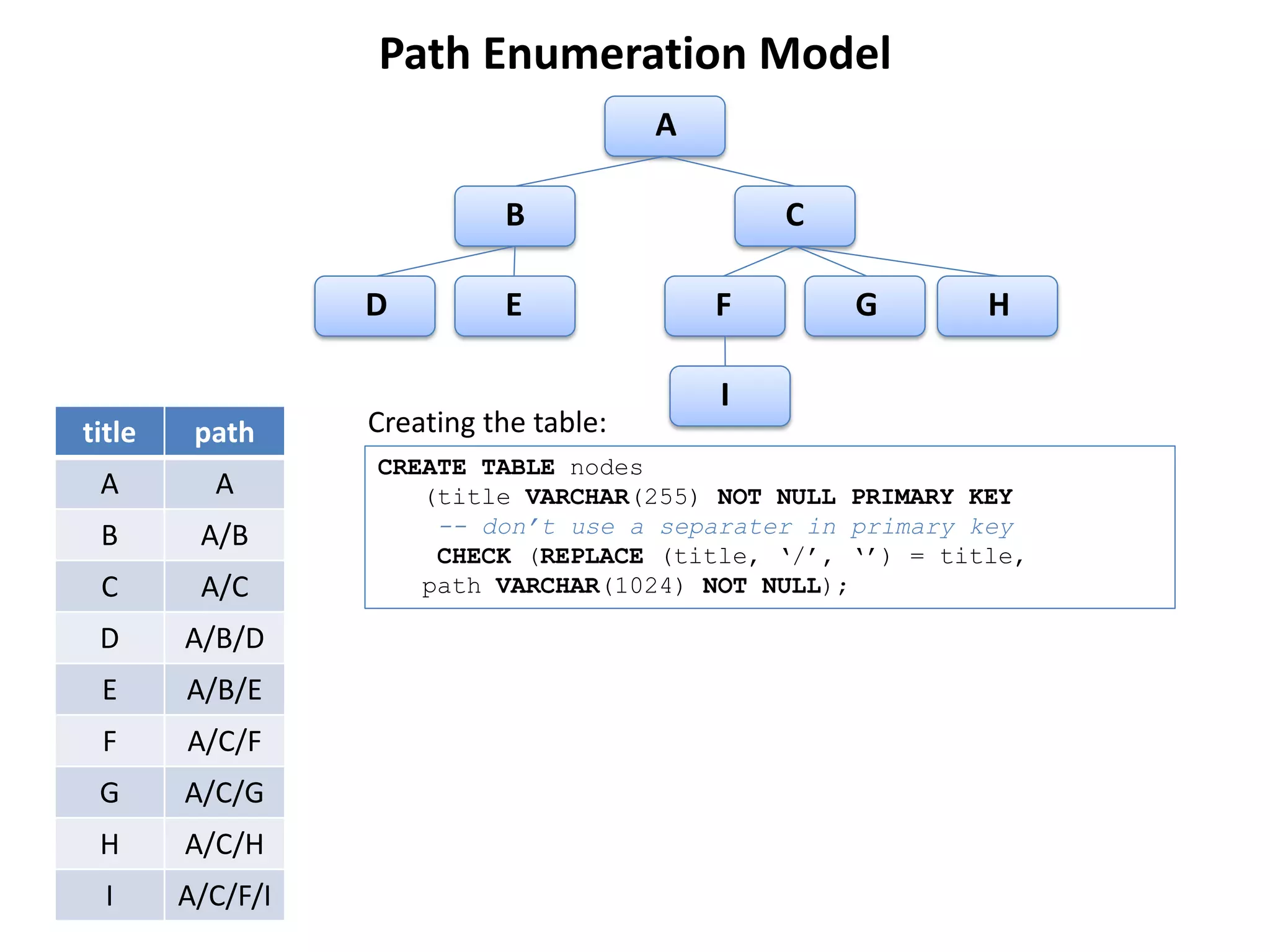
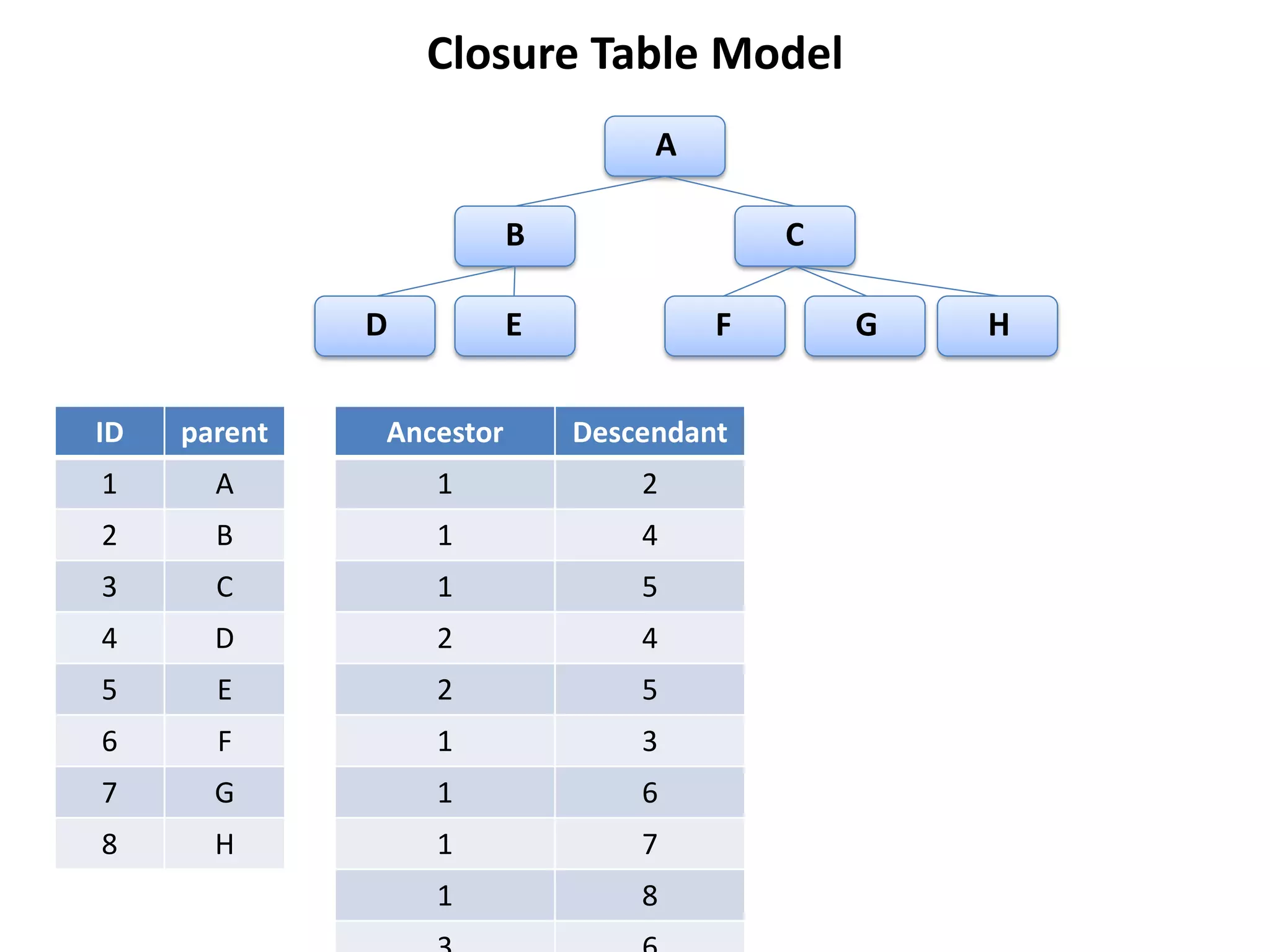
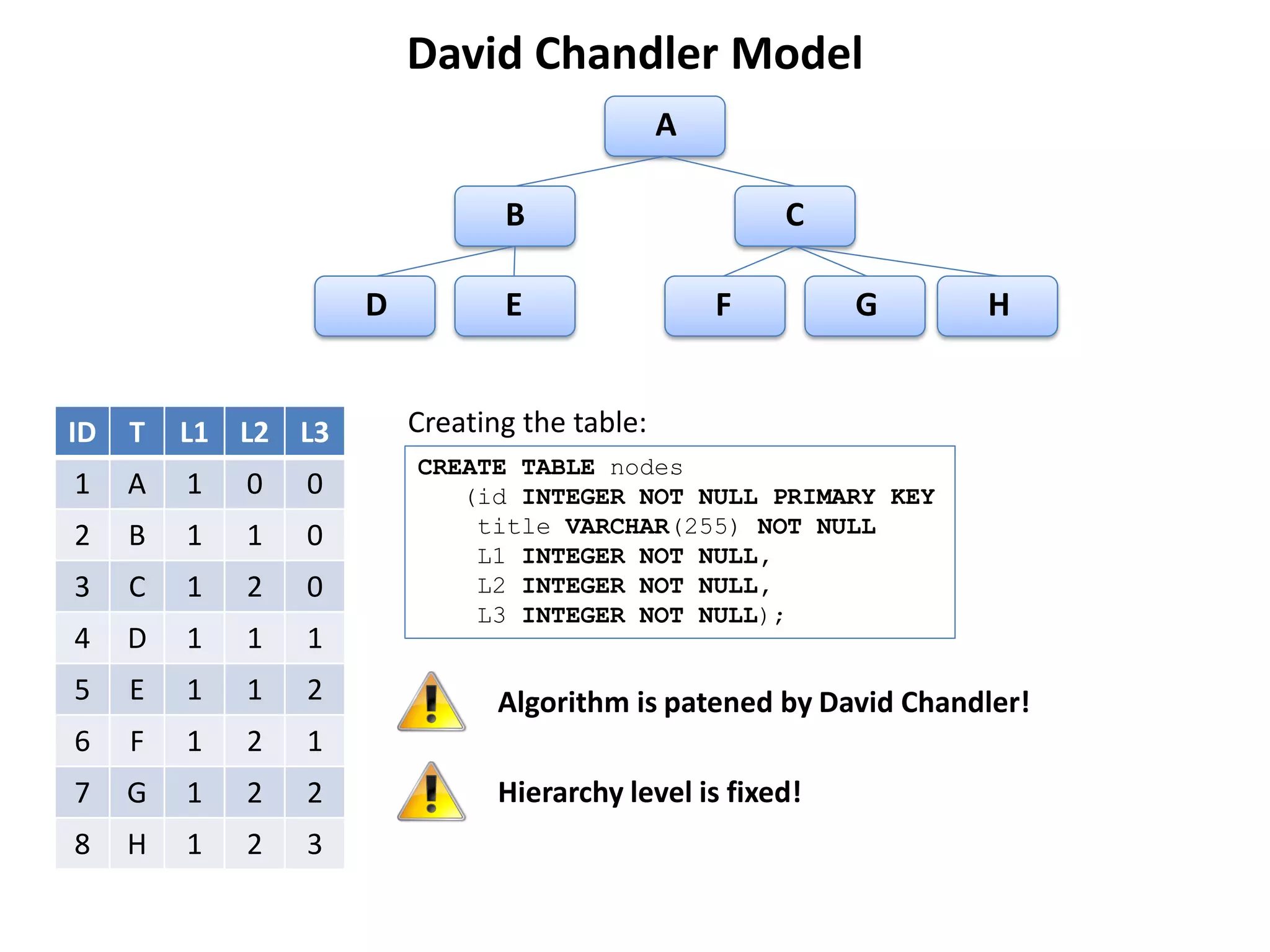
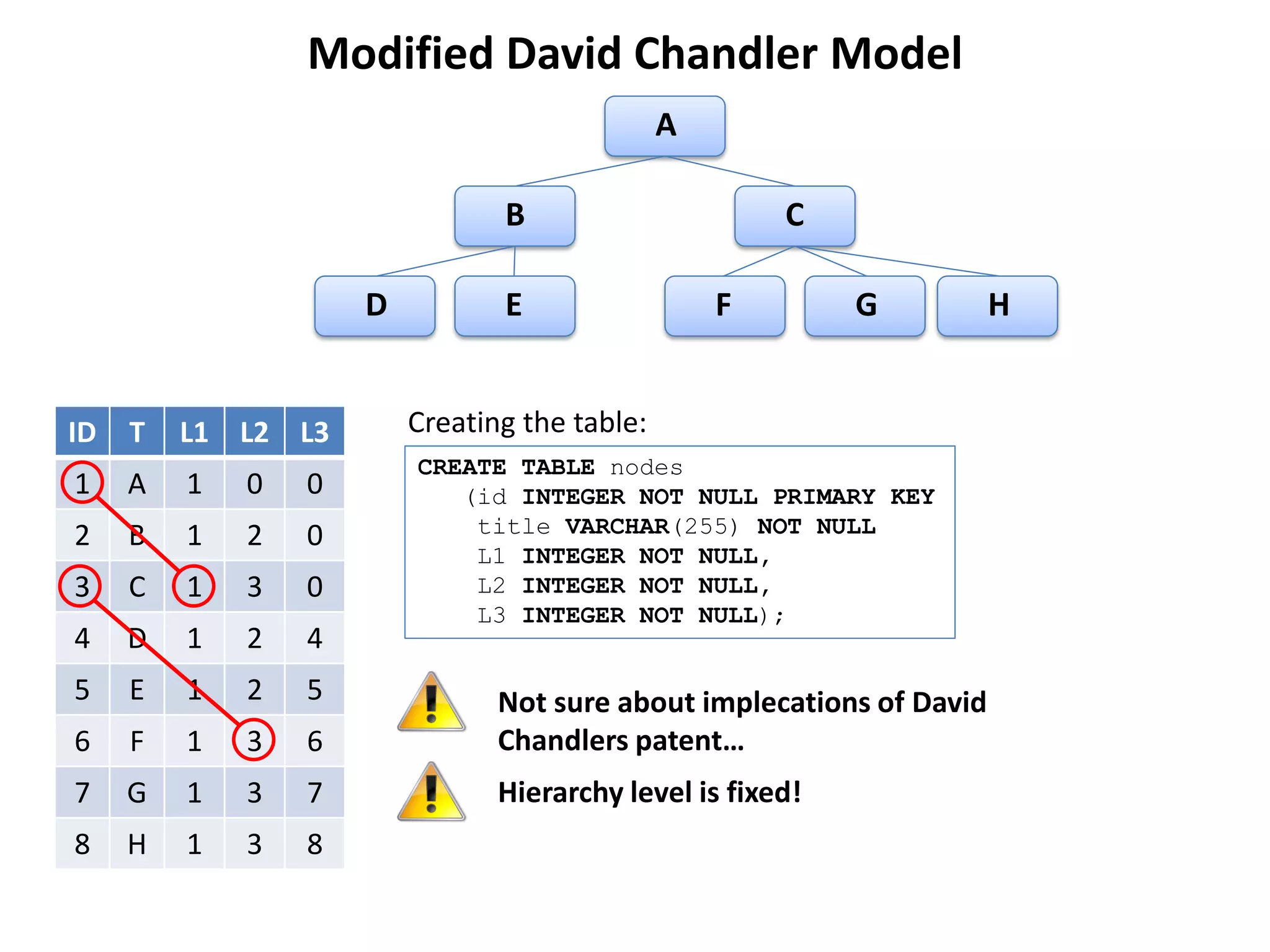
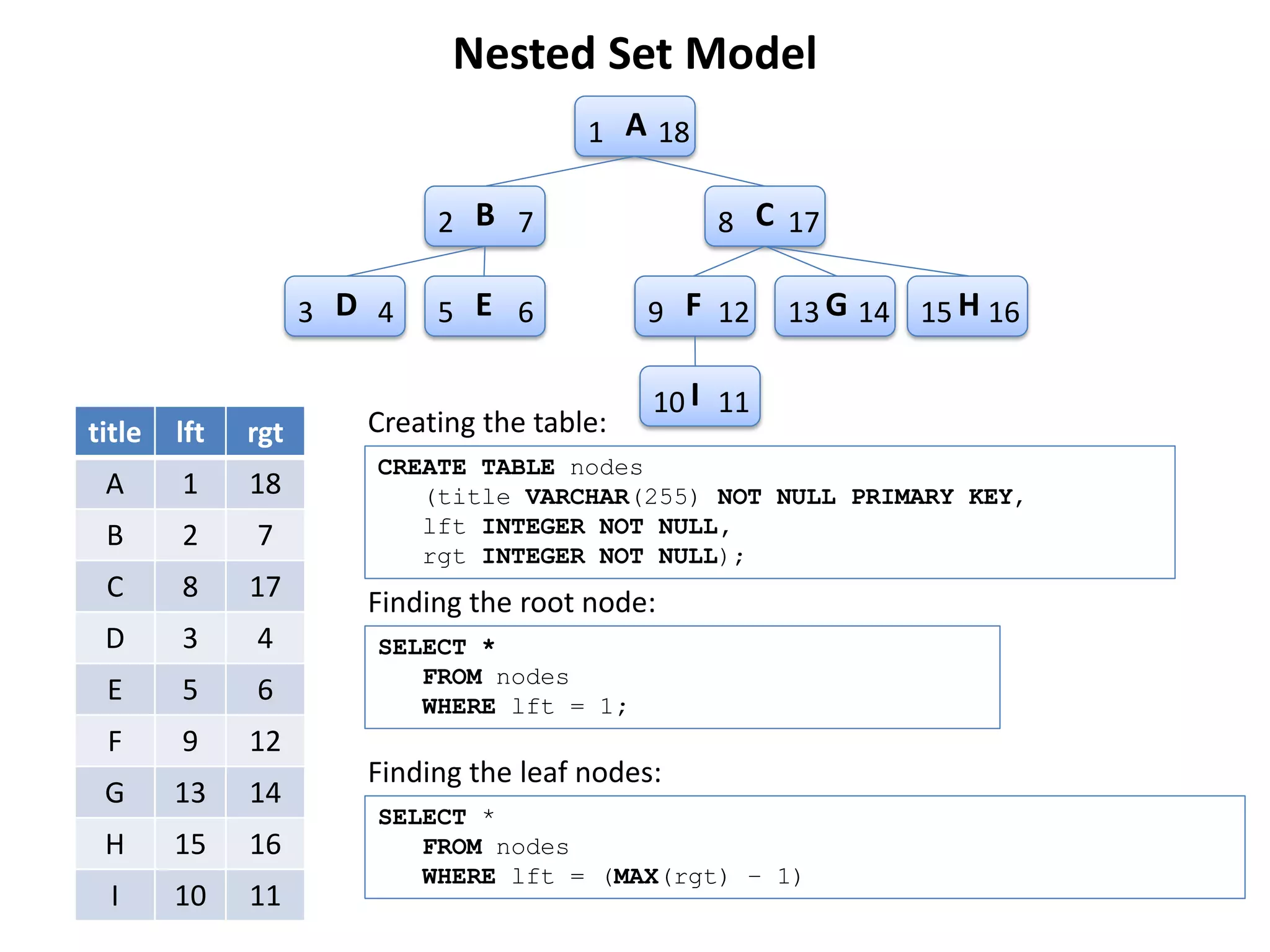
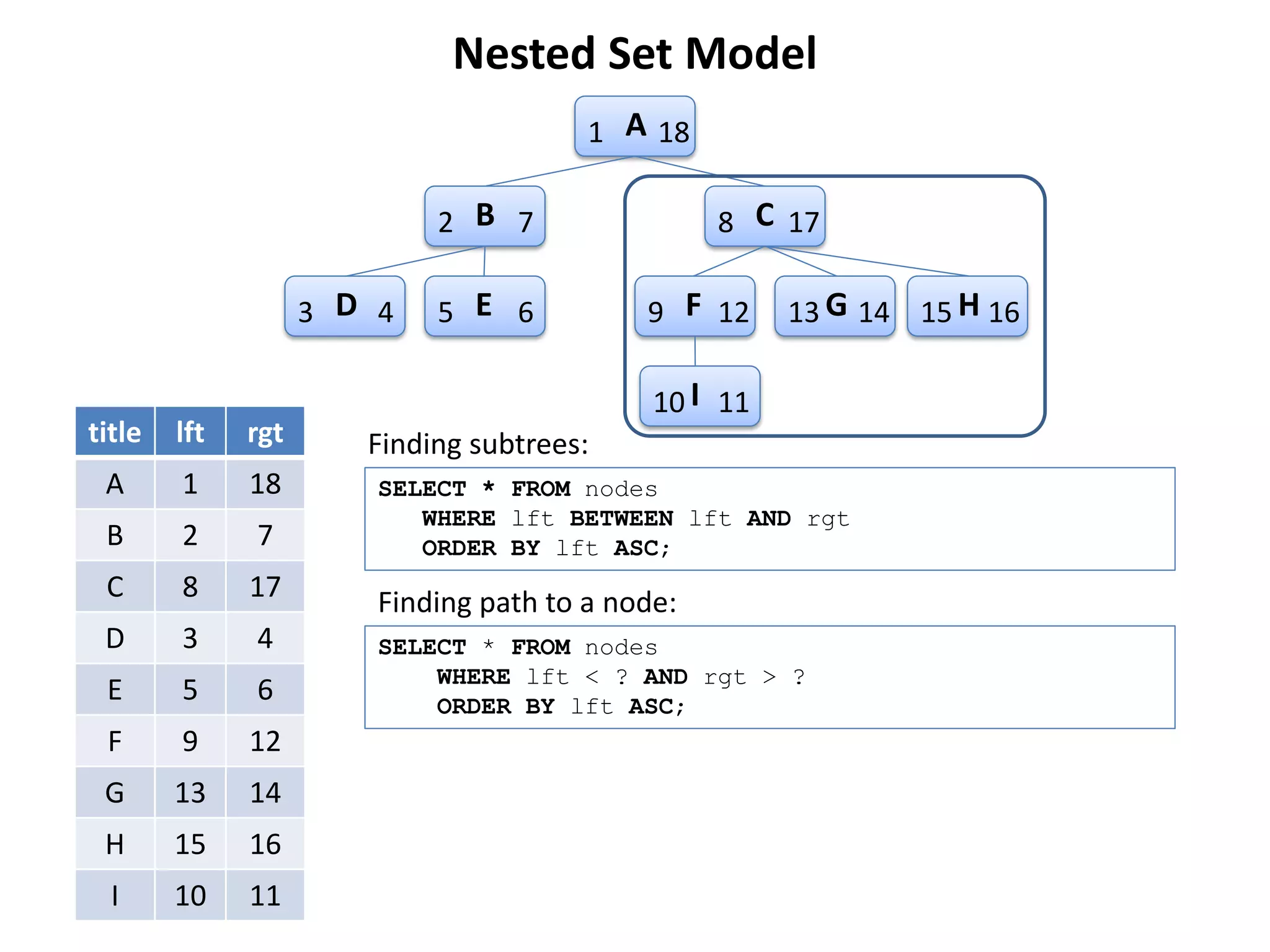
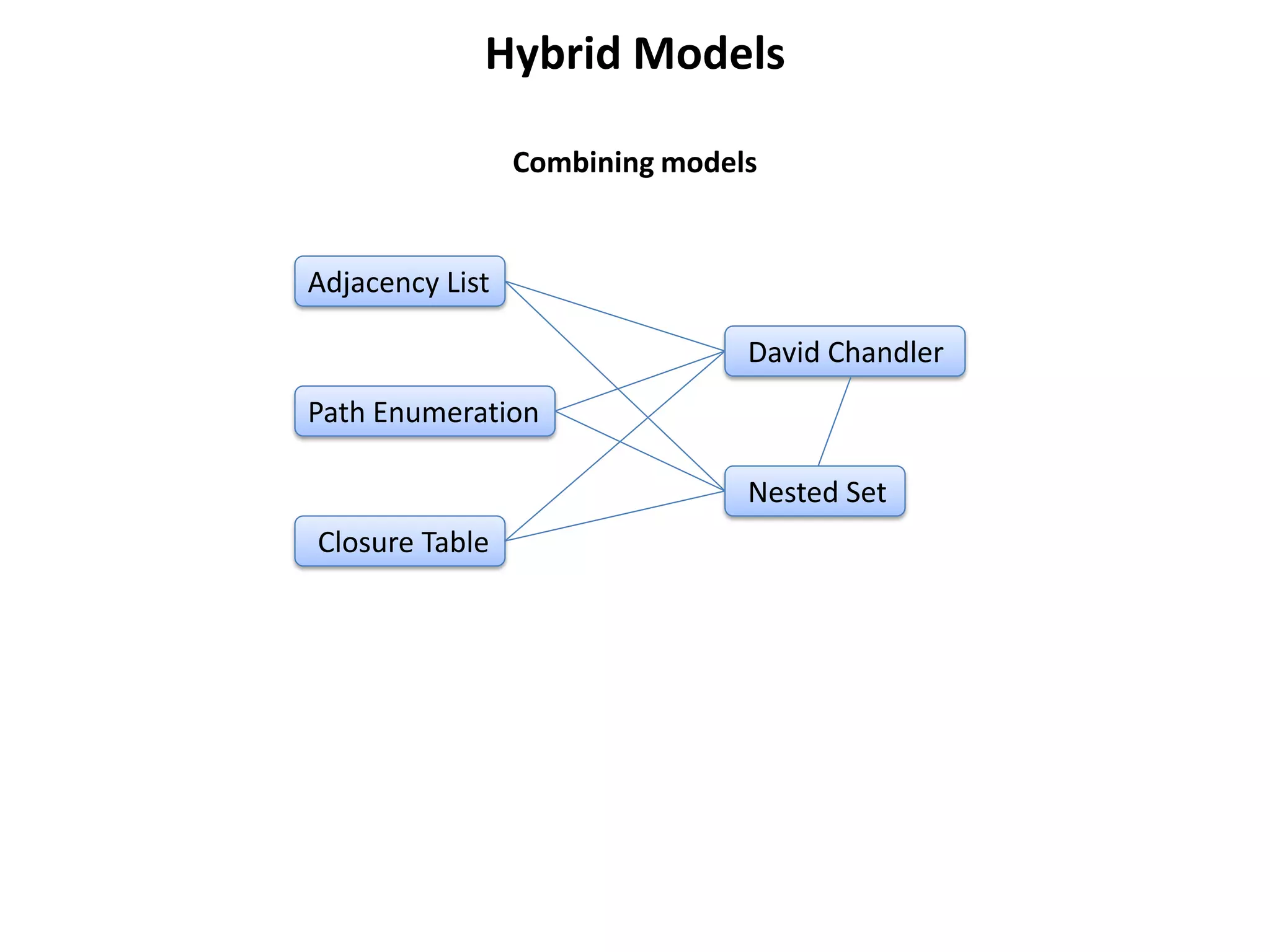
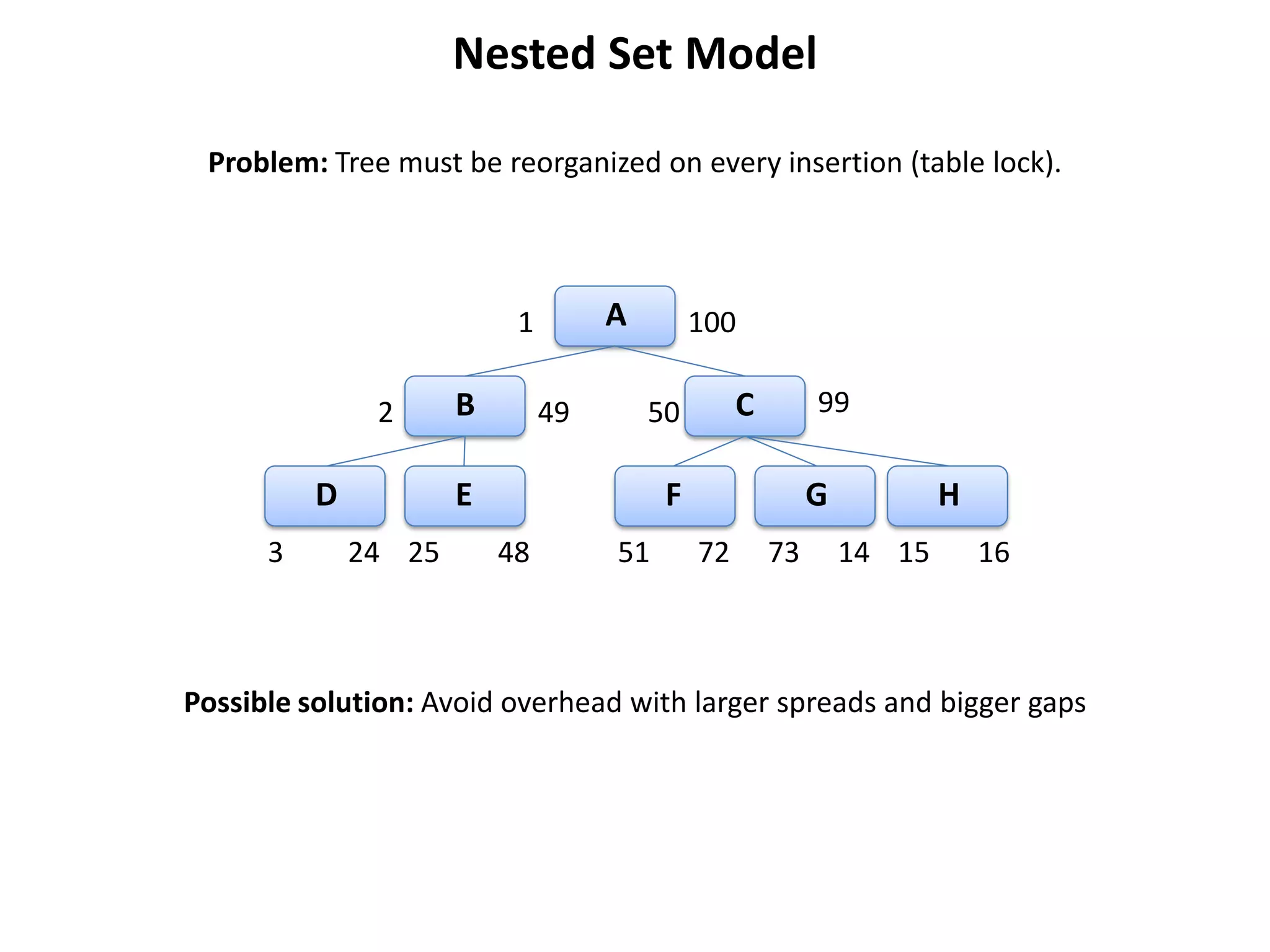
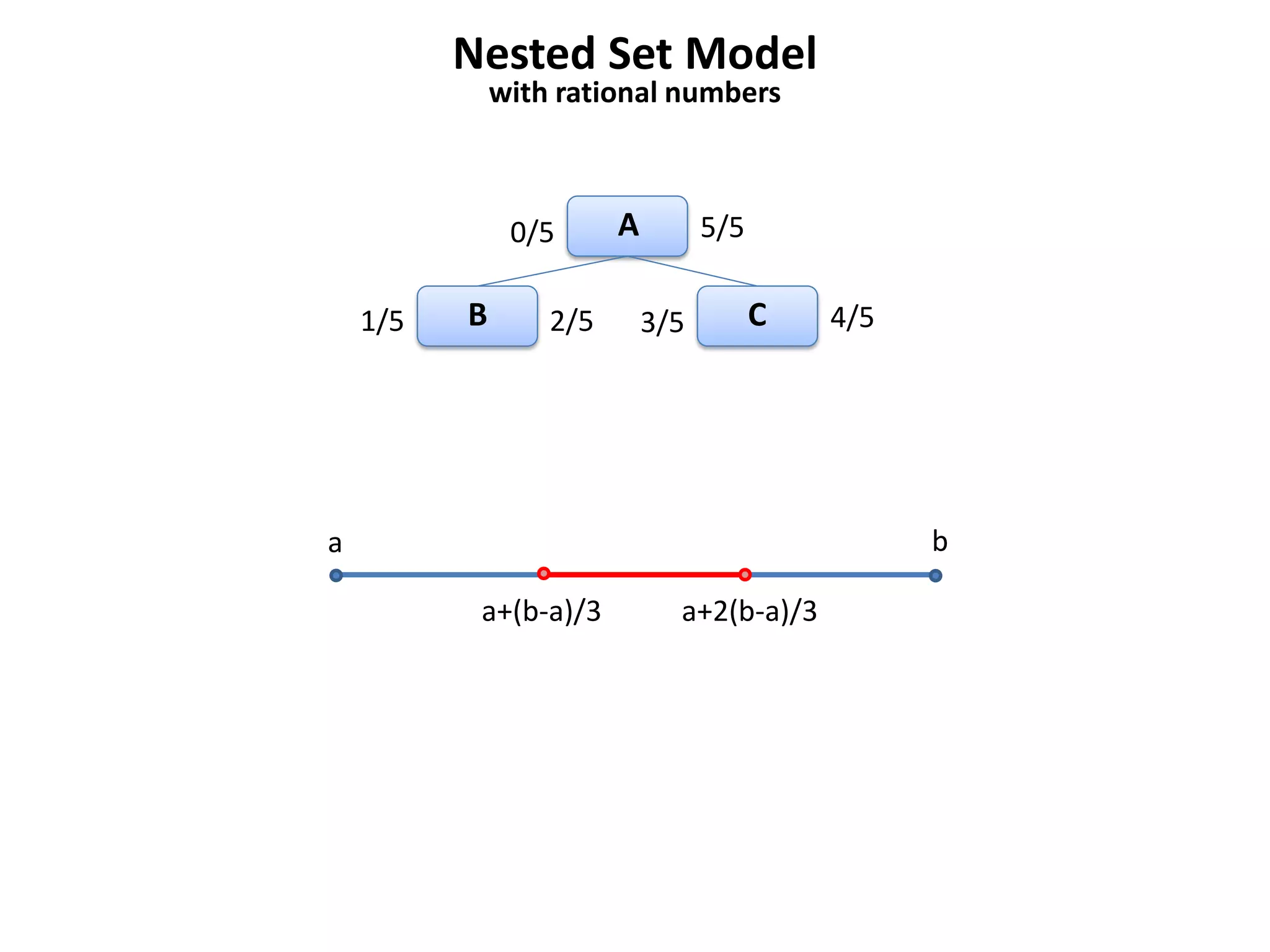
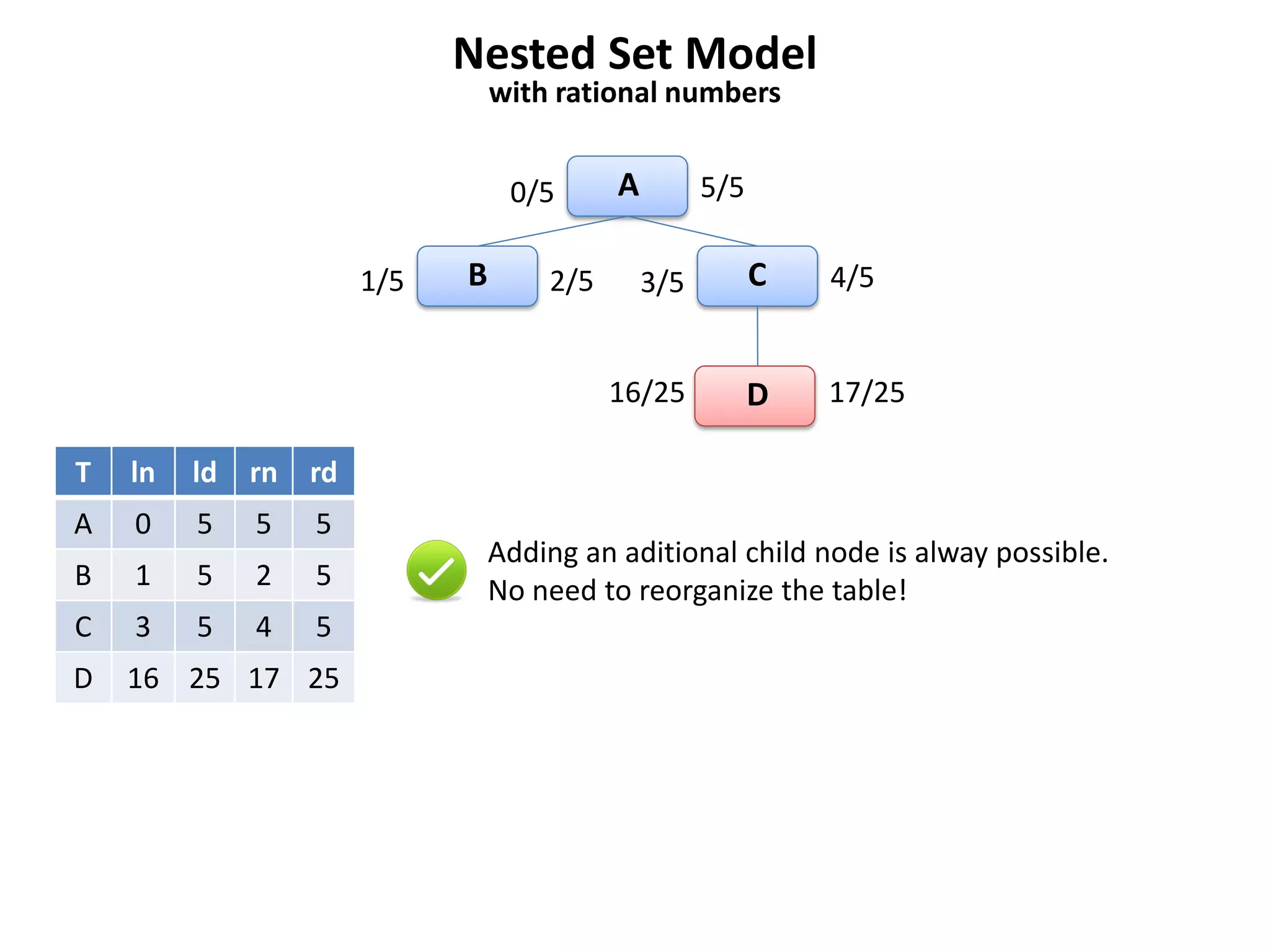
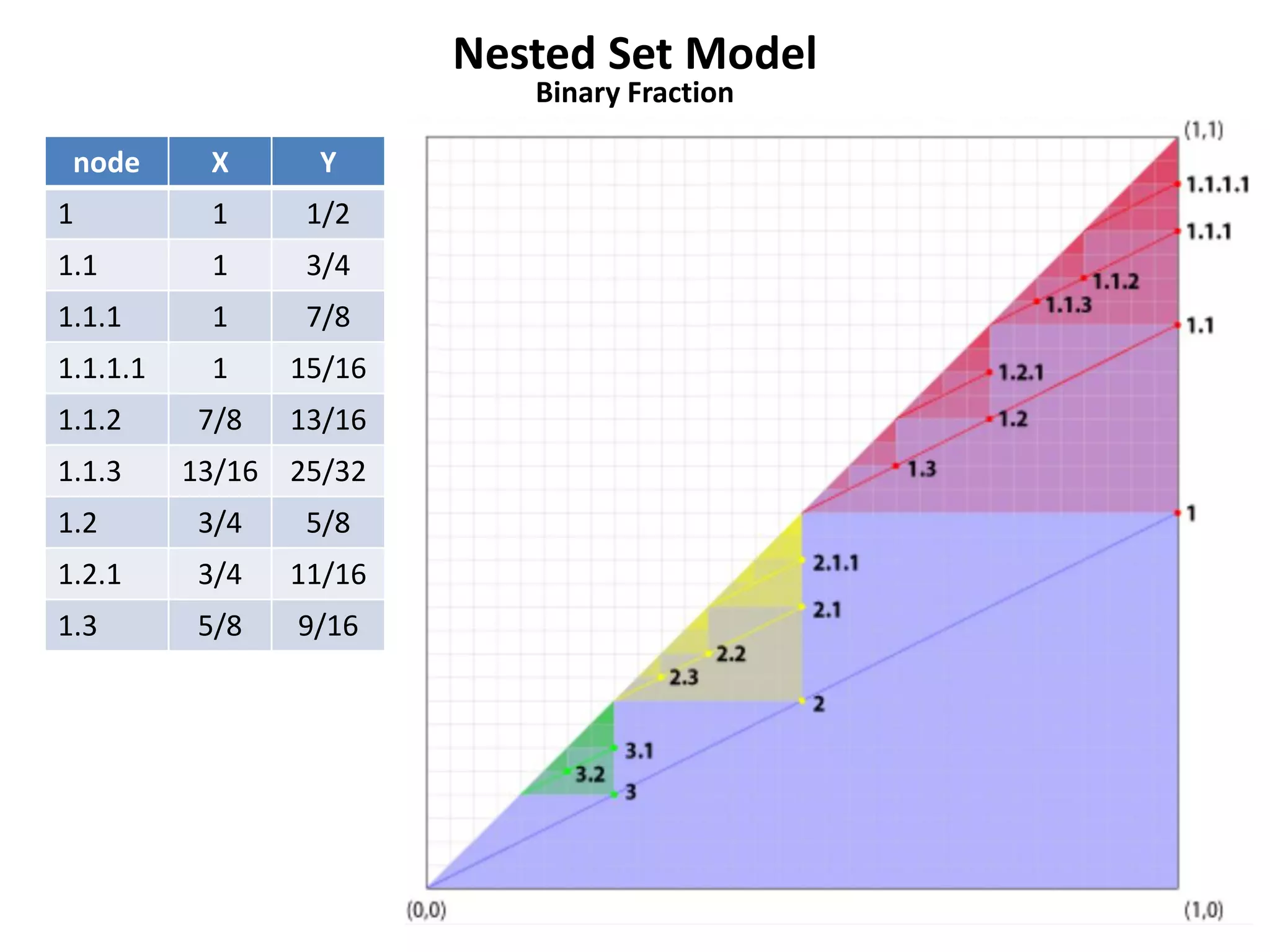
The document discusses several models for representing hierarchical or tree-like data structures in relational databases, including adjacency list, closure table, path enumeration, nested set, and various extensions of the David Chandler model. It provides examples of creating tables and querying data for each model, and notes some advantages and limitations of each approach.