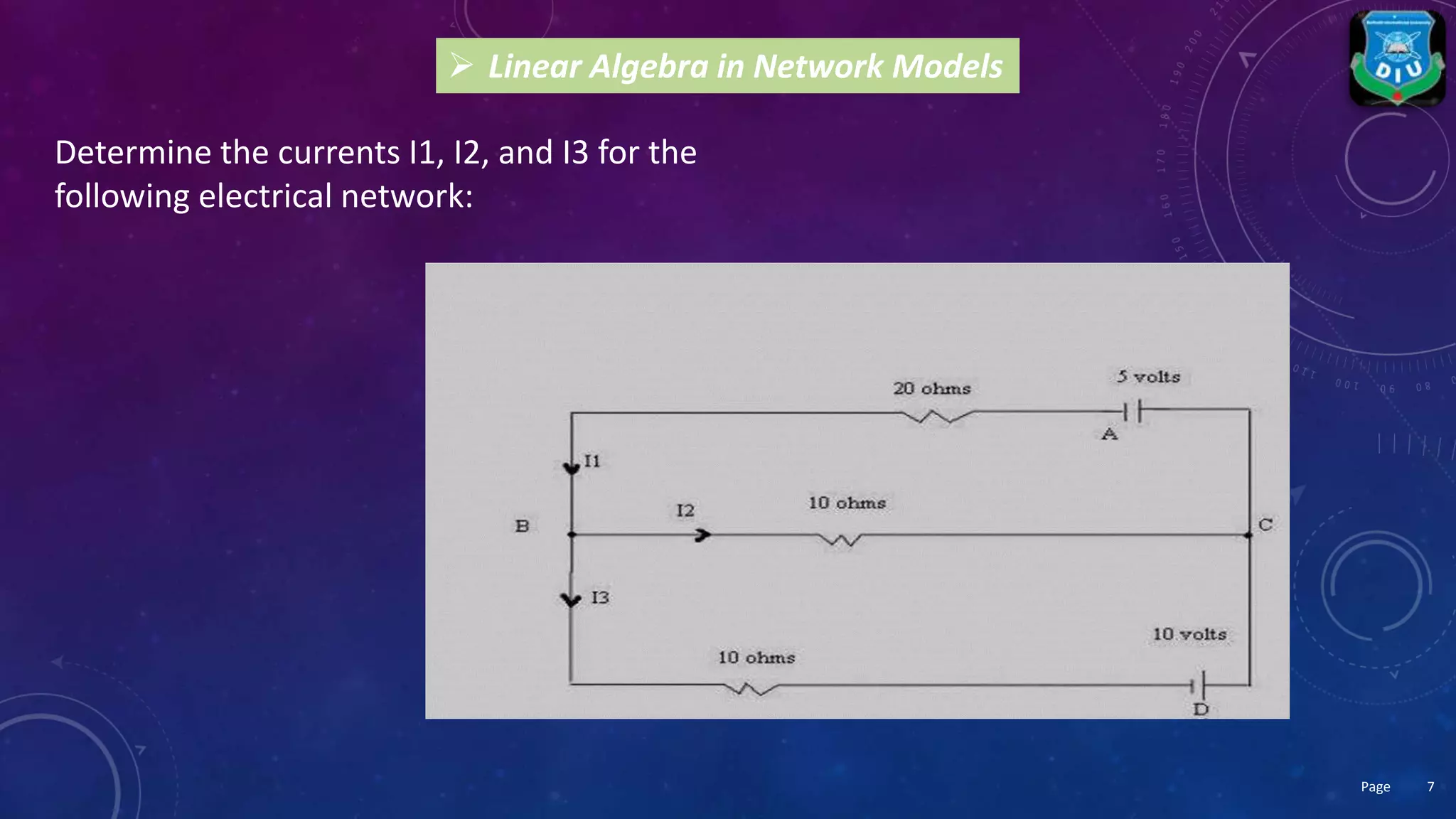
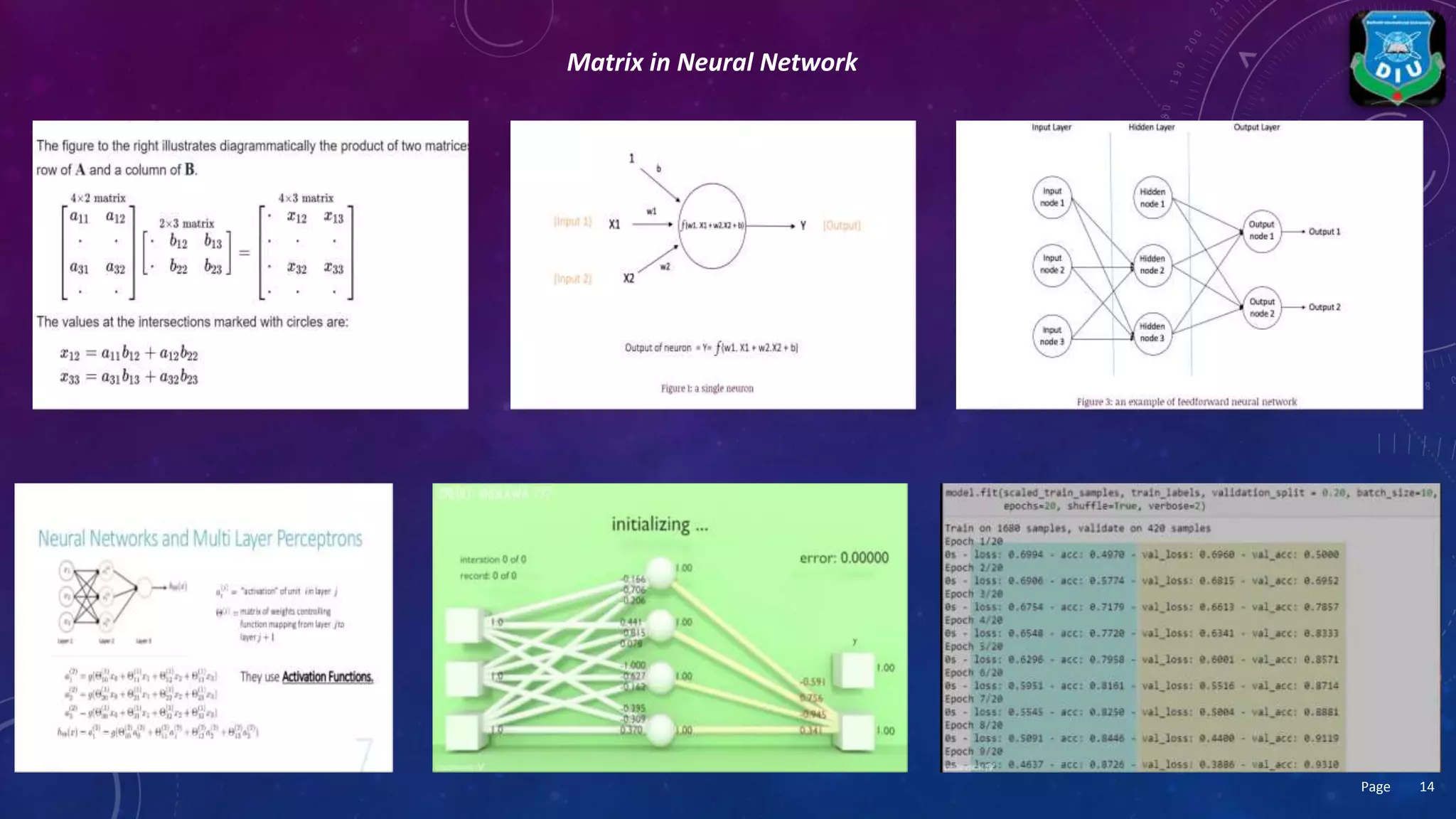
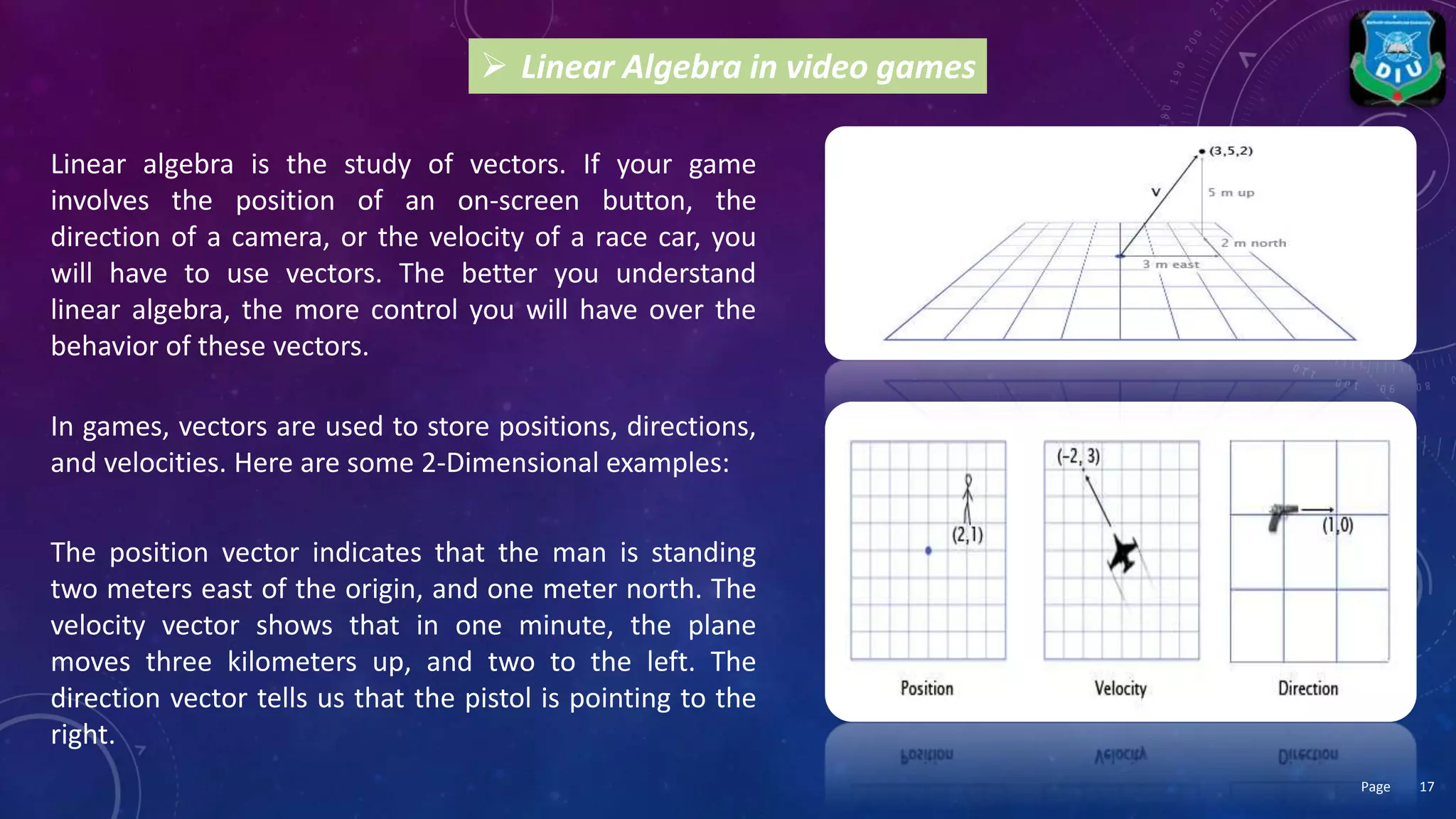
This presentation discusses the importance and applications of linear algebra in computer science. It is introduced as being vital in areas like digital photos, video games, movies and web searches. Specific uses are described, including for spatial quantities in computer graphics and statistics, network models, cryptography, computer vision, machine learning, audio/video compression, signal processing, computer graphics, and video games. It concludes that linear algebra is the foundation of computer coding schemes and encapsulated in programming languages.