Association rule mining

Lecture-27Lecture-27
Association rule miningAssociation rule mining

What Is Association Mining?What Is Association Mining?
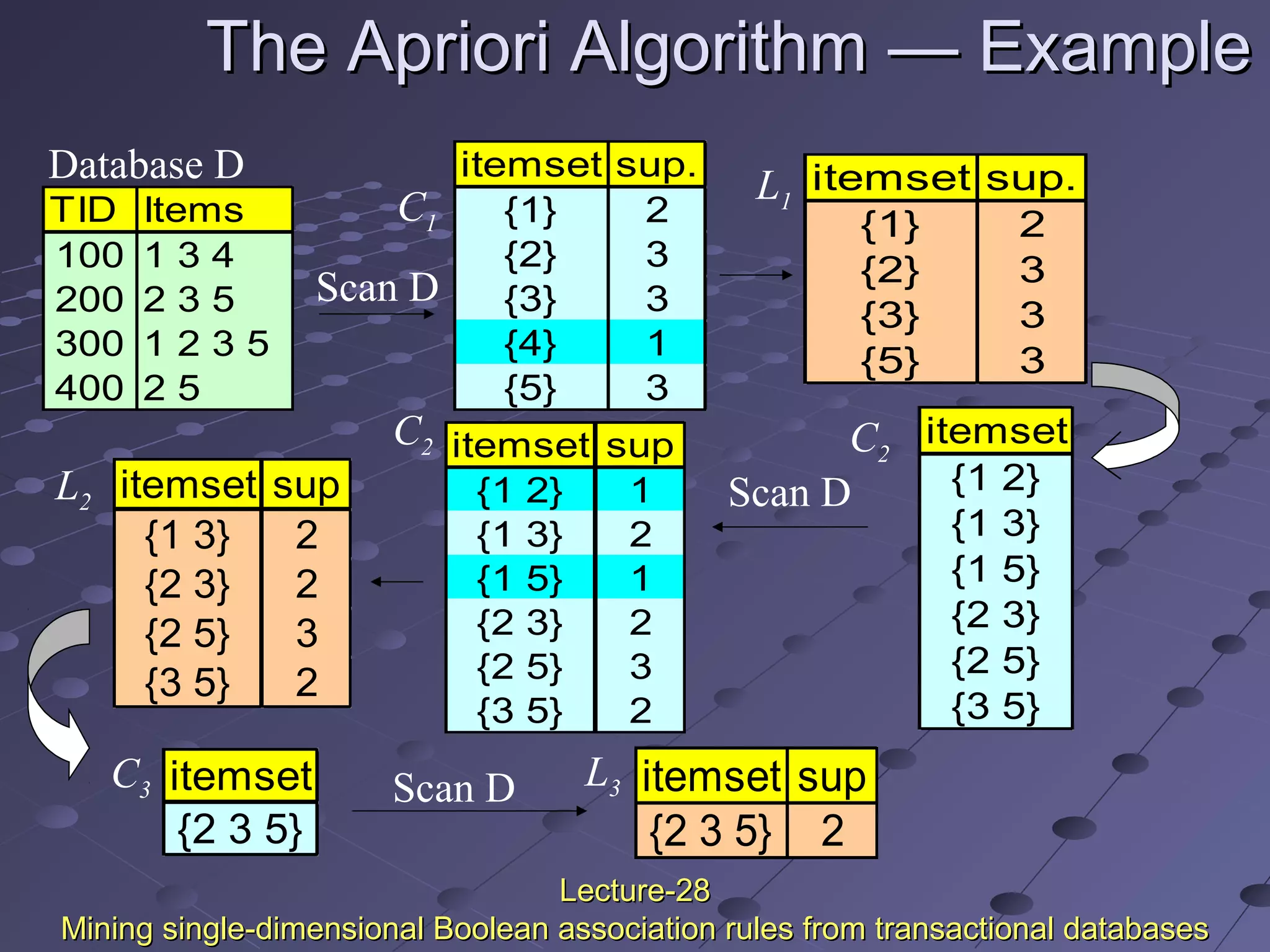
Association rule miningAssociation rule mining
 Finding frequent patterns, associations, correlations, orFinding frequent patterns, associations, correlations, or
causal structures among sets of items or objects incausal structures among sets of items or objects in
transaction databases, relational databases, and othertransaction databases, relational databases, and other
information repositories.information repositories.
ApplicationsApplications
 Basket data analysis, cross-marketing, catalog design,Basket data analysis, cross-marketing, catalog design,
loss-leader analysis, clustering, classification, etc.loss-leader analysis, clustering, classification, etc.
Lecture-27 - Association rule miningLecture-27 - Association rule mining

Association MiningAssociation Mining
Rule formRule form
prediction (Boolean variables)prediction (Boolean variables) =>=>
prediction (Boolean variables) [support,prediction (Boolean variables) [support,
confidence]confidence]
 Computer => antivirus_software [supportComputer => antivirus_software [support
=2%, confidence = 60%]=2%, confidence = 60%]
 buys (x, “computer”)buys (x, “computer”) →→ buys (x,buys (x,
“antivirus_software”) [0.5%, 60%]“antivirus_software”) [0.5%, 60%]

Association Rule: Basic ConceptsAssociation Rule: Basic Concepts
Given a database of transactions each transactionGiven a database of transactions each transaction
is a list of items (purchased by a customer in ais a list of items (purchased by a customer in a
visit)visit)
Find all rules that correlate the presence of oneFind all rules that correlate the presence of one
set of items with that of another set of itemsset of items with that of another set of items
Find frequent patternsFind frequent patterns
Example for frequent itemset mining is marketExample for frequent itemset mining is market
basket analysis.basket analysis.

Association rule performanceAssociation rule performance
measuresmeasures
ConfidenceConfidence
SupportSupport
Minimum support thresholdMinimum support threshold
Minimum confidence thresholdMinimum confidence threshold

Rule Measures: Support andRule Measures: Support and
ConfidenceConfidence
Find all the rulesFind all the rules X & YX & Y ⇒⇒ ZZ with minimumwith minimum
confidence and supportconfidence and support

support,support, ss, probability that a transaction, probability that a transaction
contains {Xcontains {X  YY  Z}Z}

confidence,confidence, c,c, conditional probabilityconditional probability
that a transaction having {Xthat a transaction having {X  Y} alsoY} also
containscontains ZZ
Transaction ID Items Bought
2000 A,B,C
1000 A,C
4000 A,D
5000 B,E,F
Let minimum support 50%, andLet minimum support 50%, and
minimum confidence 50%, we haveminimum confidence 50%, we have

AA ⇒⇒ C (50%, 66.6%)C (50%, 66.6%)

CC ⇒⇒ A (50%, 100%)A (50%, 100%)
Customer
buys diaper
Customer
buys both
Customer
buys beer

Martket Basket AnalysisMartket Basket Analysis
Shopping basketsShopping baskets
Each item has a Boolean variable representingEach item has a Boolean variable representing
the presence or absence of that item.the presence or absence of that item.
Each basket can be represented by a BooleanEach basket can be represented by a Boolean
vector of values assigned to these variables.vector of values assigned to these variables.
Identify patterns from Boolean vectorIdentify patterns from Boolean vector
Patterns can be represented by associationPatterns can be represented by association
rules.rules.

Association Rule Mining: A Road MapAssociation Rule Mining: A Road Map
Boolean vs. quantitative associationsBoolean vs. quantitative associations
- Based on the types of values handled- Based on the types of values handled
 buys(x, “SQLServer”) ^ buys(x, “DMBook”)buys(x, “SQLServer”) ^ buys(x, “DMBook”) =>=> buys(x,buys(x,
“DBMiner”) [0.2%, 60%]“DBMiner”) [0.2%, 60%]
 age(x, “30..39”) ^ income(x, “42..48K”)age(x, “30..39”) ^ income(x, “42..48K”) =>=> buys(x, “PC”)buys(x, “PC”)
[1%, 75%][1%, 75%]
Single dimension vs. multiple dimensionalSingle dimension vs. multiple dimensional
associationsassociations
Single level vs. multiple-level analysisSingle level vs. multiple-level analysis

Mining single-dimensionalMining single-dimensional
Boolean association rules fromBoolean association rules from
transactional databasestransactional databases

Apriori AlgorithmApriori Algorithm
Single dimensional, single-level, BooleanSingle dimensional, single-level, Boolean
frequent item setsfrequent item sets
Finding frequent item sets using candidateFinding frequent item sets using candidate
generationgeneration
Generating association rules fromGenerating association rules from
frequent item setsfrequent item sets
Mining single-dimensional Boolean association rules from transactional databasesMining single-dimensional Boolean association rules from transactional databases

Mining Association RulesMining Association Rules—An—An ExampleExample
For ruleFor rule AA ⇒⇒ CC::
support = support({support = support({AA CC}) = 50%}) = 50%
confidence = support({confidence = support({AA CC})/support({})/support({AA}) = 66.6%}) = 66.6%
The Apriori principle:The Apriori principle:
Any subset of a frequent itemset must be frequentAny subset of a frequent itemset must be frequent
Transaction ID Items Bought
2000 A,B,C
1000 A,C
4000 A,D
5000 B,E,F
Frequent Itemset Support
{A} 75%
{B} 50%
{C} 50%
{A,C} 50%
Min. support 50%
Min. confidence 50%

Mining Frequent Itemsets: the Key StepMining Frequent Itemsets: the Key Step
Find theFind the frequent itemsetsfrequent itemsets: the sets of items: the sets of items
that have minimum supportthat have minimum support

A subset of a frequent itemset must also be aA subset of a frequent itemset must also be a
frequent itemsetfrequent itemset
i.e., if {i.e., if {ABAB} is} is a frequent itemset, both {a frequent itemset, both {AA} and} and
{{BB} should be a frequent itemset} should be a frequent itemset

Iteratively find frequent itemsets with cardinalityIteratively find frequent itemsets with cardinality
from 1 tofrom 1 to k (k-k (k-itemsetitemset))
Use the frequent itemsets to generateUse the frequent itemsets to generate
association rules.association rules.

The Apriori AlgorithmThe Apriori Algorithm
Join StepJoin Step
 CCkk is generated by joining Lis generated by joining Lk-1k-1with itselfwith itself
Prune StepPrune Step

Any (k-1)-itemset that is not frequent cannot be aAny (k-1)-itemset that is not frequent cannot be a
subset of a frequent k-itemsetsubset of a frequent k-itemset

The Apriori AlgorithmThe Apriori Algorithm
Pseudo-codePseudo-code::
CCkk: Candidate itemset of size k: Candidate itemset of size k
LLkk : frequent itemset of size k: frequent itemset of size k
LL11 = {frequent items};= {frequent items};
forfor ((kk = 1;= 1; LLkk !=!=∅∅;; kk++)++) do begindo begin
CCk+1k+1 = candidates generated from= candidates generated from LLkk;;
for eachfor each transactiontransaction tt in database doin database do
increment the count of all candidates inincrement the count of all candidates in CCk+1k+1
that are contained inthat are contained in tt
LLk+1k+1 = candidates in= candidates in CCk+1k+1 with min_supportwith min_support
endend
returnreturn ∪∪kk LLkk;;

The Apriori AlgorithmThe Apriori Algorithm —— ExampleExample
TID Items
100 1 3 4
200 2 3 5
300 1 2 3 5
400 2 5
Database D itemset sup.
{1} 2
{2} 3
{3} 3
{4} 1
{5} 3
itemset sup.
{1} 2
{2} 3
{3} 3
{5} 3
Scan D
C1
L1
itemset
{1 2}
{1 3}
{1 5}
{2 3}
{2 5}
{3 5}
itemset sup
{1 2} 1
{1 3} 2
{1 5} 1
{2 3} 2
{2 5} 3
{3 5} 2
itemset sup
{1 3} 2
{2 3} 2
{2 5} 3
{3 5} 2
L2
C2 C2
Scan D
C3 L3itemset
{2 3 5}
Scan D itemset sup
{2 3 5} 2

How to Generate Candidates?How to Generate Candidates?
Suppose the items inSuppose the items in LLk-1k-1 are listed in an orderare listed in an order
Step 1: self-joiningStep 1: self-joining LLk-1k-1
insert into Cinsert into Ckk
select p.itemselect p.item11, p.item, p.item22, …, p.item, …, p.itemk-1k-1, q.item, q.itemk-1k-1
from Lfrom Lk-1k-1 p, Lp, Lk-1k-1 qq
where p.itemwhere p.item11=q.item=q.item11, …, p.item, …, p.itemk-2k-2=q.item=q.itemk-2k-2, p.item, p.itemk-1k-1 < q.item< q.itemk-1k-1
Step 2: pruningStep 2: pruning
forallforall itemsets c in Citemsets c in Ckk dodo
forallforall (k-1)-subsets s of c(k-1)-subsets s of c dodo
ifif (s is not in L(s is not in Lk-1k-1)) then deletethen delete cc fromfrom CCkk

How to Count Supports of Candidates?How to Count Supports of Candidates?
Why counting supports of candidates a problem?Why counting supports of candidates a problem?

The total number of candidates can be very hugeThe total number of candidates can be very huge

One transaction may contain many candidatesOne transaction may contain many candidates
MethodMethod

Candidate itemsets are stored in a hash-treeCandidate itemsets are stored in a hash-tree

Leaf node of hash-tree contains a list of itemsetsLeaf node of hash-tree contains a list of itemsets
and countsand counts

Interior node contains a hash tableInterior node contains a hash table

Subset function: finds all the candidates contained inSubset function: finds all the candidates contained in
a transactiona transaction

Example of Generating CandidatesExample of Generating Candidates
LL33=={{abc, abd, acd, ace, bcdabc, abd, acd, ace, bcd}}
Self-joining:Self-joining: LL33*L*L33

abcdabcd fromfrom abcabc andand abdabd

acdeacde fromfrom acdacd andand aceace
Pruning:Pruning:
 acdeacde is removed becauseis removed because adeade is not inis not in LL33
CC44={={abcdabcd}}

Methods to Improve Apriori’s EfficiencyMethods to Improve Apriori’s Efficiency
Hash-based itemset countingHash-based itemset counting

AA kk-itemset whose corresponding hashing bucket count is-itemset whose corresponding hashing bucket count is
below the threshold cannot be frequentbelow the threshold cannot be frequent
Transaction reductionTransaction reduction

A transaction that does not contain any frequent k-itemset isA transaction that does not contain any frequent k-itemset is
useless in subsequent scansuseless in subsequent scans
PartitioningPartitioning

Any itemset that is potentially frequent in DB must be frequentAny itemset that is potentially frequent in DB must be frequent
in at least one of the partitions of DBin at least one of the partitions of DB

Methods to Improve Apriori’s EfficiencyMethods to Improve Apriori’s Efficiency
SamplingSampling

mining on a subset of given data, lower supportmining on a subset of given data, lower support
threshold + a method to determine the completenessthreshold + a method to determine the completeness
Dynamic itemset countingDynamic itemset counting

add new candidate itemsets only when all of theiradd new candidate itemsets only when all of their
subsets are estimated to be frequentsubsets are estimated to be frequent

Mining Frequent Patterns WithoutMining Frequent Patterns Without
Candidate GenerationCandidate Generation
Compress a large database into a compact, Frequent-Compress a large database into a compact, Frequent-
Pattern tree (FP-tree) structurePattern tree (FP-tree) structure

highly condensed, but complete for frequent pattern mininghighly condensed, but complete for frequent pattern mining

avoid costly database scansavoid costly database scans
Develop an efficient, FP-tree-based frequent patternDevelop an efficient, FP-tree-based frequent pattern
mining methodmining method

A divide-and-conquer methodology: decompose mining tasks intoA divide-and-conquer methodology: decompose mining tasks into
smaller onessmaller ones

Avoid candidate generation: sub-database test onlyAvoid candidate generation: sub-database test only

Mining multilevel association rulesMining multilevel association rules
from transactional databasesfrom transactional databases

Mining various kinds of associationMining various kinds of association
rulesrules
Mining Multilevel association rulesMining Multilevel association rules

Concepts at different levelsConcepts at different levels
Mining Multidimensional association rulesMining Multidimensional association rules

More than one dimensionalMore than one dimensional
Mining Quantitative association rulesMining Quantitative association rules

Numeric attributesNumeric attributes
Lecture-29 - Mining multilevel association rules from transactional databasesLecture-29 - Mining multilevel association rules from transactional databases

Multiple-Level Association RulesMultiple-Level Association Rules
Items often form hierarchy.Items often form hierarchy.
Items at the lower level areItems at the lower level are
expected to have lowerexpected to have lower
support.support.
Rules regarding itemsets atRules regarding itemsets at
appropriate levels could beappropriate levels could be
quite useful.quite useful.
Transaction database can beTransaction database can be
encoded based onencoded based on
dimensions and levelsdimensions and levels
We can explore shared multi-We can explore shared multi-
level mininglevel mining
Food
breadmilk
skim
SunsetFraser
2% whitewheat
TID Items
T1 {111, 121, 211, 221}
T2 {111, 211, 222, 323}
T3 {112, 122, 221, 411}
T4 {111, 121}
T5 {111, 122, 211, 221, 413}

Multi-level AssociationMulti-level Association
Uniform Support- the same minimum support forUniform Support- the same minimum support for
all levelsall levels

++ One minimum support threshold. No need toOne minimum support threshold. No need to
examine itemsets containing any item whoseexamine itemsets containing any item whose
ancestors do not have minimum support.ancestors do not have minimum support.

–– Lower level items do not occur as frequently.Lower level items do not occur as frequently.
If support thresholdIf support threshold
too hightoo high ⇒⇒ miss low level associationsmiss low level associations
too lowtoo low ⇒⇒ generate too many high levelgenerate too many high level
associationsassociations

Multi-level AssociationMulti-level Association
Reduced Support- reduced minimumReduced Support- reduced minimum
support at lower levelssupport at lower levels

There are 4 search strategies:There are 4 search strategies:
Level-by-level independentLevel-by-level independent
Level-cross filtering by k-itemsetLevel-cross filtering by k-itemset
Level-cross filtering by single itemLevel-cross filtering by single item
Controlled level-cross filtering by single itemControlled level-cross filtering by single item

Uniform SupportUniform Support
Multi-level mining with uniform supportMulti-level mining with uniform support
Milk
[support = 10%]
2% Milk
[support = 6%]
Skim Milk
[support = 4%]
Level 1
min_sup = 5%
Level 2
min_sup = 5%
Back

Reduced SupportReduced Support
Multi-level mining with reduced supportMulti-level mining with reduced support
2% Milk
[support = 6%]
Skim Milk
[support = 4%]
Level 1
min_sup = 5%
Level 2
min_sup = 3%
Milk
[support = 10%]

Multi-level Association: RedundancyMulti-level Association: Redundancy
FilteringFiltering
Some rules may be redundant due to “ancestor”Some rules may be redundant due to “ancestor”
relationships between items.relationships between items.
ExampleExample

milkmilk ⇒⇒ wheat breadwheat bread [support = 8%, confidence = 70%][support = 8%, confidence = 70%]

2% milk2% milk ⇒⇒ wheat breadwheat bread [support = 2%, confidence = 72%][support = 2%, confidence = 72%]
We say the first rule is an ancestor of the secondWe say the first rule is an ancestor of the second
rule.rule.
A rule is redundant if its support is close to theA rule is redundant if its support is close to the
“expected” value, based on the rule’s ancestor.“expected” value, based on the rule’s ancestor.

Mining multidimensionalMining multidimensional
association rules fromassociation rules from
transactional databases andtransactional databases and
data warehousedata warehouse

Multi-Dimensional AssociationMulti-Dimensional Association
Single-dimensional rulesSingle-dimensional rules
buys(X, “milk”)buys(X, “milk”) ⇒⇒ buys(X, “bread”)buys(X, “bread”)
Multi-dimensional rulesMulti-dimensional rules

Inter-dimension association rules -no repeated predicatesInter-dimension association rules -no repeated predicates
age(X,”19-25”)age(X,”19-25”) ∧∧ occupation(X,“student”)occupation(X,“student”) ⇒⇒
buys(X,“coke”)buys(X,“coke”)

hybrid-dimension association rules -repeated predicateshybrid-dimension association rules -repeated predicates
age(X,”19-25”)age(X,”19-25”) ∧∧ buys(X, “popcorn”)buys(X, “popcorn”) ⇒⇒ buys(X, “coke”)buys(X, “coke”)
Lecture-30 - Mining multidimensional association rules from transactional databases andLecture-30 - Mining multidimensional association rules from transactional databases and

Multi-Dimensional AssociationMulti-Dimensional Association
Categorical AttributesCategorical Attributes

finite number of possible values, no orderingfinite number of possible values, no ordering
among valuesamong values
Quantitative AttributesQuantitative Attributes

numeric, implicit ordering among valuesnumeric, implicit ordering among values

Techniques for Mining MD AssociationsTechniques for Mining MD Associations
Search for frequentSearch for frequent kk-predicate set:-predicate set:

Example:Example: {{ageage, occupation, buys}, occupation, buys} is a 3-predicateis a 3-predicate
set.set.

Techniques can be categorized by howTechniques can be categorized by how ageage areare
treated.treated.
1. Using static discretization of quantitative attributes1. Using static discretization of quantitative attributes

Quantitative attributes are statically discretized byQuantitative attributes are statically discretized by
using predefined concept hierarchies.using predefined concept hierarchies.
2. Quantitative association rules2. Quantitative association rules

Quantitative attributes are dynamically discretizedQuantitative attributes are dynamically discretized
into “bins”based on the distribution of the data.into “bins”based on the distribution of the data.
3. Distance-based association rules3. Distance-based association rules

This is a dynamic discretization process thatThis is a dynamic discretization process that
considers the distance between data points.considers the distance between data points.

Static Discretization of Quantitative AttributesStatic Discretization of Quantitative Attributes
Discretized prior to mining using concept hierarchy.Discretized prior to mining using concept hierarchy.
Numeric values are replaced by ranges.Numeric values are replaced by ranges.
In relational database, finding all frequent k-predicate setsIn relational database, finding all frequent k-predicate sets
will requirewill require kk oror kk+1 table scans.+1 table scans.
Data cube is well suited for mining.Data cube is well suited for mining.
The cells of an n-dimensionalThe cells of an n-dimensional cuboid correspond tocuboid correspond to
the predicate sets.the predicate sets.
Mining from data cubescan be much faster.Mining from data cubescan be much faster.
(income)(age)
()
(buys)
(age, income) (age,buys) (income,buys)
(age,income,buys)Lecture-30 - Mining multidimensional association rules from transactional databases andLecture-30 - Mining multidimensional association rules from transactional databases and

Quantitative Association RulesQuantitative Association Rules
age(X,”30-34”) ∧ income(X,”24K -
48K”)
⇒ buys(X,”high resolution TV”)
Numeric attributes areNumeric attributes are dynamicallydynamically discretizeddiscretized

Such that the confidence or compactness of the rulesSuch that the confidence or compactness of the rules
mined is maximized.mined is maximized.
2-D quantitative association rules: A2-D quantitative association rules: Aquan1quan1 ∧∧ AAquan2quan2
⇒⇒ AAcatcat
Cluster “adjacent”Cluster “adjacent”
association rulesassociation rules
to form generalto form general
rules using a 2-Drules using a 2-D
grid.grid.
Example:Example:
Lecture-30 - Mining multidimensional association rules from transactional databases and data warehouseLecture-30 - Mining multidimensional association rules from transactional databases and data warehouse

From association mining toFrom association mining to
correlation analysiscorrelation analysis

Interestingness MeasurementsInterestingness Measurements
Objective measuresObjective measures

Two popular measurementsTwo popular measurements
supportsupport
confidenceconfidence
Subjective measuresSubjective measures
A rule (pattern) is interesting ifA rule (pattern) is interesting if
*it is*it is unexpectedunexpected (surprising to the user); and/or(surprising to the user); and/or
*actionable*actionable (the user can do something with it)(the user can do something with it)
Lecture-31 - From association mining to correlation analysisLecture-31 - From association mining to correlation analysis

Criticism to Support and ConfidenceCriticism to Support and Confidence
ExampleExample

Among 5000 studentsAmong 5000 students
3000 play basketball3000 play basketball
3750 eat cereal3750 eat cereal
2000 both play basket ball and eat cereal2000 both play basket ball and eat cereal

play basketballplay basketball ⇒⇒ eat cerealeat cereal [40%, 66.7%] is misleading[40%, 66.7%] is misleading
because the overall percentage of students eating cereal is 75%because the overall percentage of students eating cereal is 75%
which is higher than 66.7%.which is higher than 66.7%.

play basketballplay basketball ⇒⇒ not eat cerealnot eat cereal [20%, 33.3%] is far more[20%, 33.3%] is far more
accurate, although with lower support and confidenceaccurate, although with lower support and confidence
basketball not basketball sum(row)
cereal 2000 1750 3750
not cereal 1000 250 1250
sum(col.) 3000 2000 5000

Criticism to Support and ConfidenceCriticism to Support and Confidence
ExampleExample

X and Y: positively correlated,X and Y: positively correlated,

X and Z, negatively relatedX and Z, negatively related

support and confidence ofsupport and confidence of
X=>Z dominatesX=>Z dominates
We need a measure of dependent orWe need a measure of dependent or
correlated eventscorrelated events
P(B|A)/P(B) is also called the lift of ruleP(B|A)/P(B) is also called the lift of rule
A => BA => B
X 1 1 1 1 0 0 0 0
Y 1 1 0 0 0 0 0 0
Z 0 1 1 1 1 1 1 1
Rule Support Confidence
X=>Y 25% 50%
X=>Z 37.50% 75%
)()(
)(
,
BPAP
BAP
corr BA
∪
=

Other Interestingness Measures: InterestOther Interestingness Measures: Interest
Interest (correlation, lift)Interest (correlation, lift)

taking both P(A) and P(B) in considerationtaking both P(A) and P(B) in consideration

P(A^B)=P(B)*P(A), if A and B are independent eventsP(A^B)=P(B)*P(A), if A and B are independent events

A and B negatively correlated, if the value is less than 1;A and B negatively correlated, if the value is less than 1;
otherwise A and B positively correlatedotherwise A and B positively correlated
)()(
)(
BPAP
BAP ∧
X 1 1 1 1 0 0 0 0
Y 1 1 0 0 0 0 0 0
Z 0 1 1 1 1 1 1 1
Itemset Support Interest
X,Y 25% 2
X,Z 37.50% 0.9
Y,Z 12.50% 0.57

Constraint-based associationConstraint-based association
miningmining

Constraint-Based MiningConstraint-Based Mining
Interactive, exploratory miningInteractive, exploratory mining
kinds of constraintskinds of constraints

Knowledge type constraint- classification, association,Knowledge type constraint- classification, association,
etc.etc.

Data constraint: SQL-like queriesData constraint: SQL-like queries

Dimension/level constraintsDimension/level constraints

Rule constraintRule constraint

Interestingness constraintsInterestingness constraints
Lecture-32 - Constraint-based association miningLecture-32 - Constraint-based association mining

Rule Constraints in Association MiningRule Constraints in Association Mining
Two kind of rule constraints:Two kind of rule constraints:

Rule form constraints: meta-rule guided mining.Rule form constraints: meta-rule guided mining.
P(x, y) ^ Q(x, w)P(x, y) ^ Q(x, w) →→ takes(x, “database systems”).takes(x, “database systems”).

Rule (content) constraint: constraint-based queryRule (content) constraint: constraint-based query
optimization (Ng, et al., SIGMOD’98).optimization (Ng, et al., SIGMOD’98).
sum(LHS) < 100 ^ min(LHS) > 20 ^ count(LHS) > 3 ^ sum(RHS) >sum(LHS) < 100 ^ min(LHS) > 20 ^ count(LHS) > 3 ^ sum(RHS) >
10001000
1-variable vs. 2-variable constraints1-variable vs. 2-variable constraints

1-var: A constraint confining only one side (L/R) of the1-var: A constraint confining only one side (L/R) of the
rule, e.g., as shown above.rule, e.g., as shown above.

2-var: A constraint confining both sides (L and R).2-var: A constraint confining both sides (L and R).
sum(LHS) < min(RHS) ^ max(RHS) < 5* sum(LHS)sum(LHS) < min(RHS) ^ max(RHS) < 5* sum(LHS)

Constrain-Based Association QueryConstrain-Based Association Query
Database: (1)Database: (1) trans (TID, Itemset ),trans (TID, Itemset ), (2)(2) itemInfo (Item, Type, Price)itemInfo (Item, Type, Price)
A constrained asso. query (CAQ) is in the form of {(A constrained asso. query (CAQ) is in the form of {(SS11, S, S22 ))|C|C
},},

where C is a set of constraints on Swhere C is a set of constraints on S11, S, S22 including frequencyincluding frequency
constraintconstraint
A classification of (single-variable) constraints:A classification of (single-variable) constraints:

Class constraint: SClass constraint: S ⊂⊂ A.A. e.g. Se.g. S ⊂⊂ ItemItem

Domain constraint:Domain constraint:
SSθθ v,v, θθ ∈∈ {{ ==,, ≠≠,, <<,, ≤≤,, >>,, ≥≥ }}. e.g. S.Price < 100. e.g. S.Price < 100
vvθθ S,S, θθ isis ∈∈ oror ∉∉. e.g. snacks. e.g. snacks ∉∉ S.TypeS.Type
VVθθ S,S, oror SSθθ V,V, θθ ∈∈ {{ ⊆⊆,, ⊂⊂,, ⊄⊄,, ==,, ≠≠ }}

e.g.e.g. {{snacks, sodassnacks, sodas }} ⊆⊆ S.TypeS.Type

Aggregation constraint:Aggregation constraint: agg(S)agg(S) θθ v,v, wherewhere aggagg is in {is in {min,min,
max, sum, count, avgmax, sum, count, avg}, and}, and θθ ∈∈ {{ ==,, ≠≠,, <<,, ≤≤,, >>,, ≥≥ }.}.
e.g. count(Se.g. count(S11.Type).Type) == 1 , avg(S1 , avg(S22.Price).Price) << 100100

Constrained Association Query OptimizationConstrained Association Query Optimization
ProblemProblem
Given a CAQGiven a CAQ == { ({ (SS11, S, S22)) | C| C }, the algorithm should be :}, the algorithm should be :

sound: It only finds frequent sets that satisfy the givensound: It only finds frequent sets that satisfy the given
constraints Cconstraints C

complete: All frequent sets satisfy the givencomplete: All frequent sets satisfy the given
constraints C are foundconstraints C are found
A naïve solution:A naïve solution:

Apply Apriori for finding all frequent sets, and then toApply Apriori for finding all frequent sets, and then to
test them for constraint satisfaction one by one.test them for constraint satisfaction one by one.
Our approach:Our approach:

Comprehensive analysis of the properties ofComprehensive analysis of the properties of
constraints and try to push them as deeply asconstraints and try to push them as deeply as
possible inside the frequent set computation.possible inside the frequent set computation.

Anti-monotone and Monotone ConstraintsAnti-monotone and Monotone Constraints
A constraint CA constraint Caa is anti-monotone iff. for anyis anti-monotone iff. for any
pattern S not satisfying Cpattern S not satisfying Caa, none of the, none of the
super-patterns of S can satisfy Csuper-patterns of S can satisfy Caa
A constraint CA constraint Cmm is monotone iff. for anyis monotone iff. for any
pattern S satisfying Cpattern S satisfying Cmm, every super-, every super-
pattern of S also satisfies itpattern of S also satisfies it

Succinct ConstraintSuccinct Constraint
A subset of item IA subset of item Iss is a succinct set, if it can beis a succinct set, if it can be
expressed asexpressed as σσpp(I) for some selection predicate(I) for some selection predicate
p, wherep, where σσ is a selection operatoris a selection operator
SPSP⊆⊆22II
is a succinct power set, if there is a fixedis a succinct power set, if there is a fixed
number of succinct set Inumber of succinct set I11, …, I, …, Ikk ⊆⊆I, s.t. SP can beI, s.t. SP can be
expressed in terms of the strict power sets of Iexpressed in terms of the strict power sets of I11,,
…, I…, Ikk using union and minususing union and minus
A constraint CA constraint Css is succinct provided SATis succinct provided SATCsCs(I) is a(I) is a
succinct power setsuccinct power set

Convertible ConstraintConvertible Constraint
Suppose all items in patterns are listed in a totalSuppose all items in patterns are listed in a total
order Rorder R
A constraint C is convertible anti-monotone iff aA constraint C is convertible anti-monotone iff a
pattern S satisfying the constraint implies thatpattern S satisfying the constraint implies that
each suffix of S w.r.t. R also satisfies Ceach suffix of S w.r.t. R also satisfies C
A constraint C is convertible monotone iff aA constraint C is convertible monotone iff a
pattern S satisfying the constraint implies thatpattern S satisfying the constraint implies that
each pattern of which S is a suffix w.r.t. R alsoeach pattern of which S is a suffix w.r.t. R also
satisfies Csatisfies C

Relationships AmongRelationships Among
Categories of ConstraintsCategories of Constraints
Succinctness
Anti-monotonicity Monotonicity
Convertible constraints
Inconvertible constraints

Property of Constraints: Anti-MonotoneProperty of Constraints: Anti-Monotone
Anti-monotonicity:Anti-monotonicity: If a set S violates theIf a set S violates the
constraint, any superset of S violates theconstraint, any superset of S violates the
constraint.constraint.
Examples:Examples:

sum(S.Price)sum(S.Price) ≤≤ vv is anti-monotoneis anti-monotone

sum(S.Price)sum(S.Price) ≥≥ vv is not anti-monotoneis not anti-monotone

sum(S.Price)sum(S.Price) == vv is partly anti-monotoneis partly anti-monotone
Application:Application:

Push “Push “sum(S.price)sum(S.price) ≤≤ 1000” deeply into iterative1000” deeply into iterative
frequent set computation.frequent set computation.

Characterization ofCharacterization of
Anti-Monotonicity ConstraintsAnti-Monotonicity Constraints
S θ v, θ ∈ { =, ≤, ≥ }
v ∈ S
S ⊇ V
S ⊆ V
S = V
min(S) ≤ v
min(S) ≥ v
min(S) = v
max(S) ≤ v
max(S) ≥ v
max(S) = v
count(S) ≤ v
count(S) ≥ v
count(S) = v
sum(S) ≤ v
sum(S) ≥ v
sum(S) = v
avg(S) θ v, θ ∈ { =, ≤, ≥ }
(frequent constraint)
yes
no
no
yes
partly
no
yes
partly
yes
no
partly
yes
no
partly
yes
no
partly
convertible
(yes)

Example of Convertible Constraints: Avg(S)Example of Convertible Constraints: Avg(S) θθ VV
Let R be the value descending order overLet R be the value descending order over
the set of itemsthe set of items

E.g. I={9, 8, 6, 4, 3, 1}E.g. I={9, 8, 6, 4, 3, 1}
Avg(S)Avg(S) ≥≥ v is convertible monotone w.r.t.v is convertible monotone w.r.t.
RR
 If S is a suffix of SIf S is a suffix of S11, avg(S, avg(S11)) ≥≥ avg(S)avg(S)
{8, 4, 3} is a suffix of {9, 8, 4, 3}{8, 4, 3} is a suffix of {9, 8, 4, 3}
avg({9, 8, 4, 3})=6avg({9, 8, 4, 3})=6 ≥≥ avg({8, 4, 3})=5avg({8, 4, 3})=5
 If S satisfies avg(S)If S satisfies avg(S) ≥≥v, so does Sv, so does S11
{8, 4, 3} satisfies constraint avg(S){8, 4, 3} satisfies constraint avg(S) ≥≥ 4, so does {9,4, so does {9,
8, 4, 3}8, 4, 3}

Property of Constraints: SuccinctnessProperty of Constraints: Succinctness
Succinctness:Succinctness:

For any set SFor any set S11 and Sand S22 satisfying C, Ssatisfying C, S11 ∪∪ SS22 satisfies Csatisfies C

Given AGiven A11 is the sets of size 1 satisfying C, then any setis the sets of size 1 satisfying C, then any set
S satisfying C are based on AS satisfying C are based on A11 , i.e., it contains a subset, i.e., it contains a subset
belongs to Abelongs to A1 ,1 ,
Example :Example :

sum(S.Price )sum(S.Price ) ≥≥ vv is not succinctis not succinct

min(S.Price )min(S.Price ) ≤≤ vv is succinctis succinct
Optimization:Optimization:

If C is succinct, then C is pre-counting prunable. TheIf C is succinct, then C is pre-counting prunable. The
satisfaction of the constraint alone is not affected by thesatisfaction of the constraint alone is not affected by the
iterative support counting.iterative support counting.

Characterization of ConstraintsCharacterization of Constraints
by Succinctnessby Succinctness
S θ v, θ ∈ { =, ≤, ≥ }
v ∈ S
S ⊇V
S ⊆ V
S = V
min(S) ≤ v
min(S) ≥ v
min(S) = v
max(S) ≤ v
max(S) ≥ v
max(S) = v
count(S) ≤ v
count(S) ≥ v
count(S) = v
sum(S) ≤ v
sum(S) ≥ v
sum(S) = v
avg(S) θ v, θ ∈ { =, ≤, ≥ }
(frequent constraint)
Yes
yes
yes
yes
yes
yes
yes
yes
yes
yes
yes
weakly
weakly
weakly
no
no
no
no
(no)

Association rule mining

More Related Content

What's hot

Viewers also liked

Similar to Association rule mining

More from Acad

Recently uploaded

Association rule mining