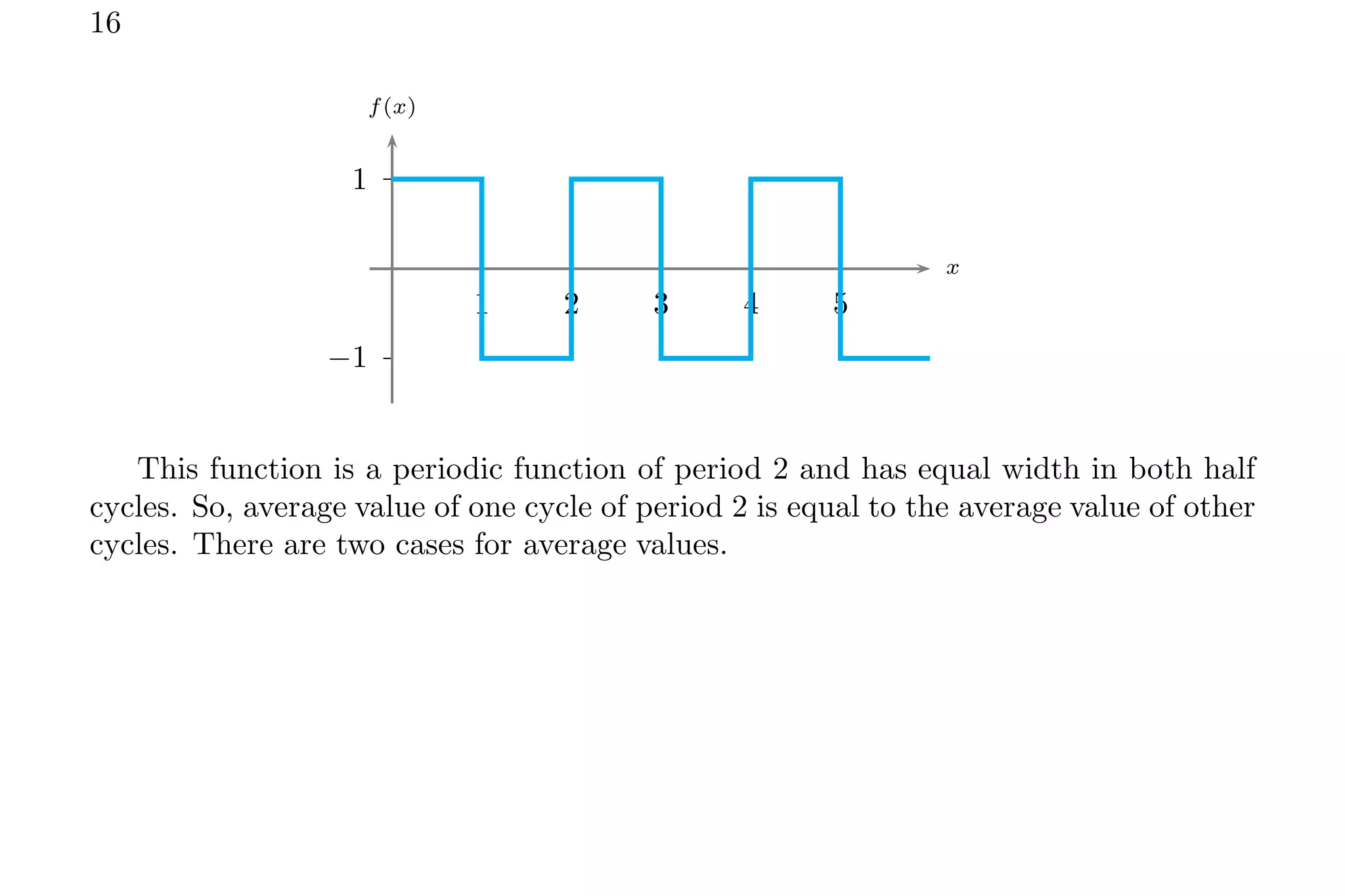
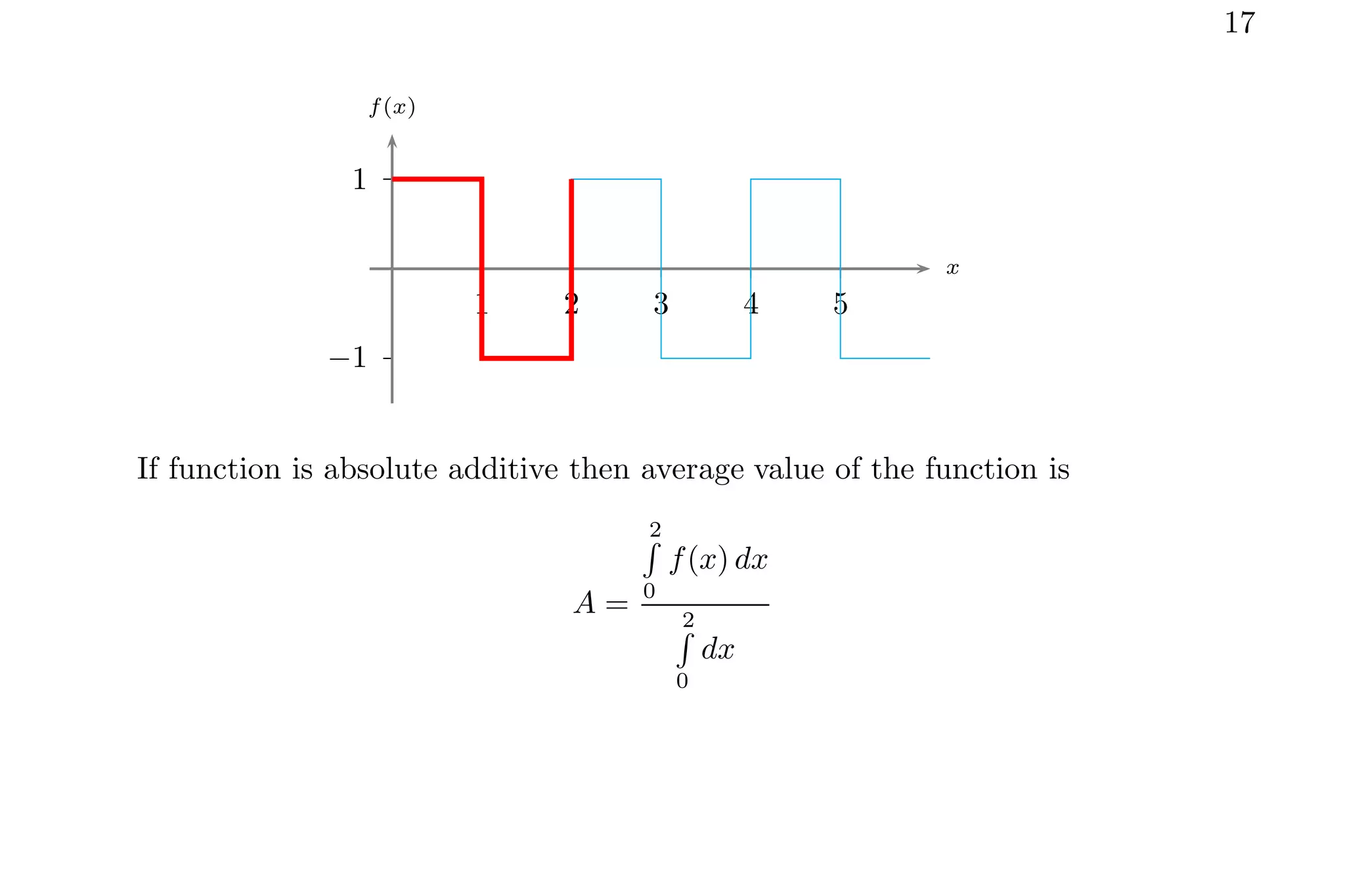
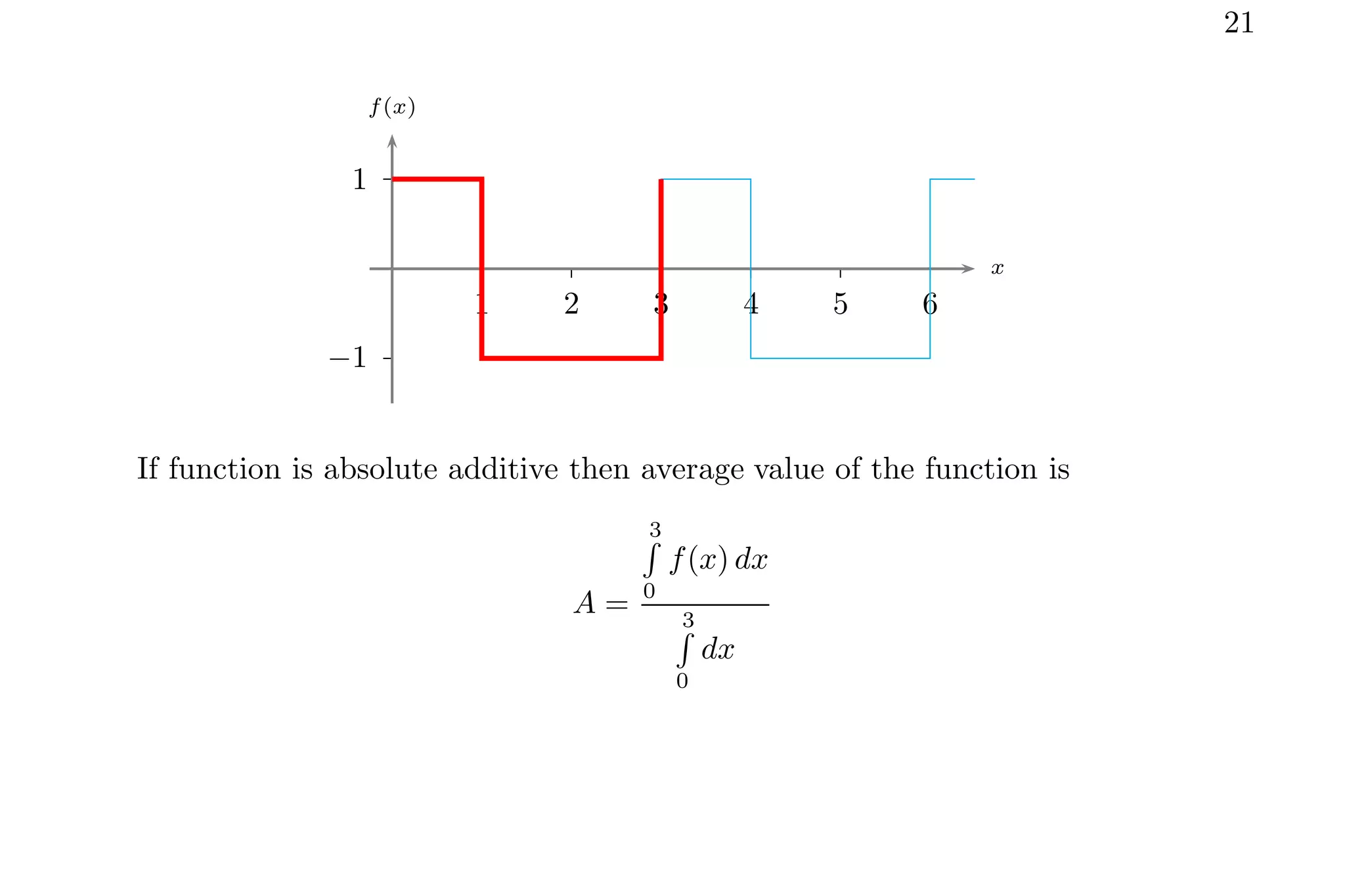
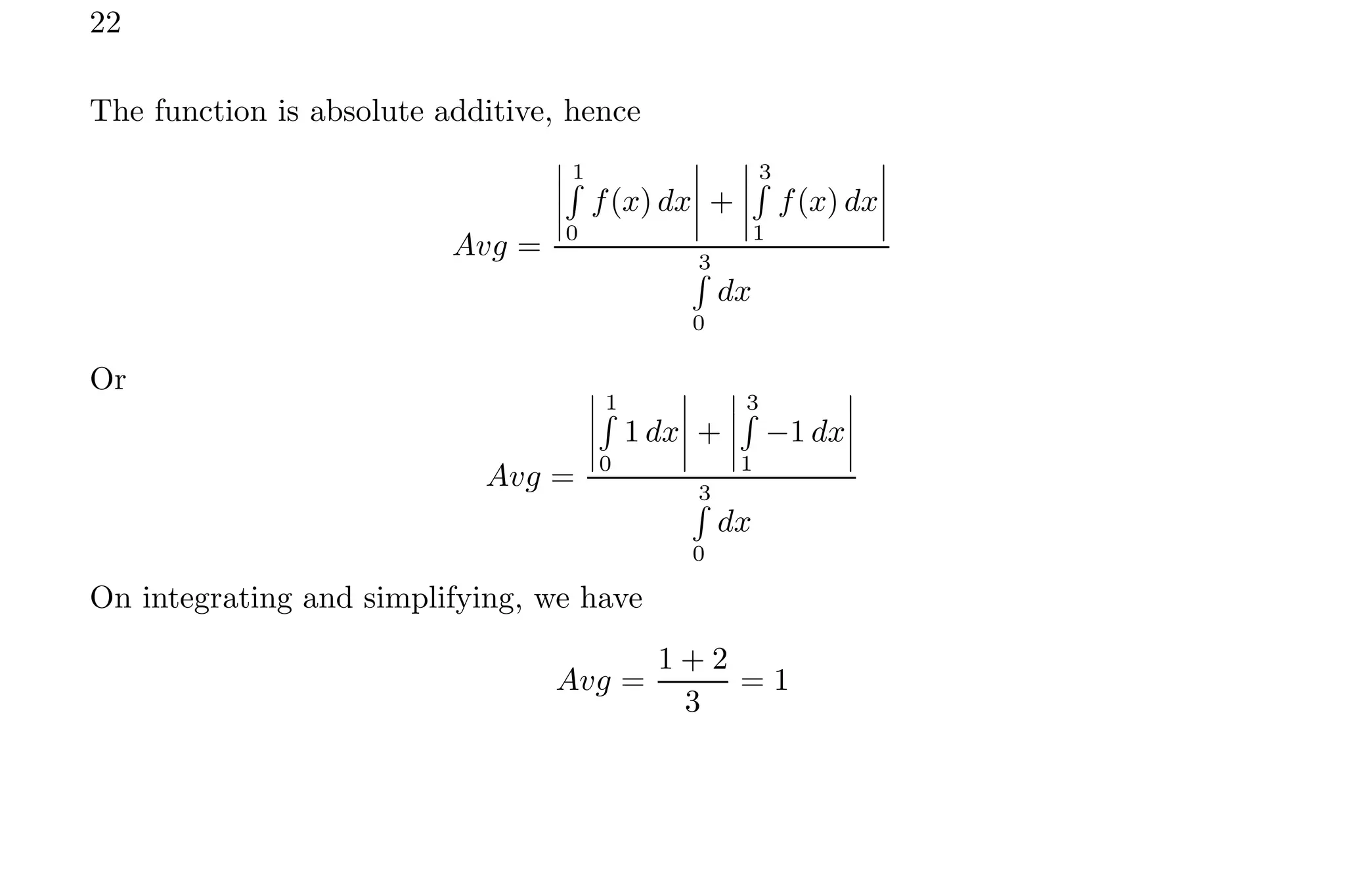
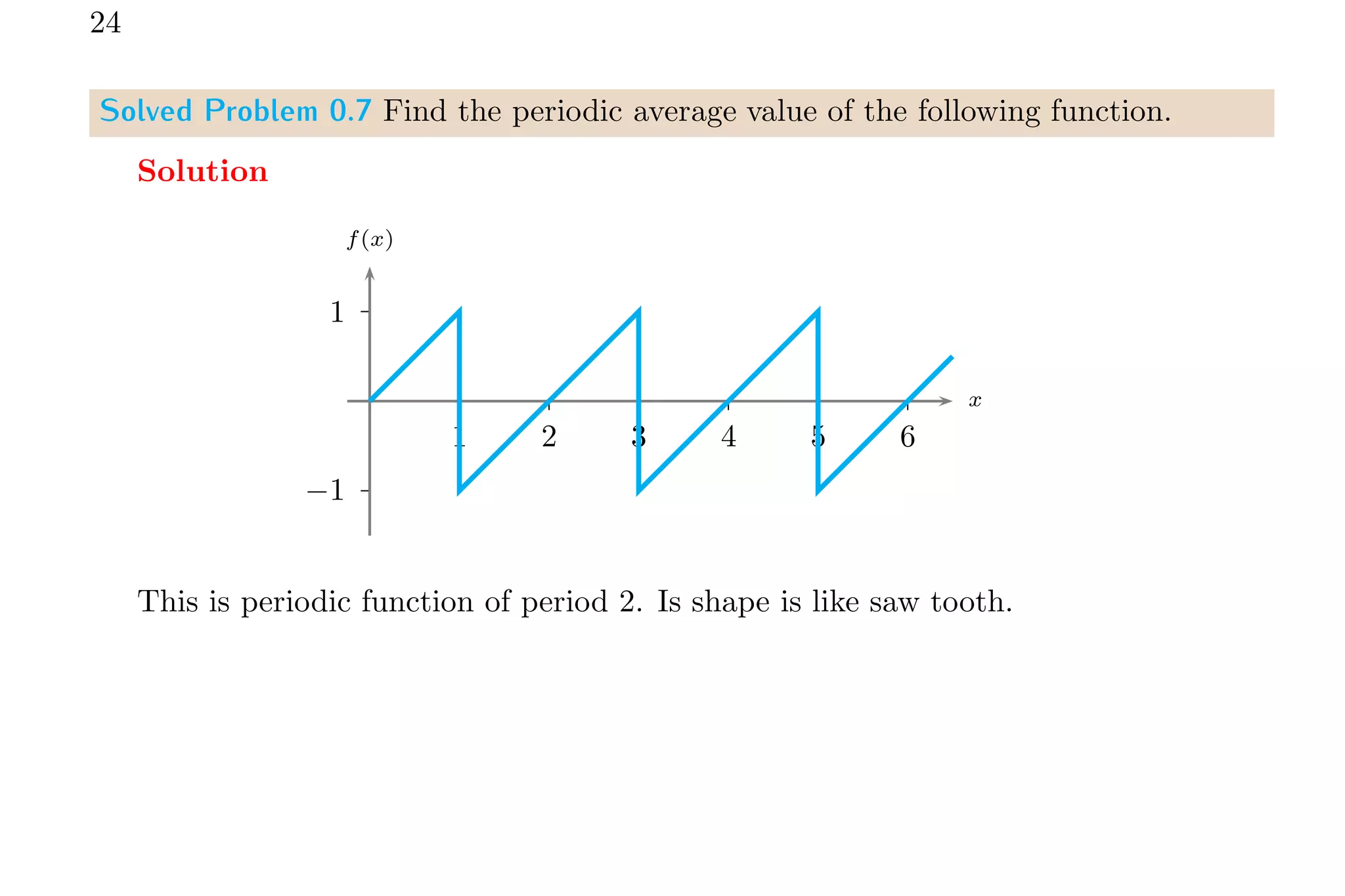
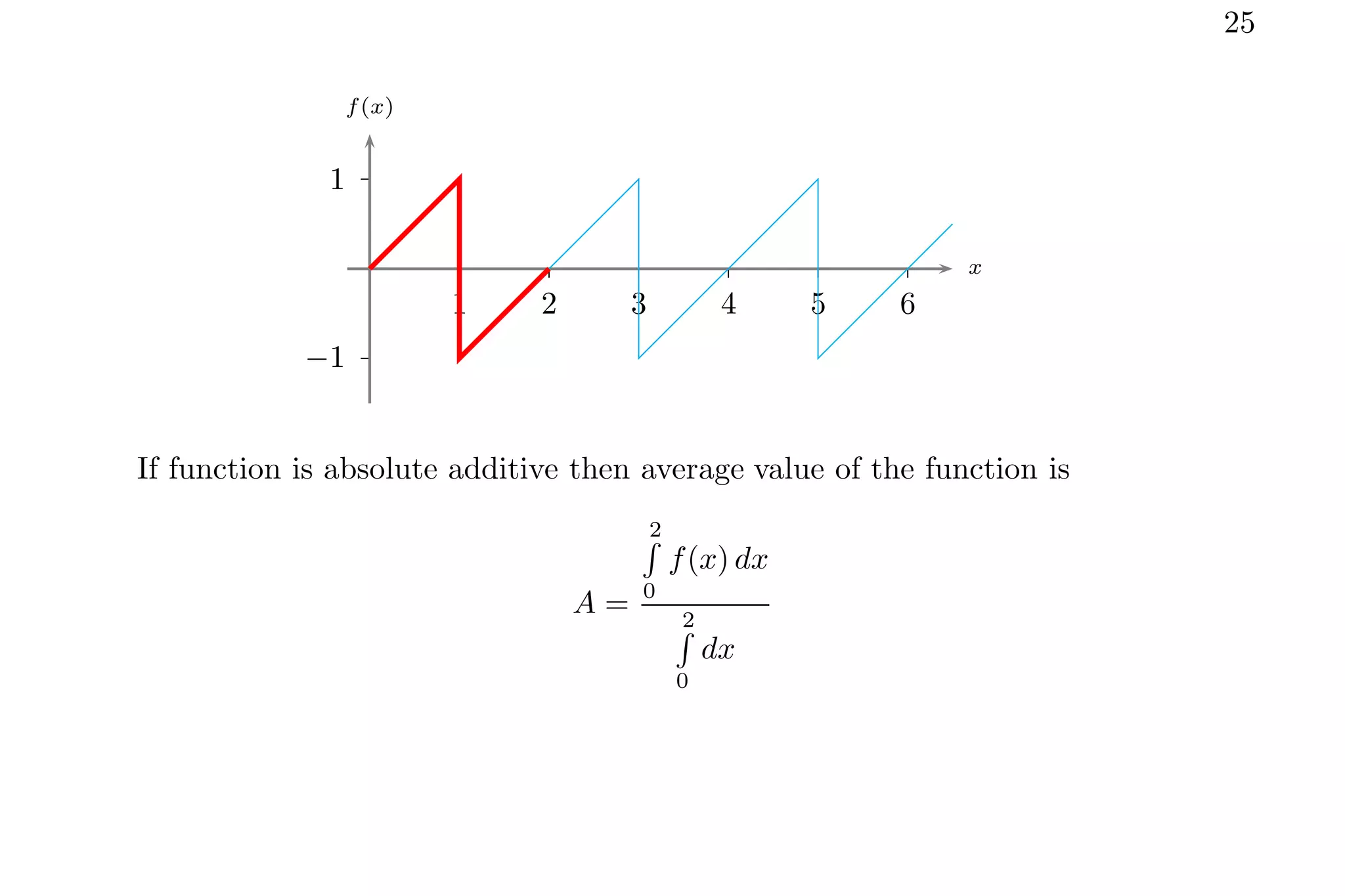
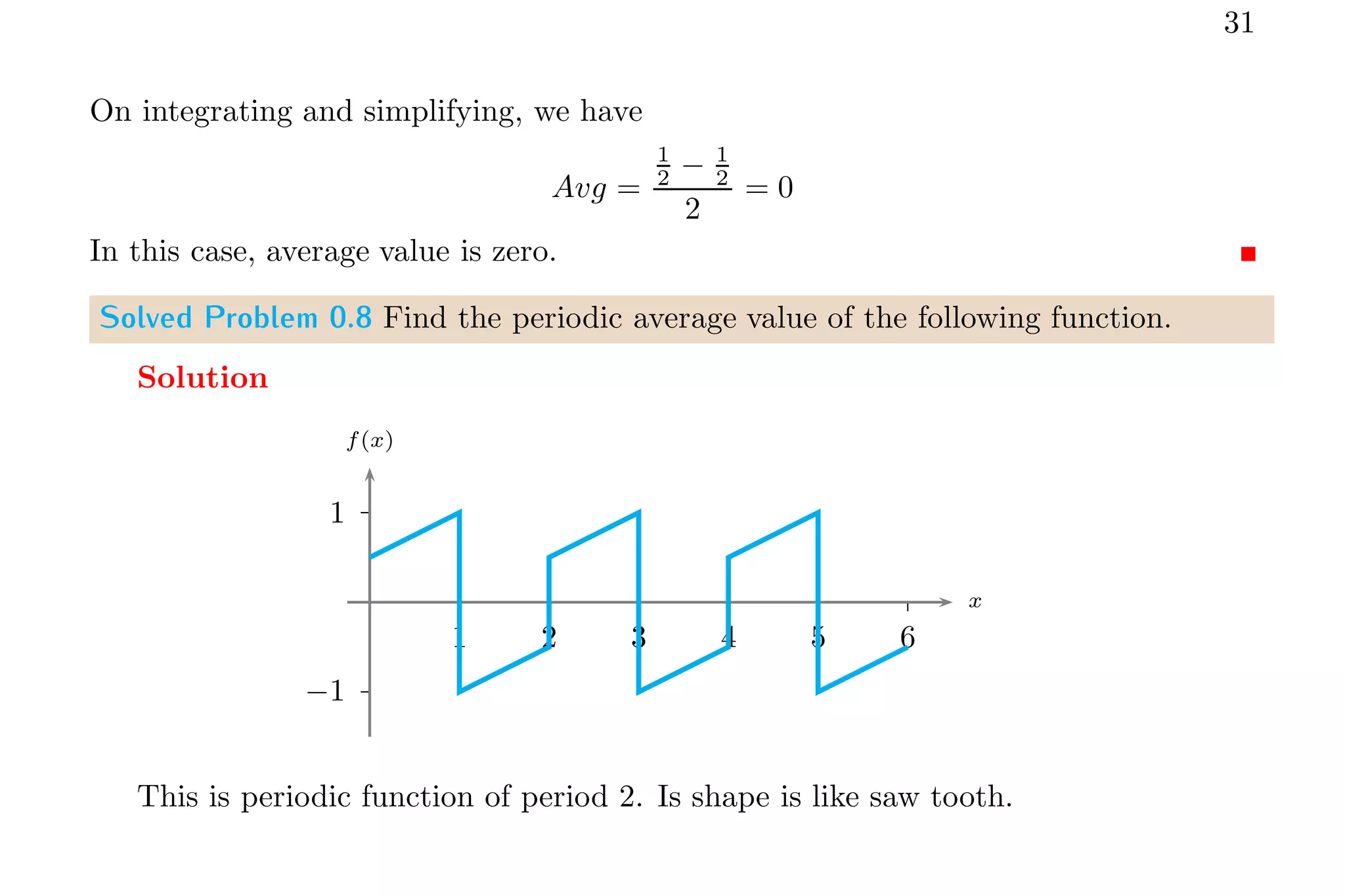
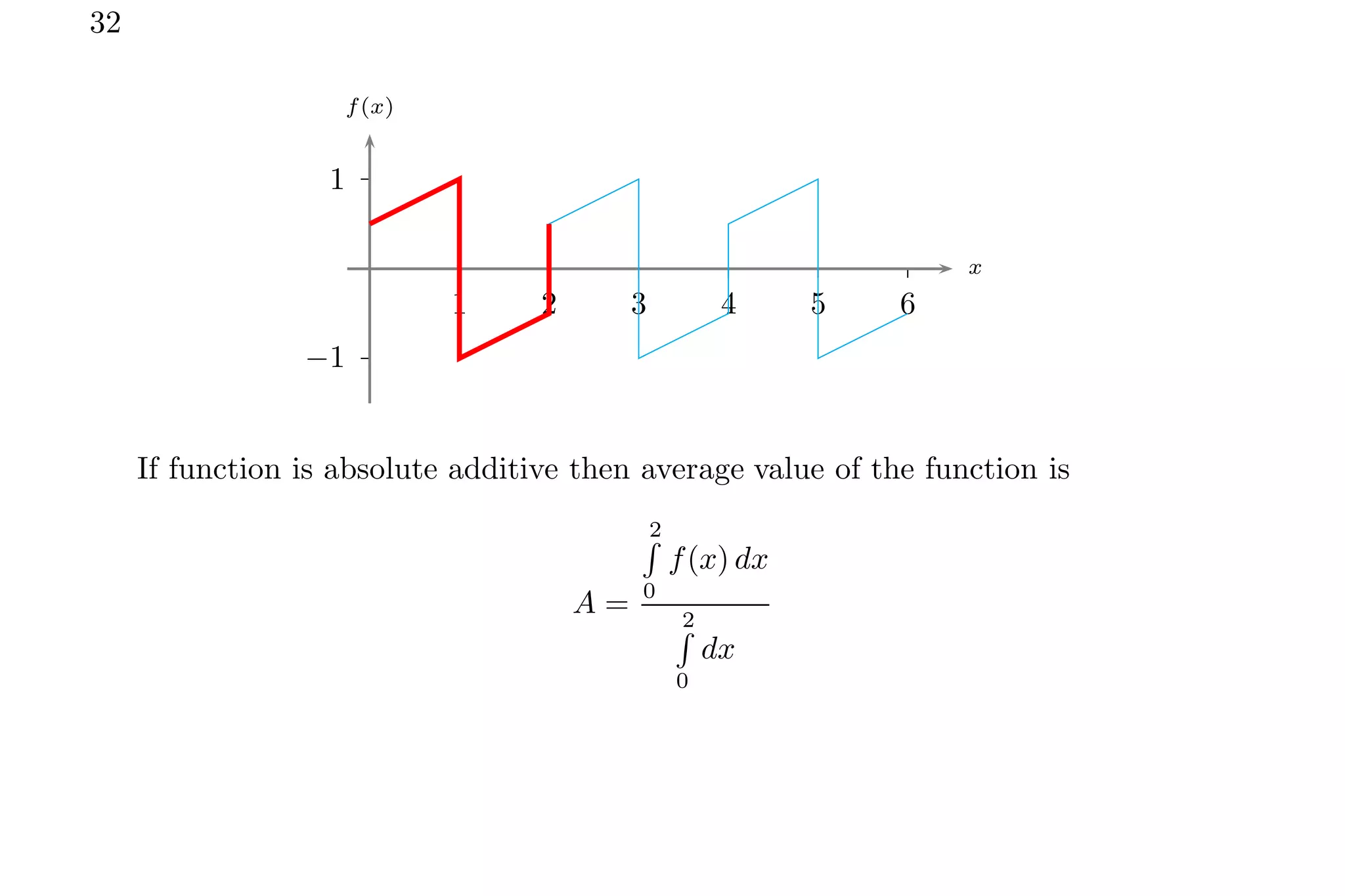
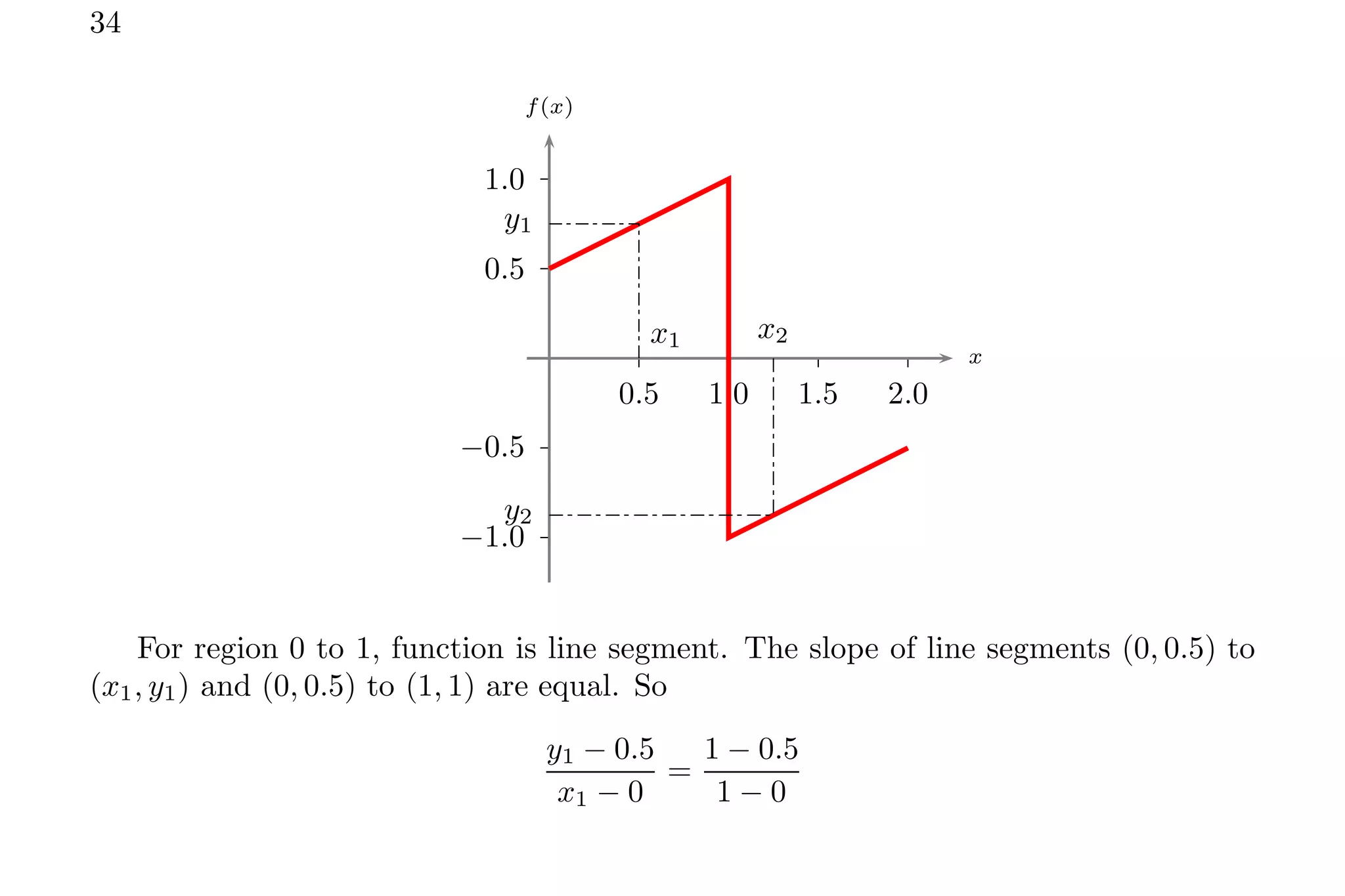
1. The document discusses calculating average values of functions using integral methods. It provides examples of finding average values over different intervals for various functions, including constants, quadratic functions, sine functions, and periodic functions.
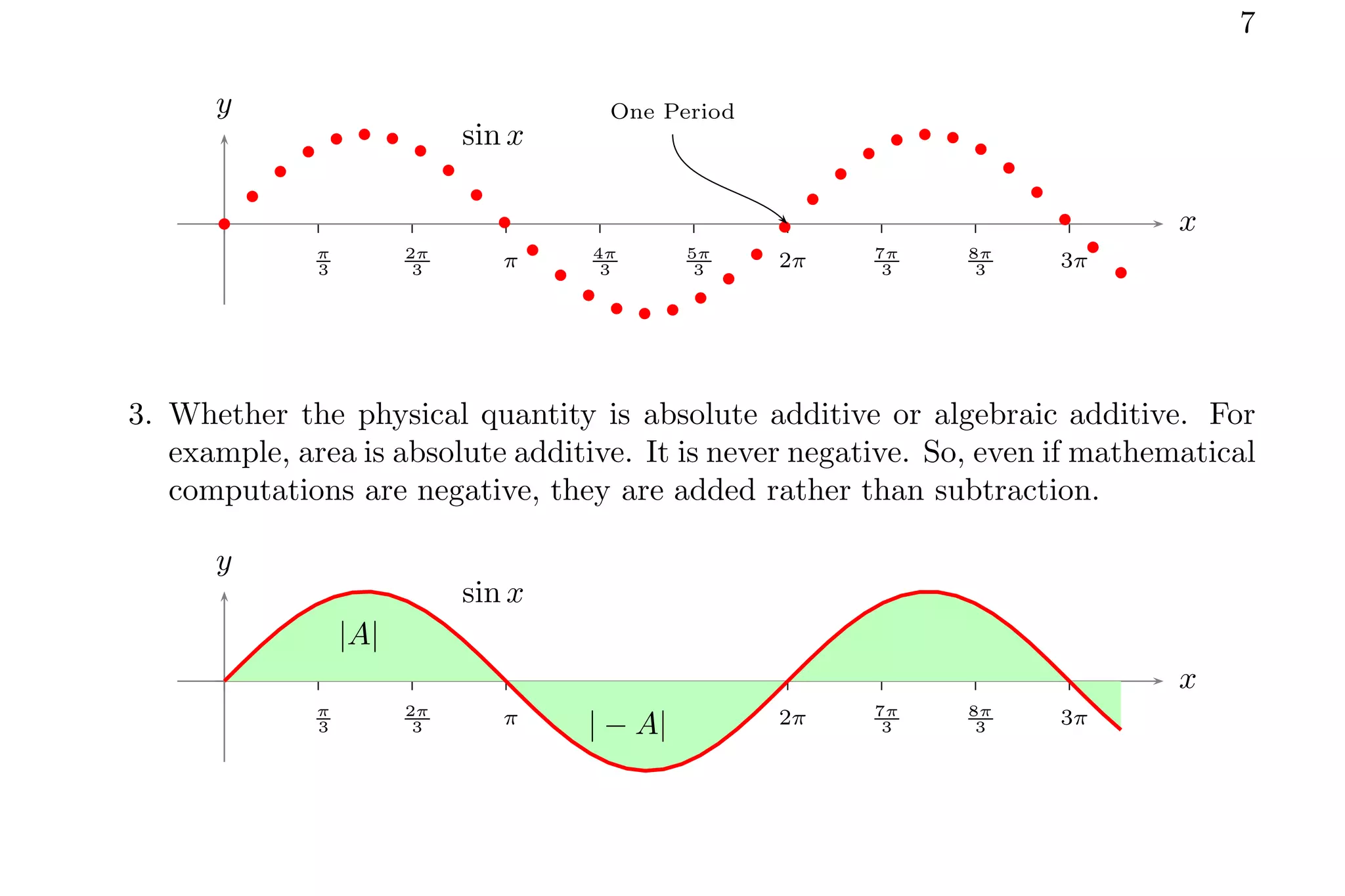
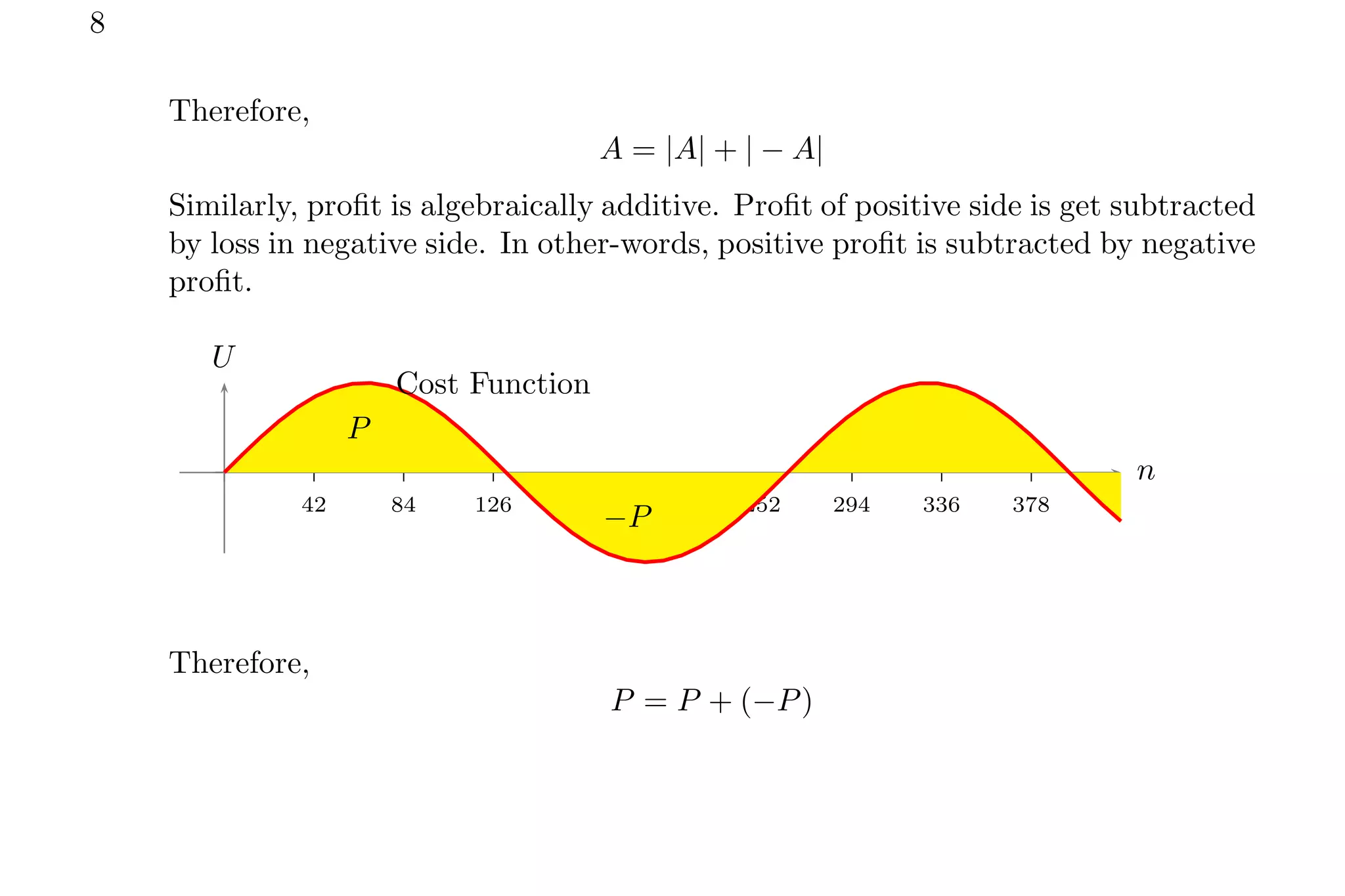
2. Key points covered include handling zero crossings, periodicity, and whether the quantity is absolute or algebraically additive. Piecewise methods and multiplying average values over one period are discussed for periodic functions.
3. Several example problems are worked through step-by-step to demonstrate finding average values over different intervals for various functions using integral relations.






![9
Solved Problem 0.1 Find the average value of constant ‘c’ for the limits ranges from
t = a to t = b.
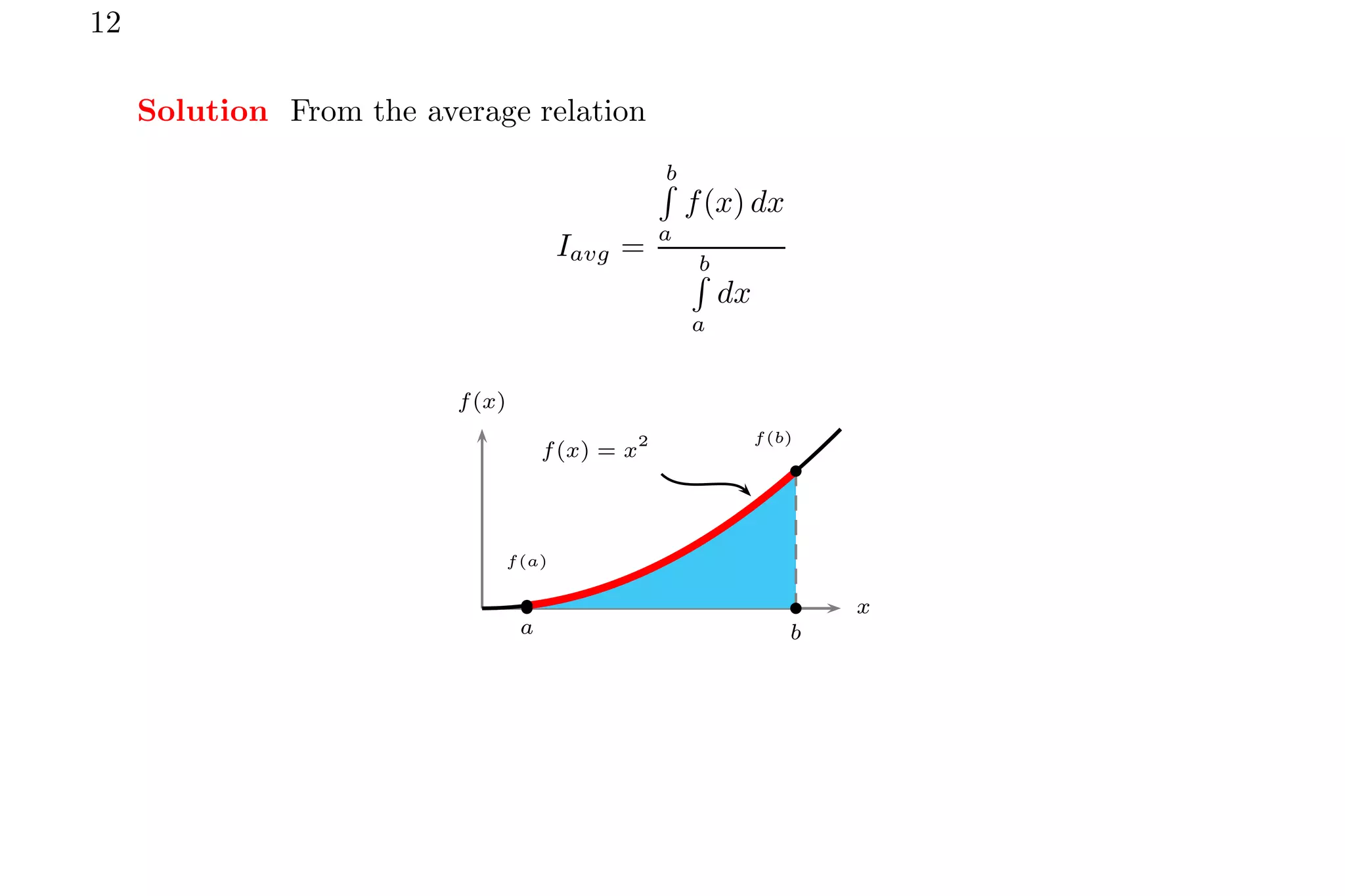
Solution The average value of function f(t) is given by
Iavg =
b
R
a
c dt
b
R
a
dt
t
c b b
c c
b b
a b
Now
Iavg = c
[t]
b
a
[t]
b
a](https://image.slidesharecdn.com/averagevaluebyintegralmethod-220120185415/75/Average-value-by-integral-method-9-2048.jpg)

![11
t
f(t)
b
b
f(a)
f(b)
b b
a b
t line
Now
Iavg =
h
t2
2
ib
a
[t]
b
a
Solving the relation
Iavg =
1
2
(a + b)
This shows that the average values of a line is average of sum of two ends of the line.
Solved Problem 0.3 Find the average value of f(x) = x2
for the x-limits ranges from
x = 2 to x = 3.](https://image.slidesharecdn.com/averagevaluebyintegralmethod-220120185415/75/Average-value-by-integral-method-11-2048.jpg)
![13
Substituting the values and integrating for the limits
Iavg =
3
R
2
x2
dx
3
R
2
dx
Or
Iavg =
h
x3
3
i3
2
[x]
3
2
Or
Iavg =
19
3
This is the required average value.
Solved Problem 0.4 Find the average value of f(x) = sin(x) within the angle limits
in radian values from x = π/3 to 2π/3.](https://image.slidesharecdn.com/averagevaluebyintegralmethod-220120185415/75/Average-value-by-integral-method-13-2048.jpg)
![14
Solution The average of function within the limits is
Iavg =
2π
3
R
π
6
sin(x)dx
2π
3
R
π
6
dx
On integration and solving it
Iavg =
[− cos(x)]
2π
3
π
6
[x]
2π
3
π
6
x
f(x)
b
b
f(π/6)
f(2π/3)
b b
π/6 2π/3
f(x) = sin(x)](https://image.slidesharecdn.com/averagevaluebyintegralmethod-220120185415/75/Average-value-by-integral-method-14-2048.jpg)