Basic data structures in python

Basic Data Structures in Python
March 1, 2018
• Courtesy : http://interactivepython.org/runestone/static/pythonds/BasicDS/toctree.html
1 Pythonds Module
• pythonds module contains implementations of all data structures
• The module can be downloaded from pythonworks.org
1.1 Objectives
- To understand the abstract data types stack, queue, deque, and list.
- To be able to implement the ADTs stack, queue and deque using Python lists.
- To be able to implement the abstract data type list as a linked list using the node and refere
1.2 Applications
- To use stacks to evaluate postfix expressions.
- To use stacks to convert expressions from infix to postfix.
- To use queues for basic timing simulations.
In [3]: # import pythonds
1.3 Stack Abstract Data Type
• An ordered collection of items where items are added to and removed from the end called
the “top.”
• Stacks are ordered LIFO.
•
• The stack operations are given below.
– Stack()
* creates a new stack that is empty.
* It needs no parameters and returns an empty stack.
1

– push(item)
* adds a new item to the top of the stack.
* It needs the item and returns nothing.
– pop()
* removes the top item from the stack.
* It needs no parameters and returns the item.
* The stack is modiﬁed.
– peek()
* returns the top item from the stack but does not remove it.
* It needs no parameters.
* The stack is not modiﬁed.
– isEmpty()
* tests to see whether the stack is empty.
* It needs no parameters and returns a boolean value.
– size()
* returns the number of items on the stack.
* It needs no parameters and returns an integer.
In [6]: # stack.py
class Stack:
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def push(self, item):
self.items.append(item)
def pop(self):
return self.items.pop()
def peek(self):
return self.items[len(self.items)-1]
def size(self):
return len(self.items)
In [23]: # from pythonds.basic.stack import Stack
s = Stack()
print(s.isEmpty())
s.push(4)
s.push('dog')
2

print(s.peek())
s.push(True)
print(s.size())
print(s.isEmpty())
s.push(8.4)
print(s.pop())
print(s.pop())
print(s.size())
True
dog
3
False
8.4
True
2
1.4 Queue as an Abstract Data Type
• An ordered collection of items which are added at one end, called the “rear,” and removed
from the other end, called the “front.”
• Queues maintain a FIFO ordering property.
•
• The queue operations are given below.
– Queue()
* creates a new queue that is empty.
* It needs no parameters and returns an empty queue.
– enqueue(item)
* adds a new item to the rear of the queue.
– dequeue()
* removes the front item from the queue.
* The queue is modiﬁed.
– isEmpty()
* tests to see whether the queue is empty.
– size()
* returns the number of items in the queue.
In [25]: class Queue:
def __init__(self):
3

self.items = []
def isEmpty(self):
def enqueue(self, item):
self.items.insert(0,item)
def dequeue(self):
def size(self):
In [32]: q=Queue()
print("Inserting 3 elements")
q.enqueue(4)
q.enqueue('dog')
q.enqueue(True)
print("Queue Size: %d" % q.size())
print("Queue Empty :", q.isEmpty())
q.enqueue(8.4)
print("Insert one more element")
q.dequeue()
q.dequeue()
print("After dequeue two elements")
print("Queue size :",q.size())
Inserting 3 elements
Queue Size: 3
Queue Empty : False
Insert one more element
After dequeue two elements
Queue size : 2
1.5 Deque as an Abstract Data Type
• A deque, also known as a double-ended queue, is an ordered collection of items similar to
the queue.
• It has two ends, a front and a rear, and the items remain positioned in the collection.
• Items are added and removed from either end, either front or rear.
•
• The deque operations are given below.
– Deque()
4

* creates a new deque that is empty.
* It needs no parameters and returns an empty deque.
– addFront(item)
* adds a new item to the front of the deque.
– addRear(item)
* adds a new item to the rear of the deque.
– removeFront()
* removes the front item from the deque.
* The deque is modiﬁed.
– removeRear()
* removes the rear item from the deque.
* The deque is modiﬁed.
– isEmpty()
* tests to see whether the deque is empty.
– size()
* returns the number of items in the deque.
In [34]: class Deque:
def __init__(self):
self.items = []
def isEmpty(self):
def addFront(self, item):
self.items.append(item)
def addRear(self, item):
self.items.insert(0,item)
def removeFront(self):
def removeRear(self):
return self.items.pop(0)
def size(self):
In [35]: d=Deque()
print(d.isEmpty())
5

d.addRear(4)
d.addRear('dog')
d.addFront('cat')
d.addFront(True)
print(d.size())
print(d.isEmpty())
d.addRear(8.4)
print(d.removeRear())
print(d.removeFront())
True
4
False
8.4
True
1.6 Linked List (Unordered List)
• A collection of items where each item holds a relative position with respect to the others.
• there is no requirement that we maintain that positioning in contiguous memory
•
• Some possible unordered list operations are given below.
– List()
* creates a new list that is empty.
* It needs no parameters and returns an empty list.
– add(item)
* adds a new item to the list.
* Assume the item is not already in the list.
*
– remove(item)
* removes the item from the list.
* It needs the item and modiﬁes the list.
* Assume the item is present in the list.
* Initialization
6

* Loacting Previous & Current node
* Removing
– search(item)
* searches for the item in the list.
* It needs the item and returns a boolean value.
– isEmpty()
* tests to see whether the list is empty.
– size()
* returns the number of items in the list.
– append(item)
* adds a new item to the end of the list making it the last item in the collection.
* Assume the item is not already in the list.
– index(item)
* returns the position of item in the list.
* It needs the item and returns the index.
* Assume the item is in the list.
– insert(pos,item)
* adds a new item to the list at position pos.
* Assume the item is not already in the list and there are enough existing items to
have position pos.
– pop()
* removes and returns the last item in the list.
* It needs nothing and returns an item.
* Assume the list has at least one item.
– pop(pos)
* removes and returns the item at position pos.
* It needs the position and returns the item.
* Assume the item is in the list.
7

1.6.1 Node Class
• The basic building block for the linked list implementation is the node.
• Each node object must hold at least two pieces of information.
– First, the node must contain the list item itself. We will call this the data field of the
node.
– In addition, each node must hold a reference to the next node.
•
In [36]: class Node:
def __init__(self,initdata):
self.data = initdata
self.next = None
def getData(self):
return self.data
def getNext(self):
return self.next
def setData(self,newdata):
self.data = newdata
def setNext(self,newnext):
self.next = newnext
1.6.2 Unordered List
• A collection of nodes, each linked to the next by explicit references.
• As long as we know where to find the first node (containing the first item), each item after
that can be found by successively following the next links.
• Hence, the UnorderedList class must maintain a reference to the first node.
In [38]: class UnorderedList:
def __init__(self):
self.head = None
# simply checks to see if the head of the list is a reference to None.
# The result of the boolean expression self.head==None will only be true if there a
# Since a new list is empty, the constructor and the check for empty must be consis
# This shows the advantage to using the reference None to denote the end of the lin
def isEmpty(self):
return self.head == None
# Each item of the list must reside in a node object.
8

# So the method creates a new node and places the item as its data.
# Then, the new node is linked to the existing structure.
# This requires two steps:
## 1. change the next reference of the new node to refer to the old first node of t
## 2. modify the head of the list to refer to the new node.
def add(self,item):
temp = Node(item)
temp.setNext(self.head)
self.head = temp
# size, search, and removeare all based on a technique known as linked list travers
# Traversal refers to the process of systematically visiting each node.
# To do this we use an external reference that starts at the first node in the list
# As we visit each node, we move the reference to the next node by traversing the n
def size(self):
current = self.head
count = 0
while current != None:
count = count + 1
current = current.getNext()
return count
def search(self,item):
current = self.head
found = False
while current != None and not found:
if current.getData() == item:
found = True
else:
return found
def remove(self,item):
current = self.head
previous = None
found = False
while not found:
if current.getData() == item:
found = True
else:
previous = current
if previous == None:
9

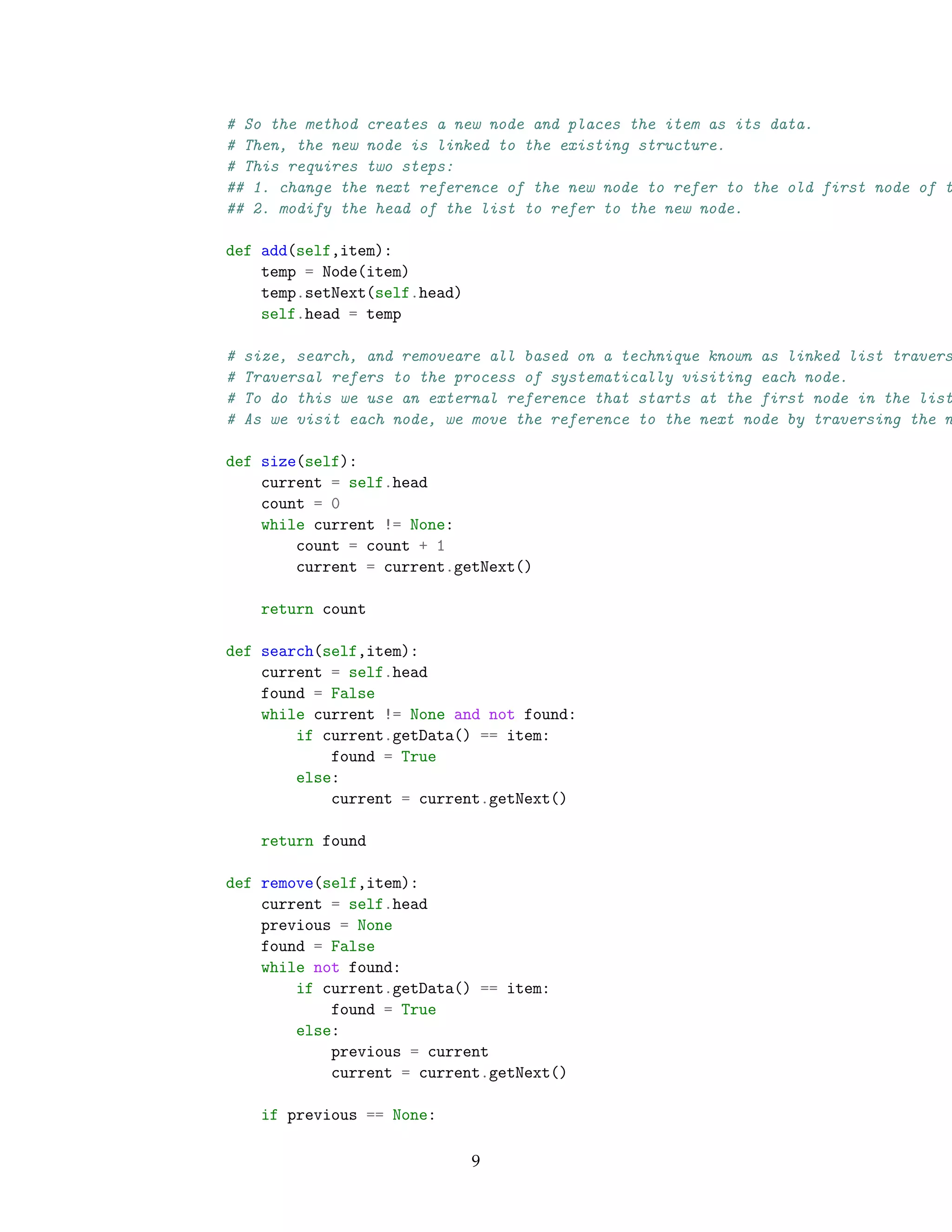
self.head = current.getNext()
else:
previous.setNext(current.getNext())
In [41]: mylist = UnorderedList()
mylist.add(31)
mylist.add(77)
mylist.add(17)
mylist.add(93)
mylist.add(26)
mylist.add(54)
print("Size of Linked List : ",mylist.size())
print("Search 93 :", mylist.search(93))
print("Search 100 :", mylist.search(100))
mylist.add(100)
print("Search 100 :",mylist.search(100))
mylist.remove(54)
mylist.remove(93)
mylist.remove(31)
print("Search 93 :",mylist.search(93))
Size of Linked List : 6
Search 93 : True
Search 100 : False
Search 100 : True
Search 93 : False
1.6.3 Application : Simple Balanced Parentheses
• Balanced parentheses means that each opening symbol has a corresponding closing symbol
and the pairs of parentheses are properly nested.
• Consider the following correctly balanced strings of parentheses:
– (()()()())
– (((())))
10

– (()((())()))
• The ability to differentiate between parentheses that are correctly balanced and those that are
unbalanced is an important part of recognizing many programming language structures.
def parChecker(symbolString):
s = Stack()
balanced = True
index = 0
while index < len(symbolString) and balanced:
symbol = symbolString[index]
if symbol == "(":
s.push(symbol)
else:
if s.isEmpty():
balanced = False
else:
s.pop()
index = index + 1
if balanced and s.isEmpty():
return True
else:
return False
print(parChecker('((()))'))
print(parChecker('(()'))
True
False
1.6.4 Application 2 : Converting Decimal Numbers to Binary Numbers
•
def divideBy2(decNumber):
11

remstack = Stack()
while decNumber > 0:
rem = decNumber % 2
remstack.push(rem)
decNumber = decNumber // 2
binString = ""
while not remstack.isEmpty():
binString = binString + str(remstack.pop())
return binString
print(divideBy2(42))
101010
• The algorithm for binary conversion can easily be extended to perform the conversion for
any base.
• In computer science it is common to use a number of different encodings.
• The most common of these are binary, octal (base 8), and hexadecimal (base 16).
def baseConverter(decNumber,base):
digits = "0123456789ABCDEF"
remstack = Stack()
while decNumber > 0:
rem = decNumber % base
remstack.push(rem)
decNumber = decNumber // base
newString = ""
while not remstack.isEmpty():
newString = newString + digits[remstack.pop()]
return newString
print(baseConverter(25,2))
print(baseConverter(25,16))
11001
19
12

1.6.5 Application 3 : Infix, Prefix and Postfix Expressions
Example :
Infix-to-Postfix Conversion
• Assume the infix expression is a string of tokens delimited by spaces.
• The operator tokens are *, /, +, and -, along with the left and right parentheses, ( and ).
• The operand tokens are the single-character identifiers A, B, C, and so on.
• Algorithm :
1. Create an empty stack called opstack for keeping operators. Create an empty list for
output.
2. Convert the input infix string to a list by using the string method split.
3. Scan the token list from left to right.
– If the token is an operand,
* append it to the end of the output list.
– If the token is a left parenthesis,
* push it on the opstack.
– If the token is a right parenthesis,
* pop the opstack until the corresponding left parenthesis is removed.
* Append each operator to the end of the output list.
– If the token is an operator, *, /, +, or -,
* push it on the opstack.
* However, first remove any operators already on the opstack that have higher
or equal precedence
* Append them to the output list.
4. When the input expression has been completely processed,
– check the opstack.
– Any operators still on the stack can be removed and appended to the end of the
output list.
•
def infixToPostfix(infixexpr):
13

prec = {}
prec["*"] = 3
prec["/"] = 3
prec["+"] = 2
prec["-"] = 2
prec["("] = 1
opStack = Stack()
postfixList = []
tokenList = infixexpr.split()
for token in tokenList:
if token in "ABCDEFGHIJKLMNOPQRSTUVWXYZ" or token in "0123456789":
postfixList.append(token)
elif token == '(':
opStack.push(token)
elif token == ')':
topToken = opStack.pop()
while topToken != '(':
postfixList.append(topToken)
topToken = opStack.pop()
else:
while (not opStack.isEmpty()) and
(prec[opStack.peek()] >= prec[token]):
postfixList.append(opStack.pop())
opStack.push(token)
while not opStack.isEmpty():
postfixList.append(opStack.pop())
return " ".join(postfixList)
print(infixToPostfix("A * B + C * D"))
print(infixToPostfix("( A + B ) * C - ( D - E ) * ( F + G )"))
A B * C D * +
A B + C * D E - F G + * -
Postﬁx Evaluation
• Assume the postﬁx expression is a string of tokens delimited by spaces.
• The operators are *, /, +, and - and the operands are assumed to be single-digit integer
values.
• The output will be an integer result.
• Algorithm :
1. Create an empty stack called operandStack.
2. Convert the string to a list by using the string method split.
3. Scan the token list from left to right.
– If the token is an operand,
14

* convert it from a string to an integer
* push the value onto the operandStack.
– If the token is an operator, *, /, +, or -, it will need two operands.
* Pop the operandStack twice.
* The ﬁrst pop is the second operand and the second pop is the ﬁrst operand.
* Perform the arithmetic operation.
* Push the result back on the operandStack.
4. When the input expression has been completely processed,
– the result is on the stack.
– Pop the operandStack and return the value.
•
In [17]: def postfixEval(postfixExpr):
operandStack = Stack()
tokenList = postfixExpr.split()
for token in tokenList:
if token in "0123456789":
operandStack.push(int(token))
else:
operand2 = operandStack.pop()
operand1 = operandStack.pop()
result = doMath(token,operand1,operand2)
operandStack.push(result)
return operandStack.pop()
def doMath(op, op1, op2):
if op == "*":
return op1 * op2
elif op == "/":
return op1 / op2
elif op == "+":
return op1 + op2
else:
return op1 - op2
print(postfixEval('7 8 + 3 2 + /'))
3.0
15

Basic data structures in python

More Related Content

What's hot

Similar to Basic data structures in python

More from Lifna C.S

Recently uploaded

In this document

Basic data structures in python