KEMBAR78
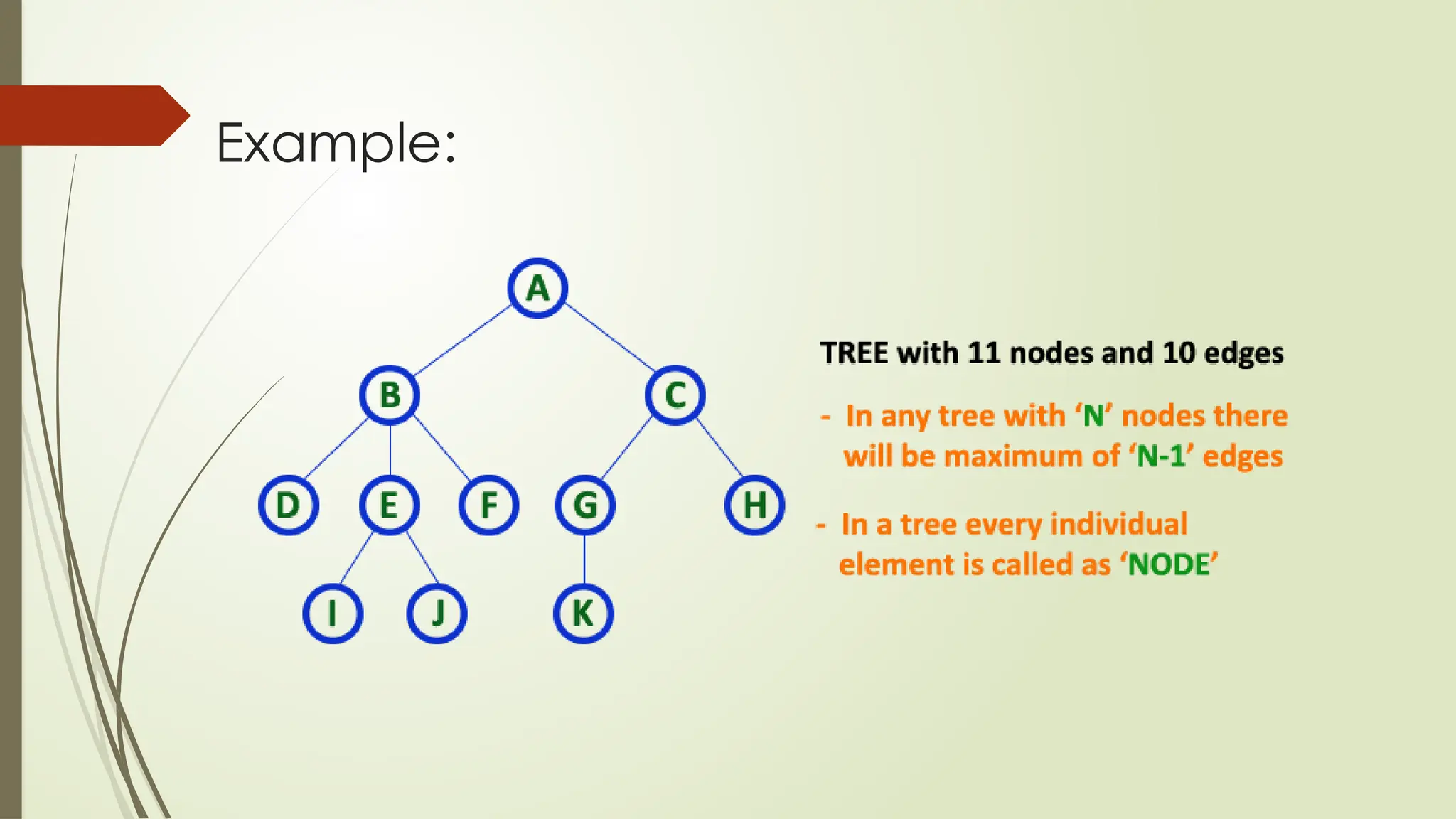
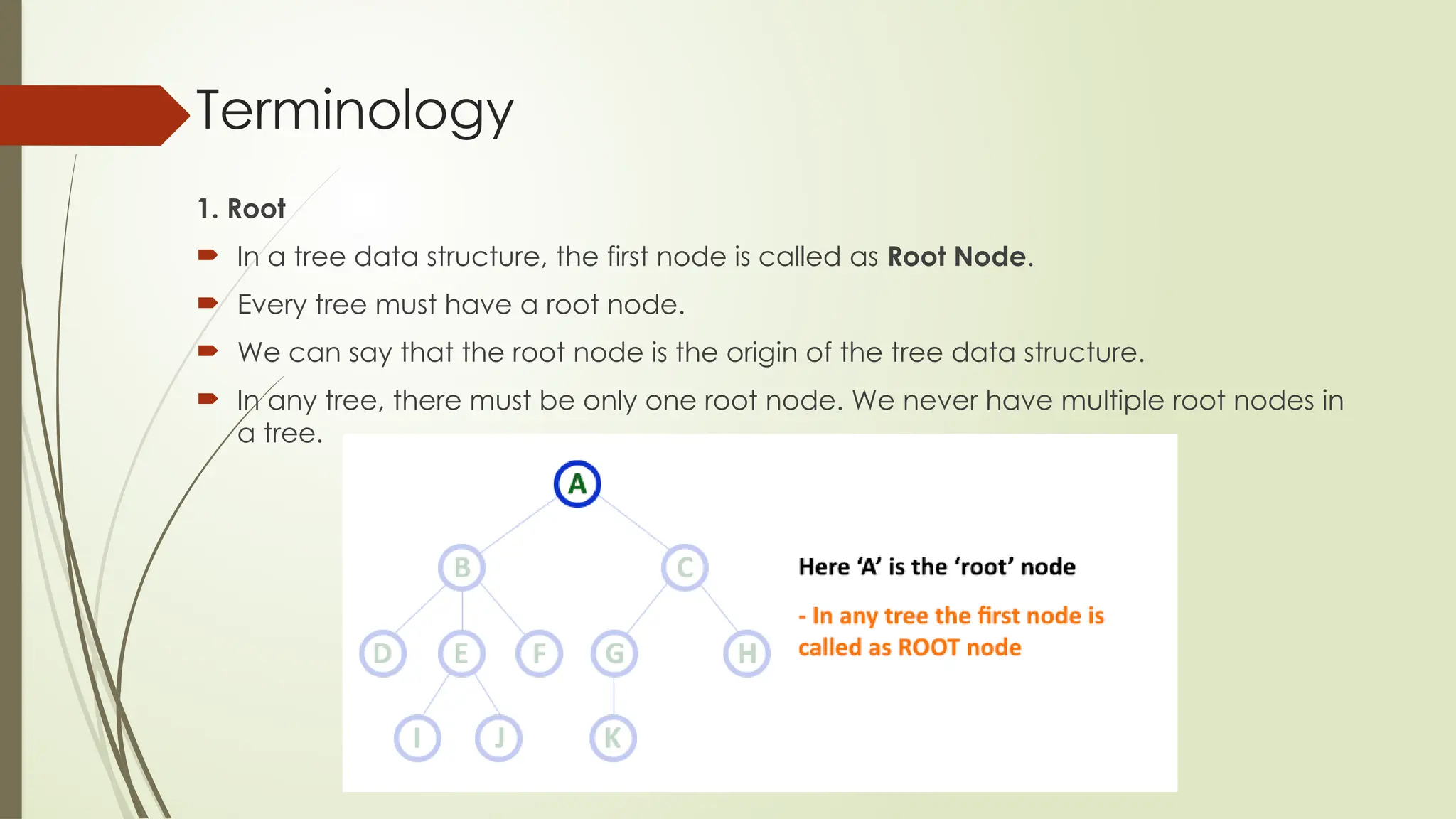
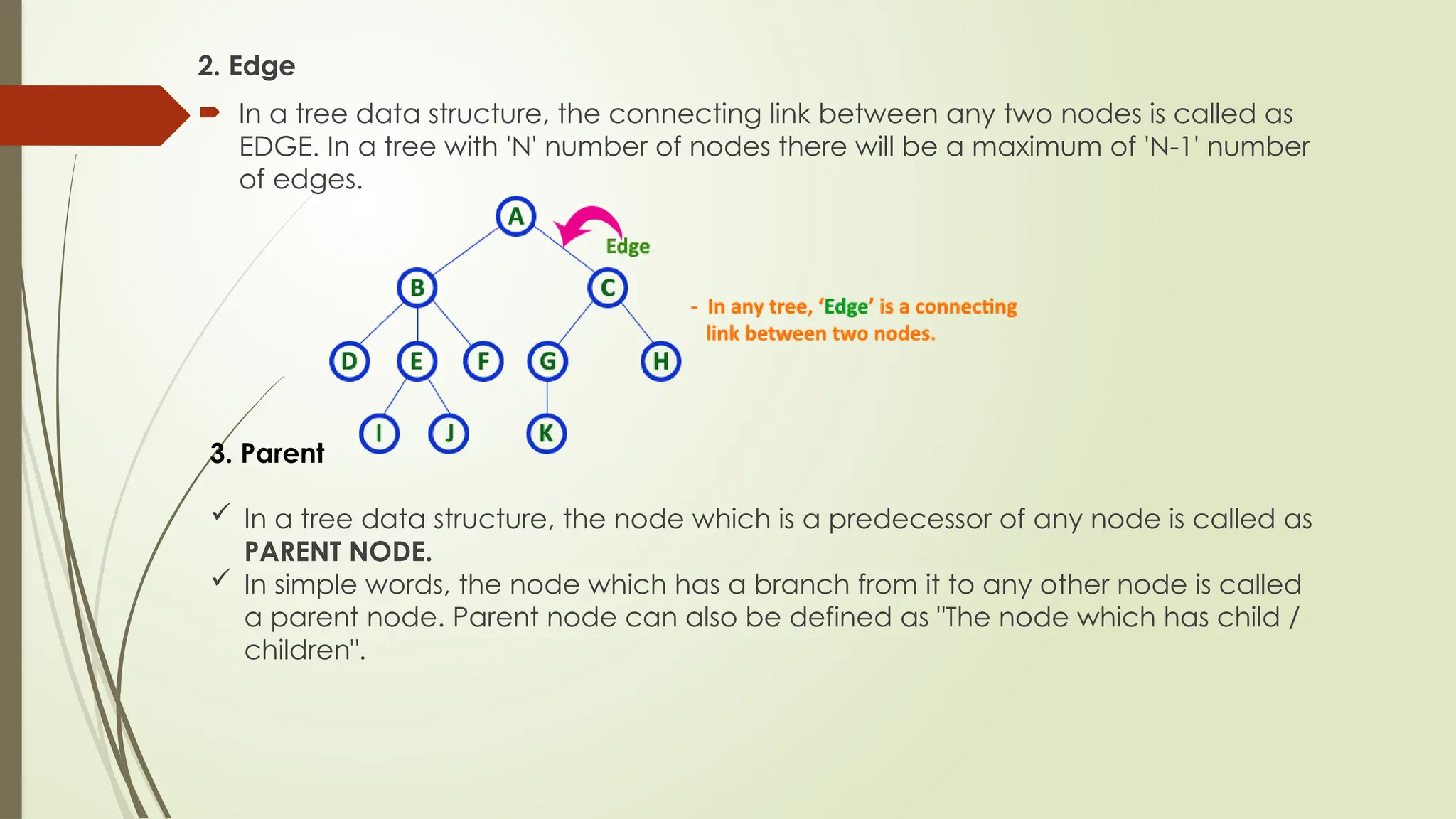
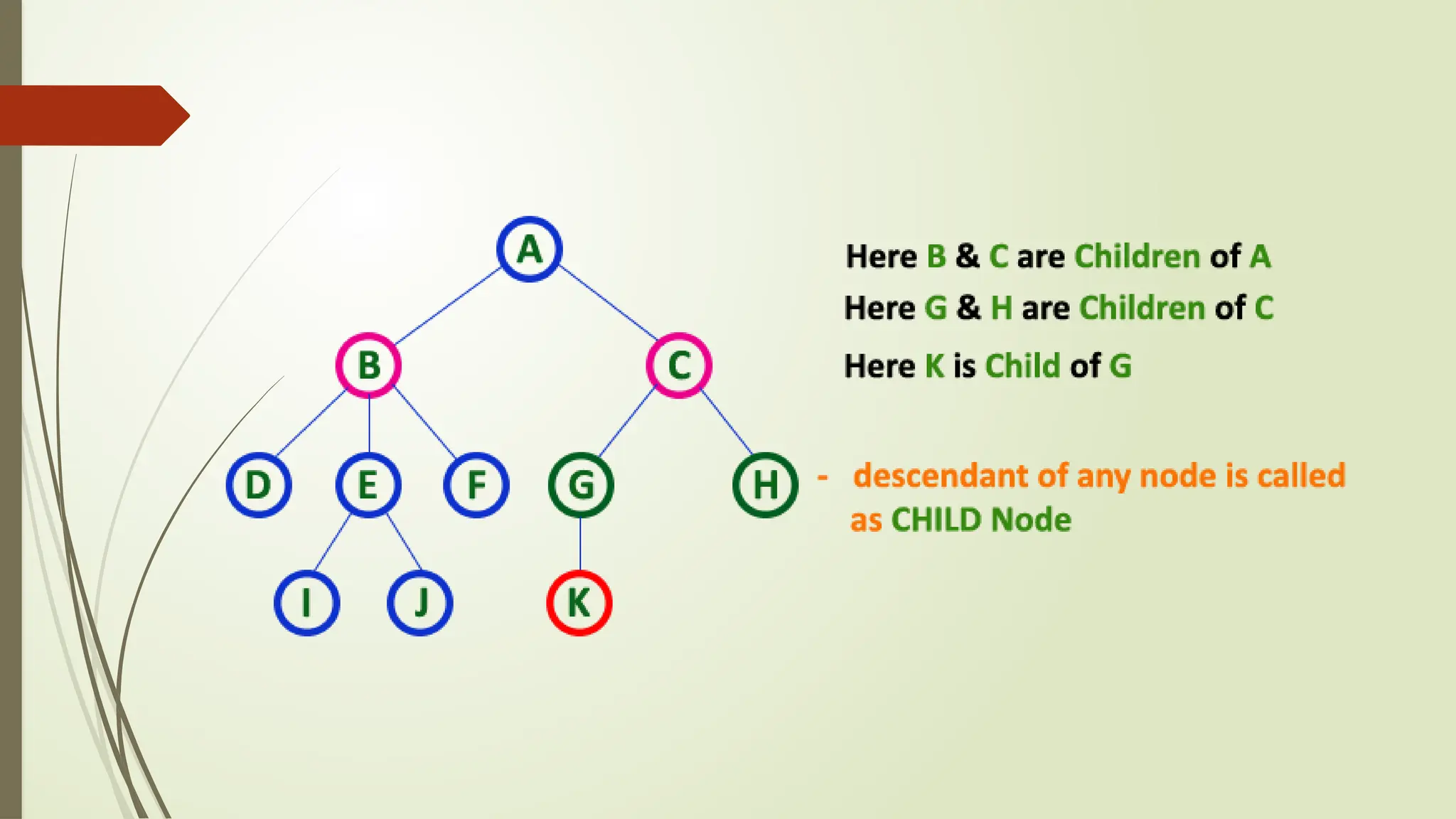
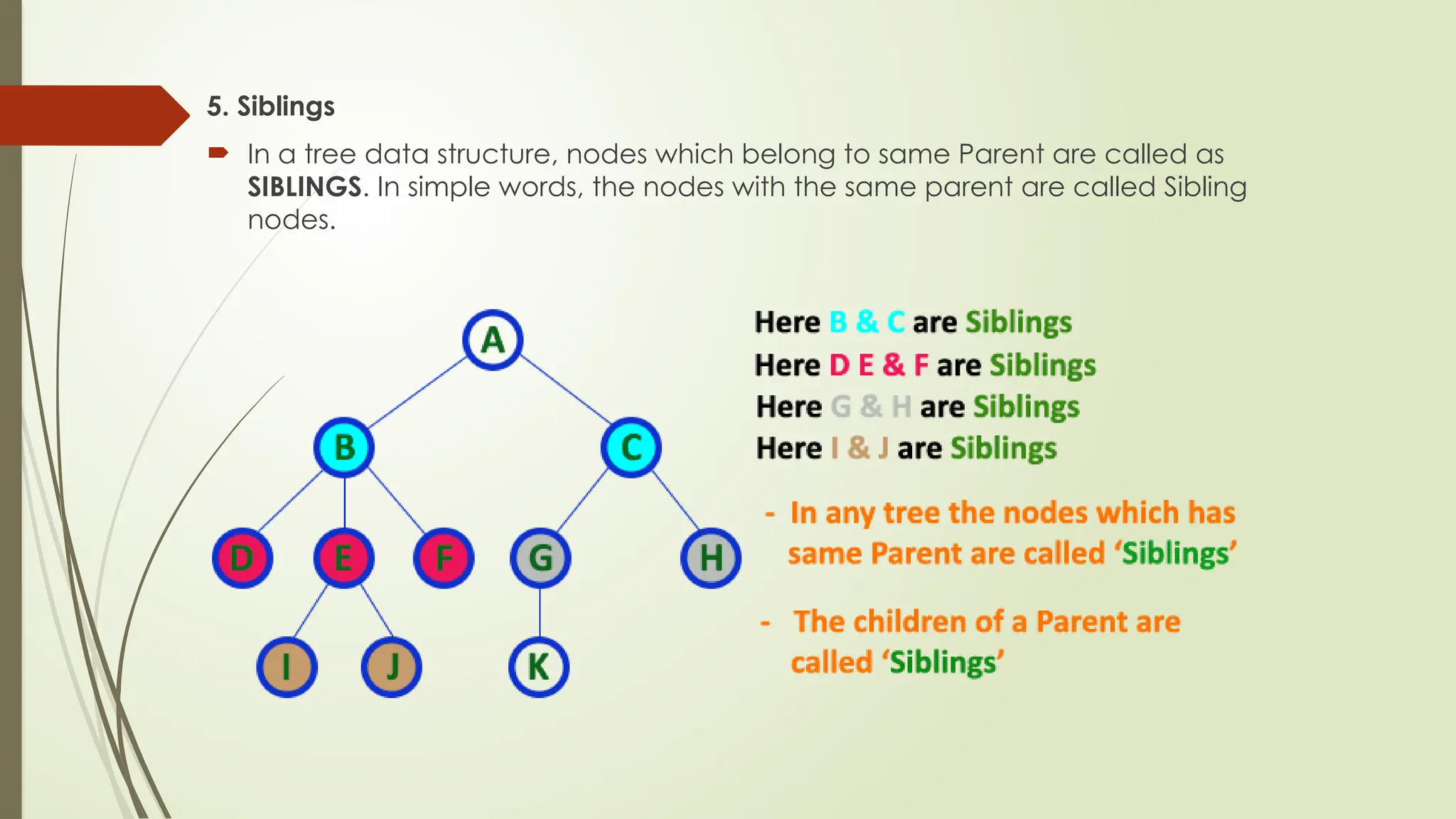
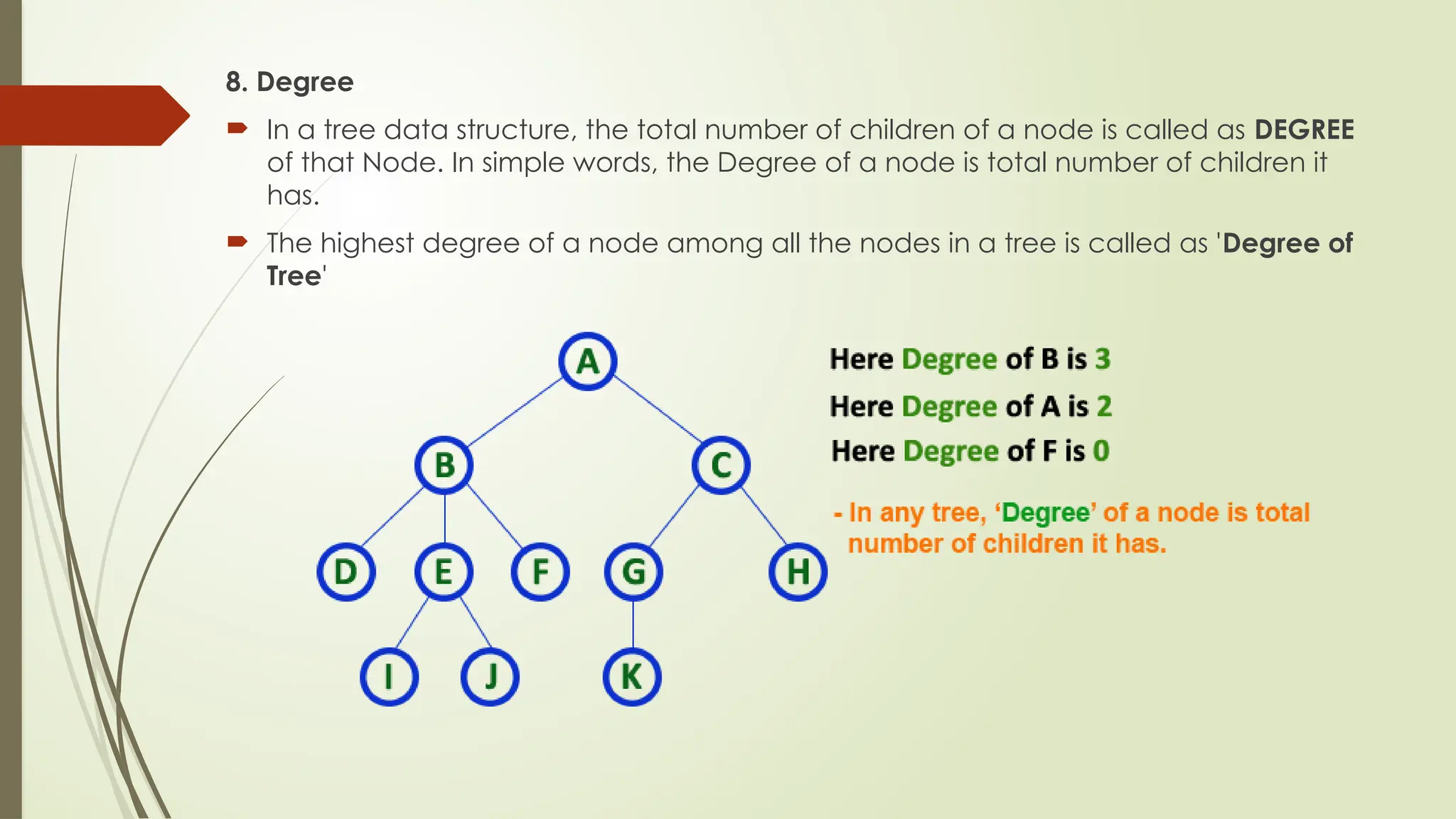
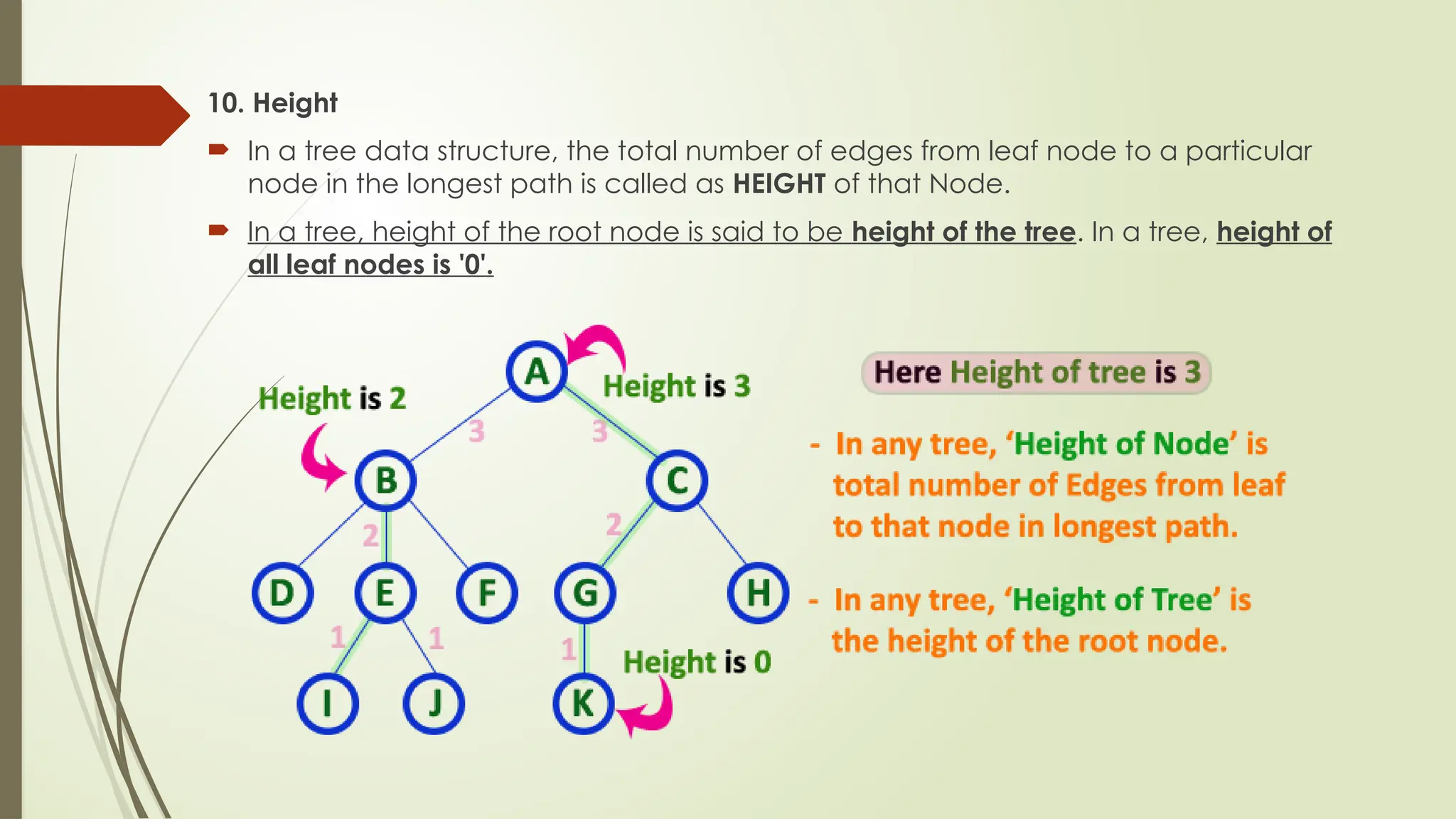
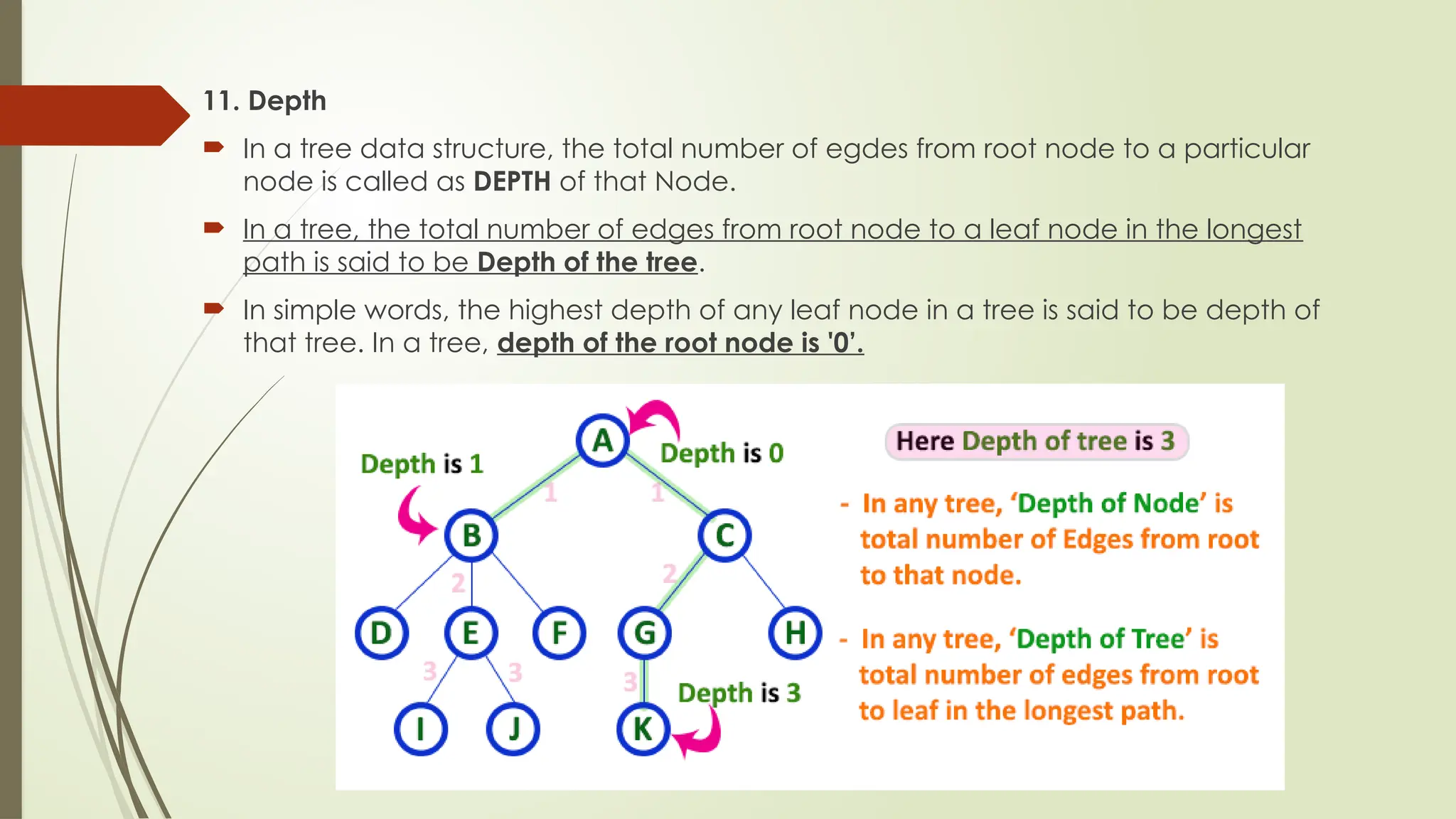
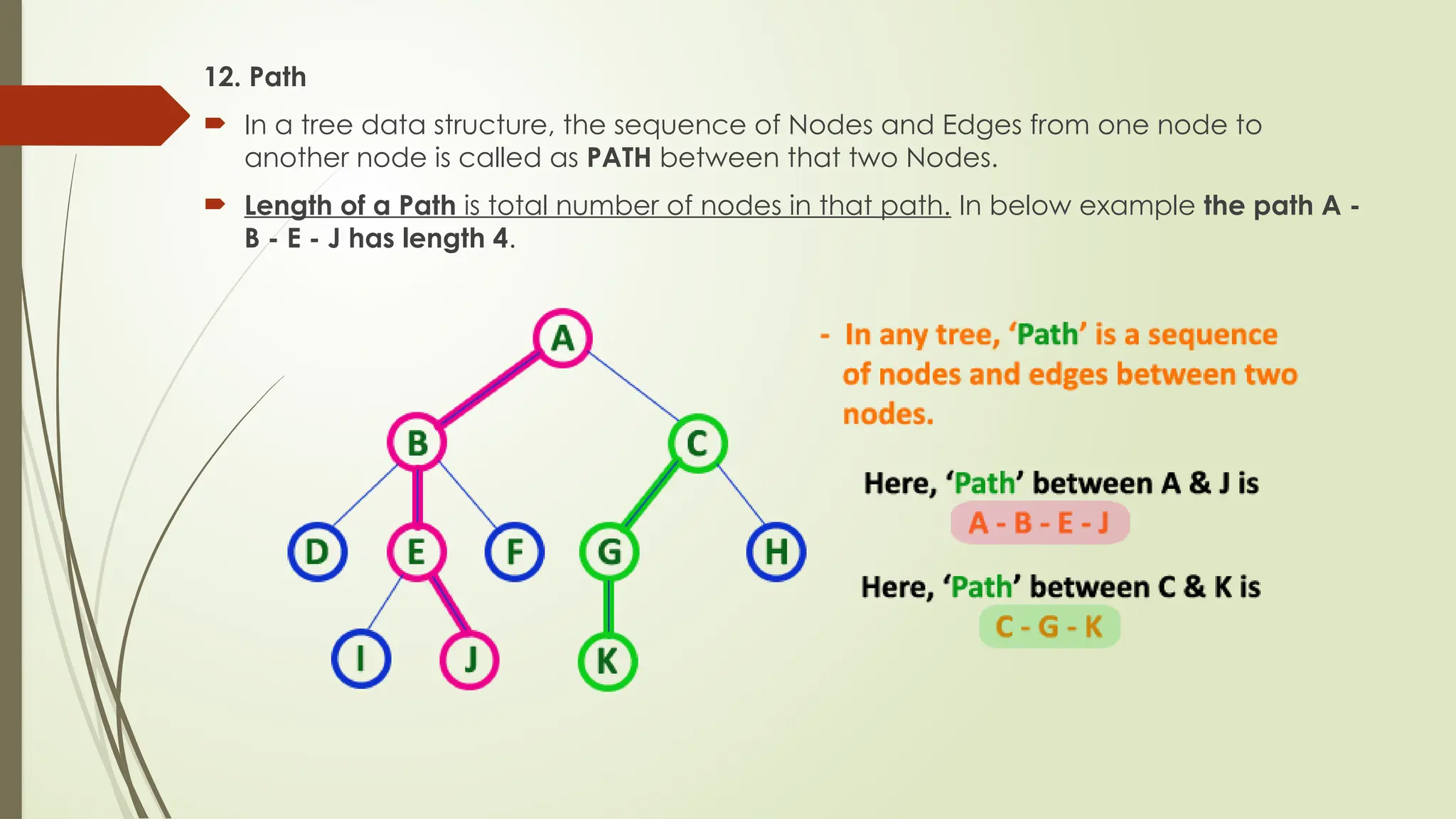
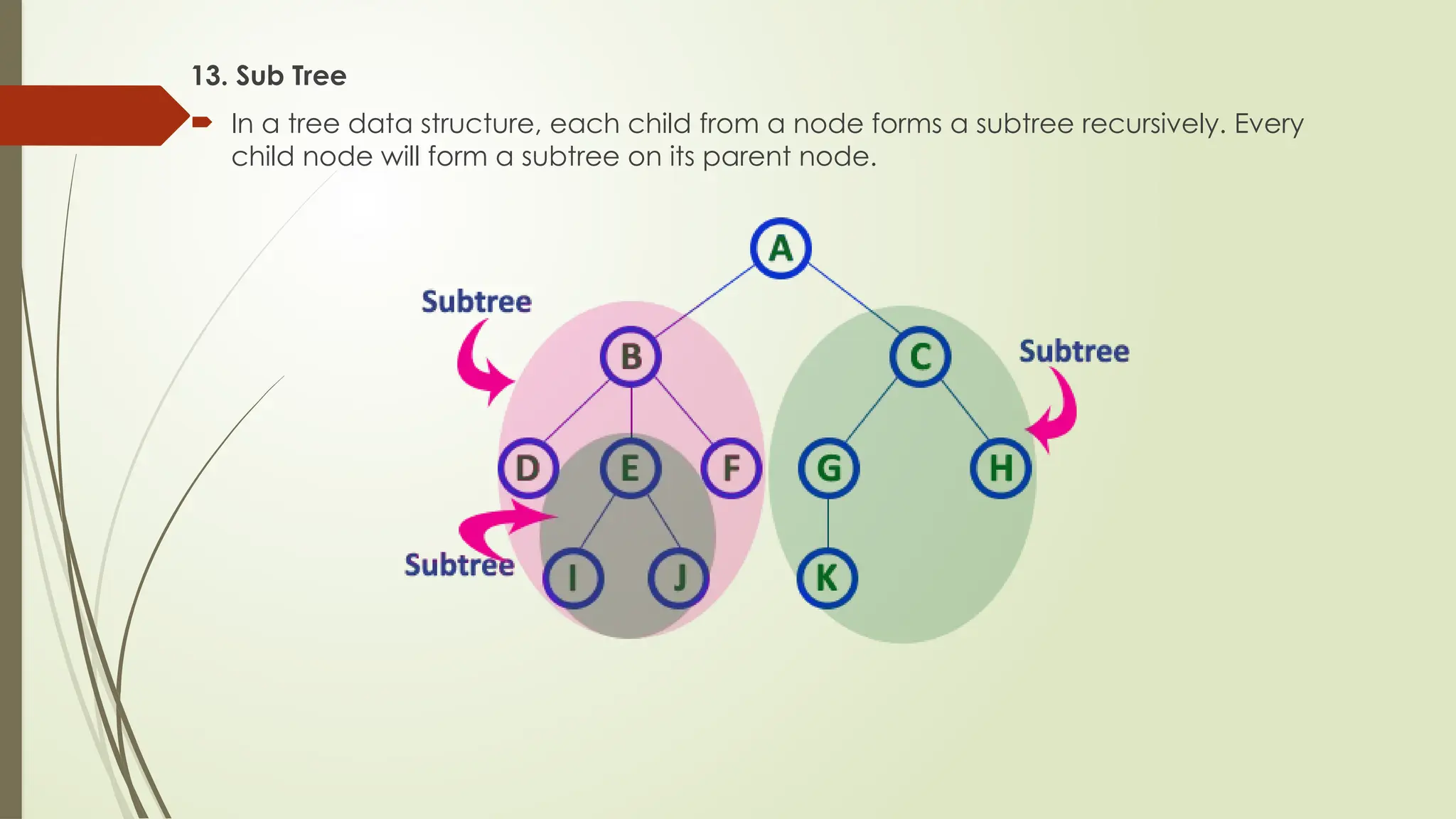
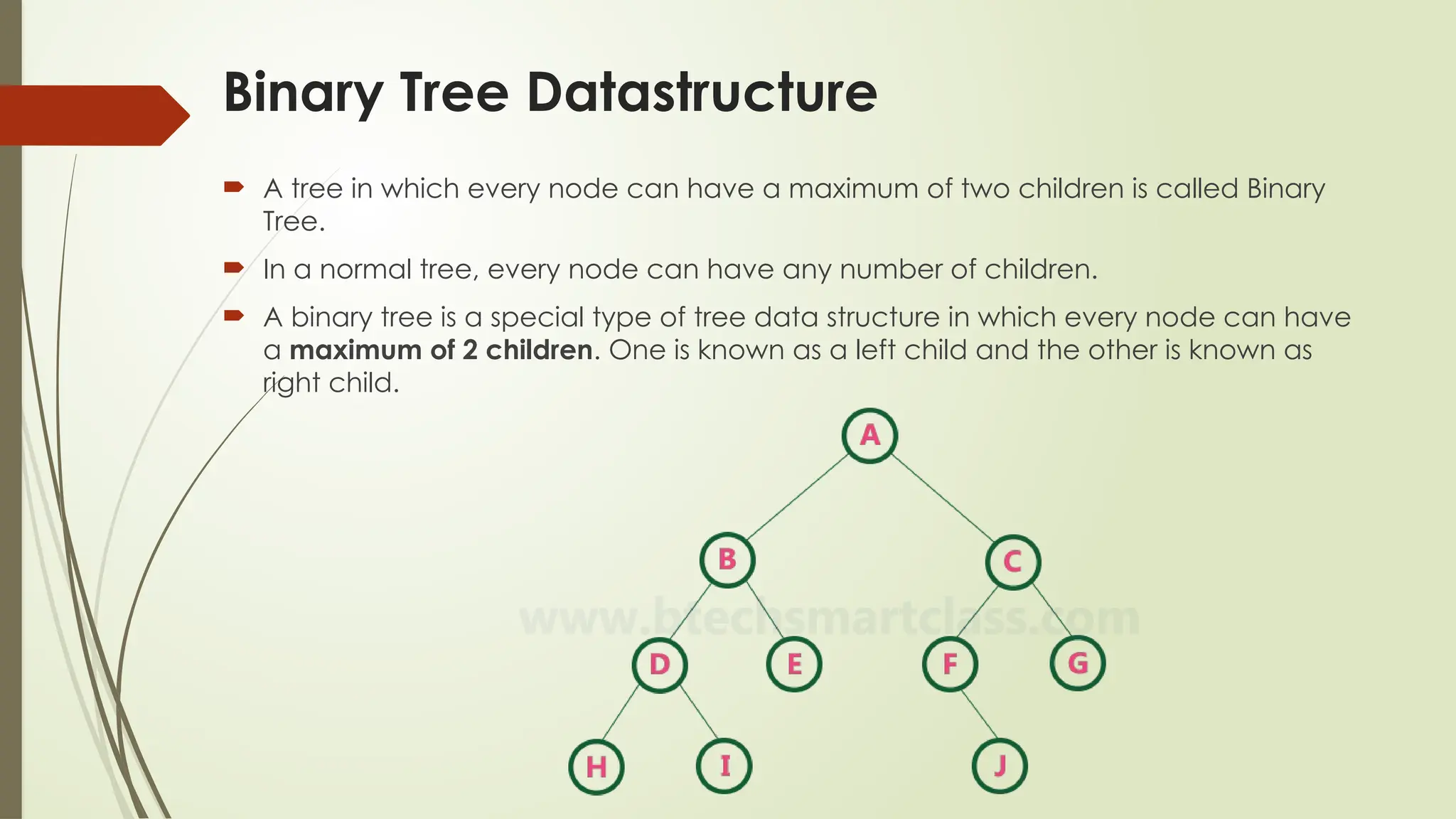
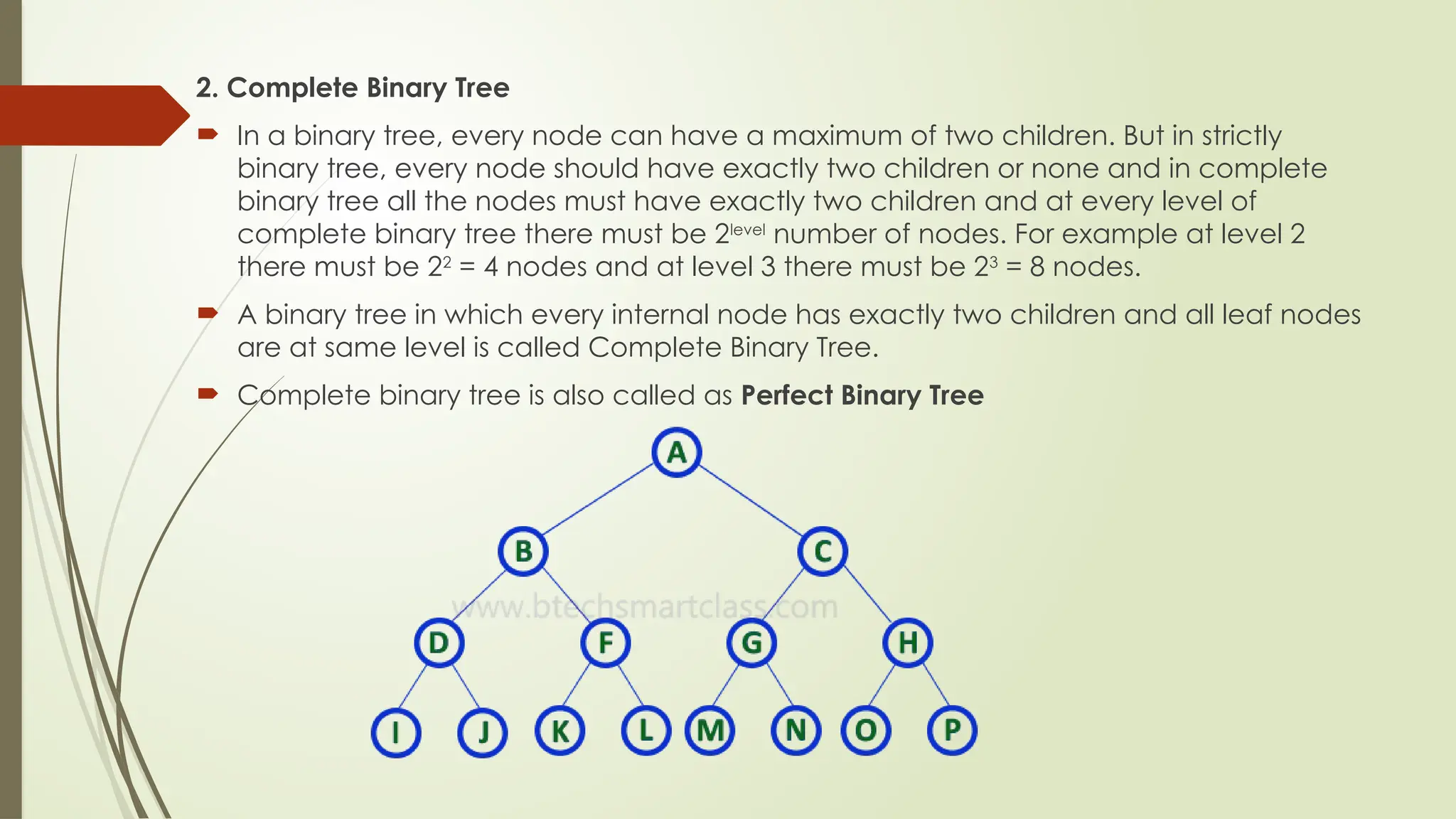
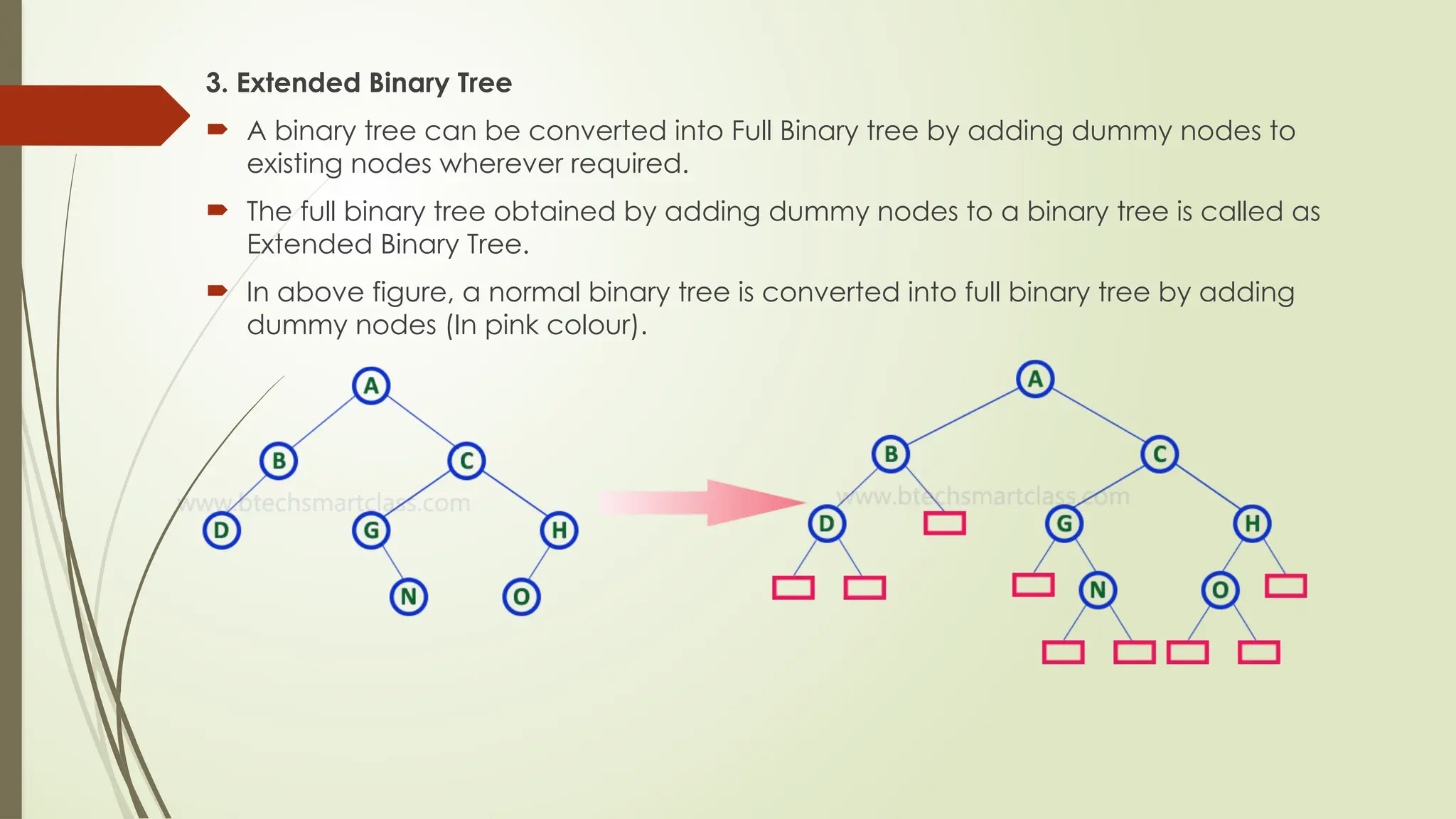
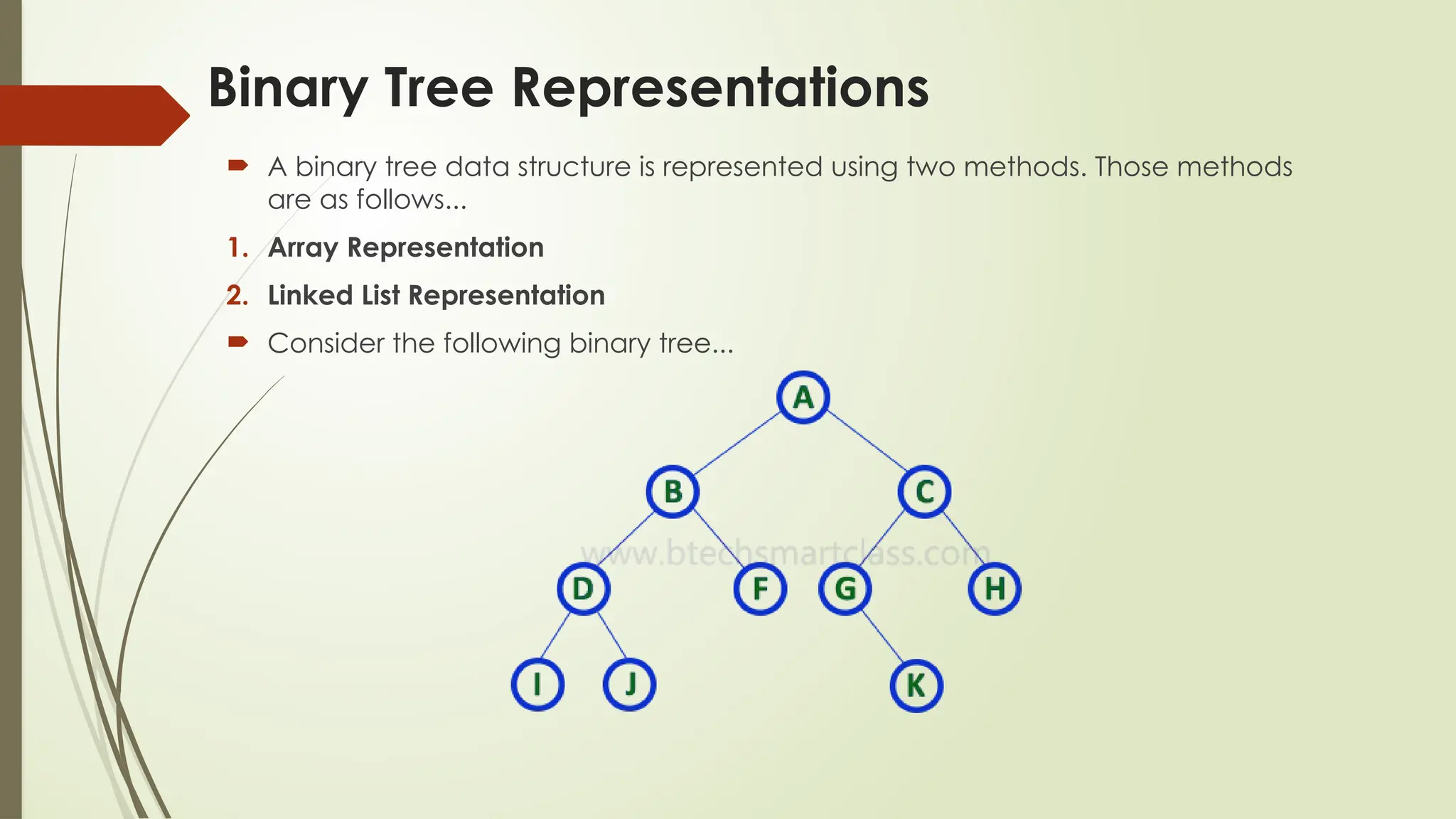
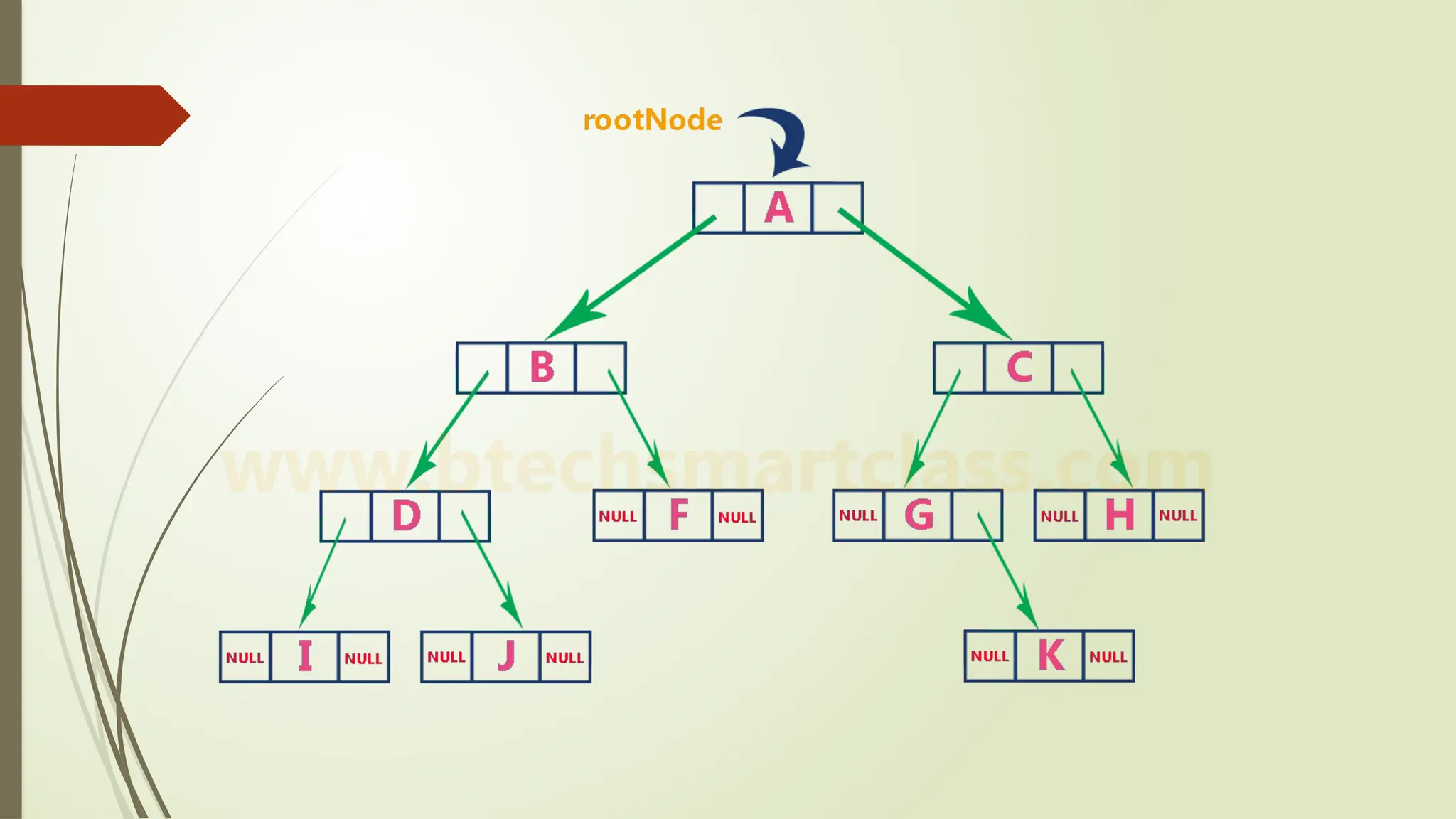
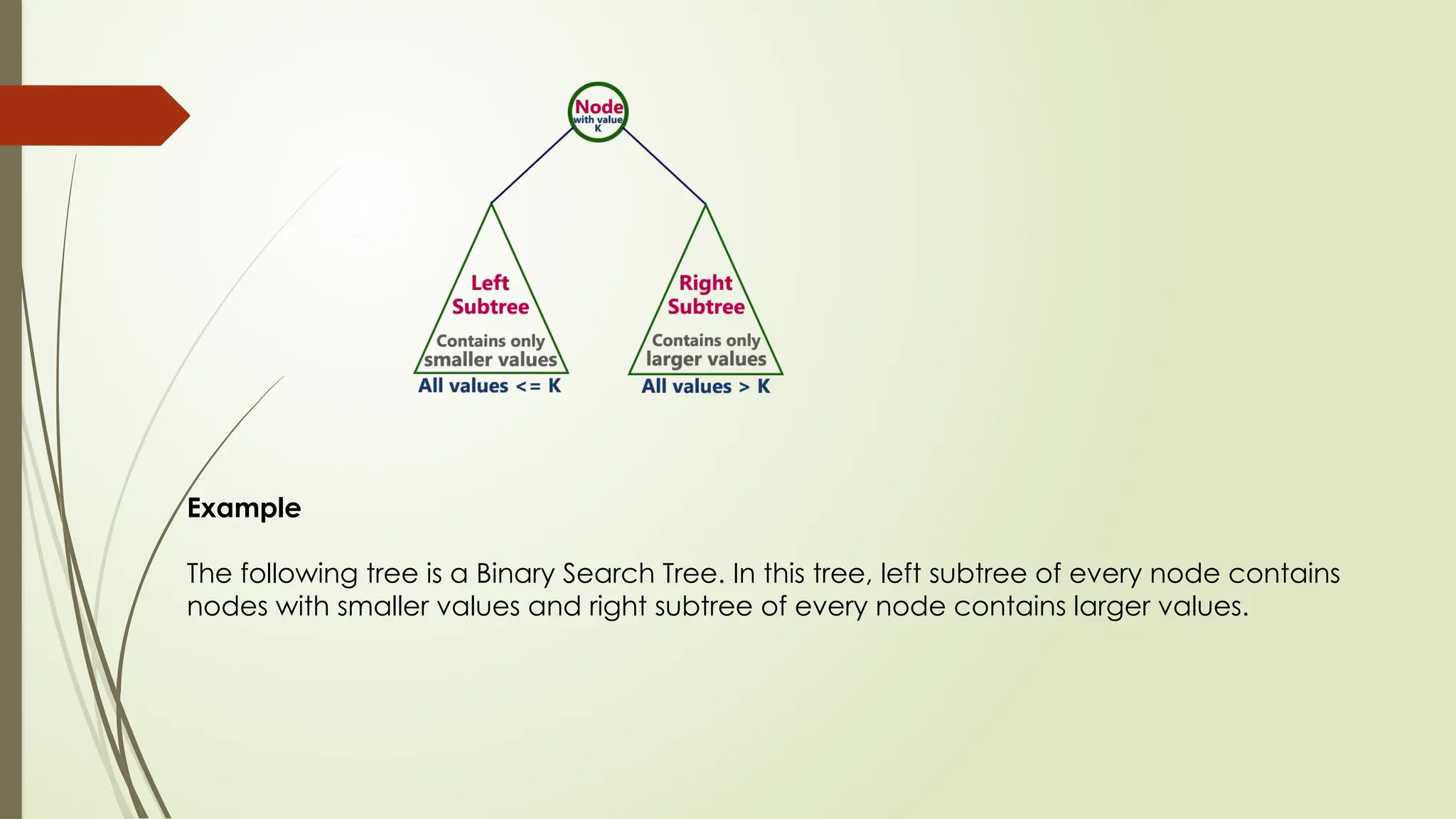
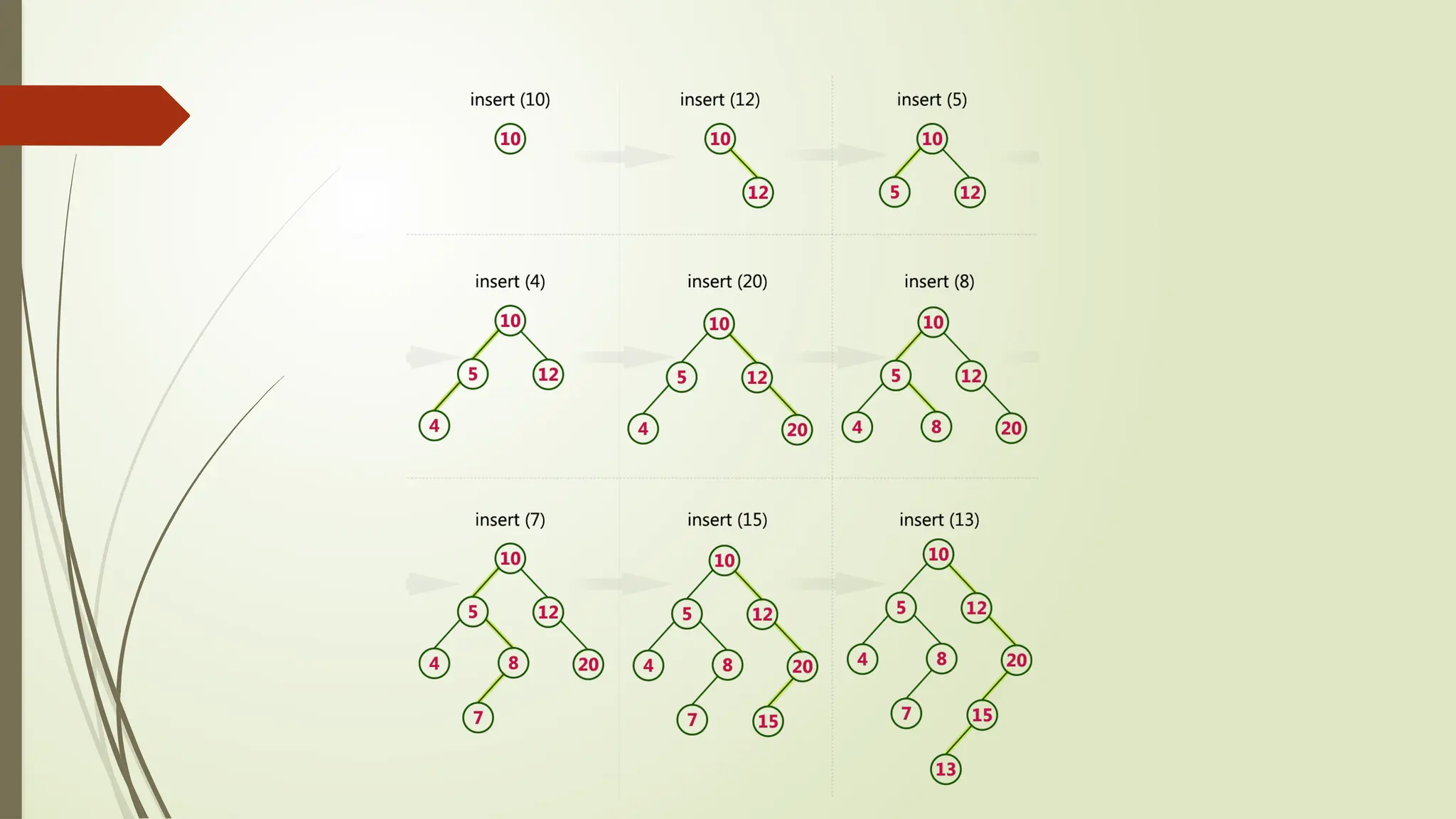
Basic Tree Data Structure BST Traversals .pptx
Uploaded byrajinooka
PPTX, PDF63 views

Basic Tree Data Structure BST Traversals .pptx

The document provides an extensive overview of tree data structures, particularly focusing on binary search trees (BST), including definitions, operations such as searching, insertion, and deletion, and various tree types like AVL trees and red-black trees. It explains essential terminologies, tree characteristics, and traversal methods, as well as the representation methods for binary trees using arrays and linked lists. Operations specific to binary search trees, including their efficiencies, are also detailed.

Download to read offline
UNIT-3 TREES
Syllabus Binary Search Trees, Definition, Implementation, Operations- Searching, Insertion. BST Deletion. AVL Trees, Height of an AVL Tree, Operations, AVL Trees, Height of an AVL Tree, Operations, AVL Trees- Deletion and Searching, Red –Black Tree, Splay Trees, Previous question papers discussion
Tree Data Structure Definition:  Tree is a non-linear data structure which organizes data in hierarchical structure and this is a recursive definition. A tree data structure can also be defined as follows...  Tree data structure is a collection of data (Node) which is organized in hierarchical structure recursively  In tree data structure, every individual element is called as Node.  Node in a tree data structure stores the actual data of that particular element and link to next element in hierarchical structure.  In a tree data structure, if we have N number of nodes then we can have a maximum of N-1 number of links.
Example:
Terminology 1. Root  In a tree data structure, the first node is called as Root Node.  Every tree must have a root node.  We can say that the root node is the origin of the tree data structure.  In any tree, there must be only one root node. We never have multiple root nodes in a tree.
2. Edge  In a tree data structure, the connecting link between any two nodes is called as EDGE. In a tree with 'N' number of nodes there will be a maximum of 'N-1' number of edges. 3. Parent  In a tree data structure, the node which is a predecessor of any node is called as PARENT NODE.  In simple words, the node which has a branch from it to any other node is called a parent node. Parent node can also be defined as "The node which has child / children".
4. Child  In a tree data structure, the node which is descendant of any node is called as CHILD Node.  In simple words, the node which has a link from its parent node is called as child node. In a tree, any parent node can have any number of child nodes. In a tree, all the nodes except root are child nodes.
5. Siblings  In a tree data structure, nodes which belong to same Parent are called as SIBLINGS. In simple words, the nodes with the same parent are called Sibling nodes.
6. Leaf  In a tree data structure, the node which does not have a child is called as LEAF Node. In simple words, a leaf is a node with no child.  In a tree data structure, the leaf nodes are also called as External Nodes. External node is also a node with no child. In a tree, leaf node is also called as 'Terminal' node.
7. Internal Nodes  In a tree data structure, the node which has at least one child is called as INTERNAL Node. In simple words, an internal node is a node with at least one child.  In a tree data structure, nodes other than leaf nodes are called as Internal Nodes. The root node is also said to be Internal Node if the tree has more than one node. Internal nodes are also called as 'Non-Terminal' nodes.
8. Degree  In a tree data structure, the total number of children of a node is called as DEGREE of that Node. In simple words, the Degree of a node is total number of children it has.  The highest degree of a node among all the nodes in a tree is called as 'Degree of Tree'
9. Level  In a tree data structure, the root node is said to be at Level 0 and the children of root node are at Level 1 and the children of the nodes which are at Level 1 will be at Level 2 and so on... In simple words, in a tree each step from top to bottom is called as a Level and the Level count starts with '0' and incremented by one at each level (Step).
10. Height  In a tree data structure, the total number of edges from leaf node to a particular node in the longest path is called as HEIGHT of that Node.  In a tree, height of the root node is said to be height of the tree. In a tree, height of all leaf nodes is '0'.
11. Depth  In a tree data structure, the total number of egdes from root node to a particular node is called as DEPTH of that Node.  In a tree, the total number of edges from root node to a leaf node in the longest path is said to be Depth of the tree.  In simple words, the highest depth of any leaf node in a tree is said to be depth of that tree. In a tree, depth of the root node is '0’.
12. Path  In a tree data structure, the sequence of Nodes and Edges from one node to another node is called as PATH between that two Nodes.  Length of a Path is total number of nodes in that path. In below example the path A - B - E - J has length 4.
13. Sub Tree  In a tree data structure, each child from a node forms a subtree recursively. Every child node will form a subtree on its parent node.
Binary Tree Datastructure  A tree in which every node can have a maximum of two children is called Binary Tree.  In a normal tree, every node can have any number of children.  A binary tree is a special type of tree data structure in which every node can have a maximum of 2 children. One is known as a left child and the other is known as right child.
 There are different types of binary trees and they are...  1. Strictly Binary Tree  In a binary tree, every node can have a maximum of two children. But in strictly binary tree, every node should have exactly two children or none. That means every internal node must have exactly two children. A strictly Binary Tree can be defined as follows...  A binary tree in which every node has either two or zero number of children is called Strictly Binary Tree  Strictly binary tree is also called as Full Binary Tree or Proper Binary Tree or 2-Tree.  Strictly binary tree data structure is used to represent mathematical expressions.
Example
2. Complete Binary Tree  In a binary tree, every node can have a maximum of two children. But in strictly binary tree, every node should have exactly two children or none and in complete binary tree all the nodes must have exactly two children and at every level of complete binary tree there must be 2level number of nodes. For example at level 2 there must be 22 = 4 nodes and at level 3 there must be 23 = 8 nodes.  A binary tree in which every internal node has exactly two children and all leaf nodes are at same level is called Complete Binary Tree.  Complete binary tree is also called as Perfect Binary Tree
3. Extended Binary Tree  A binary tree can be converted into Full Binary tree by adding dummy nodes to existing nodes wherever required.  The full binary tree obtained by adding dummy nodes to a binary tree is called as Extended Binary Tree.  In above figure, a normal binary tree is converted into full binary tree by adding dummy nodes (In pink colour).
Binary Tree Representations  A binary tree data structure is represented using two methods. Those methods are as follows... 1. Array Representation 2. Linked List Representation  Consider the following binary tree...
1. Array Representation of Binary Tree  In array representation of a binary tree, we use one-dimensional array (1-D Array) to represent a binary tree.  Consider the above example of a binary tree and it is represented as follows...  To represent a binary tree of depth 'n' using array representation, we need one dimensional array with a maximum size of 2n + 1.
2. Linked List Representation of Binary Tree  We use a double linked list to represent a binary tree. In a double linked list, every node consists of three fields.  First field for storing left child address, second for storing actual data and third for storing right child address.  In this linked list representation, a node has the following structure...  The above example of the binary tree represented using Linked list representation is shown as follows...
Binary Tree Traversals  When we wanted to display a binary tree, we need to follow some order in which all the nodes of that binary tree must be displayed. In any binary tree, displaying order of nodes depends on the traversal method.  Displaying (or) visiting order of nodes in a binary tree is called as Binary Tree Traversal.  There are three types of binary tree traversals. 1. In - Order Traversal 2. Pre - Order Traversal 3. Post - Order Traversal  Consider the following binary tree...
1. In - Order Traversal ( leftChild - root - rightChild )  In In-Order traversal, the root node is visited between the left child and right child. In this traversal, the left child node is visited first, then the root node is visited and later we go for visiting the right child node. This in-order traversal is applicable for every root node of all subtrees in the tree. This is performed recursively for all nodes in the tree.  In the above example of a binary tree, first we try to visit left child of root node 'A', but A's left child 'B' is a root node for left subtree. so we try to visit its (B's) left child 'D' and again D is a root for subtree with nodes D, I and J.  So we try to visit its left child 'I' and it is the leftmost child. So first we visit 'I' then go for its root node 'D' and later we visit D's right child 'J'. With this we have completed the left part of node B. Then visit 'B' and next B's right child 'F' is visited.  With this we have completed left part of node A. Then visit root node 'A'. With this we have completed left and root parts of node A. Then we go for the right part of the node A. In right of A again there is a subtree with root C.  So go for left child of C and again it is a subtree with root G. But G does not have left part so we visit 'G' and then visit G's right child K.  With this we have completed the left part of node C. Then visit root node 'C' and next visit C's right child 'H' which is the rightmost child in the tree. So we stop the process.  That means here we have visited in the order of I - D - J - B - F - A - G - K - C - H using In-Order Traversal.
 In-Order Traversal for above example of binary tree is I - D - J - B - F - A - G - K - C - H Pre - Order Traversal ( root - leftChild - rightChild )  In Pre-Order traversal, the root node is visited before the left child and right child nodes.  In this traversal, the root node is visited first, then its left child and later its right child. This pre-order traversal is applicable for every root node of all subtrees in the tree.  In the above example of binary tree, first we visit root node 'A' then visit its left child 'B' which is a root for D and F.  So we visit B's left child 'D' and again D is a root for I and J. So we visit D's left child 'I' which is the leftmost child. So next we go for visiting D's right child 'J’.  With this we have completed root, left and right parts of node D and root, left parts of node B. Next visit B's right child 'F'. With this we have completed root and left parts of node A.  So we go for A's right child 'C' which is a root node for G and H. After visiting C, we go for its left child 'G' which is a root for node K. So next we visit left of G, but it does not have left child so we go for G's right child 'K’.  With this, we have completed node C's root and left parts. Next visit C's right child 'H' which is the rightmost child in the tree. So we stop the process.  That means here we have visited in the order of A-B-D-I-J-F-C-G-K-H using Pre-Order Traversal.  Pre-Order Traversal for above example binary tree is A - B - D - I - J - F - C - G - K - H
3. Post - Order Traversal ( leftChild - rightChild - root )  In Post-Order traversal, the root node is visited after left child and right child. In this traversal, left child node is visited first, then its right child and then its root node. This is recursively performed until the right most node is visited.  Here we have visited in the order of I - J - D - F - B - K - G - H - C - A using Post-Order Traversal.  Post-Order Traversal for above example binary tree is I - J - D - F - B - K - G - H - C – A
Binary Search Tree  In a binary tree, every node can have a maximum of two children but there is no need to maintain the order of nodes basing on their values. In a binary tree, the elements are arranged in the order they arrive at the tree from top to bottom and left to right.  A binary tree has the following time complexities... Search Operation - O(n) Insertion Operation - O(1) Deletion Operation - O(n)  To enhance the performance of binary tree, we use a special type of binary tree known as Binary Search Tree. Binary search tree mainly focuses on the search operation in a binary tree.  Binary search tree can be defined as follows...  Binary Search Tree is a binary tree in which every node contains only smaller values in its left subtree and only larger values in its right subtree.  In a binary search tree, all the nodes in the left subtree of any node contains smaller values and all the nodes in the right subtree of any node contains larger values as shown in the following figure...
Example The following tree is a Binary Search Tree. In this tree, left subtree of every node contains nodes with smaller values and right subtree of every node contains larger values.
Every binary search tree is a binary tree but every binary tree need not to be binary search tree.
 Operations on a Binary Search Tree  The following operations are performed on a binary search tree... 1. Search 2. Insertion 3. Deletion
Search Operation in BST In a binary search tree, the search operation is performed with O(log n) time complexity. The search operation is performed as follows... Step 1 - Read the search element from the user. Step 2 - Compare the search element with the value of root node in the tree. Step 3 - If both are matched, then display "Given node is found!!!" and terminate the function Step 4 - If both are not matched, then check whether search element is smaller or larger than that node value. Step 5 - If search element is smaller, then continue the search process in left subtree. Step 6- If search element is larger, then continue the search process in right subtree. Step 7 - Repeat the same until we find the exact element or until the search element is compared with the leaf node Step 8 - If we reach to the node having the value equal to the search value then display "Element is found" and terminate the function. Step 9 - If we reach to the leaf node and if it is also not matched with the search element, then display "Element is not found" and terminate the function.
Insertion Operation in BST  In a binary search tree, the insertion operation is performed with O(log n) time complexity. In binary search tree, new node is always inserted as a leaf node. The insertion operation is performed as follows... • Step 1 - Create a newNode with given value and set its left and right to NULL. • Step 2 - Check whether tree is Empty. • Step 3 - If the tree is Empty, then set root to newNode. • Step 4 - If the tree is Not Empty, then check whether the value of newNode is smaller or larger than the node (here it is root node). • Step 5 - If newNode is smaller than or equal to the node then move to its left child. If newNode is larger than the node then move to its right child. • Step 6- Repeat the above steps until we reach to the leaf node (i.e., reaches to NULL). • Step 7 - After reaching the leaf node, insert the newNode as left child if the newNode is smaller or equal to that leaf node or else insert it as right child.
Deletion Operation in BST  In a binary search tree, the deletion operation is performed with O(log n) time complexity. Deleting a node from Binary search tree includes following three cases...  Case 1: Deleting a Leaf node (A node with no children)  Case 2: Deleting a node with one child  Case 3: Deleting a node with two children
 Case 1: Deleting a leaf node  We use the following steps to delete a leaf node from BST... • Step 1 - Find the node to be deleted using search operation • Step 2 - Delete the node using free function (If it is a leaf) and terminate the function.
Case 2: Deleting a node with one child  We use the following steps to delete a node with one child from BST... • Step 1 - Find the node to be deleted using search operation • Step 2 - If it has only one child then create a link between its parent node and child node. • Step 3 - Delete the node using free function and terminate the function.
Case 3: Deleting a node with two children  We use the following steps to delete a node with two children from BST... • Step 1 - Find the node to be deleted using search operation • Step 2 - If it has two children, then find the largest node in its left subtree (OR) the smallest node in its right subtree. • Step 3 - Swap both deleting node and node which is found in the above step. • Step 4 - Then check whether deleting node came to case 1 or case 2 or else goto step 2 • Step 5 - If it comes to case 1, then delete using case 1 logic. • Step 6- If it comes to case 2, then delete using case 2 logic. • Step 7 - Repeat the same process until the node is deleted from the tree.
Example  Construct a Binary Search Tree by inserting the following sequence of numbers...  10,12,5,4,20,8,7,15 and 13  Above elements are inserted into a Binary Search Tree as follows...
Basic Tree Data Structure BST Traversals .pptx
Basic Tree Data Structure BST Traversals .pptx

More Related Content

DOCX
data structures Unit 3 notes.docxdata structures Unit 3 notes.docx
byyatakonakiran2
 
PPT
UNIT-4 TREES.ppt
bySIVAKUMARM603675
 
PPTX
Data Structures -Non Linear DS-Basics ofTrees
bysailaja156145
 
PPTX
UNIT III Non Linear Data Structures - Trees.pptx
bykncetaruna
 
PPTX
Tree Data Structure in Advanced Data Structure
byshailajacse
 
PPT
Data structure lecture of tree in daa -07.ppt
byatif11nh
 
PPTX
TREE PRESENTATION COMPUTER SCIENCE/DATA STRUCTURE
byHaroldOmega1
 
PPTX
UNIT III Non Linear Data Structures - Trees.pptx
byVISWANATHAN R V
 
data structures Unit 3 notes.docxdata structures Unit 3 notes.docx
byyatakonakiran2
 
UNIT-4 TREES.ppt
bySIVAKUMARM603675
 
Data Structures -Non Linear DS-Basics ofTrees
bysailaja156145
 
UNIT III Non Linear Data Structures - Trees.pptx
bykncetaruna
 
Tree Data Structure in Advanced Data Structure
byshailajacse
 
Data structure lecture of tree in daa -07.ppt
byatif11nh
 
TREE PRESENTATION COMPUTER SCIENCE/DATA STRUCTURE
byHaroldOmega1
 
UNIT III Non Linear Data Structures - Trees.pptx
byVISWANATHAN R V
 

Similar to Basic Tree Data Structure BST Traversals .pptx

PPT
Final tree.ppt tells about tree presentation
bynakulvarshney371
 
PPTX
A binary tree is a hierarchical data structure where each node has at most tw...
bybeaulah5219
 
PPT
9. TREE Data Structure Non Linear Data Structure
bykejika1215
 
PPTX
DS-UNIT-4zjufrusefihfacbciauhfbaiuhc.pptx
byDRCARIBOU
 
PPTX
Data Structure of computer science and technology
bybhaskarsai499
 
PPTX
NON-LINEAR DATA STRUCTURE-TREES.pptx
byRajitha Reddy Alugati
 
PPTX
TREES 1.pptx
bySanGeet25
 
PPTX
TREES basics simple introduction .pptx
bySanGeet25
 
PPTX
Presentation1-Data structure S-Tree.pptx
byPraveen156918
 
PPTX
Tree.pptx
byworldchannel
 
PPTX
Data structure using c module 2
bysmruti sarangi
 
PPTX
Tree
bybhumish
 
DOCX
Trees in data structrures
byGaurav Sharma
 
PPTX
Tree
byRaj Sarode
 
PPTX
Lecture 2-Trees in Data Structure Complete Lecture Slide
byKrishnenduRarhi
 
PPTX
unit-2-data structure and algorithms-tree-2024-1.pptx
bypritimalkhede
 
PPTX
TERMINOLOGIES OF TREE, TYPES OF TREE.pptx
byKALPANAC20
 
PPTX
Unit 5 Tree.pptx
bySurajSharma266169
 
PPTX
Binary and B+tree in data structure.pptx
byumanggargcse
 
PPTX
Binary tree
byMKalpanaDevi
 
Final tree.ppt tells about tree presentation
bynakulvarshney371
 
A binary tree is a hierarchical data structure where each node has at most tw...
bybeaulah5219
 
9. TREE Data Structure Non Linear Data Structure
bykejika1215
 
DS-UNIT-4zjufrusefihfacbciauhfbaiuhc.pptx
byDRCARIBOU
 
Data Structure of computer science and technology
bybhaskarsai499
 
NON-LINEAR DATA STRUCTURE-TREES.pptx
byRajitha Reddy Alugati
 
TREES 1.pptx
bySanGeet25
 
TREES basics simple introduction .pptx
bySanGeet25
 
Presentation1-Data structure S-Tree.pptx
byPraveen156918
 
Tree.pptx
byworldchannel
 
Data structure using c module 2
bysmruti sarangi
 
Tree
bybhumish
 
Trees in data structrures
byGaurav Sharma
 
Tree
byRaj Sarode
 
Lecture 2-Trees in Data Structure Complete Lecture Slide
byKrishnenduRarhi
 
unit-2-data structure and algorithms-tree-2024-1.pptx
bypritimalkhede
 
TERMINOLOGIES OF TREE, TYPES OF TREE.pptx
byKALPANAC20
 
Unit 5 Tree.pptx
bySurajSharma266169
 
Binary and B+tree in data structure.pptx
byumanggargcse
 
Binary tree
byMKalpanaDevi
 

More from rajinooka

PPT
Security topic in OS from Galvin book chp 14
byrajinooka
 
PPT
Deadlocks PPT Presentation from galvin book
byrajinooka
 
PPT
Linear Datsructure_stacks_Data Structure_PPT.ppt
byrajinooka
 
PPT
stack data structure , applications, advantages
byrajinooka
 
PPT
stack data structure and its applications , advantages, disadvantages etc
byrajinooka
 
PDF
l4a.pdf
byrajinooka
 
PDF
80x86_2.pdf
byrajinooka
 
PPT
UNIT-V.ppt
byrajinooka
 
PPT
Introduction to LaTeX - Dumitrescu.ppt
byrajinooka
 
PPTX
8-Queens Problem.pptx
byrajinooka
 
Security topic in OS from Galvin book chp 14
byrajinooka
 
Deadlocks PPT Presentation from galvin book
byrajinooka
 
Linear Datsructure_stacks_Data Structure_PPT.ppt
byrajinooka
 
stack data structure , applications, advantages
byrajinooka
 
stack data structure and its applications , advantages, disadvantages etc
byrajinooka
 
l4a.pdf
byrajinooka
 
80x86_2.pdf
byrajinooka
 
UNIT-V.ppt
byrajinooka
 
Introduction to LaTeX - Dumitrescu.ppt
byrajinooka
 
8-Queens Problem.pptx
byrajinooka
 

Recently uploaded

PPTX
GEMM tiling for weight stationary NCKU AISlab
bye24111071
 
PPTX
Optimizing Wave Energy Capture: Utilizing Variable-Pitch Turbine Blades in We...
byArijit Biswas
 
PDF
How Are Learning-Based Methods Reshaping Trajectory Planning in Autonomous D...
byimagnejane
 
PPTX
Hydrocarbon traps, migration and accumulation of petroleum
byAhmadnawaz144515
 
PPTX
Understanding UL Wire Options that Surpass Industry Standards
byEpec Engineered Technologies
 
PDF
Boundary Conditions of field components.pdf
byRCC Institute of Information Technology
 
PPTX
UNIT - V - Flexible Manufacturing System.pptx
byrameshrajendhra
 
PPT
23 EL PGS Sec-I (Shared).ppt power generation systems
byMehran university of engineering technology Pakistan
 
PPTX
An improved feature extraction algorithm of EEG signals
byAnirban Nath
 
PDF
Project photos of Caliagua's new Telemark project for FivePoint.
byjhines4
 
PPTX
AUV DESIGN and DEVELOPMENT FOR DEEP SEA MINING ( POLYMETALLIC NODULES) in MRC...
byArijit Biswas
 
PDF
Certified Cloud Security Professional (CCSP): Unit 4
byVICTOR MAESTRE RAMIREZ
 
PPTX
All About Introduction to Artificial IntelligenceAI.pptx
byRAJASEKARAN G
 
PPTX
COLLAGE PLACEMENT MANAGEMENT SYSTEM.pptx
bychaitanyachopade08
 
PDF
Somnath Mukherjee_BIM Specialist_Portfolio.pdf
bySomnathMukherjee980757
 
PDF
TOPIC 1.2 THE CONSTRUCTION PROJECT BY KJFF
byKHEN49
 
PPTX
Blockchain for Digital identity security
bysamirsarar2
 
PPTX
Heat Transfer Power Point presentation 1.1.pptx
bySolomon Raj
 
PPTX
DECARBONAZING REFINING INDUSTRY rev2.pptx
bygonzalezolabarriaped
 
PDF
International Journal of Network Security & Its Applications (IJNSA)
byIJNSA Journal
 
GEMM tiling for weight stationary NCKU AISlab
bye24111071
 
Optimizing Wave Energy Capture: Utilizing Variable-Pitch Turbine Blades in We...
byArijit Biswas
 
How Are Learning-Based Methods Reshaping Trajectory Planning in Autonomous D...
byimagnejane
 
Hydrocarbon traps, migration and accumulation of petroleum
byAhmadnawaz144515
 
Understanding UL Wire Options that Surpass Industry Standards
byEpec Engineered Technologies
 
Boundary Conditions of field components.pdf
byRCC Institute of Information Technology
 
UNIT - V - Flexible Manufacturing System.pptx
byrameshrajendhra
 
23 EL PGS Sec-I (Shared).ppt power generation systems
byMehran university of engineering technology Pakistan
 
An improved feature extraction algorithm of EEG signals
byAnirban Nath
 
Project photos of Caliagua's new Telemark project for FivePoint.
byjhines4
 
AUV DESIGN and DEVELOPMENT FOR DEEP SEA MINING ( POLYMETALLIC NODULES) in MRC...
byArijit Biswas
 
Certified Cloud Security Professional (CCSP): Unit 4
byVICTOR MAESTRE RAMIREZ
 
All About Introduction to Artificial IntelligenceAI.pptx
byRAJASEKARAN G
 
COLLAGE PLACEMENT MANAGEMENT SYSTEM.pptx
bychaitanyachopade08
 
Somnath Mukherjee_BIM Specialist_Portfolio.pdf
bySomnathMukherjee980757
 
TOPIC 1.2 THE CONSTRUCTION PROJECT BY KJFF
byKHEN49
 
Blockchain for Digital identity security
bysamirsarar2
 
Heat Transfer Power Point presentation 1.1.pptx
bySolomon Raj
 
DECARBONAZING REFINING INDUSTRY rev2.pptx
bygonzalezolabarriaped
 
International Journal of Network Security & Its Applications (IJNSA)
byIJNSA Journal
 

Basic Tree Data Structure BST Traversals .pptx

  • 1.
  • 2.
    Syllabus Binary Search Trees,Definition, Implementation, Operations- Searching, Insertion. BST Deletion. AVL Trees, Height of an AVL Tree, Operations, AVL Trees, Height of an AVL Tree, Operations, AVL Trees- Deletion and Searching, Red –Black Tree, Splay Trees, Previous question papers discussion
  • 3.
    Tree Data Structure Definition: Tree is a non-linear data structure which organizes data in hierarchical structure and this is a recursive definition. A tree data structure can also be defined as follows...  Tree data structure is a collection of data (Node) which is organized in hierarchical structure recursively  In tree data structure, every individual element is called as Node.  Node in a tree data structure stores the actual data of that particular element and link to next element in hierarchical structure.  In a tree data structure, if we have N number of nodes then we can have a maximum of N-1 number of links.
  • 4.
  • 5.
    Terminology 1. Root  Ina tree data structure, the first node is called as Root Node.  Every tree must have a root node.  We can say that the root node is the origin of the tree data structure.  In any tree, there must be only one root node. We never have multiple root nodes in a tree.
  • 6.
    2. Edge  Ina tree data structure, the connecting link between any two nodes is called as EDGE. In a tree with 'N' number of nodes there will be a maximum of 'N-1' number of edges. 3. Parent  In a tree data structure, the node which is a predecessor of any node is called as PARENT NODE.  In simple words, the node which has a branch from it to any other node is called a parent node. Parent node can also be defined as "The node which has child / children".
  • 7.
    4. Child  Ina tree data structure, the node which is descendant of any node is called as CHILD Node.  In simple words, the node which has a link from its parent node is called as child node. In a tree, any parent node can have any number of child nodes. In a tree, all the nodes except root are child nodes.
  • 9.
    5. Siblings  Ina tree data structure, nodes which belong to same Parent are called as SIBLINGS. In simple words, the nodes with the same parent are called Sibling nodes.
  • 10.
    6. Leaf  Ina tree data structure, the node which does not have a child is called as LEAF Node. In simple words, a leaf is a node with no child.  In a tree data structure, the leaf nodes are also called as External Nodes. External node is also a node with no child. In a tree, leaf node is also called as 'Terminal' node.
  • 11.
    7. Internal Nodes In a tree data structure, the node which has at least one child is called as INTERNAL Node. In simple words, an internal node is a node with at least one child.  In a tree data structure, nodes other than leaf nodes are called as Internal Nodes. The root node is also said to be Internal Node if the tree has more than one node. Internal nodes are also called as 'Non-Terminal' nodes.
  • 12.
    8. Degree  Ina tree data structure, the total number of children of a node is called as DEGREE of that Node. In simple words, the Degree of a node is total number of children it has.  The highest degree of a node among all the nodes in a tree is called as 'Degree of Tree'
  • 13.
    9. Level  Ina tree data structure, the root node is said to be at Level 0 and the children of root node are at Level 1 and the children of the nodes which are at Level 1 will be at Level 2 and so on... In simple words, in a tree each step from top to bottom is called as a Level and the Level count starts with '0' and incremented by one at each level (Step).
  • 14.
    10. Height  Ina tree data structure, the total number of edges from leaf node to a particular node in the longest path is called as HEIGHT of that Node.  In a tree, height of the root node is said to be height of the tree. In a tree, height of all leaf nodes is '0'.
  • 15.
    11. Depth  Ina tree data structure, the total number of egdes from root node to a particular node is called as DEPTH of that Node.  In a tree, the total number of edges from root node to a leaf node in the longest path is said to be Depth of the tree.  In simple words, the highest depth of any leaf node in a tree is said to be depth of that tree. In a tree, depth of the root node is '0’.
  • 16.
    12. Path  Ina tree data structure, the sequence of Nodes and Edges from one node to another node is called as PATH between that two Nodes.  Length of a Path is total number of nodes in that path. In below example the path A - B - E - J has length 4.
  • 17.
    13. Sub Tree In a tree data structure, each child from a node forms a subtree recursively. Every child node will form a subtree on its parent node.
  • 18.
    Binary Tree Datastructure A tree in which every node can have a maximum of two children is called Binary Tree.  In a normal tree, every node can have any number of children.  A binary tree is a special type of tree data structure in which every node can have a maximum of 2 children. One is known as a left child and the other is known as right child.
  • 19.
     There aredifferent types of binary trees and they are...  1. Strictly Binary Tree  In a binary tree, every node can have a maximum of two children. But in strictly binary tree, every node should have exactly two children or none. That means every internal node must have exactly two children. A strictly Binary Tree can be defined as follows...  A binary tree in which every node has either two or zero number of children is called Strictly Binary Tree  Strictly binary tree is also called as Full Binary Tree or Proper Binary Tree or 2-Tree.  Strictly binary tree data structure is used to represent mathematical expressions.
  • 20.
  • 21.
    2. Complete BinaryTree  In a binary tree, every node can have a maximum of two children. But in strictly binary tree, every node should have exactly two children or none and in complete binary tree all the nodes must have exactly two children and at every level of complete binary tree there must be 2level number of nodes. For example at level 2 there must be 22 = 4 nodes and at level 3 there must be 23 = 8 nodes.  A binary tree in which every internal node has exactly two children and all leaf nodes are at same level is called Complete Binary Tree.  Complete binary tree is also called as Perfect Binary Tree
  • 22.
    3. Extended BinaryTree  A binary tree can be converted into Full Binary tree by adding dummy nodes to existing nodes wherever required.  The full binary tree obtained by adding dummy nodes to a binary tree is called as Extended Binary Tree.  In above figure, a normal binary tree is converted into full binary tree by adding dummy nodes (In pink colour).
  • 23.
    Binary Tree Representations A binary tree data structure is represented using two methods. Those methods are as follows... 1. Array Representation 2. Linked List Representation  Consider the following binary tree...
  • 24.
    1. Array Representationof Binary Tree  In array representation of a binary tree, we use one-dimensional array (1-D Array) to represent a binary tree.  Consider the above example of a binary tree and it is represented as follows...  To represent a binary tree of depth 'n' using array representation, we need one dimensional array with a maximum size of 2n + 1.
  • 25.
    2. Linked ListRepresentation of Binary Tree  We use a double linked list to represent a binary tree. In a double linked list, every node consists of three fields.  First field for storing left child address, second for storing actual data and third for storing right child address.  In this linked list representation, a node has the following structure...  The above example of the binary tree represented using Linked list representation is shown as follows...
  • 27.
    Binary Tree Traversals When we wanted to display a binary tree, we need to follow some order in which all the nodes of that binary tree must be displayed. In any binary tree, displaying order of nodes depends on the traversal method.  Displaying (or) visiting order of nodes in a binary tree is called as Binary Tree Traversal.  There are three types of binary tree traversals. 1. In - Order Traversal 2. Pre - Order Traversal 3. Post - Order Traversal  Consider the following binary tree...
  • 28.
    1. In -Order Traversal ( leftChild - root - rightChild )  In In-Order traversal, the root node is visited between the left child and right child. In this traversal, the left child node is visited first, then the root node is visited and later we go for visiting the right child node. This in-order traversal is applicable for every root node of all subtrees in the tree. This is performed recursively for all nodes in the tree.  In the above example of a binary tree, first we try to visit left child of root node 'A', but A's left child 'B' is a root node for left subtree. so we try to visit its (B's) left child 'D' and again D is a root for subtree with nodes D, I and J.  So we try to visit its left child 'I' and it is the leftmost child. So first we visit 'I' then go for its root node 'D' and later we visit D's right child 'J'. With this we have completed the left part of node B. Then visit 'B' and next B's right child 'F' is visited.  With this we have completed left part of node A. Then visit root node 'A'. With this we have completed left and root parts of node A. Then we go for the right part of the node A. In right of A again there is a subtree with root C.  So go for left child of C and again it is a subtree with root G. But G does not have left part so we visit 'G' and then visit G's right child K.  With this we have completed the left part of node C. Then visit root node 'C' and next visit C's right child 'H' which is the rightmost child in the tree. So we stop the process.  That means here we have visited in the order of I - D - J - B - F - A - G - K - C - H using In-Order Traversal.
  • 29.
     In-Order Traversalfor above example of binary tree is I - D - J - B - F - A - G - K - C - H Pre - Order Traversal ( root - leftChild - rightChild )  In Pre-Order traversal, the root node is visited before the left child and right child nodes.  In this traversal, the root node is visited first, then its left child and later its right child. This pre-order traversal is applicable for every root node of all subtrees in the tree.  In the above example of binary tree, first we visit root node 'A' then visit its left child 'B' which is a root for D and F.  So we visit B's left child 'D' and again D is a root for I and J. So we visit D's left child 'I' which is the leftmost child. So next we go for visiting D's right child 'J’.  With this we have completed root, left and right parts of node D and root, left parts of node B. Next visit B's right child 'F'. With this we have completed root and left parts of node A.  So we go for A's right child 'C' which is a root node for G and H. After visiting C, we go for its left child 'G' which is a root for node K. So next we visit left of G, but it does not have left child so we go for G's right child 'K’.  With this, we have completed node C's root and left parts. Next visit C's right child 'H' which is the rightmost child in the tree. So we stop the process.  That means here we have visited in the order of A-B-D-I-J-F-C-G-K-H using Pre-Order Traversal.  Pre-Order Traversal for above example binary tree is A - B - D - I - J - F - C - G - K - H
  • 30.
    3. Post -Order Traversal ( leftChild - rightChild - root )  In Post-Order traversal, the root node is visited after left child and right child. In this traversal, left child node is visited first, then its right child and then its root node. This is recursively performed until the right most node is visited.  Here we have visited in the order of I - J - D - F - B - K - G - H - C - A using Post-Order Traversal.  Post-Order Traversal for above example binary tree is I - J - D - F - B - K - G - H - C – A
  • 31.
    Binary Search Tree In a binary tree, every node can have a maximum of two children but there is no need to maintain the order of nodes basing on their values. In a binary tree, the elements are arranged in the order they arrive at the tree from top to bottom and left to right.  A binary tree has the following time complexities... Search Operation - O(n) Insertion Operation - O(1) Deletion Operation - O(n)  To enhance the performance of binary tree, we use a special type of binary tree known as Binary Search Tree. Binary search tree mainly focuses on the search operation in a binary tree.  Binary search tree can be defined as follows...  Binary Search Tree is a binary tree in which every node contains only smaller values in its left subtree and only larger values in its right subtree.  In a binary search tree, all the nodes in the left subtree of any node contains smaller values and all the nodes in the right subtree of any node contains larger values as shown in the following figure...
  • 32.
    Example The following treeis a Binary Search Tree. In this tree, left subtree of every node contains nodes with smaller values and right subtree of every node contains larger values.
  • 33.
    Every binary searchtree is a binary tree but every binary tree need not to be binary search tree.
  • 34.
     Operations ona Binary Search Tree  The following operations are performed on a binary search tree... 1. Search 2. Insertion 3. Deletion
  • 35.
    Search Operation inBST In a binary search tree, the search operation is performed with O(log n) time complexity. The search operation is performed as follows... Step 1 - Read the search element from the user. Step 2 - Compare the search element with the value of root node in the tree. Step 3 - If both are matched, then display "Given node is found!!!" and terminate the function Step 4 - If both are not matched, then check whether search element is smaller or larger than that node value. Step 5 - If search element is smaller, then continue the search process in left subtree. Step 6- If search element is larger, then continue the search process in right subtree. Step 7 - Repeat the same until we find the exact element or until the search element is compared with the leaf node Step 8 - If we reach to the node having the value equal to the search value then display "Element is found" and terminate the function. Step 9 - If we reach to the leaf node and if it is also not matched with the search element, then display "Element is not found" and terminate the function.
  • 36.
    Insertion Operation inBST  In a binary search tree, the insertion operation is performed with O(log n) time complexity. In binary search tree, new node is always inserted as a leaf node. The insertion operation is performed as follows... • Step 1 - Create a newNode with given value and set its left and right to NULL. • Step 2 - Check whether tree is Empty. • Step 3 - If the tree is Empty, then set root to newNode. • Step 4 - If the tree is Not Empty, then check whether the value of newNode is smaller or larger than the node (here it is root node). • Step 5 - If newNode is smaller than or equal to the node then move to its left child. If newNode is larger than the node then move to its right child. • Step 6- Repeat the above steps until we reach to the leaf node (i.e., reaches to NULL). • Step 7 - After reaching the leaf node, insert the newNode as left child if the newNode is smaller or equal to that leaf node or else insert it as right child.
  • 37.
    Deletion Operation inBST  In a binary search tree, the deletion operation is performed with O(log n) time complexity. Deleting a node from Binary search tree includes following three cases...  Case 1: Deleting a Leaf node (A node with no children)  Case 2: Deleting a node with one child  Case 3: Deleting a node with two children
  • 38.
     Case 1:Deleting a leaf node  We use the following steps to delete a leaf node from BST... • Step 1 - Find the node to be deleted using search operation • Step 2 - Delete the node using free function (If it is a leaf) and terminate the function.
  • 39.
    Case 2: Deletinga node with one child  We use the following steps to delete a node with one child from BST... • Step 1 - Find the node to be deleted using search operation • Step 2 - If it has only one child then create a link between its parent node and child node. • Step 3 - Delete the node using free function and terminate the function.
  • 40.
    Case 3: Deletinga node with two children  We use the following steps to delete a node with two children from BST... • Step 1 - Find the node to be deleted using search operation • Step 2 - If it has two children, then find the largest node in its left subtree (OR) the smallest node in its right subtree. • Step 3 - Swap both deleting node and node which is found in the above step. • Step 4 - Then check whether deleting node came to case 1 or case 2 or else goto step 2 • Step 5 - If it comes to case 1, then delete using case 1 logic. • Step 6- If it comes to case 2, then delete using case 2 logic. • Step 7 - Repeat the same process until the node is deleted from the tree.
  • 41.
    Example  Construct aBinary Search Tree by inserting the following sequence of numbers...  10,12,5,4,20,8,7,15 and 13  Above elements are inserted into a Binary Search Tree as follows...