Binary Searching Algorithm PowerPoint Presentation

Binary search is the search technique that works
efficiently on sorted lists. Hence, to search an element
into some list using the binary search technique, we
must ensure that the list is sorted.
Binary search follows the divide and conquer approach
in which the list is divided into two halves, and the item is
compared with the middle element of the list. If the match
is found then, the location of the middle element is
returned. Otherwise, we search into either of the halves
depending upon the result produced through the match.

Binary_Search(a, lower_bound, upper_bound, val) // 'a' is the
given array, 'lower_bound' is the index of the first array element, 'upper_bound' is
the index of the last array element, 'val' is the value to search
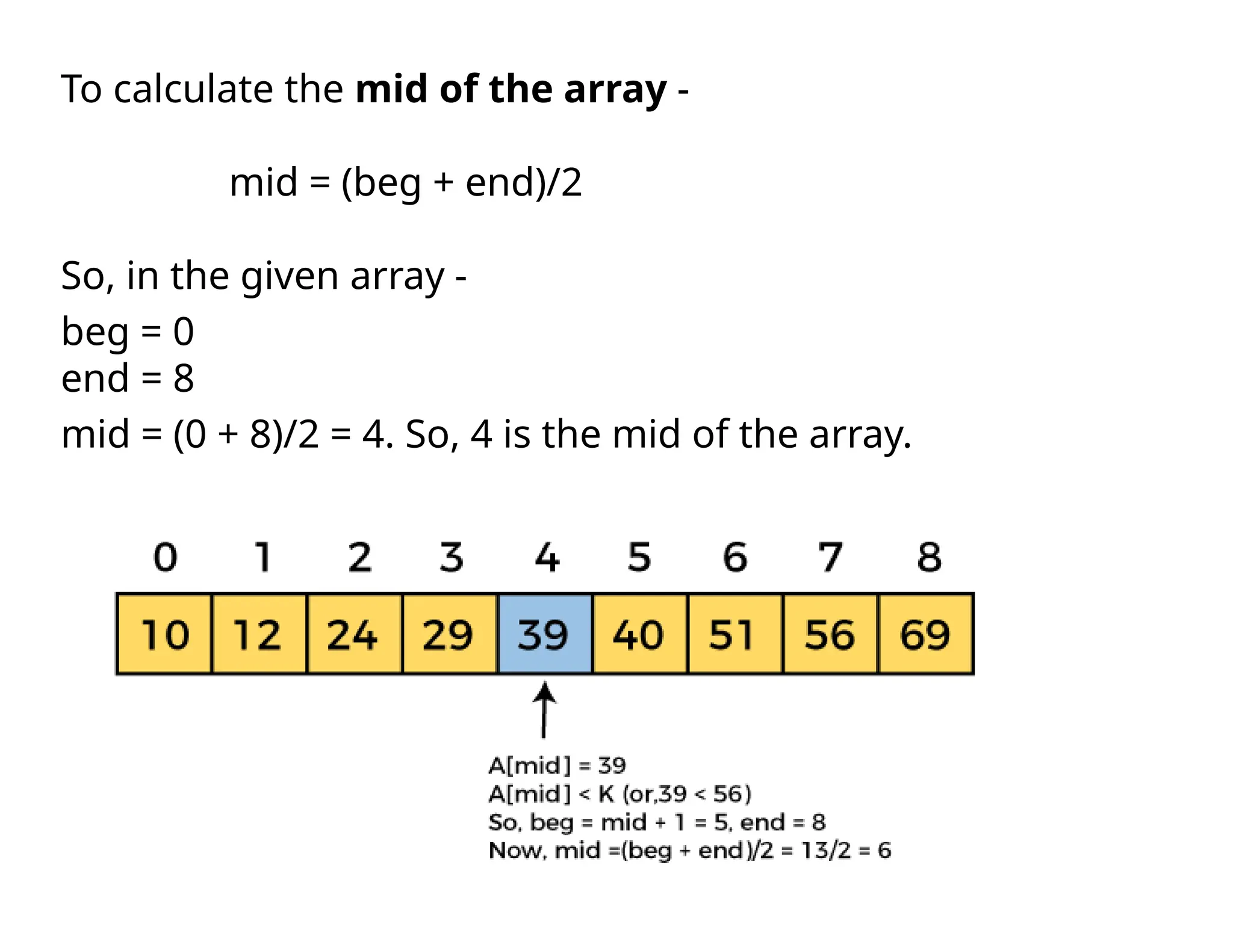
Step 1: set beg = lower_bound, end = upper_bound, pos = - 1
Step 2: repeat steps 3 and 4 while beg <=end
Step 3: set mid = (beg + end)/2
Step 4: if a[mid] = val
set pos = mid
print pos
go to step 6
else if a[mid] > val
set end = mid - 1
else
set beg = mid + 1
[end of if]
[end of loop]
Step 5: if pos = -1
print "value is not present in the array"
[end of if]
Step 6: exit

Working of Binary search
There are two methods to implement the binary search
algorithm -
■ Iterative method
■ Recursive method
The recursive method of binary search follows the divide
and conquer approach.
Let the elements of array are -
Let the element to search is, K =
56

To calculate the mid of the array -
mid = (beg + end)/2
So, in the given array -
beg = 0
end = 8
mid = (0 + 8)/2 = 4. So, 4 is the mid of the array.

Now, the element to search is found. So algorithm will return
the index of the element matched.

Binary search in C language
#include <stdio.h>
int binarySearch(int a[], int beg, int end, int val)
{
int mid;
if(end >= beg)
{
mid = (beg + end)/2;
if(a[mid] == val)
{
return mid+1;
}
else if(a[mid] < val)
{
return binarySearch(a, mid+1, end, val);
}
else
{
return binarySearch(a, beg, mid-1, val);
}
}
return -1;
}

int main() {
int a[] = {11, 14, 25, 30, 40, 41, 52, 57, 70};
int val = 40;
int n = sizeof(a) / sizeof(a[0]);
int res = binarySearch(a, 0, n-1, val);
printf("The elements of the array are - ");
for (int i = 0; i < n; i++)
printf("%d ", a[i]);
printf("nElement to be searched is - %d", val);
if (res == -1)
printf("nElement is not present in the array");
else
printf("nElement is present at %d position of array", res);
return 0;
}

Binary search in Java language
class BinarySearch {
static int binarySearch(int a[], int beg, int end, int val)
{
int mid;
if(end >= beg)
{
mid = (beg + end)/2;
if(a[mid] == val)
{
return mid+1;
}
else if(a[mid] < val)
{
return binarySearch(a, mid+1, end, val);
}
else
{
return binarySearch(a, beg, mid-1, val);
}
}
return -1;
}

public static void main(String args[]) {
int a[] = {8, 10, 22, 27, 37, 44, 49, 55, 69};
int val = 37;
int n = a.length;
int res = binarySearch(a, 0, n-1, val);
System.out.print("The elements of the array are: ");
for (int i = 0; i < n; i++)
{
System.out.print(a[i] + " ");
}
System.out.println();
System.out.println("Element to be searched is: " + val);
if (res == -1)
System.out.println("Element is not present in the array");
else
System.out.println("Element is present at " + res + " position of
array");
}
}

Binary Searching Algorithm PowerPoint Presentation

More Related Content

Similar to Binary Searching Algorithm PowerPoint Presentation

Recently uploaded

Binary Searching Algorithm PowerPoint Presentation