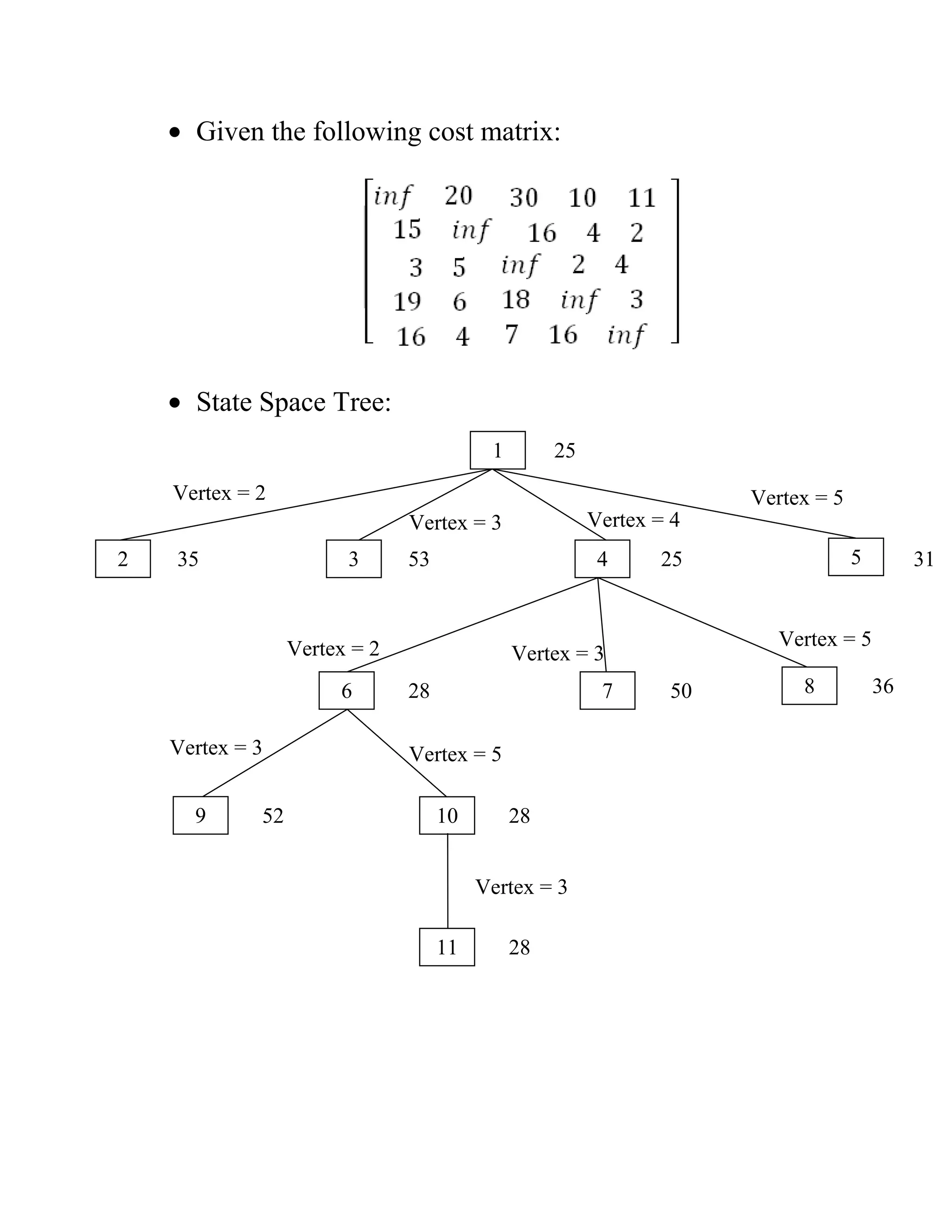
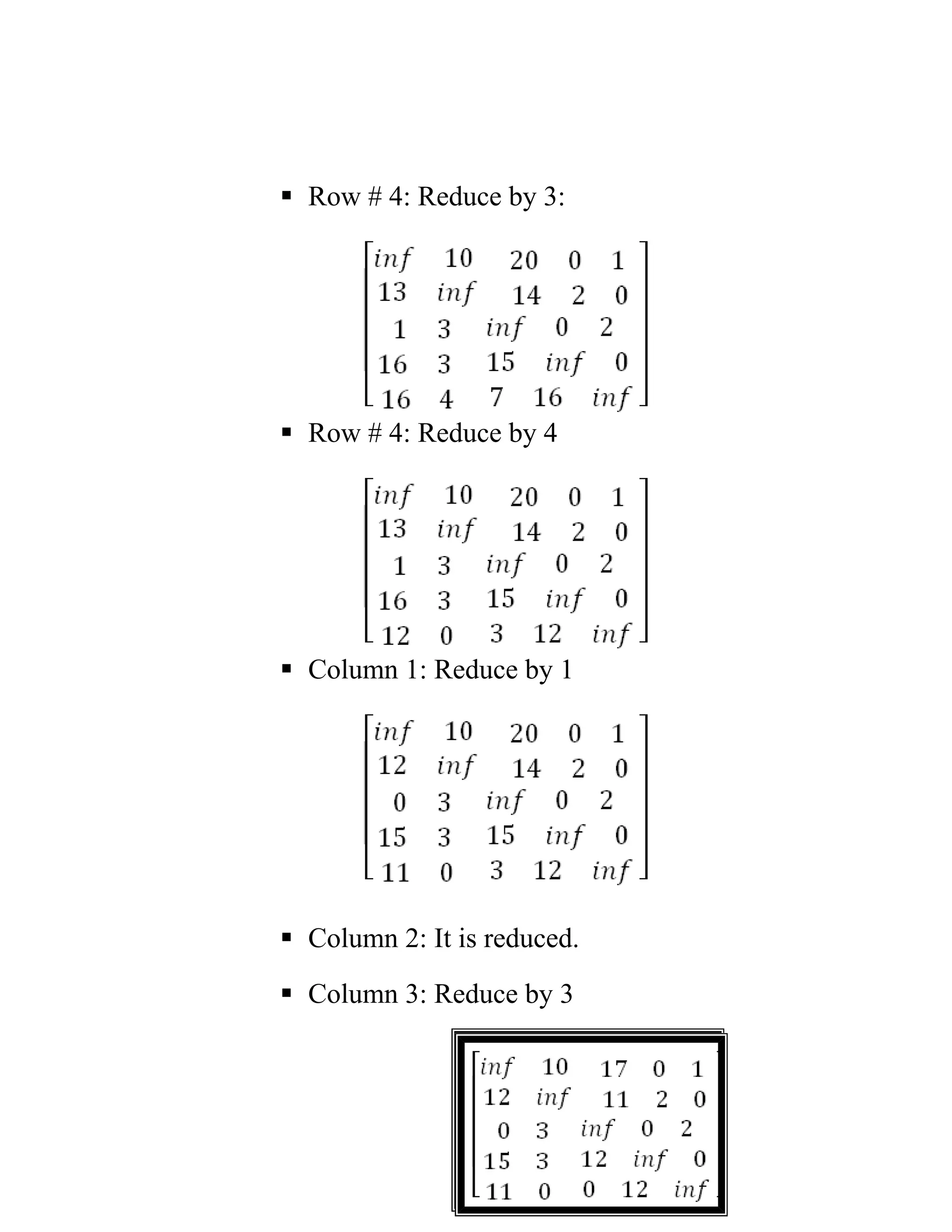
Branch and Bound is a state space search algorithm that involves generating all children of a node before exploring any children. It uses lower bounds to prune parts of the search tree that cannot produce better solutions than what has already been found. The algorithm is demonstrated on problems like the 8-puzzle and Travelling Salesman Problem. For TSP, it works by reducing the cost matrix at each node to calculate lower bounds, and exploring the child with the lowest estimated total cost.