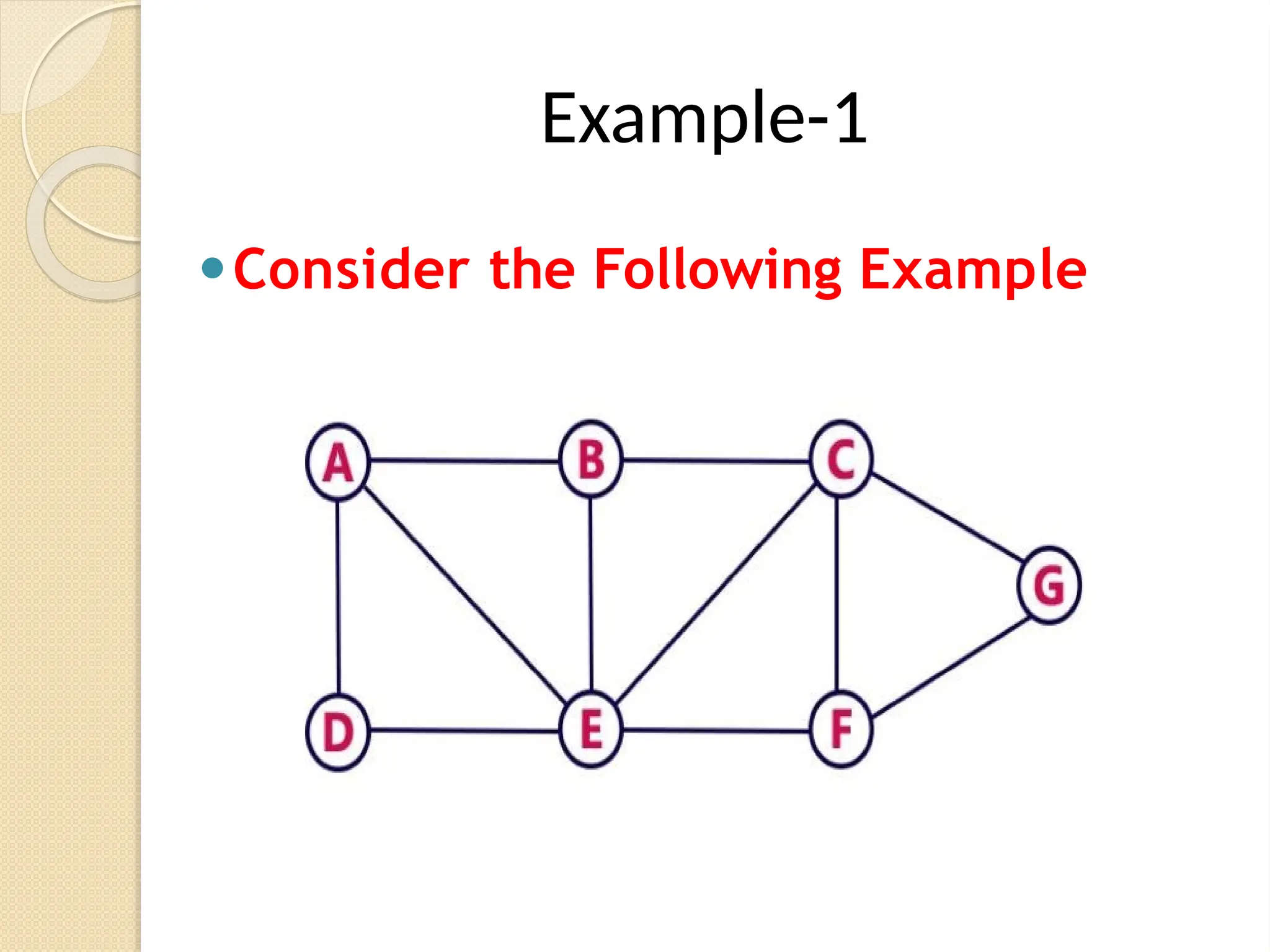
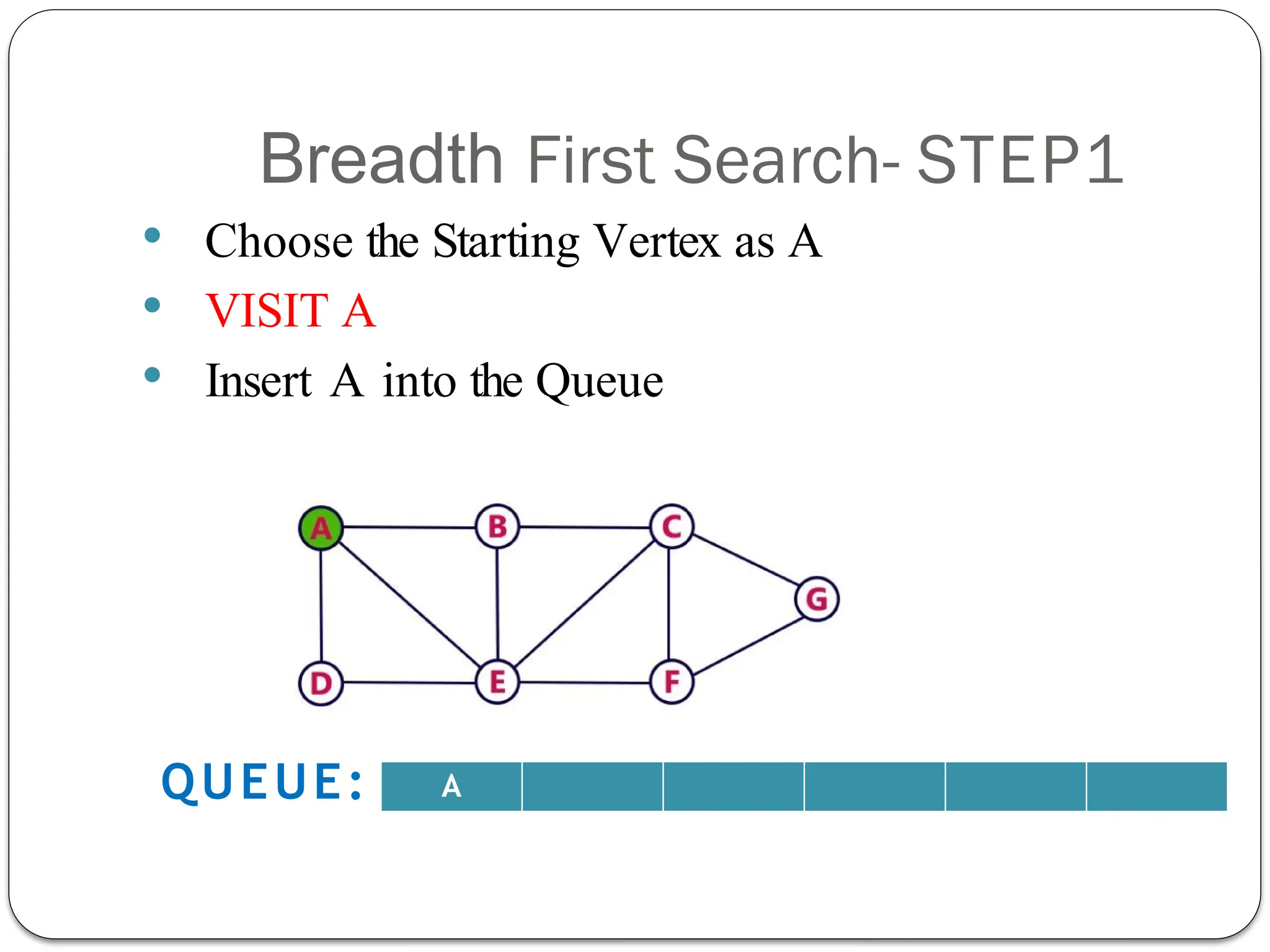
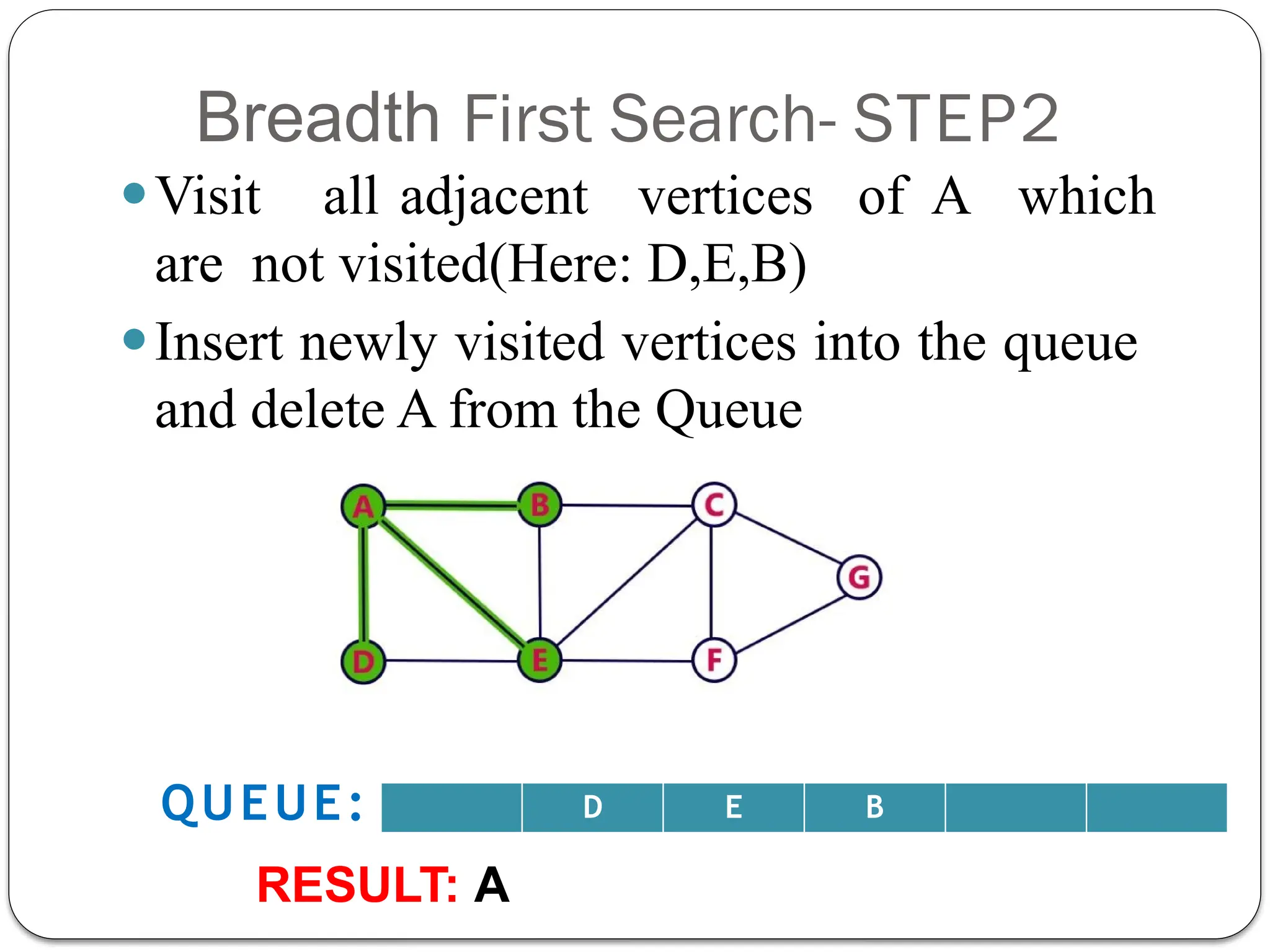
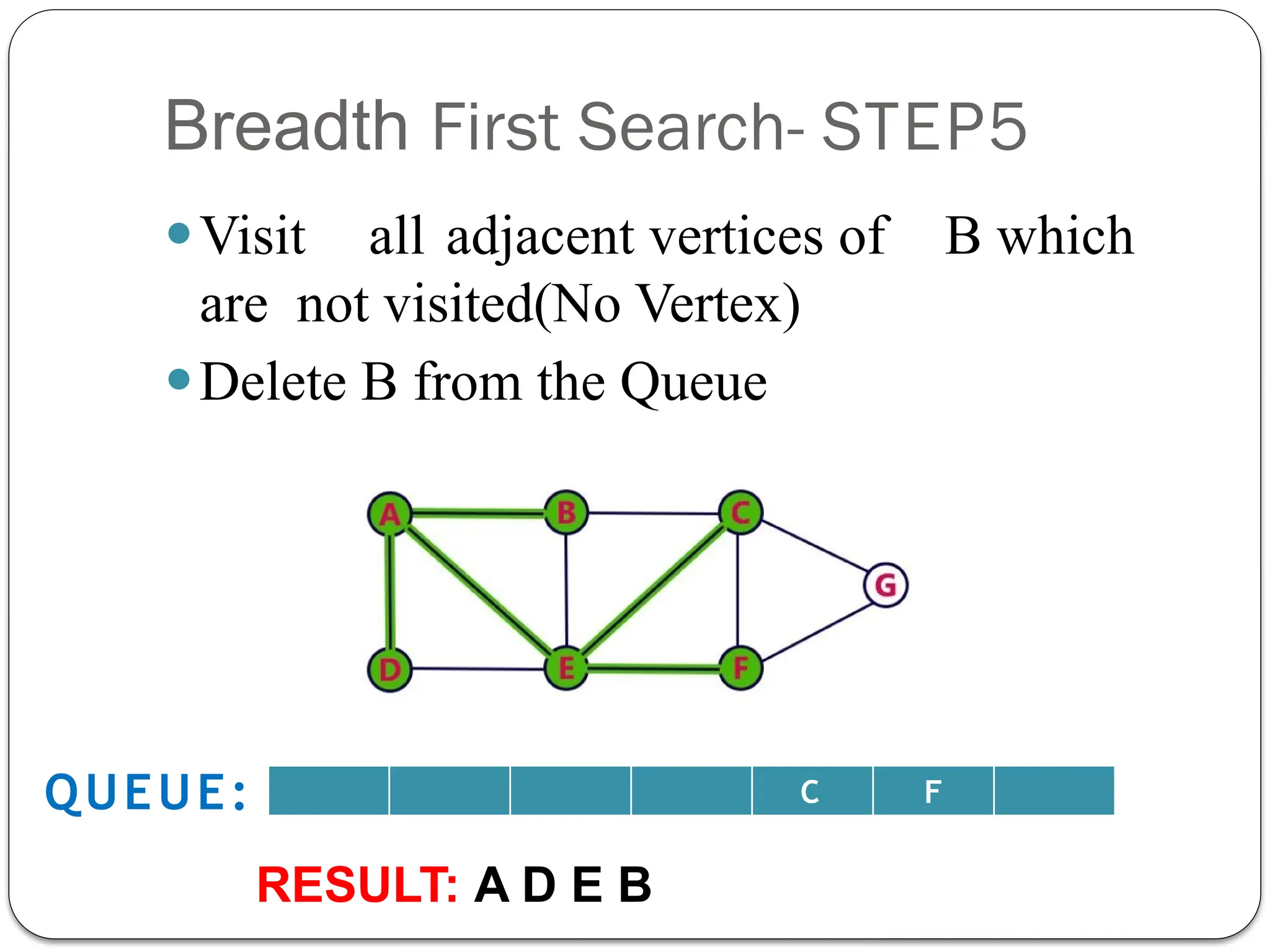
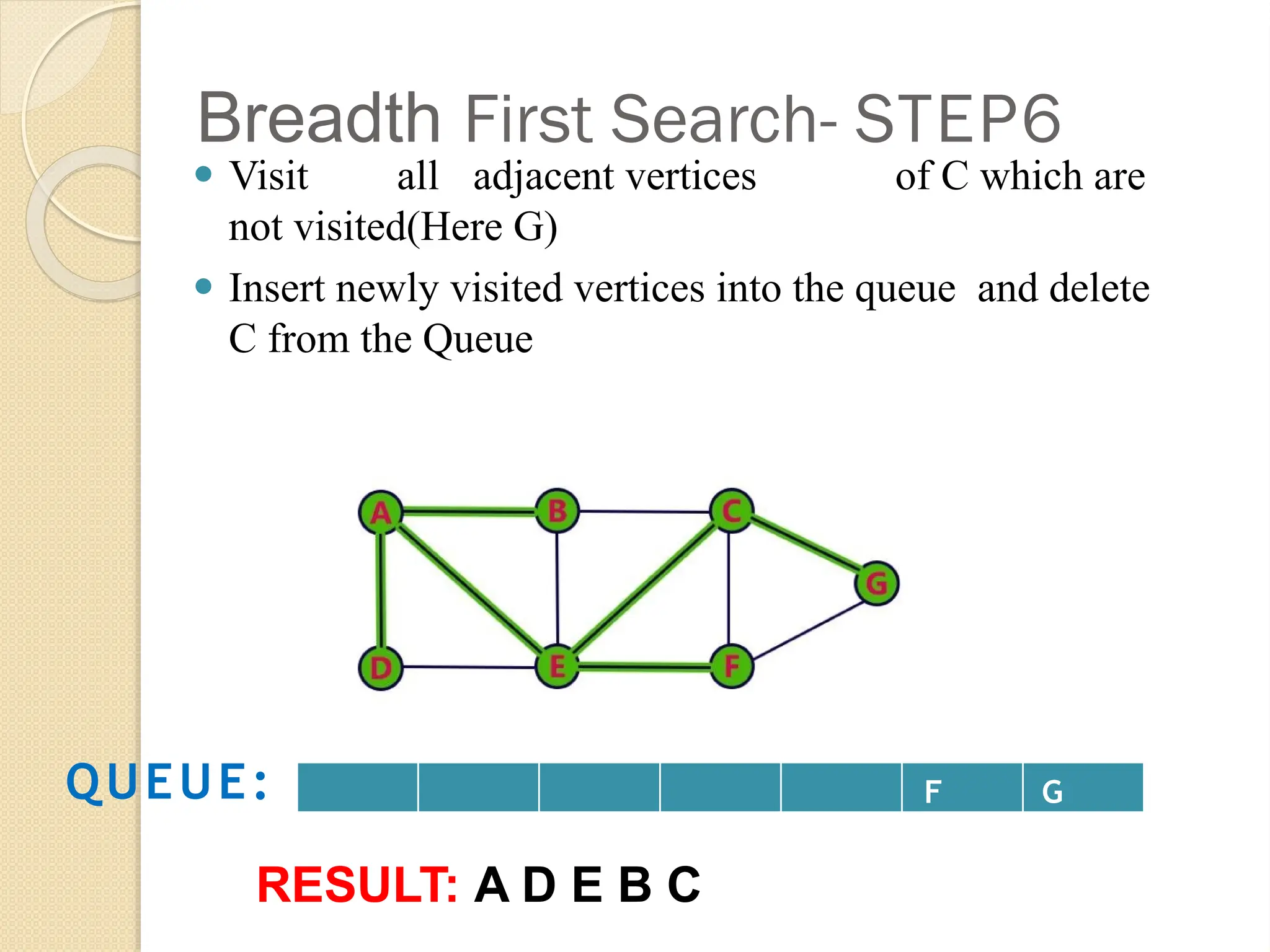
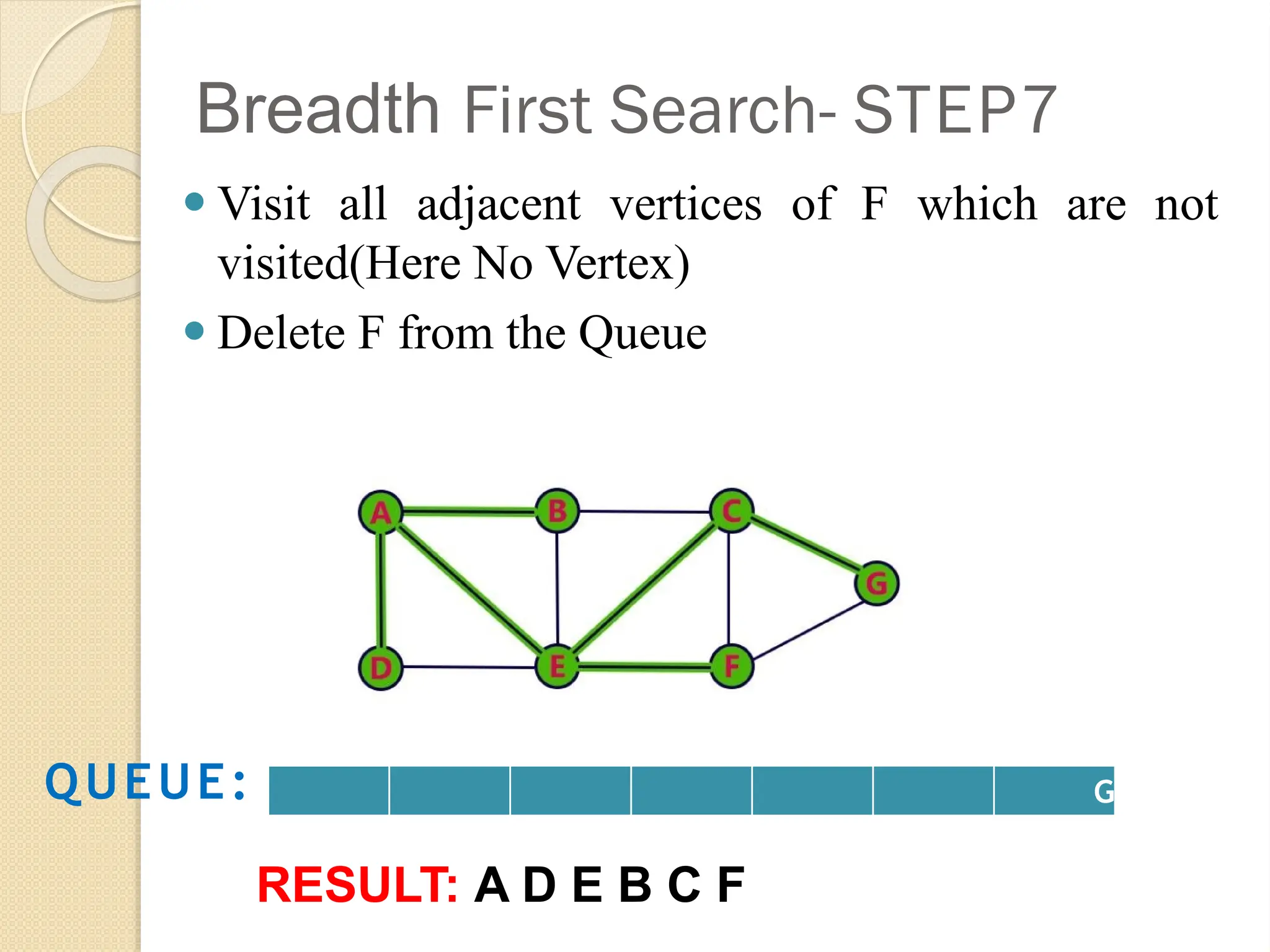
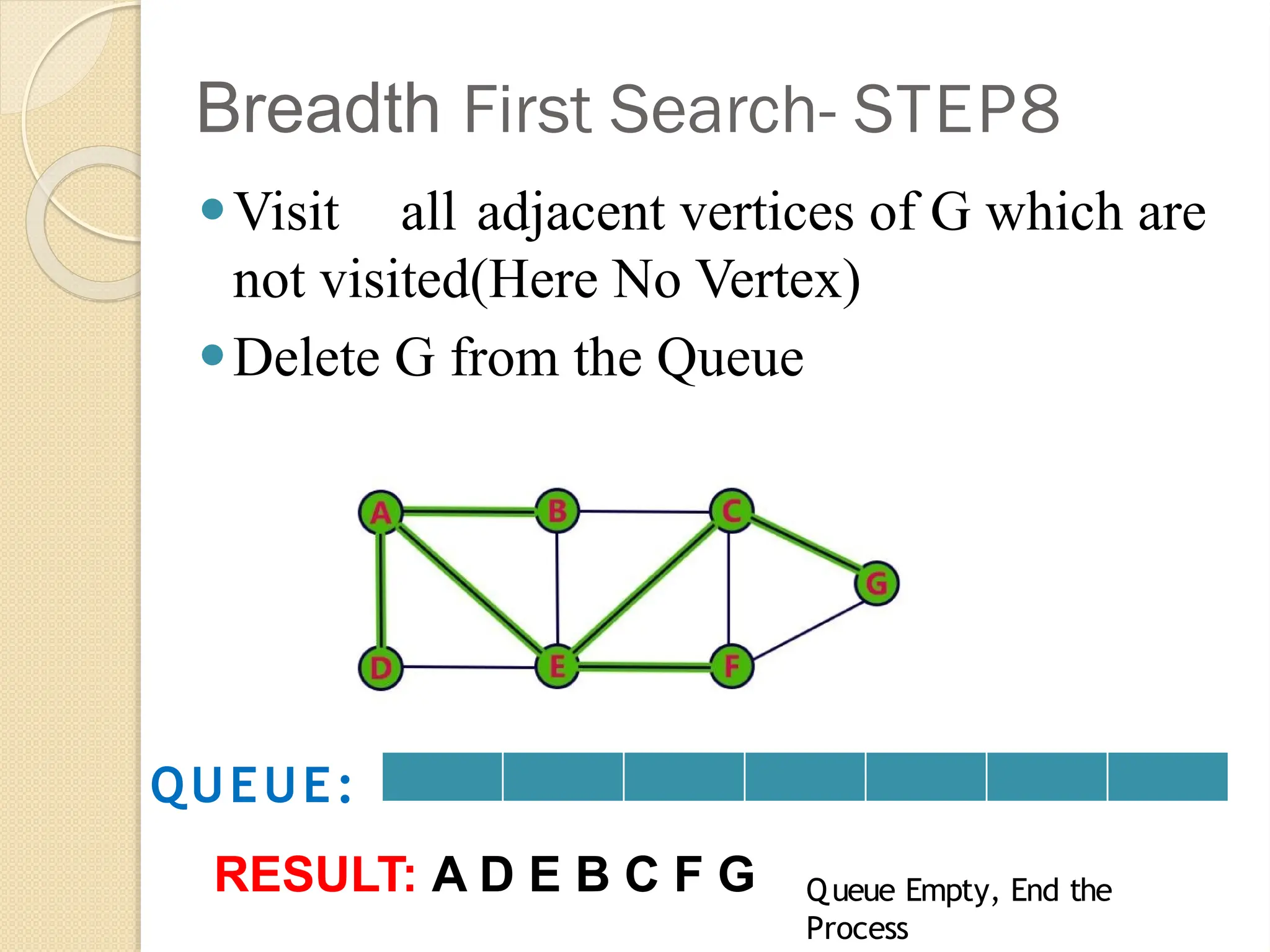
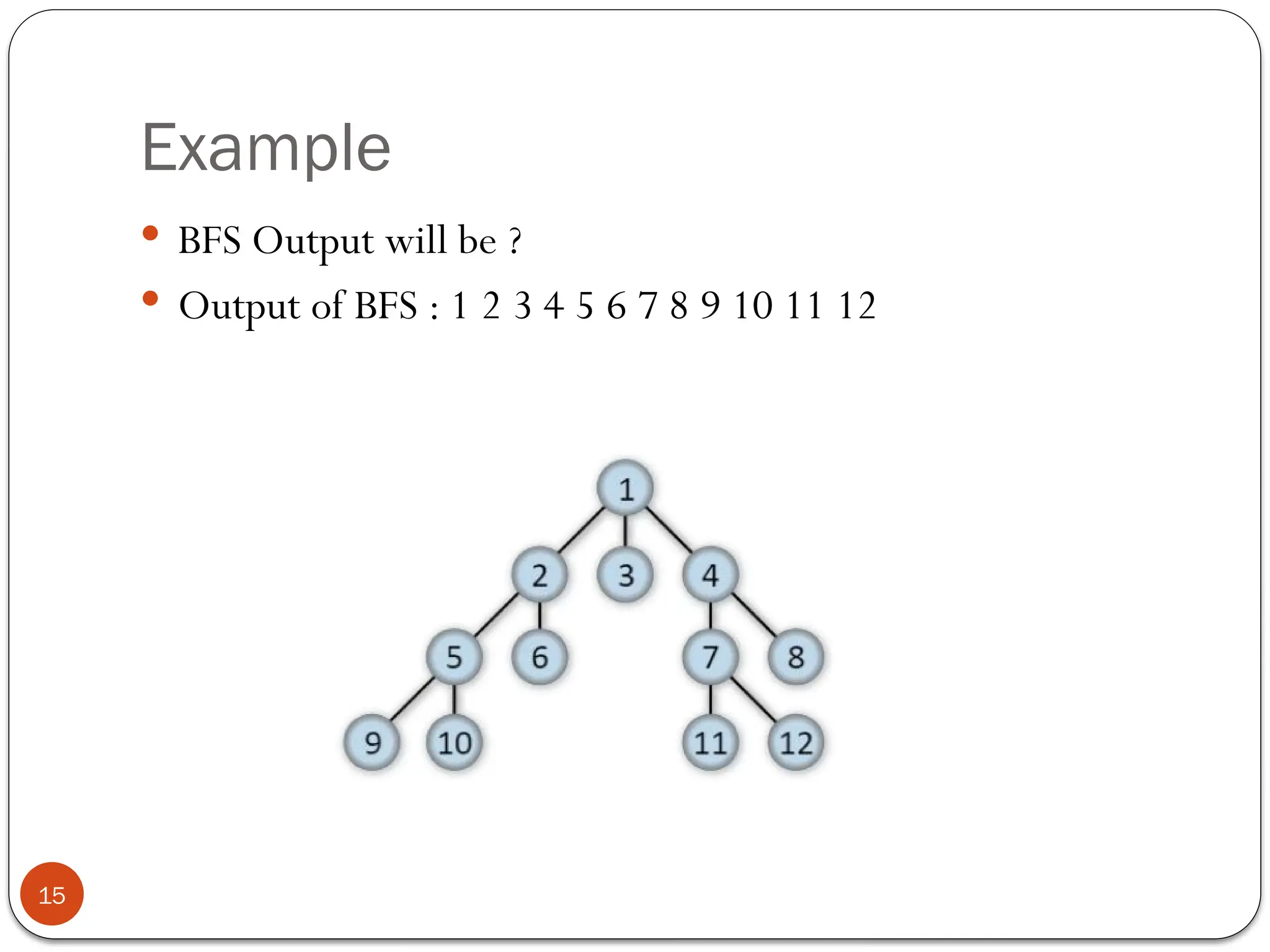
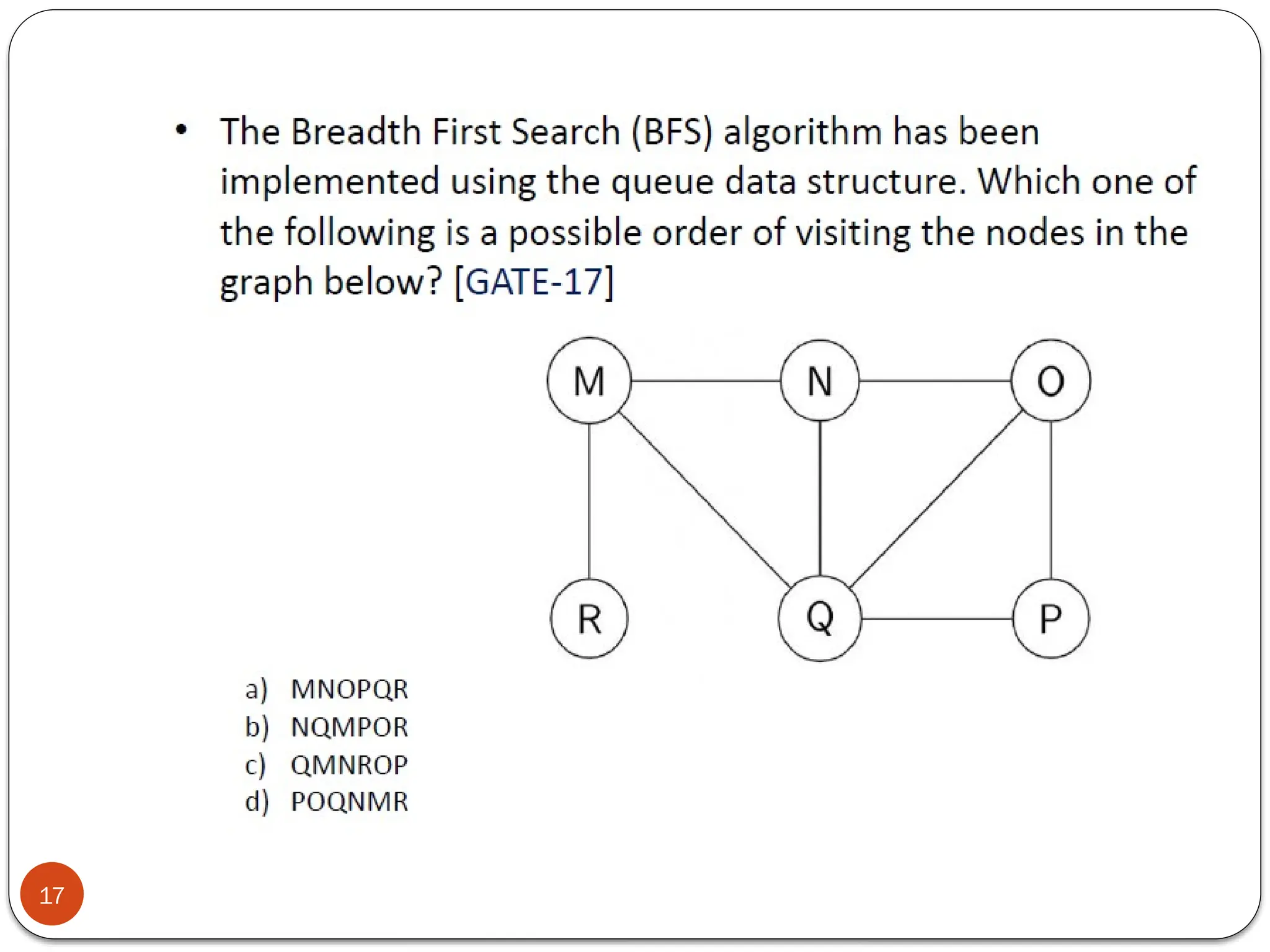
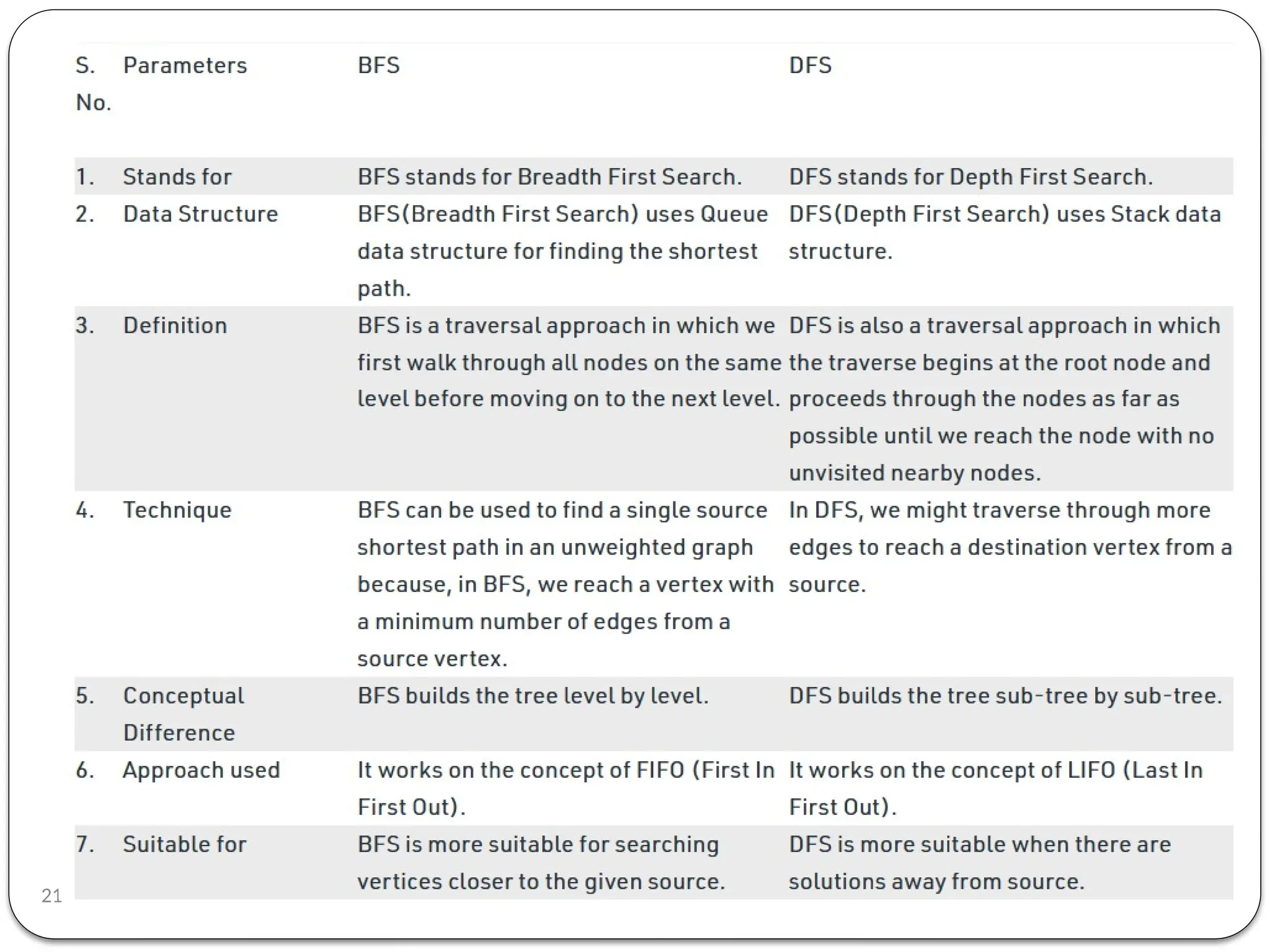
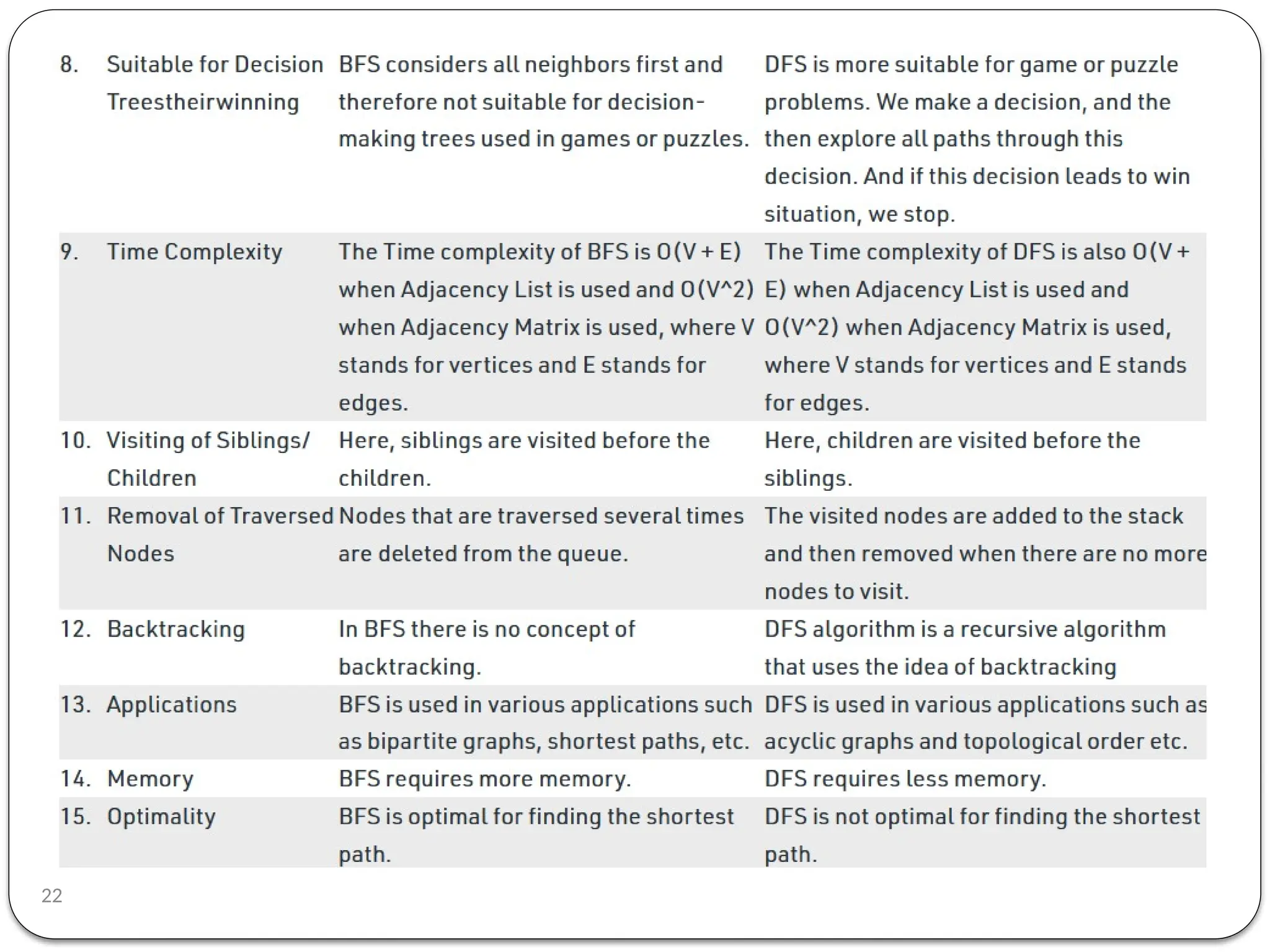
Breadth-First Search (BFS) is an algorithm used to traverse tree or graph data structures, exploring all neighbor nodes at the current depth before moving deeper. It involves using a queue to track nodes, marking them as visited, and inserting unvisited neighbors until the queue is empty. BFS guarantees a solution if one exists and is optimal for unweighted graphs, but requires significant memory and can be time-consuming for distant solutions.