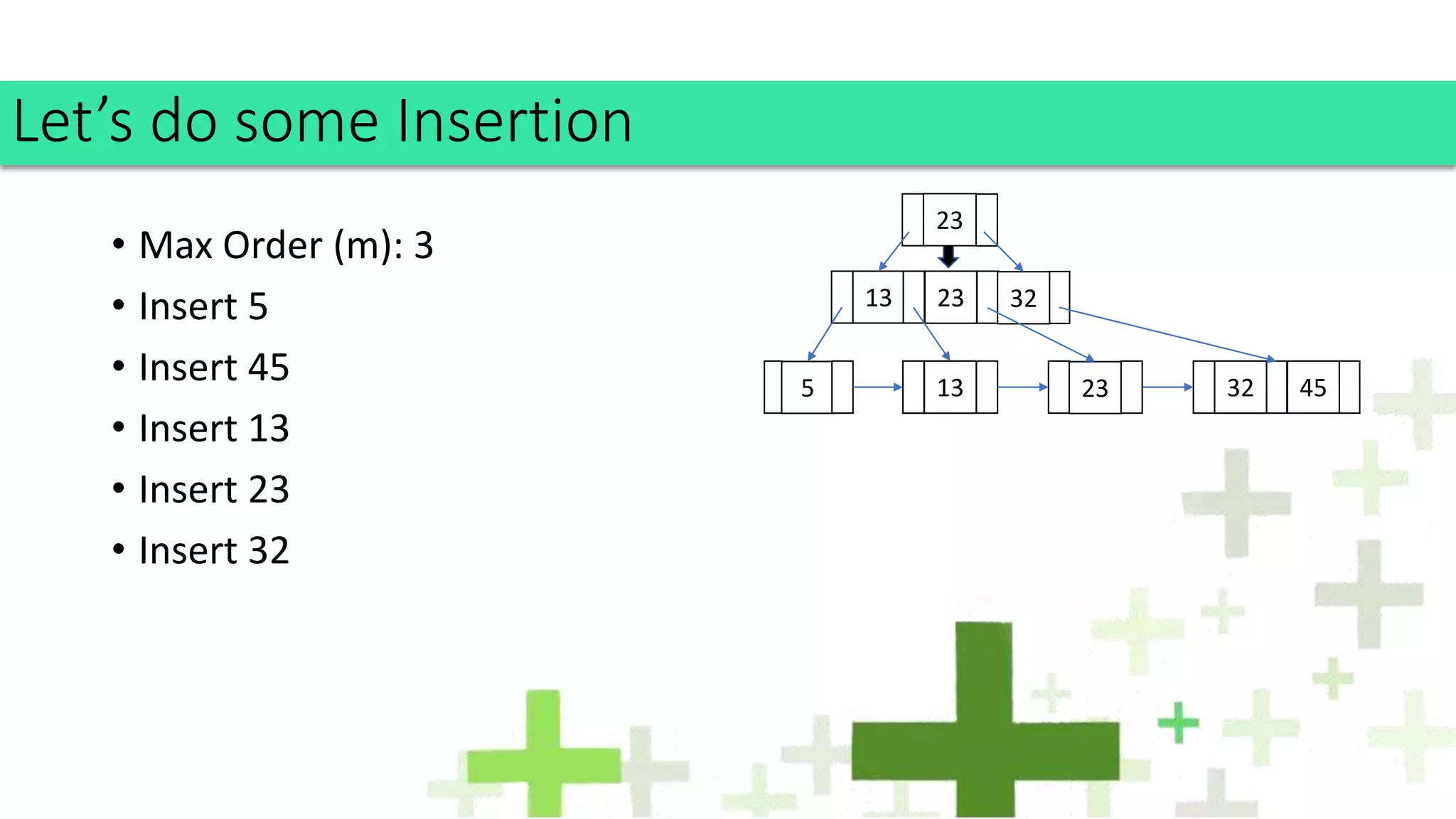
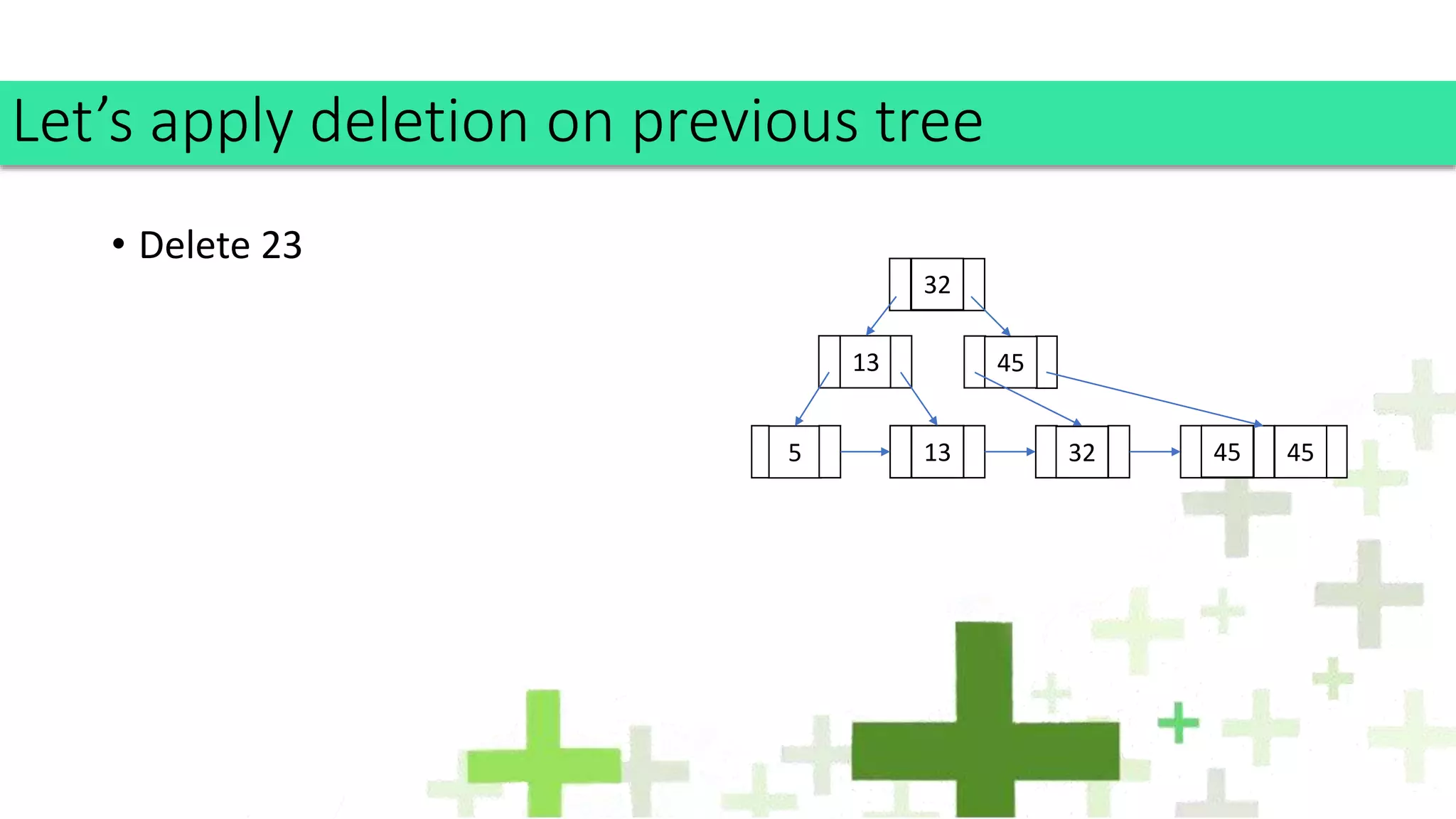
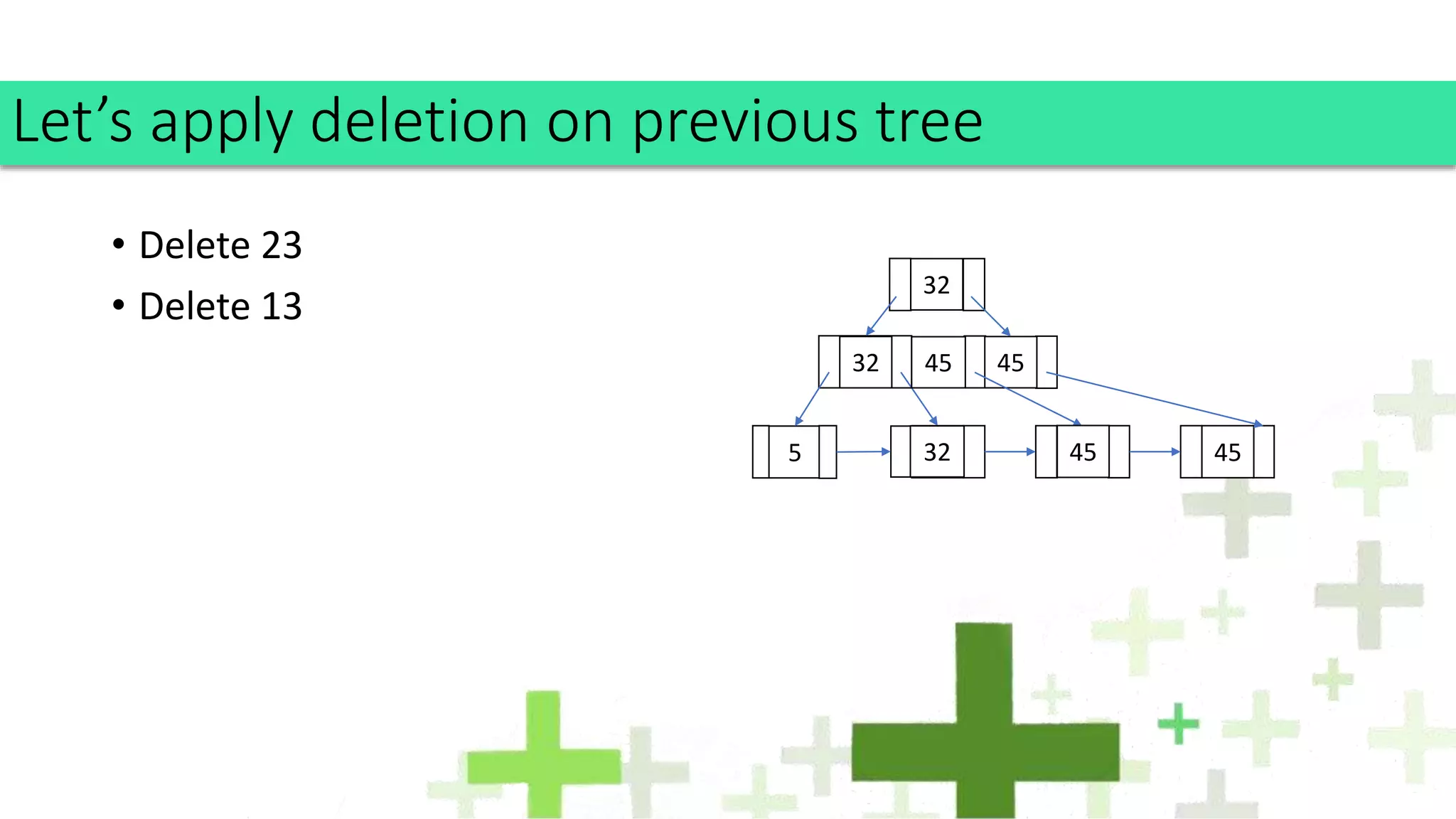
The document discusses B+ trees, an optimization of B trees, highlighting their structure, properties, and operational rules for insertion and deletion. Key features include storing all data in leaf nodes, maximizing branching factors for improved performance, and facilitating efficient searching due to ordered leaves. Applications of B+ trees span various file systems and databases, making them integral for indexing and data storage.