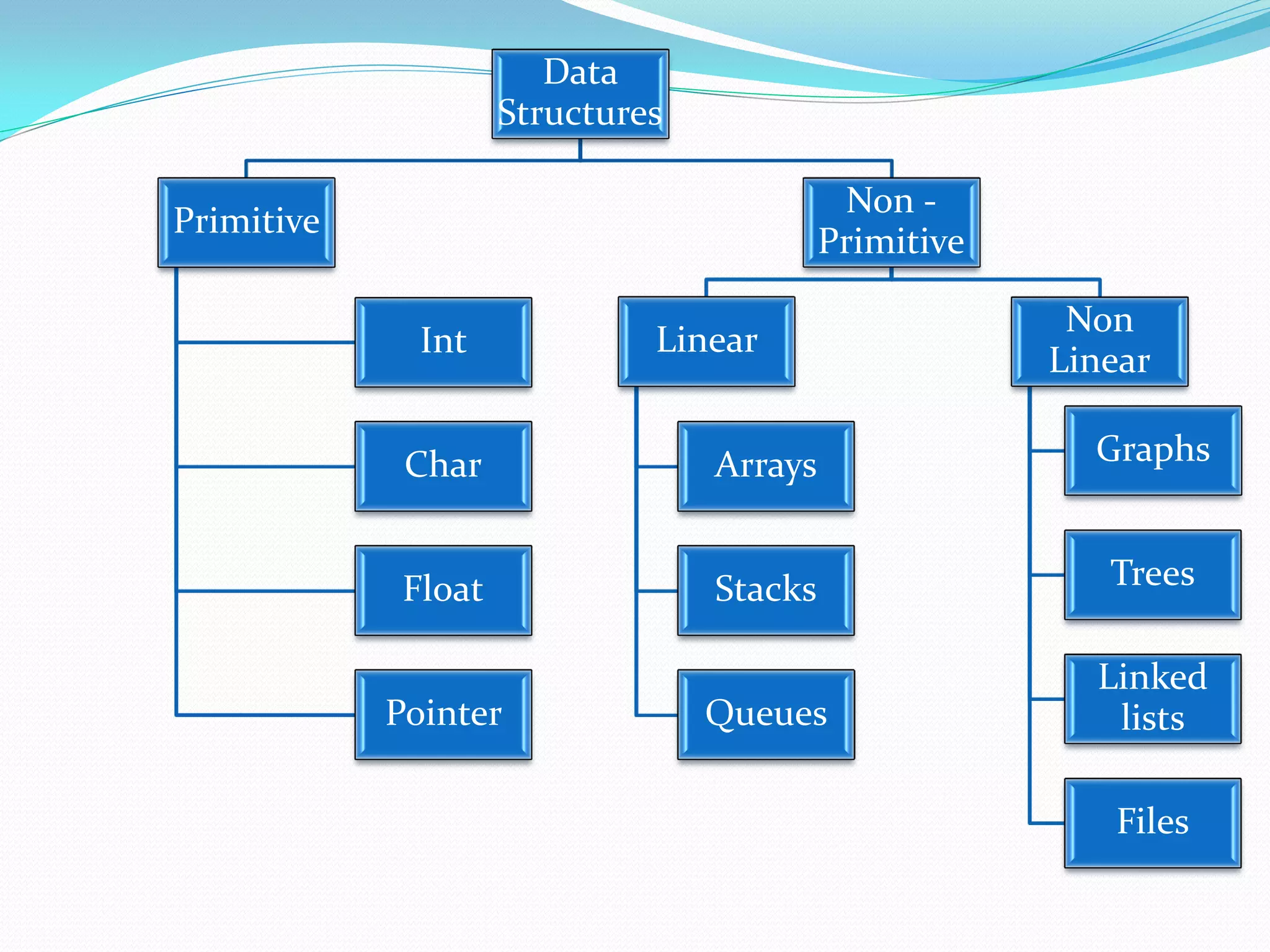
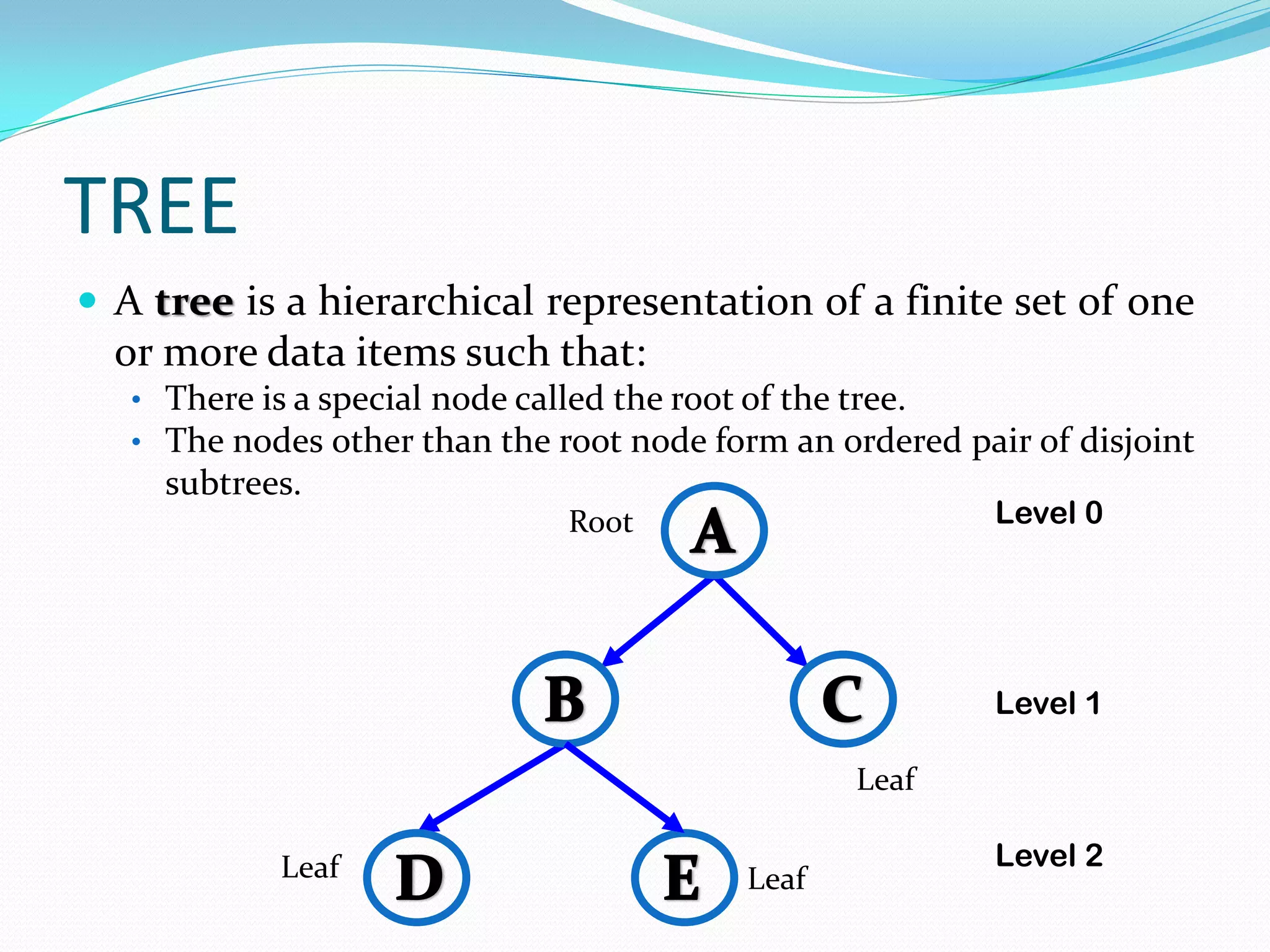
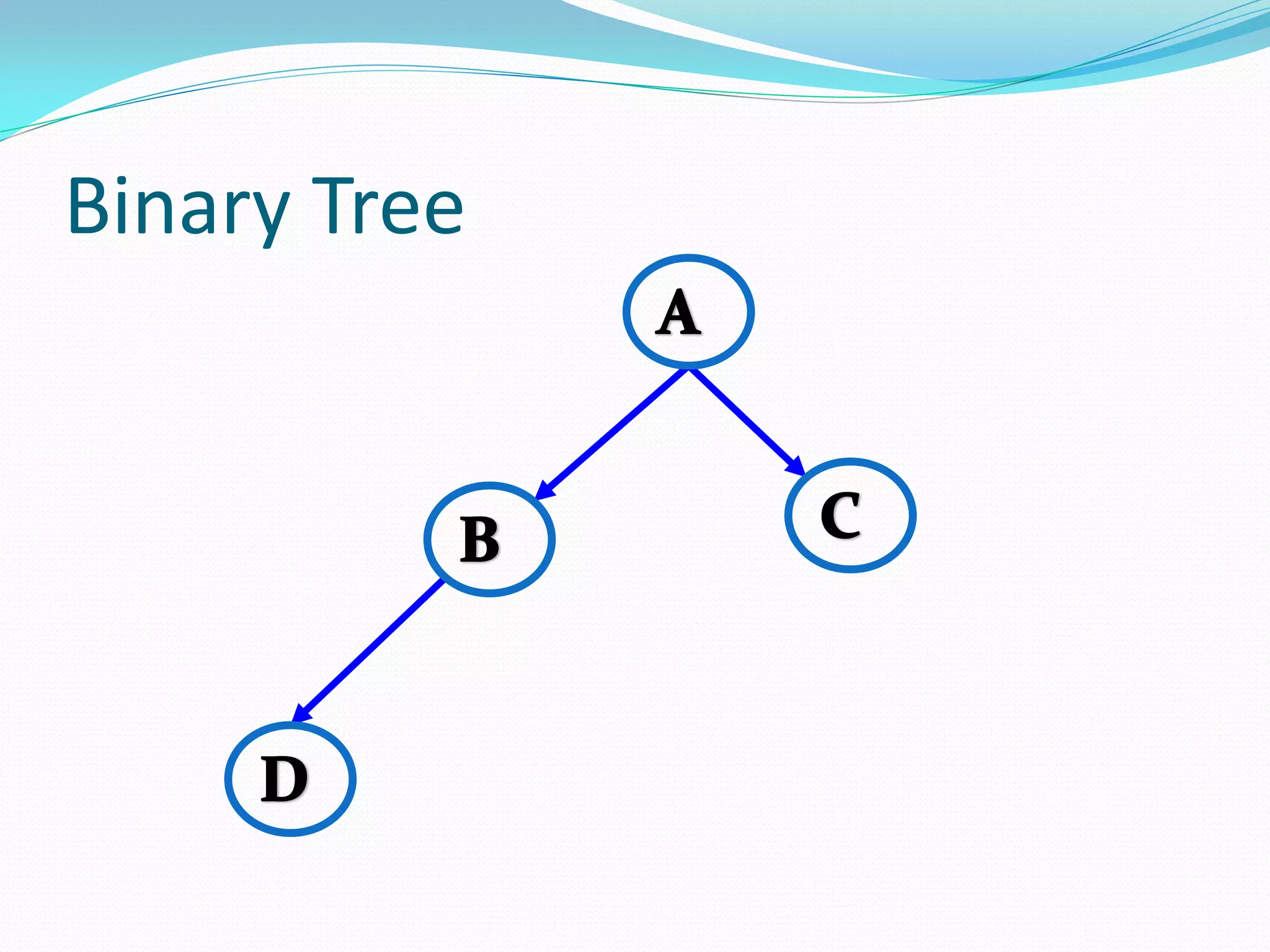
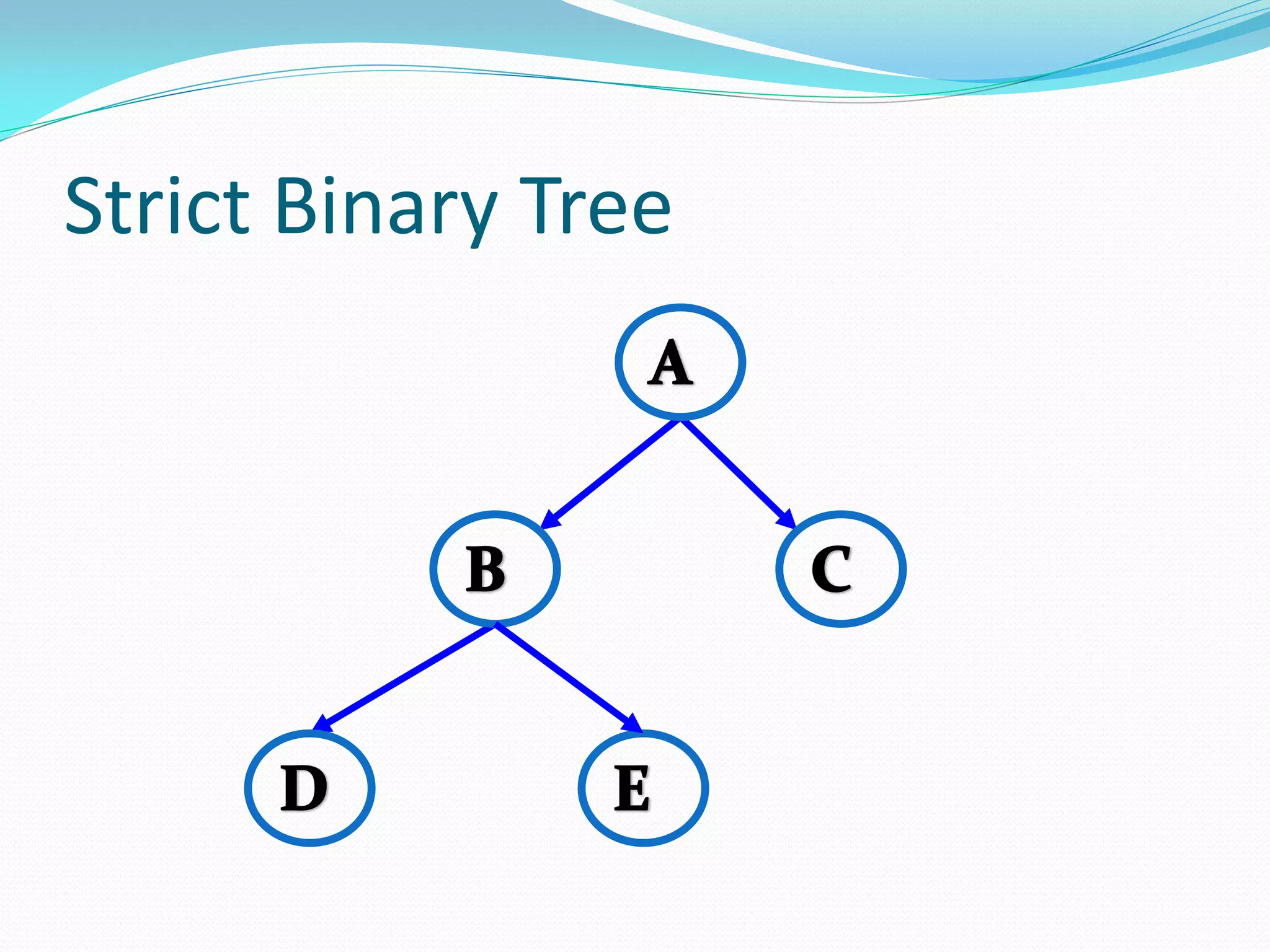
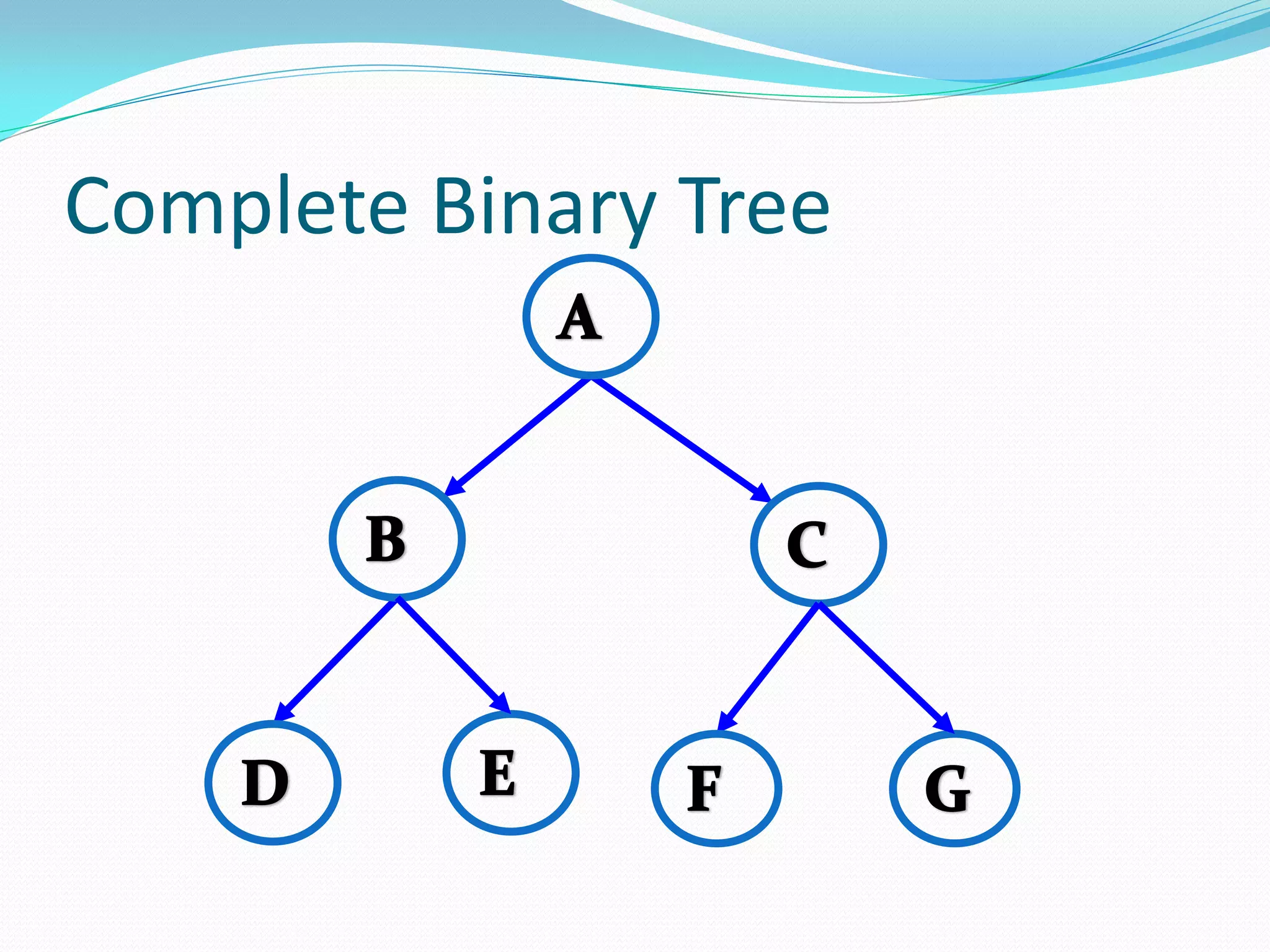
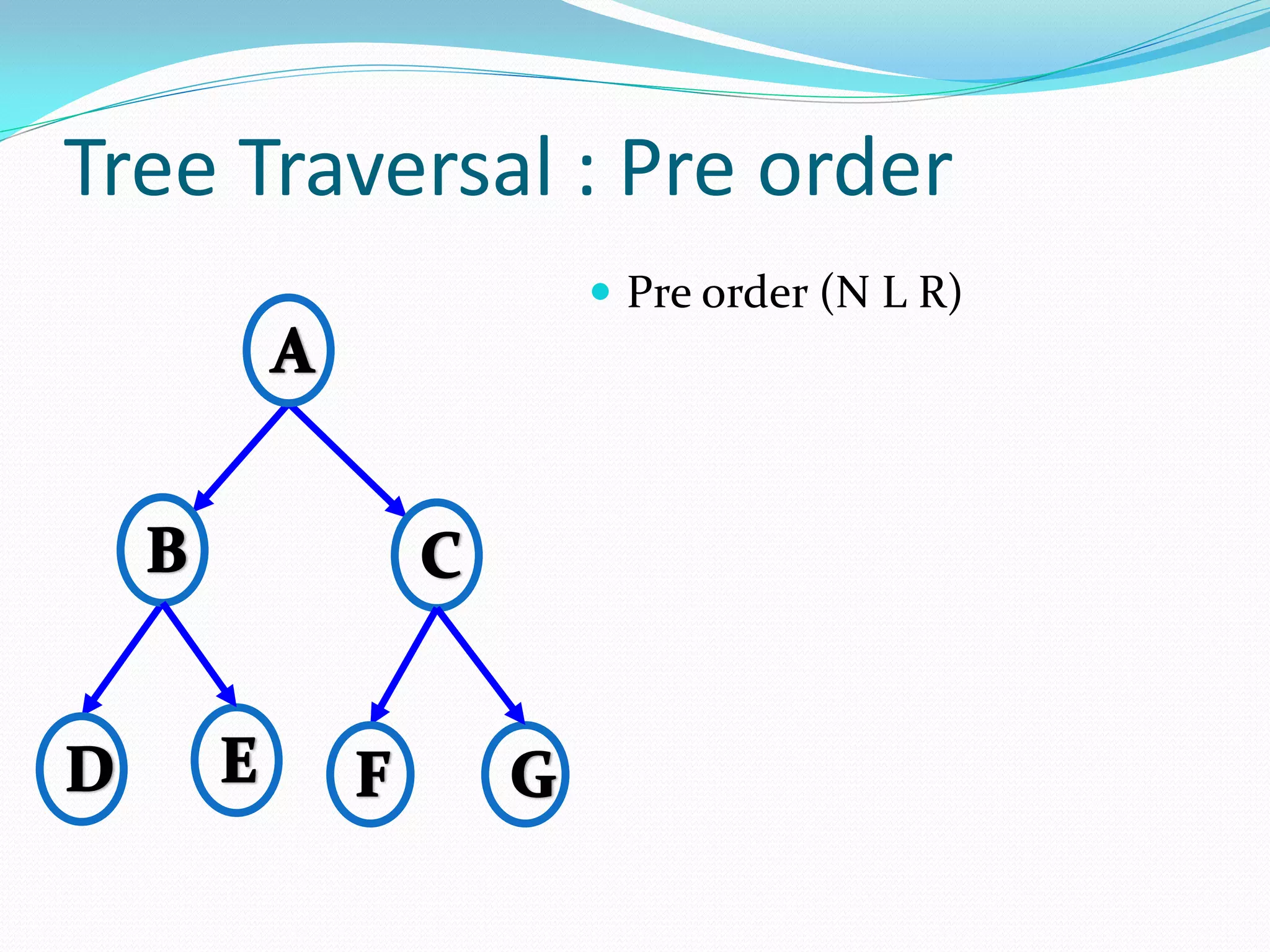
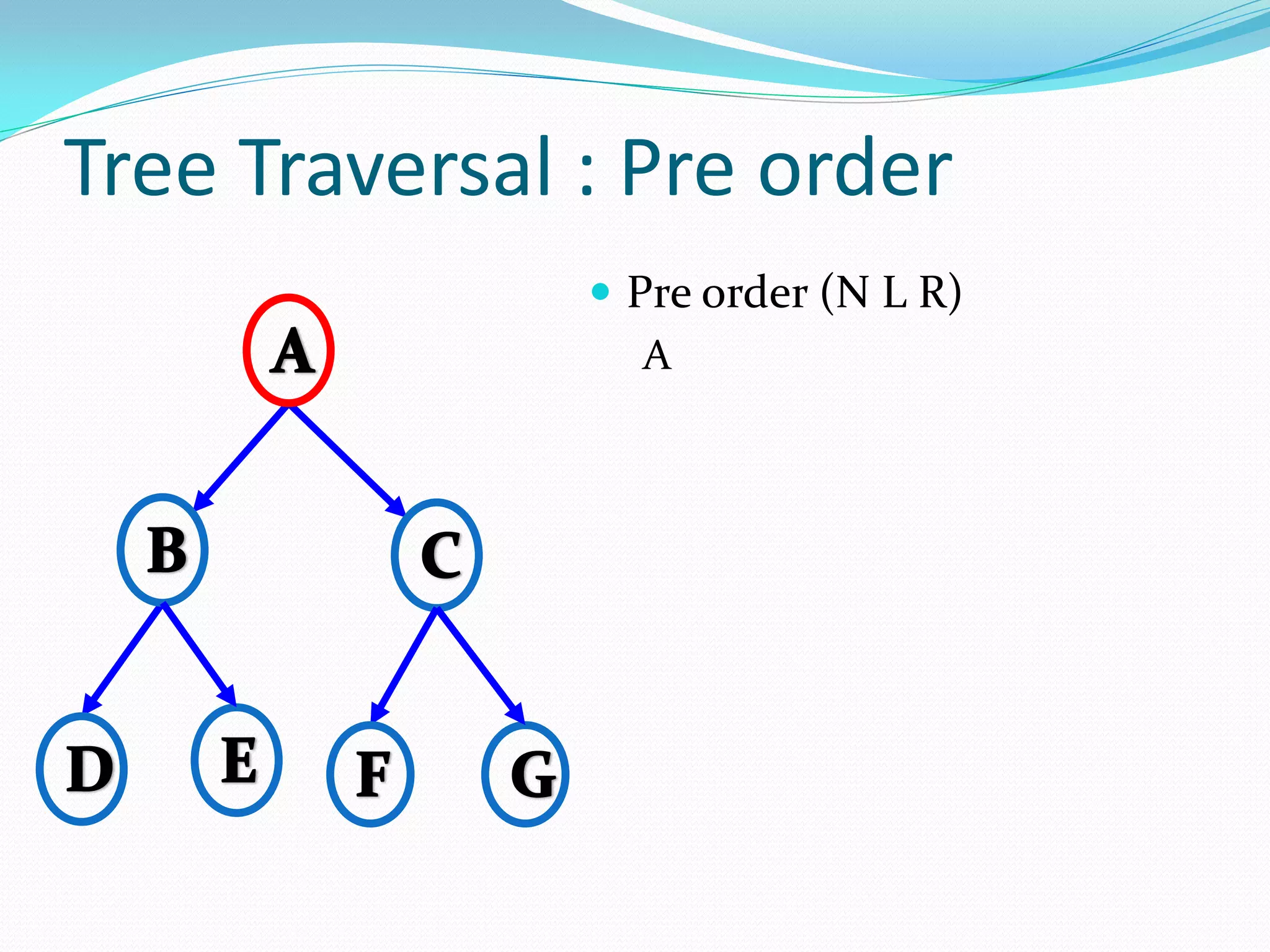
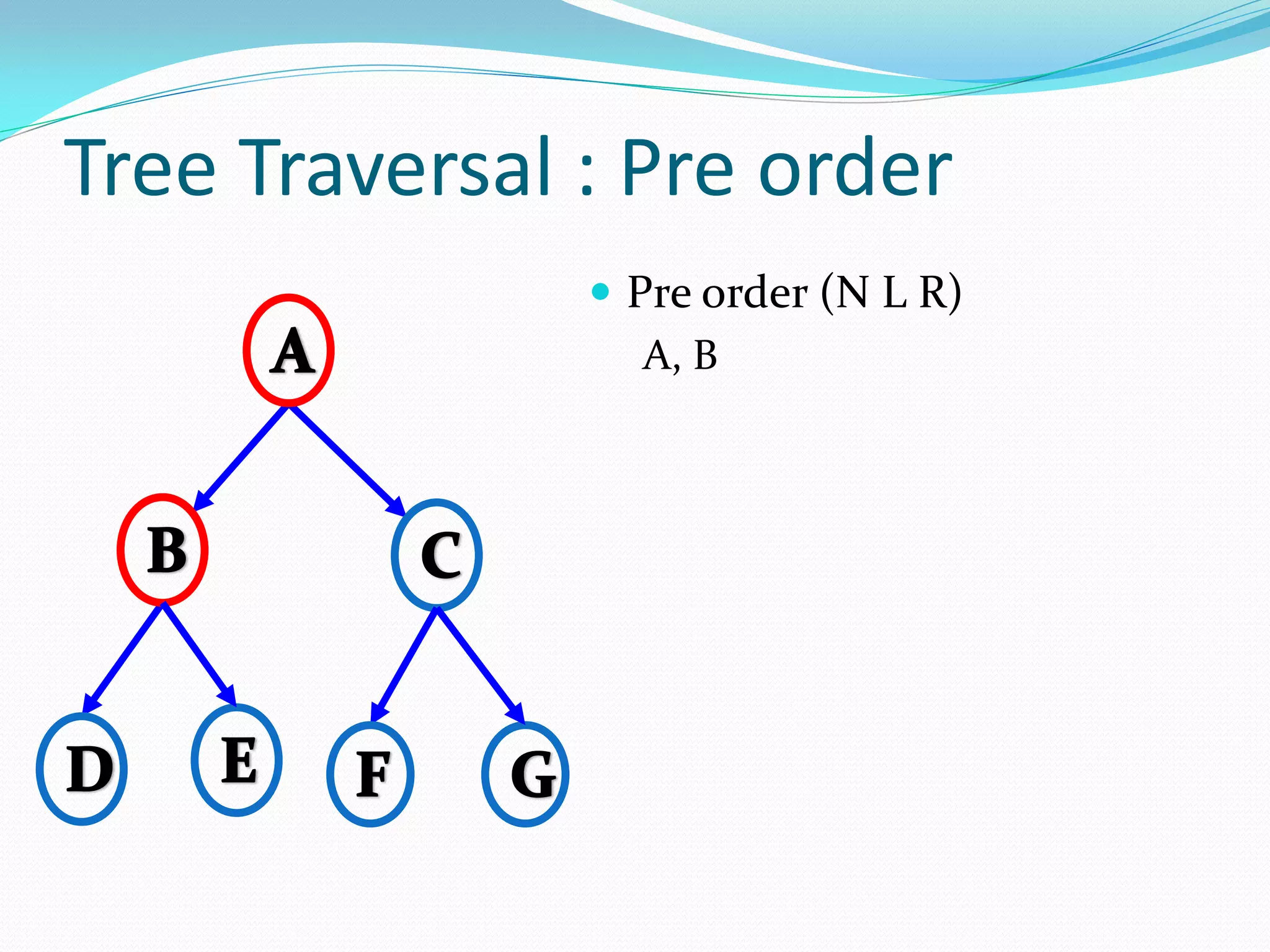
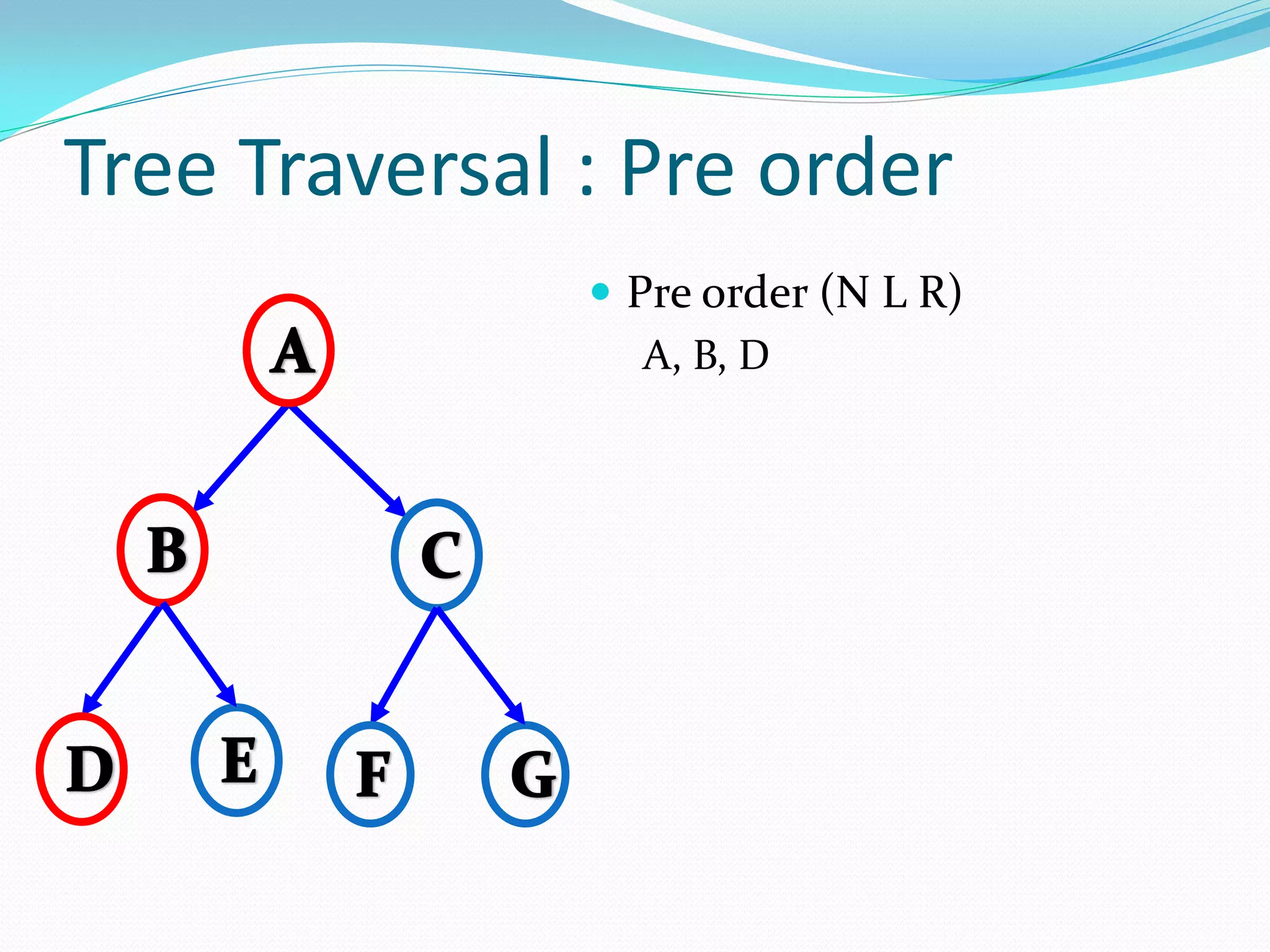
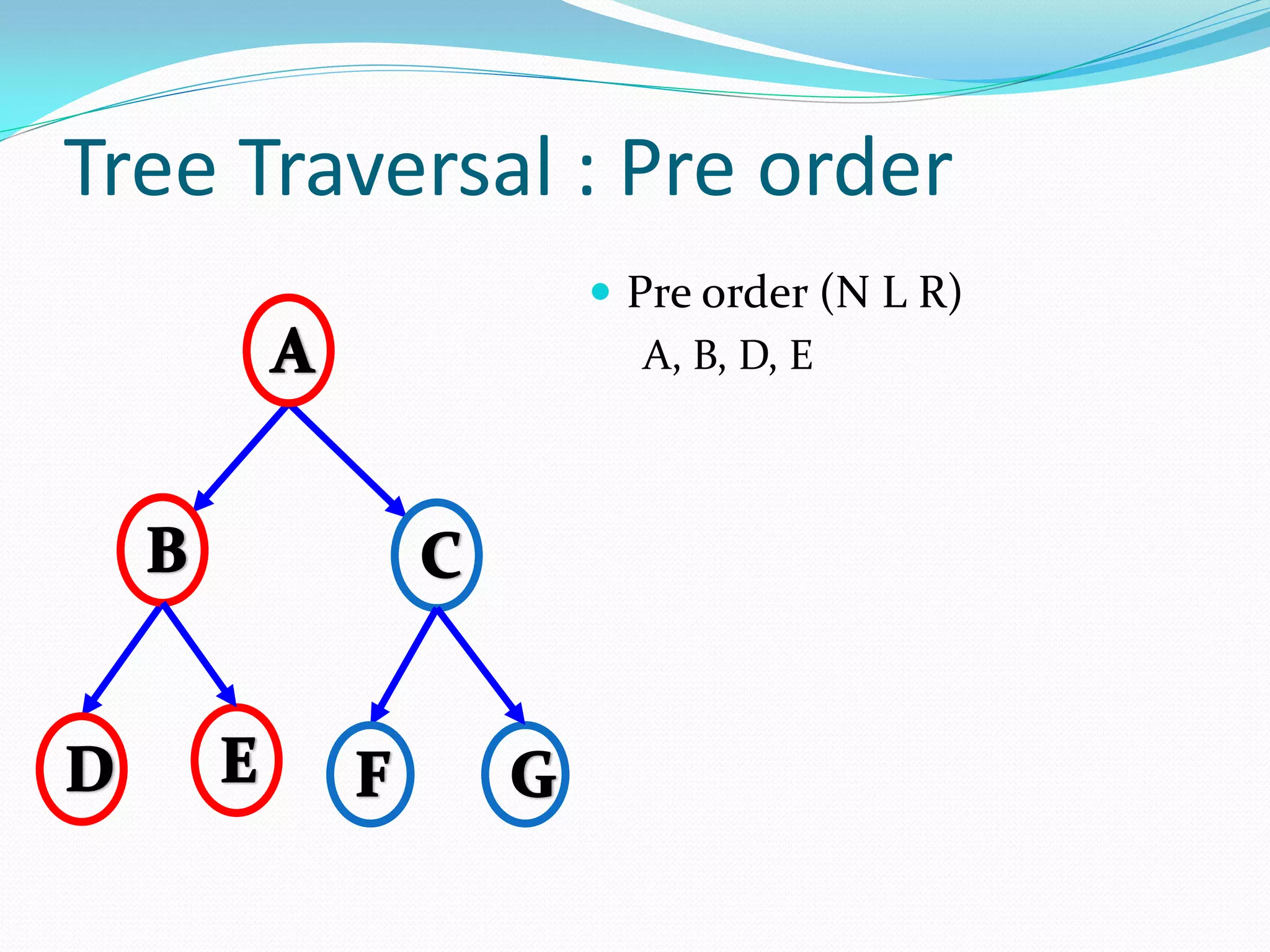
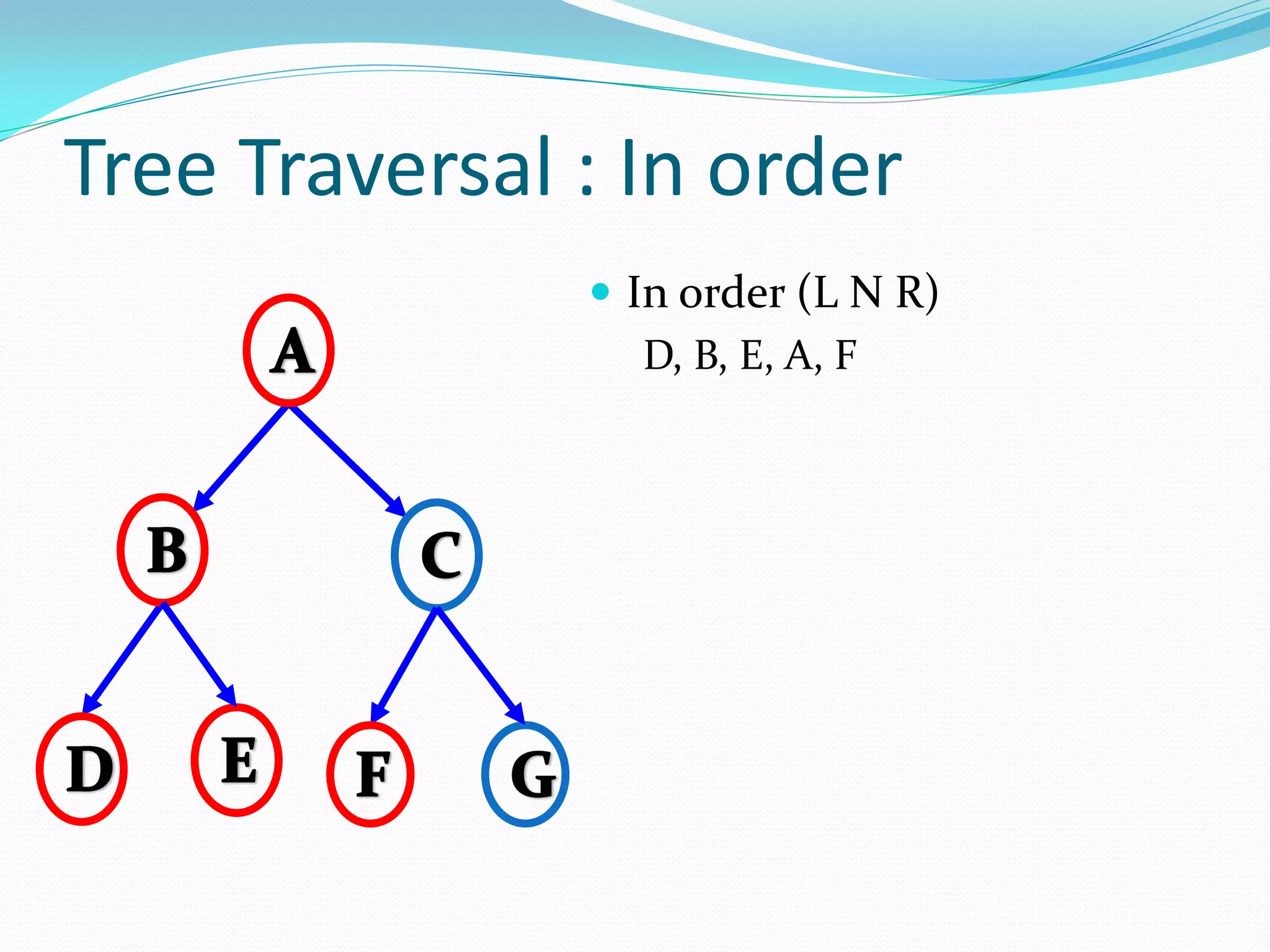
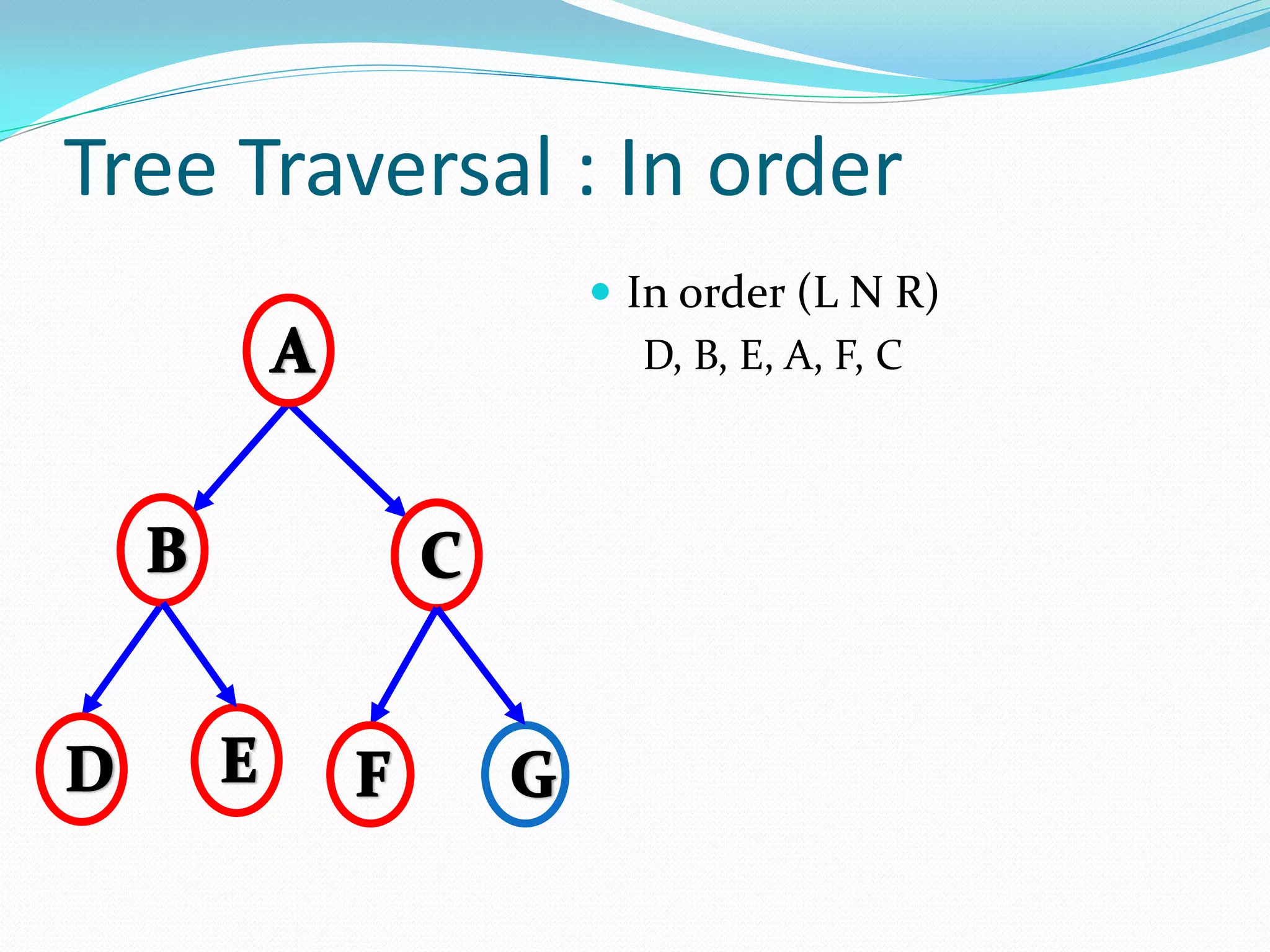
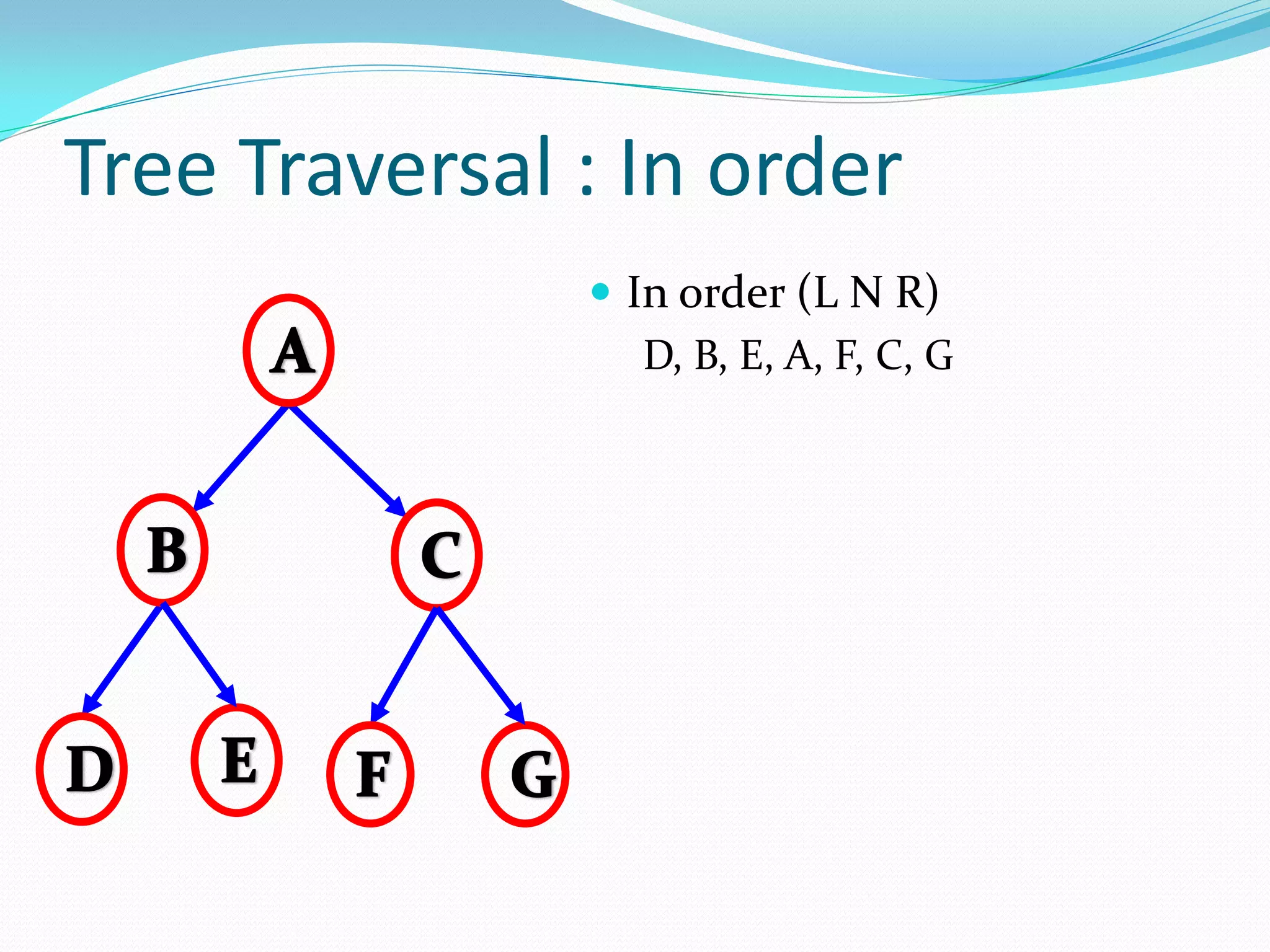
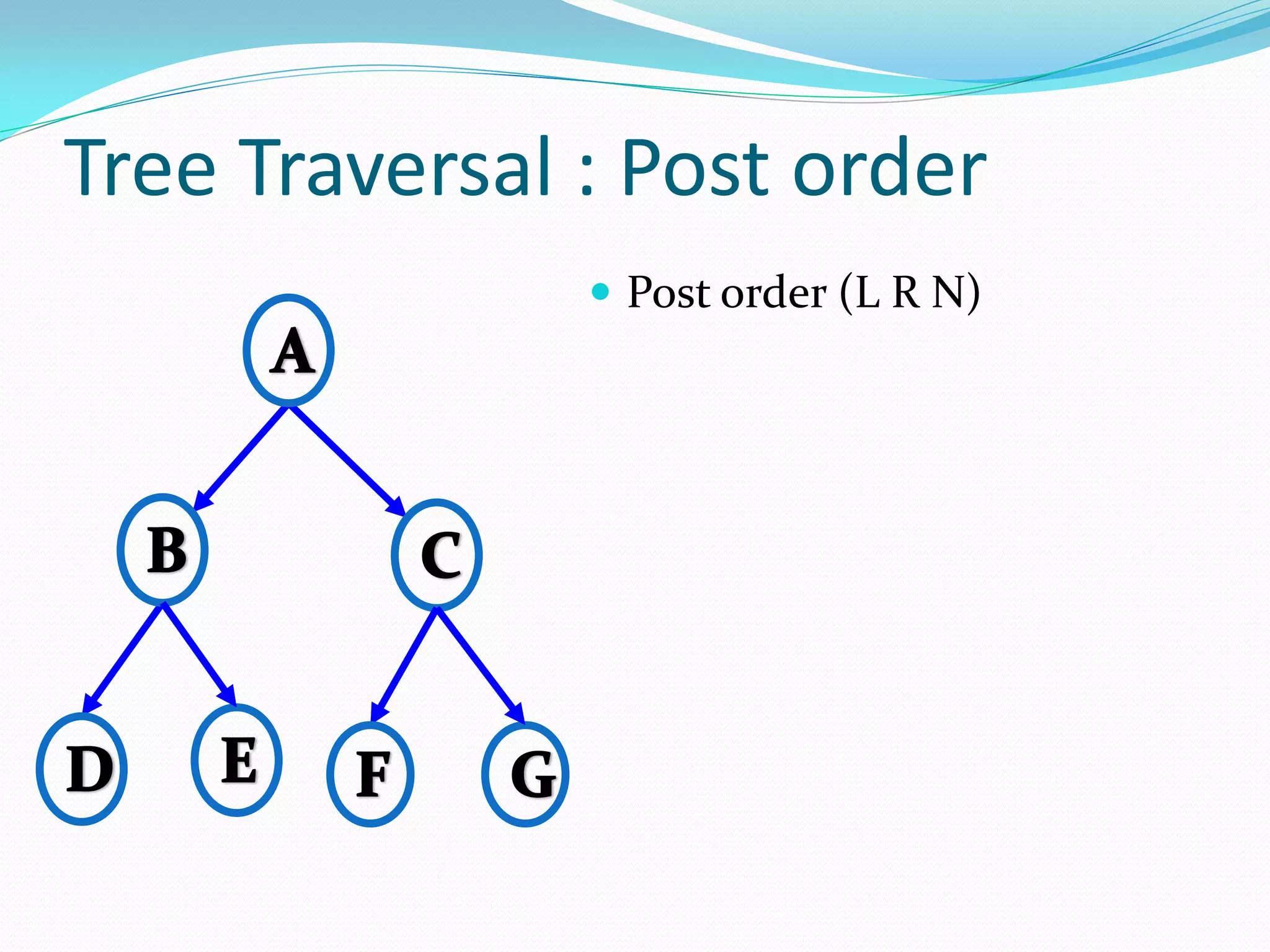
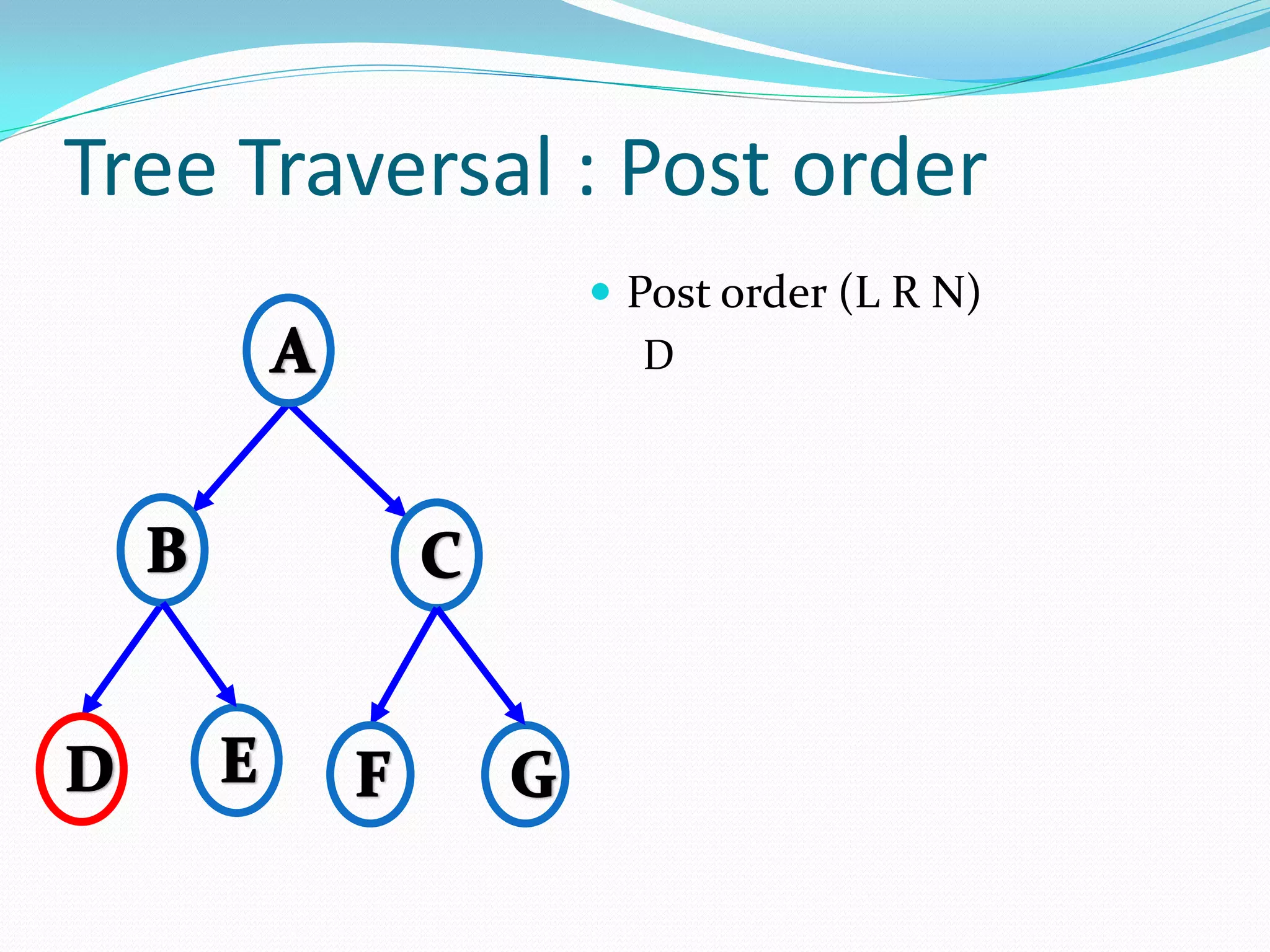
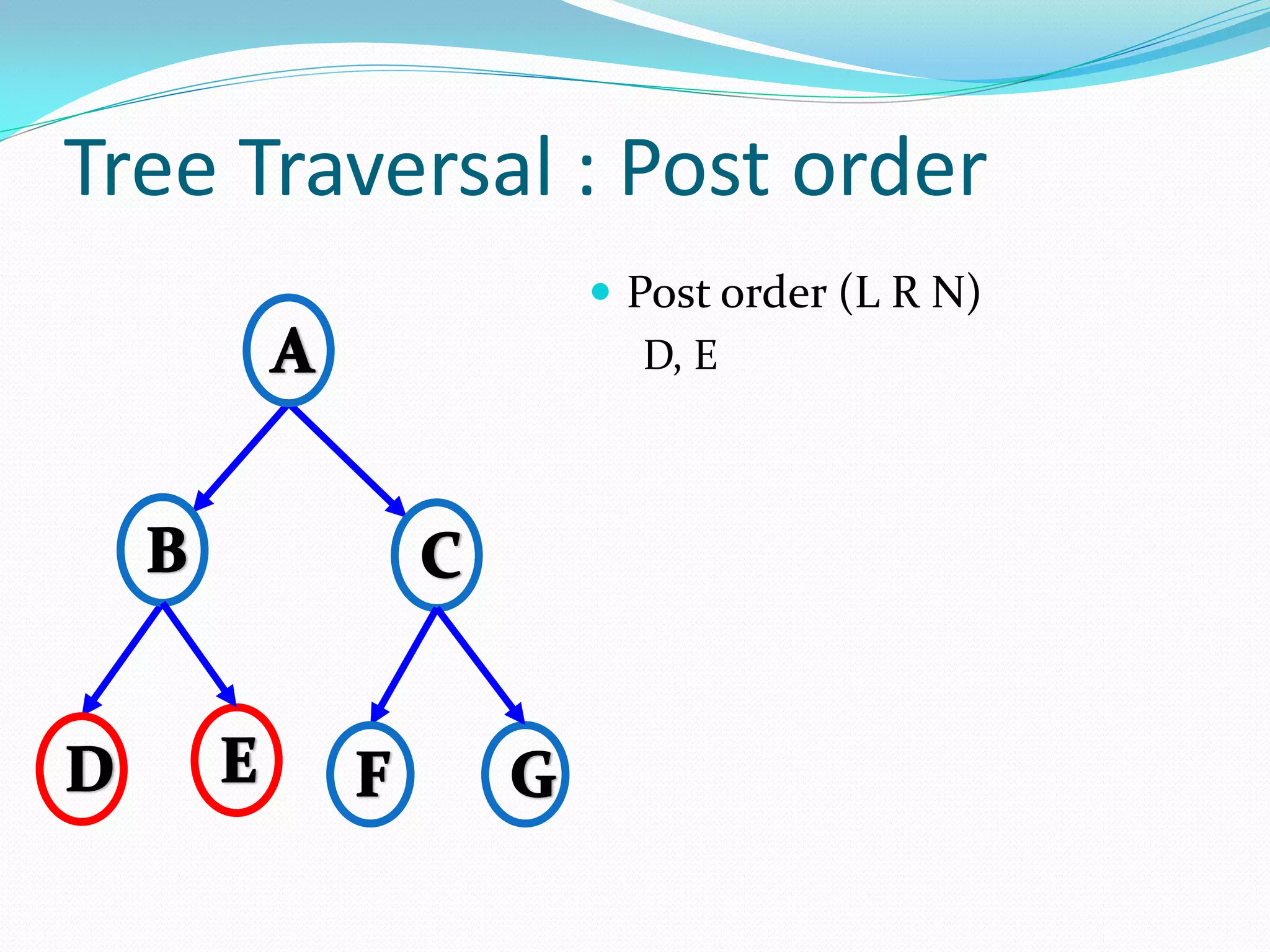
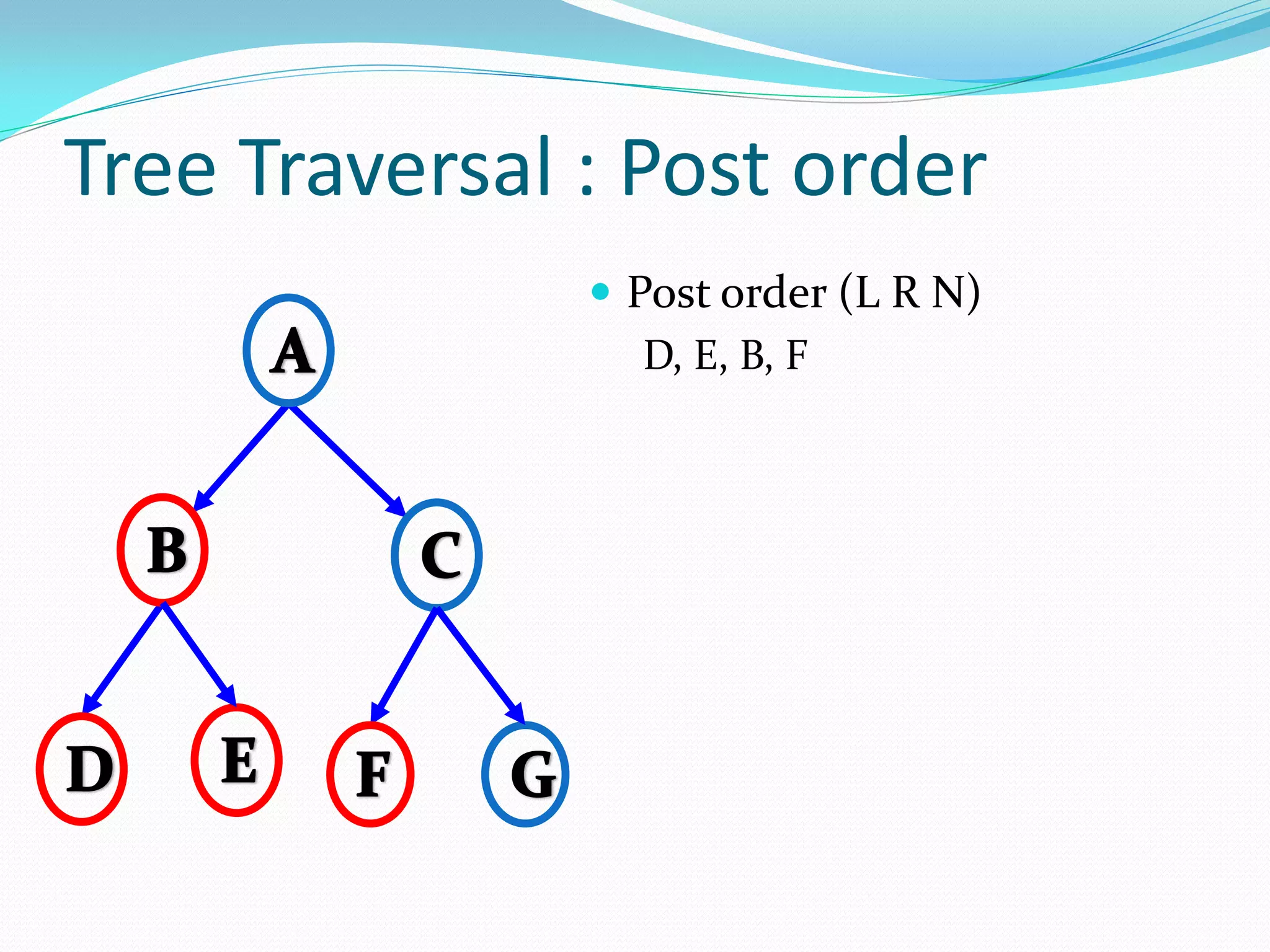
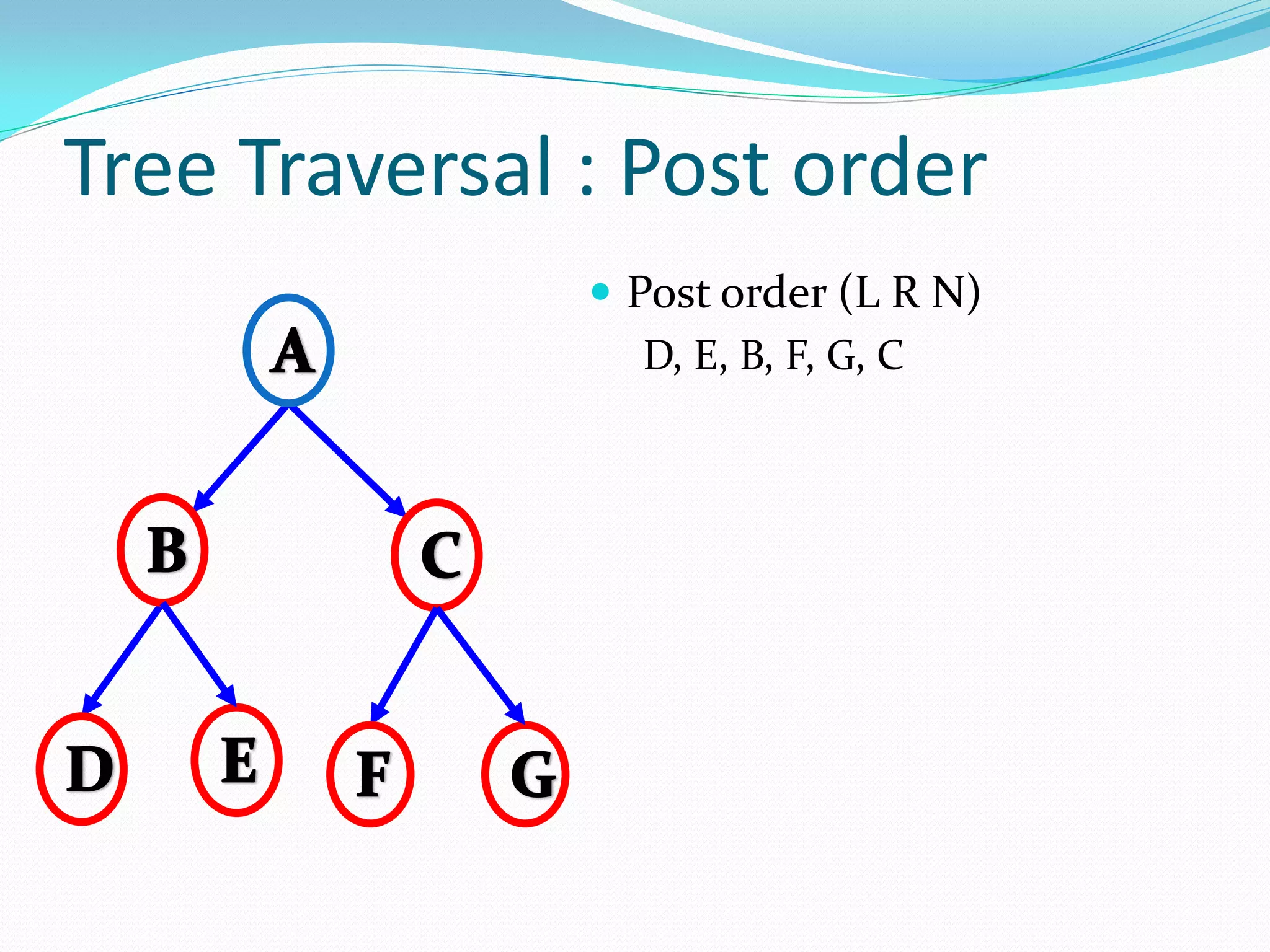
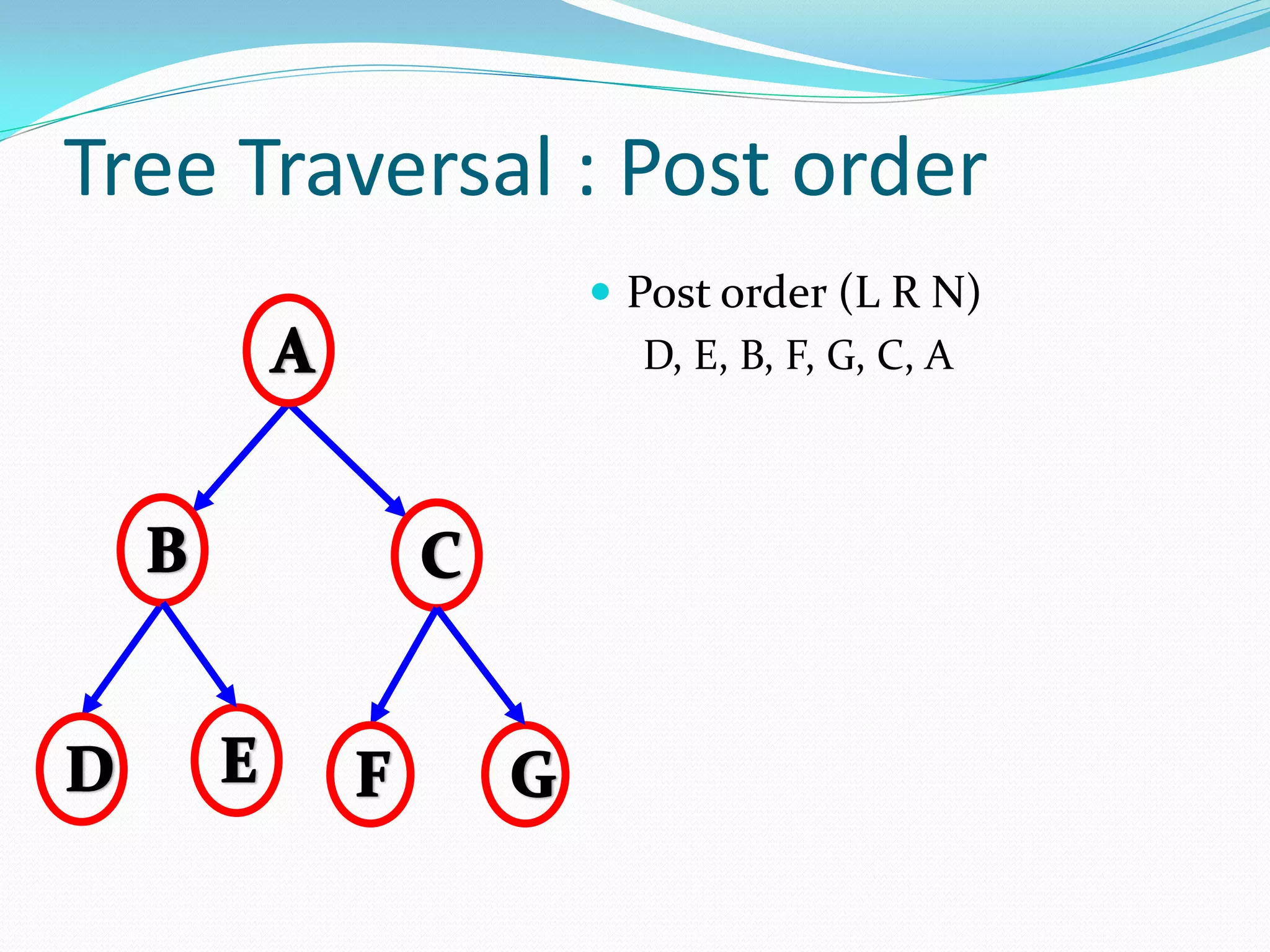
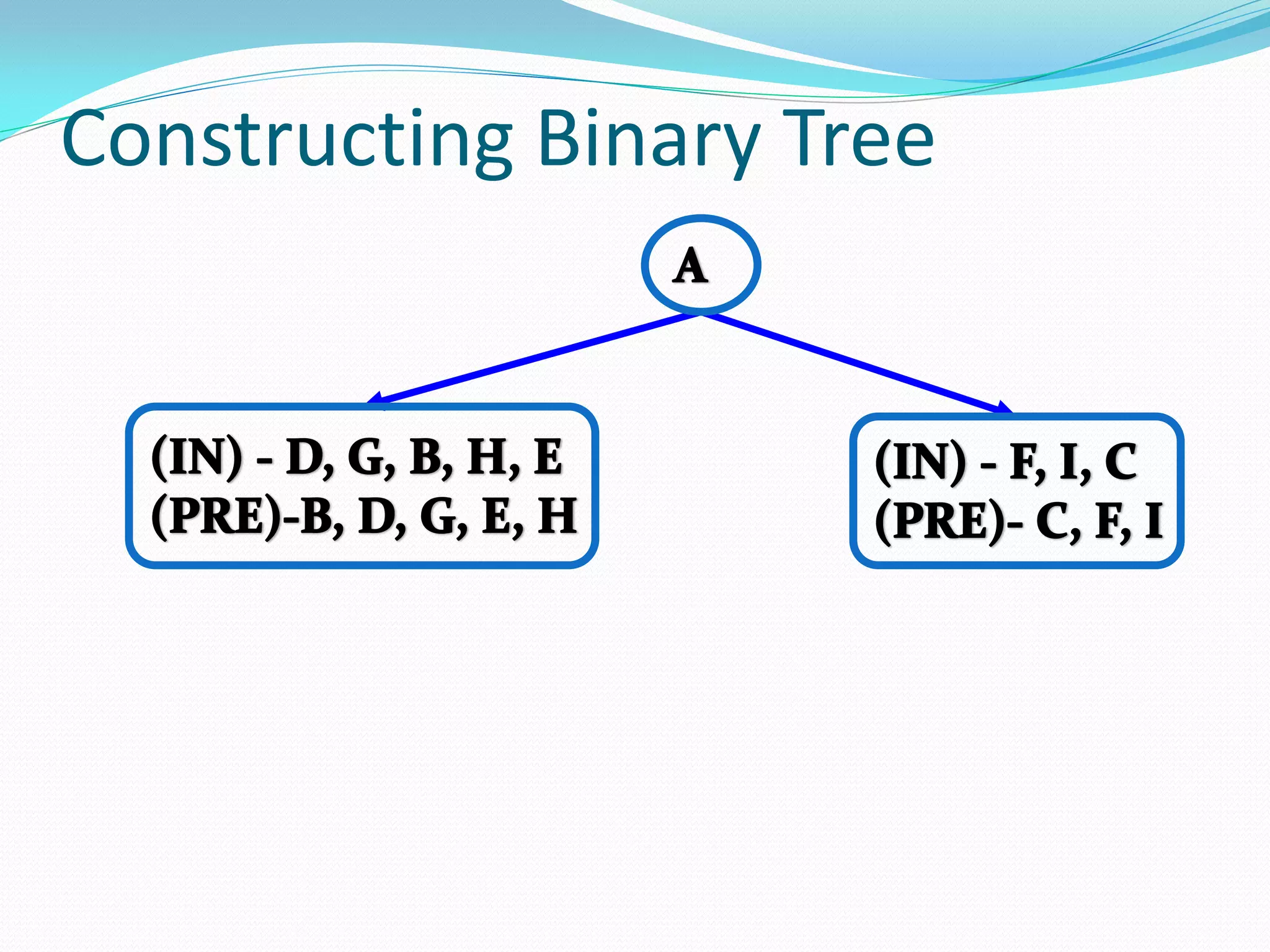
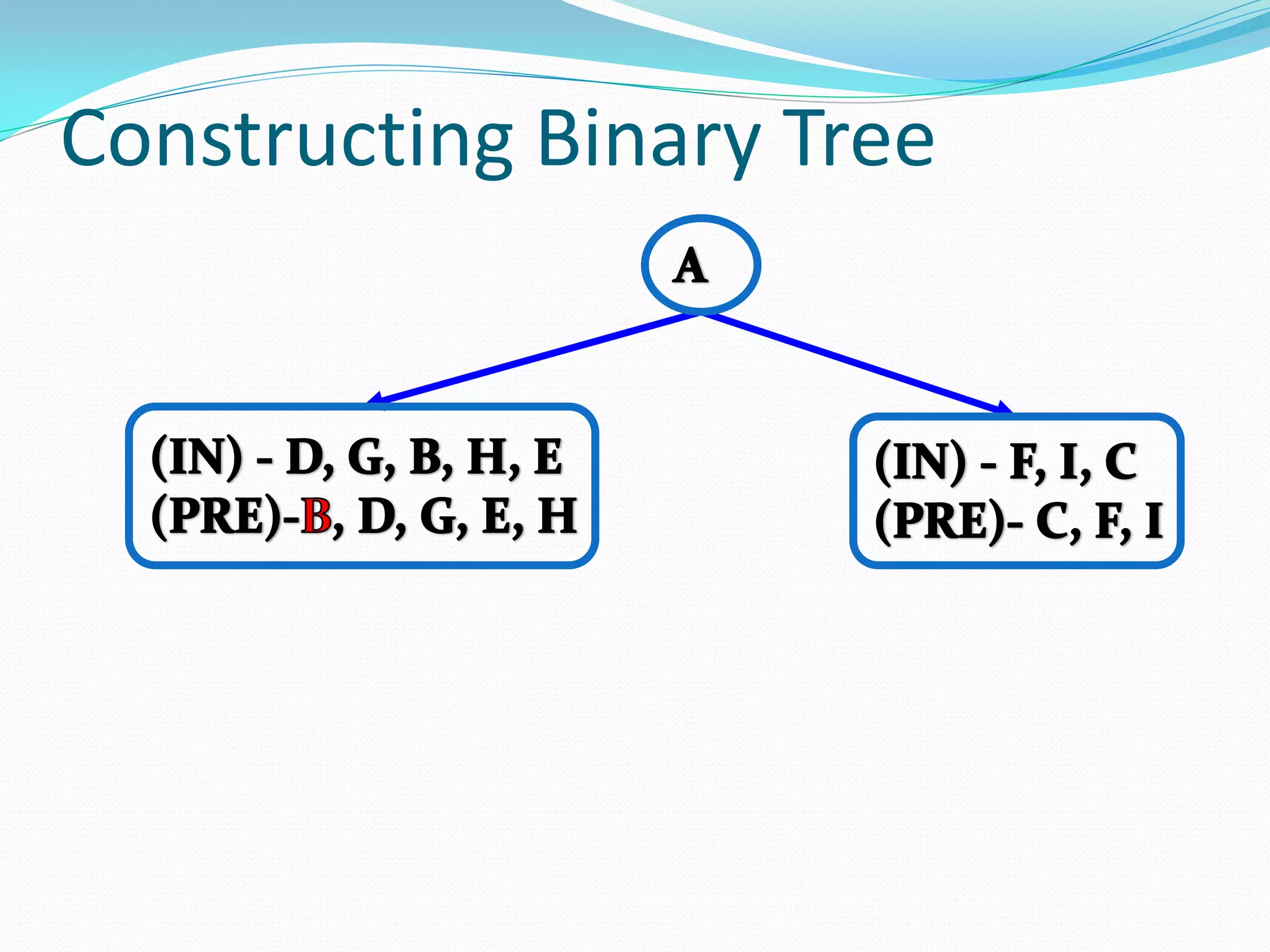
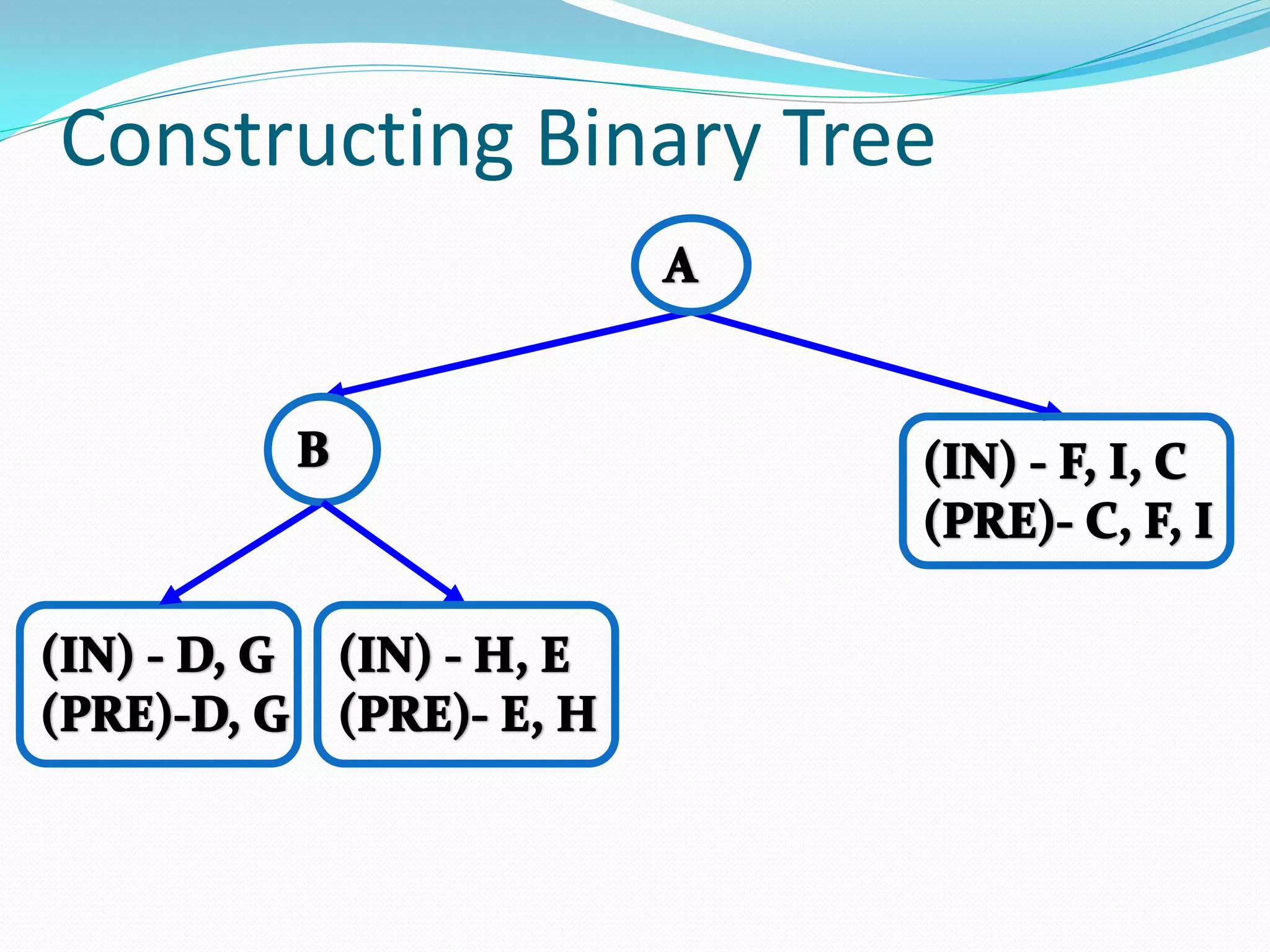
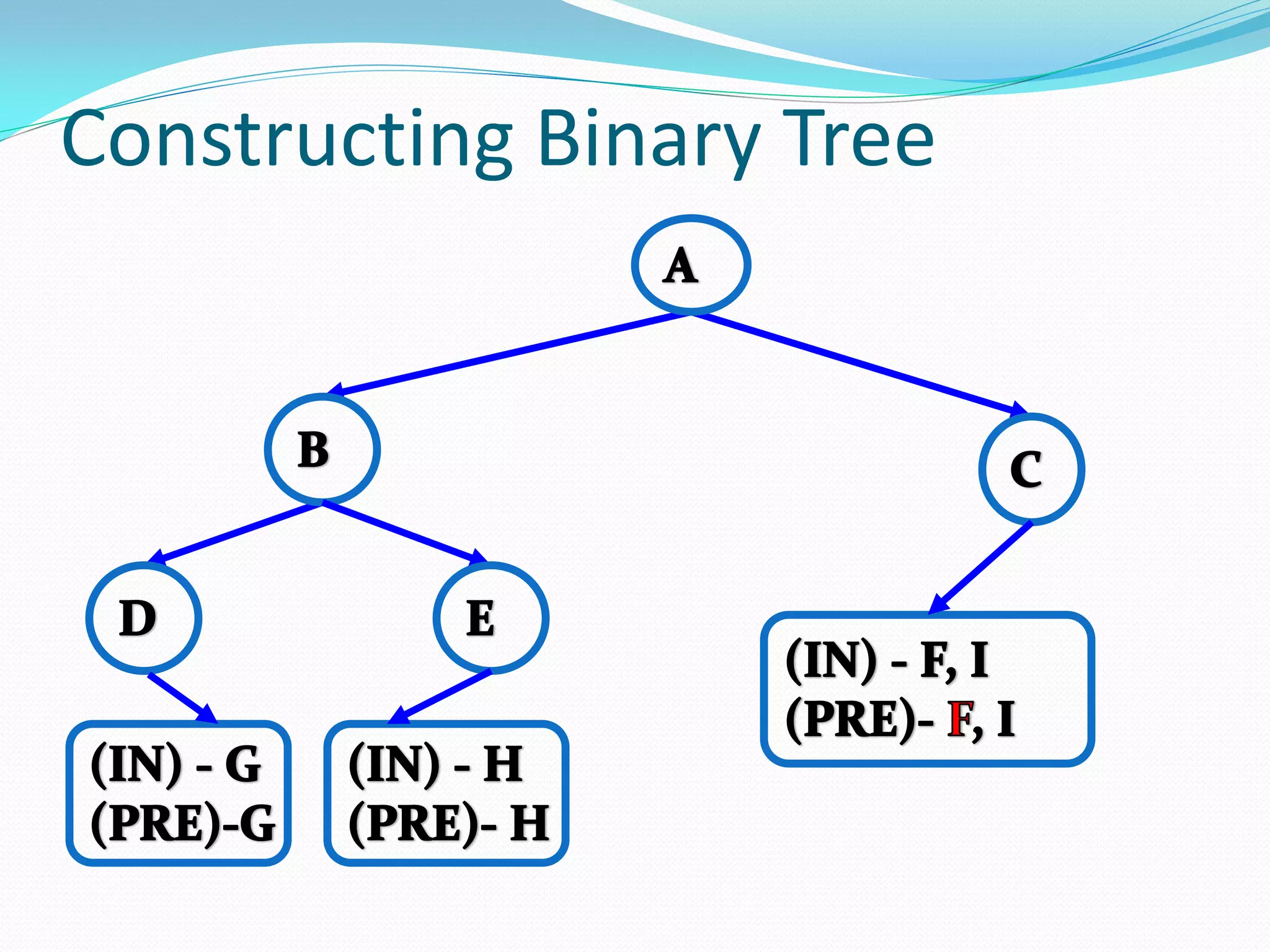
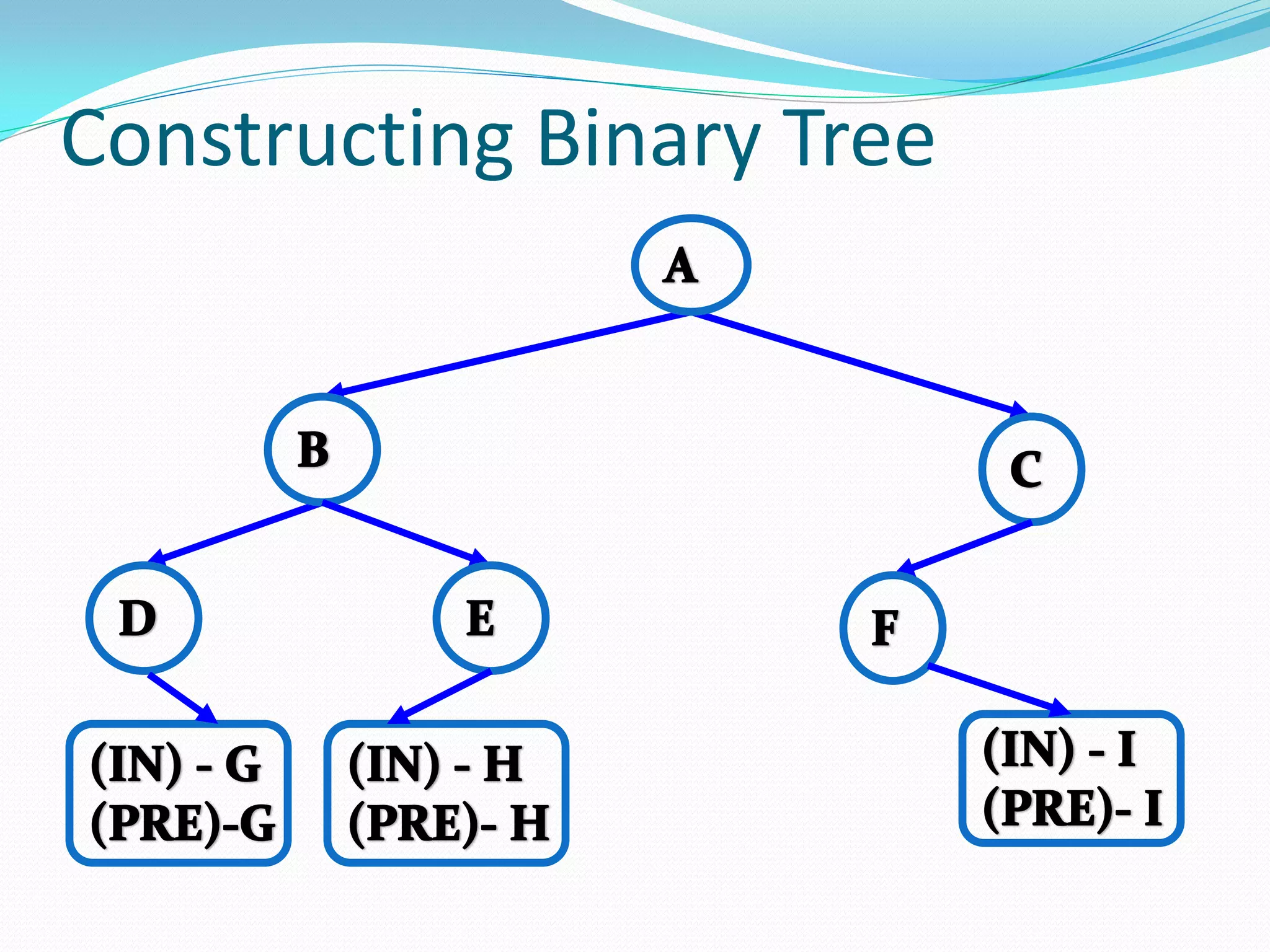
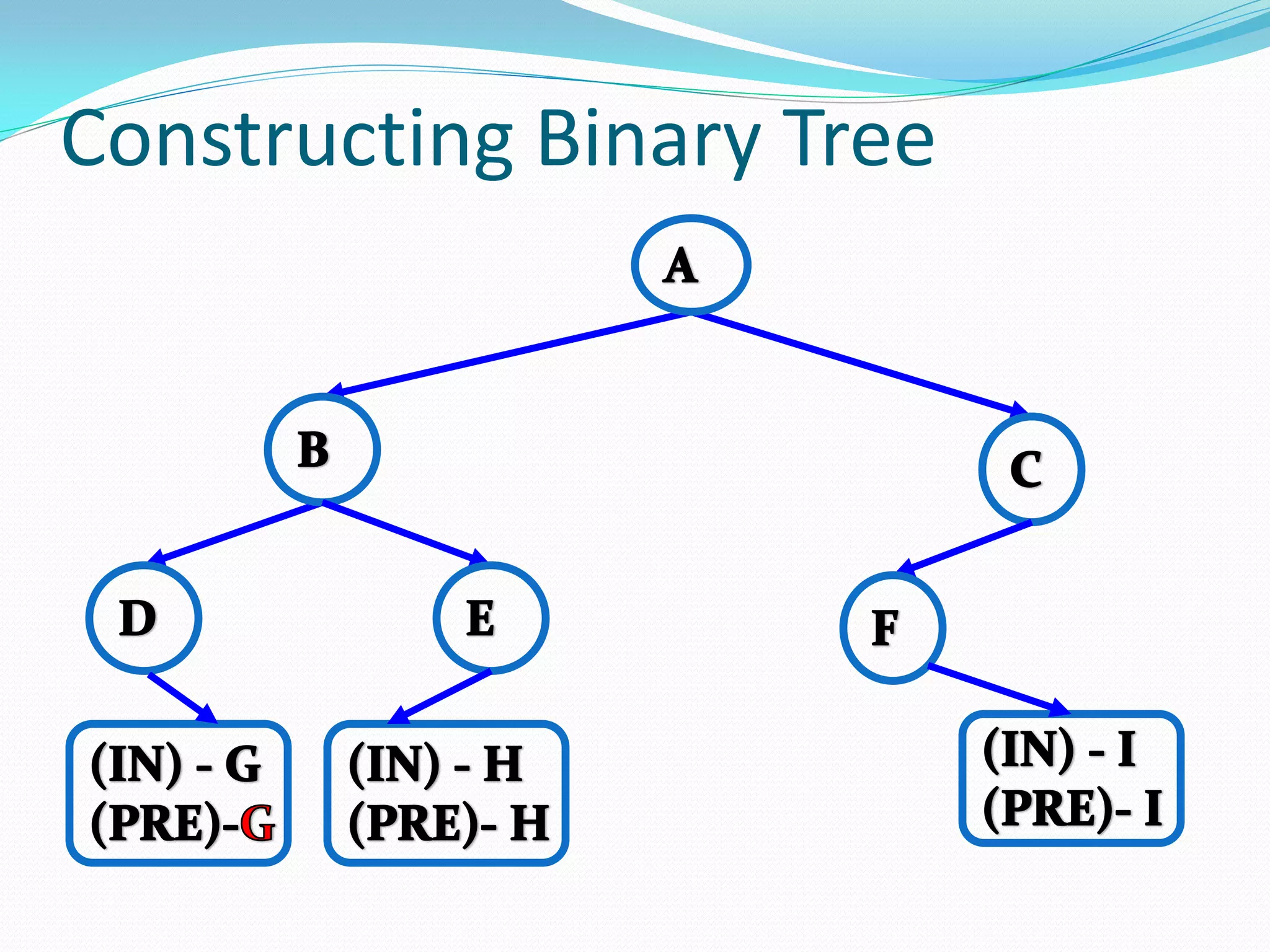
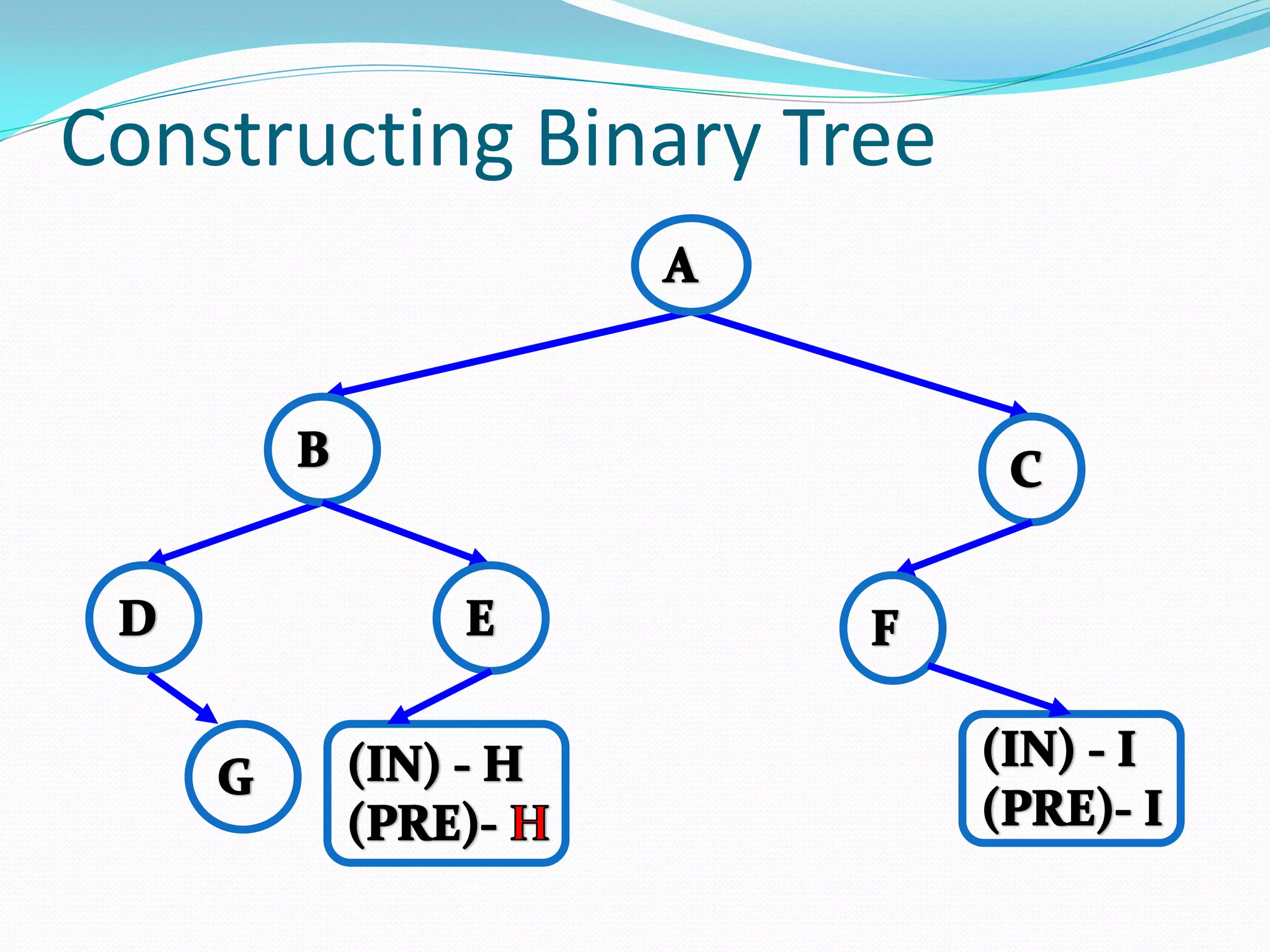
The document discusses various tree data structures and algorithms related to binary trees. It begins with an introduction to different types of binary trees such as strict binary trees, complete binary trees, and extended binary trees. It then covers tree traversal algorithms including preorder, inorder and postorder traversal. The document also discusses representations of binary trees using arrays and linked lists. Finally, it explains algorithms for operations on binary search trees such as searching, insertion, deletion and rebalancing through rotations in AVL trees.


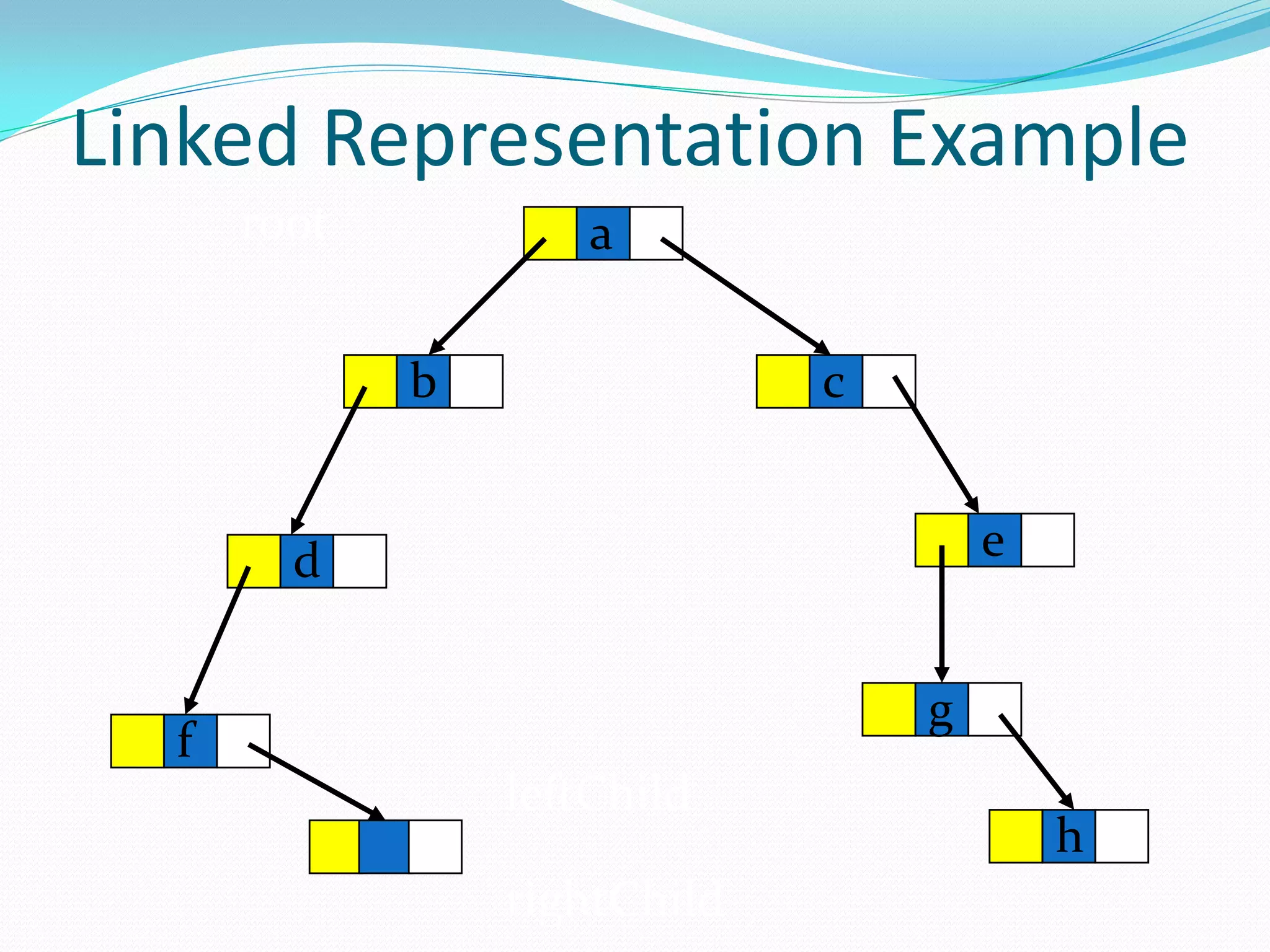
![Array Representation
Number the nodes using the numbering scheme for a
full binary tree. The node that is numbered i is stored in
tree[i].
tree[]
0 5 10
a b c d e f g h i j
b
a
c
d e f g
h i j
1
2 3
4 5 6 7
8 9 10](https://image.slidesharecdn.com/datastructuresunit3-151009070317-lva1-app6892/75/Trees-Binary-Search-Tree-AVL-Tree-in-Data-Structures-5-2048.jpg)
![Right-Skewed Binary Tree
An n node binary tree needs an array whose
length is between n+1 and 2n.
a
b
1
3
c
7
d
15
tree[]
0 5 10
a - b - - - c - - - - - - -
15
d](https://image.slidesharecdn.com/datastructuresunit3-151009070317-lva1-app6892/75/Trees-Binary-Search-Tree-AVL-Tree-in-Data-Structures-6-2048.jpg)








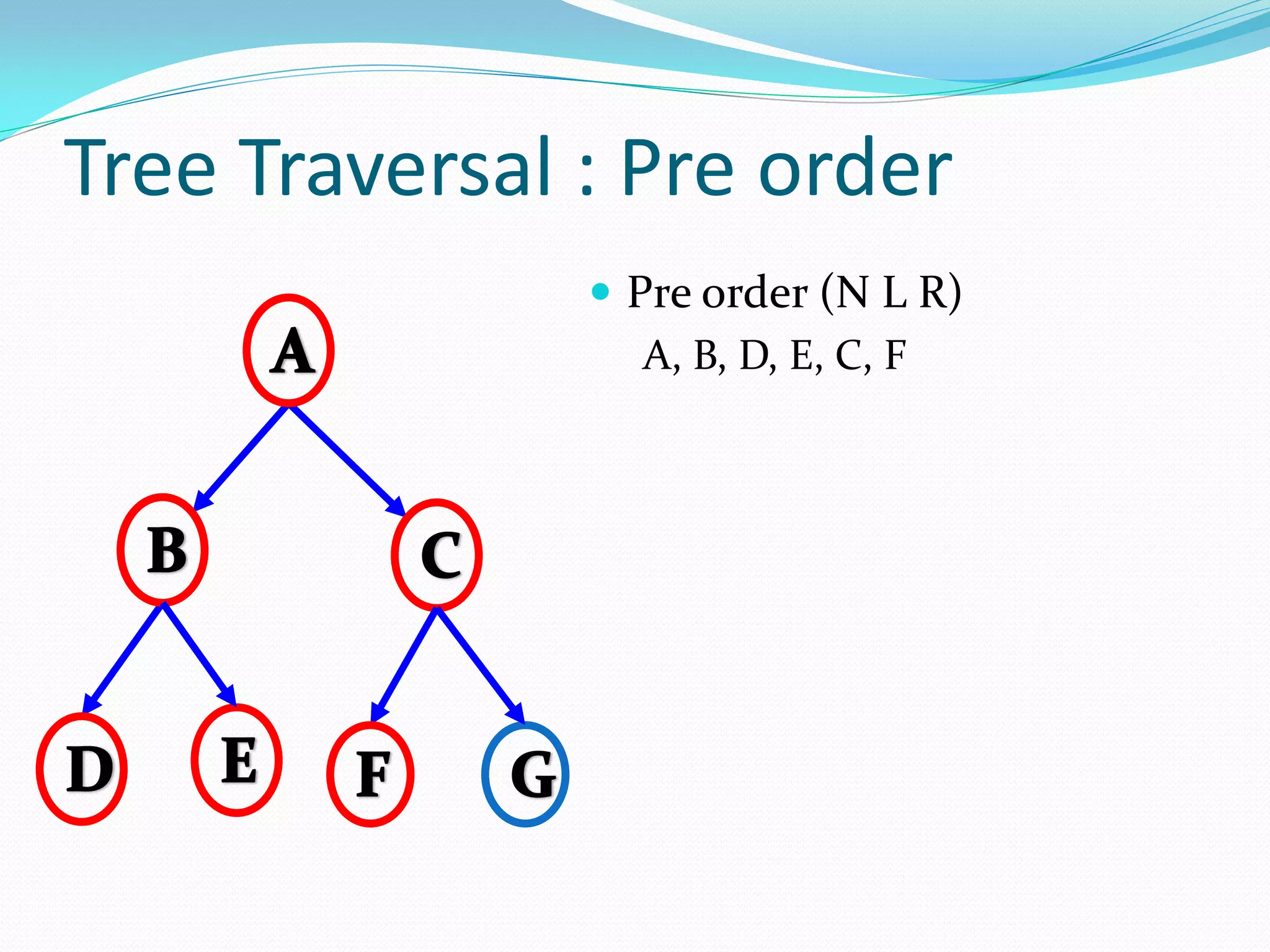


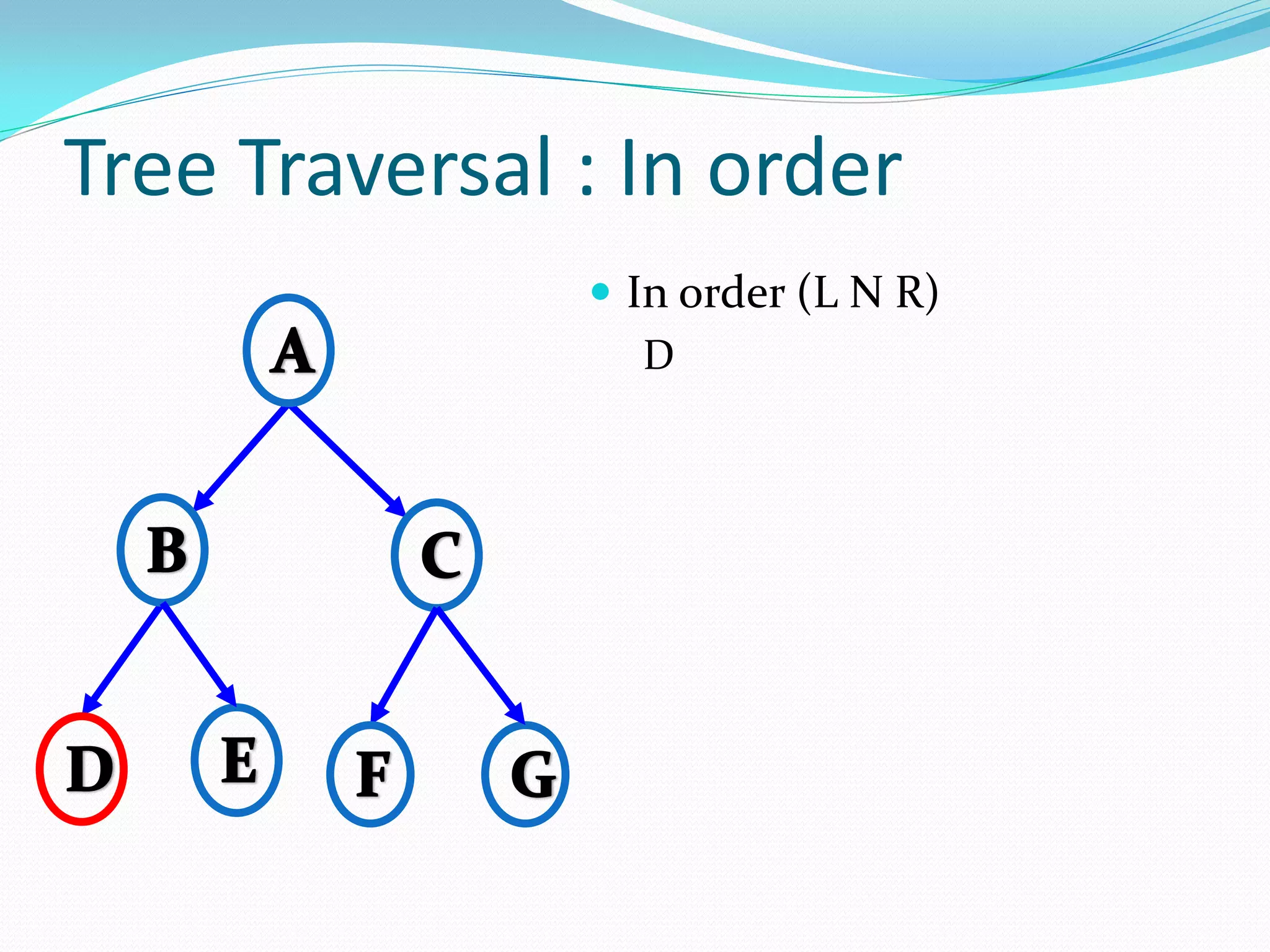
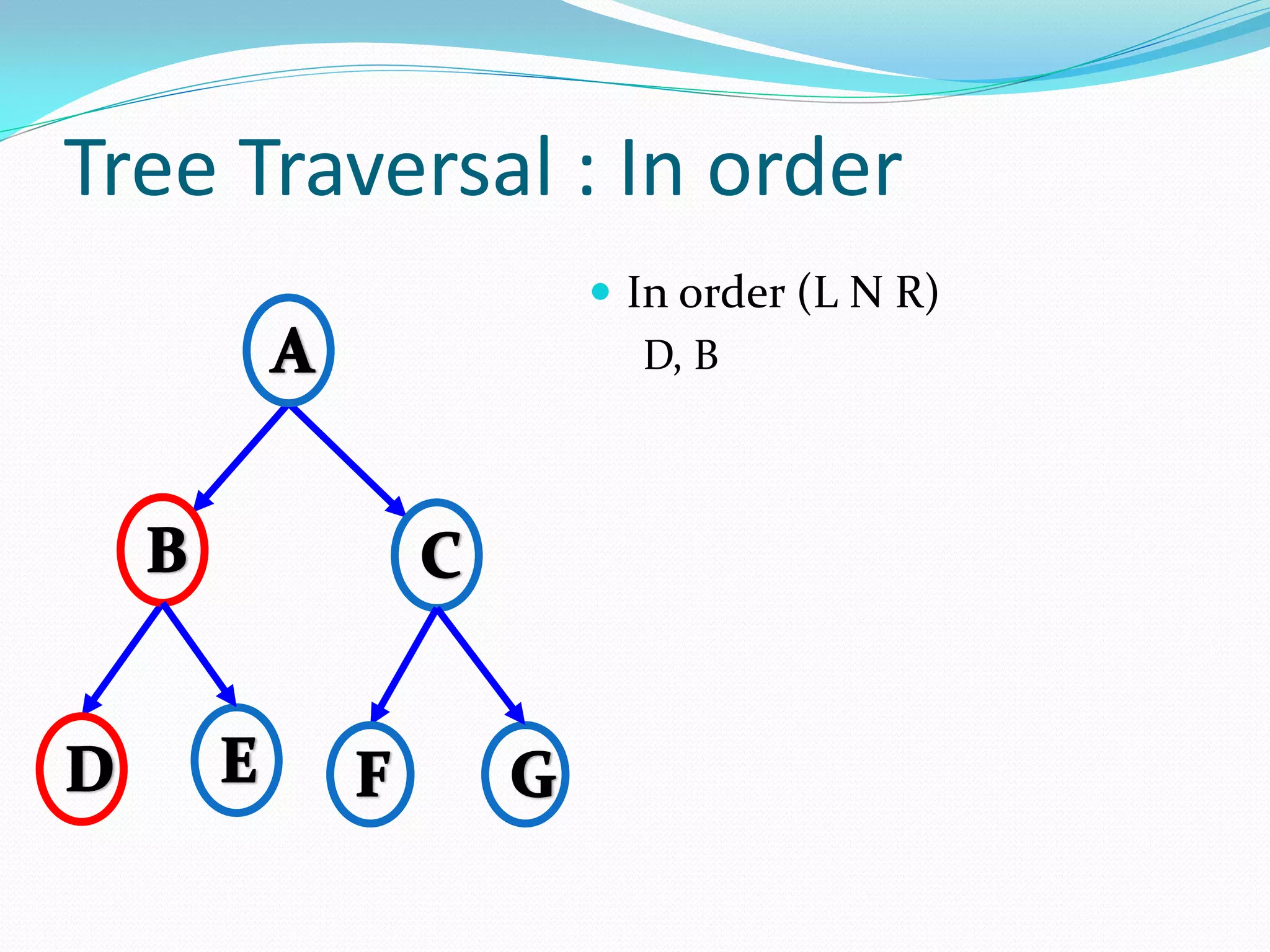
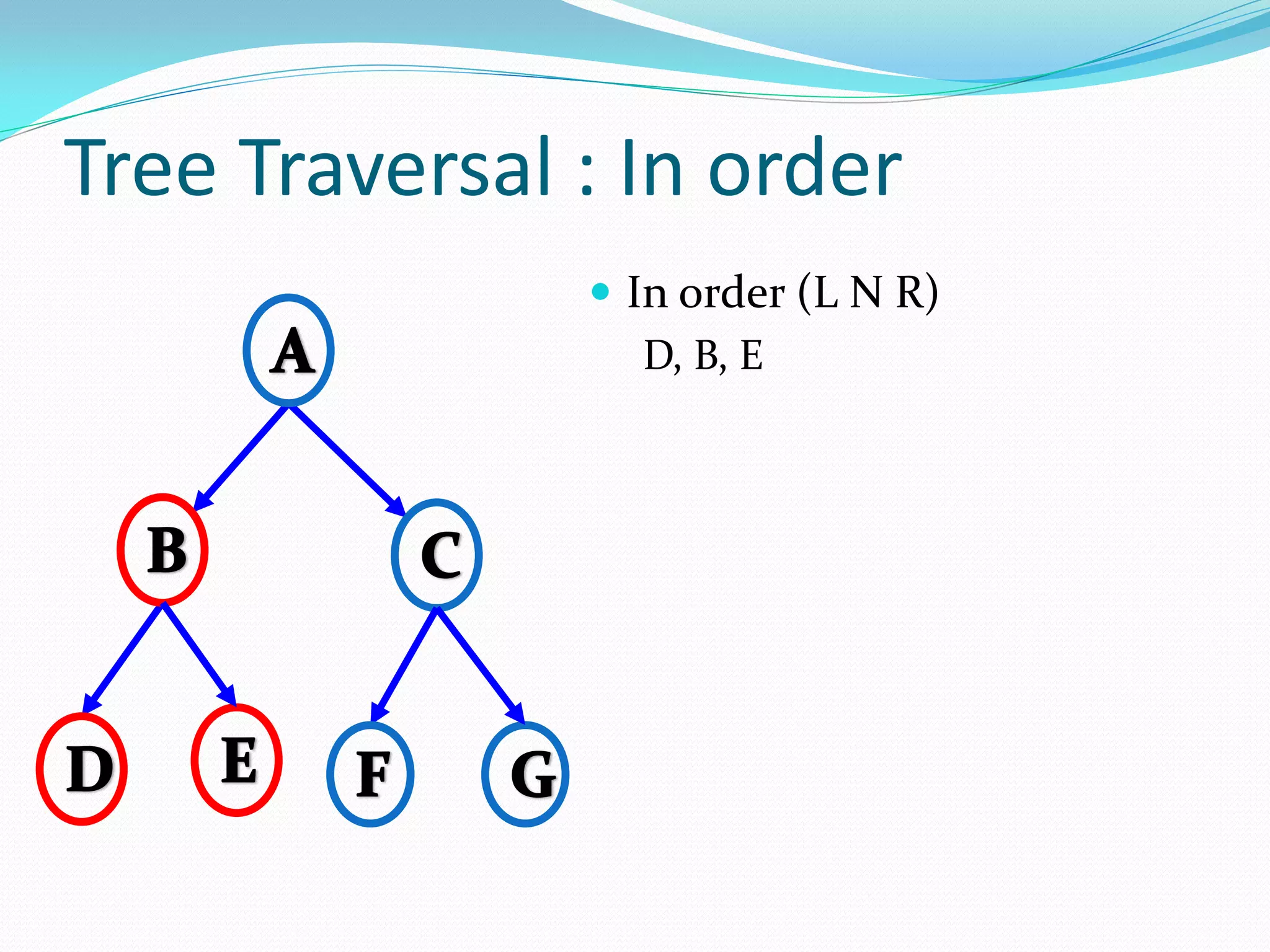




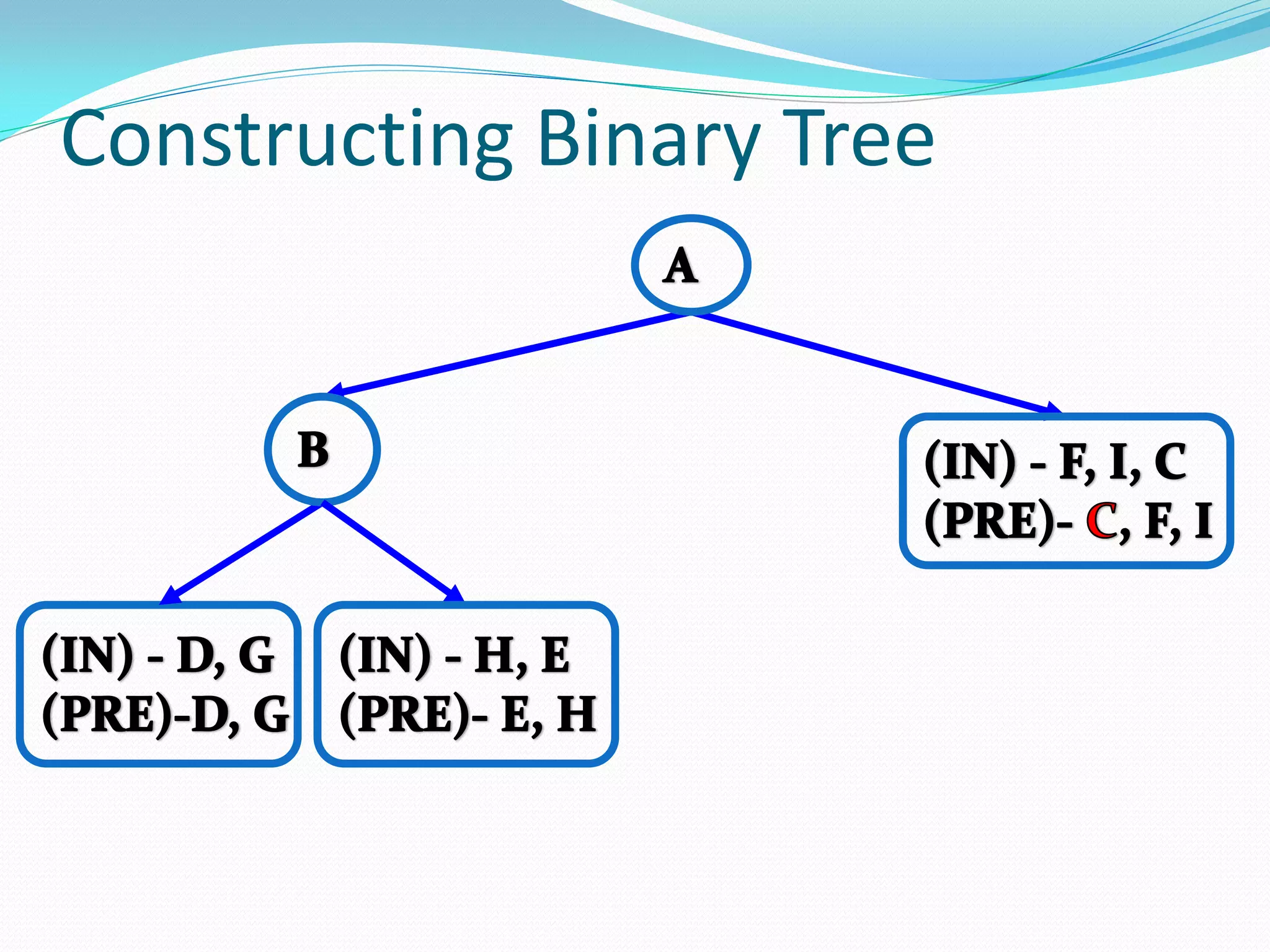
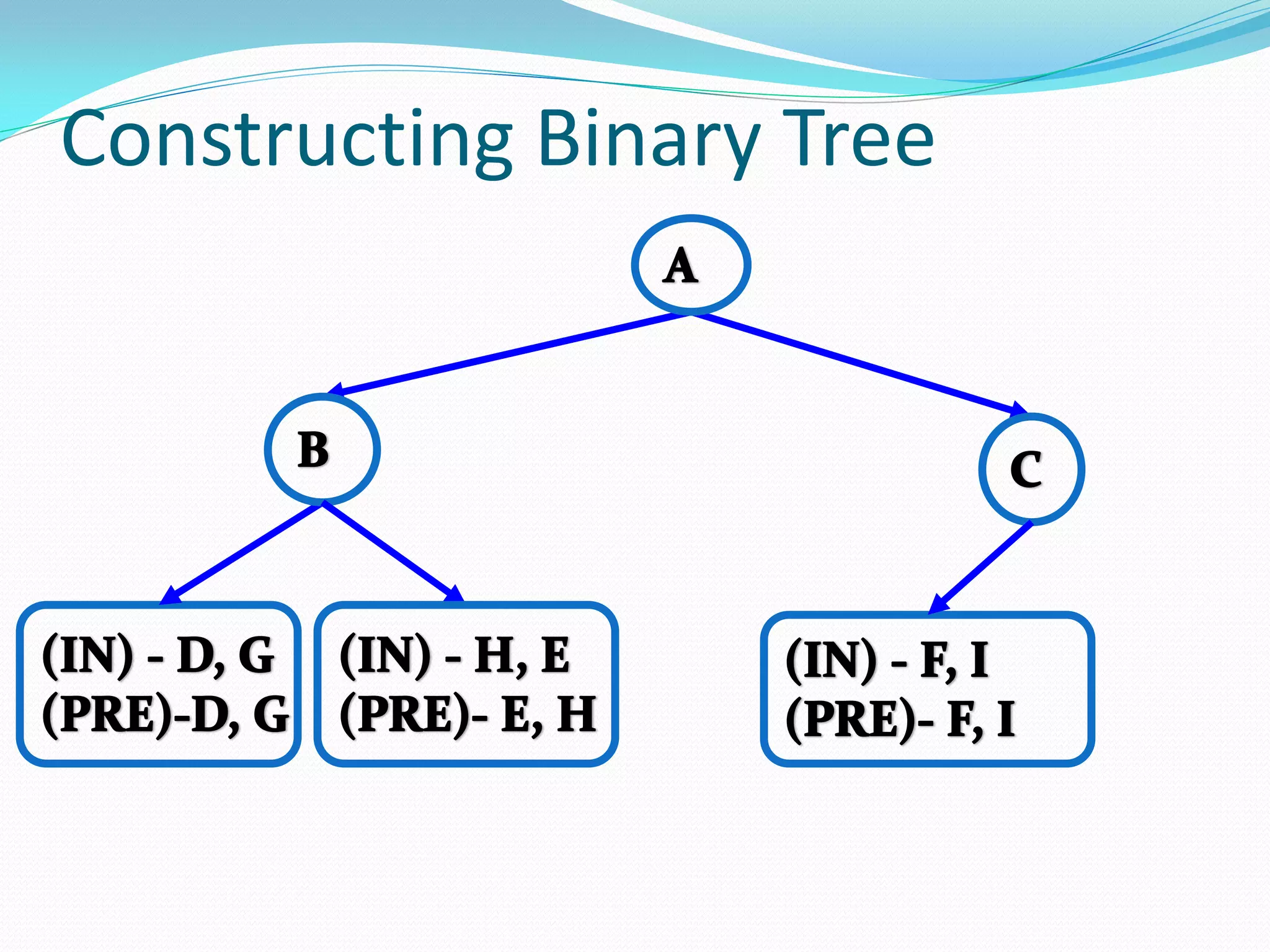
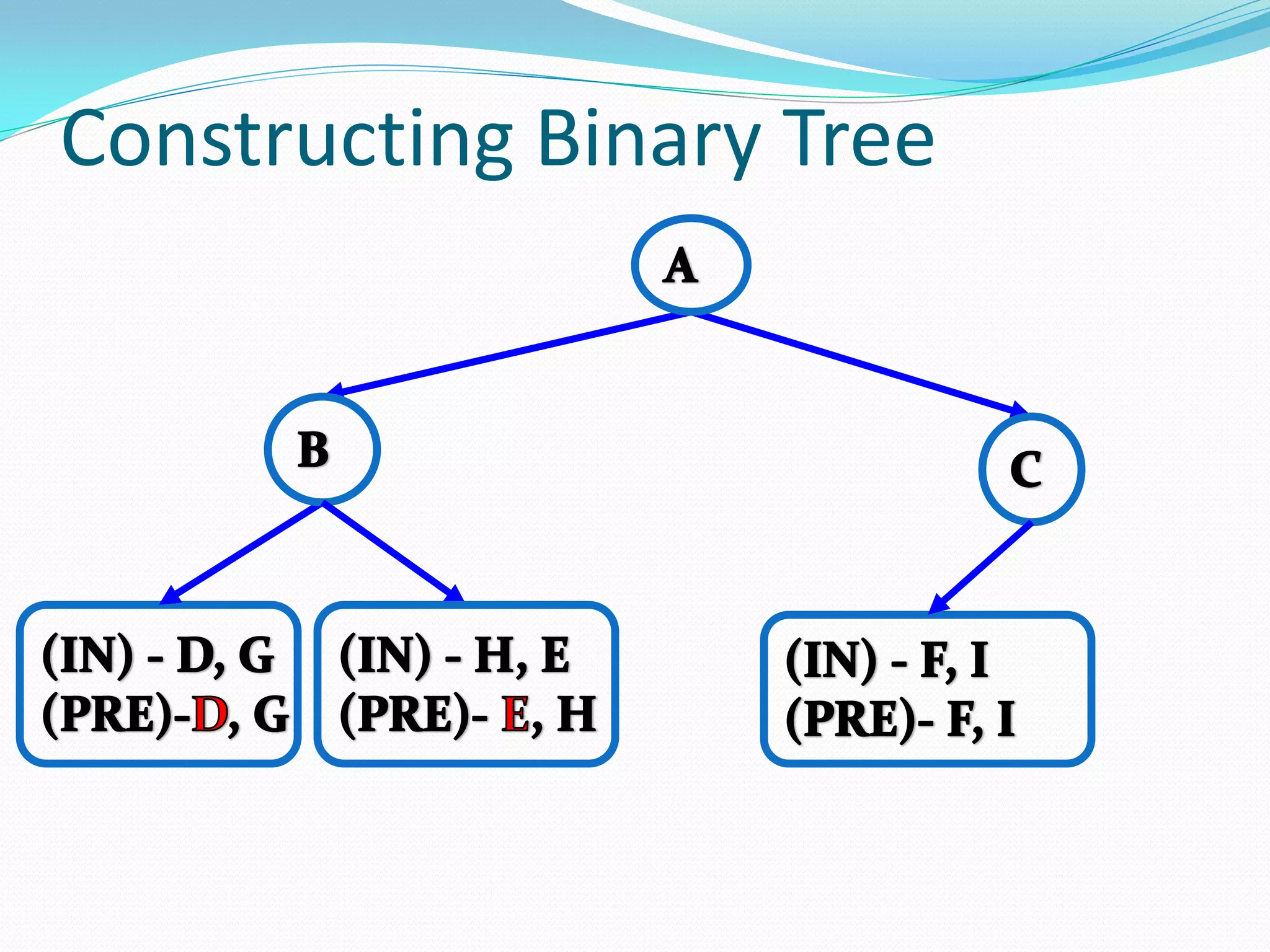
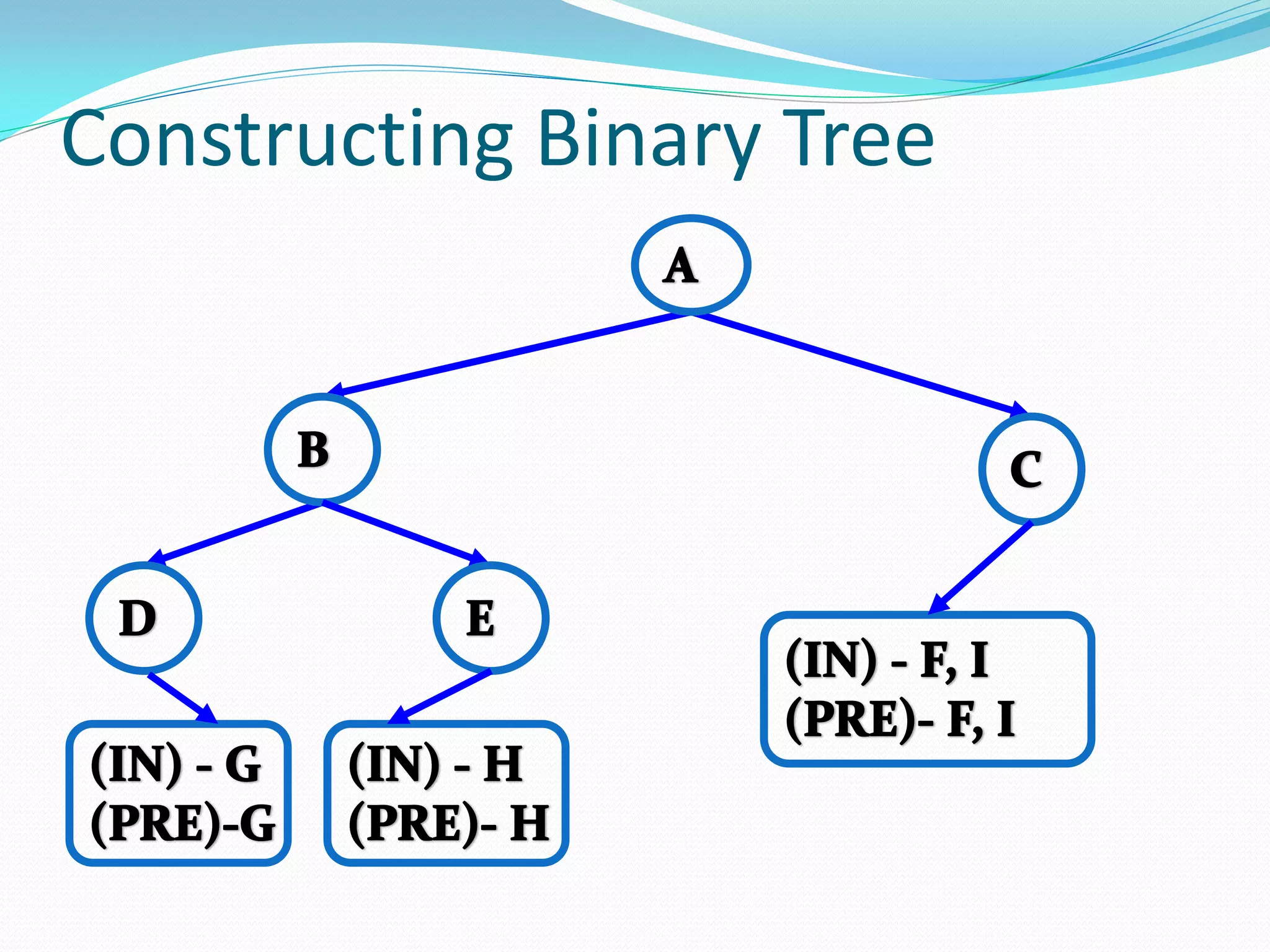
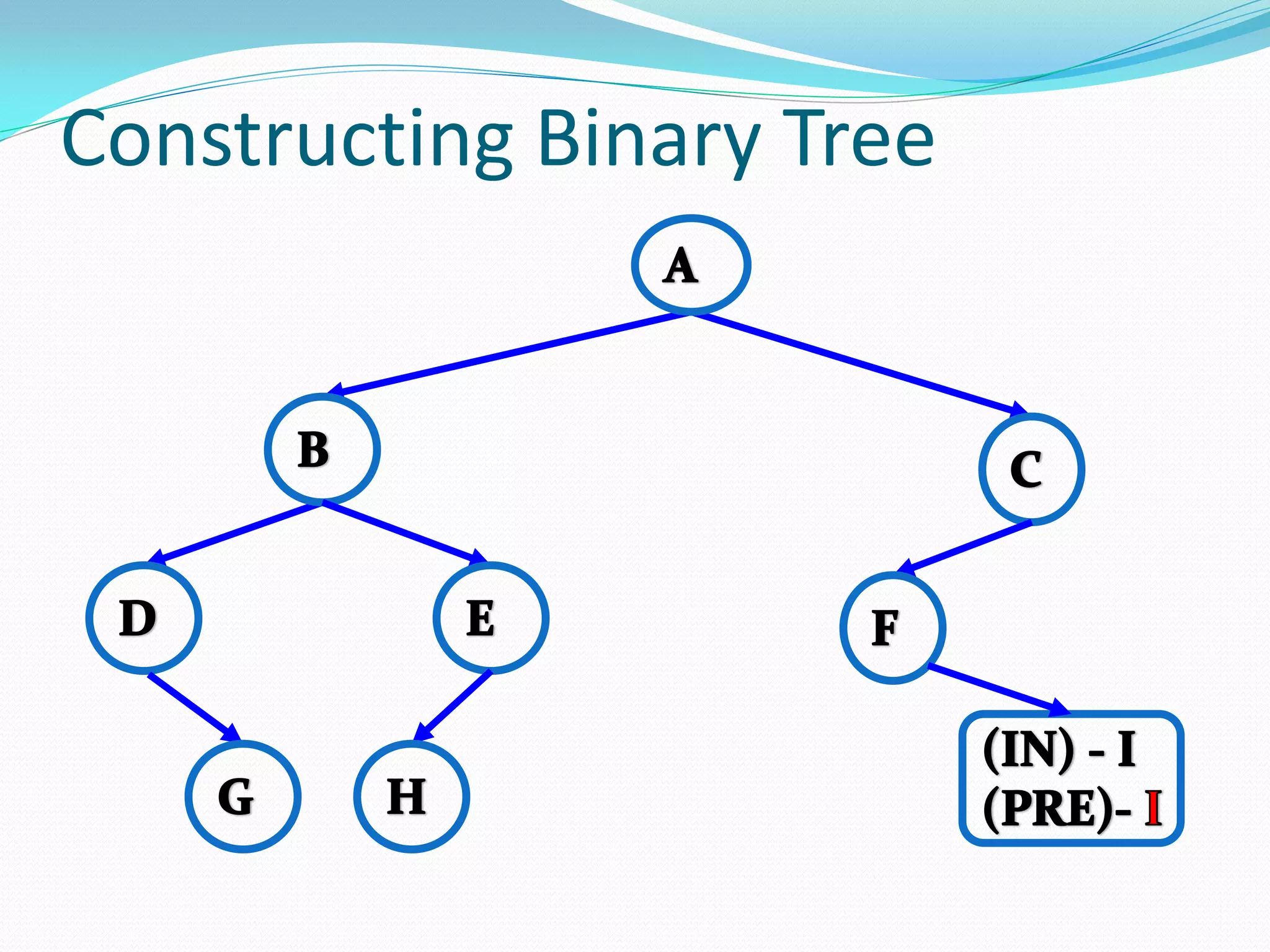











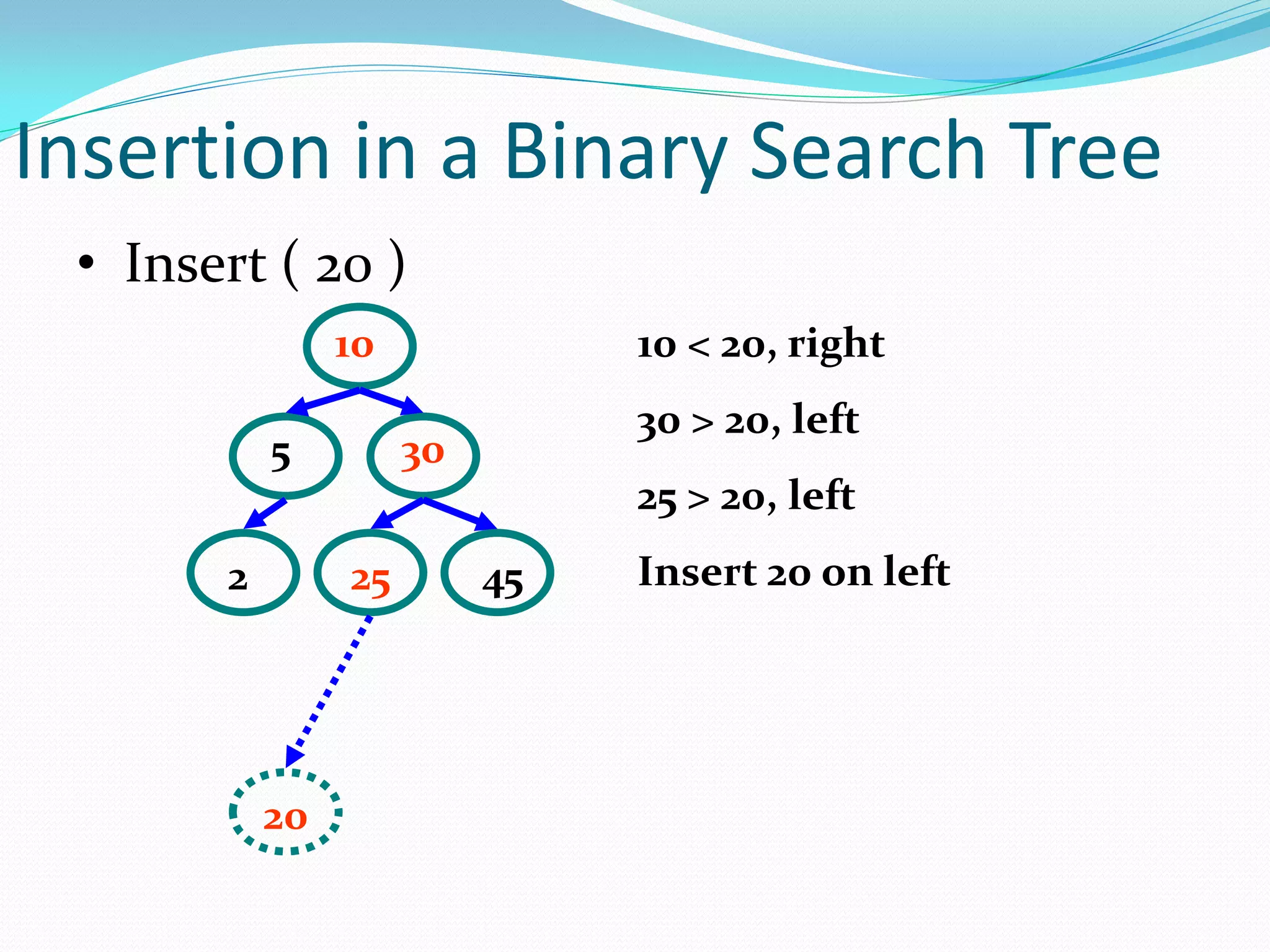








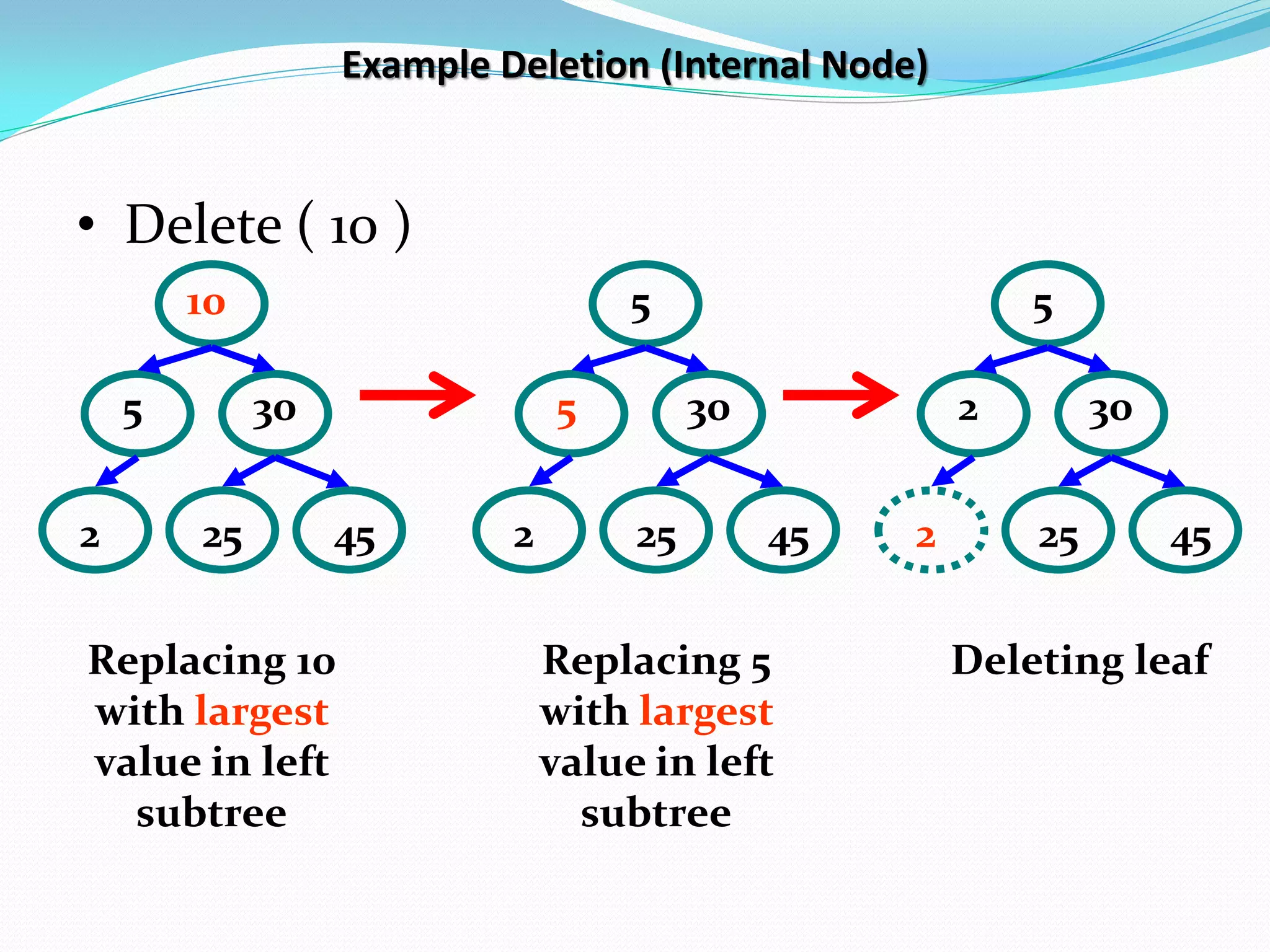
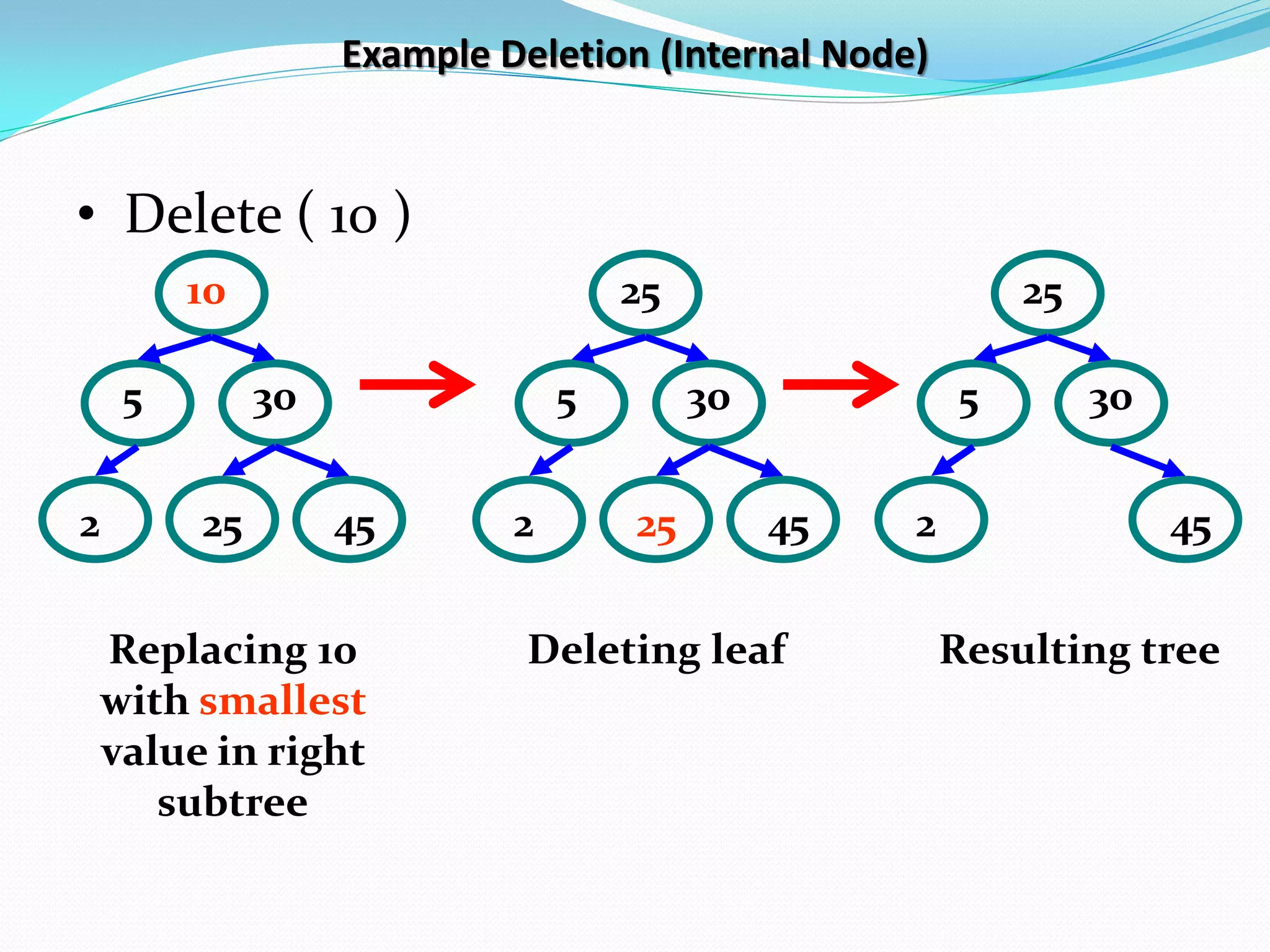



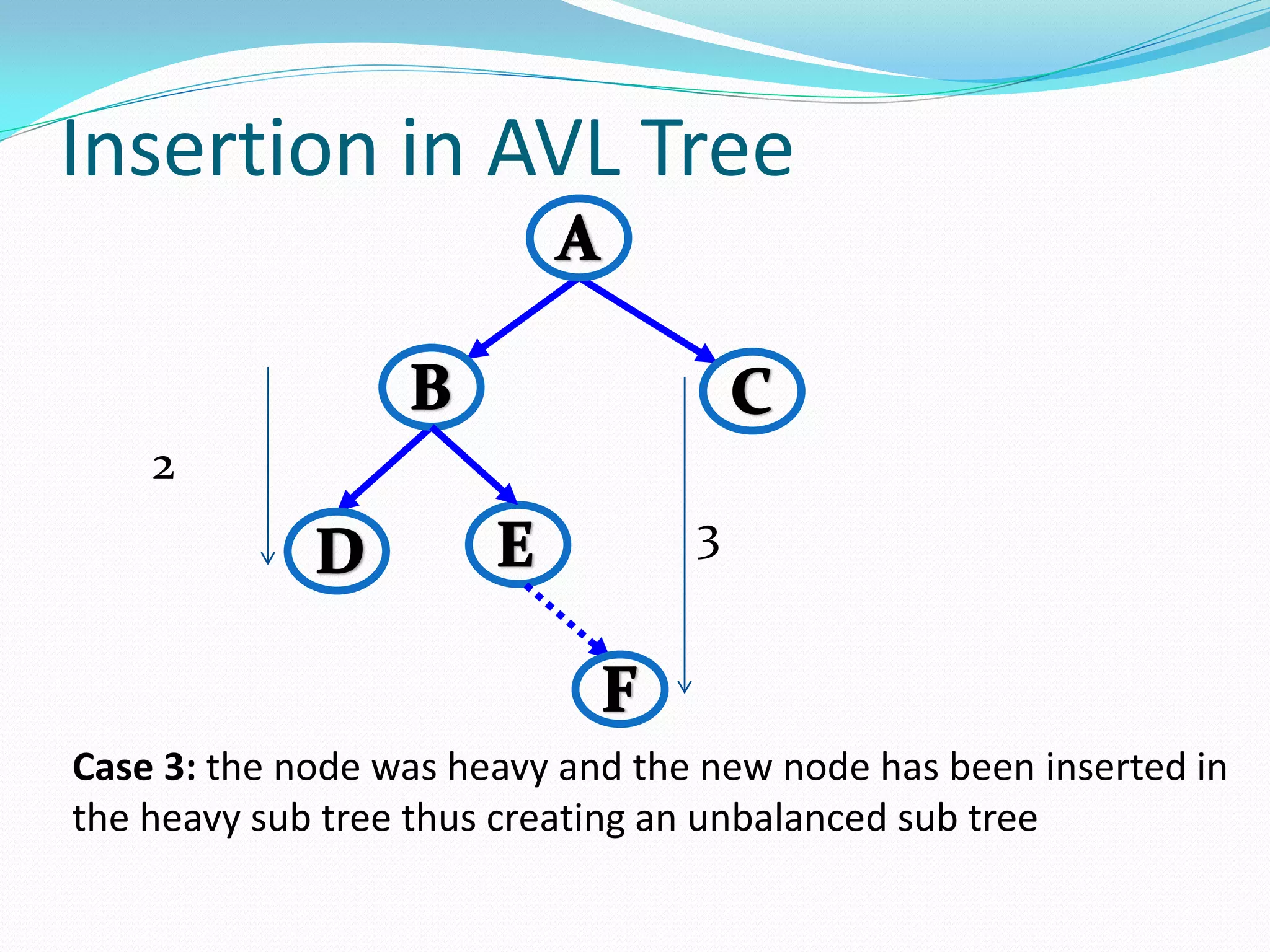



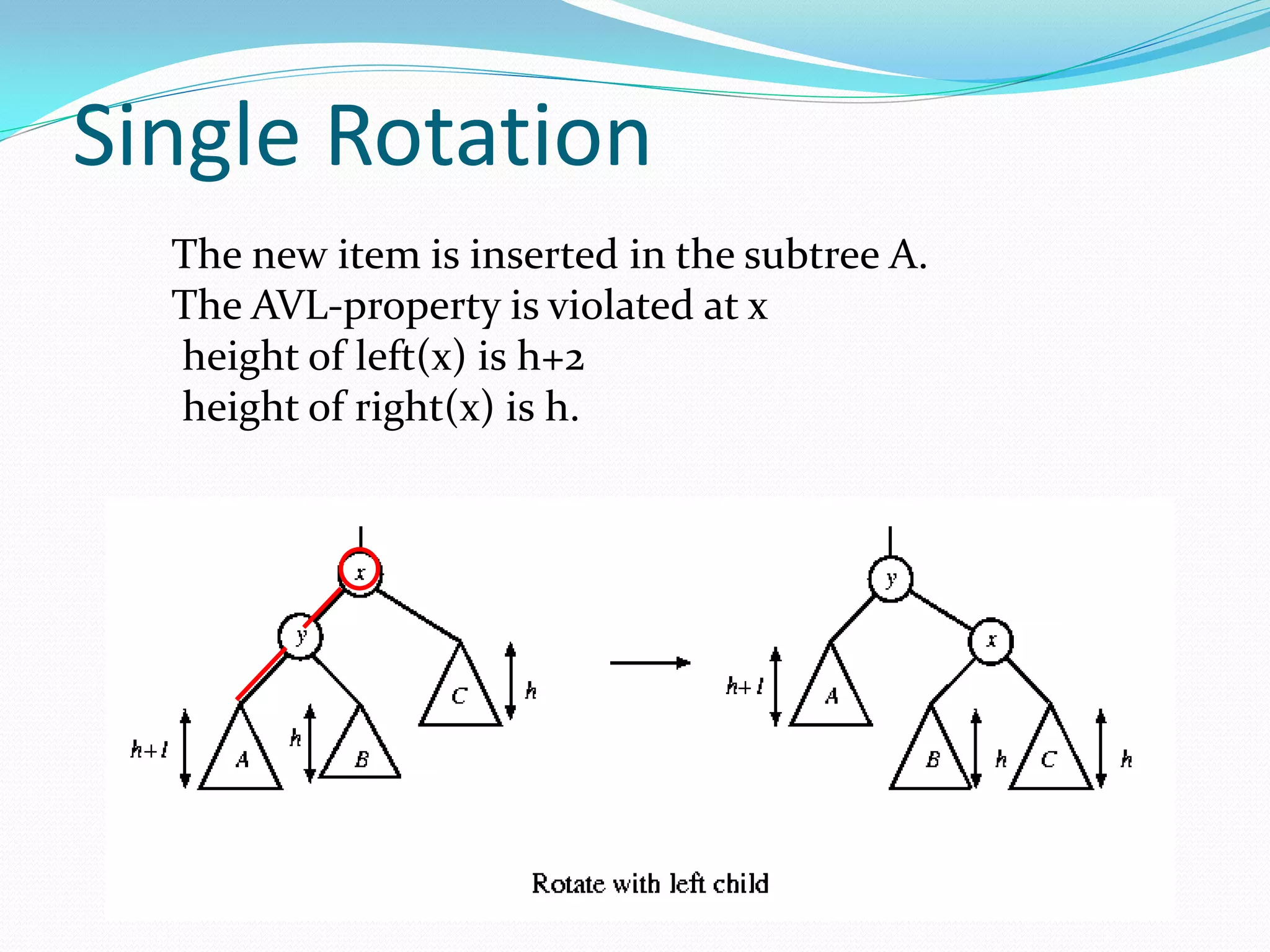
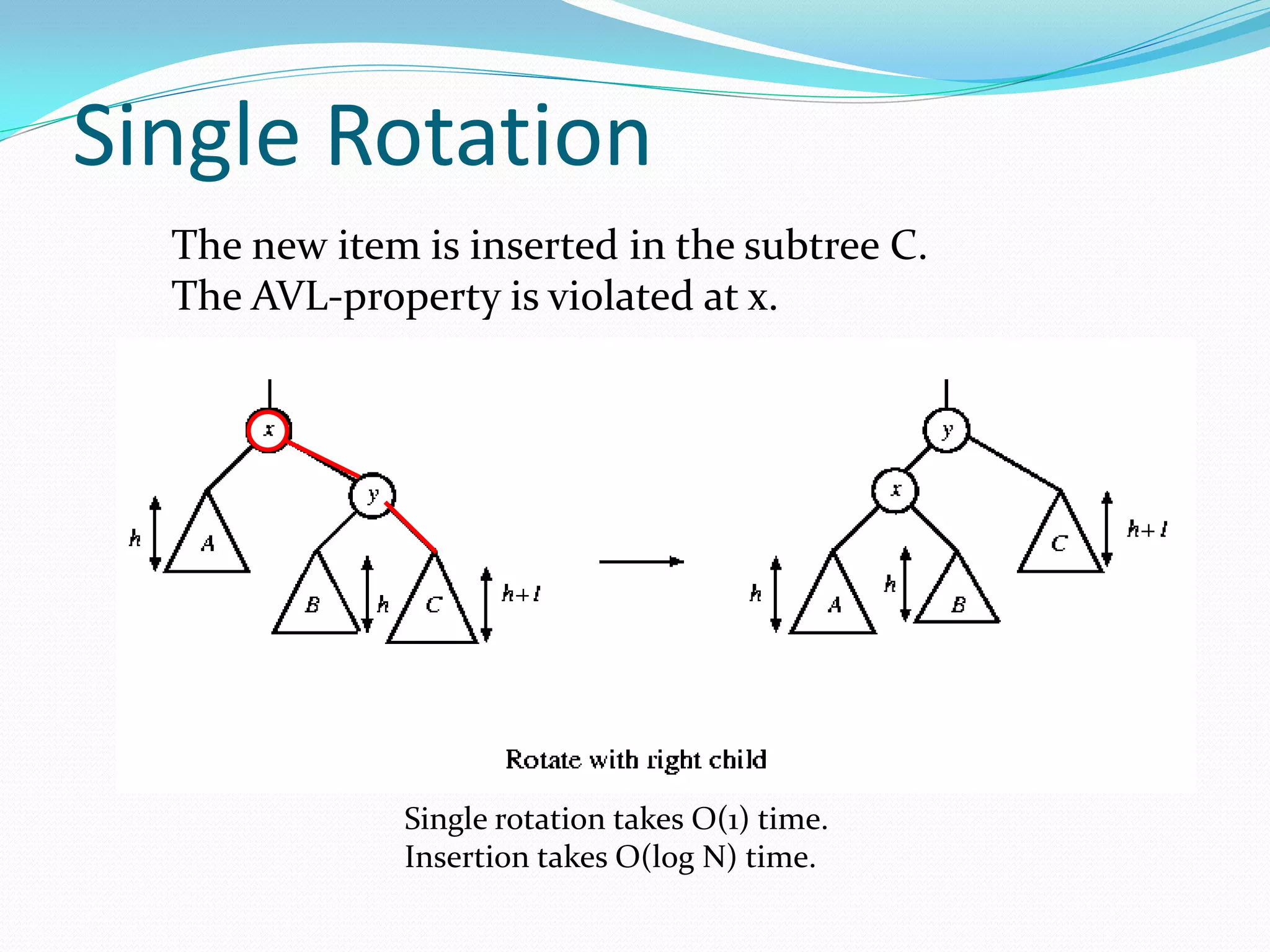
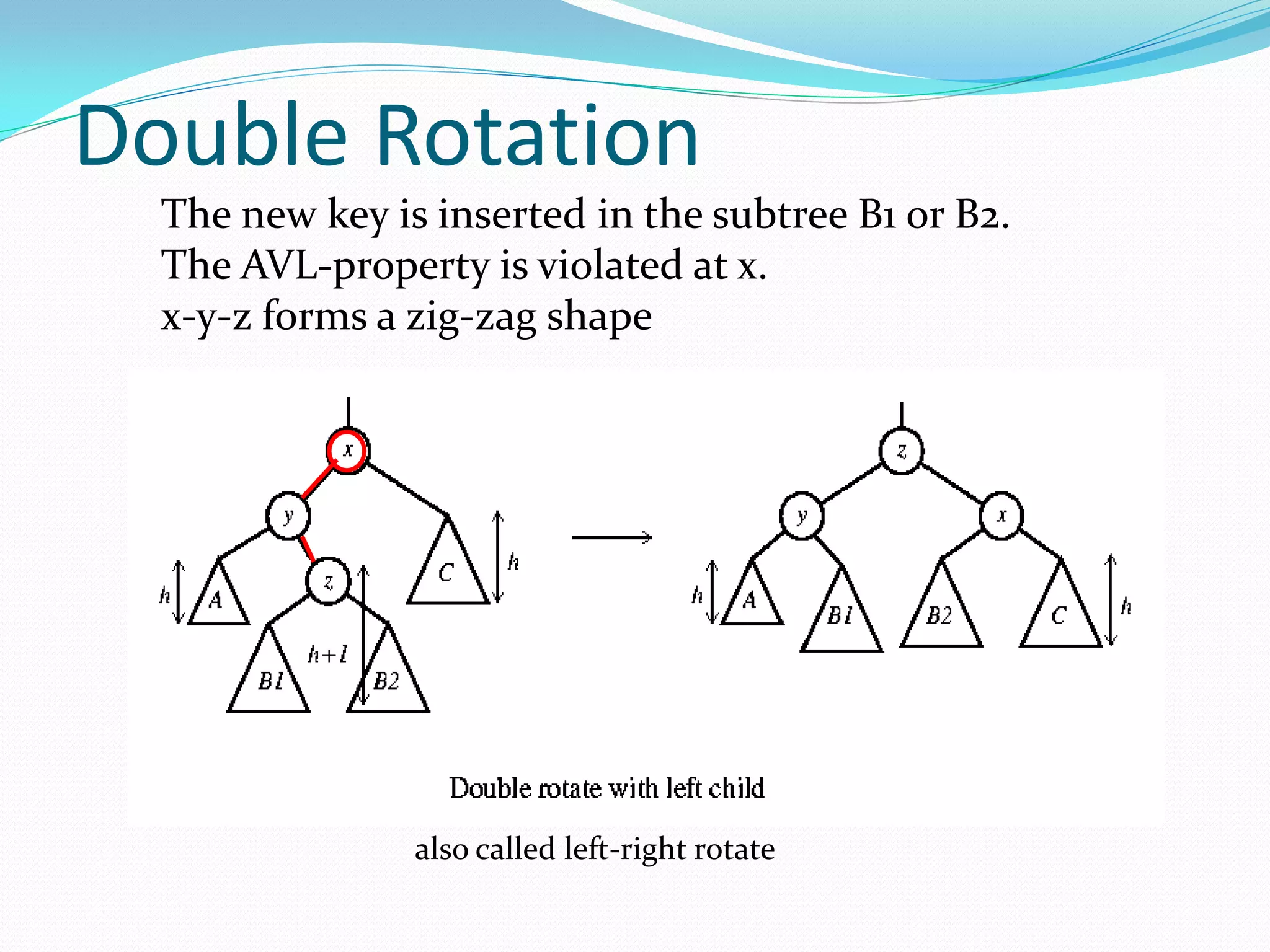















![14
12 7
810 6
9
6 3
5
30
25
[1]
[2] [3]
[5] [6]
[1]
[2] [3]
[4]
[1]
[2]
2
7 4
810 6
10
20 83
50
11
21
[1]
[2] [3]
[5] [6]
[1]
[2] [3]
[4]
[1]
[2]
[4]
Max Heap
Min Heap](https://image.slidesharecdn.com/datastructuresunit3-151009070317-lva1-app6892/75/Trees-Binary-Search-Tree-AVL-Tree-in-Data-Structures-129-2048.jpg)

![Insertion into a Max Heap
void insert_max_heap(element item, int *n)
{
int i;
if (HEAP_FULL(*n)) {
fprintf(stderr, “the heap is full.n”);
exit(1);
}
i = ++(*n);
while ((i!=1)&&(item.key>heap[i/2].key)) {
heap[i] = heap[i/2];
i /= 2;
}
heap[i]= item;
}
2k-1=n ==> k=log2(n+1)
O(log2n)](https://image.slidesharecdn.com/datastructuresunit3-151009070317-lva1-app6892/75/Trees-Binary-Search-Tree-AVL-Tree-in-Data-Structures-131-2048.jpg)
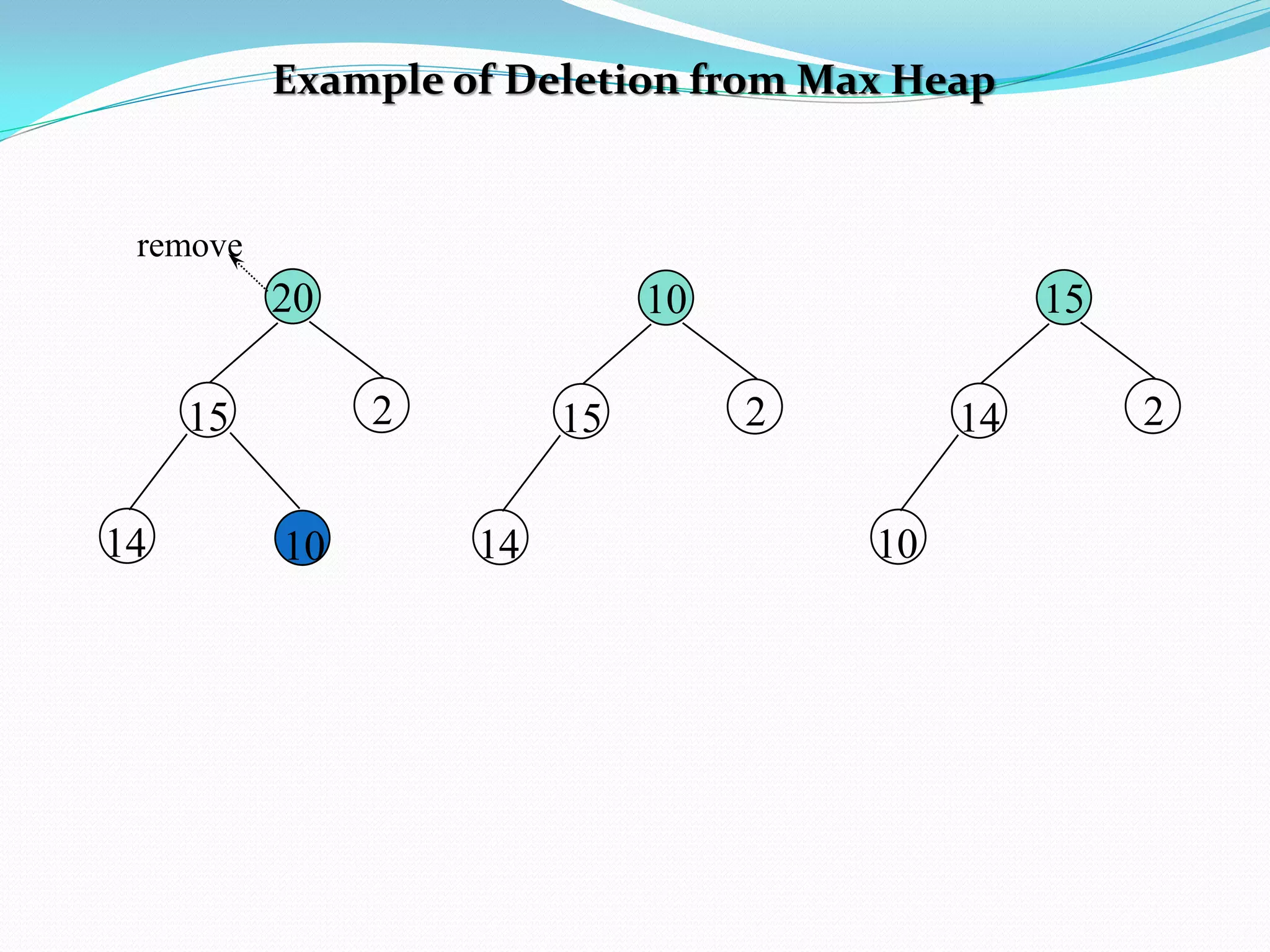
![Deletion from a Max Heap
element delete_max_heap(int *n)
{
int parent, child;
element item, temp;
if (HEAP_EMPTY(*n)) {
fprintf(stderr, “The heap is emptyn”);
exit(1);
}
/* save value of the element with the
highest key */
item = heap[1];
/* use last element in heap to adjust heap */
temp = heap[(*n)--];
parent = 1;
child = 2;](https://image.slidesharecdn.com/datastructuresunit3-151009070317-lva1-app6892/75/Trees-Binary-Search-Tree-AVL-Tree-in-Data-Structures-133-2048.jpg)
![while (child <= *n) {
/* find the larger child of the current
parent */
if ((child < *n)&&
(heap[child].key<heap[child+1].key))
child++;
if (temp.key >= heap[child].key) break;
/* move to the next lower level */
heap[parent] = heap[child];
child *= 2;
}
heap[parent] = temp;
return item;
}](https://image.slidesharecdn.com/datastructuresunit3-151009070317-lva1-app6892/75/Trees-Binary-Search-Tree-AVL-Tree-in-Data-Structures-134-2048.jpg)
