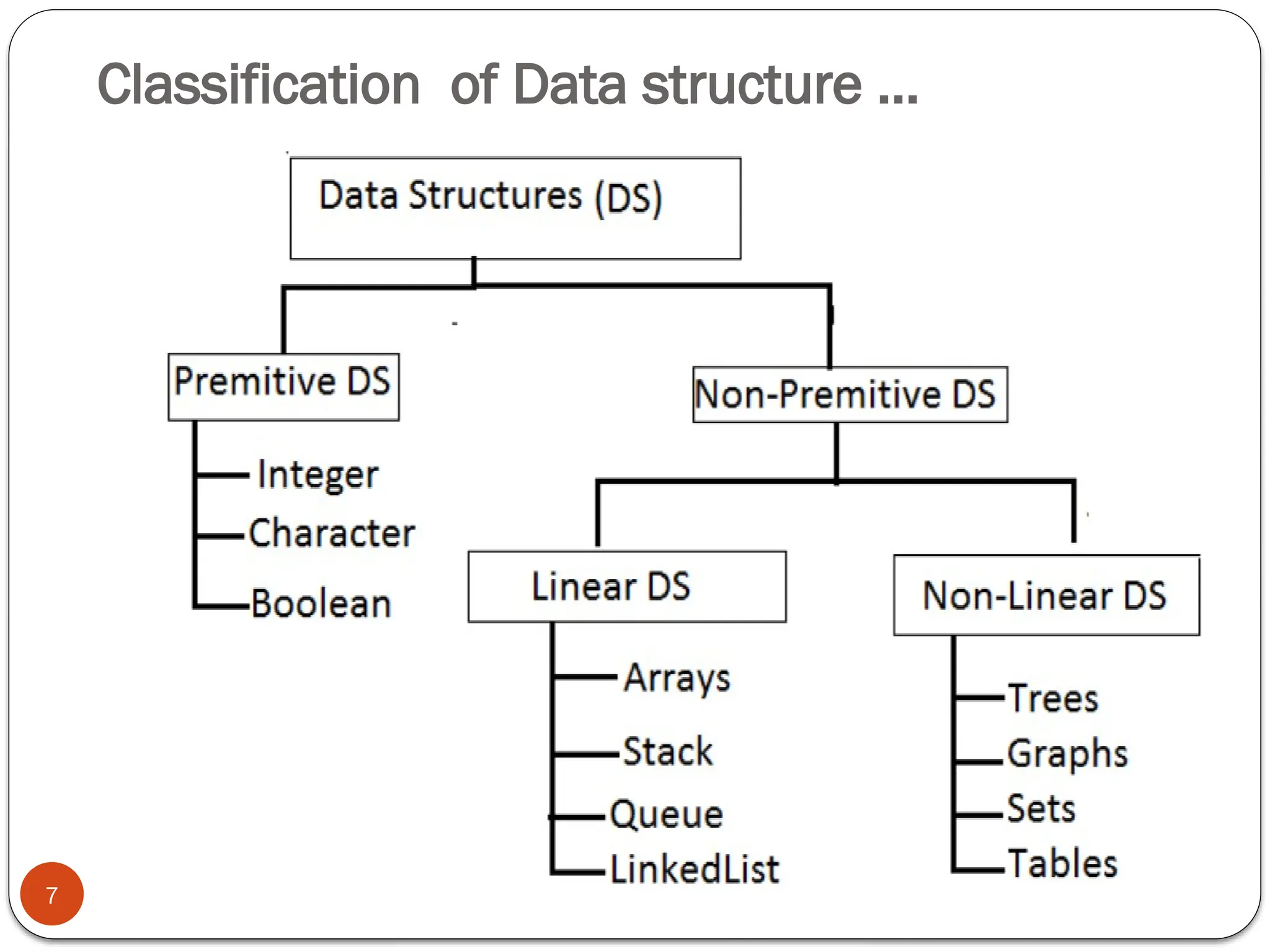
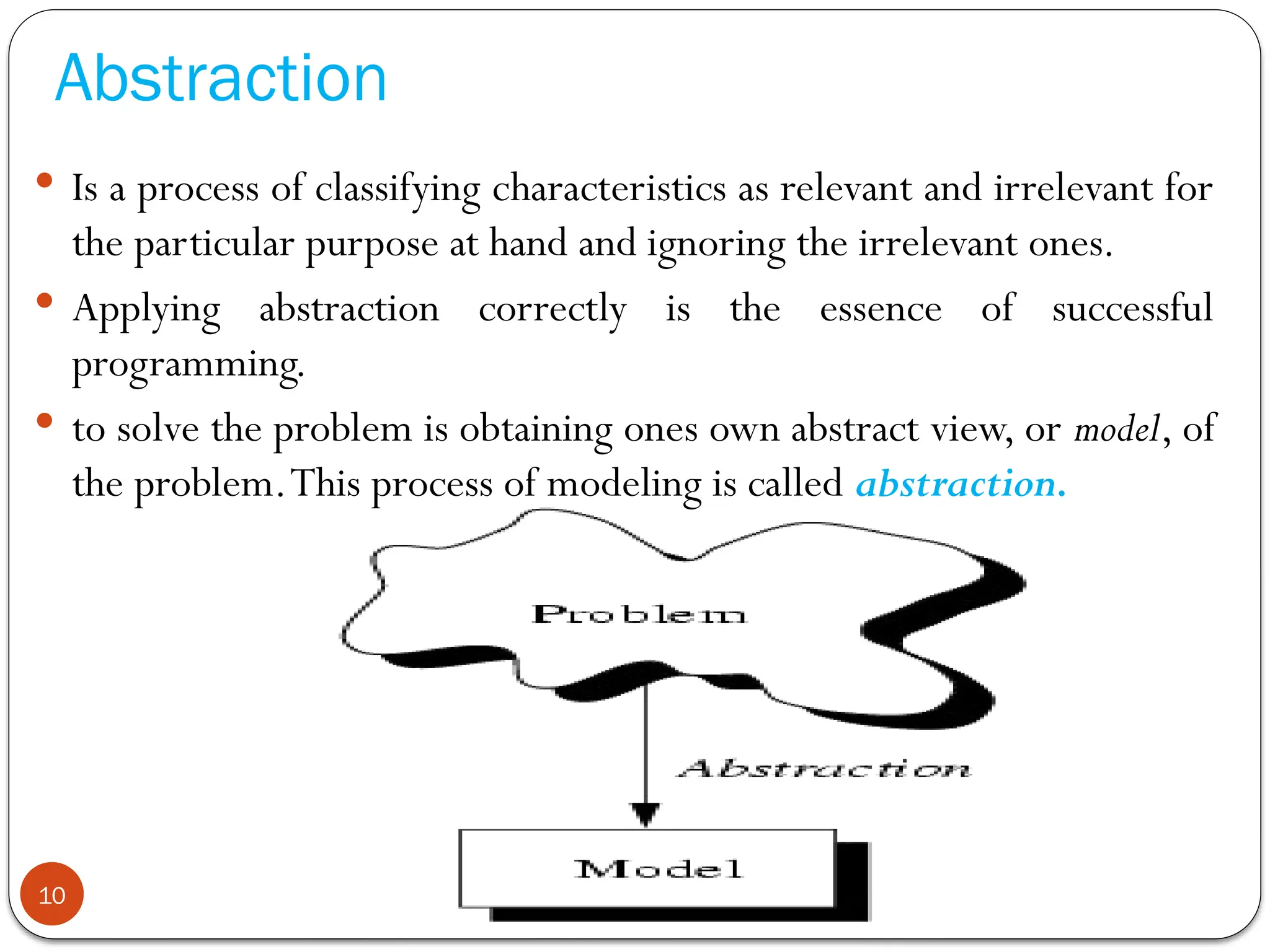
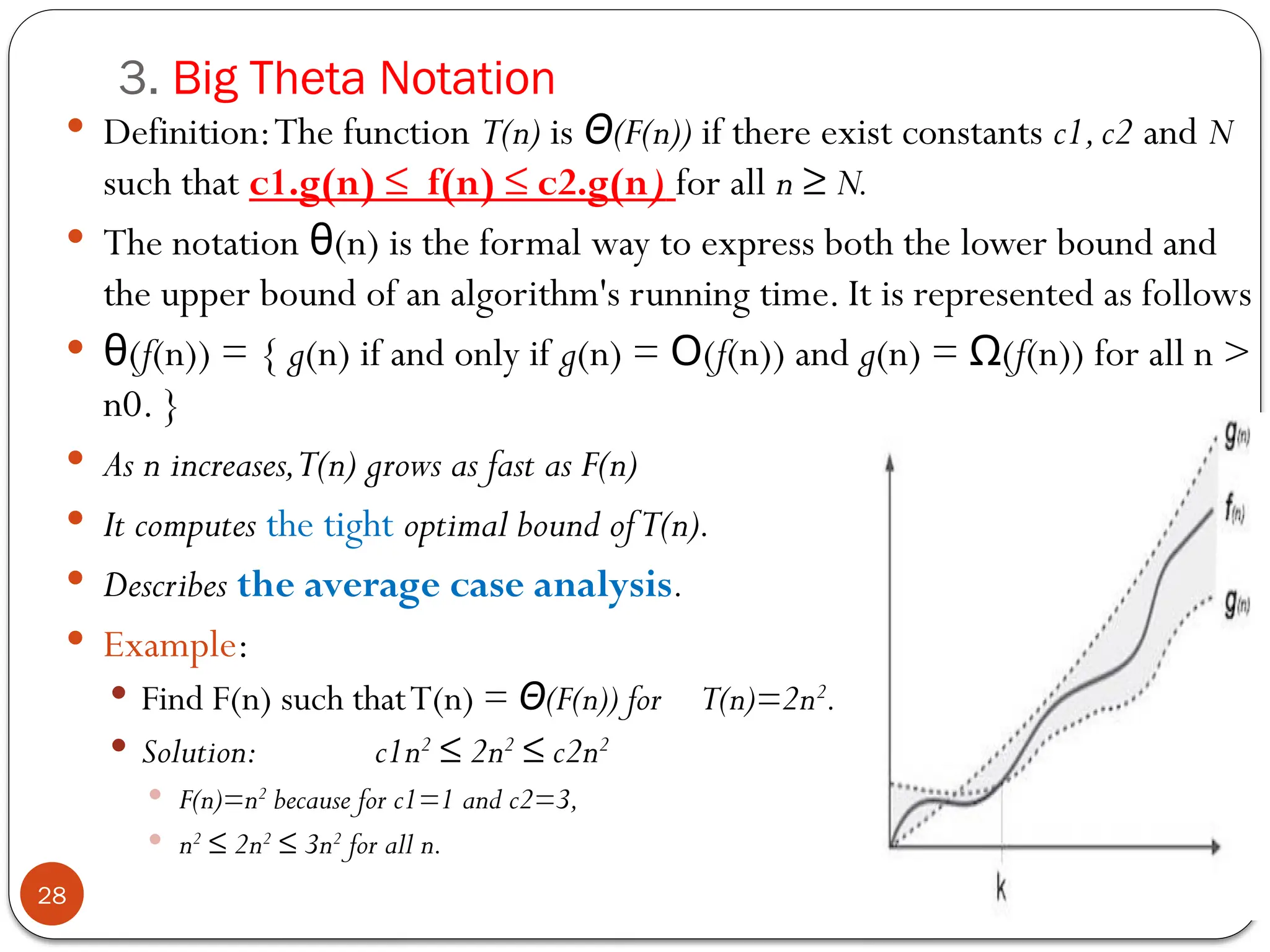
This document is an introduction to data structures and algorithms, covering key concepts such as data structure definitions, classifications, and properties of algorithms. It explains the importance of algorithm analysis including time and space complexity, and introduces various notations like big-O, big-omega, and big-theta for evaluating algorithm efficiency. The document also delineates different operations on data structures and the significance of abstraction in programming.