KEMBAR78
Clustering Methods with R | PDF
Akira Murakami, profile picture
Uploaded byAkira Murakami
PDF, PPTX1,983 views

Clustering Methods with R

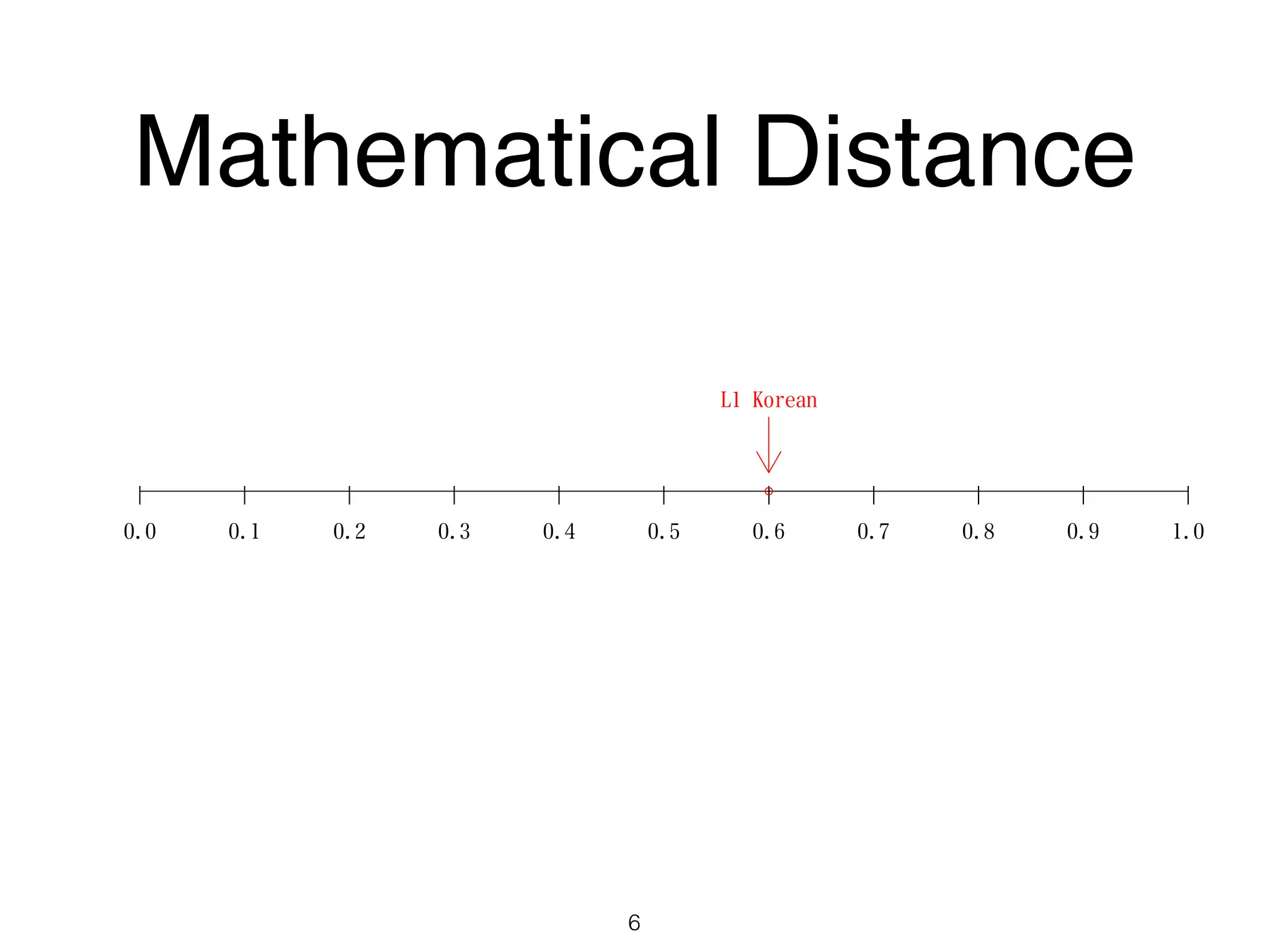
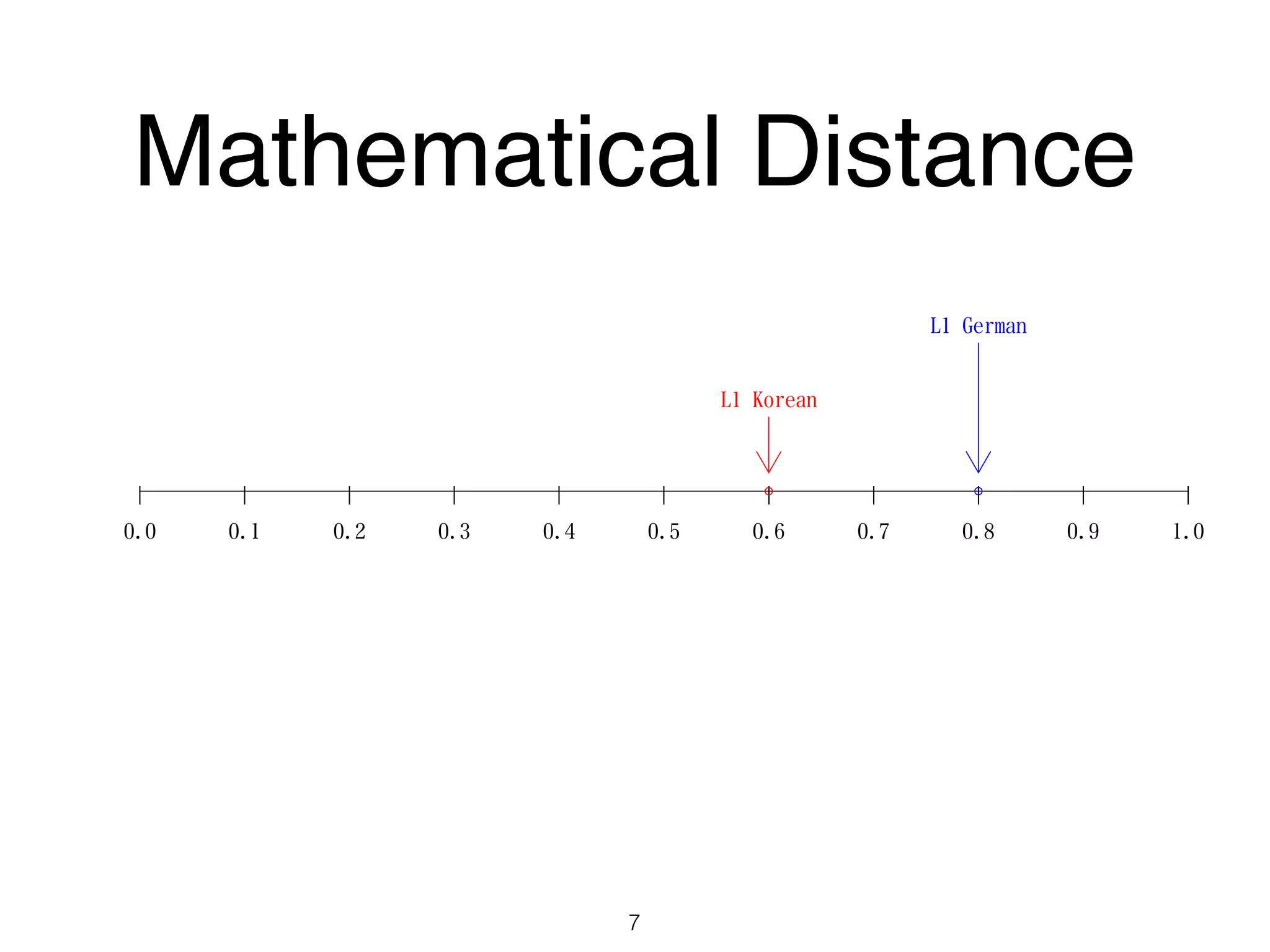
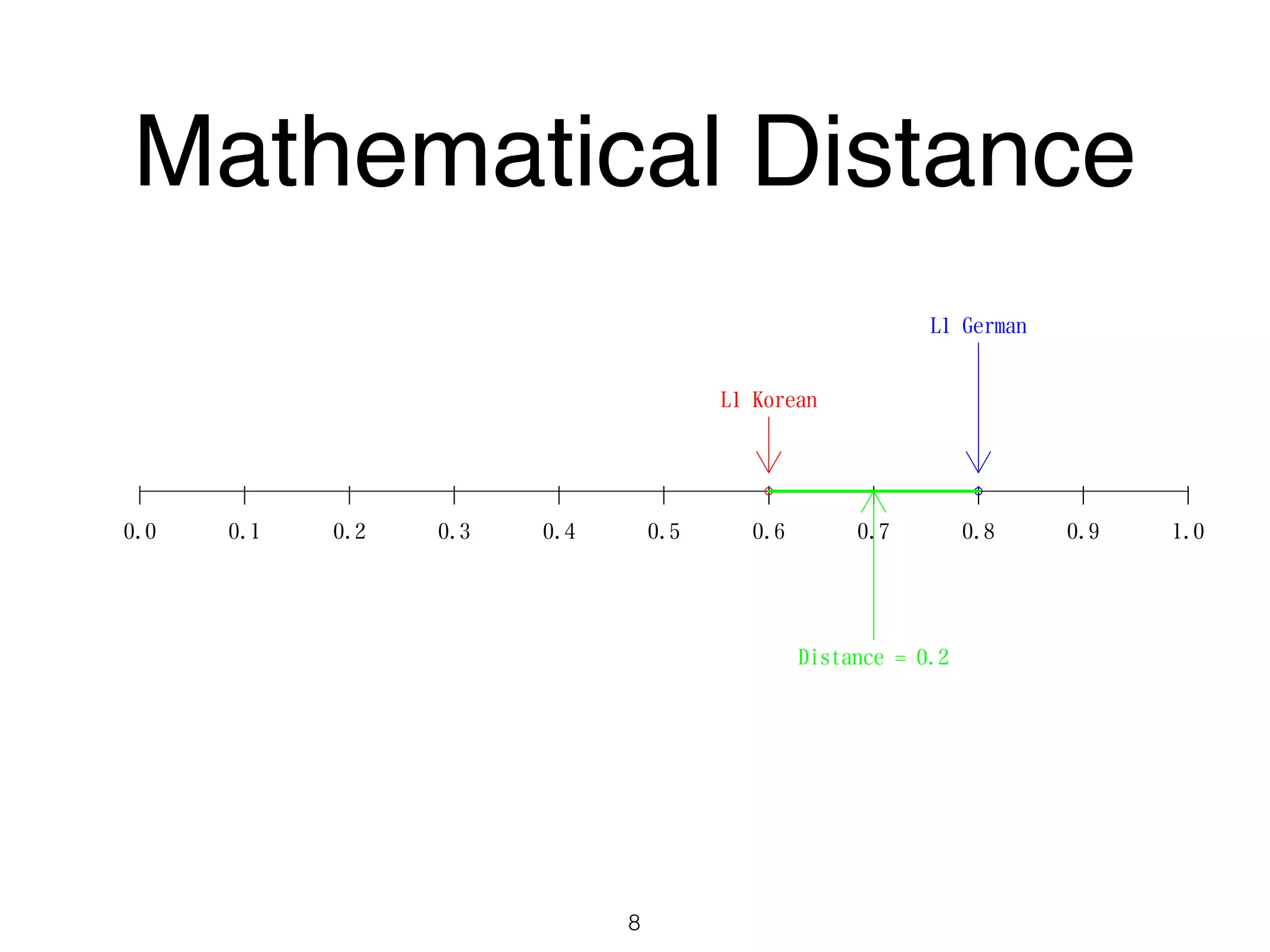
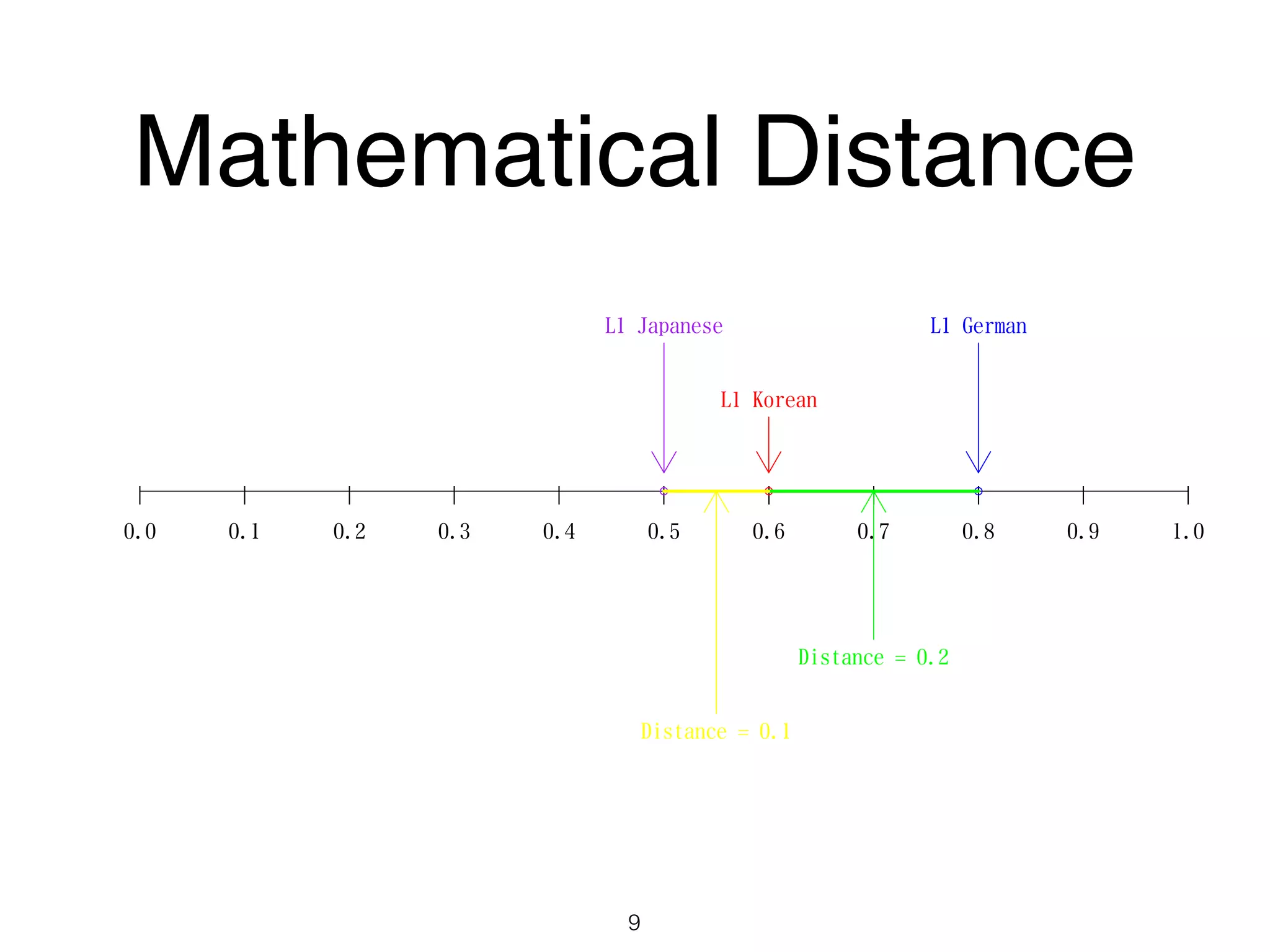
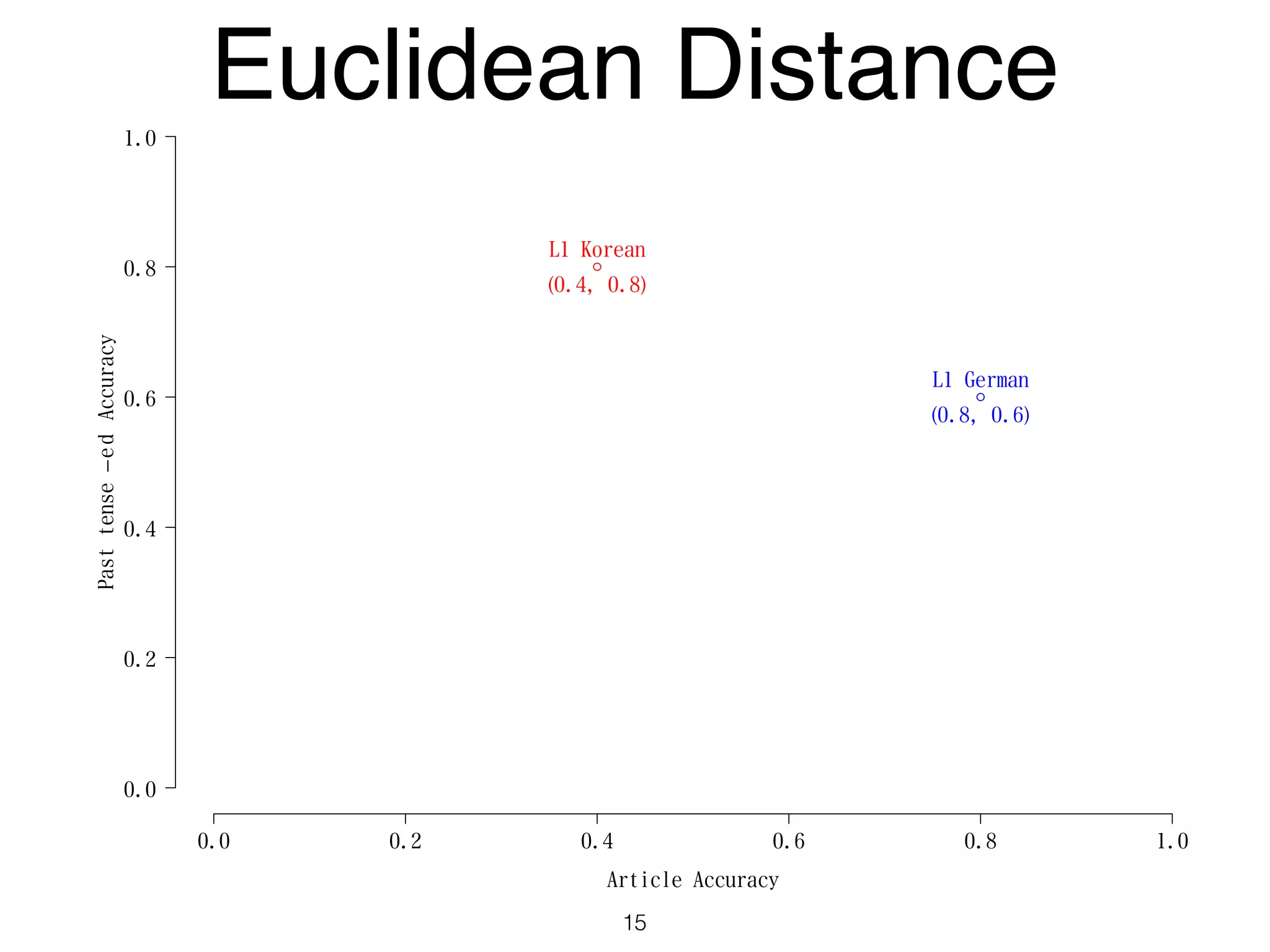
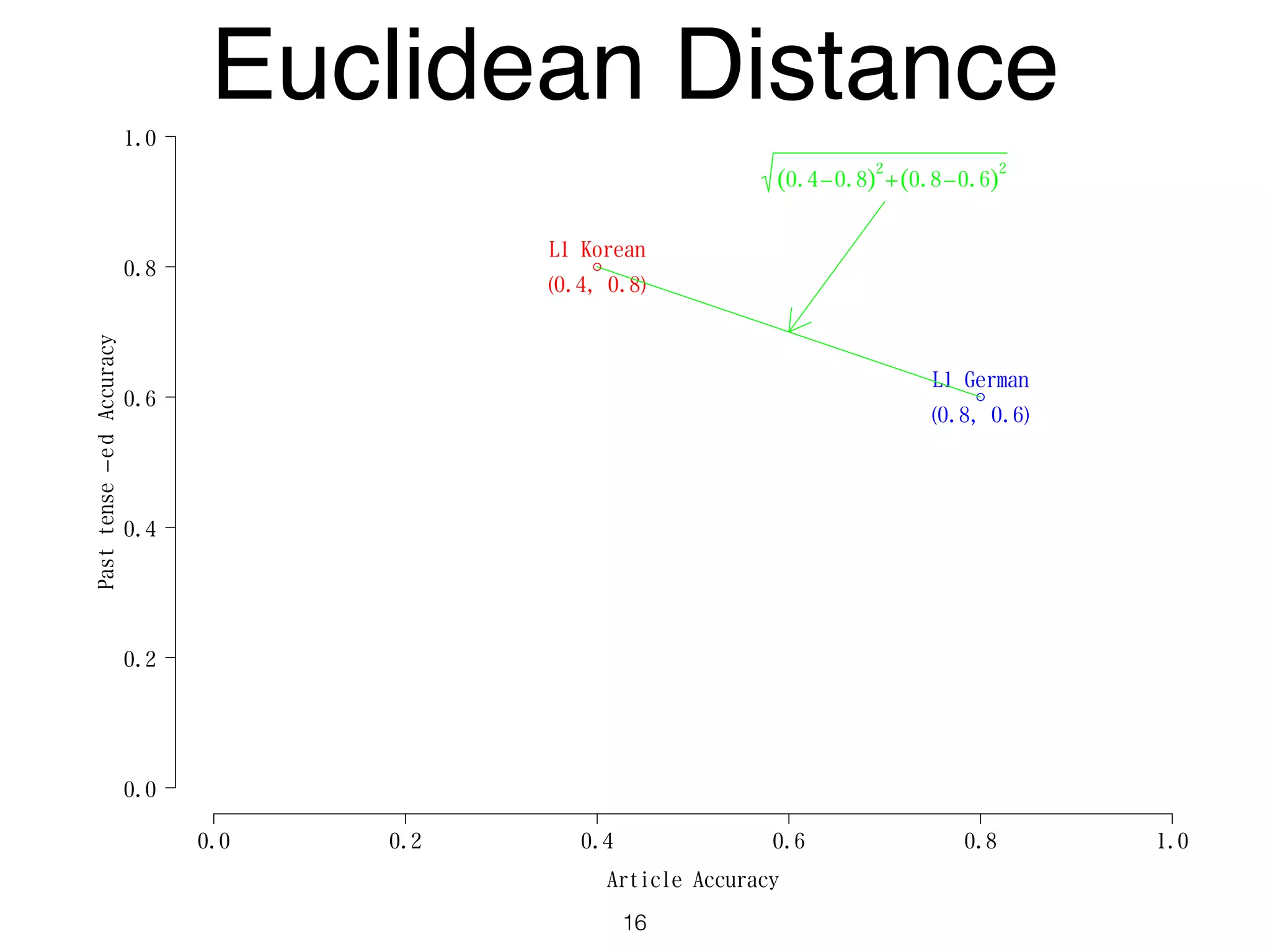
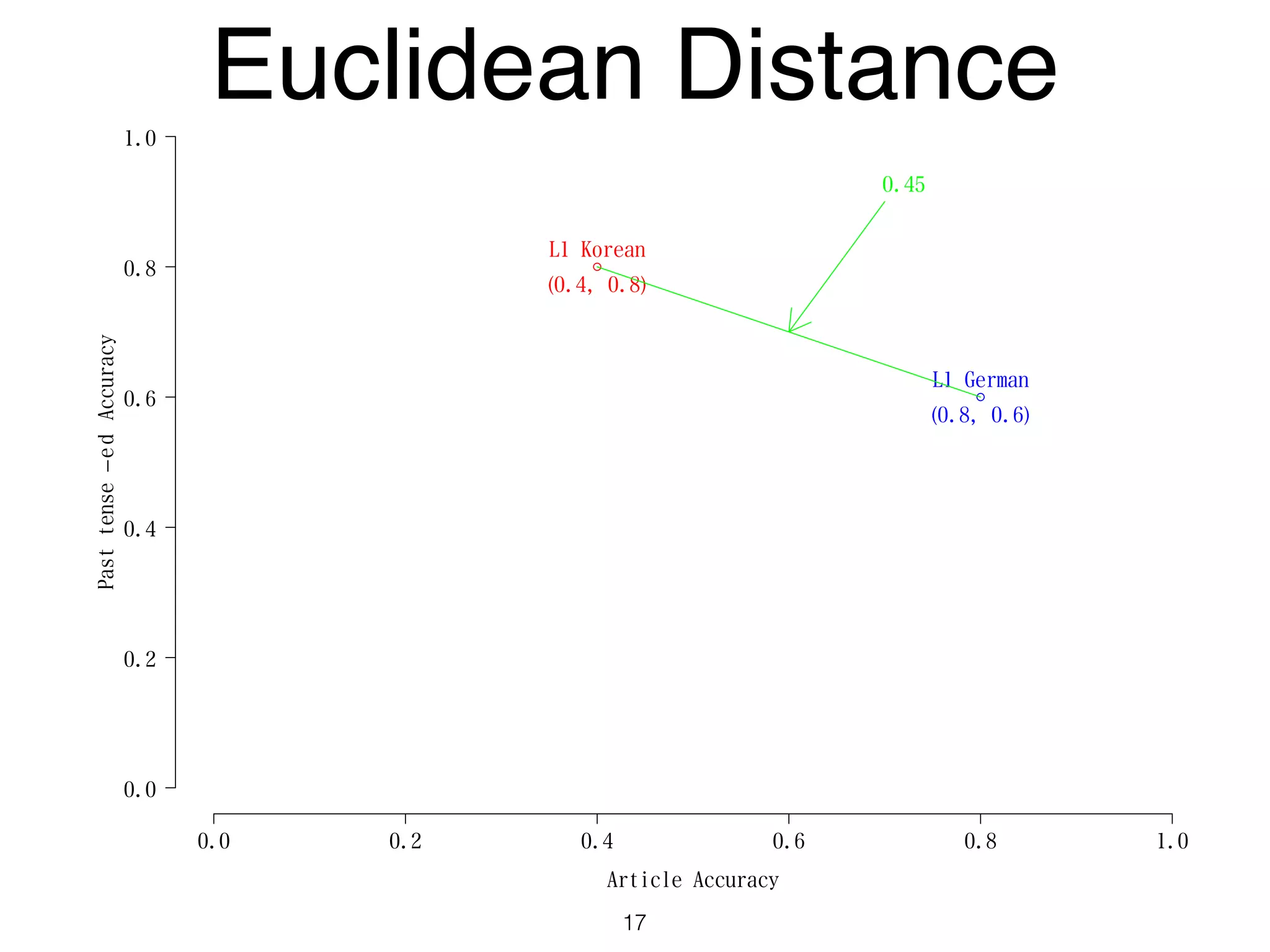
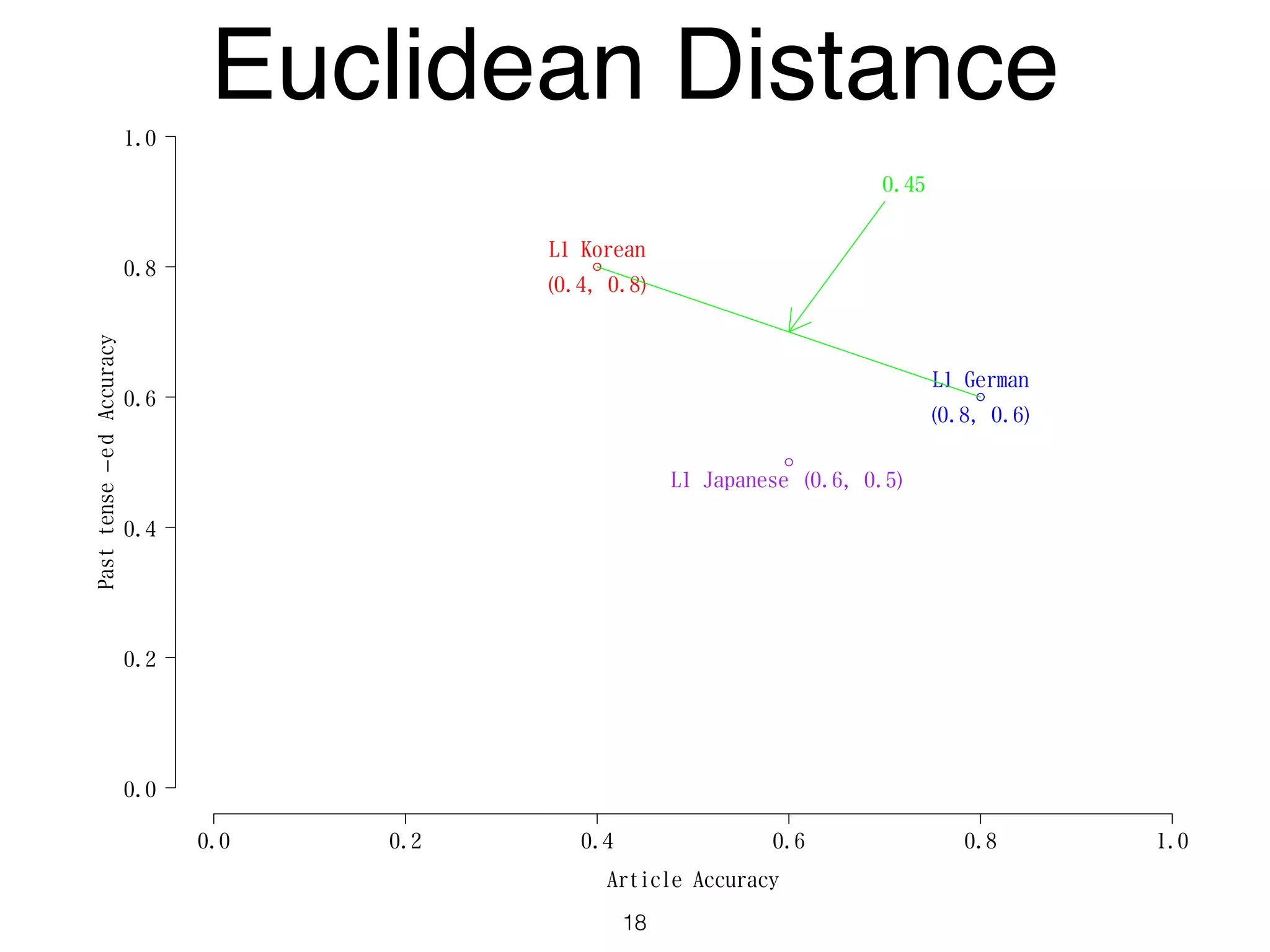
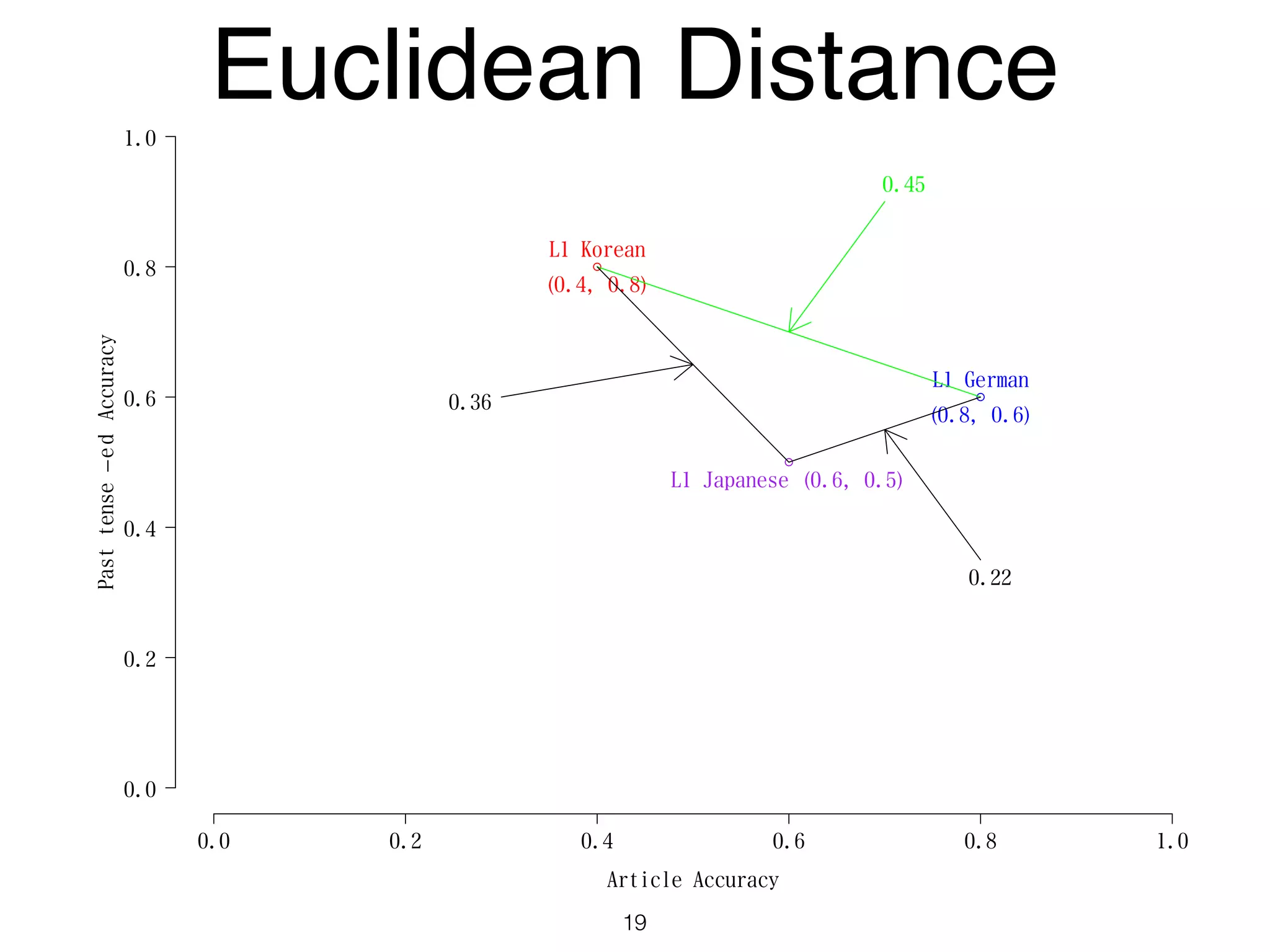
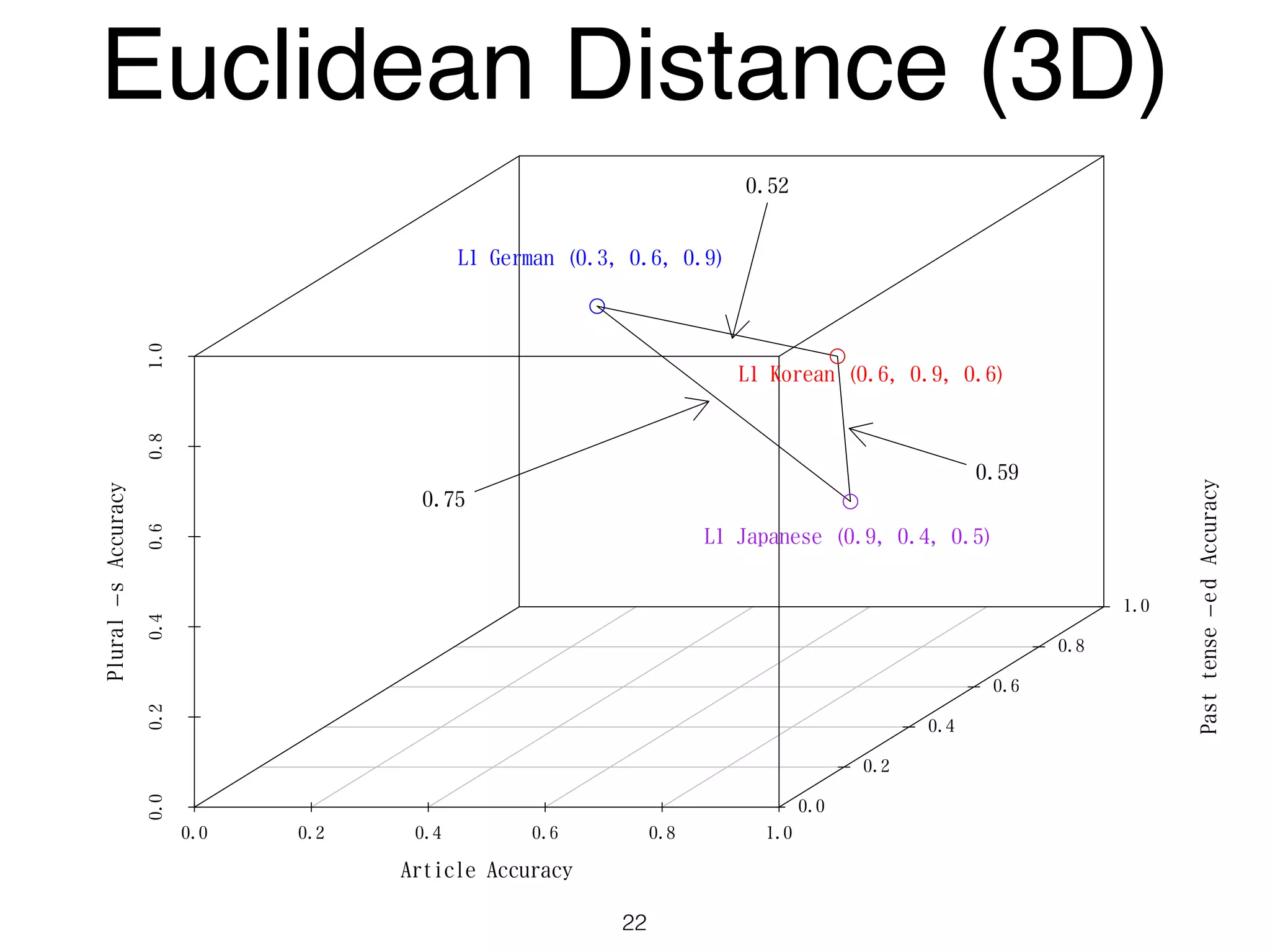
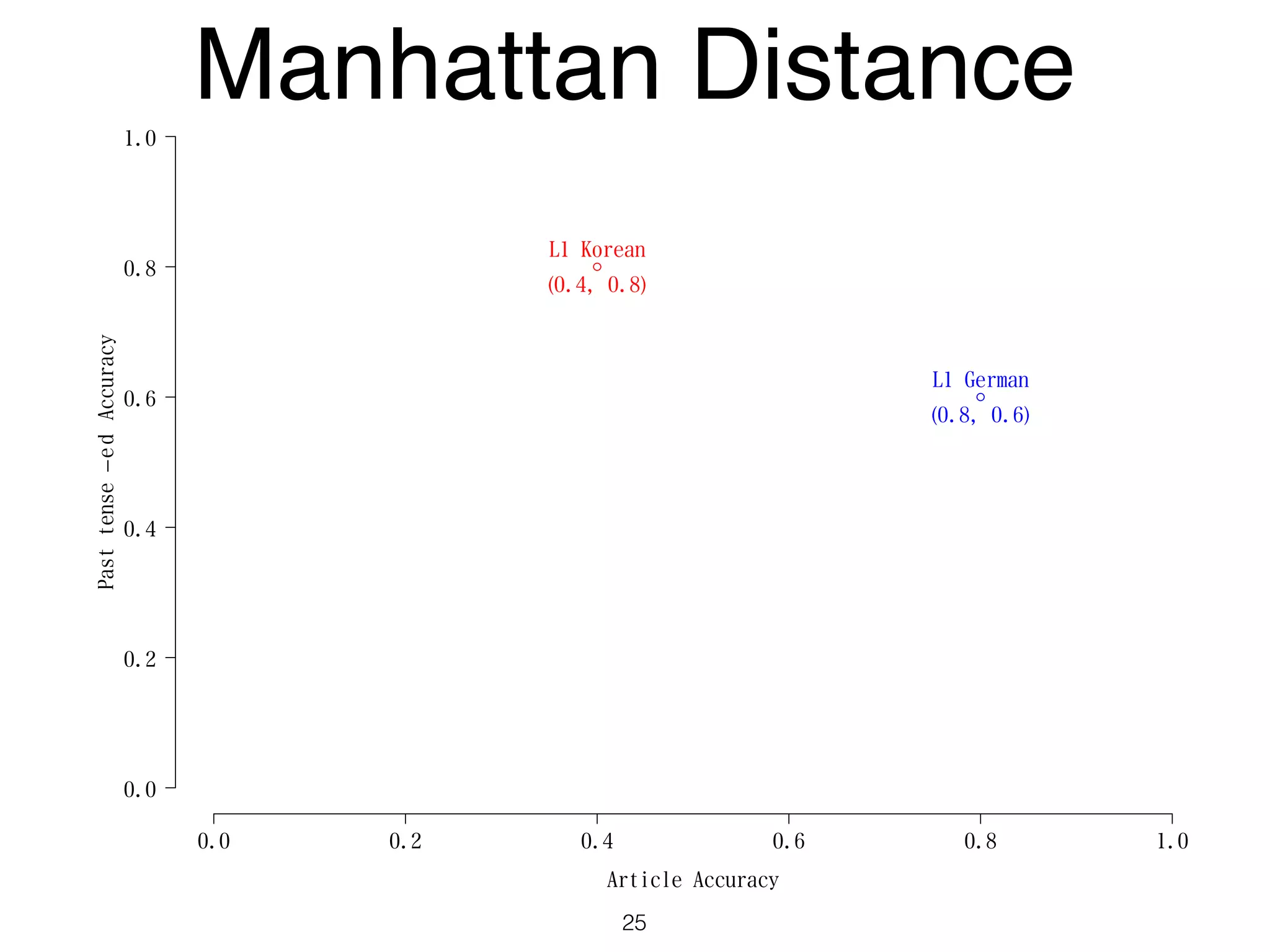
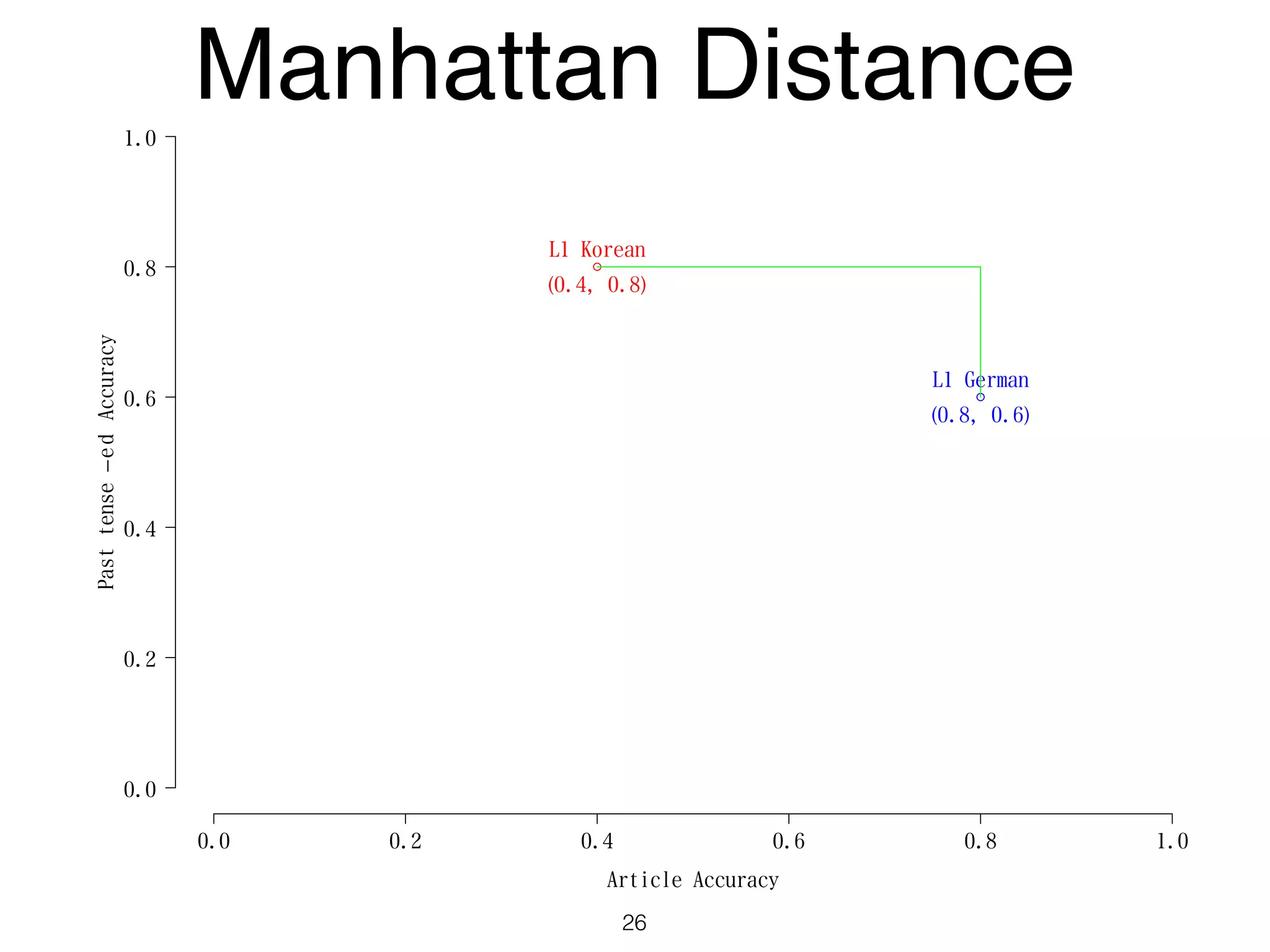
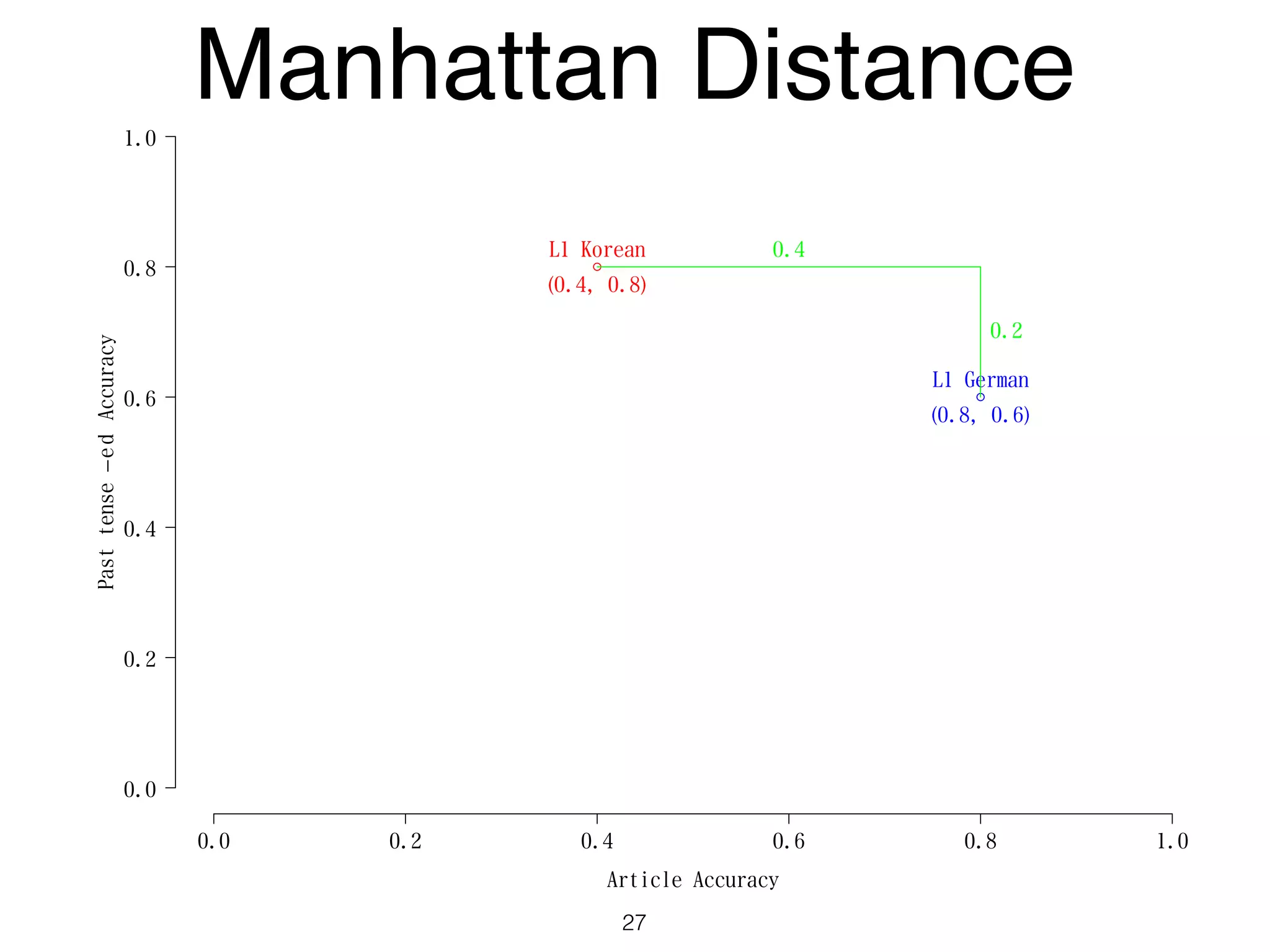
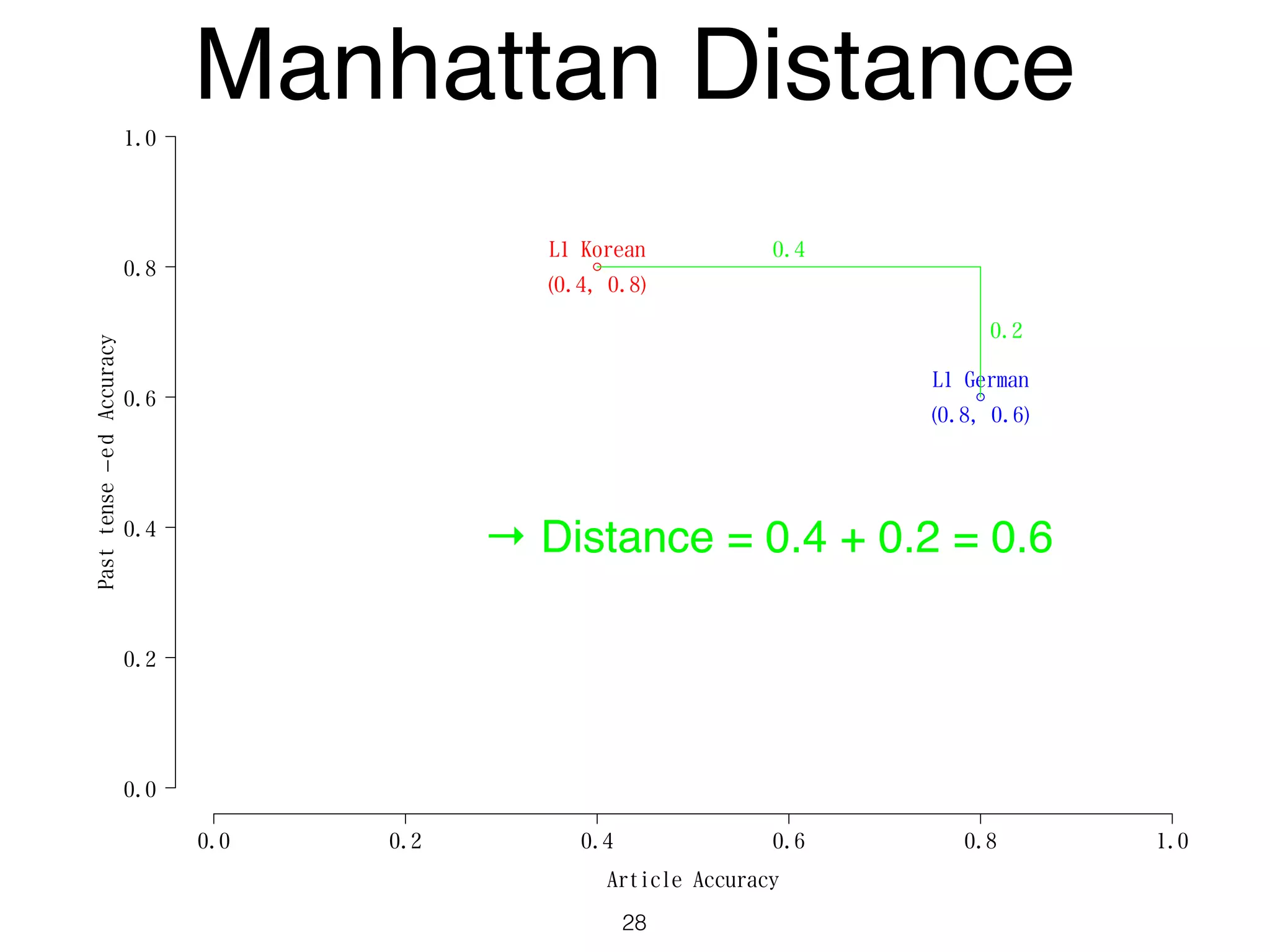
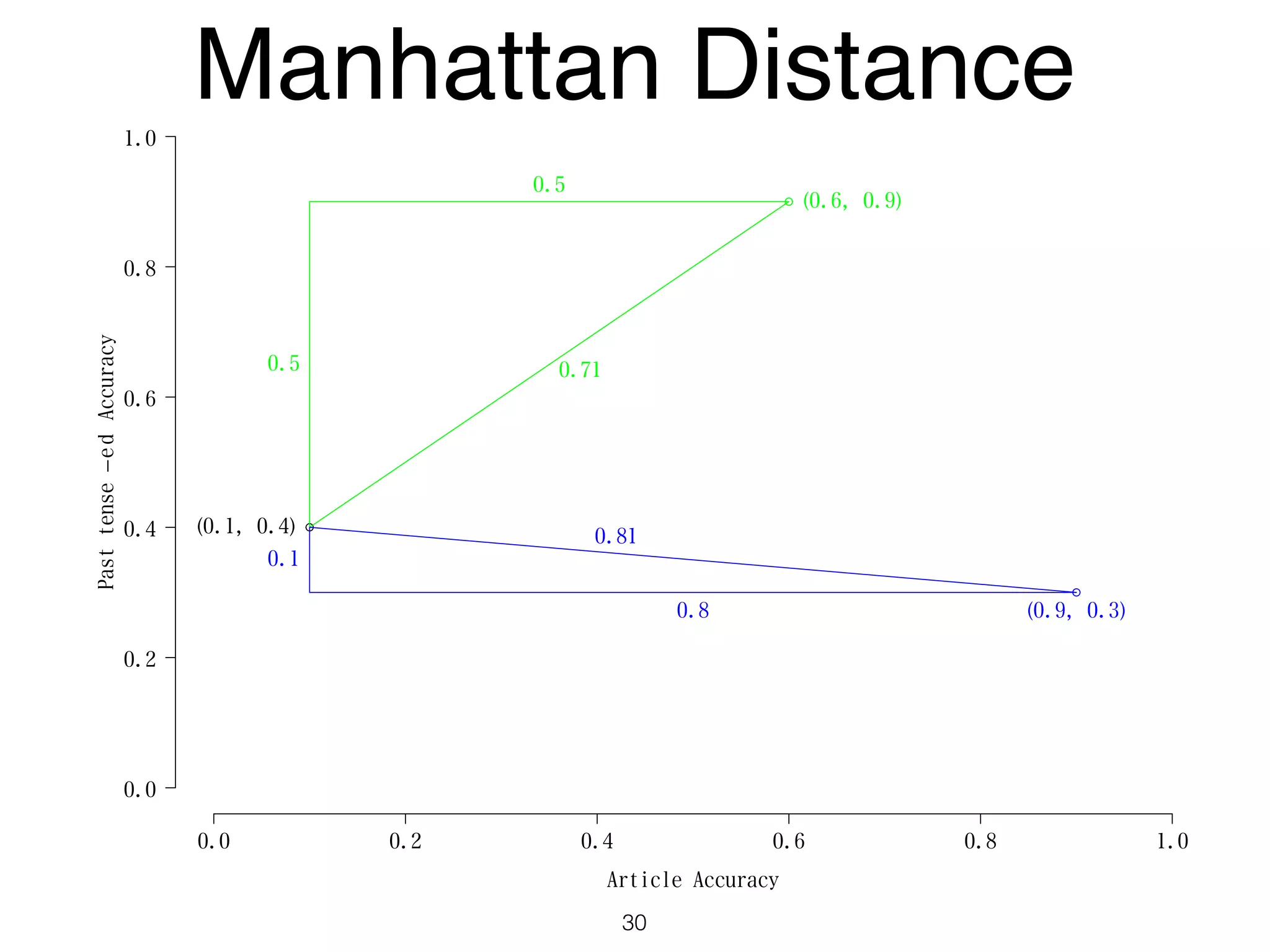
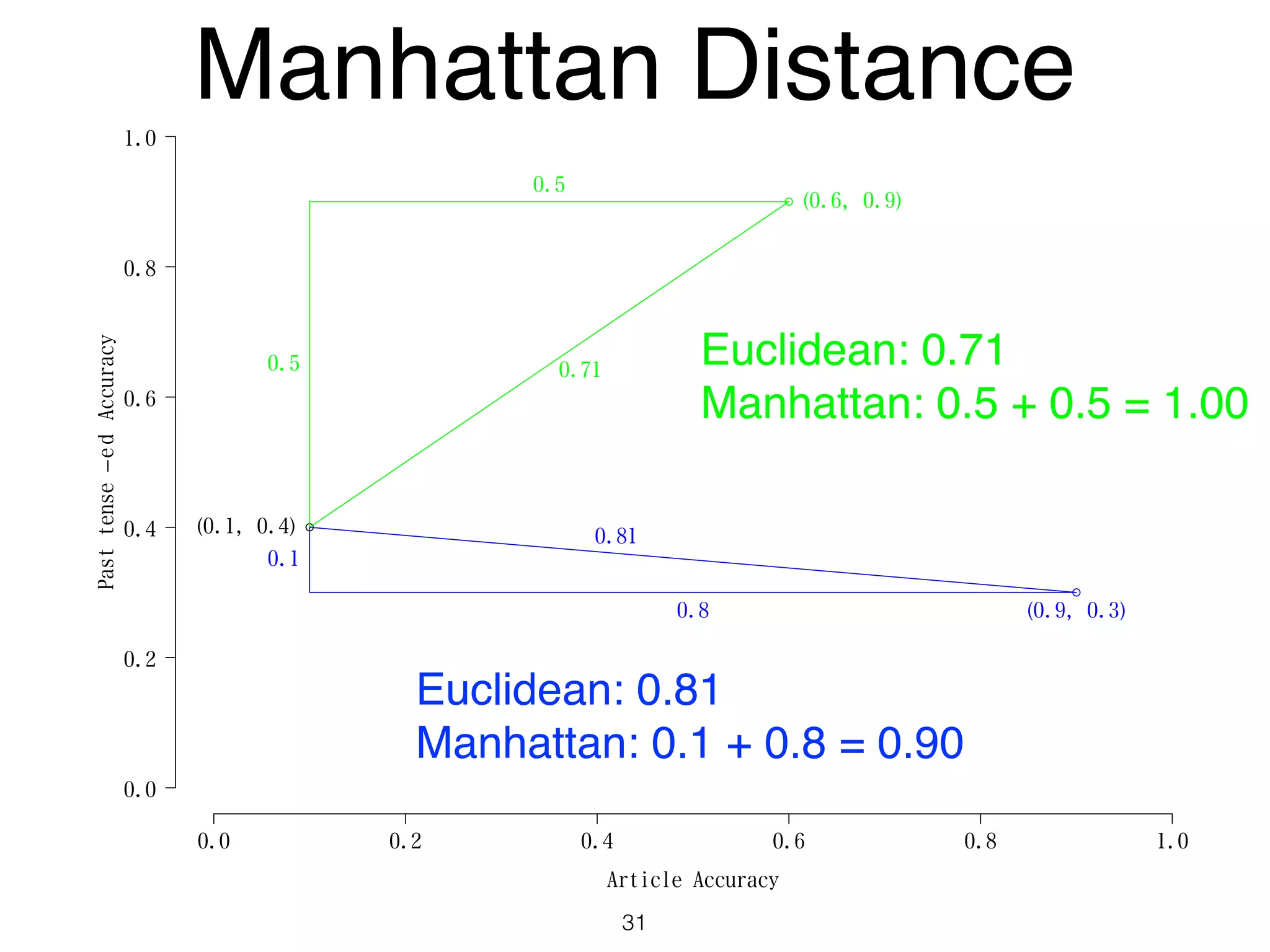
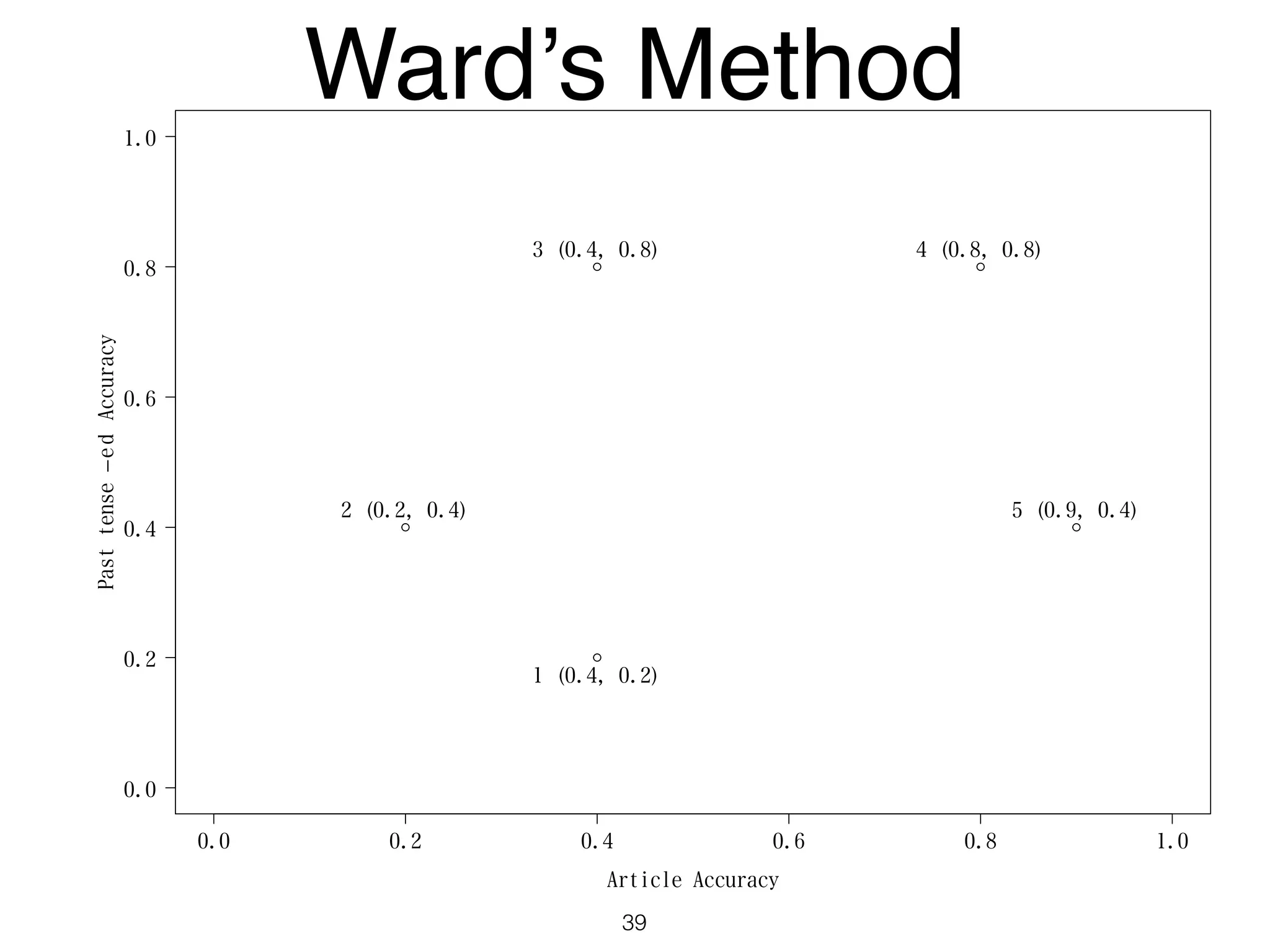
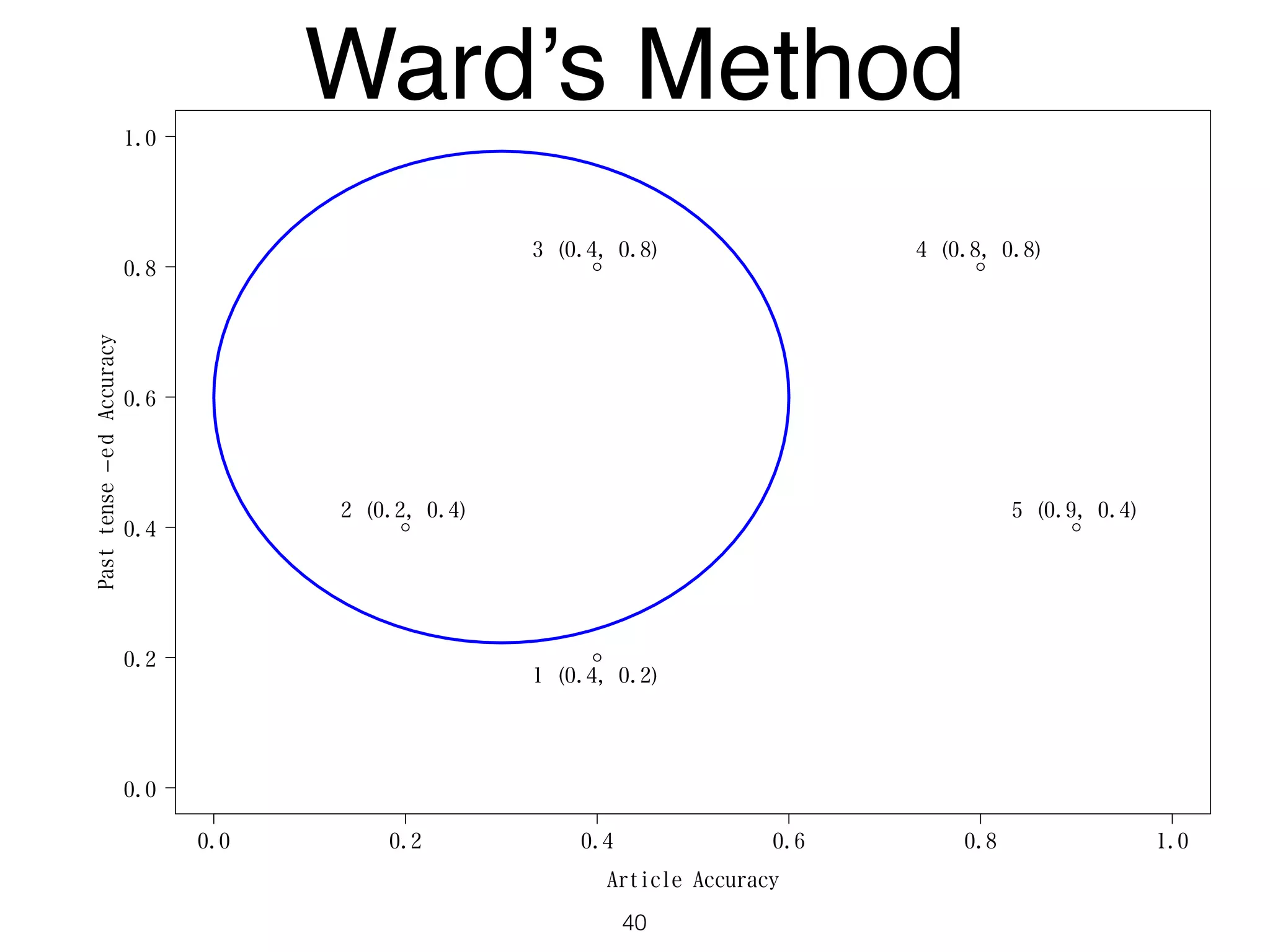
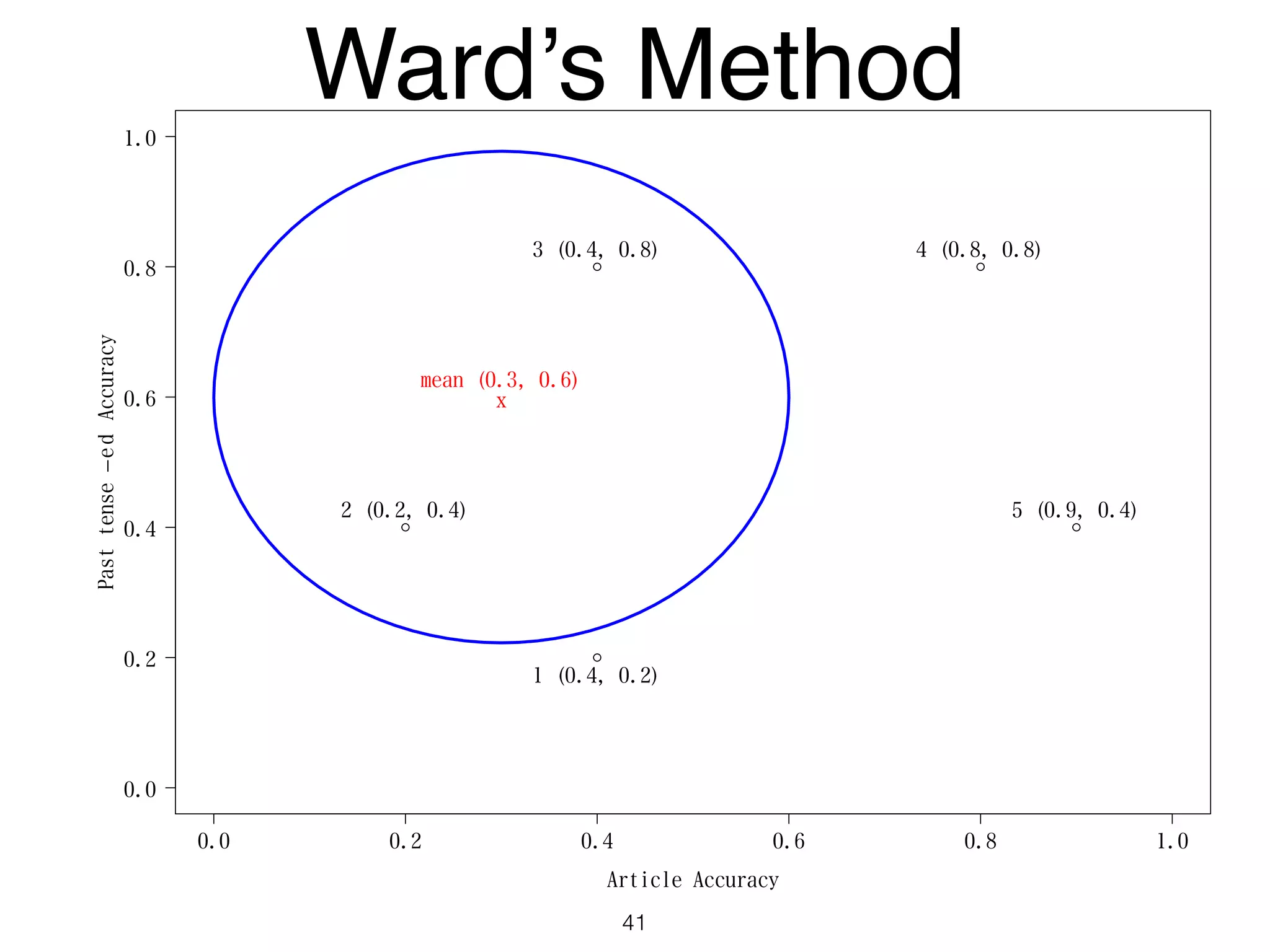
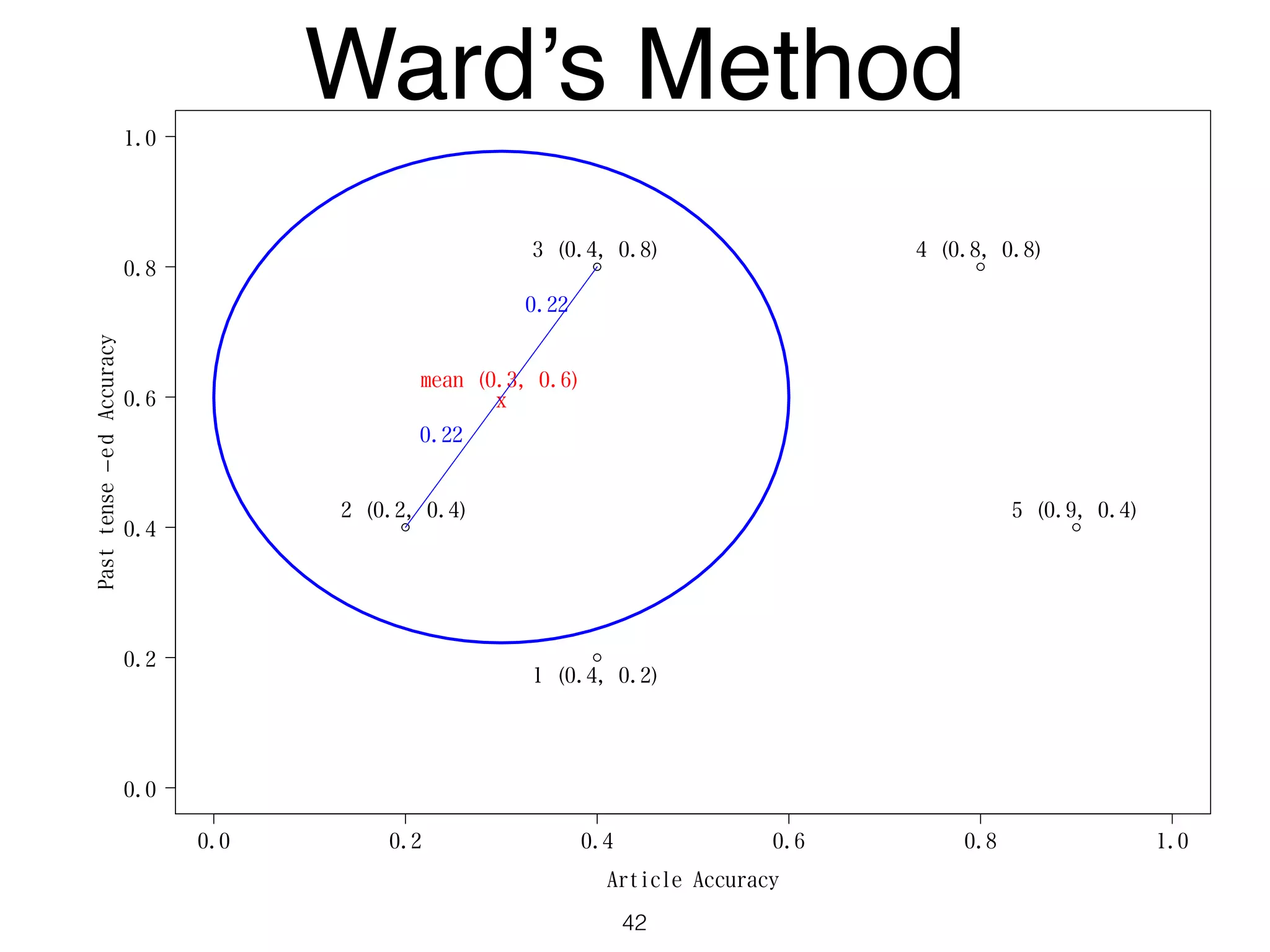
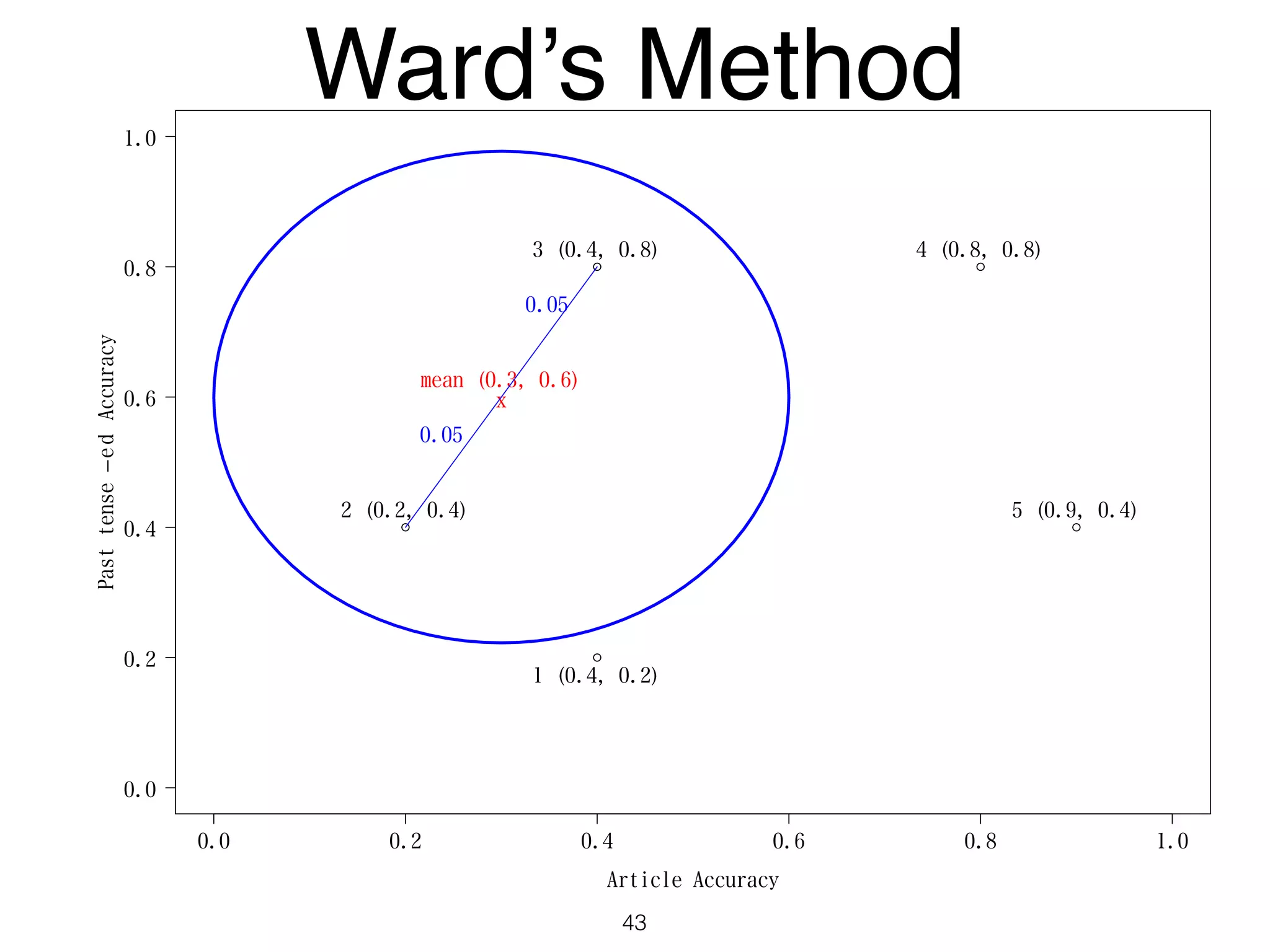
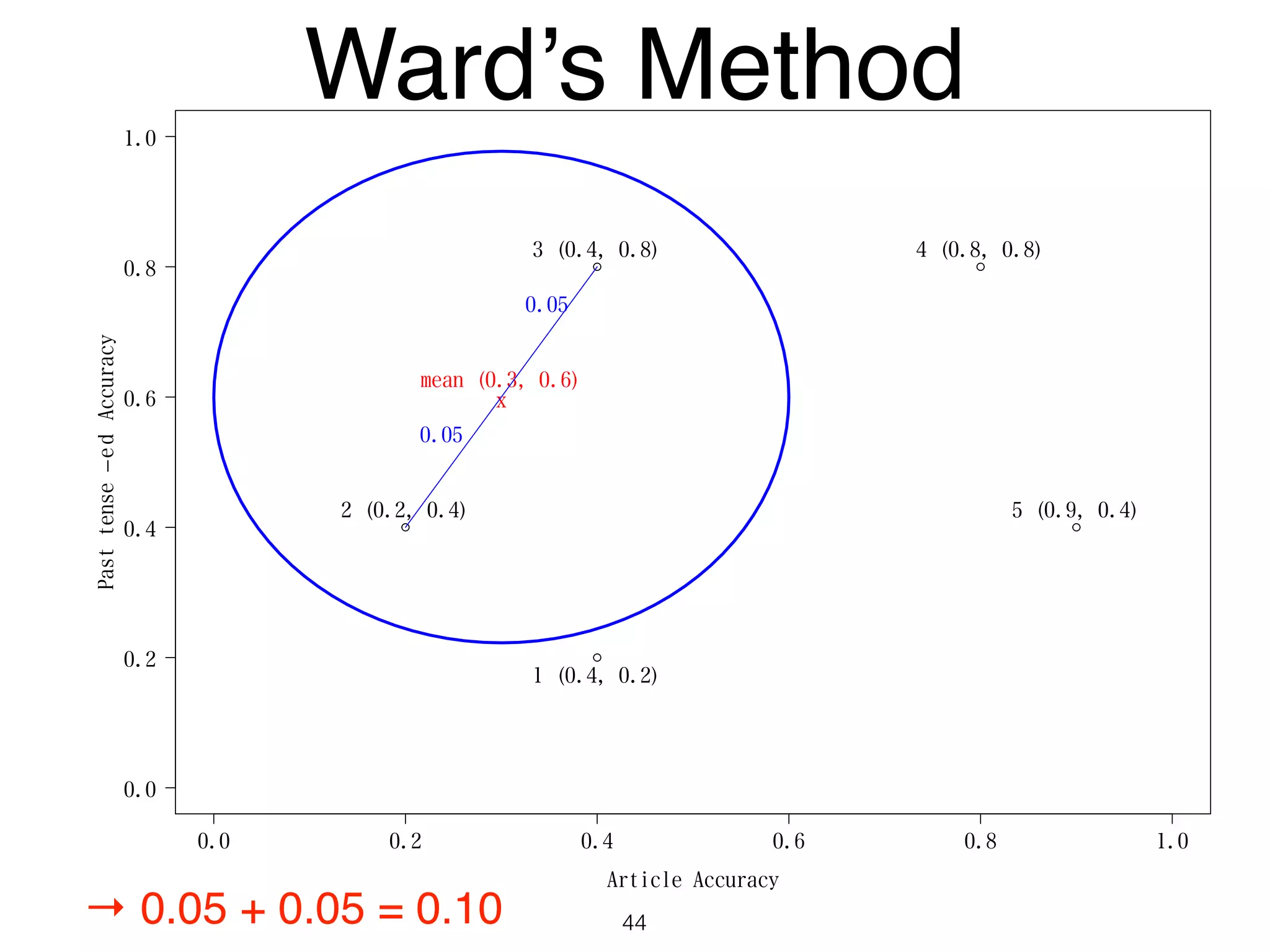
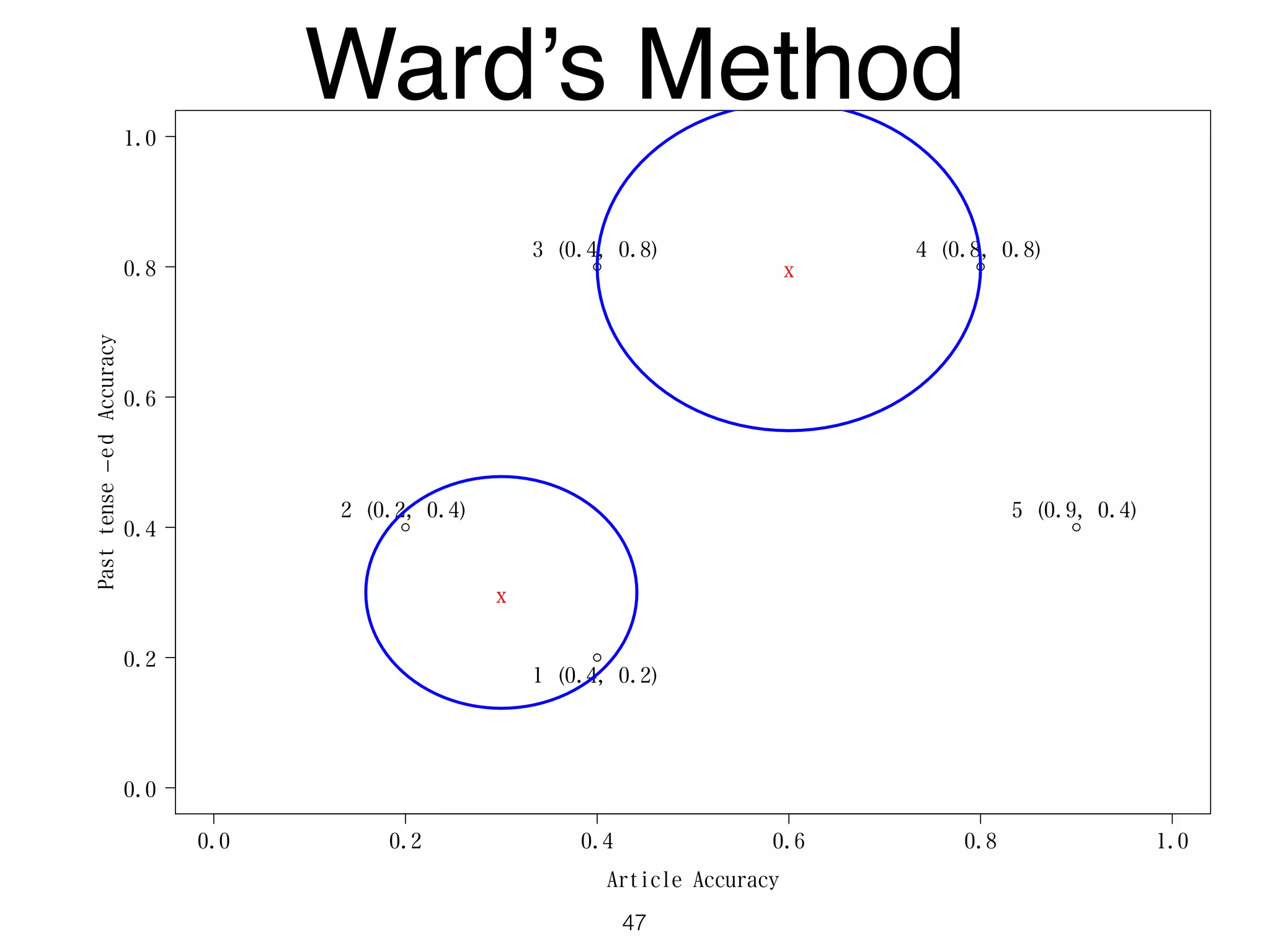
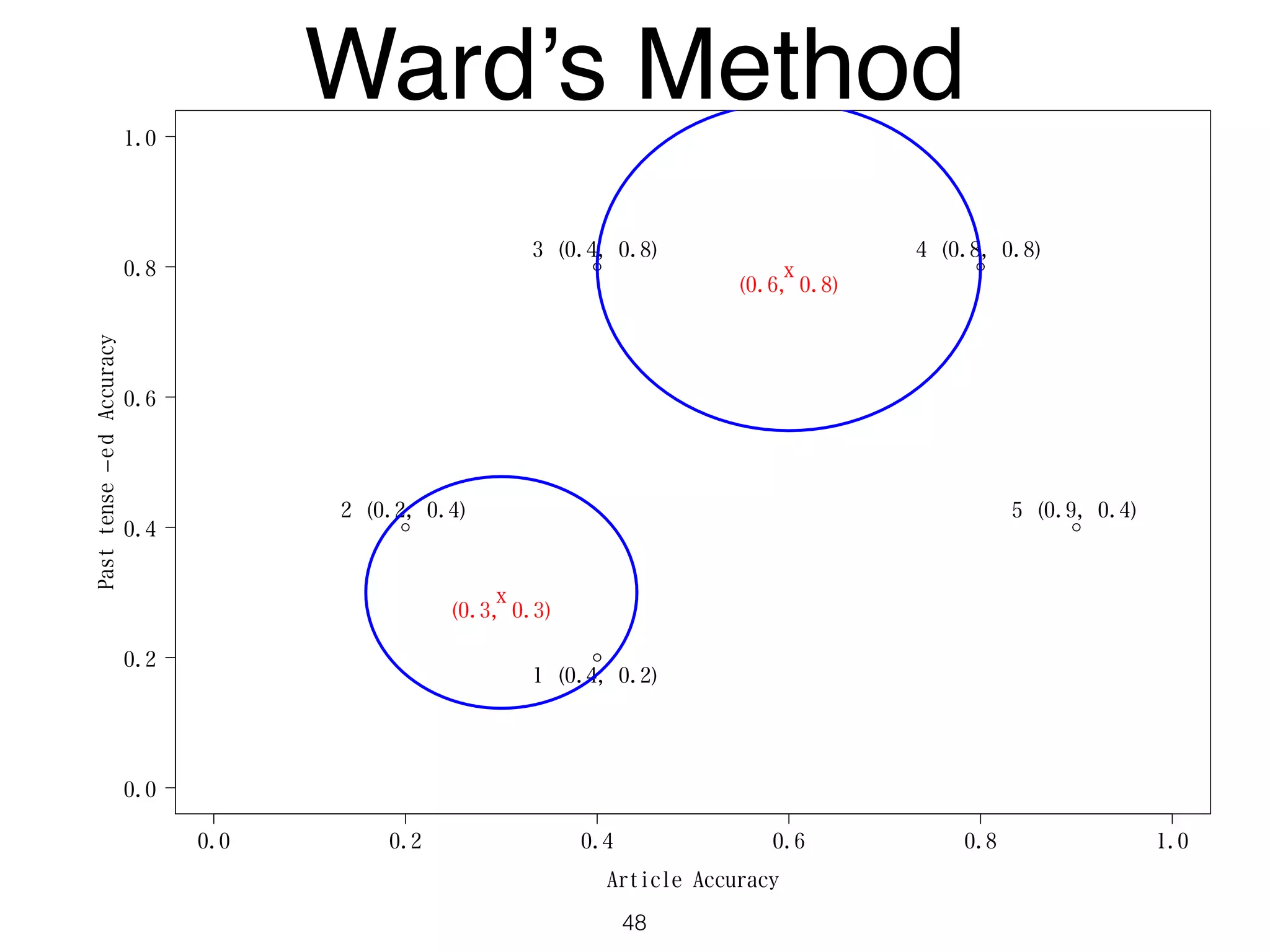
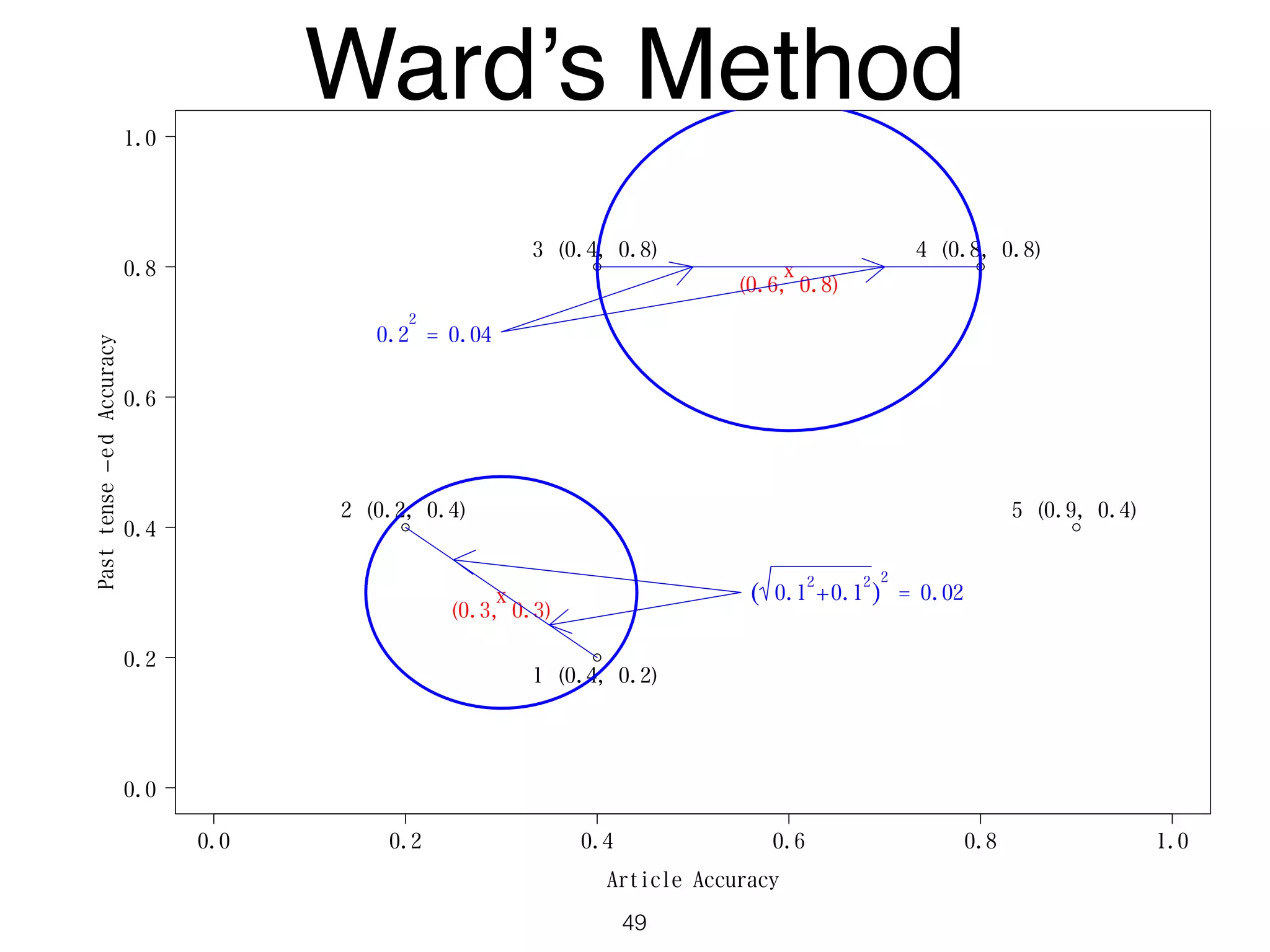
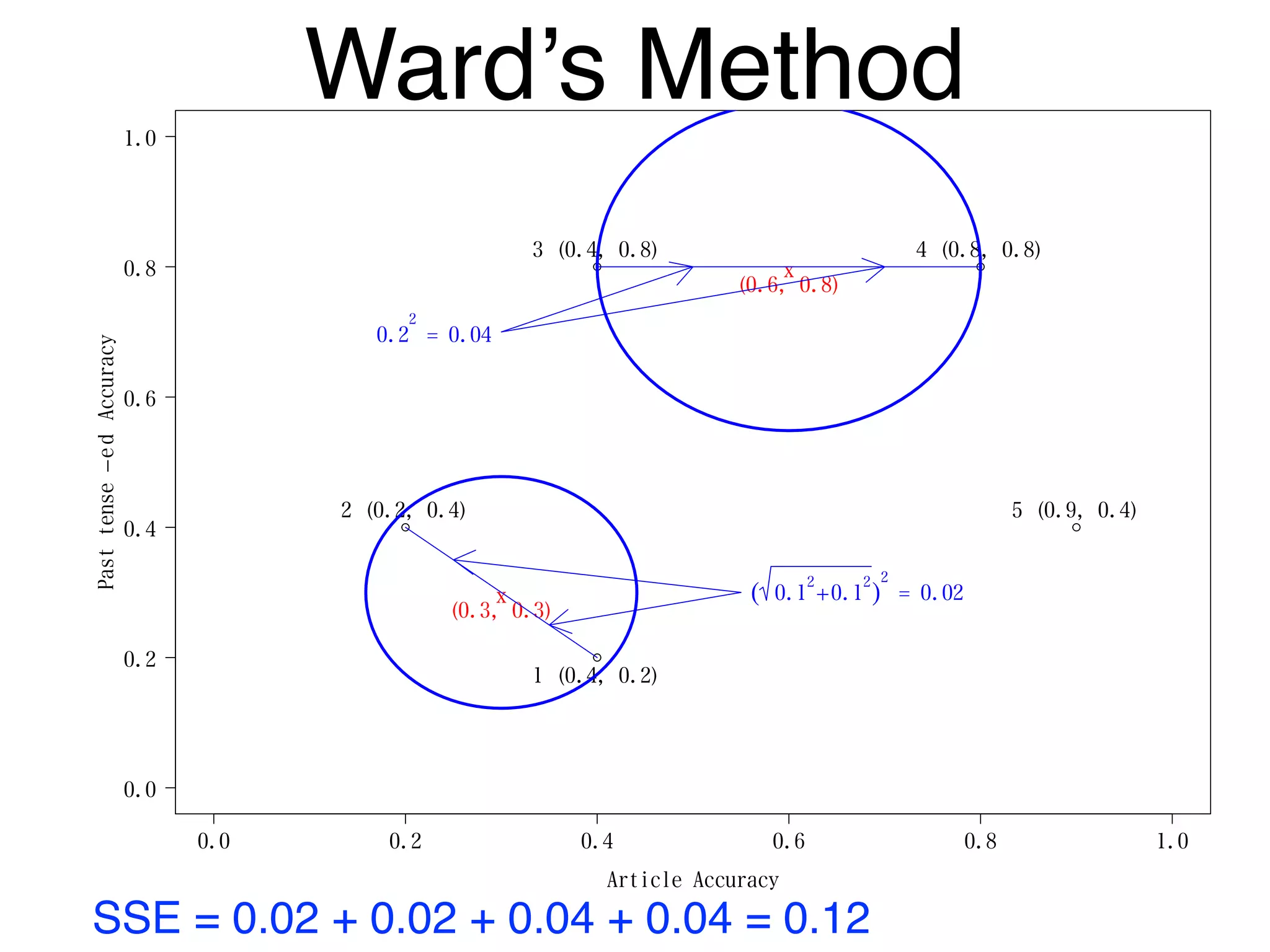
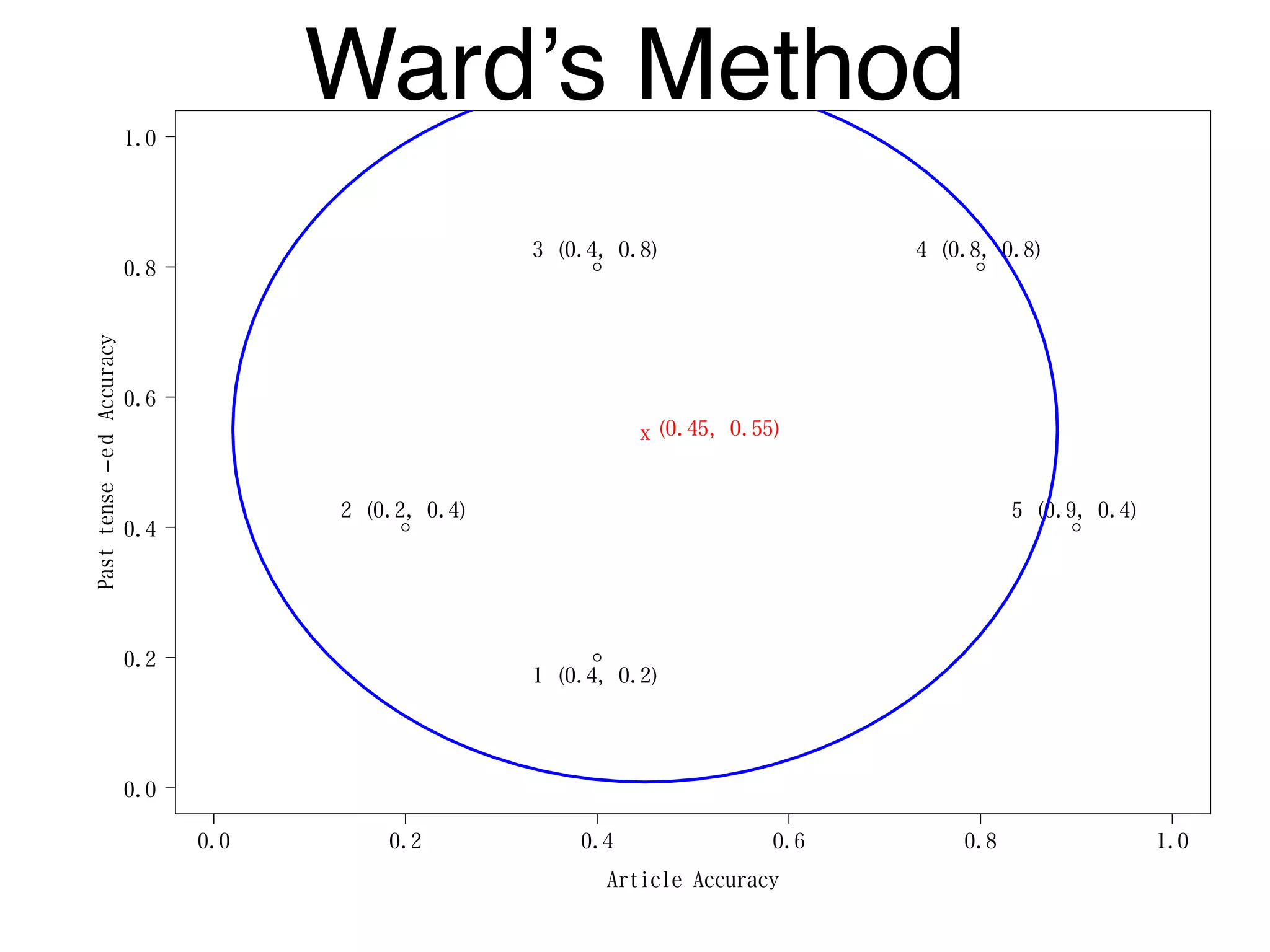
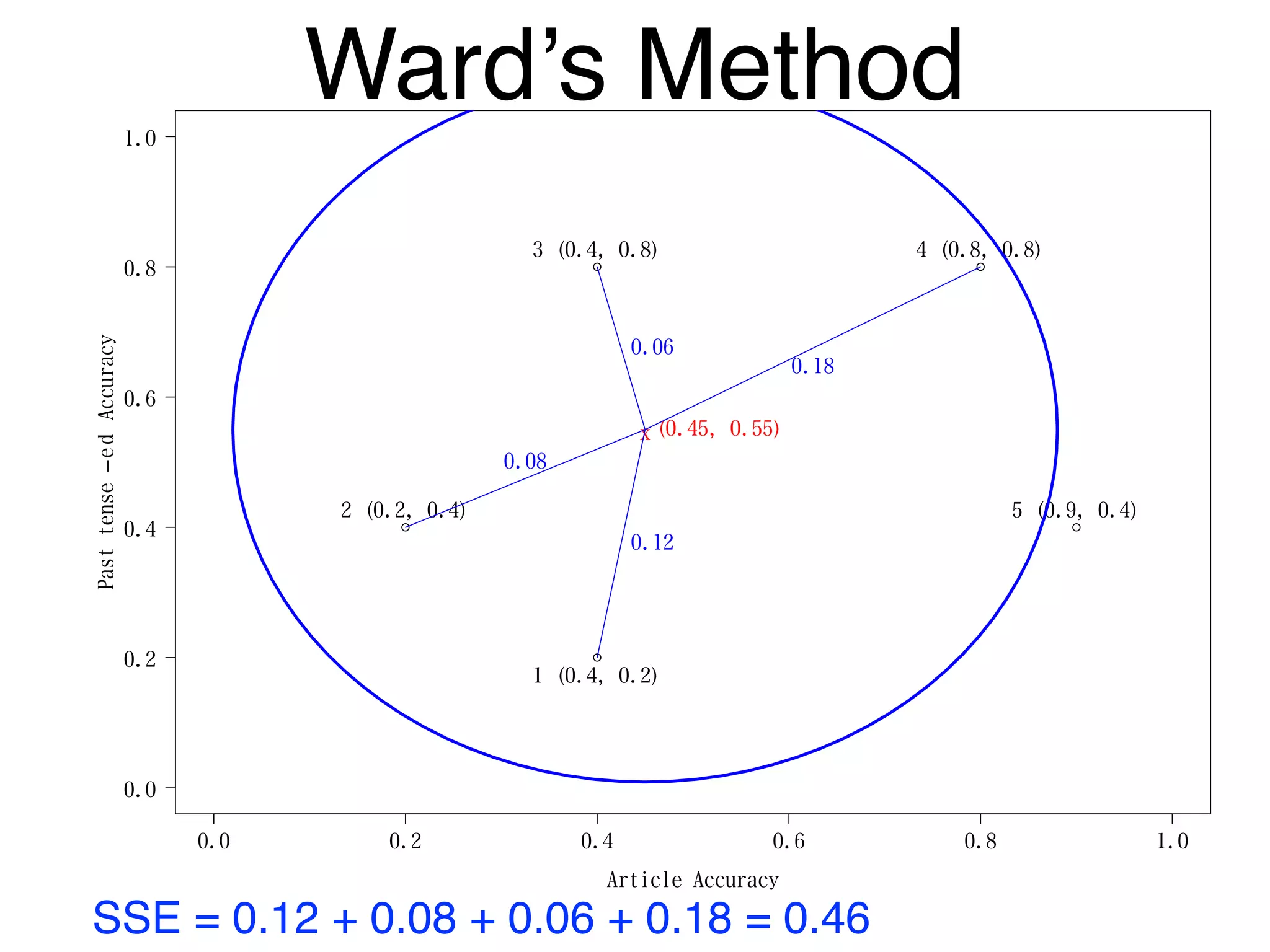
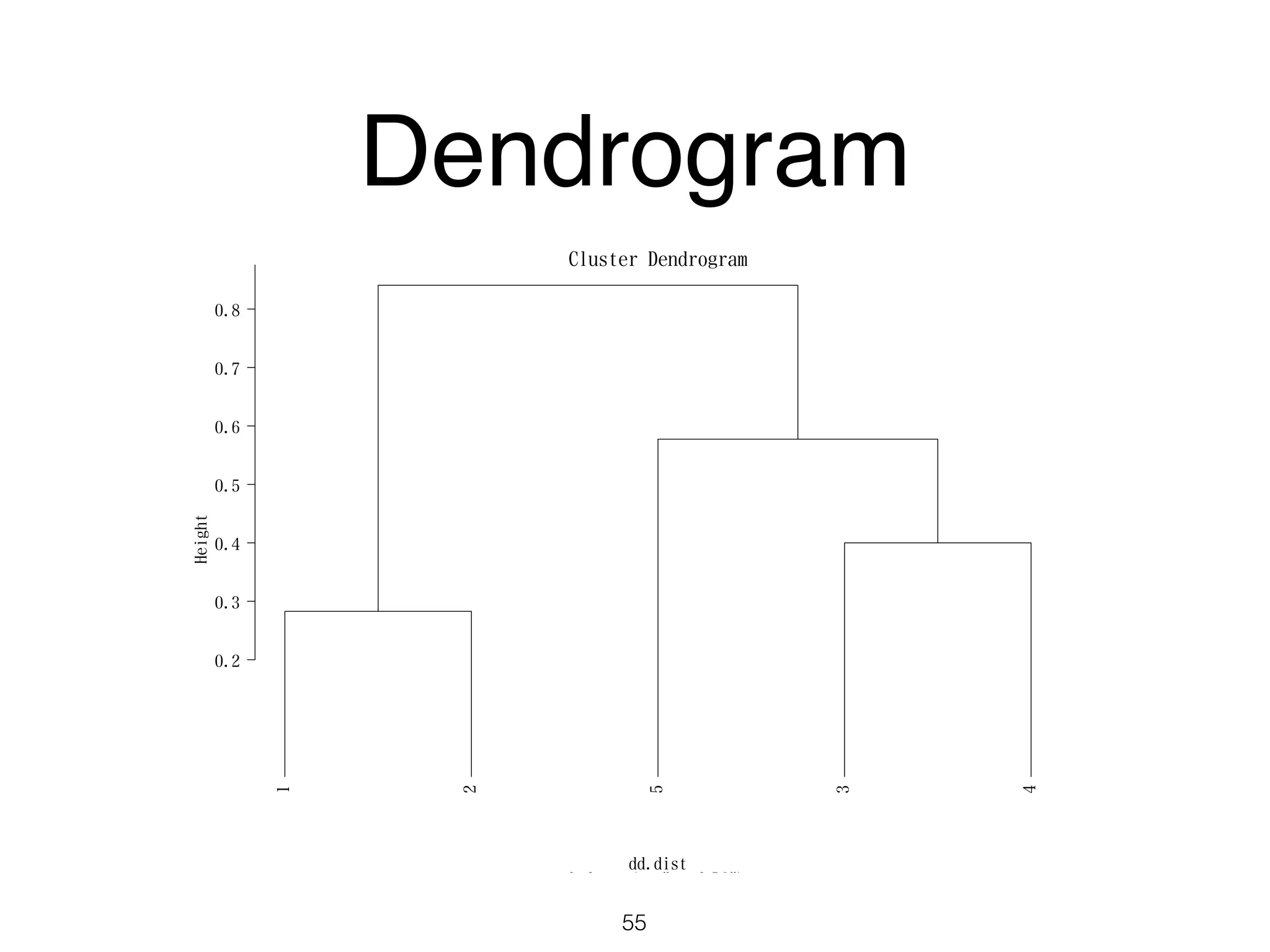
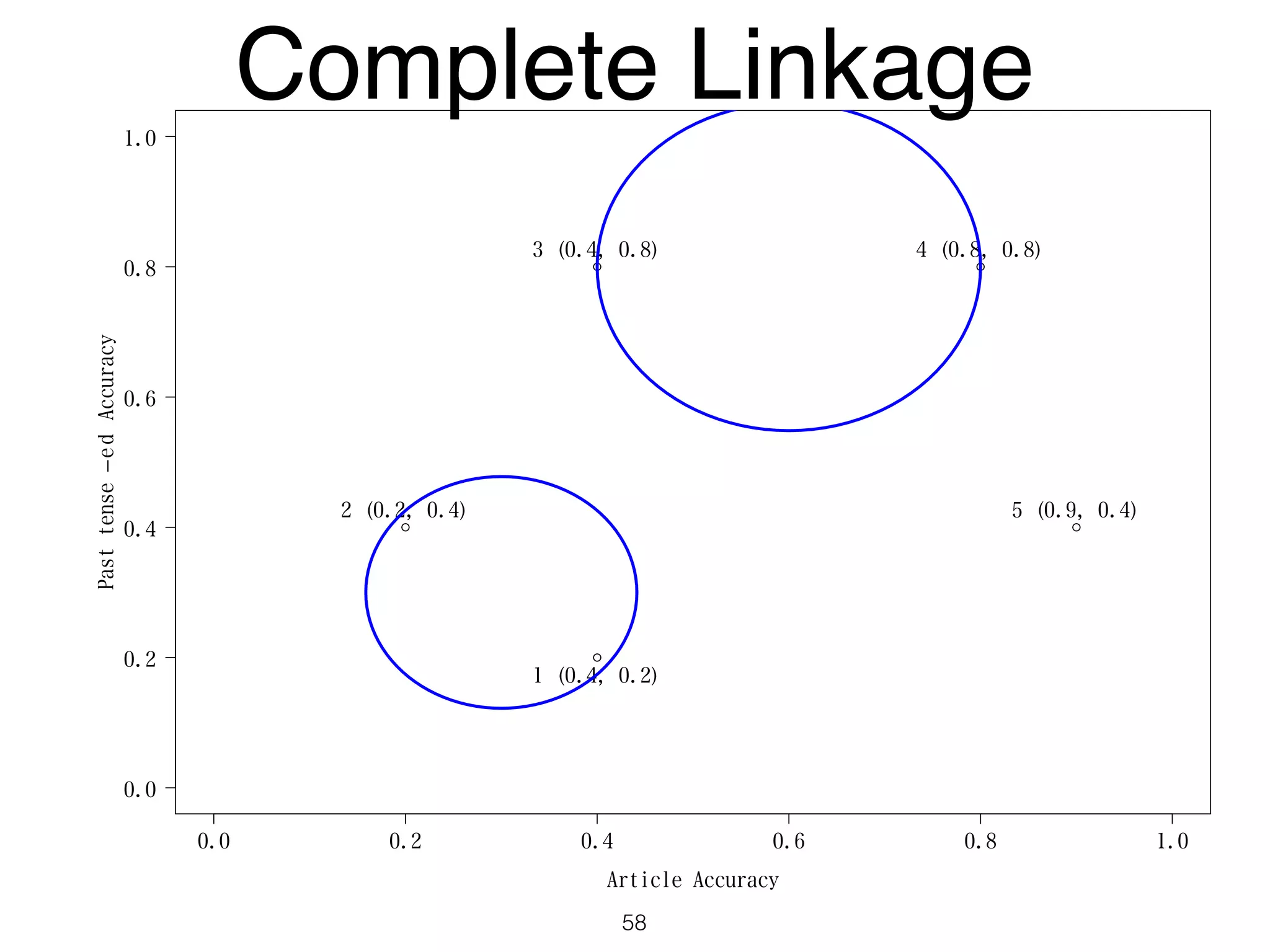
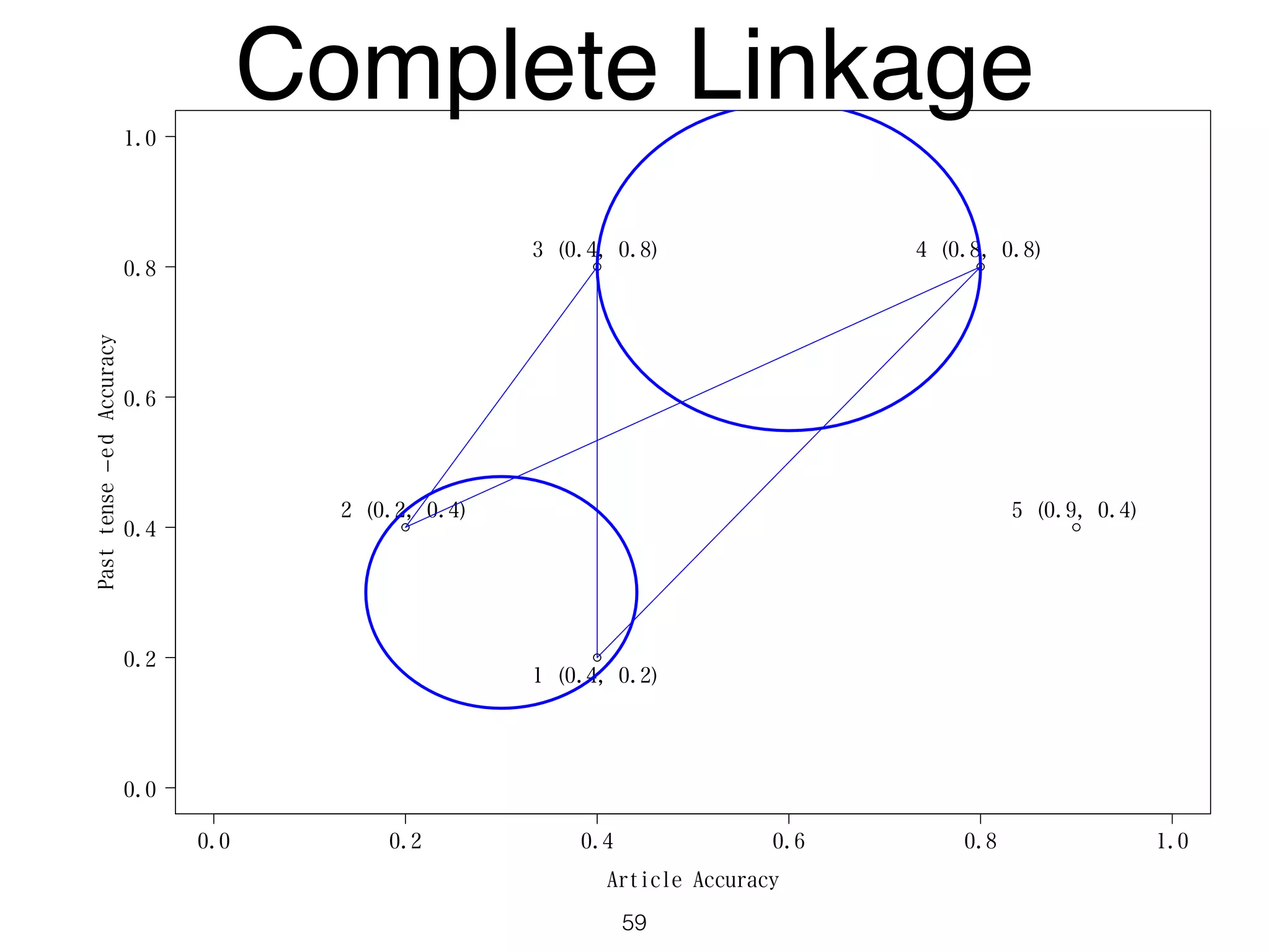
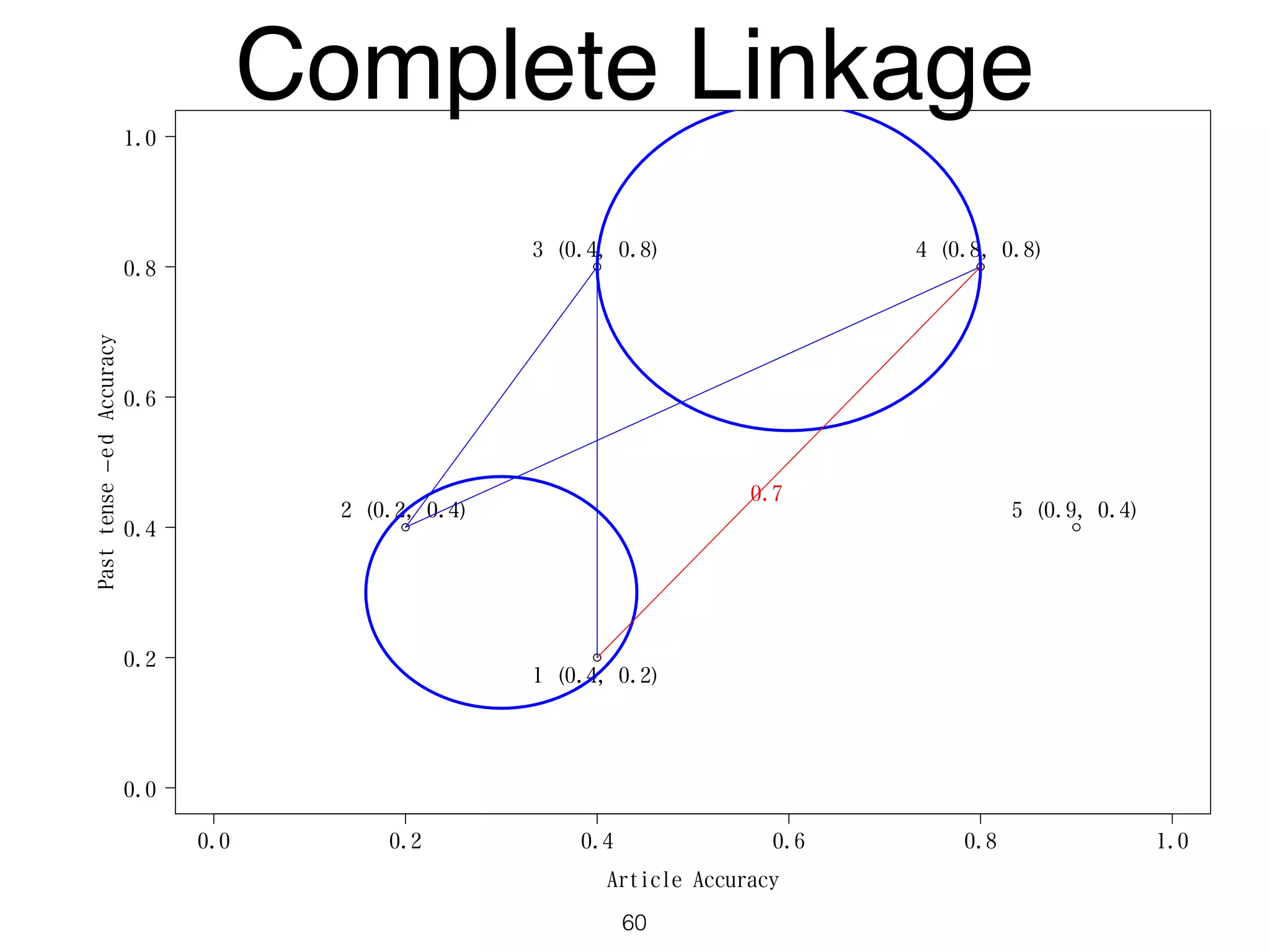
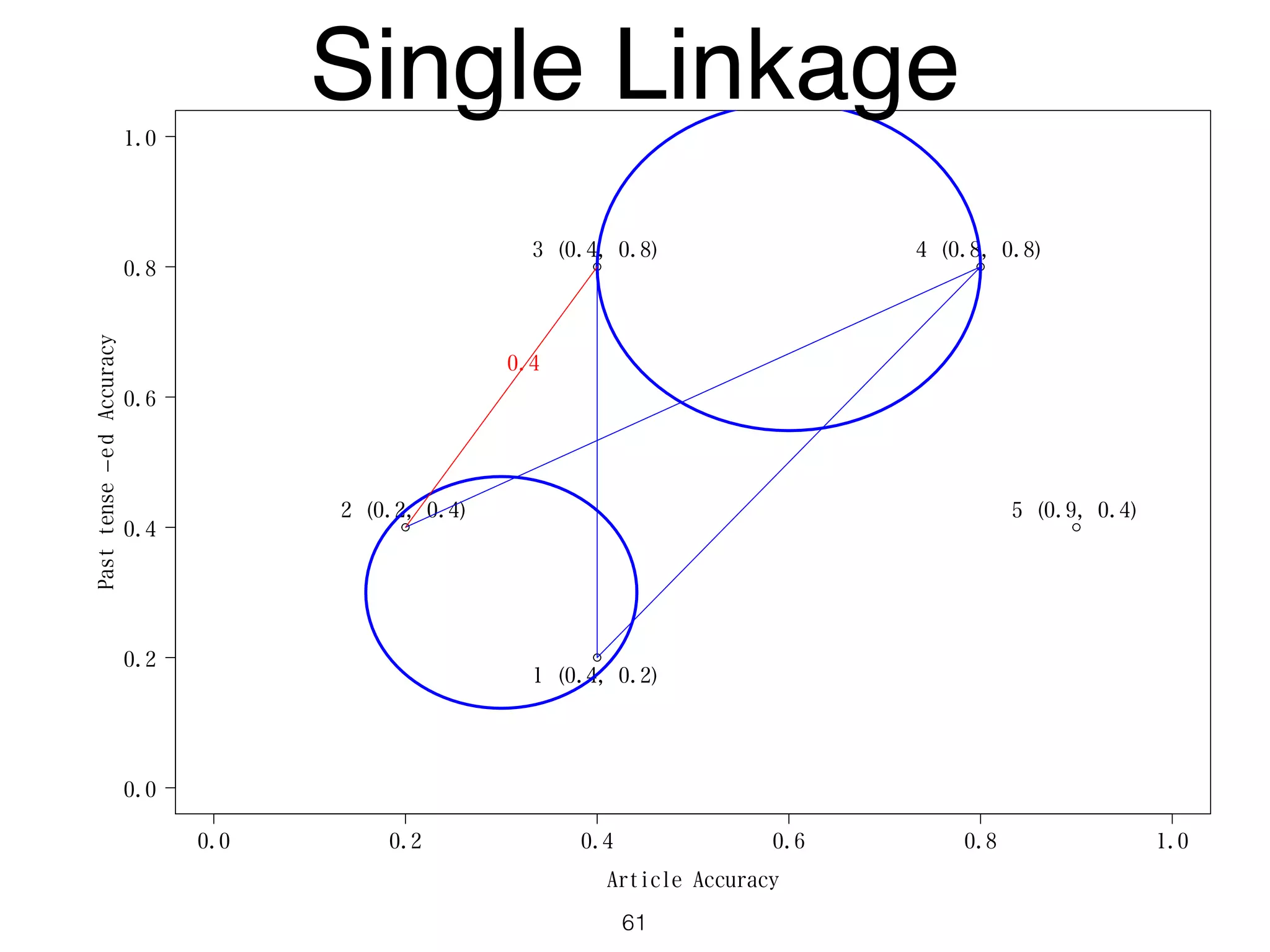
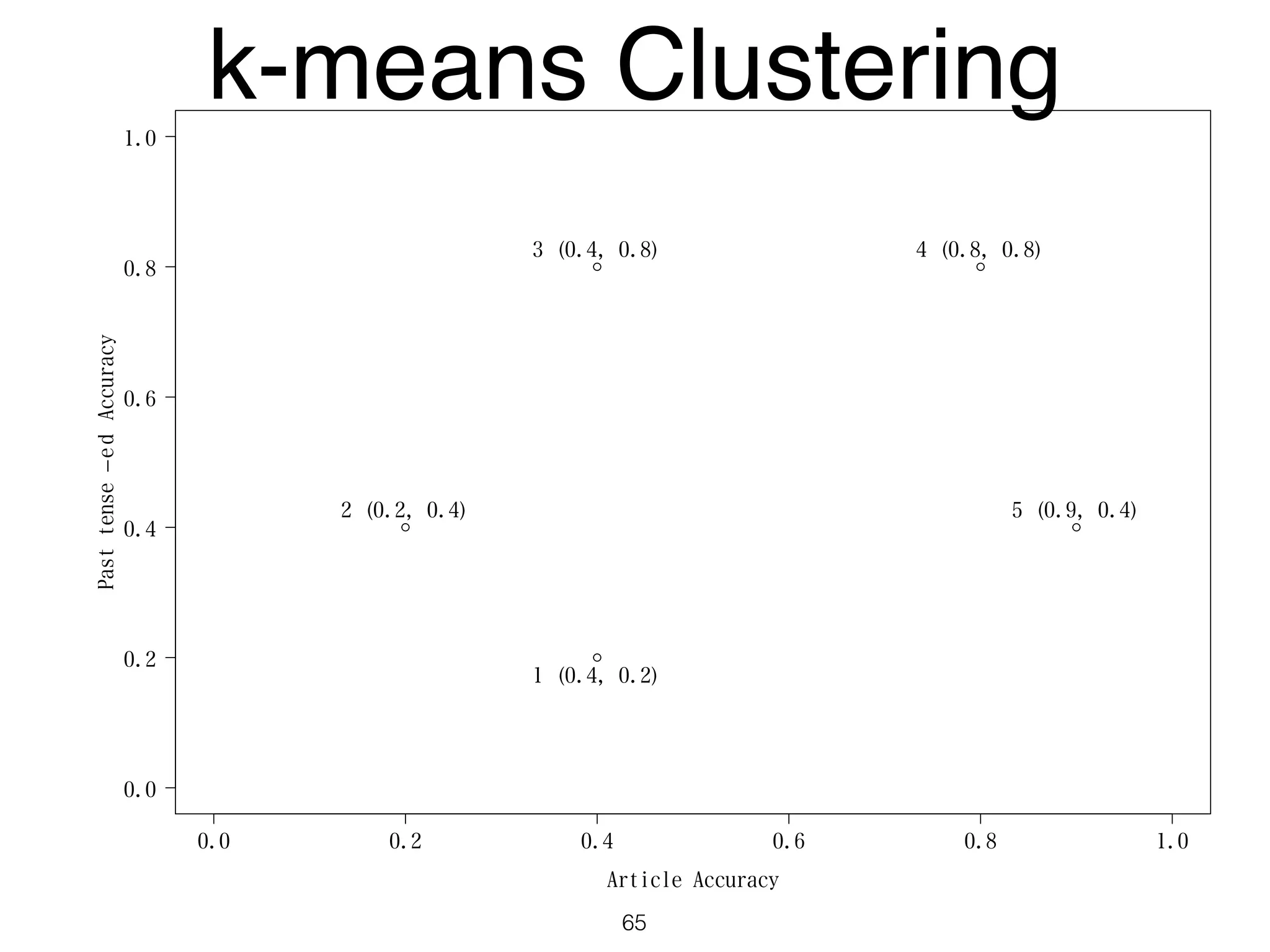
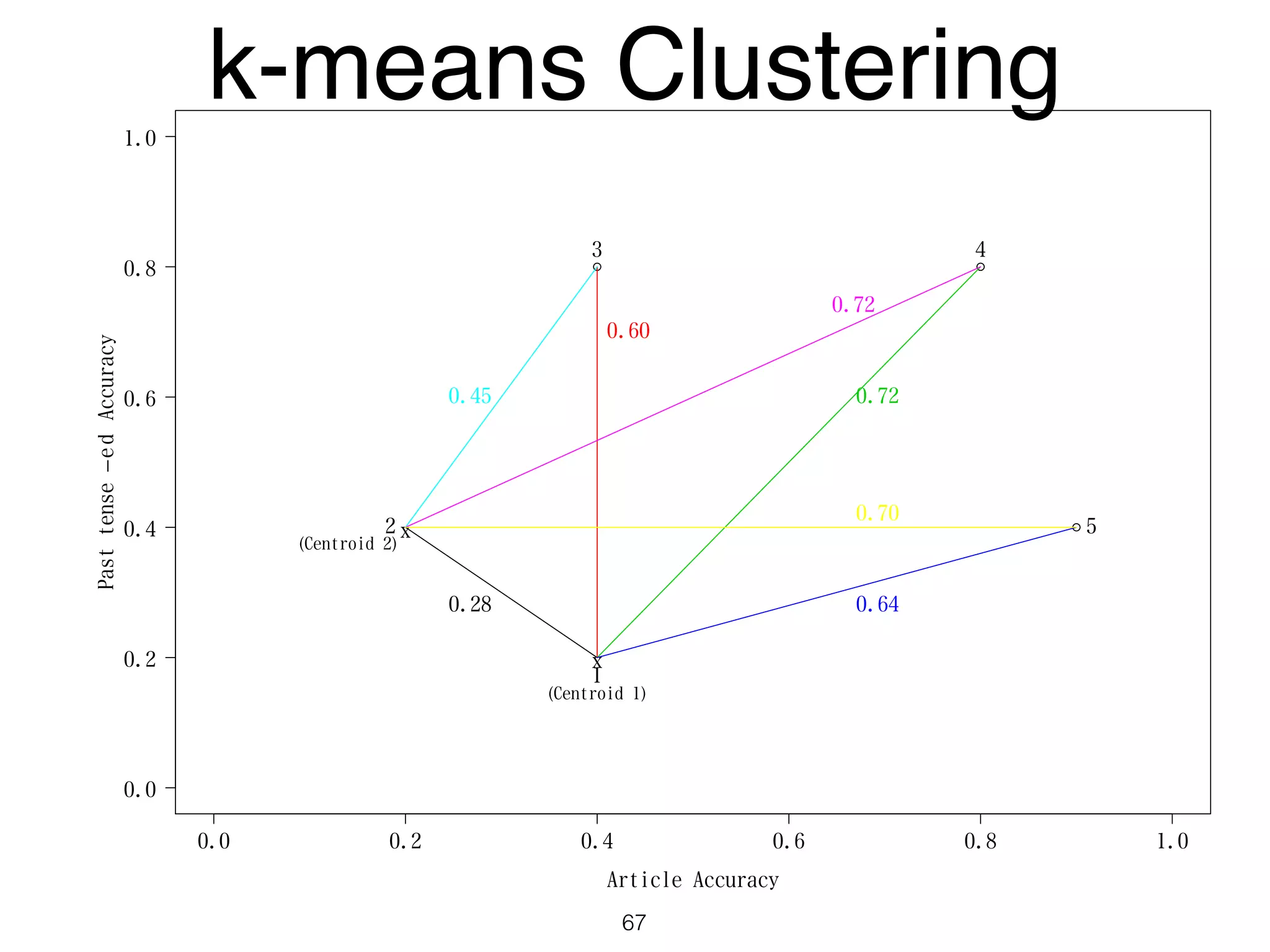
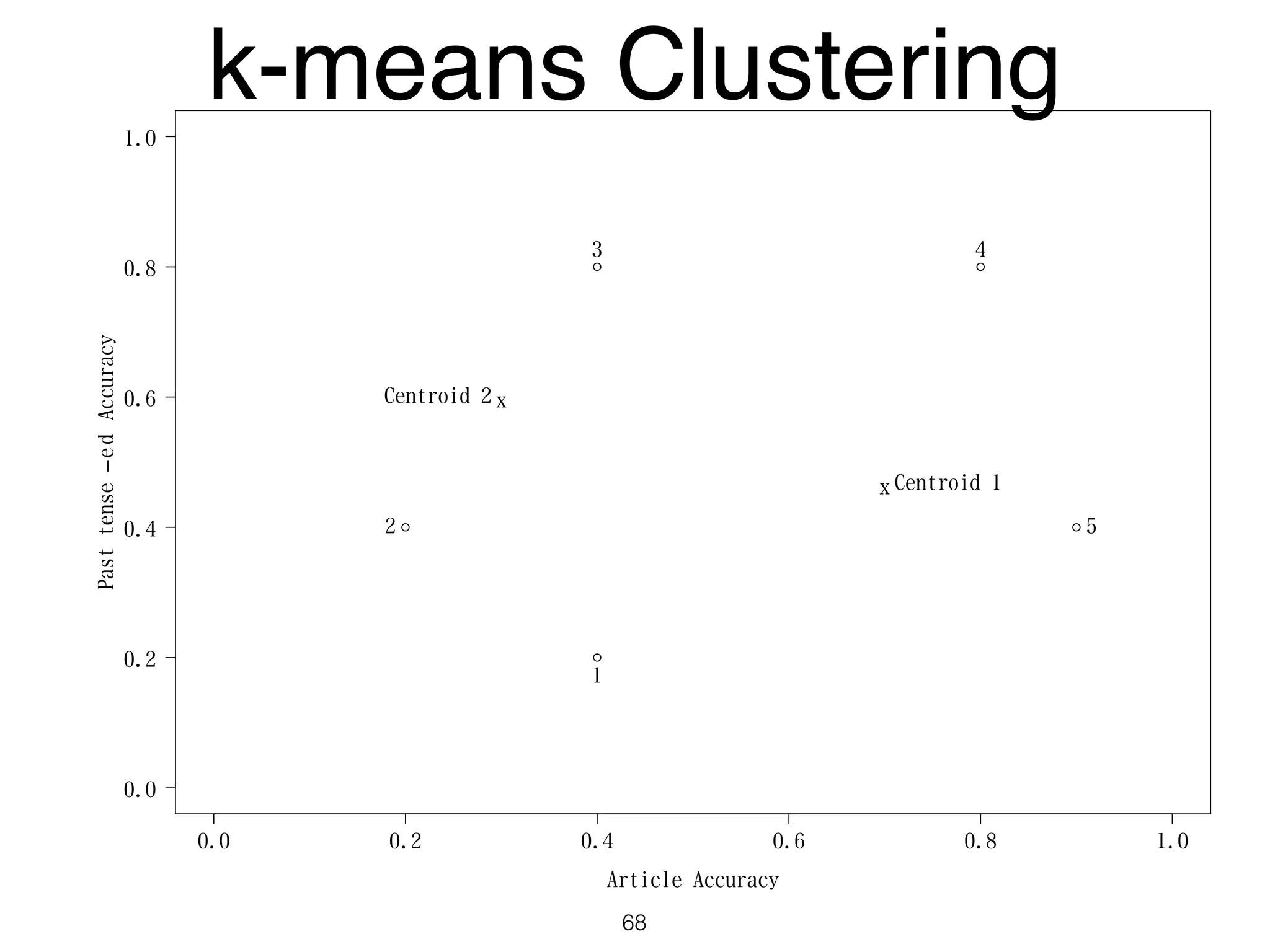
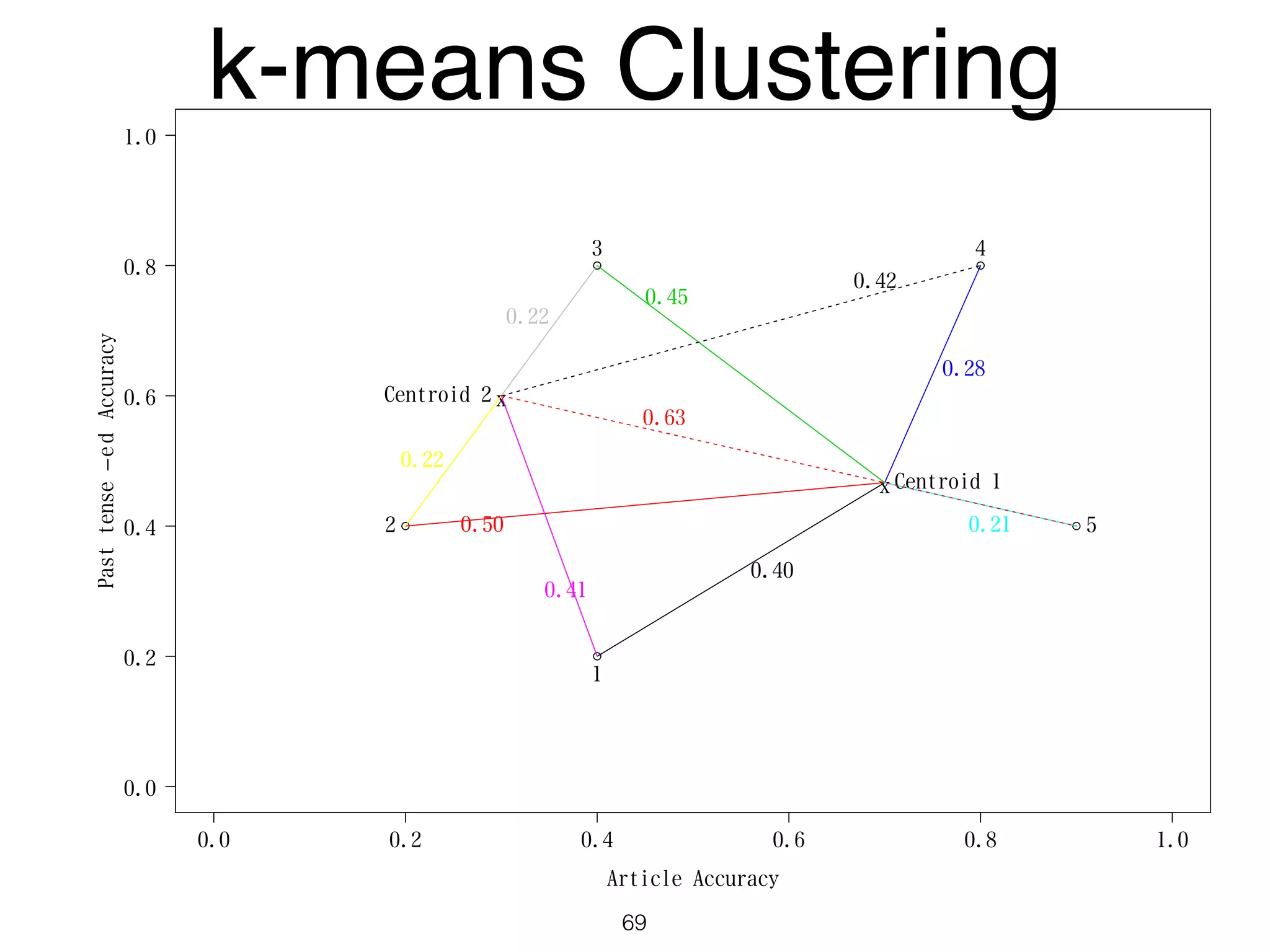
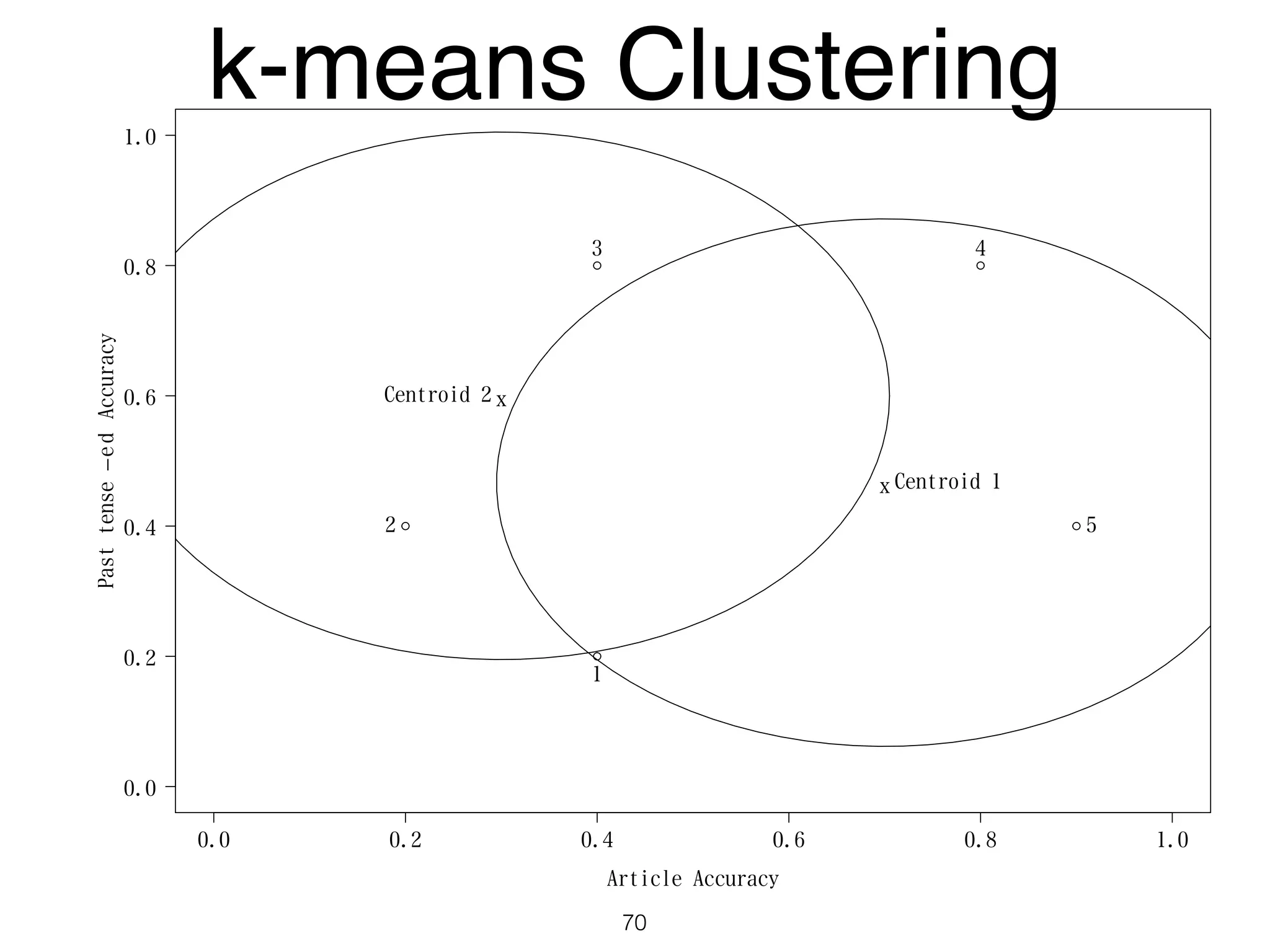
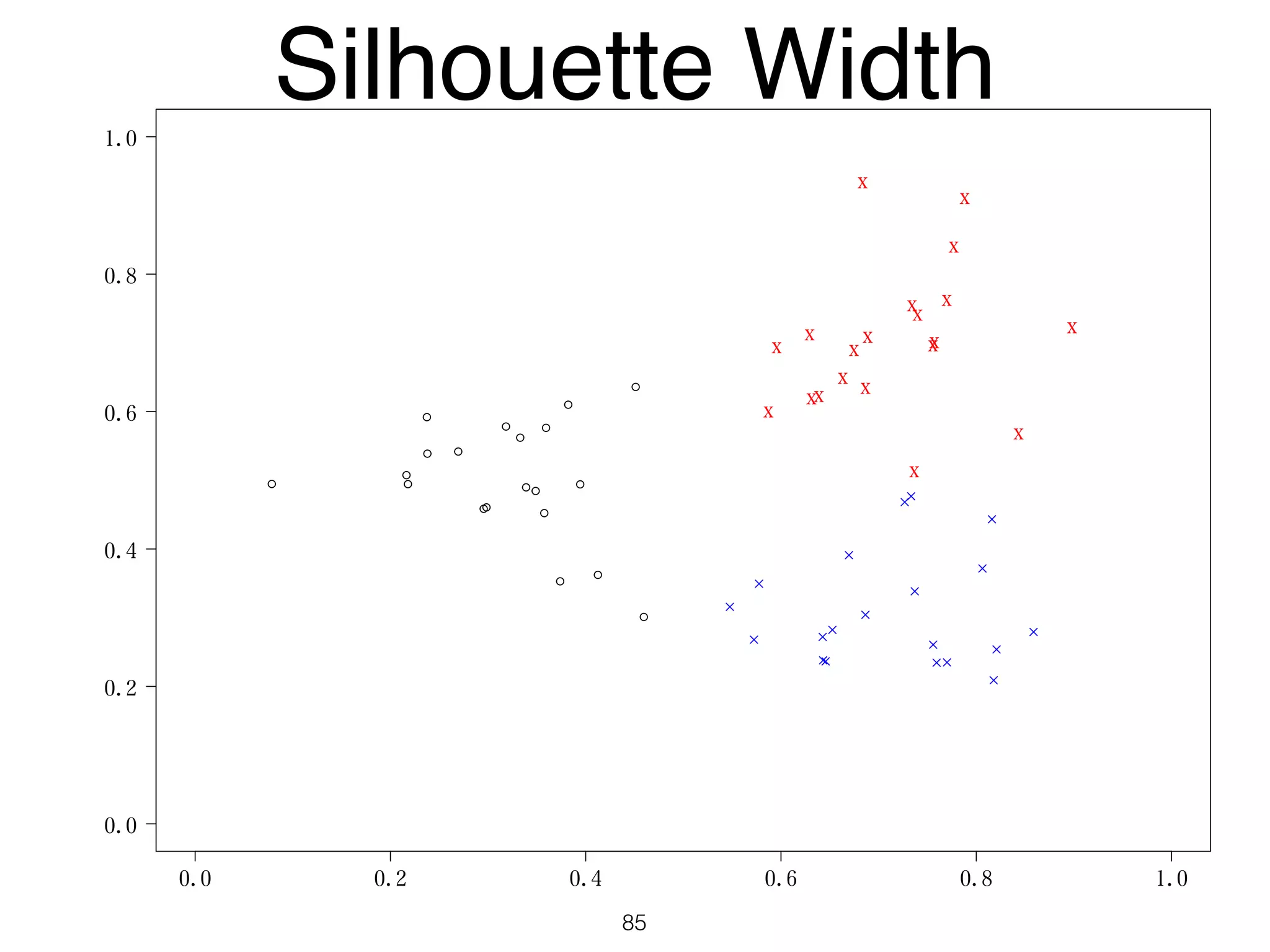
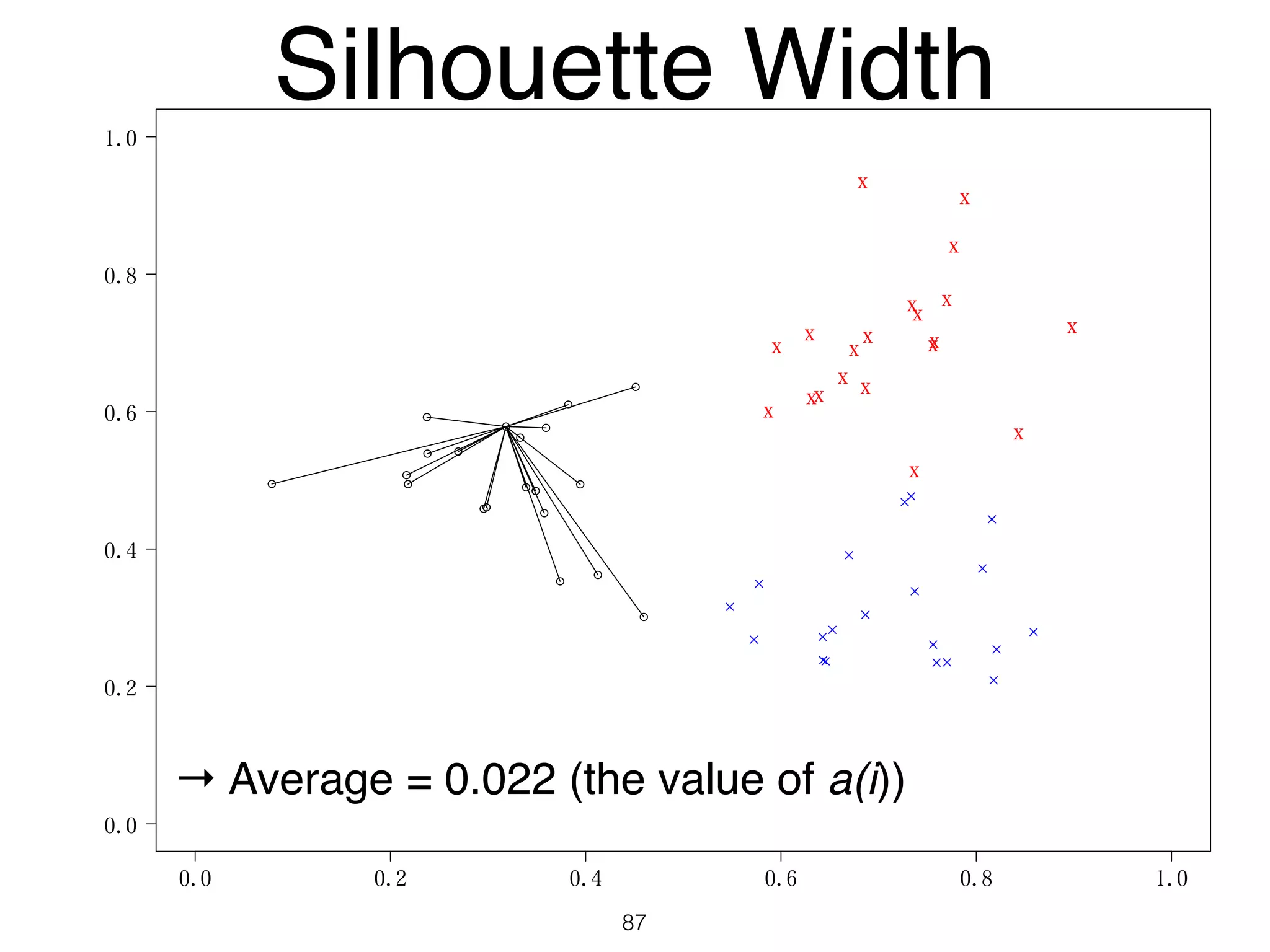
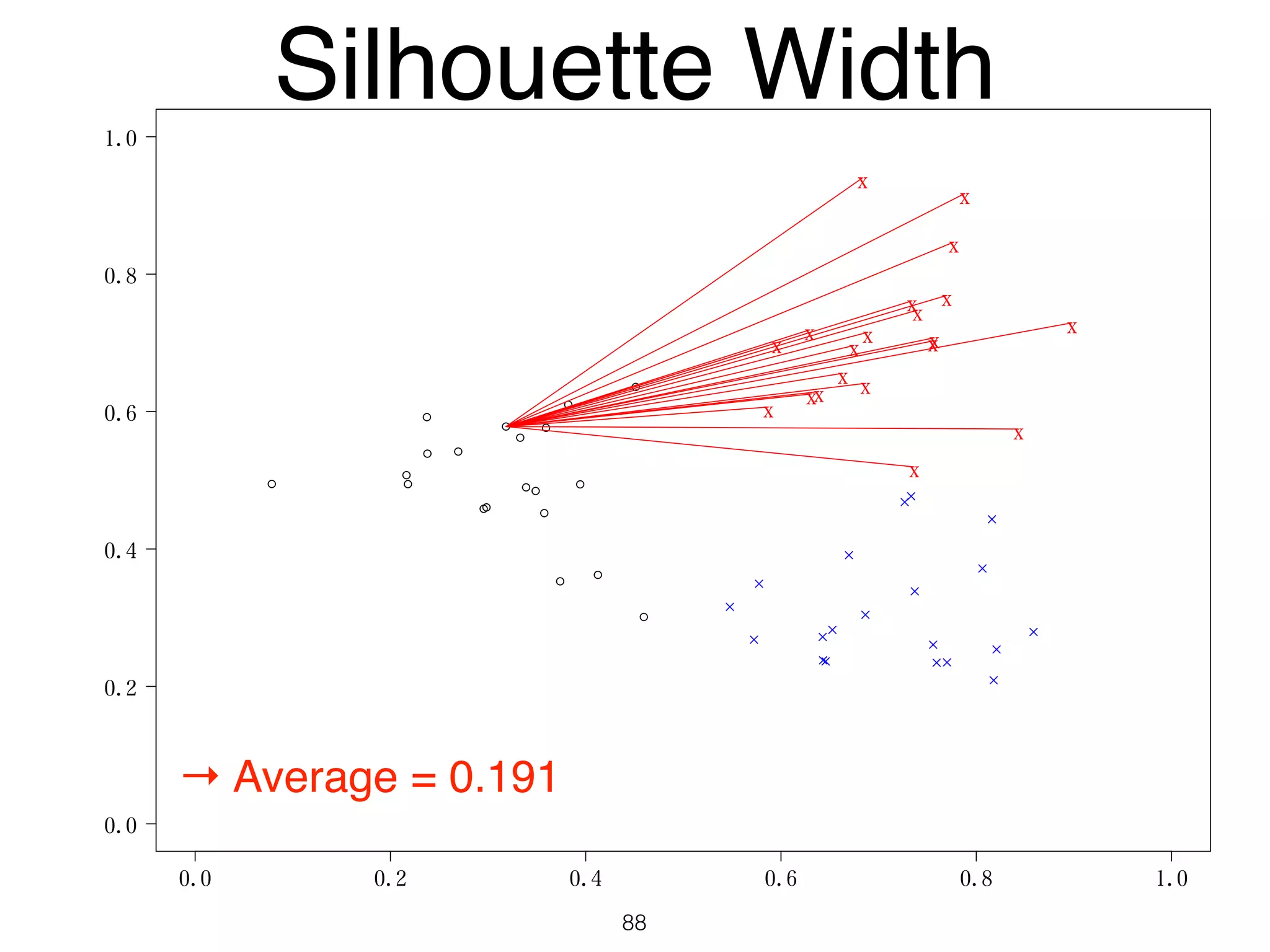
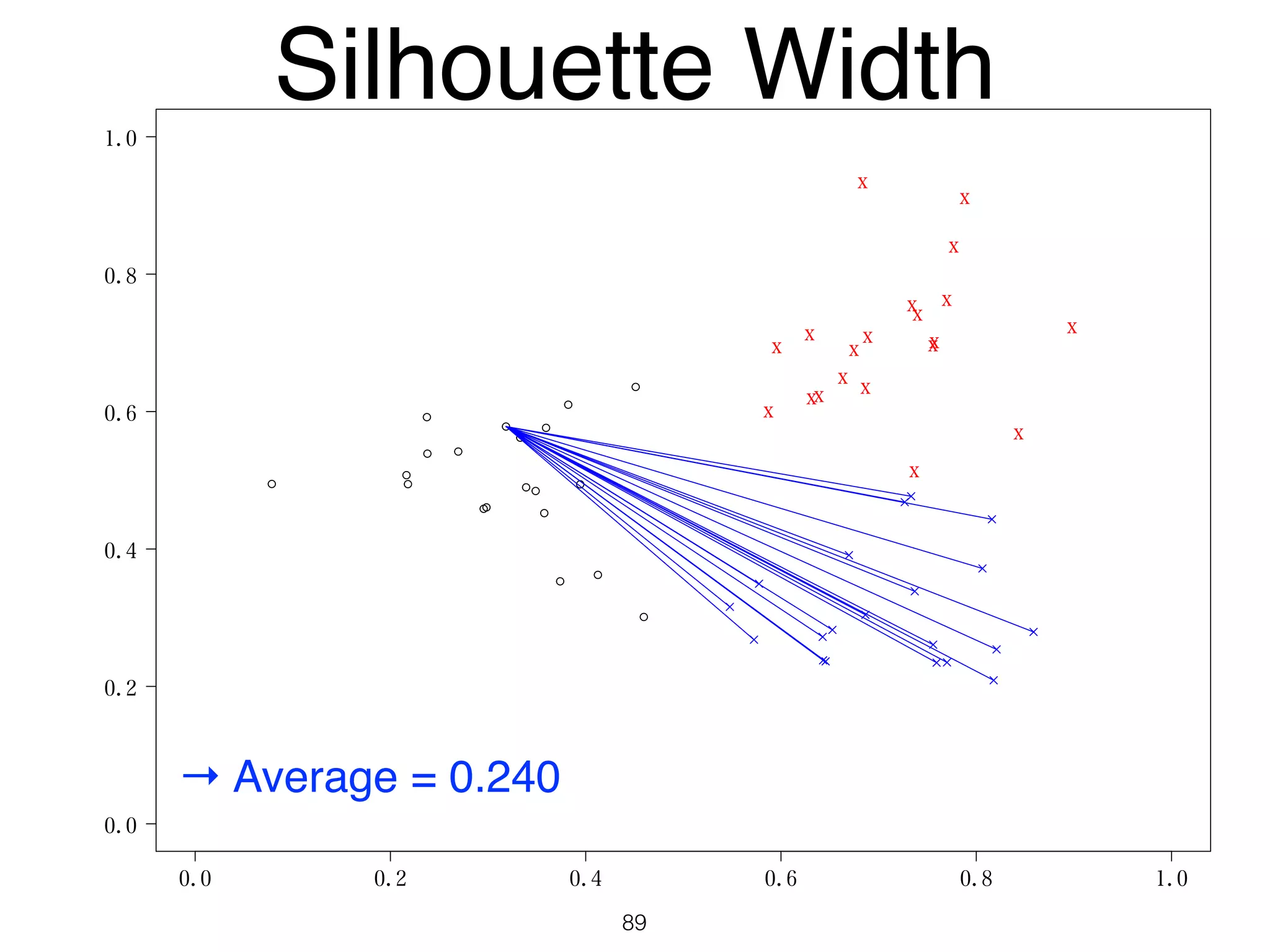
The document discusses clustering methods in R, emphasizing cluster analysis to identify groups based on similarity among data points. Various distance measures and clustering algorithms, such as agglomerative hierarchical clustering and k-means, are examined, including techniques for calculating cluster similarity. The content is particularly focused on applications in second language acquisition, exploring typologies of learner profiles through statistical methods.

Download as PDF, PPTX
Clustering Methods with R Akira Murakami Department of English Language and Applied Linguistics University of Birmingham a.murakami@bham.ac.uk
Cluster Analysis • Cluster analysis finds groups in data. • Objects in the same cluster are similar to each other. • Objects in different clusters are dissimilar. • A variety of algorithms have been proposed. • Saying “I ran a cluster analysis” does not mean much. • Used in data mining or as a statistical analysis. • Unsupervised machine learning technique. 2
Cluster Analysis in SLA • In SLA, clustering has been applied to identify the typology of learners’ • motivational profiles (Csizér & Dörnyei, 2005), • ability/aptitude profiles (Rysiewicz, 2008), • developmental profiles based on international posture, L2 willingness to communicate, and frequency of communication in L2 (Yashima & Zenuk-Nishide, 2008), • cognitive and achievement profiles based on L1 achievement, intelligence, L2 aptitude, and L2 proficiency (Sparks, Patton, & Ganschow, 2012). 3
Similarity Measure • Cluster analysis groups the observations that are “similar”. But how do we measure similarity? • Let’s suppose that we are interested in clustering L1 groups according to their accuracy of different linguistic features (i.e., accuracy profile of L1 groups). • As the measure of accuracy, we use an index that takes the value between 0 and 1, such as the TLU score. 4
￨ ￨ ￨ ￨ ￨ ￨ ￨ ￨ ￨ ￨ ￨ 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 Mathematical Distance 5
￨ ￨ ￨ ￨ ￨ ￨ ￨ ￨ ￨ ￨ ￨ 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 L1 Korean Mathematical Distance 6
￨ ￨ ￨ ￨ ￨ ￨ ￨ ￨ ￨ ￨ ￨ 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 L1 Korean L1 German Mathematical Distance 7
￨ ￨ ￨ ￨ ￨ ￨ ￨ ￨ ￨ ￨ ￨ 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 L1 Korean L1 German Distance = 0.2 Mathematical Distance 8
￨ ￨ ￨ ￨ ￨ ￨ ￨ ￨ ￨ ￨ ￨ 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 L1 Korean L1 German Distance = 0.2 L1 Japanese Distance = 0.1 Mathematical Distance 9
(Dis)Similarity Matrix 10 L1 Korean L1 German L1 Japanese L1 Korean 0.0 L1 German 0.2 0.0 L1 Japanese 0.1 0.3 0.0
Distance Measures • Things are simple in 1D, but get more complicated in 2D or above. • Different measures of distance • Euclidean distance • Manhattan distance • Maximum distance • Mahalanobis distance • Hamming distance • etc 11
Distance Measures • Things are simple in 1D, but get more complicated in 2D or above. • Different measures of distance • Euclidean distance • Manhattan distance • Maximum distance • Mahalanobis distance • Hamming distance • etc 12
Article Accuracy Pasttense−edAccuracy 0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Euclidean Distance 13
Article Accuracy Pasttense−edAccuracy 0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 L1 German (0.8, 0.6) Euclidean Distance 14
Article Accuracy Pasttense−edAccuracy 0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 L1 German (0.8, 0.6) L1 Korean (0.4, 0.8) Euclidean Distance 15
Article Accuracy Pasttense−edAccuracy 0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 L1 German (0.8, 0.6) L1 Korean (0.4, 0.8) (0.4−0.8)2 +(0.8−0.6)2 Euclidean Distance 16
Article Accuracy Pasttense−edAccuracy 0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 L1 German (0.8, 0.6) L1 Korean (0.4, 0.8) 0.45 Euclidean Distance 17
Article Accuracy Pasttense−edAccuracy 0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 L1 German (0.8, 0.6) L1 Korean (0.4, 0.8) 0.45 L1 Japanese (0.6, 0.5) Euclidean Distance 18
Article Accuracy Pasttense−edAccuracy 0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 L1 German (0.8, 0.6) L1 Korean (0.4, 0.8) 0.45 L1 Japanese (0.6, 0.5) 0.36 0.22 Euclidean Distance 19
(Dis)Similarity Matrix 20 L1 Korean L1 German L1 Japanese L1 Korean 0.00 L1 German 0.45 0.00 L1 Japanese 0.36 0.22 0.00
0.0 0.2 0.4 0.6 0.8 1.0 0.00.20.40.60.81.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy Plural−sAccuracy L1 German (0.3, 0.6, 0.9) L1 Korean (0.6, 0.9, 0.6) L1 Japanese (0.9, 0.4, 0.5) Euclidean Distance (3D) 21
0.0 0.2 0.4 0.6 0.8 1.0 0.00.20.40.60.81.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy Plural−sAccuracy L1 German (0.3, 0.6, 0.9) L1 Korean (0.6, 0.9, 0.6) L1 Japanese (0.9, 0.4, 0.5) 0.75 0.52 0.59 Euclidean Distance (3D) 22
(Dis)Similarity Matrix 23 L1 Korean L1 German L1 Japanese L1 Korean 0.00 L1 German 0.52 0.00 L1 Japanese 0.59 0.75 0.00
Distance Measures • Things are simple in 1D, but get more complicated in 2D or above. • Different measures of distance • Euclidean distance • Manhattan distance • Maximum distance • Mahalanobis distance • Hamming distance • etc 24
Article Accuracy Pasttense−edAccuracy 0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 L1 German (0.8, 0.6) L1 Korean (0.4, 0.8) Manhattan Distance 25
Article Accuracy Pasttense−edAccuracy 0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 L1 German (0.8, 0.6) L1 Korean (0.4, 0.8) Manhattan Distance 26
Article Accuracy Pasttense−edAccuracy 0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 L1 German (0.8, 0.6) L1 Korean (0.4, 0.8) 0.4 0.2 Manhattan Distance 27
Article Accuracy Pasttense−edAccuracy 0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 L1 German (0.8, 0.6) L1 Korean (0.4, 0.8) 0.4 0.2 Manhattan Distance 28 → Distance = 0.4 + 0.2 = 0.6
Article Accuracy Pasttense−edAccuracy 0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 (0.1, 0.4) (0.9, 0.3) (0.6, 0.9) Manhattan Distance 29
Article Accuracy Pasttense−edAccuracy 0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 (0.1, 0.4) (0.9, 0.3) (0.6, 0.9) 0.5 0.5 0.71 0.1 0.8 0.81 Manhattan Distance 30
Article Accuracy Pasttense−edAccuracy 0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 (0.1, 0.4) (0.9, 0.3) (0.6, 0.9) 0.5 0.5 0.71 0.1 0.8 0.81 Manhattan Distance 31 Euclidean: 0.71 Manhattan: 0.5 + 0.5 = 1.00 Euclidean: 0.81 Manhattan: 0.1 + 0.8 = 0.90
dist() • In R, dist function is used to obtain dissimilarity matrices. • Practicals 32
Clustering Methods • Now that we know the concept of similarity, we move on to the clustering of objects based on the similarity. • A number of methods have been proposed for clustering. We will look at the following two: • agglomerative hierarchical cluster analysis • k-means 33
Clustering Methods • Now that we know the concept of similarity, we move on to the clustering of objects based on the similarity. • A number of methods have been proposed for clustering. We will look at the following two: • agglomerative hierarchical cluster analysis • k-means 34
Agglomerative Hierarchical Cluster Analysis • In agglomerative hierarchical clustering, observations are clustered in a bottom-up manner. 1. Each observation forms an independent cluster at the beginning. 2. The two clusters that are most similar are clustered together. 3. 2 is repeated until all the observations are clustered in a single cluster. 35
Linkage Criteria • How do we calculate the similarity between clusters that each includes multiple observations? • Ward’s criterion (Ward’s method) • complete-linkage • single-linkage • etc. 36
Linkage Criteria • How do we calculate the similarity between clusters that each includes multiple observations? • Ward’s criterion (Ward’s method) • complete-linkage • single-linkage • etc. 37
Ward’s Method • Ward’s method leads to the smallest within-cluster variance. • At each iteration, two clusters are merged so that it yields the smallest increase of the sum of squared errors. • Sum of Squared Errors (SSE): the sum of the squared difference between the mean of the cluster and individual data points. 38
0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 (0.4, 0.2) 2 (0.2, 0.4) 3 (0.4, 0.8) 4 (0.8, 0.8) 5 (0.9, 0.4) Ward’s Method 39
0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 (0.4, 0.2) 2 (0.2, 0.4) 3 (0.4, 0.8) 4 (0.8, 0.8) 5 (0.9, 0.4) Ward’s Method 40
0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 (0.4, 0.2) 2 (0.2, 0.4) 3 (0.4, 0.8) 4 (0.8, 0.8) 5 (0.9, 0.4) x mean (0.3, 0.6) Ward’s Method 41
0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 (0.4, 0.2) 2 (0.2, 0.4) 3 (0.4, 0.8) 4 (0.8, 0.8) 5 (0.9, 0.4) x mean (0.3, 0.6) 0.22 0.22 Ward’s Method 42
0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 (0.4, 0.2) 2 (0.2, 0.4) 3 (0.4, 0.8) 4 (0.8, 0.8) 5 (0.9, 0.4) x mean (0.3, 0.6) 0.05 0.05 Ward’s Method 43
0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 (0.4, 0.2) 2 (0.2, 0.4) 3 (0.4, 0.8) 4 (0.8, 0.8) 5 (0.9, 0.4) x mean (0.3, 0.6) 0.05 0.05 Ward’s Method 44→ 0.05 + 0.05 = 0.10
• This procedure is repeated for all of the pairs. 45
0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 (0.4, 0.2) 2 (0.2, 0.4) 3 (0.4, 0.8) 4 (0.8, 0.8) 5 (0.9, 0.4) x Ward’s Method 46
0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 (0.4, 0.2) 2 (0.2, 0.4) 3 (0.4, 0.8) 4 (0.8, 0.8) 5 (0.9, 0.4) x x Ward’s Method 47
0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 (0.4, 0.2) 2 (0.2, 0.4) 3 (0.4, 0.8) 4 (0.8, 0.8) 5 (0.9, 0.4) x x (0.3, 0.3) (0.6, 0.8) Ward’s Method 48
0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 (0.4, 0.2) 2 (0.2, 0.4) 3 (0.4, 0.8) 4 (0.8, 0.8) 5 (0.9, 0.4) x x (0.3, 0.3) (0.6, 0.8) ( 0.1 2 +0.1 2 ) 2 = 0.02 0.2 2 = 0.04 Ward’s Method 49
0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 (0.4, 0.2) 2 (0.2, 0.4) 3 (0.4, 0.8) 4 (0.8, 0.8) 5 (0.9, 0.4) x x (0.3, 0.3) (0.6, 0.8) ( 0.1 2 +0.1 2 ) 2 = 0.02 0.2 2 = 0.04 Ward’s Method SSE = 0.02 + 0.02 + 0.04 + 0.04 = 0.12
0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 (0.4, 0.2) 2 (0.2, 0.4) 3 (0.4, 0.8) 4 (0.8, 0.8) 5 (0.9, 0.4) x (0.45, 0.55) Ward’s Method
0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 (0.4, 0.2) 2 (0.2, 0.4) 3 (0.4, 0.8) 4 (0.8, 0.8) 5 (0.9, 0.4) x (0.45, 0.55) 0.12 0.08 0.06 0.18 Ward’s Method SSE = 0.12 + 0.08 + 0.06 + 0.18 = 0.46
ΔSSE • SSE before the merger: 0.12 • SSE after the merger: 0.46 • Difference (ΔSSE): 0.46 - 0.12 = 0.34 53
0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 (0.4, 0.2) 2 (0.2, 0.4) 3 (0.4, 0.8) 4 (0.8, 0.8) 5 (0.9, 0.4) x x Ward’s Method 54
Dendrogram 55 1 2 5 3 4 0.2 0.3 0.4 0.5 0.6 0.7 0.8 Cluster Dendrogram hclust (*, "ward.D2") dd.dist Height
56 Practicals
Linkage Criteria • How do we know the similarity between clusters that each includes multiple observations? • Ward’s criterion (Ward’s method) • complete-linkage • single-linkage • etc. 57
0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 (0.4, 0.2) 2 (0.2, 0.4) 3 (0.4, 0.8) 4 (0.8, 0.8) 5 (0.9, 0.4) Complete Linkage 58
0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 (0.4, 0.2) 2 (0.2, 0.4) 3 (0.4, 0.8) 4 (0.8, 0.8) 5 (0.9, 0.4) Complete Linkage 59
0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 (0.4, 0.2) 2 (0.2, 0.4) 3 (0.4, 0.8) 4 (0.8, 0.8) 5 (0.9, 0.4) 0.7 Complete Linkage 60
0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 (0.4, 0.2) 2 (0.2, 0.4) 3 (0.4, 0.8) 4 (0.8, 0.8) 5 (0.9, 0.4) 0.4 Single Linkage 61
Potential Pitfall of Hierarchical Clustering • It assumes hierarchical structure in the clustering. • Let us say that our data included two L1 groups over three proficiency levels. • If we group the data into two clusters, the best split may be between the two L1 groups. • If we group them into three clusters, the best groups may be by proficiency groups. • In this case, three-cluster solution is not nested within two- cluster solution, and hierarchical clustering may fail to identify the two clusters. 62
63 k-means Clustering
k-means Clustering • K-means clustering does not assume a hierarchical structure of clusters. • i.e., no parent/child clusters • Analysts need to specify the number of clusters. 64
0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 (0.4, 0.2) 2 (0.2, 0.4) 3 (0.4, 0.8) 4 (0.8, 0.8) 5 (0.9, 0.4) k-means Clustering 65
0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy x x 1 2 3 4 5 (Centroid 1) (Centroid 2) k-means Clustering 66
0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy x x 1 2 3 4 5 (Centroid 1) (Centroid 2) 0.28 0.60 0.45 0.72 0.72 0.64 0.70 k-means Clustering 67
0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 2 3 4 5 x x Centroid 1 Centroid 2 k-means Clustering 68
0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 2 3 4 5 x x Centroid 1 Centroid 2 0.40 0.41 0.50 0.22 0.45 0.22 0.28 0.42 0.21 0.63 k-means Clustering 69
0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 2 3 4 5 x x Centroid 1 Centroid 2 k-means Clustering 70
k-Means Clustering • The optimal number of clusters depends on the intended use. • There is no “correct” or “wrong” choice in the number of clusters. • NP hard • The algorithm only approximates solutions. • Randomness is involved in the solution. You get different solutions every time you run it. • It assumes convex clusters. 71
0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 y1 Concave 72
0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 y1 x x xx x x x x x xx x x x x x x x x xx x xx x x x xx x x xx x x x xx x x x x x x x x x x xx x x x x x x x x x x x x xx x x x x x x x x x x x x x x x x x x xx x xx x x x x x x x x x x x x x x x x x x xx x x xx x x x x x x x x x x x x x x x x x x xx x xx x x x x x x x x x x x x x x x x x x x x x x x xx x x x x xx x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x Concave 73
74 Practicals
Within-Learner Centering • The mean accuracy value of each learner was subtracted from all the data points of the learner. • For example, let's suppose the mean sentence length (MSL) of Learner A over 10 writings was • {4.0, 4.2, 4.4, 4.6, 4.8, 5.0, 5.2, 5.4, 5.6, 5.8} 
 
 and that of Learner B was • {8.0, 8.2, 8.4, 8.6, 8.8, 9.0, 9.2, 9.4, 9.6, 9.8} • The difference in MSL is identical in the two learners (+0.2 per writing). • But the absolute MSL is widely different. 75
Within-Learner Centering • The mean value of Learner A (4.9) is subtracted from all the data points of Learner A: • → {-0.90, -0.70, -0.50, -0.30, -0.10, 0.10, 0.30, 0.50, 0.70, 0.90}. • Similarly, the mean value of Learner B (8.90) is subtracted from all the data points of Learner B: • → {-0.90, -0.70, -0.50, -0.30, -0.10, 0.10, 0.30, 0.50, 0.70, 0.90}. • It is guaranteed that these two learners are clustered into the same group as they have exactly the same set of values. 76
77 Cluster Validation
Cluster Validation/Evaluation • We got clusters and explored them, but how do we know how good the clusters are, or whether they indeed capture signal and not just noise? • Are the clusters ‘real’? • Is it the difference in the true learning curve that the earlier clustering captured or is it just the random noise? 78
Two Types of Validation • External Validation • Internal Validation 79
External Validation • If there is a a systematic pattern between clusters and some external criteria, such as the proficiency or L1 of learners, then what the cluster analysis captured is unlikely to be just noise. 80
Internal Validation • Measures of goodness of clusters • silhouette width • Davies–Bouldin index • Dunn index • etc. 81
Internal Validation • Measures of goodness of clusters • silhouette width • Davies–Bouldin index • Dunn index • etc. 82
Silhouette Width • Intuitively, the silhouette value is large if within- cluster dissimilarity is small (i.e., learners within each cluster have similar developmental trajectories) and between-cluster dissimilarity is large (i.e., learners in different clusters have different learning curves). • The silhouette is given to each data point (i.e., learner), and all the silhouette values are averaged to measure the cluster distinctiveness of a cluster analysis. 83
• Let’s say there are three clusters, A through C. • Let’s further say that i is a member of Cluster A. • Let a(i) be the average distance between that learner and all the other learners that belong to the same cluster. • We also calculate the average distances 1. between the learner and all the other learners that belong to Cluster B 2. between the learner and all the other learners that belong to Cluster C • Let b(i) be the smaller of the two above (1-2). • s(i) = (b(i) - a(i)) / max(a(i), b(i)) 84 Silhouette Width
0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 y1 x x x x x x x x x x x x x x x x x x x x Silhouette Width 85
0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 y1 x x x x x x x x x x x x x x x x x x x x Silhouette Width 86
0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 y1 x x x x x x x x x x x x x x x x x x x x Silhouette Width 87 → Average = 0.022 (the value of a(i))
0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 y1 x x x x x x x x x x x x x x x x x x x x Silhouette Width 88 → Average = 0.191
0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 y1 x x x x x x x x x x x x x x x x x x x x Silhouette Width 89 → Average = 0.240
Silhouette Width • a(i) = 0.022 • b(i) = 0.191 (the smaller of the other two) • s(i) = (b(i) - a(i)) / max(a(i), b(i)) • s(i) = (0.191 - 0.022) / 0.191 = 0.882 • This is repeated for all the data points. • Goodness of clustering: mean silhouette width across all the data points. 90
Bootstrapping • Now that we have a measure of how good our clustering is, the next question is whether it is good enough to be considered non-random. • We can address this question through the technique called bootstrapping. • The idea is similar to the usual hypothesis-testing procedure. • We obtain the null distribution of the silhouette value and see where our value falls. 91
• More specific procedure is as follows: 1. For each learner, we sample 30 writings (with replacement). 2. We run a k-means cluster analysis with the data obtained in 1 and calculate the mean silhouette value. 3. 1 and 2 are repeated e.g., 10,000 times, resulting in 10,000 mean silhouette values which we consider as the null distribution. 4. We examine whether the 95% range of 3 includes our observed mean silhouette value. 92 Bootstrapping
• The idea here is that we practically randomize the order of the writings within individual learners and follow the same procedure as our main analysis. • Since the order of writings is random, there should not be any systematic pattern of development observed. • The clusters obtained in this manner thus captures noise alone. We calculate the mean silhouette value on the noise-only, random clusters, and obtain its distribution by repeating the whole procedure a large number of times. 93 Bootstrapping
94 langtest.jp
langtest.jp 95 http://langtest.jp
Paper Introducing langtest.jp 96 http://applij.oxfordjournals.org/content/early/2015/06/24/applin.amv025.abstract
langtest.jp 97
98 Demo

More Related Content

PPTX
Marketing analytics - clustering Types
bySuryakumar Thangarasu
 
PPTX
Cluster Analysis
byBaivab Nag
 
PPTX
Cluster analysis
byJewel Refran
 
PPTX
Cluster Analysis
byguest0edcaf
 
DOCX
Cluster Analysis Assignment 2013-2014(2)
byTIEZHENG YUAN
 
DOC
Graph Clustering and cluster
byAdil Mehmoood
 
PPTX
Rajia cluster analysis
byCollege of Fisheries, KVAFSU, Mangalore, Karnataka
 
PPTX
Cluster Validation
byUdaya Arangala
 
Marketing analytics - clustering Types
bySuryakumar Thangarasu
 
Cluster Analysis
byBaivab Nag
 
Cluster analysis
byJewel Refran
 
Cluster Analysis
byguest0edcaf
 
Cluster Analysis Assignment 2013-2014(2)
byTIEZHENG YUAN
 
Graph Clustering and cluster
byAdil Mehmoood
 
Rajia cluster analysis
byCollege of Fisheries, KVAFSU, Mangalore, Karnataka
 
Cluster Validation
byUdaya Arangala
 

What's hot

PPTX
Hierarchical Clustering in Data Mining
byYashraj Nigam
 
PDF
Cluster Analysis
byDr Athar Khan
 
PPTX
Cluster analysis
byAvijit Famous
 
PPT
cluster analysis
bysudesh regmi
 
PPT
Cluster spss week7
byBirat Sharma
 
PDF
Cluster Analysis
bySSA KPI
 
PPT
Cluster analysis for market segmentation
byVishal Tandel
 
PPT
Malhotra20
byUzair Javed Siddiqui
 
PPTX
Introduction to Linear Discriminant Analysis
byJaclyn Kokx
 
PPTX
Cluster analysis
bysaba khan
 
PPTX
03 Data Mining Techniques
byValerii Klymchuk
 
PPTX
SPSS Step-by-Step Tutorial and Statistical Guides by Statswork
byStats Statswork
 
PDF
Clustering
byLearnbay Datascience
 
PPTX
02 Related Concepts
byValerii Klymchuk
 
PDF
Canonical correlation
byNational Institute of Biologics
 
PDF
IJCSI-10-6-1-288-292
byHARDIK SINGH
 
PDF
Higgs Boson Machine Learning Challenge - Kaggle
bySajith Edirisinghe
 
PPTX
Clustering
byAlberto Labarga
 
PPTX
Classification techniques in data mining
byKamal Acharya
 
Hierarchical Clustering in Data Mining
byYashraj Nigam
 
Cluster Analysis
byDr Athar Khan
 
Cluster analysis
byAvijit Famous
 
cluster analysis
bysudesh regmi
 
Cluster spss week7
byBirat Sharma
 
Cluster Analysis
bySSA KPI
 
Cluster analysis for market segmentation
byVishal Tandel
 
Malhotra20
byUzair Javed Siddiqui
 
Introduction to Linear Discriminant Analysis
byJaclyn Kokx
 
Cluster analysis
bysaba khan
 
03 Data Mining Techniques
byValerii Klymchuk
 
SPSS Step-by-Step Tutorial and Statistical Guides by Statswork
byStats Statswork
 
Clustering
byLearnbay Datascience
 
02 Related Concepts
byValerii Klymchuk
 
Canonical correlation
byNational Institute of Biologics
 
IJCSI-10-6-1-288-292
byHARDIK SINGH
 
Higgs Boson Machine Learning Challenge - Kaggle
bySajith Edirisinghe
 
Clustering
byAlberto Labarga
 
Classification techniques in data mining
byKamal Acharya
 

Similar to Clustering Methods with R

PDF
Clustering Methods with R
byAkira Murakami
 
PPT
Statistical Clustering
bytim_hare
 
PPTX
Hierarchical clustering
byishmecse13
 
PDF
Clustering Algorithms - Kmeans,Min ALgorithm
bySharmila Chidaravalli
 
PPTX
01 Statistika Lanjut - Cluster Analysis part 1 with sound (1).pptx
byniawiya
 
PDF
Cluster Analysis: Measuring Similarity & Dissimilarity
byShivarkarSandip
 
PDF
Unit III Unsupervised learning-clustering
byShivarkarSandip
 
PPTX
Clusteranalysis
bydeepti gupta
 
PPTX
Read first few slides cluster analysis
byKritika Jain
 
PPTX
Clusteranalysis 121206234137-phpapp01
bydeepti gupta
 
PDF
Artificial Intelligence and machine learning
byabhaykumar804670
 
PPTX
Hierachical clustering
byTilani Gunawardena PhD(UNIBAS), BSc(Pera), FHEA(UK), CEng, MIESL
 
PDF
Clustering.pdf
bynadimhossain24
 
PPTX
Cluster Analysis.pptx
byAdityaRajput317826
 
PPT
clustering and their types explanation of data mining
byvandanasharma862095
 
PPTX
kmean clustering
byTilani Gunawardena PhD(UNIBAS), BSc(Pera), FHEA(UK), CEng, MIESL
 
PPT
Slide-TIF311-DM-10-11.ppt
bySandinoBerutu1
 
PPT
Slide-TIF311-DM-10-11.ppt
byImXaib
 
PDF
clustering_hierarchical ckustering notes.pdf
byp_manimozhi
 
PPTX
Clustering_Overview.pptx
bynyomans1
 
Clustering Methods with R
byAkira Murakami
 
Statistical Clustering
bytim_hare
 
Hierarchical clustering
byishmecse13
 
Clustering Algorithms - Kmeans,Min ALgorithm
bySharmila Chidaravalli
 
01 Statistika Lanjut - Cluster Analysis part 1 with sound (1).pptx
byniawiya
 
Cluster Analysis: Measuring Similarity & Dissimilarity
byShivarkarSandip
 
Unit III Unsupervised learning-clustering
byShivarkarSandip
 
Clusteranalysis
bydeepti gupta
 
Read first few slides cluster analysis
byKritika Jain
 
Clusteranalysis 121206234137-phpapp01
bydeepti gupta
 
Artificial Intelligence and machine learning
byabhaykumar804670
 
Hierachical clustering
byTilani Gunawardena PhD(UNIBAS), BSc(Pera), FHEA(UK), CEng, MIESL
 
Clustering.pdf
bynadimhossain24
 
Cluster Analysis.pptx
byAdityaRajput317826
 
clustering and their types explanation of data mining
byvandanasharma862095
 
kmean clustering
byTilani Gunawardena PhD(UNIBAS), BSc(Pera), FHEA(UK), CEng, MIESL
 
Slide-TIF311-DM-10-11.ppt
bySandinoBerutu1
 
Slide-TIF311-DM-10-11.ppt
byImXaib
 
clustering_hierarchical ckustering notes.pdf
byp_manimozhi
 
Clustering_Overview.pptx
bynyomans1
 

Recently uploaded

PPTX
Expt 15_biostatistics, expermiental colo edited.pptx
bymagsjtae
 
PPTX
ETL DRIVEN ANALYTICS DATA WAREHOUSE (DATA ENGINEERING)
byZaidMAHSOUNE
 
PPTX
Group project mgtkspgo gj a akf alkn mkla.pptx
bymadaminbekmahmudov02
 
PPTX
最新版加拿大卡莫森学院毕业证（CC毕业证书）原版定制成绩单在读证明学历认证
by西澳大利亚大学学历认证【Q微号:1954 292 140】办理学位证(UWA毕业证成绩单)
 
PPT
Reporting ov conducting cd analysiss.ppt
byDaffaFauziIrwanto
 
PPTX
"Data Analysis Dashboard in Excel & Power BI
bySara Ebrahim
 
PPTX
How to Leverage a PIM for a Successful Data Migration 10 2025.pptx
byPaula Levy
 
PPTX
IFR_Phraseology_Exercises_Jose_Antonio_Davila_Chapeyquen.pptx
byAntonio Davila
 
PDF
MSc_Dissertation — Remote Work On Mental Health
byRobertSolomon23
 
PPTX
Agentic Systems and Compliance - A brief intro [1.2]
byrobertowilliams
 
PDF
gis based document for apparture radar analysis
byBedassaDessalegn3
 
DOCX
Knowledge Management Information Sheet(58f671121fa4e5fd56cf1025ded949ee).docx
byjesusjeager
 
PPTX
MongoDB Developers Best Practices12.pptx
bysivasanniboina1
 
PDF
An Artificial Intelligence-driven Approach to Mineral Exploration in Botswana
byJames AH Campbell
 
PPTX
Morgan (Kumpulan Tabel).pptx Morgan (Kumpulan Tabel).pptx
byDhika Adhi Pratama
 
PPTX
Matrix and determinant URT [Autosaved].pptx
bymom91284
 
DOC
Bài Tập Bổ trợ Anh 7 Global năm học 2022 2023 UNIT 4 GLOBAL SUCCESS 7HS.doc
byThyHng893134
 
PDF
RTP_AR_Basic_Learners' Workbook_KS2 [FOR REPRODUCTION] (1).pdf
byRHODABADTING
 
PPTX
Feed Formulation PEARSON'S SQUARE METHOD.pptx
bybaginareca
 
DOCX
researchmethodologyreport-140226083638-phpapp02.docx
byomgorde230
 
Expt 15_biostatistics, expermiental colo edited.pptx
bymagsjtae
 
ETL DRIVEN ANALYTICS DATA WAREHOUSE (DATA ENGINEERING)
byZaidMAHSOUNE
 
Group project mgtkspgo gj a akf alkn mkla.pptx
bymadaminbekmahmudov02
 
最新版加拿大卡莫森学院毕业证（CC毕业证书）原版定制成绩单在读证明学历认证
by西澳大利亚大学学历认证【Q微号:1954 292 140】办理学位证(UWA毕业证成绩单)
 
Reporting ov conducting cd analysiss.ppt
byDaffaFauziIrwanto
 
"Data Analysis Dashboard in Excel & Power BI
bySara Ebrahim
 
How to Leverage a PIM for a Successful Data Migration 10 2025.pptx
byPaula Levy
 
IFR_Phraseology_Exercises_Jose_Antonio_Davila_Chapeyquen.pptx
byAntonio Davila
 
MSc_Dissertation — Remote Work On Mental Health
byRobertSolomon23
 
Agentic Systems and Compliance - A brief intro [1.2]
byrobertowilliams
 
gis based document for apparture radar analysis
byBedassaDessalegn3
 
Knowledge Management Information Sheet(58f671121fa4e5fd56cf1025ded949ee).docx
byjesusjeager
 
MongoDB Developers Best Practices12.pptx
bysivasanniboina1
 
An Artificial Intelligence-driven Approach to Mineral Exploration in Botswana
byJames AH Campbell
 
Morgan (Kumpulan Tabel).pptx Morgan (Kumpulan Tabel).pptx
byDhika Adhi Pratama
 
Matrix and determinant URT [Autosaved].pptx
bymom91284
 
Bài Tập Bổ trợ Anh 7 Global năm học 2022 2023 UNIT 4 GLOBAL SUCCESS 7HS.doc
byThyHng893134
 
RTP_AR_Basic_Learners' Workbook_KS2 [FOR REPRODUCTION] (1).pdf
byRHODABADTING
 
Feed Formulation PEARSON'S SQUARE METHOD.pptx
bybaginareca
 
researchmethodologyreport-140226083638-phpapp02.docx
byomgorde230
 

Clustering Methods with R

  • 1.
    Clustering Methods withR Akira Murakami Department of English Language and Applied Linguistics University of Birmingham a.murakami@bham.ac.uk
  • 2.
    Cluster Analysis • Clusteranalysis finds groups in data. • Objects in the same cluster are similar to each other. • Objects in different clusters are dissimilar. • A variety of algorithms have been proposed. • Saying “I ran a cluster analysis” does not mean much. • Used in data mining or as a statistical analysis. • Unsupervised machine learning technique. 2
  • 3.
    Cluster Analysis inSLA • In SLA, clustering has been applied to identify the typology of learners’ • motivational profiles (Csizér & Dörnyei, 2005), • ability/aptitude profiles (Rysiewicz, 2008), • developmental profiles based on international posture, L2 willingness to communicate, and frequency of communication in L2 (Yashima & Zenuk-Nishide, 2008), • cognitive and achievement profiles based on L1 achievement, intelligence, L2 aptitude, and L2 proficiency (Sparks, Patton, & Ganschow, 2012). 3
  • 4.
    Similarity Measure • Clusteranalysis groups the observations that are “similar”. But how do we measure similarity? • Let’s suppose that we are interested in clustering L1 groups according to their accuracy of different linguistic features (i.e., accuracy profile of L1 groups). • As the measure of accuracy, we use an index that takes the value between 0 and 1, such as the TLU score. 4
  • 5.
    ￨ ￨ ￨￨ ￨ ￨ ￨ ￨ ￨ ￨ ￨ 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 Mathematical Distance 5
  • 6.
    ￨ ￨ ￨￨ ￨ ￨ ￨ ￨ ￨ ￨ ￨ 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 L1 Korean Mathematical Distance 6
  • 7.
    ￨ ￨ ￨￨ ￨ ￨ ￨ ￨ ￨ ￨ ￨ 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 L1 Korean L1 German Mathematical Distance 7
  • 8.
    ￨ ￨ ￨￨ ￨ ￨ ￨ ￨ ￨ ￨ ￨ 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 L1 Korean L1 German Distance = 0.2 Mathematical Distance 8
  • 9.
    ￨ ￨ ￨￨ ￨ ￨ ￨ ￨ ￨ ￨ ￨ 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 L1 Korean L1 German Distance = 0.2 L1 Japanese Distance = 0.1 Mathematical Distance 9
  • 10.
    (Dis)Similarity Matrix 10 L1 KoreanL1 German L1 Japanese L1 Korean 0.0 L1 German 0.2 0.0 L1 Japanese 0.1 0.3 0.0
  • 11.
    Distance Measures • Thingsare simple in 1D, but get more complicated in 2D or above. • Different measures of distance • Euclidean distance • Manhattan distance • Maximum distance • Mahalanobis distance • Hamming distance • etc 11
  • 12.
    Distance Measures • Thingsare simple in 1D, but get more complicated in 2D or above. • Different measures of distance • Euclidean distance • Manhattan distance • Maximum distance • Mahalanobis distance • Hamming distance • etc 12
  • 13.
    Article Accuracy Pasttense−edAccuracy 0.0 0.20.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Euclidean Distance 13
  • 14.
    Article Accuracy Pasttense−edAccuracy 0.0 0.20.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 L1 German (0.8, 0.6) Euclidean Distance 14
  • 15.
    Article Accuracy Pasttense−edAccuracy 0.0 0.20.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 L1 German (0.8, 0.6) L1 Korean (0.4, 0.8) Euclidean Distance 15
  • 16.
    Article Accuracy Pasttense−edAccuracy 0.0 0.20.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 L1 German (0.8, 0.6) L1 Korean (0.4, 0.8) (0.4−0.8)2 +(0.8−0.6)2 Euclidean Distance 16
  • 17.
    Article Accuracy Pasttense−edAccuracy 0.0 0.20.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 L1 German (0.8, 0.6) L1 Korean (0.4, 0.8) 0.45 Euclidean Distance 17
  • 18.
    Article Accuracy Pasttense−edAccuracy 0.0 0.20.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 L1 German (0.8, 0.6) L1 Korean (0.4, 0.8) 0.45 L1 Japanese (0.6, 0.5) Euclidean Distance 18
  • 19.
    Article Accuracy Pasttense−edAccuracy 0.0 0.20.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 L1 German (0.8, 0.6) L1 Korean (0.4, 0.8) 0.45 L1 Japanese (0.6, 0.5) 0.36 0.22 Euclidean Distance 19
  • 20.
    (Dis)Similarity Matrix 20 L1 KoreanL1 German L1 Japanese L1 Korean 0.00 L1 German 0.45 0.00 L1 Japanese 0.36 0.22 0.00
  • 21.
    0.0 0.2 0.40.6 0.8 1.0 0.00.20.40.60.81.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy Plural−sAccuracy L1 German (0.3, 0.6, 0.9) L1 Korean (0.6, 0.9, 0.6) L1 Japanese (0.9, 0.4, 0.5) Euclidean Distance (3D) 21
  • 22.
    0.0 0.2 0.40.6 0.8 1.0 0.00.20.40.60.81.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy Plural−sAccuracy L1 German (0.3, 0.6, 0.9) L1 Korean (0.6, 0.9, 0.6) L1 Japanese (0.9, 0.4, 0.5) 0.75 0.52 0.59 Euclidean Distance (3D) 22
  • 23.
    (Dis)Similarity Matrix 23 L1 KoreanL1 German L1 Japanese L1 Korean 0.00 L1 German 0.52 0.00 L1 Japanese 0.59 0.75 0.00
  • 24.
    Distance Measures • Thingsare simple in 1D, but get more complicated in 2D or above. • Different measures of distance • Euclidean distance • Manhattan distance • Maximum distance • Mahalanobis distance • Hamming distance • etc 24
  • 25.
    Article Accuracy Pasttense−edAccuracy 0.0 0.20.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 L1 German (0.8, 0.6) L1 Korean (0.4, 0.8) Manhattan Distance 25
  • 26.
    Article Accuracy Pasttense−edAccuracy 0.0 0.20.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 L1 German (0.8, 0.6) L1 Korean (0.4, 0.8) Manhattan Distance 26
  • 27.
    Article Accuracy Pasttense−edAccuracy 0.0 0.20.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 L1 German (0.8, 0.6) L1 Korean (0.4, 0.8) 0.4 0.2 Manhattan Distance 27
  • 28.
    Article Accuracy Pasttense−edAccuracy 0.0 0.20.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 L1 German (0.8, 0.6) L1 Korean (0.4, 0.8) 0.4 0.2 Manhattan Distance 28 → Distance = 0.4 + 0.2 = 0.6
  • 29.
    Article Accuracy Pasttense−edAccuracy 0.0 0.20.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 (0.1, 0.4) (0.9, 0.3) (0.6, 0.9) Manhattan Distance 29
  • 30.
    Article Accuracy Pasttense−edAccuracy 0.0 0.20.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 (0.1, 0.4) (0.9, 0.3) (0.6, 0.9) 0.5 0.5 0.71 0.1 0.8 0.81 Manhattan Distance 30
  • 31.
    Article Accuracy Pasttense−edAccuracy 0.0 0.20.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 (0.1, 0.4) (0.9, 0.3) (0.6, 0.9) 0.5 0.5 0.71 0.1 0.8 0.81 Manhattan Distance 31 Euclidean: 0.71 Manhattan: 0.5 + 0.5 = 1.00 Euclidean: 0.81 Manhattan: 0.1 + 0.8 = 0.90
  • 32.
    dist() • In R,dist function is used to obtain dissimilarity matrices. • Practicals 32
  • 33.
    Clustering Methods • Nowthat we know the concept of similarity, we move on to the clustering of objects based on the similarity. • A number of methods have been proposed for clustering. We will look at the following two: • agglomerative hierarchical cluster analysis • k-means 33
  • 34.
    Clustering Methods • Nowthat we know the concept of similarity, we move on to the clustering of objects based on the similarity. • A number of methods have been proposed for clustering. We will look at the following two: • agglomerative hierarchical cluster analysis • k-means 34
  • 35.
    Agglomerative Hierarchical ClusterAnalysis • In agglomerative hierarchical clustering, observations are clustered in a bottom-up manner. 1. Each observation forms an independent cluster at the beginning. 2. The two clusters that are most similar are clustered together. 3. 2 is repeated until all the observations are clustered in a single cluster. 35
  • 36.
    Linkage Criteria • Howdo we calculate the similarity between clusters that each includes multiple observations? • Ward’s criterion (Ward’s method) • complete-linkage • single-linkage • etc. 36
  • 37.
    Linkage Criteria • Howdo we calculate the similarity between clusters that each includes multiple observations? • Ward’s criterion (Ward’s method) • complete-linkage • single-linkage • etc. 37
  • 38.
    Ward’s Method • Ward’smethod leads to the smallest within-cluster variance. • At each iteration, two clusters are merged so that it yields the smallest increase of the sum of squared errors. • Sum of Squared Errors (SSE): the sum of the squared difference between the mean of the cluster and individual data points. 38
  • 39.
    0.0 0.2 0.40.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 (0.4, 0.2) 2 (0.2, 0.4) 3 (0.4, 0.8) 4 (0.8, 0.8) 5 (0.9, 0.4) Ward’s Method 39
  • 40.
    0.0 0.2 0.40.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 (0.4, 0.2) 2 (0.2, 0.4) 3 (0.4, 0.8) 4 (0.8, 0.8) 5 (0.9, 0.4) Ward’s Method 40
  • 41.
    0.0 0.2 0.40.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 (0.4, 0.2) 2 (0.2, 0.4) 3 (0.4, 0.8) 4 (0.8, 0.8) 5 (0.9, 0.4) x mean (0.3, 0.6) Ward’s Method 41
  • 42.
    0.0 0.2 0.40.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 (0.4, 0.2) 2 (0.2, 0.4) 3 (0.4, 0.8) 4 (0.8, 0.8) 5 (0.9, 0.4) x mean (0.3, 0.6) 0.22 0.22 Ward’s Method 42
  • 43.
    0.0 0.2 0.40.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 (0.4, 0.2) 2 (0.2, 0.4) 3 (0.4, 0.8) 4 (0.8, 0.8) 5 (0.9, 0.4) x mean (0.3, 0.6) 0.05 0.05 Ward’s Method 43
  • 44.
    0.0 0.2 0.40.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 (0.4, 0.2) 2 (0.2, 0.4) 3 (0.4, 0.8) 4 (0.8, 0.8) 5 (0.9, 0.4) x mean (0.3, 0.6) 0.05 0.05 Ward’s Method 44→ 0.05 + 0.05 = 0.10
  • 45.
    • This procedureis repeated for all of the pairs. 45
  • 46.
    0.0 0.2 0.40.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 (0.4, 0.2) 2 (0.2, 0.4) 3 (0.4, 0.8) 4 (0.8, 0.8) 5 (0.9, 0.4) x Ward’s Method 46
  • 47.
    0.0 0.2 0.40.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 (0.4, 0.2) 2 (0.2, 0.4) 3 (0.4, 0.8) 4 (0.8, 0.8) 5 (0.9, 0.4) x x Ward’s Method 47
  • 48.
    0.0 0.2 0.40.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 (0.4, 0.2) 2 (0.2, 0.4) 3 (0.4, 0.8) 4 (0.8, 0.8) 5 (0.9, 0.4) x x (0.3, 0.3) (0.6, 0.8) Ward’s Method 48
  • 49.
    0.0 0.2 0.40.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 (0.4, 0.2) 2 (0.2, 0.4) 3 (0.4, 0.8) 4 (0.8, 0.8) 5 (0.9, 0.4) x x (0.3, 0.3) (0.6, 0.8) ( 0.1 2 +0.1 2 ) 2 = 0.02 0.2 2 = 0.04 Ward’s Method 49
  • 50.
    0.0 0.2 0.40.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 (0.4, 0.2) 2 (0.2, 0.4) 3 (0.4, 0.8) 4 (0.8, 0.8) 5 (0.9, 0.4) x x (0.3, 0.3) (0.6, 0.8) ( 0.1 2 +0.1 2 ) 2 = 0.02 0.2 2 = 0.04 Ward’s Method SSE = 0.02 + 0.02 + 0.04 + 0.04 = 0.12
  • 51.
    0.0 0.2 0.40.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 (0.4, 0.2) 2 (0.2, 0.4) 3 (0.4, 0.8) 4 (0.8, 0.8) 5 (0.9, 0.4) x (0.45, 0.55) Ward’s Method
  • 52.
    0.0 0.2 0.40.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 (0.4, 0.2) 2 (0.2, 0.4) 3 (0.4, 0.8) 4 (0.8, 0.8) 5 (0.9, 0.4) x (0.45, 0.55) 0.12 0.08 0.06 0.18 Ward’s Method SSE = 0.12 + 0.08 + 0.06 + 0.18 = 0.46
  • 53.
    ΔSSE • SSE beforethe merger: 0.12 • SSE after the merger: 0.46 • Difference (ΔSSE): 0.46 - 0.12 = 0.34 53
  • 54.
    0.0 0.2 0.40.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 (0.4, 0.2) 2 (0.2, 0.4) 3 (0.4, 0.8) 4 (0.8, 0.8) 5 (0.9, 0.4) x x Ward’s Method 54
  • 55.
  • 56.
  • 57.
    Linkage Criteria • Howdo we know the similarity between clusters that each includes multiple observations? • Ward’s criterion (Ward’s method) • complete-linkage • single-linkage • etc. 57
  • 58.
    0.0 0.2 0.40.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 (0.4, 0.2) 2 (0.2, 0.4) 3 (0.4, 0.8) 4 (0.8, 0.8) 5 (0.9, 0.4) Complete Linkage 58
  • 59.
    0.0 0.2 0.40.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 (0.4, 0.2) 2 (0.2, 0.4) 3 (0.4, 0.8) 4 (0.8, 0.8) 5 (0.9, 0.4) Complete Linkage 59
  • 60.
    0.0 0.2 0.40.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 (0.4, 0.2) 2 (0.2, 0.4) 3 (0.4, 0.8) 4 (0.8, 0.8) 5 (0.9, 0.4) 0.7 Complete Linkage 60
  • 61.
    0.0 0.2 0.40.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 (0.4, 0.2) 2 (0.2, 0.4) 3 (0.4, 0.8) 4 (0.8, 0.8) 5 (0.9, 0.4) 0.4 Single Linkage 61
  • 62.
    Potential Pitfall ofHierarchical Clustering • It assumes hierarchical structure in the clustering. • Let us say that our data included two L1 groups over three proficiency levels. • If we group the data into two clusters, the best split may be between the two L1 groups. • If we group them into three clusters, the best groups may be by proficiency groups. • In this case, three-cluster solution is not nested within two- cluster solution, and hierarchical clustering may fail to identify the two clusters. 62
  • 63.
  • 64.
    k-means Clustering • K-meansclustering does not assume a hierarchical structure of clusters. • i.e., no parent/child clusters • Analysts need to specify the number of clusters. 64
  • 65.
    0.0 0.2 0.40.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 (0.4, 0.2) 2 (0.2, 0.4) 3 (0.4, 0.8) 4 (0.8, 0.8) 5 (0.9, 0.4) k-means Clustering 65
  • 66.
    0.0 0.2 0.40.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy x x 1 2 3 4 5 (Centroid 1) (Centroid 2) k-means Clustering 66
  • 67.
    0.0 0.2 0.40.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy x x 1 2 3 4 5 (Centroid 1) (Centroid 2) 0.28 0.60 0.45 0.72 0.72 0.64 0.70 k-means Clustering 67
  • 68.
    0.0 0.2 0.40.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 2 3 4 5 x x Centroid 1 Centroid 2 k-means Clustering 68
  • 69.
    0.0 0.2 0.40.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 2 3 4 5 x x Centroid 1 Centroid 2 0.40 0.41 0.50 0.22 0.45 0.22 0.28 0.42 0.21 0.63 k-means Clustering 69
  • 70.
    0.0 0.2 0.40.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 Article Accuracy Pasttense−edAccuracy 1 2 3 4 5 x x Centroid 1 Centroid 2 k-means Clustering 70
  • 71.
    k-Means Clustering • Theoptimal number of clusters depends on the intended use. • There is no “correct” or “wrong” choice in the number of clusters. • NP hard • The algorithm only approximates solutions. • Randomness is involved in the solution. You get different solutions every time you run it. • It assumes convex clusters. 71
  • 72.
    0.0 0.2 0.40.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 y1 Concave 72
  • 73.
    0.0 0.2 0.40.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 y1 x x xx x x x x x xx x x x x x x x x xx x xx x x x xx x x xx x x x xx x x x x x x x x x x xx x x x x x x x x x x x x xx x x x x x x x x x x x x x x x x x x xx x xx x x x x x x x x x x x x x x x x x x xx x x xx x x x x x x x x x x x x x x x x x x xx x xx x x x x x x x x x x x x x x x x x x x x x x x xx x x x x xx x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x Concave 73
  • 74.
  • 75.
    Within-Learner Centering • Themean accuracy value of each learner was subtracted from all the data points of the learner. • For example, let's suppose the mean sentence length (MSL) of Learner A over 10 writings was • {4.0, 4.2, 4.4, 4.6, 4.8, 5.0, 5.2, 5.4, 5.6, 5.8} 
 
 and that of Learner B was • {8.0, 8.2, 8.4, 8.6, 8.8, 9.0, 9.2, 9.4, 9.6, 9.8} • The difference in MSL is identical in the two learners (+0.2 per writing). • But the absolute MSL is widely different. 75
  • 76.
    Within-Learner Centering • Themean value of Learner A (4.9) is subtracted from all the data points of Learner A: • → {-0.90, -0.70, -0.50, -0.30, -0.10, 0.10, 0.30, 0.50, 0.70, 0.90}. • Similarly, the mean value of Learner B (8.90) is subtracted from all the data points of Learner B: • → {-0.90, -0.70, -0.50, -0.30, -0.10, 0.10, 0.30, 0.50, 0.70, 0.90}. • It is guaranteed that these two learners are clustered into the same group as they have exactly the same set of values. 76
  • 77.
  • 78.
    Cluster Validation/Evaluation • Wegot clusters and explored them, but how do we know how good the clusters are, or whether they indeed capture signal and not just noise? • Are the clusters ‘real’? • Is it the difference in the true learning curve that the earlier clustering captured or is it just the random noise? 78
  • 79.
    Two Types ofValidation • External Validation • Internal Validation 79
  • 80.
    External Validation • Ifthere is a a systematic pattern between clusters and some external criteria, such as the proficiency or L1 of learners, then what the cluster analysis captured is unlikely to be just noise. 80
  • 81.
    Internal Validation • Measuresof goodness of clusters • silhouette width • Davies–Bouldin index • Dunn index • etc. 81
  • 82.
    Internal Validation • Measuresof goodness of clusters • silhouette width • Davies–Bouldin index • Dunn index • etc. 82
  • 83.
    Silhouette Width • Intuitively,the silhouette value is large if within- cluster dissimilarity is small (i.e., learners within each cluster have similar developmental trajectories) and between-cluster dissimilarity is large (i.e., learners in different clusters have different learning curves). • The silhouette is given to each data point (i.e., learner), and all the silhouette values are averaged to measure the cluster distinctiveness of a cluster analysis. 83
  • 84.
    • Let’s saythere are three clusters, A through C. • Let’s further say that i is a member of Cluster A. • Let a(i) be the average distance between that learner and all the other learners that belong to the same cluster. • We also calculate the average distances 1. between the learner and all the other learners that belong to Cluster B 2. between the learner and all the other learners that belong to Cluster C • Let b(i) be the smaller of the two above (1-2). • s(i) = (b(i) - a(i)) / max(a(i), b(i)) 84 Silhouette Width
  • 85.
    0.0 0.2 0.40.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 y1 x x x x x x x x x x x x x x x x x x x x Silhouette Width 85
  • 86.
    0.0 0.2 0.40.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 y1 x x x x x x x x x x x x x x x x x x x x Silhouette Width 86
  • 87.
    0.0 0.2 0.40.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 y1 x x x x x x x x x x x x x x x x x x x x Silhouette Width 87 → Average = 0.022 (the value of a(i))
  • 88.
    0.0 0.2 0.40.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 y1 x x x x x x x x x x x x x x x x x x x x Silhouette Width 88 → Average = 0.191
  • 89.
    0.0 0.2 0.40.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 y1 x x x x x x x x x x x x x x x x x x x x Silhouette Width 89 → Average = 0.240
  • 90.
    Silhouette Width • a(i)= 0.022 • b(i) = 0.191 (the smaller of the other two) • s(i) = (b(i) - a(i)) / max(a(i), b(i)) • s(i) = (0.191 - 0.022) / 0.191 = 0.882 • This is repeated for all the data points. • Goodness of clustering: mean silhouette width across all the data points. 90
  • 91.
    Bootstrapping • Now thatwe have a measure of how good our clustering is, the next question is whether it is good enough to be considered non-random. • We can address this question through the technique called bootstrapping. • The idea is similar to the usual hypothesis-testing procedure. • We obtain the null distribution of the silhouette value and see where our value falls. 91
  • 92.
    • More specificprocedure is as follows: 1. For each learner, we sample 30 writings (with replacement). 2. We run a k-means cluster analysis with the data obtained in 1 and calculate the mean silhouette value. 3. 1 and 2 are repeated e.g., 10,000 times, resulting in 10,000 mean silhouette values which we consider as the null distribution. 4. We examine whether the 95% range of 3 includes our observed mean silhouette value. 92 Bootstrapping
  • 93.
    • The ideahere is that we practically randomize the order of the writings within individual learners and follow the same procedure as our main analysis. • Since the order of writings is random, there should not be any systematic pattern of development observed. • The clusters obtained in this manner thus captures noise alone. We calculate the mean silhouette value on the noise-only, random clusters, and obtain its distribution by repeating the whole procedure a large number of times. 93 Bootstrapping
  • 94.
  • 95.
  • 96.
  • 97.
  • 98.