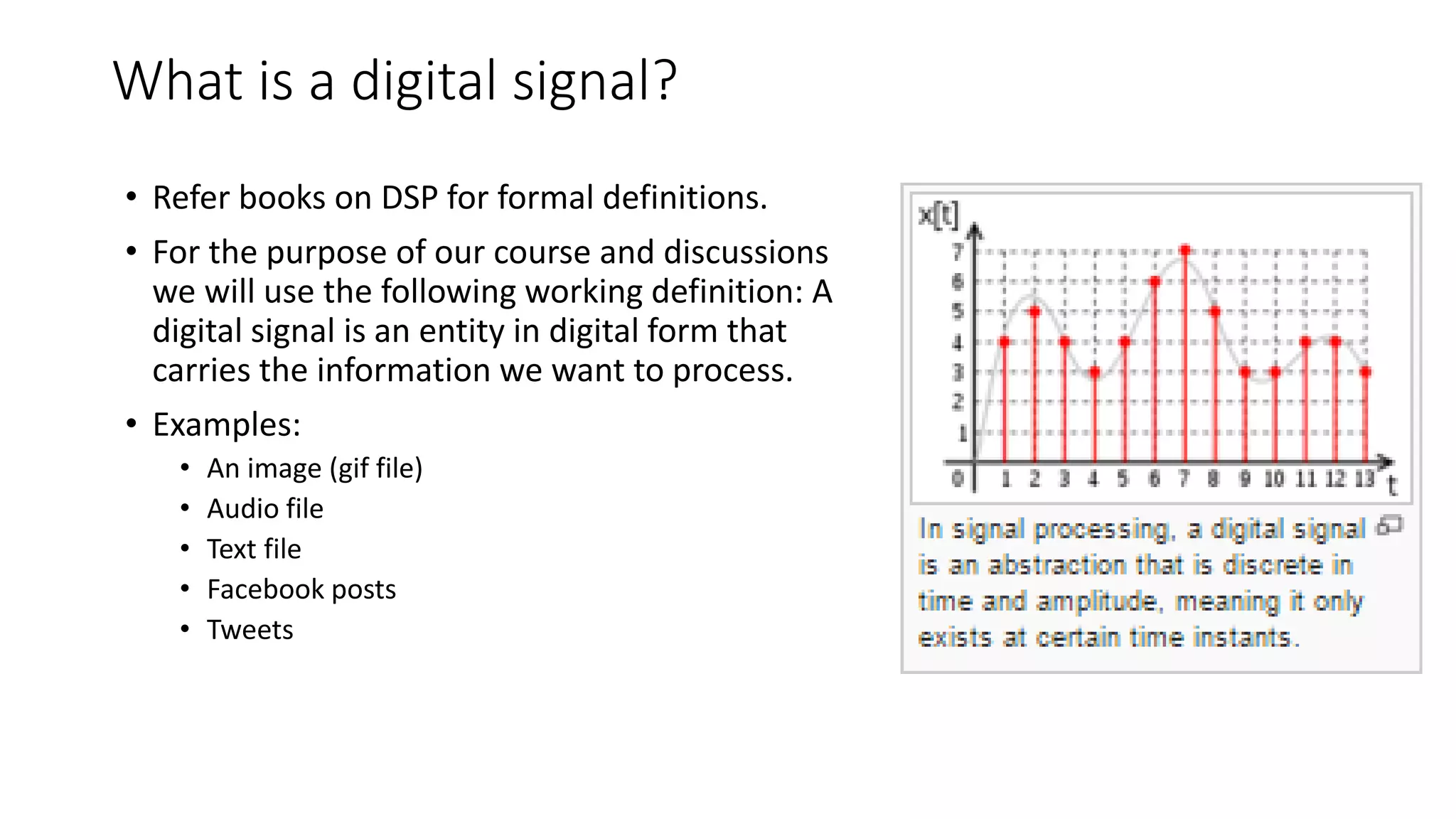
Convolutional Neural Networks: Part 1

Convolutional Neural Networks: Part 1

• 1.
  Introduction to Convolutional NeuralNetworks Applied Machine Learning Anantharaman Narayana Iyer JNResearch narayana dot Anantharaman at gmail dot com 23 March 2016
• 2.
  Topics • Motivation: Whywe need CNN? • What is the principle of convolution? • From ANN to CNN • CNN Architecture
• 3.
  Motivation for CNN •Suppose we are required to perform image classification on a colour image of 100 x 100 dimensions. • If we are to implement this brute force using a standard feed forward neural network that has an input, hidden and an output layer, how many model parameters we need for: hidden units (nh) = 1000, output classes = 10 and Softmax output layer • Input layer = 10k pixels * 3 = 30k, weight matrix for hidden to input layer = 1k * 30k = 30 M and output layer matrix size = 10 * 1000 = 10k • We can easily see that the parameters blow up if we need to process larger sized images because an image is 2 dimensional and has a depth also if the colour information is to be taken in to account • One way to handle this is by extracting the features using image processing techniques (pre processing) and presenting a lower dimensional input to the Neural Network. But this requires expert engineered features and hence domain knowledge • Can we do better by using some properties of images? • CNNs allow us to substantially reduce the model parameters without needing to perform hand crafted feature engineering
• 4.
  Convolution: From firstprinciples
• 5.
  What is adigital signal? • Refer books on DSP for formal definitions. • For the purpose of our course and discussions we will use the following working definition: A digital signal is an entity in digital form that carries the information we want to process. • Examples: • An image (gif file) • Audio file • Text file • Facebook posts • Tweets
• 6.
  What is asystem? • For the purpose of our class, we consider the system as a function that transforms the input signal. • A linear system satisfies the properties of: • Scaling • Superposition • Shift Invariant Systems: If the input is shifted by a distance k, the output is also shifted exactly by the same distance. • A linear shift invariant system is both linear as well as shift invariant. • If a system is linear shift invariant, its output is fully characterized by its impulse response and is determined as the convolution of the input and the impulse response • Important implications: • Impulse Response fully characterizes the system and so we can treat the system as a black box. • Inputs can be looked at as scaling factors to the impulse response and so don’t play a role in modifying the nature of output except for scaling
• 7.
  Convolution 𝐶𝑜𝑛𝑣𝑜𝑙𝑢𝑡𝑖𝑜𝑛 𝑖𝑛 1𝐷𝑖𝑚𝑒𝑛𝑠𝑖𝑜𝑛: 𝑦 𝑛 = 𝑘=−∞ 𝑘=∞ 𝑥 𝑘 ℎ[𝑛 − 𝑘] 𝐶𝑜𝑛𝑣𝑜𝑙𝑢𝑡𝑖𝑜𝑛 𝑖𝑛 2 𝐷𝑖𝑚𝑒𝑛𝑠𝑖𝑜𝑛𝑠: 𝑦 𝑛1, 𝑛2 = 𝑘1=−∞ 𝑘1=−∞ 𝑘2=−∞ 𝑘2=∞ 𝑥 𝑘1, 𝑘2 ℎ[ 𝑛1 − 𝑘1 , 𝑛2 − 𝑘2 ]
• 8.
  CNNs for applicationsthat involve images • Why CNNs are more suitable to process images? • Pixels in an image correlate to each other. However, nearby pixels correlate stronger and distant pixels don’t influence much • Local features are important: Local Receptive Fields • Affine transformations: e.g the class of an image doesn’t change with respect to translation. So we can build a feature detector that can look for a particular feature (e.g an edge) anywhere in the image plane by moving across. A convolutional layer may have several such filters constituting the depth dimension of the layer.
• 9.
  Before we discussCNNs… • CNNs operate on images that have a 2d surface and a depth in terms of RGB colours. Hence they are 3 dimensional. • The standard neural network architecture has a linear input layer structure. • When we discuss CNN architecture, it helps to decouple in our minds the abstraction CNNs deal with and the practical realization of these principles on a linear layer based neural network architectures.
• 10.
  CNN Architecture –Refer Slides from Andrej Karpathy’s course (Stanford)
• 11.
  FNN to CNN:Conceptual Understanding • Inputs • The input layer of FNN is a linear arrangement of input elements. This is typically represented as an input vector. • CNNs operate on a 3d input “volume”. • Hidden Layers of the architecture • Neural networks use one or more hidden layers with the units typically performing some non linear transformations (e.g tanh) • Convolutional networks use: convolutional layers and pooling layers • Local receptive fields and shared weights for a given filter across the complete input • Strides • Filters arranged depthwise: small size • Output layer • In a traditional NN the output layer (such as Softmax or Logistic) connect to the linear hidden layer in a fully connected pattern • CNNs follow a similar pattern where the “volume” represented by the final internal layer is fully connected to the output layer