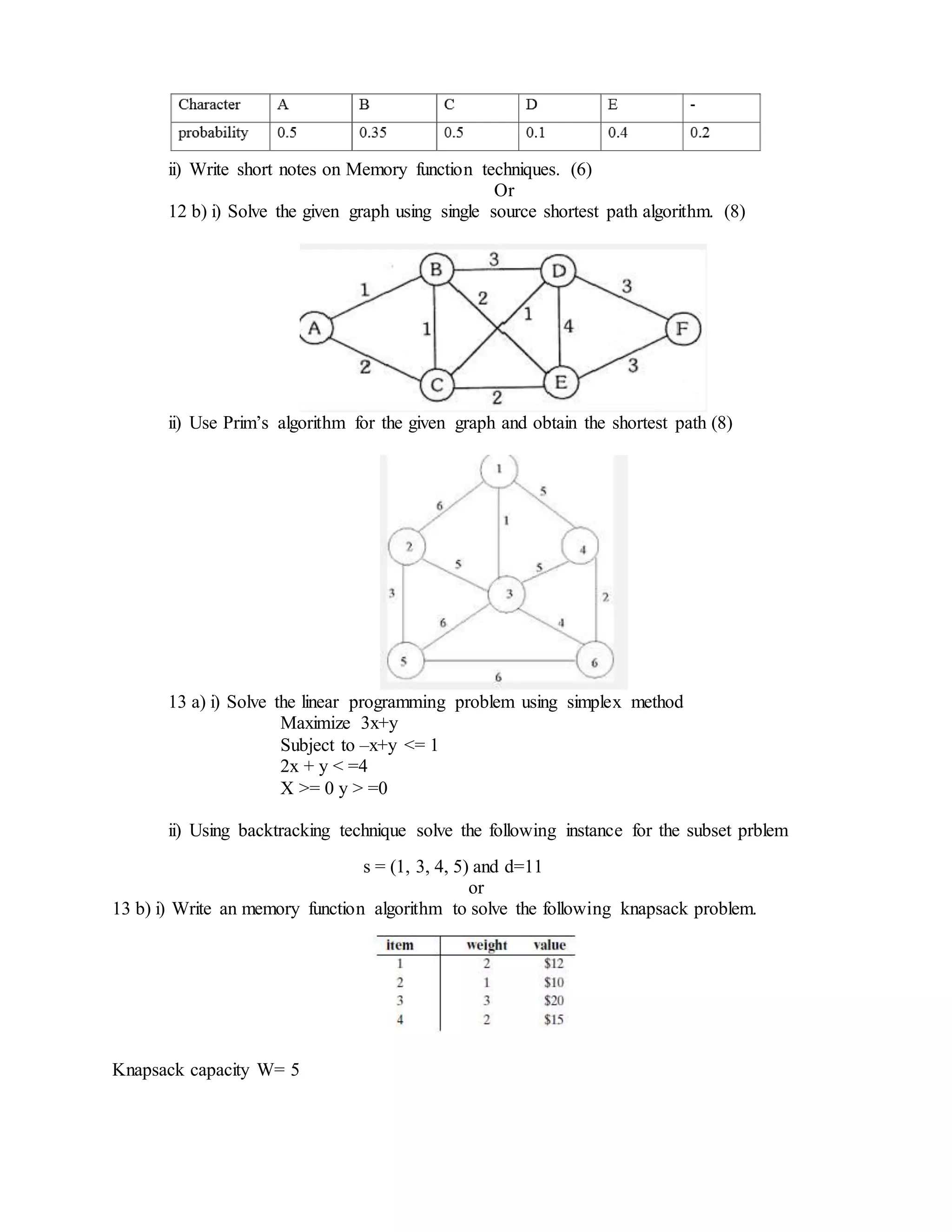
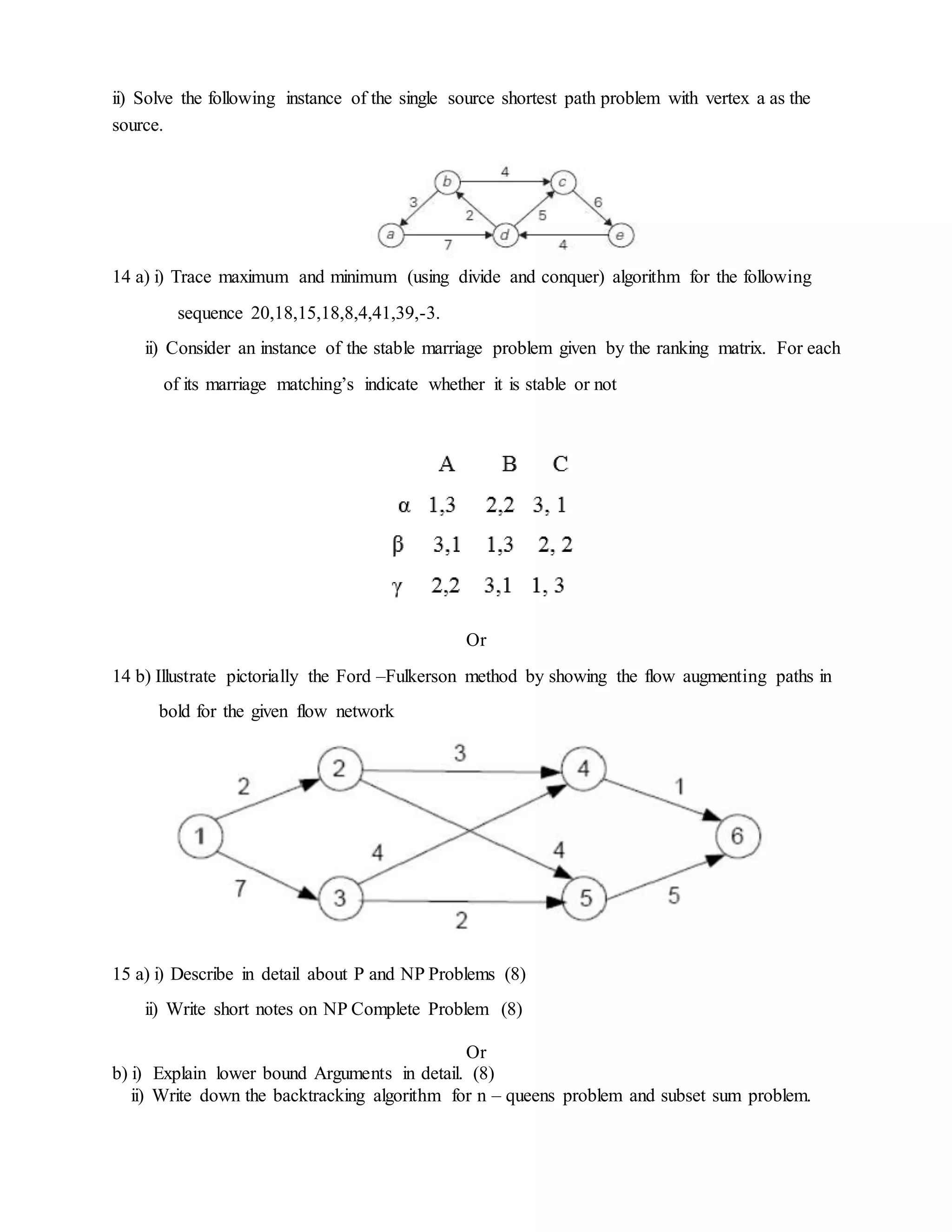
This document contains a past exam paper for the subject "Design and Analysis of Algorithms". It has 2 parts with a total of 15 questions. Part A covers basic algorithm concepts like recurrence relations, efficiency classes, minimum spanning trees, and more. Part B involves solving algorithm problems using techniques like dynamic programming, Huffman coding, shortest paths, and more. It also tests concepts like P vs NP, approximation algorithms, and analysis of algorithm efficiency.