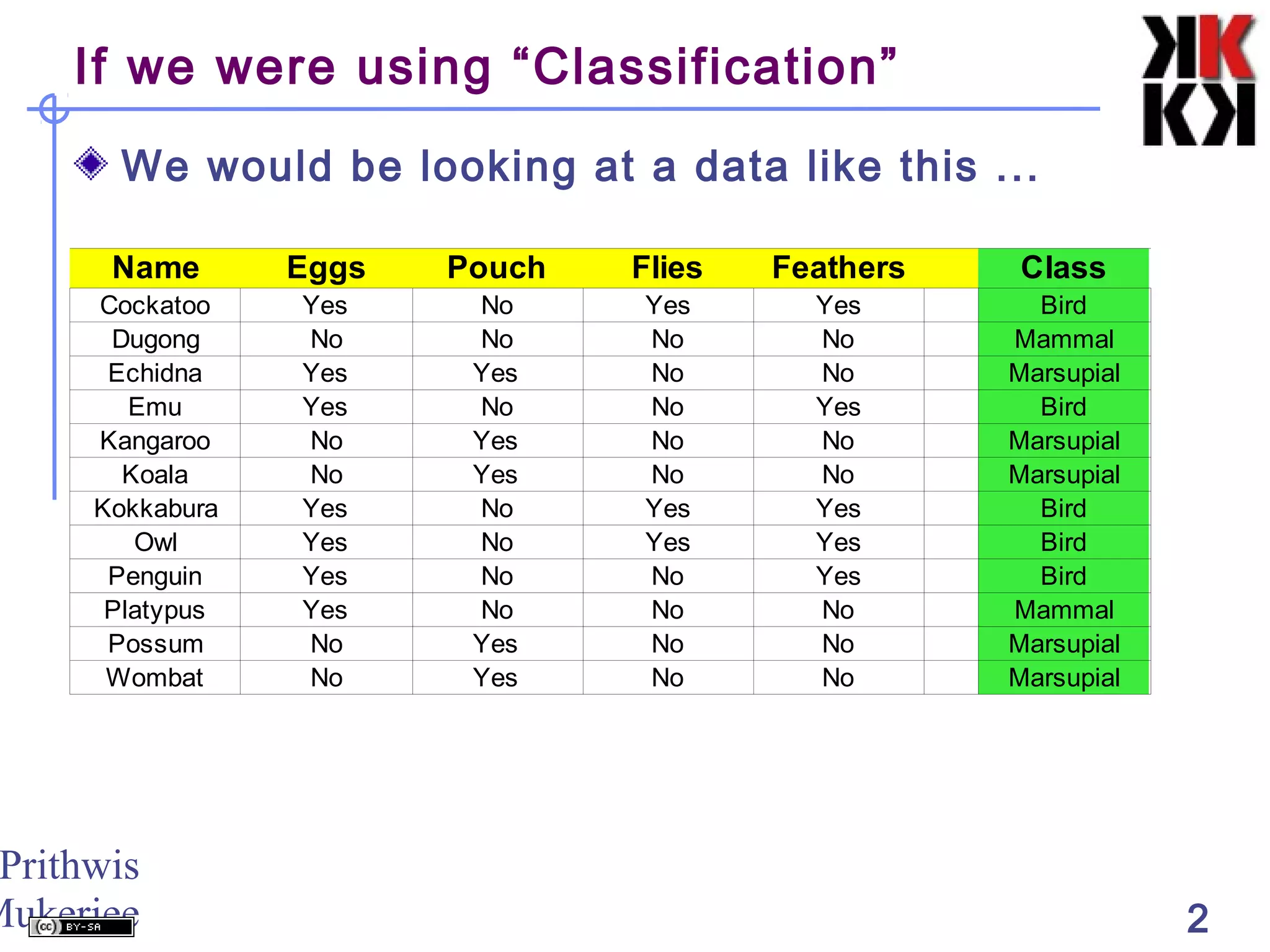
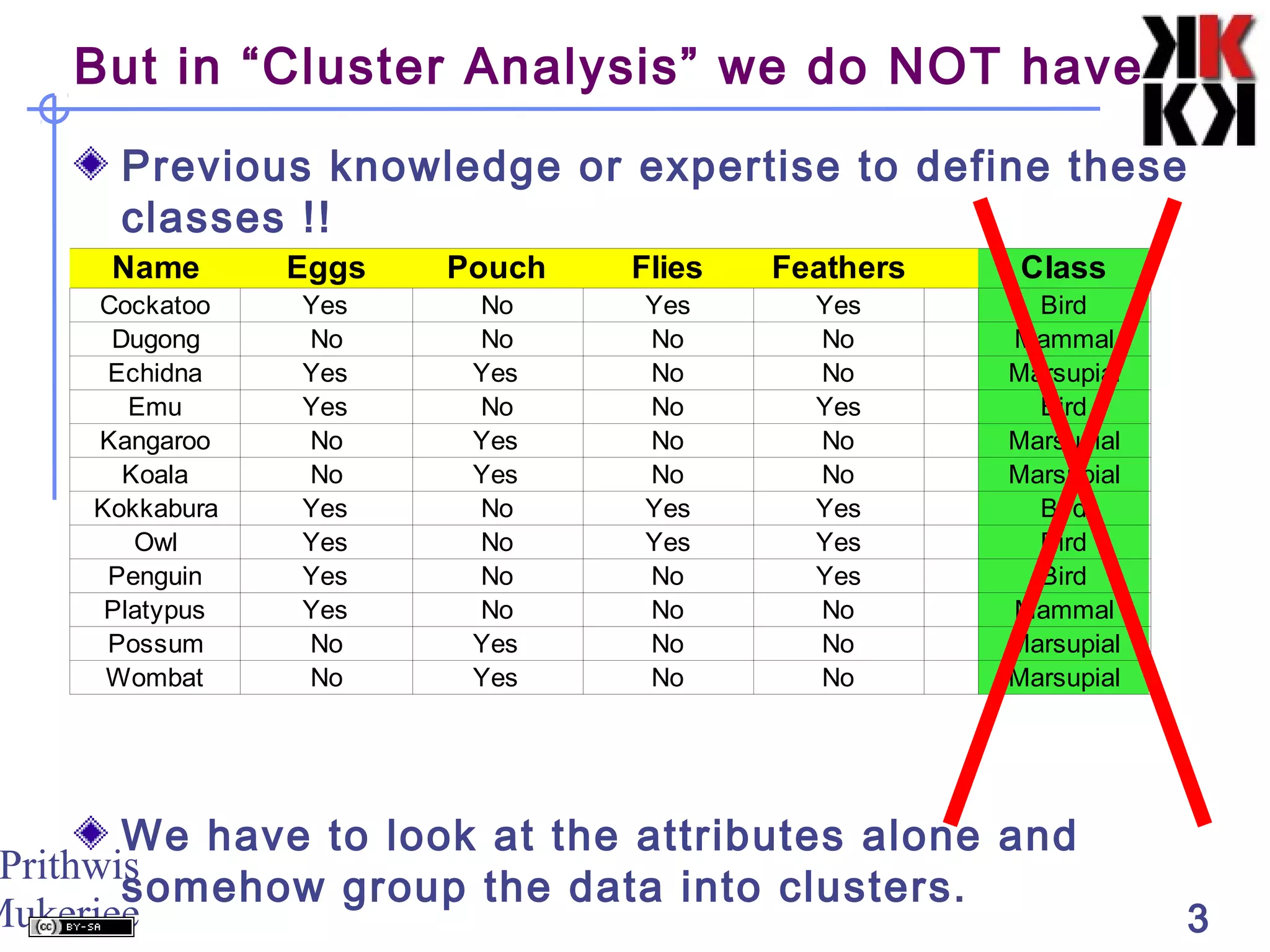
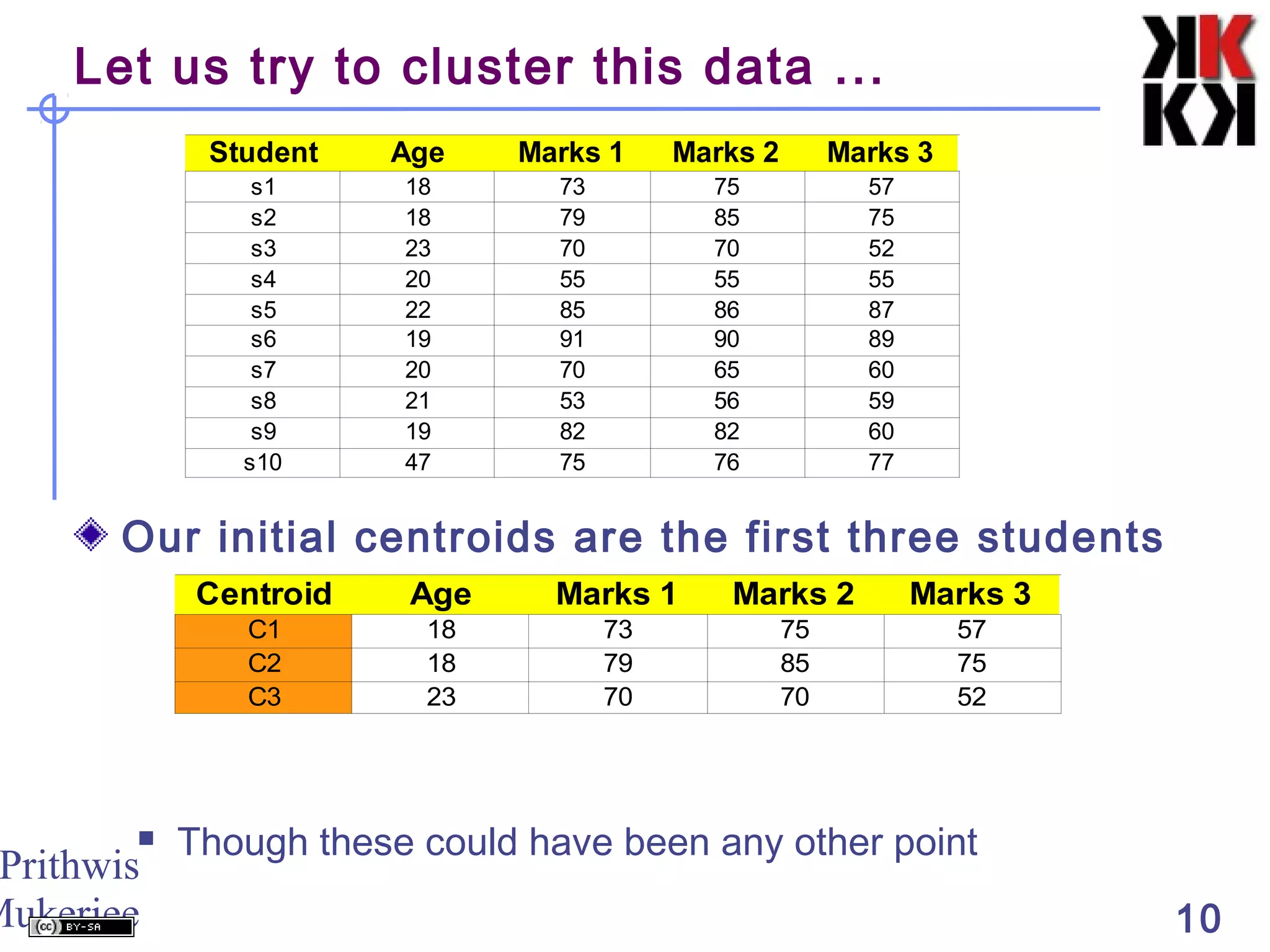
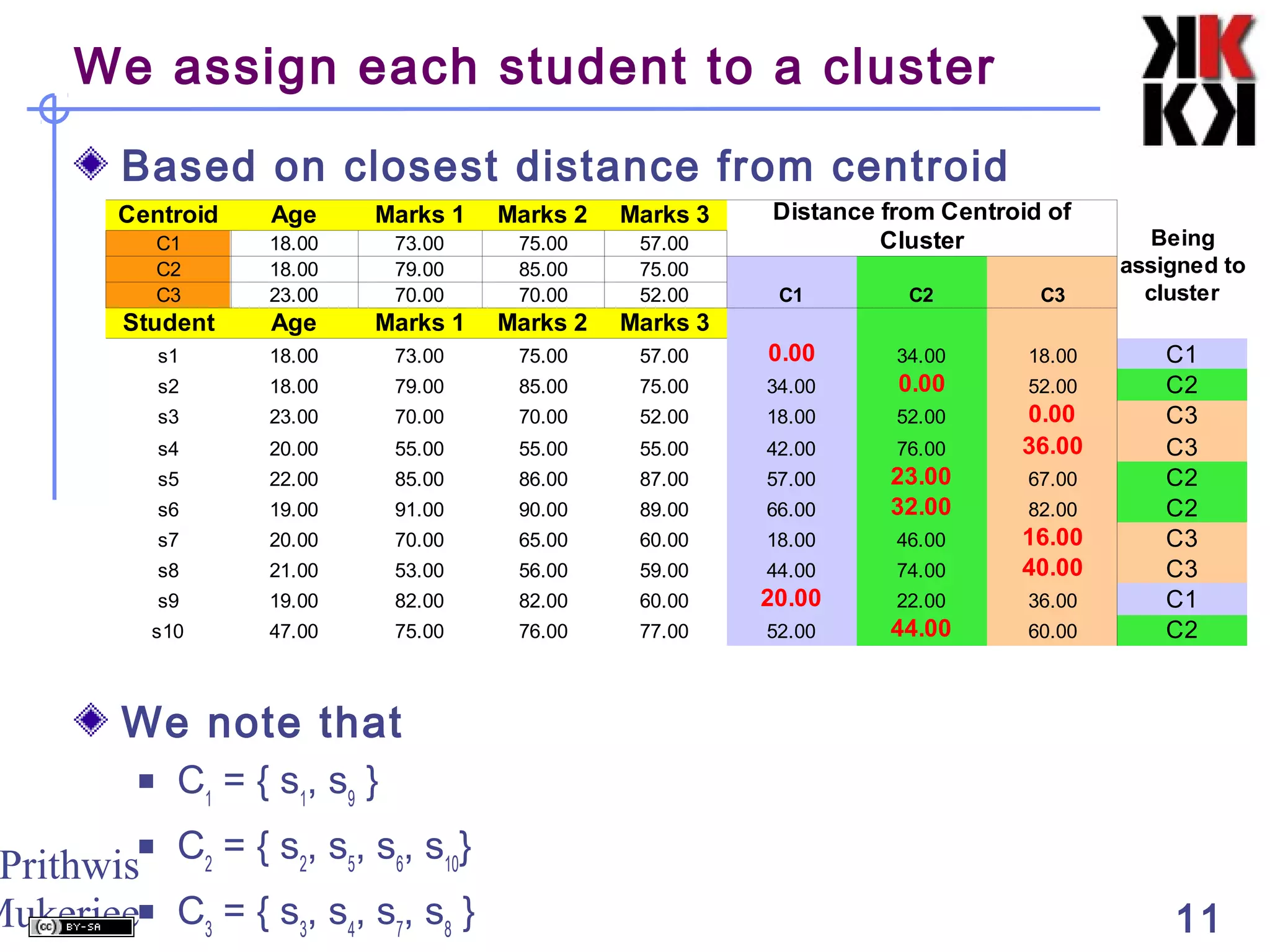
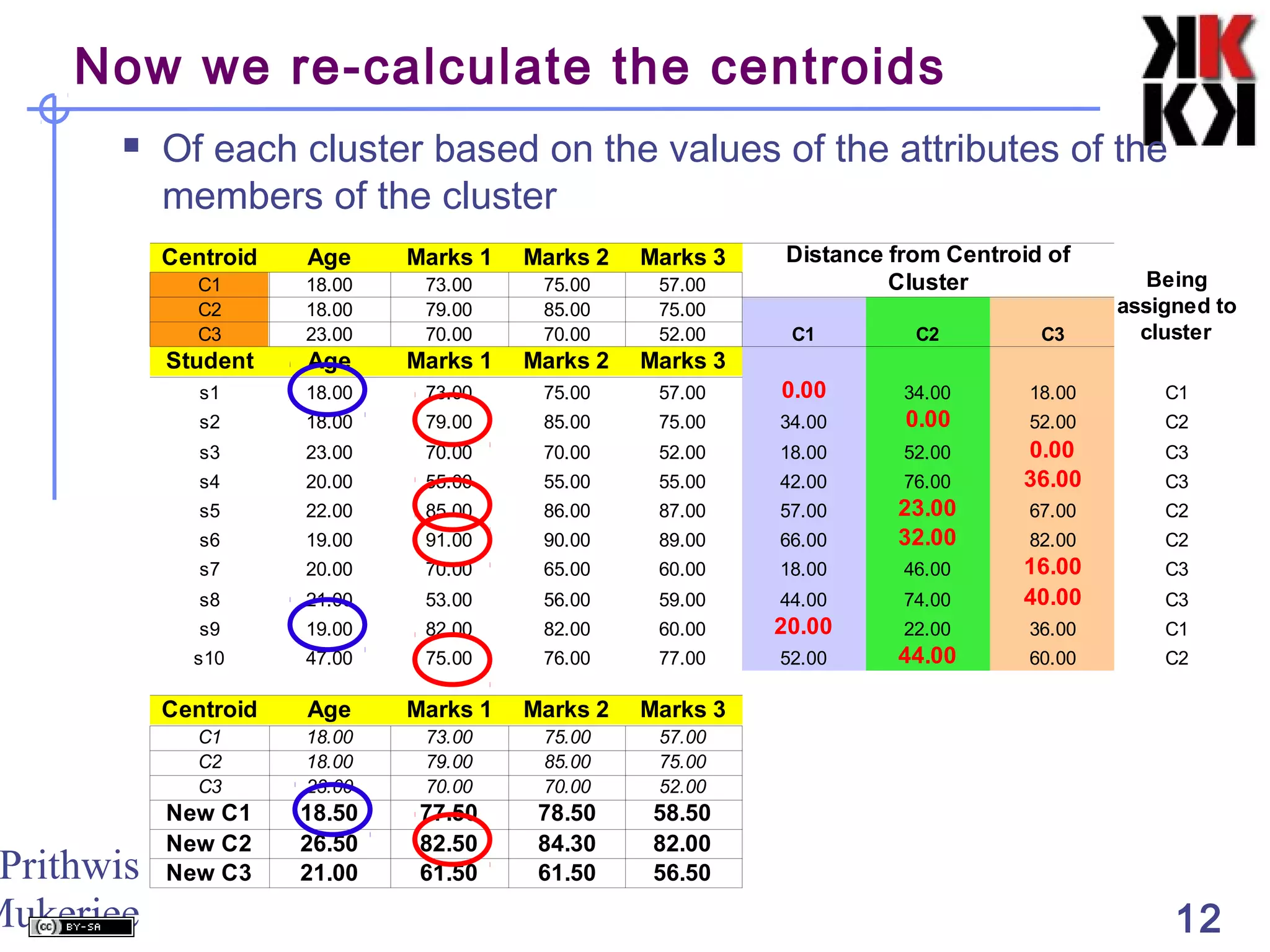
This document discusses cluster analysis, an unsupervised machine learning technique. It begins by explaining that cluster analysis differs from classification in that it does not rely on predefined classes, but instead aims to group similar objects into clusters based solely on their attribute values. It then covers key aspects of cluster analysis, including how to calculate distance between objects, common distance metrics, and partitioning clustering methods like k-means which assign objects to clusters iteratively until cluster membership stabilizes.