Downloaded 55 times
Uploaded byMachine Learning Valencia
L13. Cluster Analysis
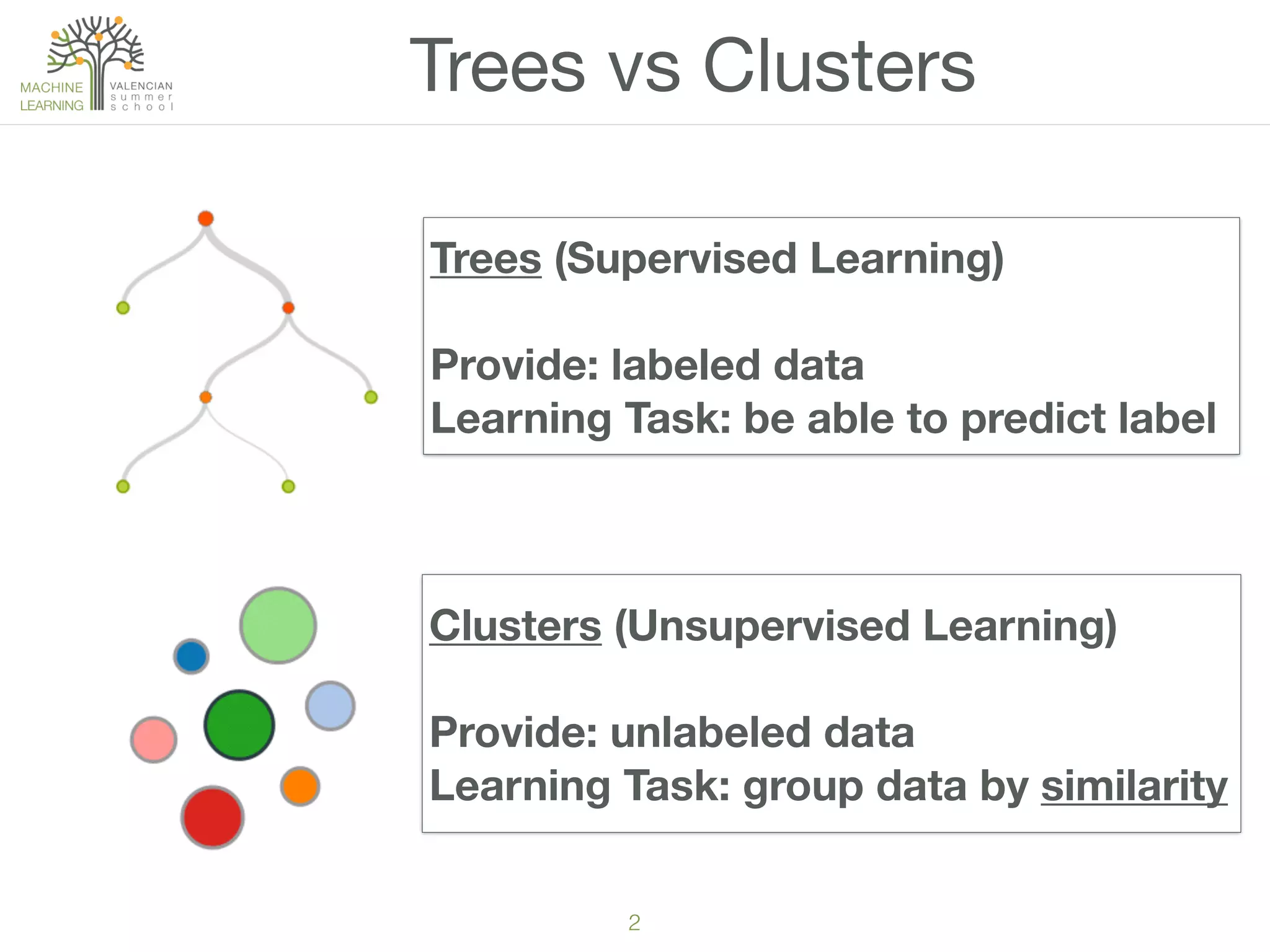
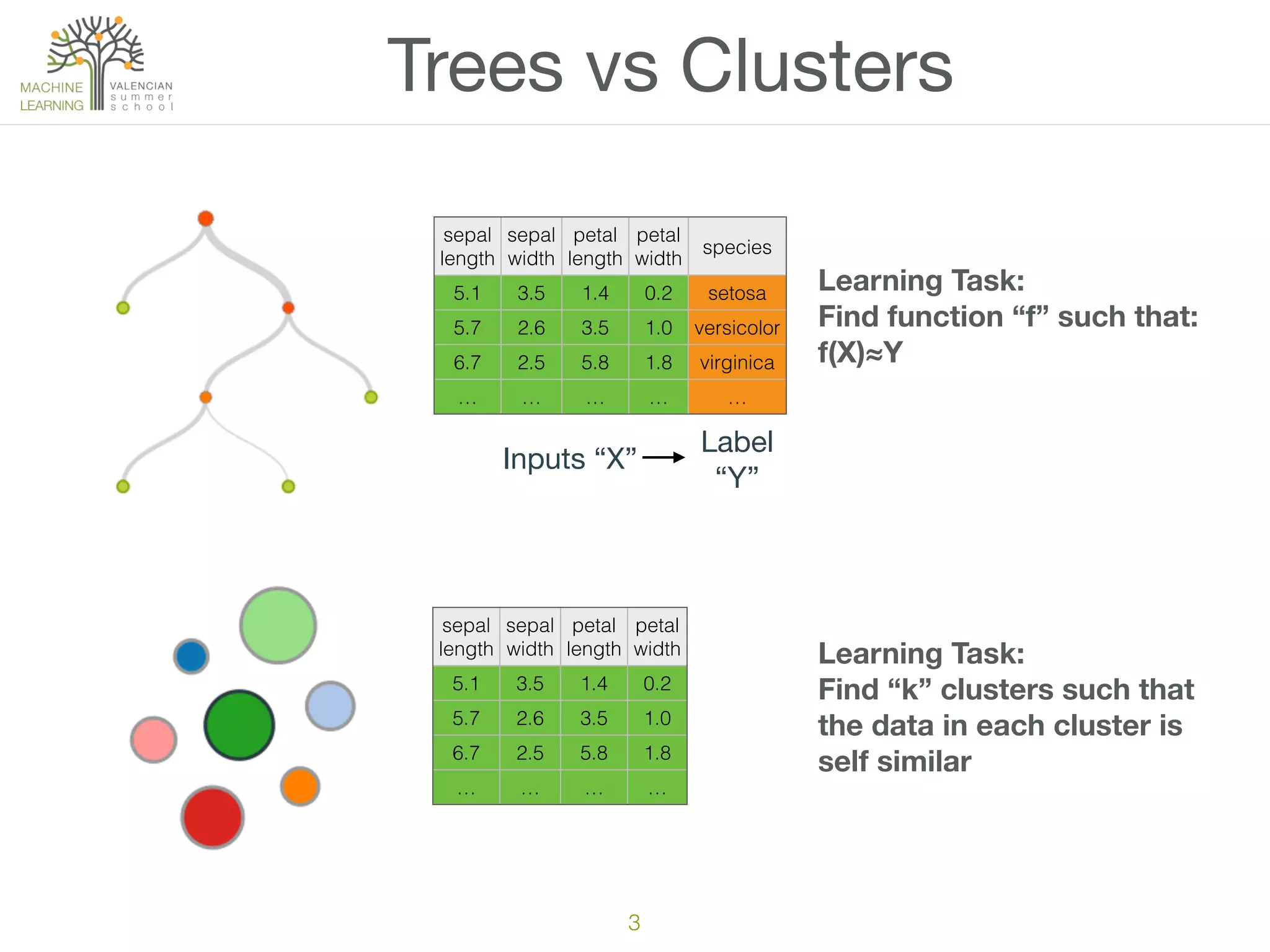
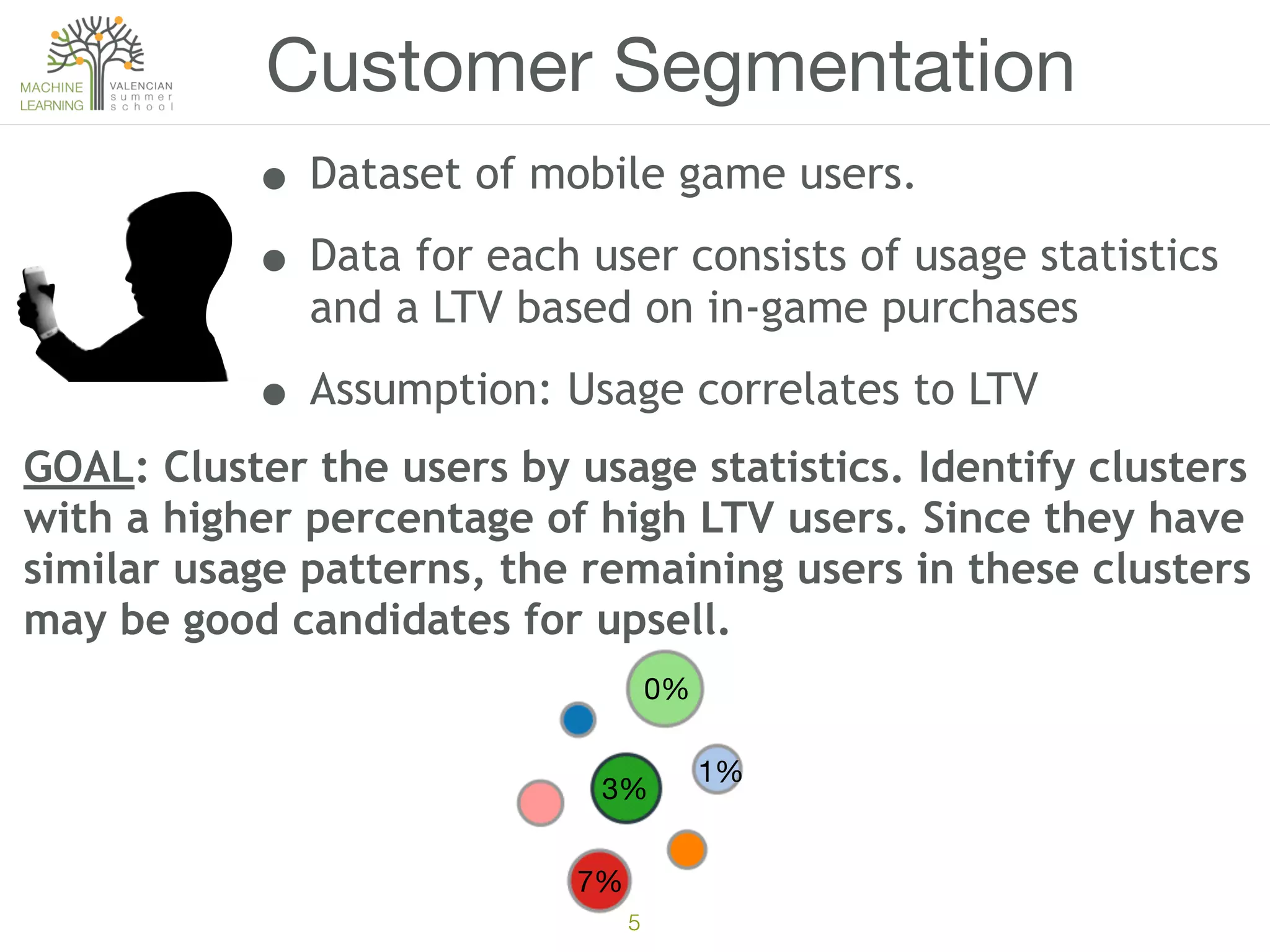
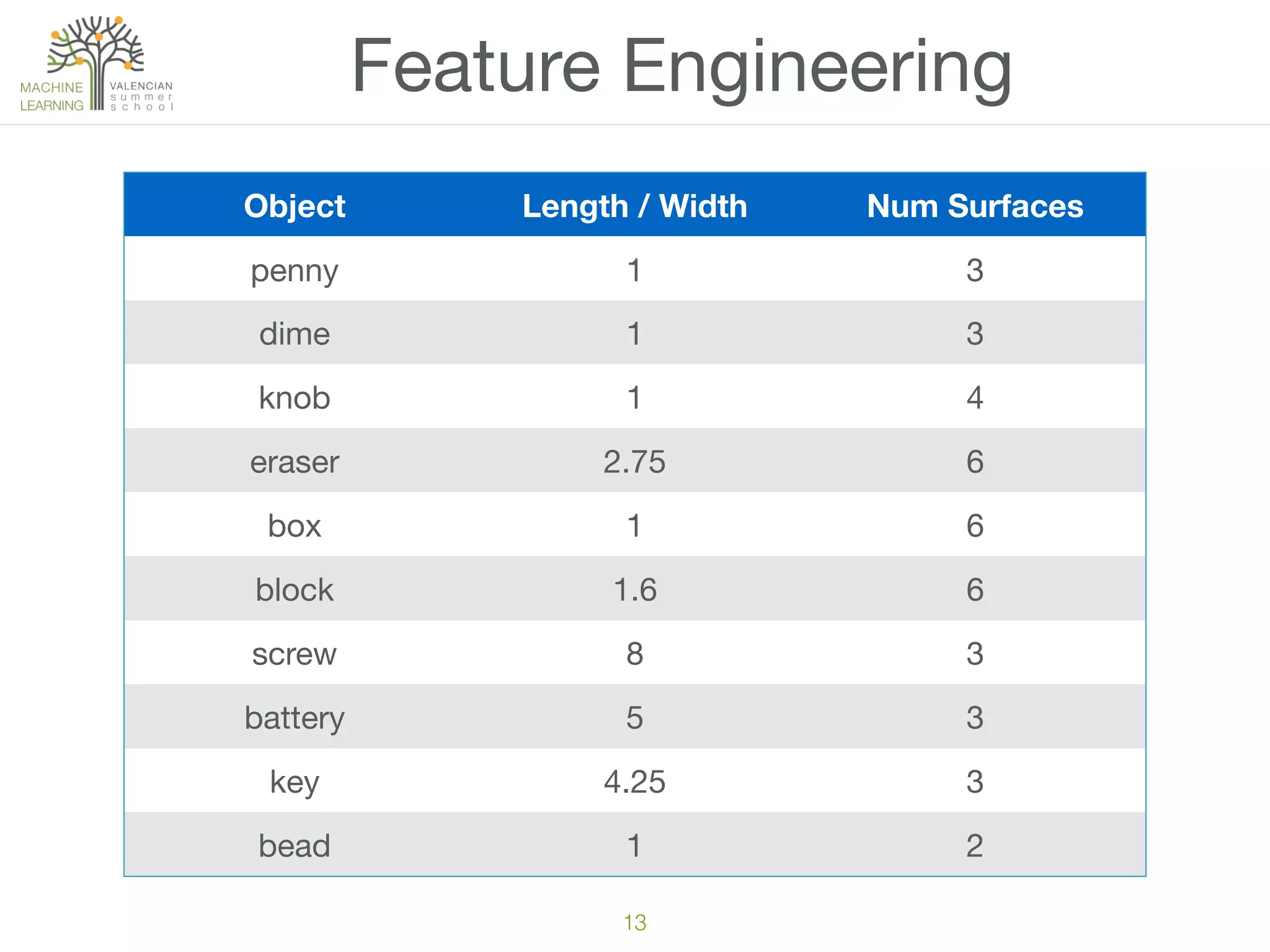
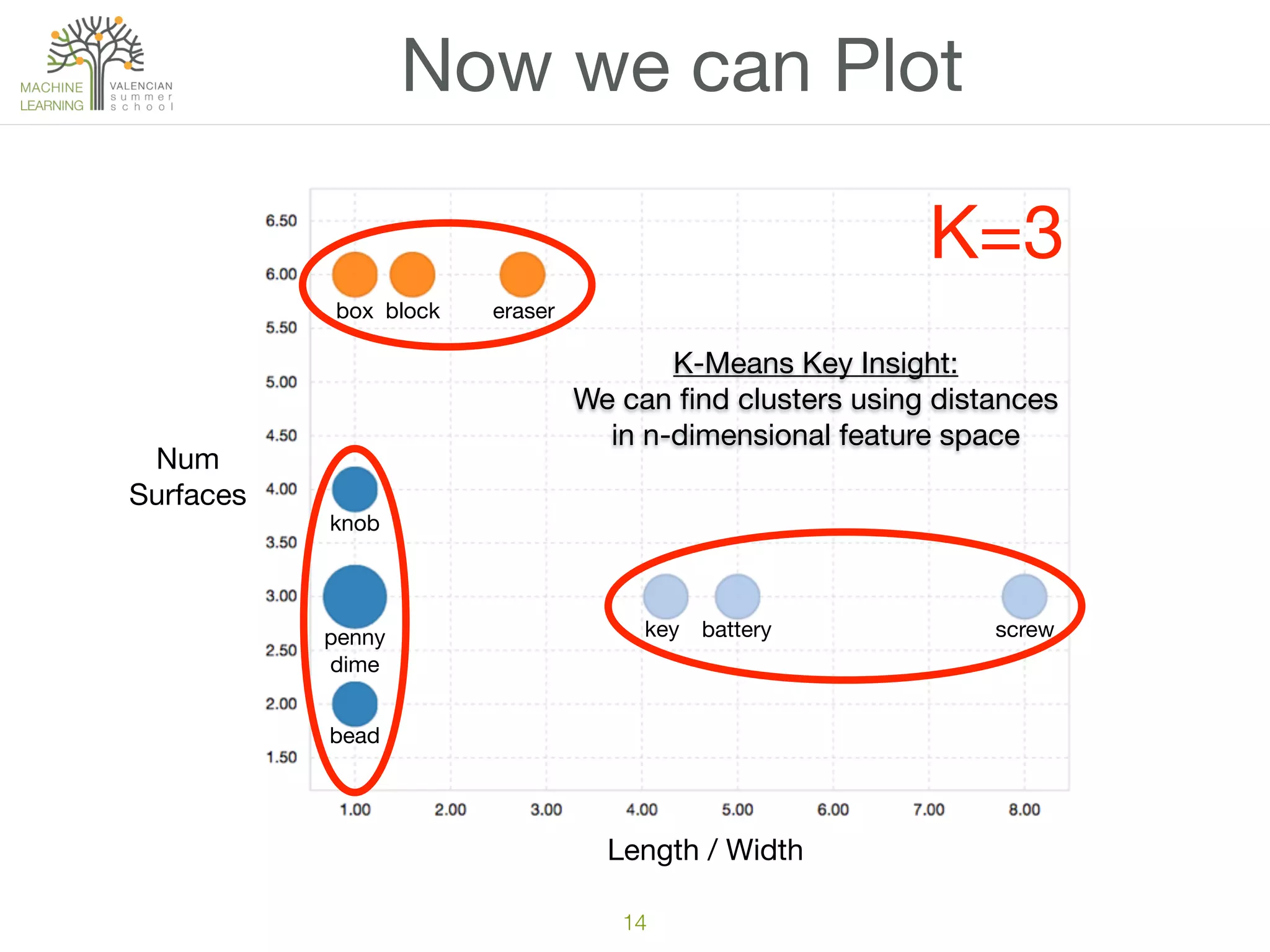
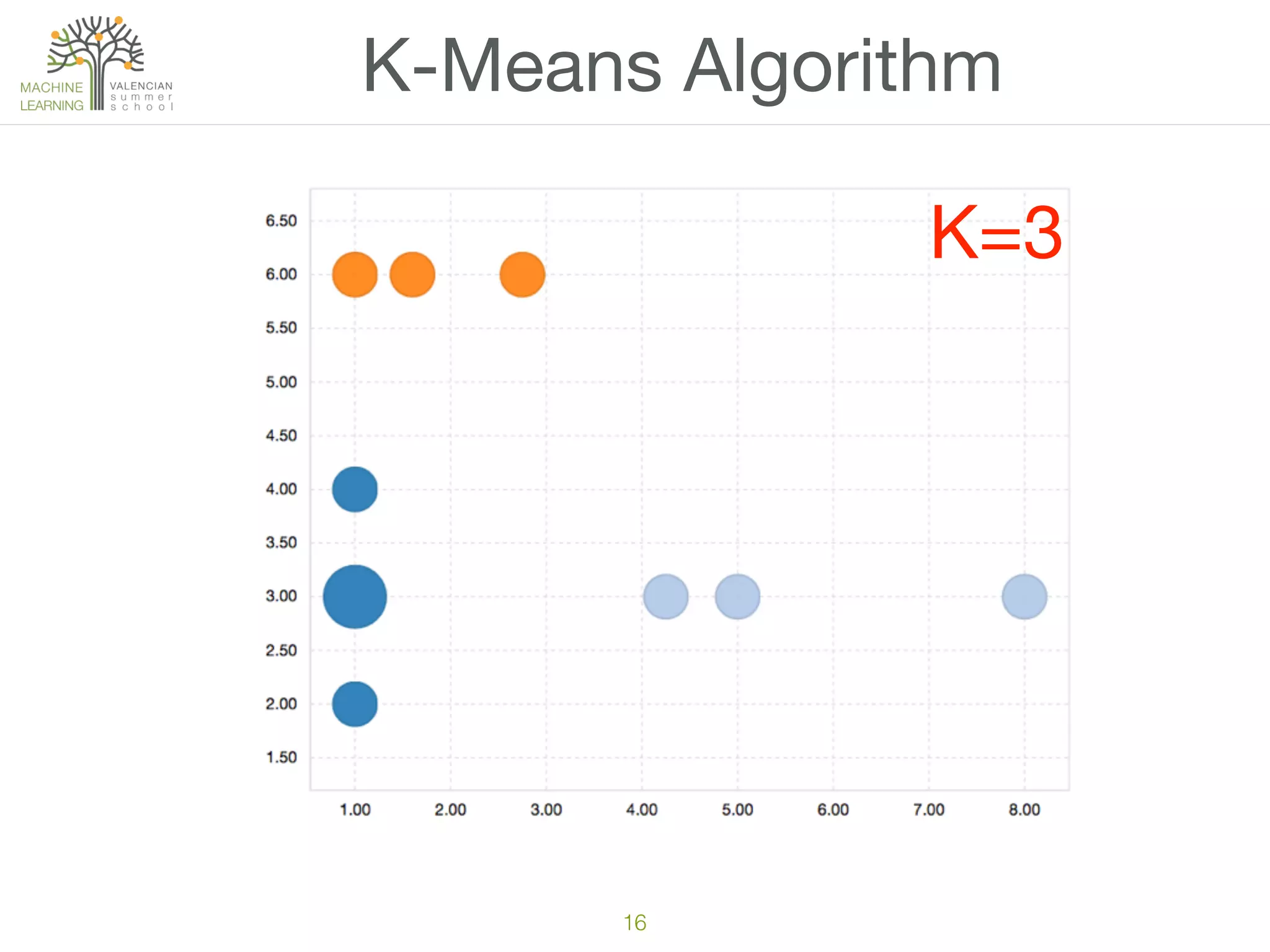
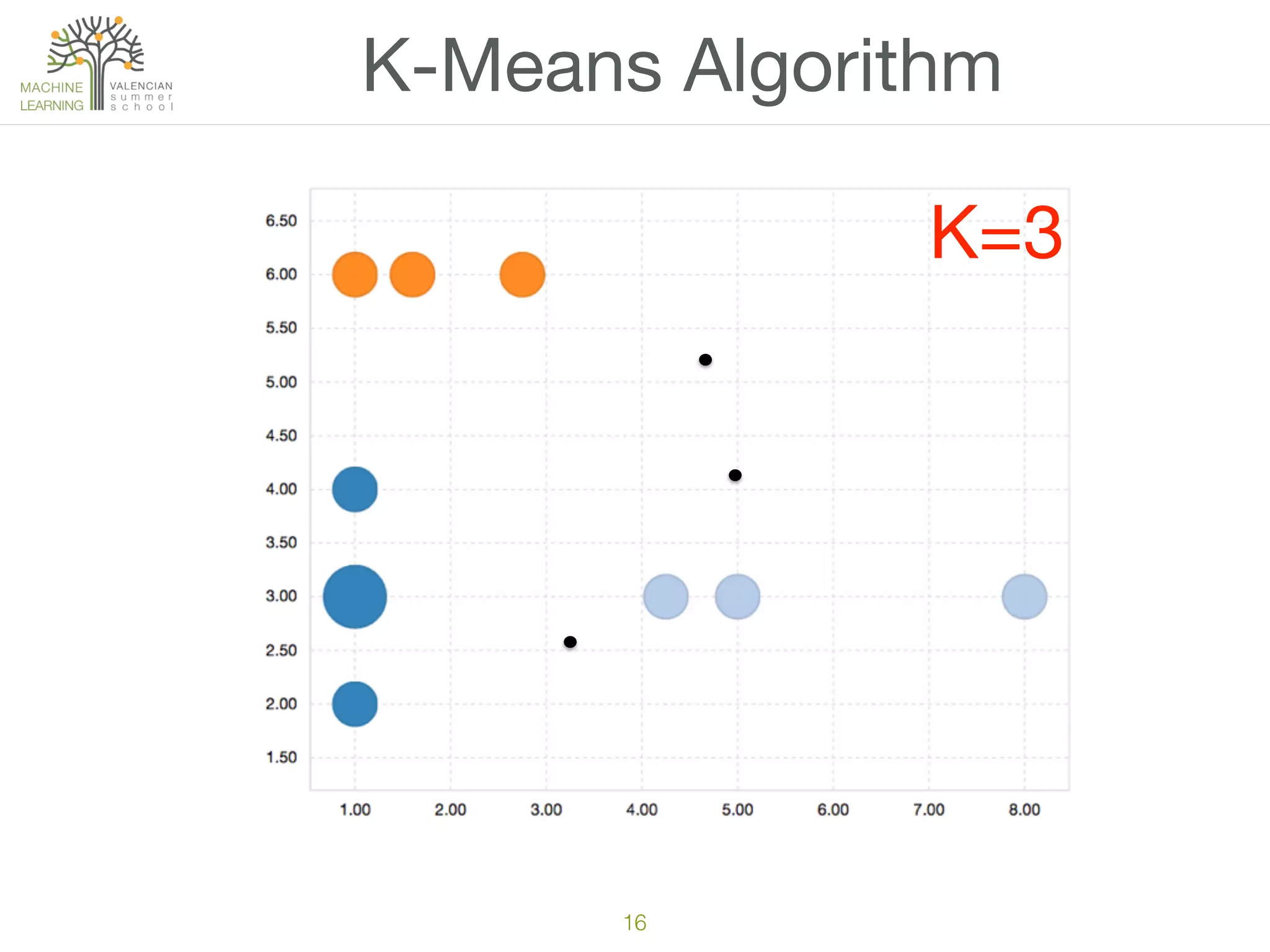
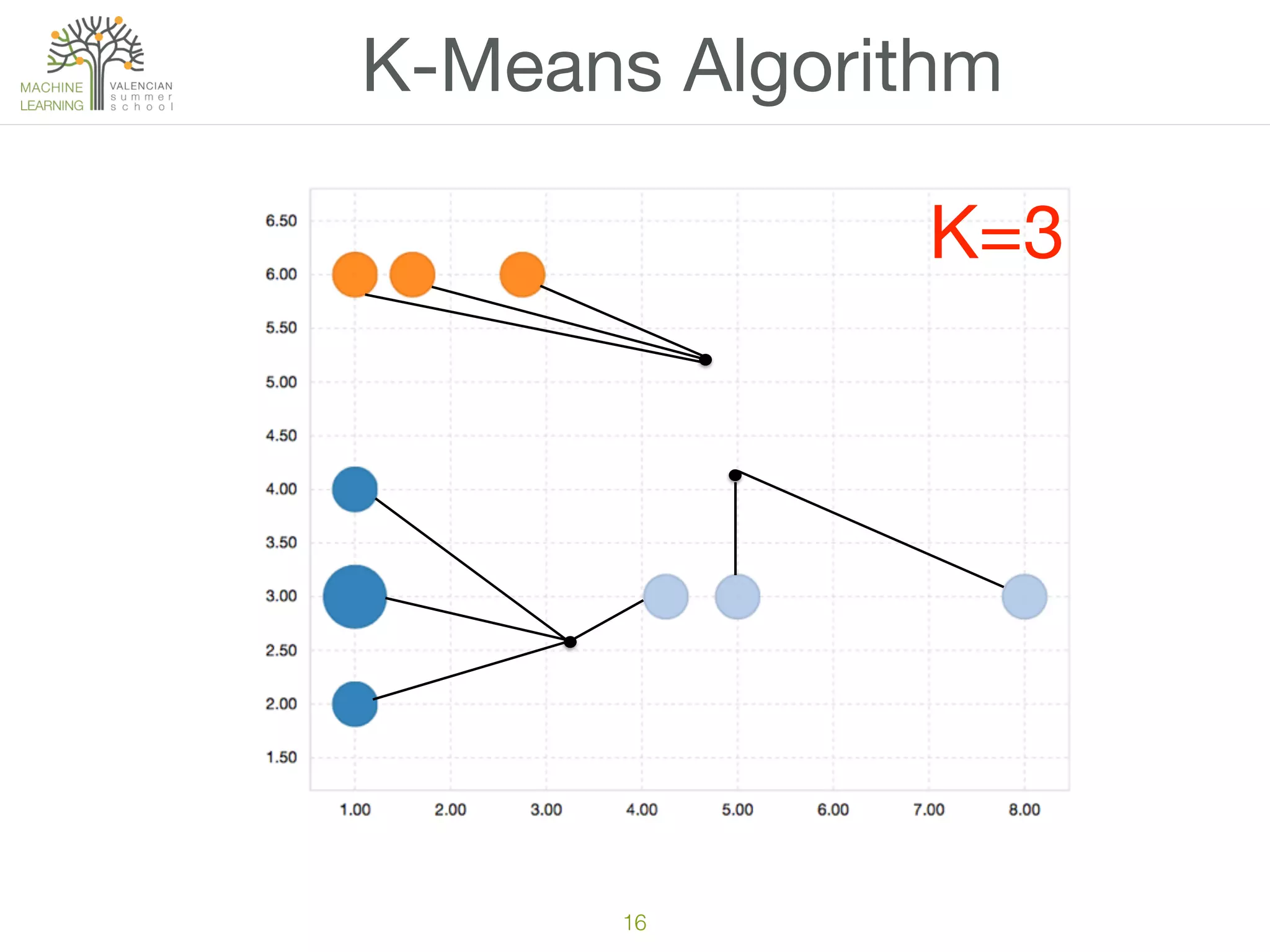
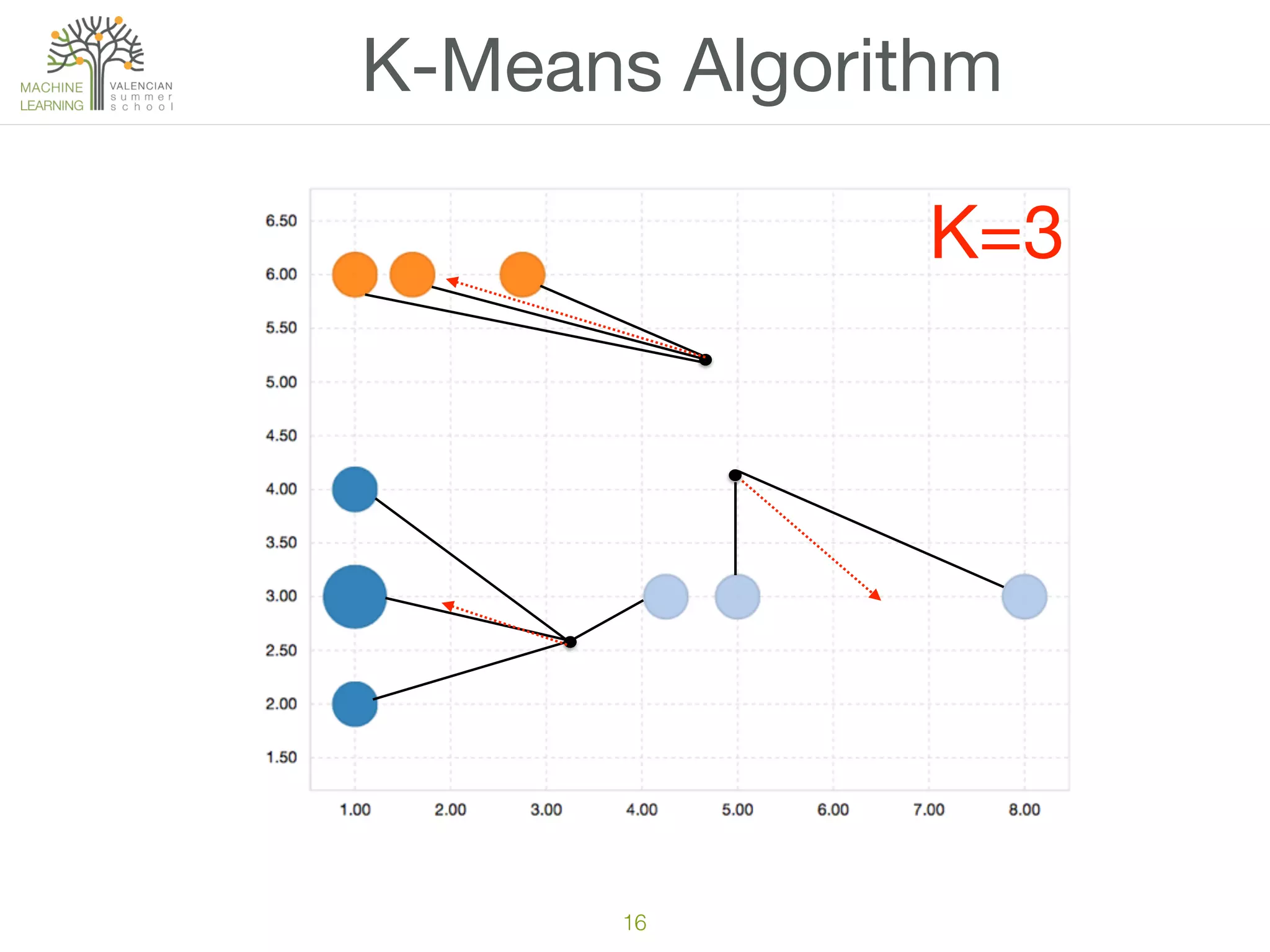
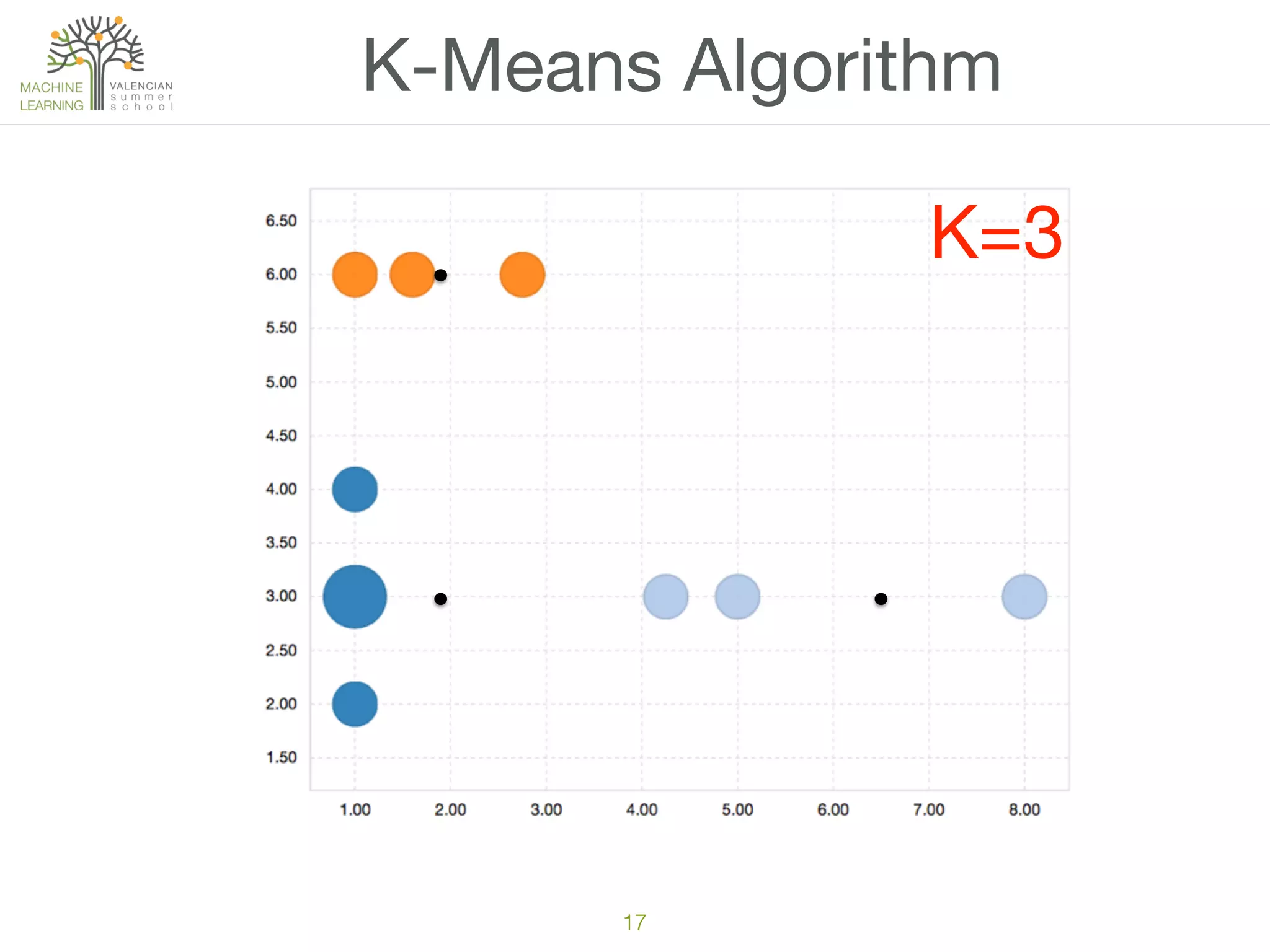
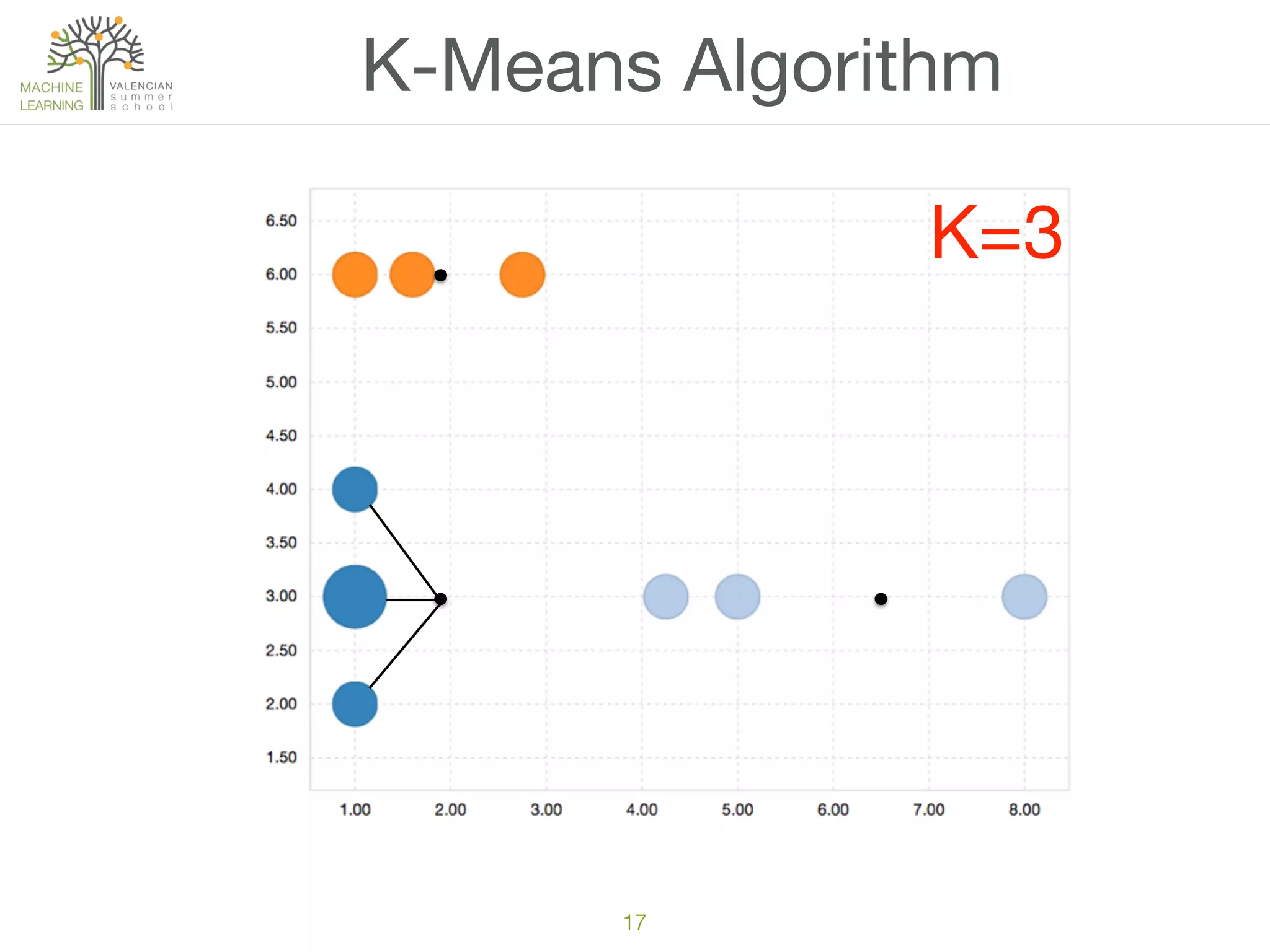
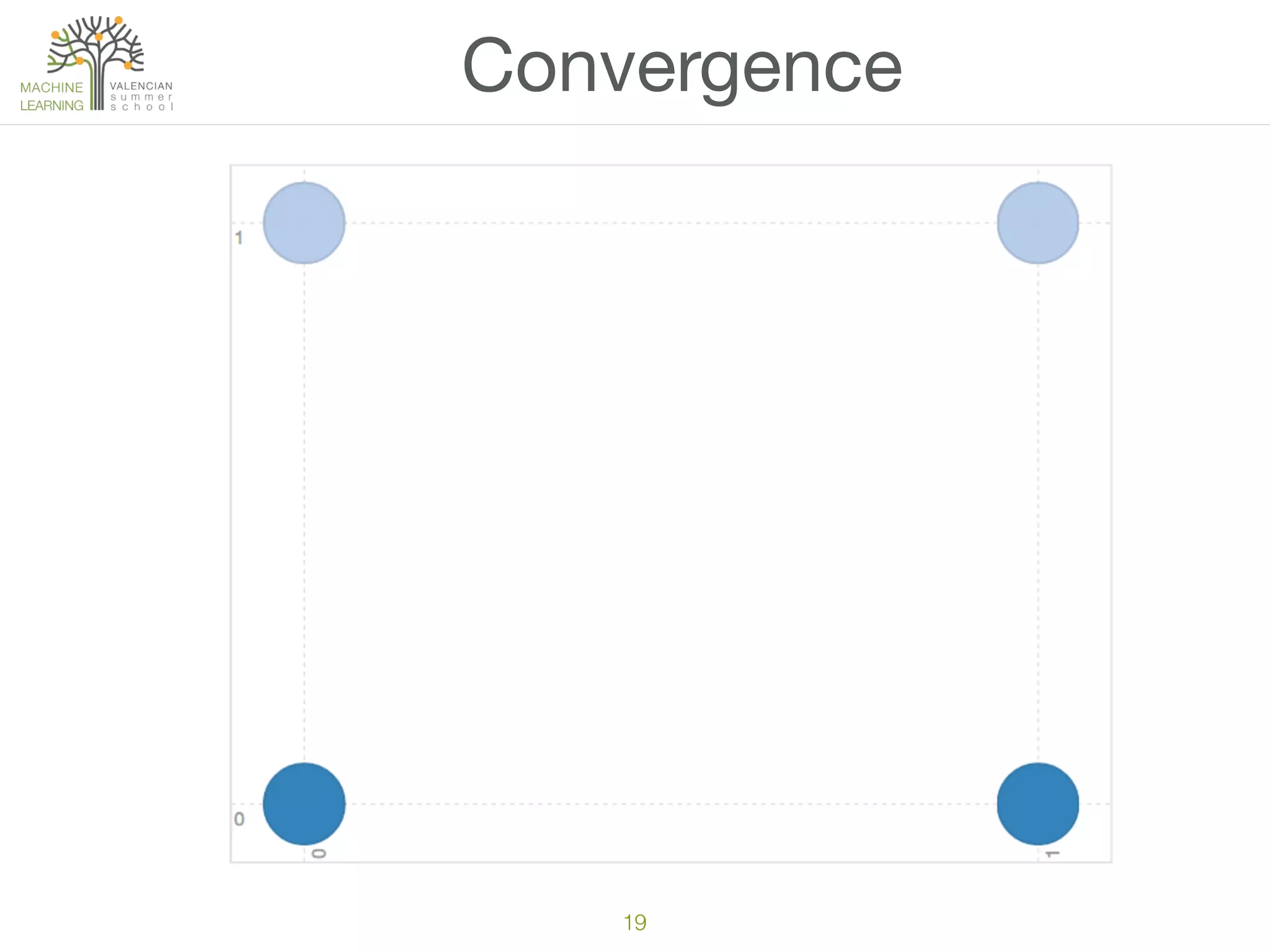
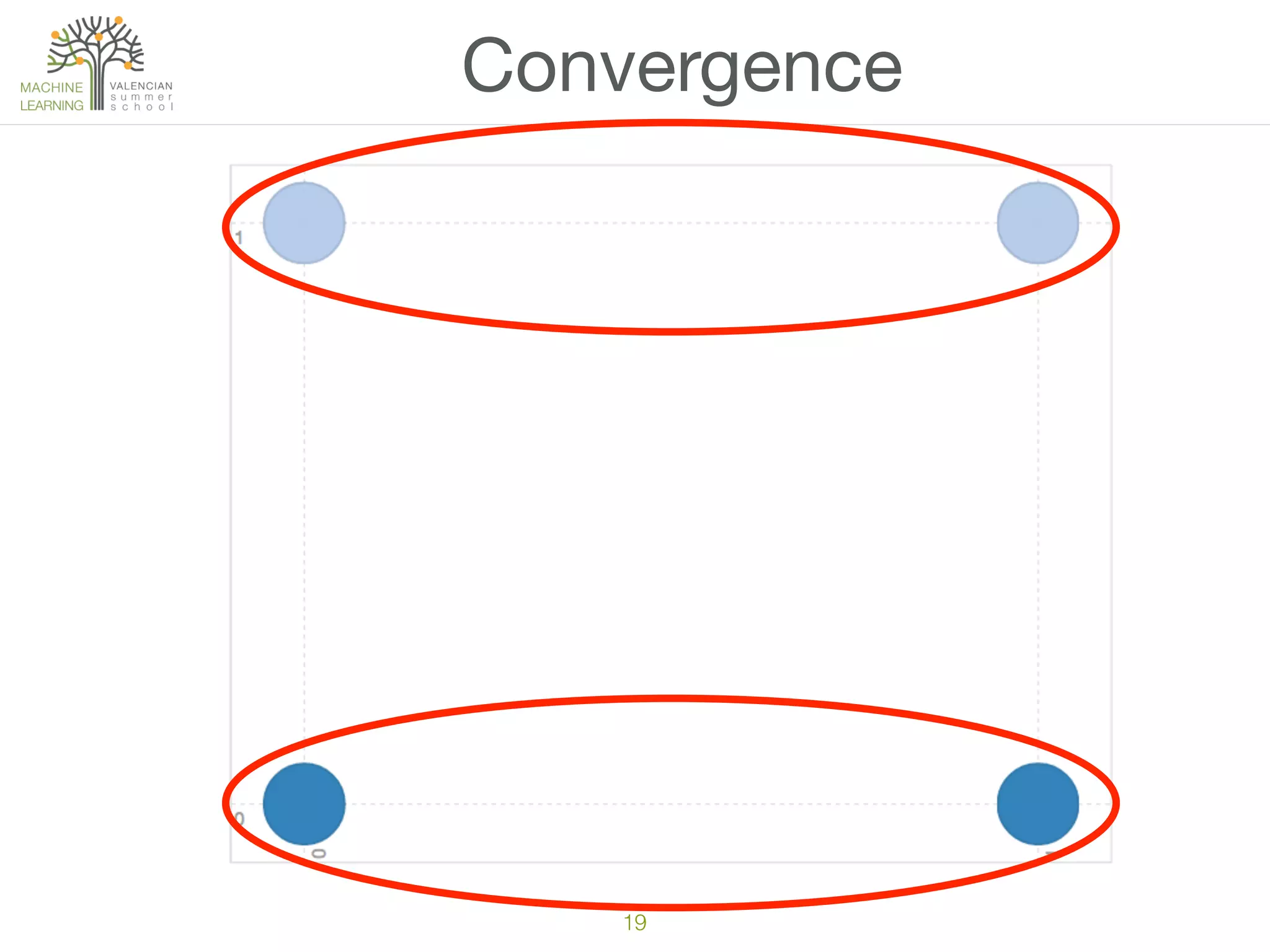
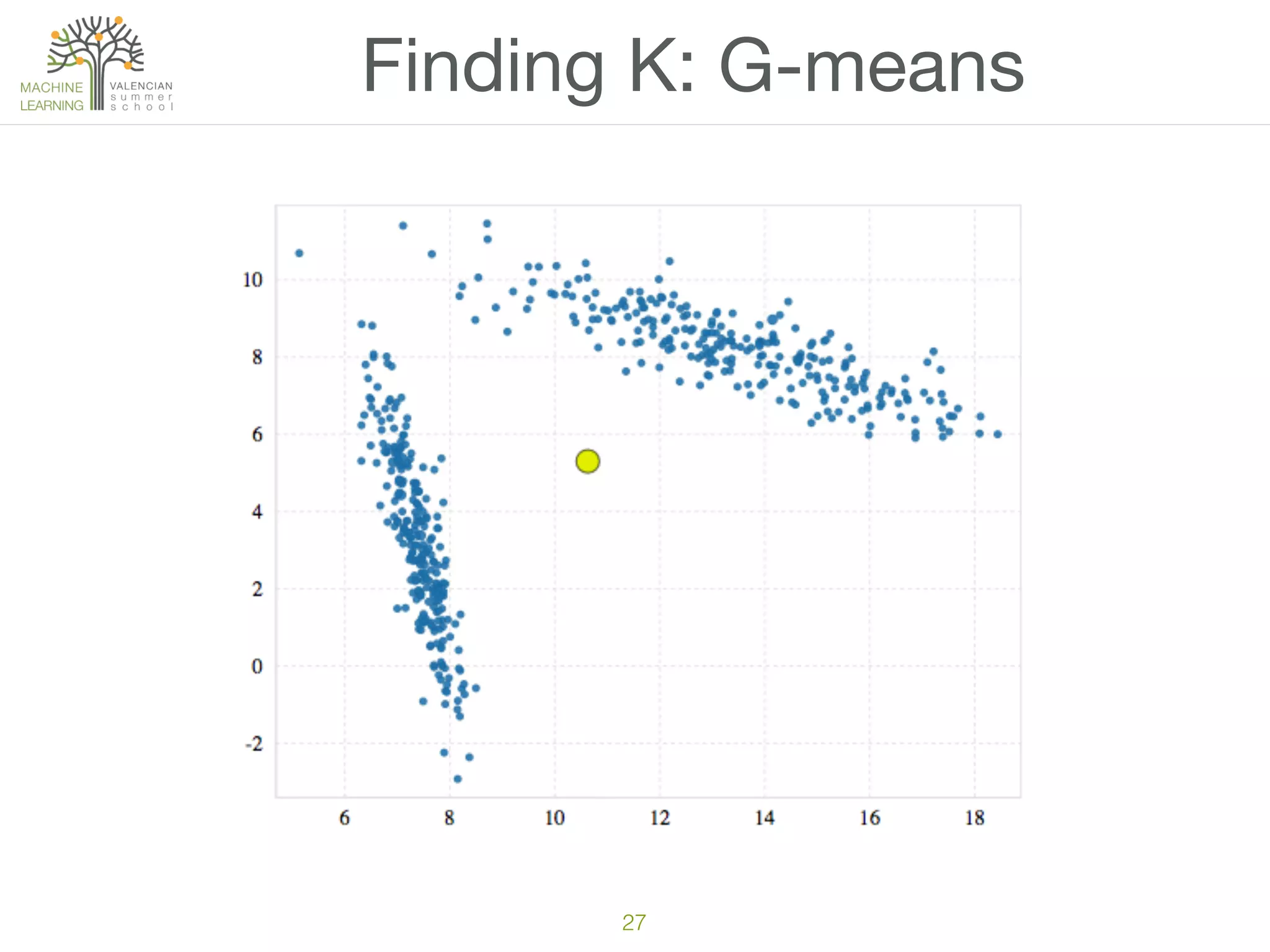
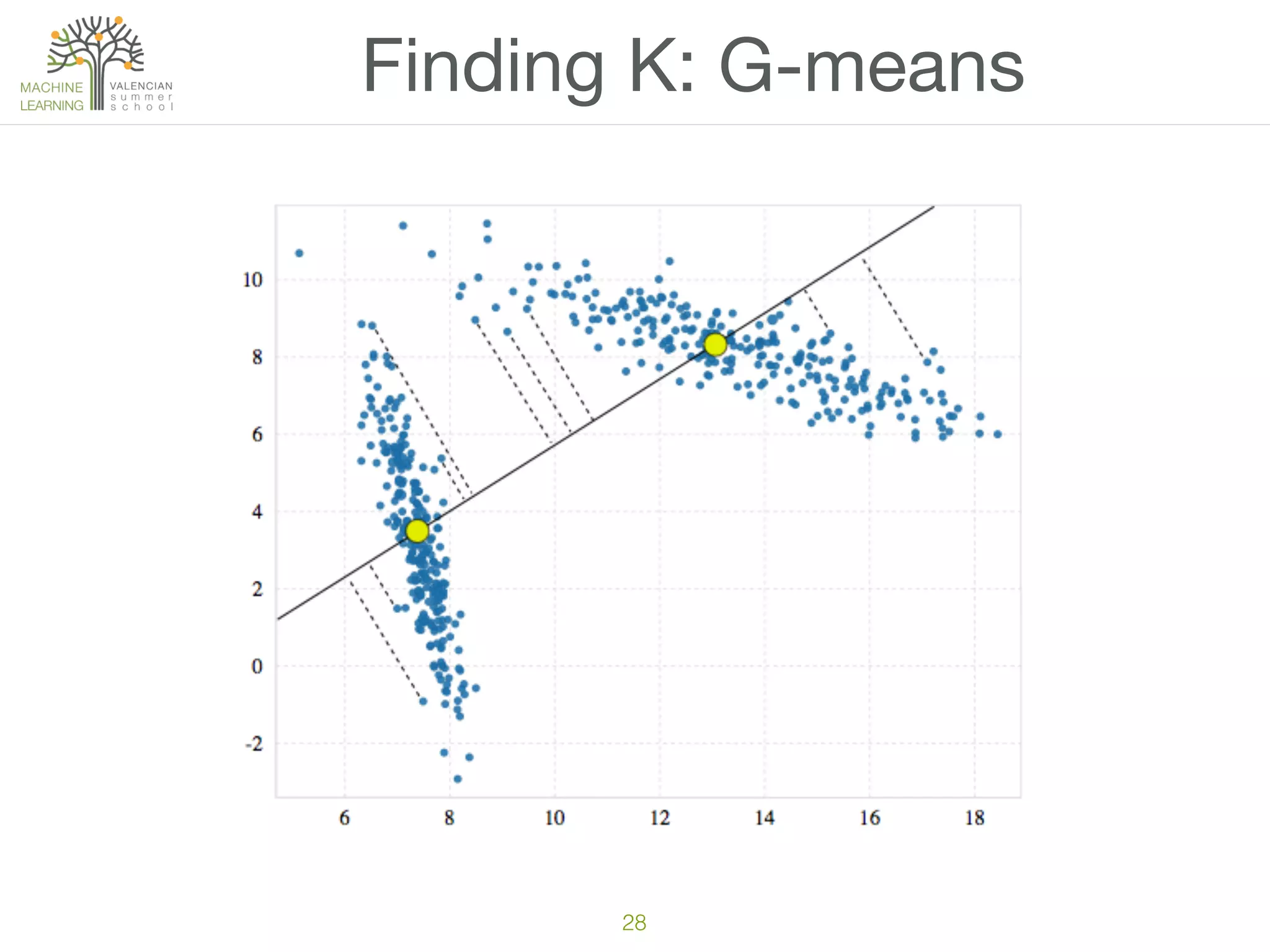
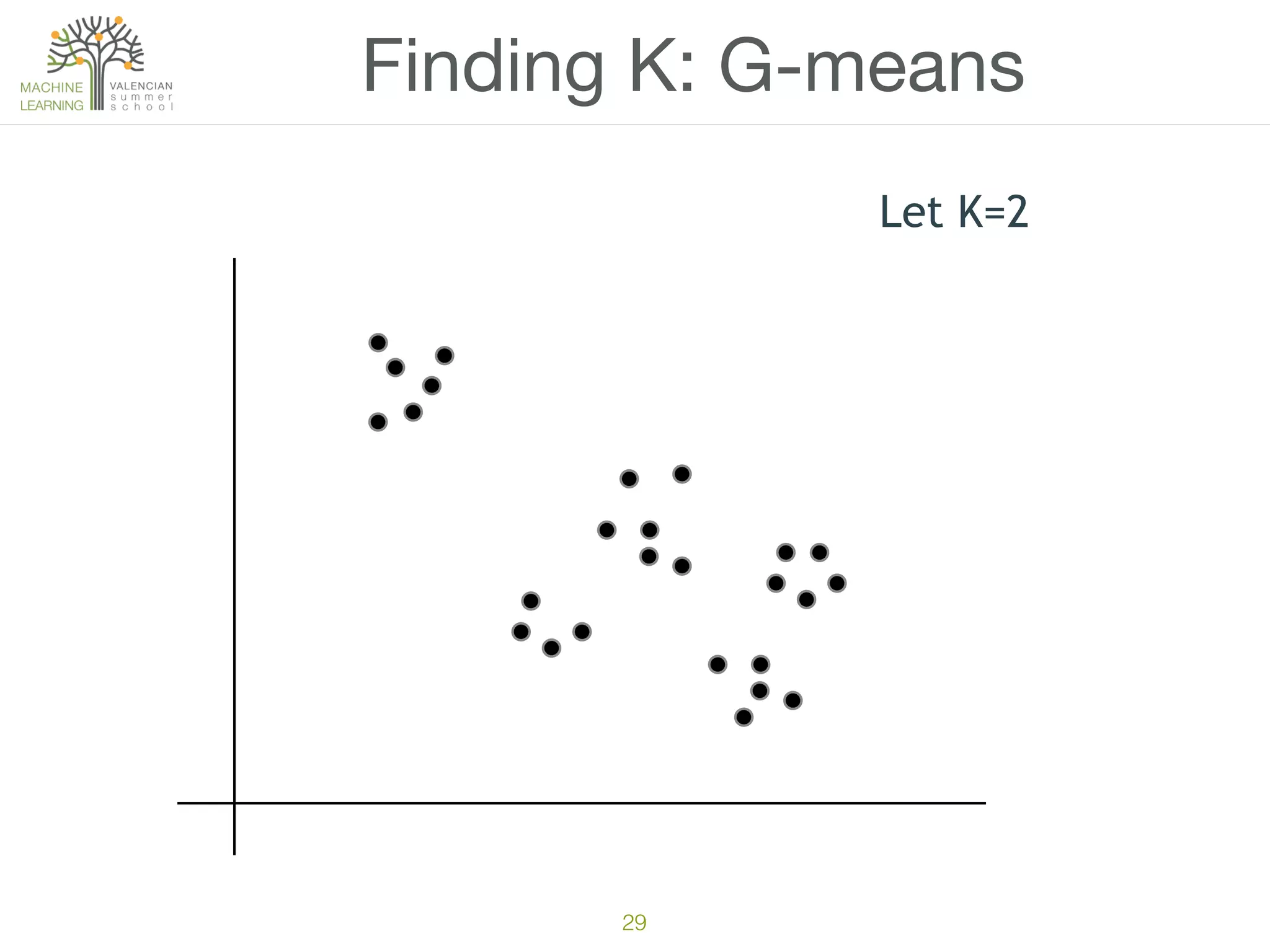
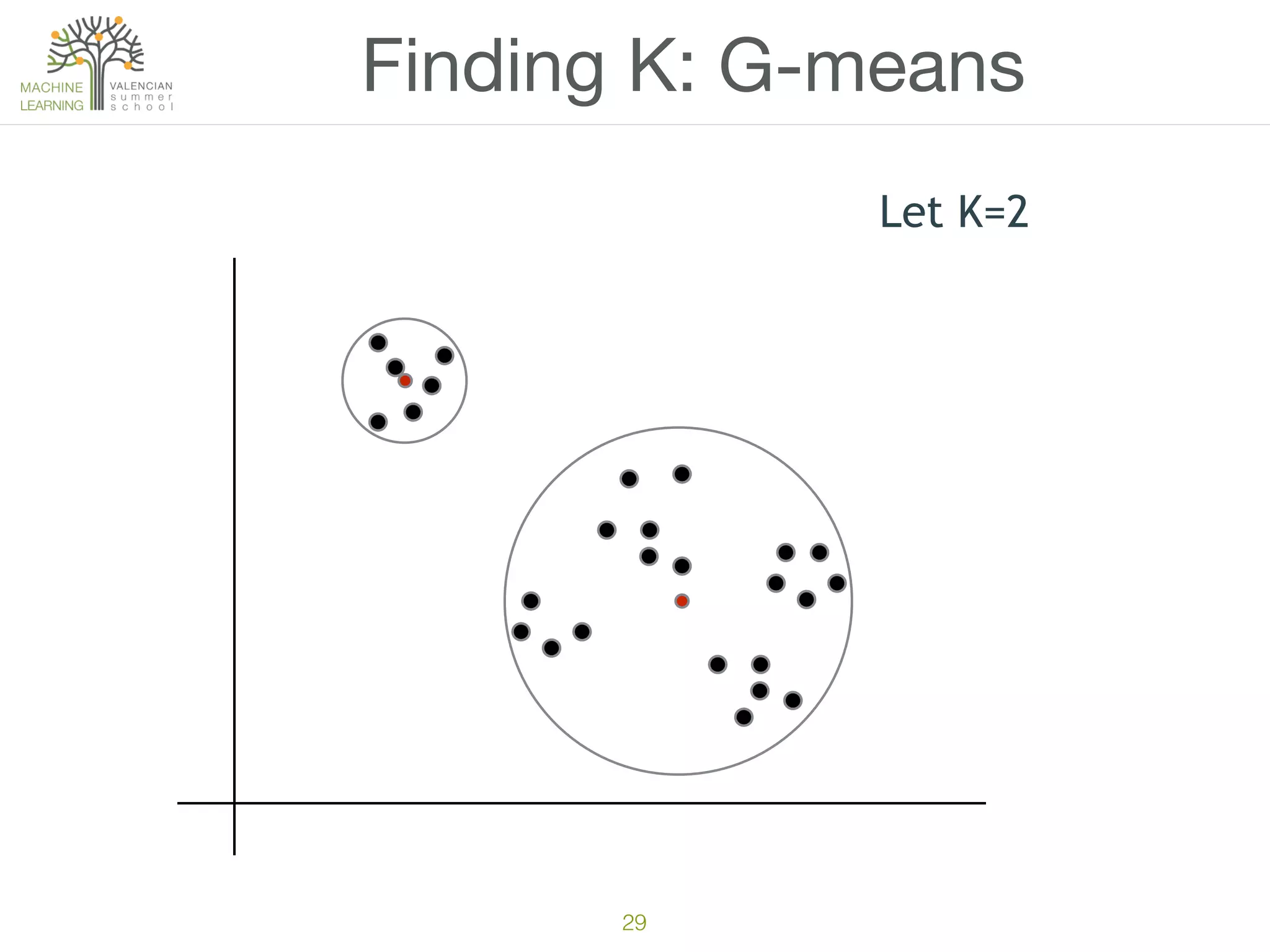
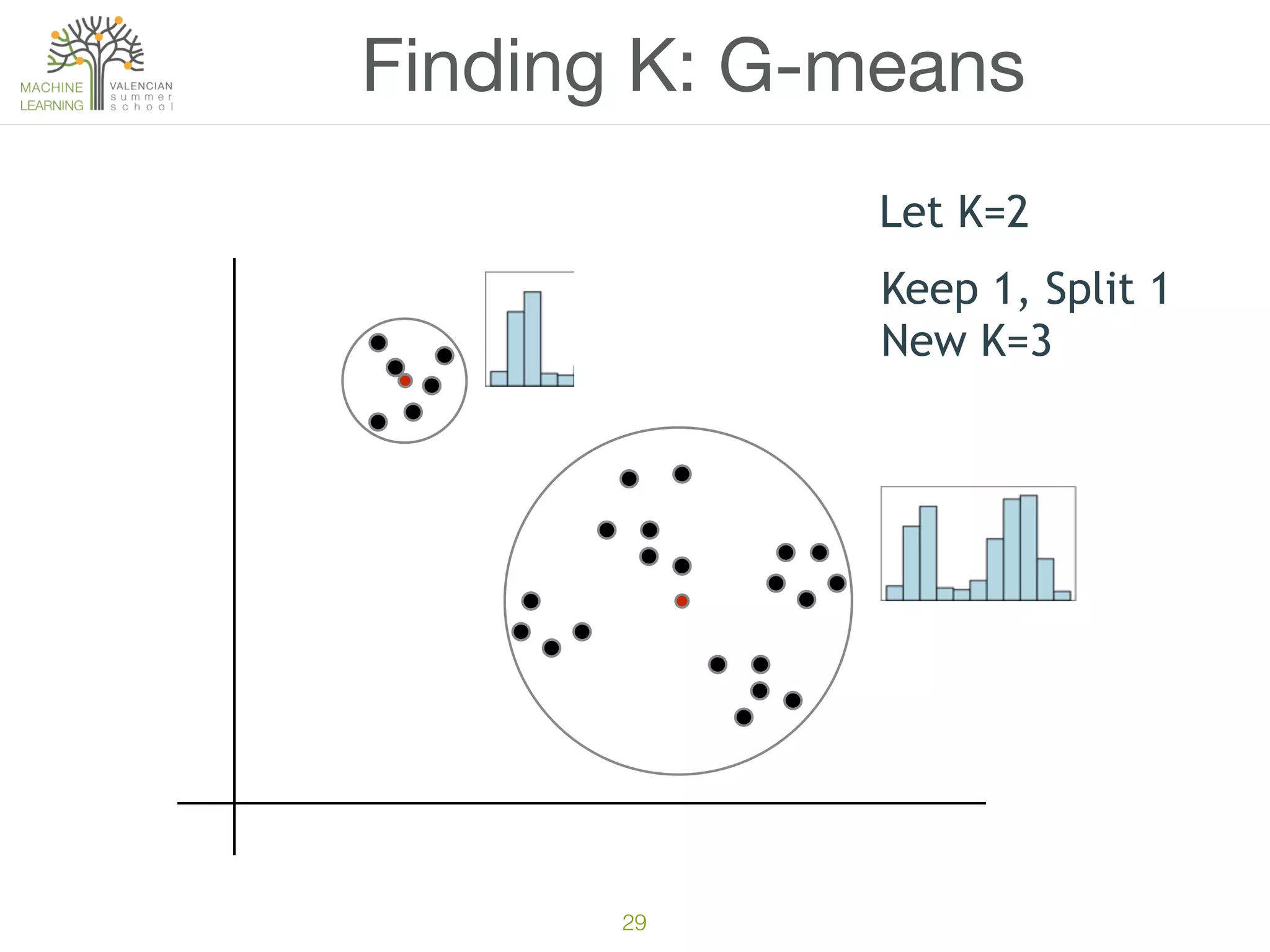
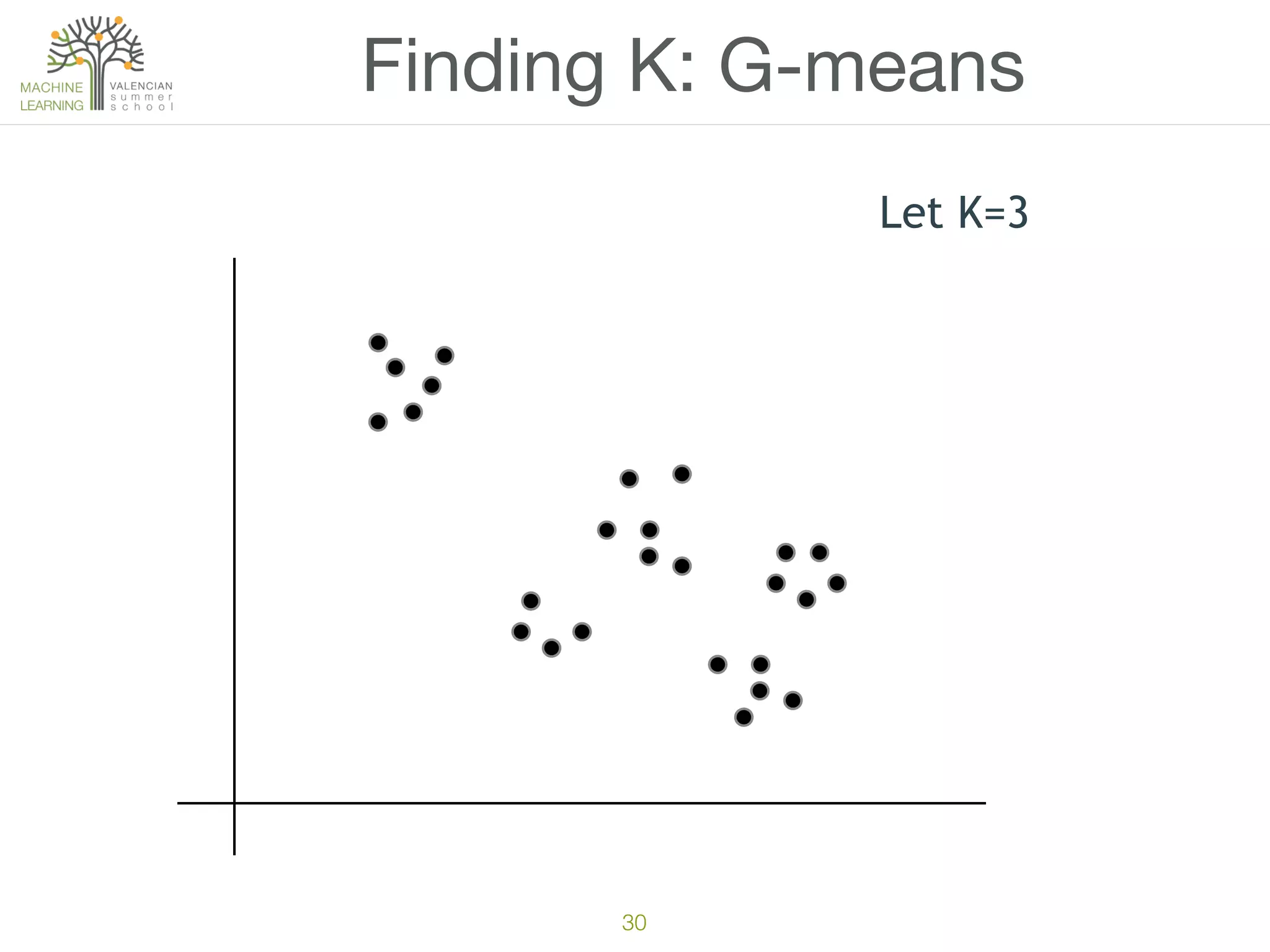
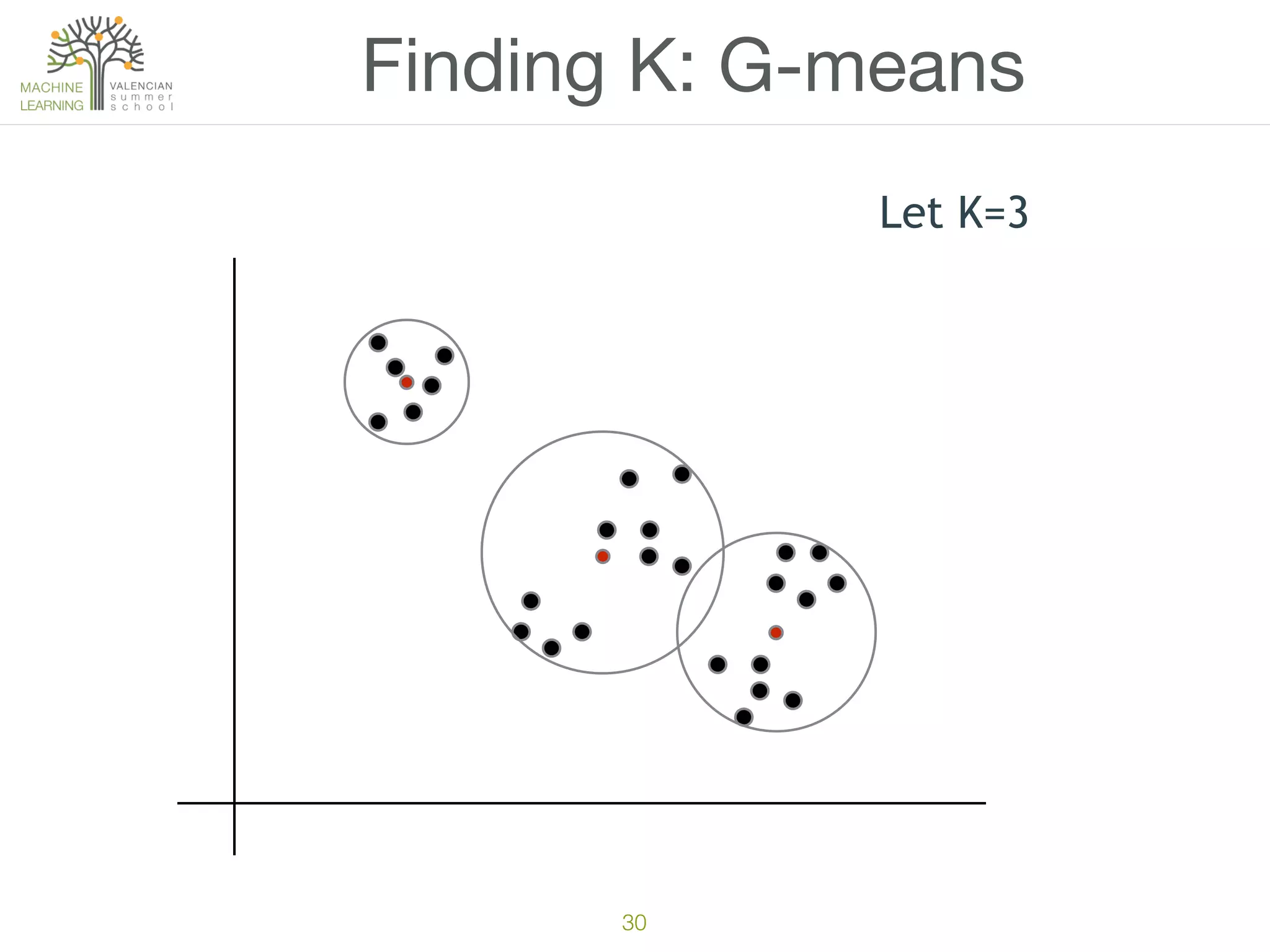
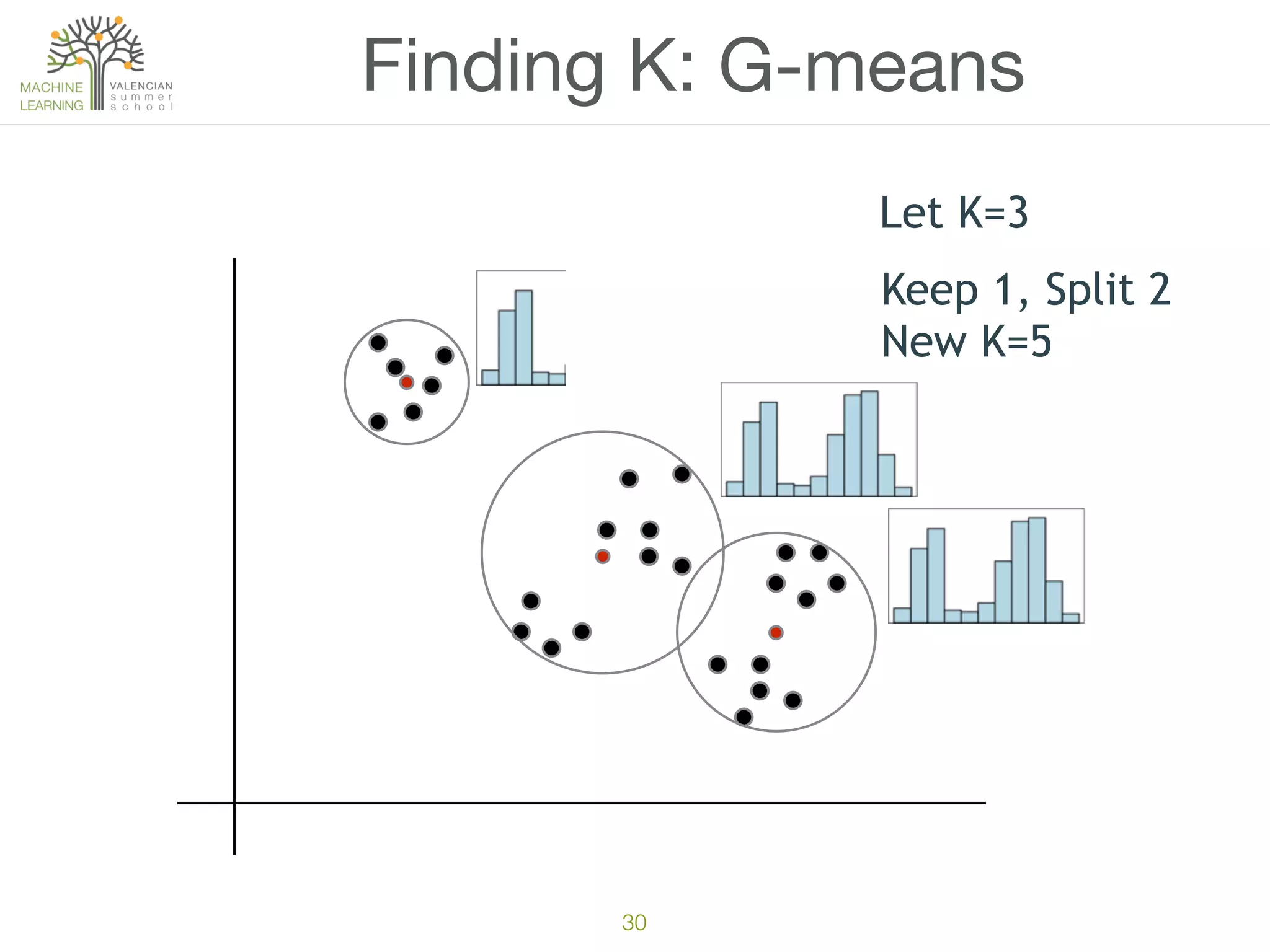
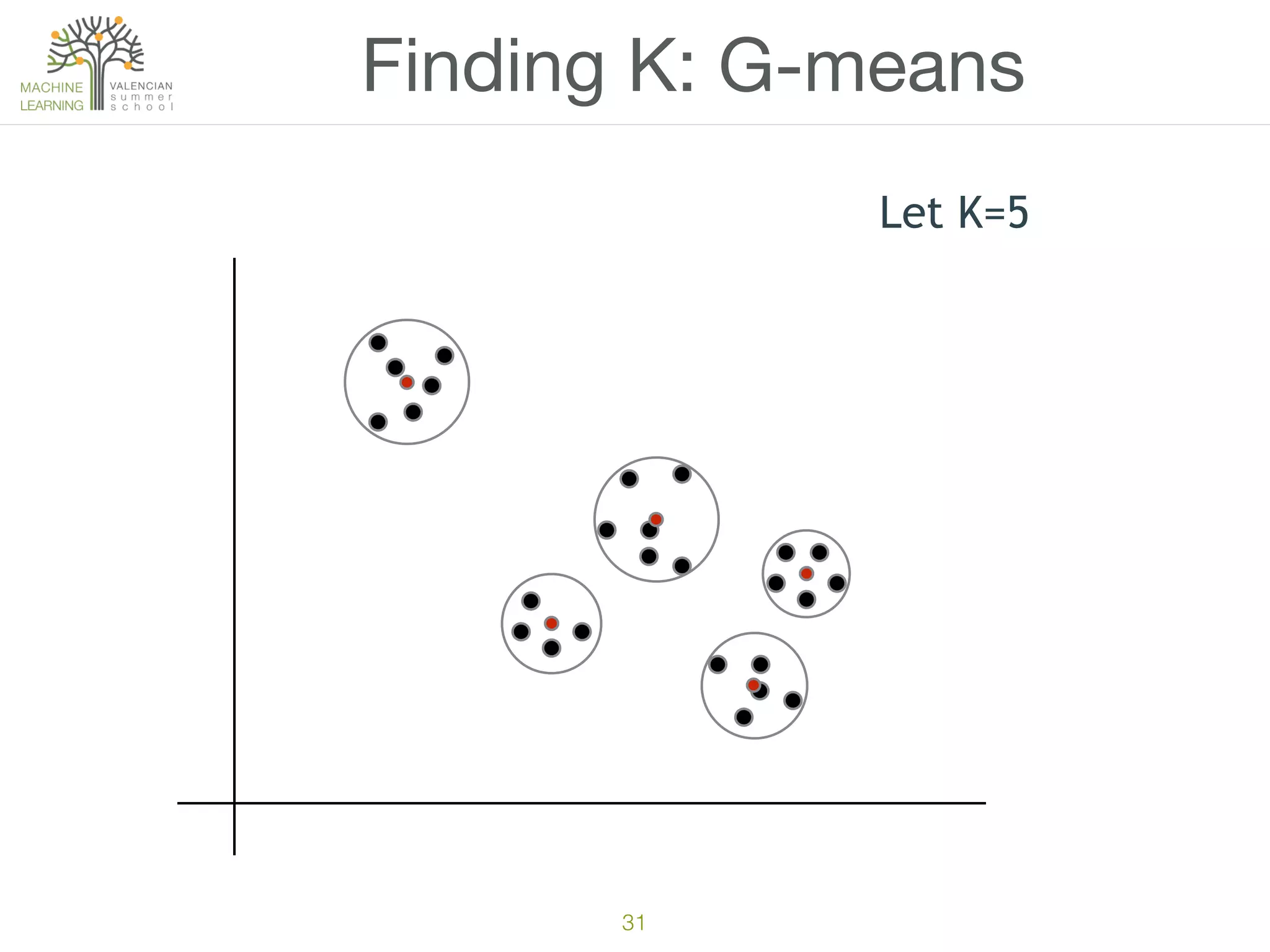
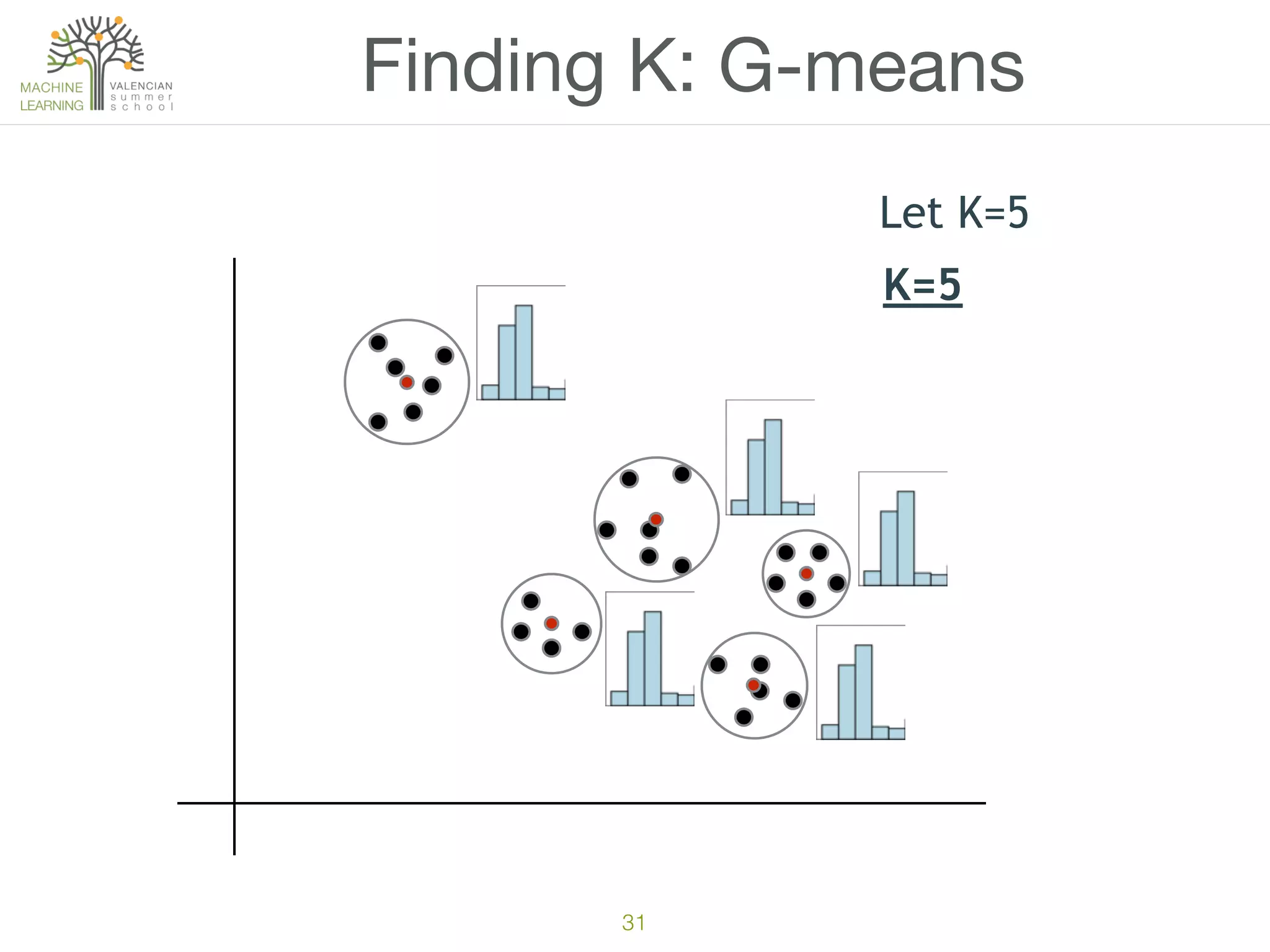
The document discusses concepts of cluster analysis in machine learning, contrasting supervised and unsupervised learning, and showcasing applications such as customer segmentation and item discovery. It introduces the k-means algorithm, feature engineering, and methods for handling missing values and categorical data in clustering contexts. Additionally, it describes techniques for determining the optimal number of clusters (k) using approaches like g-means.
More Related Content
![Matrix and determinant URT [Autosaved].pptx](https://cdn.slidesharecdn.com/ss_thumbnails/matrixanddeterminanturtautosaved-251018190340-9e6a6deb-thumbnail.jpg?width=600ounds&width=560&fit=bounds)
L13. Cluster Analysis
- 1.
- 2. 2 Trees vs Clusters Trees(Supervised Learning) Provide: labeled data Learning Task: be able to predict label Clusters (Unsupervised Learning) Provide: unlabeled data Learning Task: group data by similarity
- 3. 3 Trees vs Clusters sepal length sepal width petal length petal width species 5.13.5 1.4 0.2 setosa 5.7 2.6 3.5 1.0 versicolor 6.7 2.5 5.8 1.8 virginica … … … … … sepal length sepal width petal length petal width 5.1 3.5 1.4 0.2 5.7 2.6 3.5 1.0 6.7 2.5 5.8 1.8 … … … … Learning Task: Find function “f” such that: f(X)≈Y Learning Task: Find “k” clusters such that the data in each cluster is self similar Inputs “X” Label “Y”
- 4. 4 • Customer segmentation •Item discovery • Association • Recommender • Active learning Use Cases
- 5. 5 Customer Segmentation GOAL: Clusterthe users by usage statistics. Identify clusters with a higher percentage of high LTV users. Since they have similar usage patterns, the remaining users in these clusters may be good candidates for upsell. • Dataset of mobile game users. • Data for each user consists of usage statistics and a LTV based on in-game purchases • Assumption: Usage correlates to LTV 5 0% 3% 7% 1%
- 6. 6 Item Discovery • Datasetof 86 whiskies • Each whiskey scored on a scale from 0 to 4 for each of 12 possible flavor characteristics. GOAL: Cluster the whiskies by flavor profile to discover whiskies that have similar taste. Smoky Fruity Body
- 7. 7 Association • Dataset ofLending Club Loans • Mark any loan that is currently or has even been late as “trouble” GOAL: Cluster the loans by application profile to rank loan quality by percentage of trouble loans in population 0% 3% 7% 1%
- 8. 8 Active Learning GOAL: Ratherthan sample randomly, use clustering to group patients by similarity and then test a sample from each cluster to label the data. • Dataset of diagnostic measurements of 768 patients. • Want to test each patient for diabetes and label the dataset to build a model but the test is expensive* *For a more realistic example of high cost, imagine a dataset with a billion transactions, each one needing to be labelled as fraud/not-fraud. Or a million images which need to be labeled as cat/not-cat. 2323
- 9.
- 10.
- 11. 11 Human Example • Humanused prior knowledge to select possible features that separated the objects. • “round”, “skinny”, “edges”, “hard”, etc • Items were then separated based on the chosen features • Separation quality was then tested to ensure: • met criteria of K=3 • groups were sufficiently “distant” • no crossover
- 12. 12 Learning from Humans •Length/Width • greater than 1 => “skinny” • equal to 1 => “round” • less than 1 => invert • Number of Surfaces • distinct surfaces require “edges” which have corners • easier to count Create features that capture these object differences
- 13. 13 Feature Engineering Object Length/ Width Num Surfaces penny 1 3 dime 1 3 knob 1 4 eraser 2.75 6 box 1 6 block 1.6 6 screw 8 3 battery 5 3 key 4.25 3 bead 1 2
- 14. 14 Now we canPlot K=3 Num Surfaces Length / Width box block eraser knob penny dime bead key battery screw K-Means Key Insight: We can find clusters using distances in n-dimensional feature space
- 15. 15 Now we canPlot Num Surfaces Length / Width box block eraser knob penny dime bead key battery screw K-Means Find “best” (minimum distance) circles that include all points
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25. 19 Convergence Convergence guaranteed but notnecessarily unique Starting points important (K++)
- 26. 20 Starting Points • Randompoints or instances in n-dimensional space • Chose points “farthest” away from each other • but this is sensitive to outliers • k++ • the first center is chosen randomly from instance • each subsequent center is chosen from the remaining instances with probability proportional to its squared distance from the point's closest existing cluster center
- 27. 21 Scaling price number of bedrooms d= 160,000 d = 1
- 28. 22 Other Tricks • Whatis the distance to a “missing value”? • What is the distance between categorical values? • What is the distance between text features? • Does it have to be Euclidean distance? • Unknown “K”?
- 29. 23 Distance to MissingValue? • Nonsense! Try replacing missing values with: • Maximum • Mean • Median • Minimum • Zero • Ignore instances with missing values
- 30. 24 Distance to Categorical? •Special distance function • if valA == valB then distance = 0 (or scaling value) else distance = 1 • Assign centroid the most common category of the member instances • Compute Euclidean distance as normal One approach: similar to “k-prototypes”
- 31. 25 Distance to Categorical? feature_1feature_2 feature_3 instance_1 red cat ball instance_2 red cat ball instance_3 red cat box instance_4 blue dog fridge D = 0 D = 1 D = sqrt(3)
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38. 29 Finding K: G-means LetK=2 Keep 1, Split 1 New K=3
- 39.
- 40.
- 41. 30 Finding K: G-means LetK=3 Keep 1, Split 2 New K=5
- 42.
- 43.
- 44. 31 Finding K: G-means LetK=5 K=5