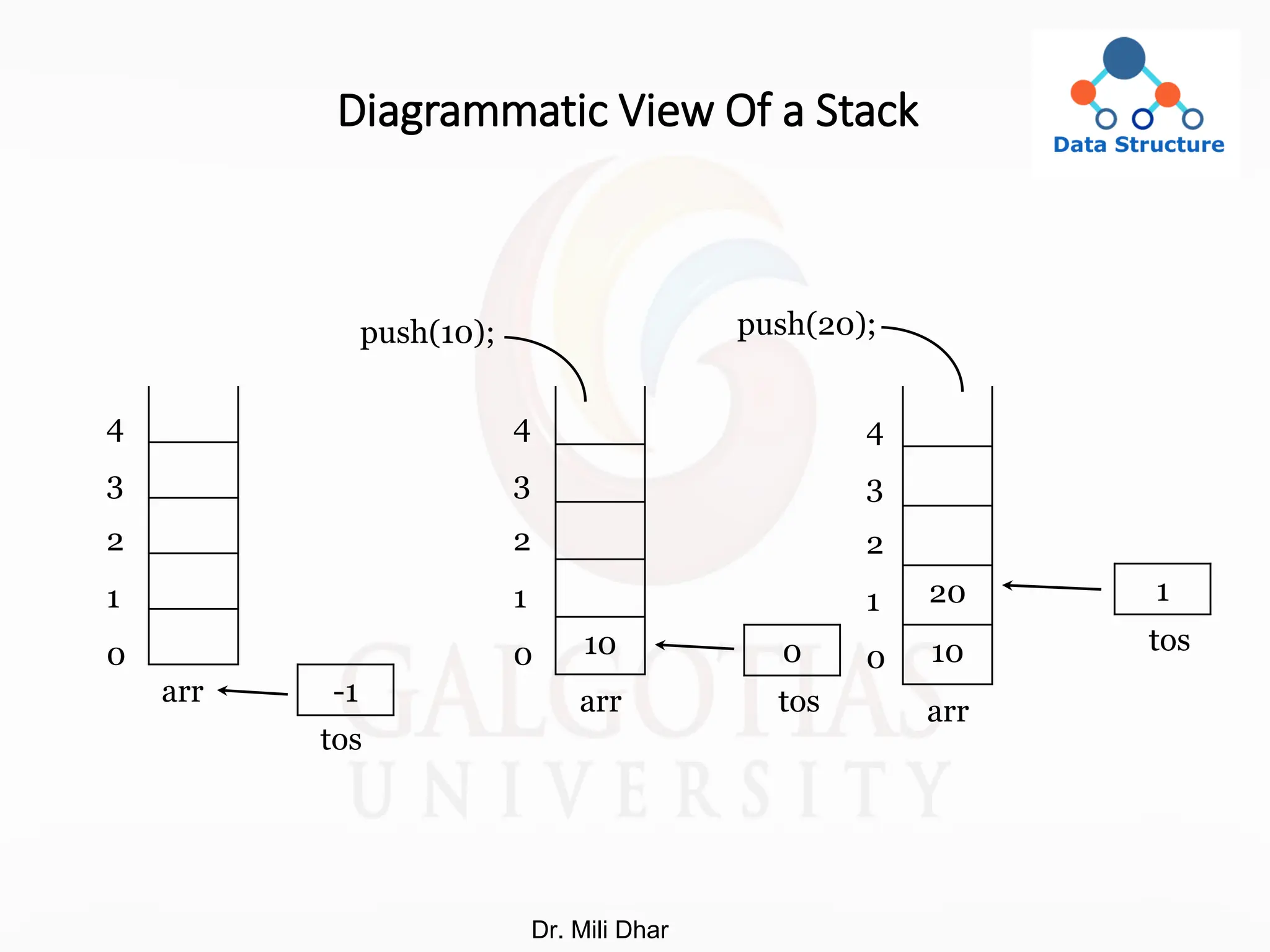
The lecture covers data structures, focusing on arrays and stacks, their definitions, declarations, and operations such as insertion and access. It discusses the address calculation for one-dimensional and two-dimensional arrays, and introduces sparse matrices, including their representations and benefits. Furthermore, it explains arithmetic operations on matrices and provides examples to demonstrate these concepts in programming.



![Declaring an Array
#include <conio.h>
#include<stdio.h>
void main()
{
int arr[5];
int i;
for(i=0;i<5;i++)
{
……
……
}
getch();
}
10 20 30 40 50 int i;
0 1 2 3 4
index
arr
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-4-2048.jpg)
![Declaration of an Array
type array-name[];
OR
type[] array-name;
Example:
int Arr[];
OR
int [] Arr;
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-5-2048.jpg)
![Initialization of an Array
var-name = new type [size];
Example:
int Arr[];
Arr = new int [20];
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-6-2048.jpg)
![Insert elements in an Array
int[] myNum = {10, 20, 30, 40};
String[] cars = {"Volvo", "BMW", "Ford", "Mazda"};
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-7-2048.jpg)
![Accessing of an Array
for (int i = 0; i < arr.length; i++)
System.out.println("Element at index " +
i + " : "+ arr[i]);
System.out.println(cars[0]);
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-8-2048.jpg)

![class DS {
public static void main(String[] args)
{
char [] arr; declaration
arr = new char[5]; initialization
arr[0] = ‘10’; inserting elements
arr[1] = ‘20’;
arr[2] = ‘30’;
arr[3] = ‘40’;
arr[4] = ‘50’;
// accessing the elements of the specified array
for (int i = 0; i < arr.length; i++)
System.out.println("Element at index " + i + " : " + arr[i]);
}
}
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-10-2048.jpg)
![import java.util.*;
class HelloWorld {
public static void main(String[] args)
{
int []arr = new int[3];
Scanner sc = new Scanner(System.in);
for (int i =0; i<arr.length; i++) {
System.out.println("Enter the elements "+i);
arr[i]= sc.nextInt(); }
for (int i =0; i<arr.length; i++)
{
System.out.println(arr[i]);
}
}
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-11-2048.jpg)
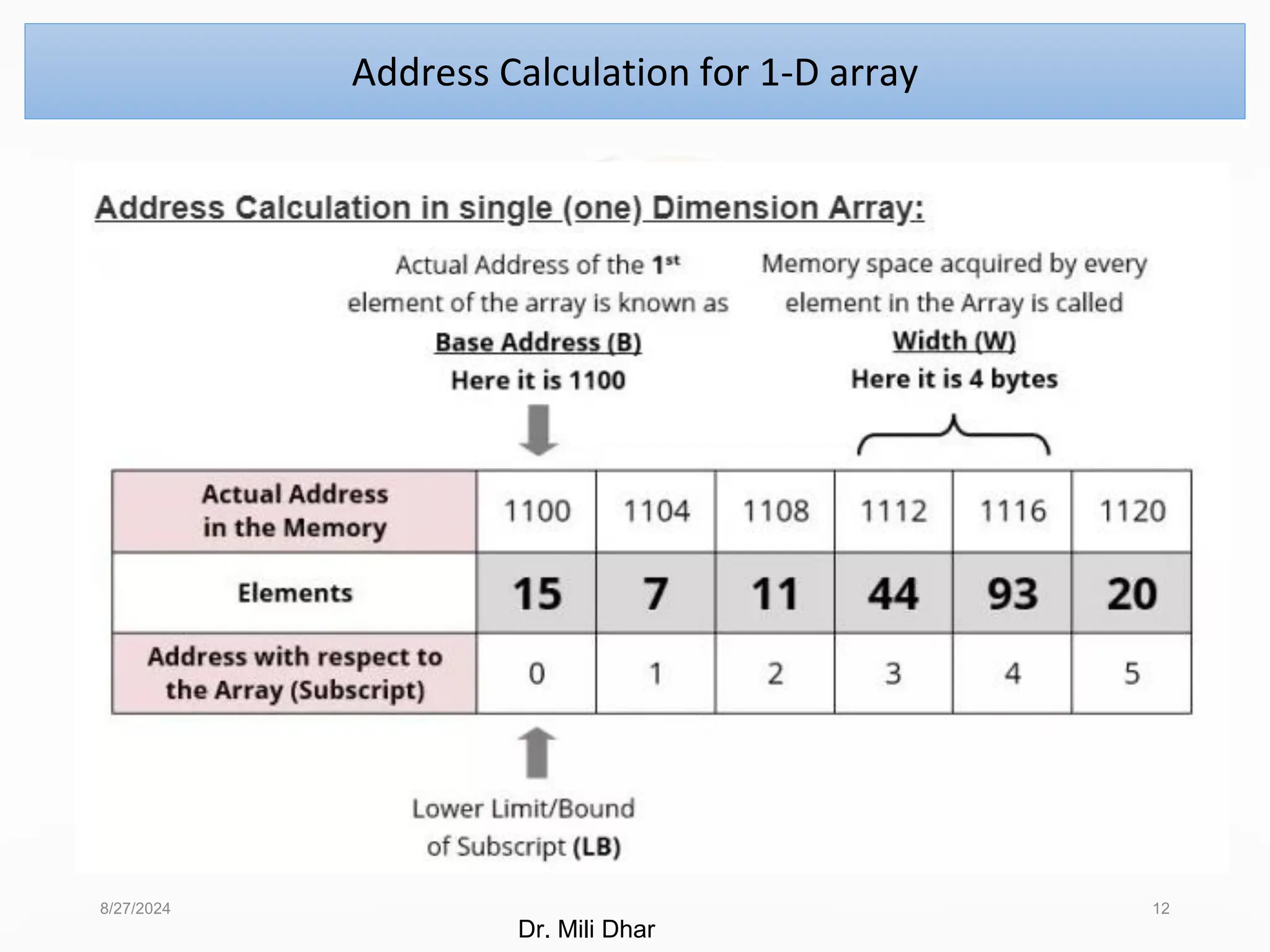
![• Array of an element of an array say “A[ I ]” is calculated using the
following formula:
Address of A [ I ] = B + W * ( I – LB )
Where,
B = Base address
W = Storage Size of one element stored in the array (in byte)
I = Subscript of element whose address is to be found
LB = Lower limit / Lower Bound of subscript, if not specified assume 0
(zero)
8/27/2024 13
Address Calculation for 1-D array
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-13-2048.jpg)
![Example 1:
• Given the base address of an array B[1300…..1900] as
1020 and size of each element is 2 bytes in the memory.
Find the address of B[1700].
• Solution:
The given values are: B = 1020, LB = 1300, W = 2, I = 1700
Address of A [ I ] = B + W * ( I – LB )
= 1020 + 2 * (1700 – 1300)
= 1020 + 2 * 400
= 1020 + 800
= 1820 [Ans]
8/27/2024 14
Address Calculation for 1-D array
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-14-2048.jpg)
![Example 2:
• Find the base address of an array A[-15:65]. The size of each
element is 2 bytes in the memory and the location of A[37] is 4279.
Solution:
The given values are: LB = -15, UB = 65, W = 2, I = 37, A[37] = 4279
Address of A [ I ] = B + W * ( I – LB )
4279= B + 2 * (37 – (-15))
4279= B + 2 * 52
4279= B + 104
B= 4175 [Ans]
8/27/2024 15
Address Calculation
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-15-2048.jpg)
![Declaration of 2D-Array
type arr-name[][];
OR
type[][] arr-name;
Example:
int Arr[][];
OR
int [][] Arr;
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-16-2048.jpg)
![Initialization of an 2D-Array
var-name = new type [size][size];
Example:
int Arr[] [];
Arr = new int [20][20];
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-17-2048.jpg)
![Insert elements in an Array
int[][] myNum = {{10, 20}, {30, 40}};
String[] []cars = {{"Volvo", "BMW“}, {"Ford", "Mazda"}};
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-18-2048.jpg)
![Insert elements in an Array
import java.util.*;
class HelloWorld {public static void main(String[] args)
{
int [][]arr = new int[3][3];
Scanner sc = new Scanner(System.in);
for (int i =0; i<arr.length; i++) {
for (int j =0; j<arr.length; j++) {
System.out.println("Enter the elements "+i,j);
arr[i][j]= sc.nextInt(); } }
for (int i =0; i<arr.length; i++)
{
for (int j =0; j<arr.length; j++) {
System.out.println(arr[i][j]);
}}
}
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-19-2048.jpg)
![Display elements of 2D Array
public class Main
{
public static void main(String[] args)
{
int[][] myNumbers = { {1, 2, 3, 4}, {5, 6, 7} };
for (int i = 0; i < myNumbers.length; ++i)
{
for(int j = 0; j < myNumbers[i].length; ++j)
{
System.out.println(myNumbers[i][j]);
}
}
}
}
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-20-2048.jpg)
![Row Major Array
In row major order, the elements of a particular row are
stored at adjacent memory locations. The first element
of the array (arr[0][0]) is stored at the first location
followed by the arr[0][1] and so on. After the first row,
elements of the next row are stored next.
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-21-2048.jpg)
![Column Major Array
In column major order, the elements of a column are
stored adjacent to each other in the memory.The first
element of the array (arr[0][0]) is stored at the first
location followed by the arr[1][0] and so on. After the
first column, elements of the next column are stored
stating from the top.
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-22-2048.jpg)
![address[i][j] = I + W * [(i - l_row) * N + (j - l_col)]
•I : Base address
l_row : lower bound for row
l_col : lower bound for column
W : sizeof (data type)
N : Number of columns
8/27/2024 23
Address Calculation row major array
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-23-2048.jpg)
![• Example:
Consider an integer array of size 3X3. The address of the first
element is 1048. Calculate the address of the element at index i =
2, j = 1. (0 based index)
• I = 1048, l_row = 0 = l_col, i = 2, j = 1, W = 2, N = 3
• address[2][1] = I + W * [(i-l_row) * N + (j - l_col)]
• address[2][1] = 1048 + 2 *[ 2 * 3 + 1 ]= 1048 + 12 + 2 = 1062
8/27/2024 24
Address Calculation row major array
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-24-2048.jpg)
![• Example:
Example: Given an array, arr[1………10][1………15] with base
value 100 and the size of each element is 1 Byte in memory. Find
the address of arr[8][6] with the help of row-major order.
8/27/2024 25
Address Calculation row major array
Base address B = 100
W = 1 Bytes, I = 8, J = 6
LR = 1, LC = 1
N = Upper Bound – Lower Bound + 1
= 15 – 1 + 1 = 15
Solution:
Address of A[8][6] = 100 + 1 * ((8 – 1) * 15 + (6 – 1))
= 100 + 1 * ((7) * 15 + (5))
= 100 + 1 * (110)
Address of A[I][J] = 210
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-25-2048.jpg)
![address[i][j] = I + W * ((j – l_col) * M + (i – l_row))
I : Base address
l_row : lower bound for row
l_col : lower bound for column
W : sizeof (data type)
M : Number of rows
8/27/2024 26
Address Calculation column major array
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-26-2048.jpg)
![• Example:
• Consider an integer array of size 3X3. The address of the first
element is 1048. Calculate the address of the element at index i = 2, j
= 1. (0 based index)
• I = 1048, l_row = 0 = l_col, i = 2, j = 1, W = 2, M = 3
• address[2][1] = I + W * [(j - l_col) * M + (i - l_row)]
• address[2][1] = 1048 + 2 * [1 * 3 + 2 ]= 1048 + 6 + 4 = 1058
8/27/2024 27
Address Calculation column major array
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-27-2048.jpg)
![• Example:
Example: Given an array, arr[1………10][1………15] with base
value 100 and the size of each element is 1 Byte in memory. Find
the address of arr[8][6] with the help of column-major order.
8/27/2024 28
Address Calculation column major array
Base address B = 100
W = 1 Bytes, I = 8, J = 6
LR = 1, LC = 1
N = Upper Bound – Lower Bound + 1
= 10 – 1 + 1 = 10
Solution:
Address of A[8][6] = 100 + 1 * ((6 – 1) * 10 + (8 – 1))
= 100 + 1 * ((5) * 10 + (7))
= 100 + 1 * (57)
Address of A[I][J] = 157
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-28-2048.jpg)


![8/27/2024 32
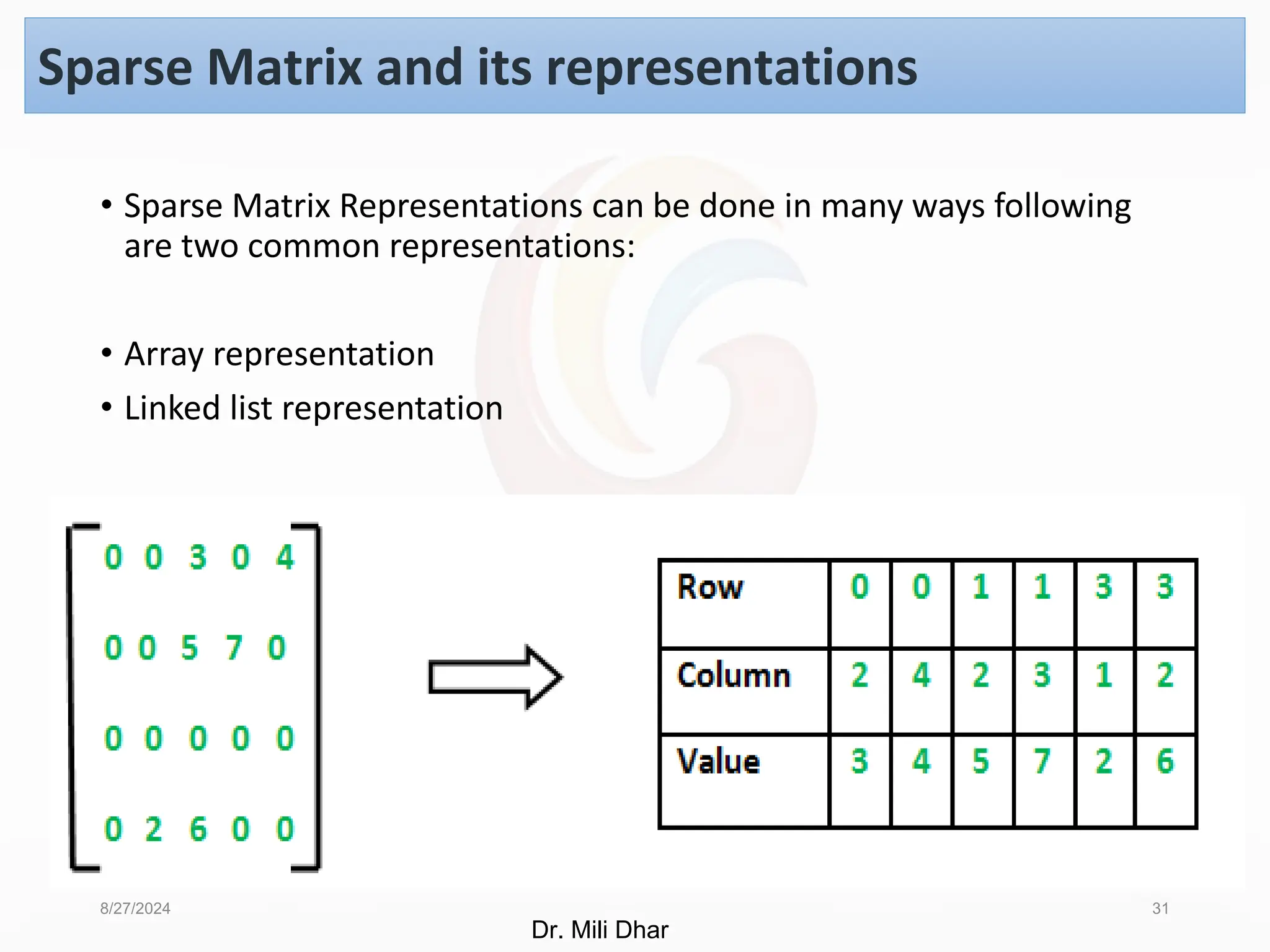
Sparse Matrix and its representations
int size = 0;
for (int i = 0; i < 4; i++)
{
for (int j = 0; j < 5; j++)
{
if (sparseMatrix[i][j] != 0)
{
size++;
}
}
}
class DS
{
public static void main(String[]
args)
{
int sparseMatrix[][]
= {
{0, 0, 3, 0, 4},
{0, 0, 5, 7, 0},
{0, 0, 0, 0, 0},
{0, 2, 6, 0, 0}
};
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-32-2048.jpg)
![8/27/2024 33
Sparse Matrix and its representations
// number of columns in compactMatrix (size) must be
// equal to number of non - zero elements in sparseMatrix
int compactMatrix[][] = new int[3][size];
// Making of new matrix
int k = 0;
for (int i = 0; i < 4; i++)
{
for (int j = 0; j < 5; j++)
{
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-33-2048.jpg)
![8/27/2024 34
Sparse Matrix and its representations
if (sparseMatrix[i][j] != 0)
{
compactMatrix[0][k] = i;
compactMatrix[1][k] = j;
compactMatrix[2][k] = sparseMatrix[i][j];
k++;
}
}
}
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-34-2048.jpg)
![8/27/2024 35
Sparse Matrix and its representations
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < size; j++)
{
System.out.printf("%d ", compactMatrix[i][j]);
}
System.out.printf("n");
}
}
}
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-35-2048.jpg)

![8/27/2024 37
Arithmetic operations on matrices
public class MatrixAdditionExample{
public static void main(String args[]){
//creating two matrices
int a[][]={{1,3,4},{2,4,3},{3,4,5}};
int b[][]={{1,3,4},{2,4,3},{1,2,4}};
//creating another matrix to store the sum of two matrices
int c[][]=new int[3][3]; //3 rows and 3 columns
//adding and printing addition of 2 matrices
for(int i=0;i<3;i++){
for(int j=0;j<3;j++){
c[i][j]=a[i][j]+b[i][j]; //use - for subtraction
System.out.print(c[i][j]+" ");
}
System.out.println(); //new line
}
}}
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-37-2048.jpg)
![8/27/2024 39
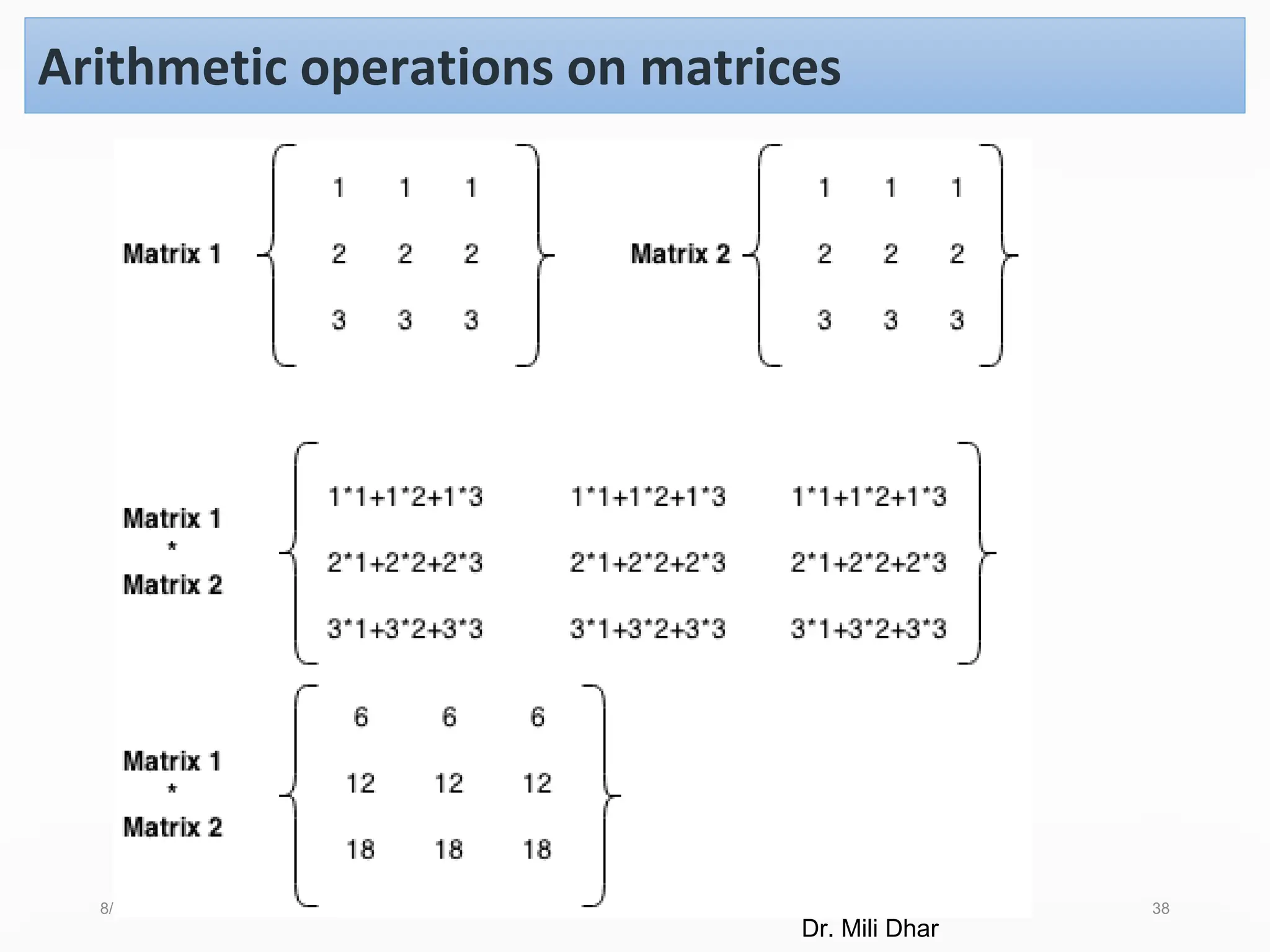
Arithmetic operations on matrices
public class MM{
public static void main(String
args[]){
//creating two matrices
int a[][]={{1,1,1},{2,2,2},{3,3,3}};
int b[][]={{1,1,1},{2,2,2},{3,3,3}};
//creating another matrix to store
the multiplication of two matrices
int c[][]=new int[3][3];
//multiplying and printing
multiplication of 2 matrices
for(int i=0;i<3;i++){
for(int j=0;j<3;j++){
c[i][j]=0;
for(int k=0;k<3;k++)
{
c[i][j]+=a[i][k]*b[k][j];
}
System.out.print(c[i][j]+" ");}
System.out.println();//new line
}
}}
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-39-2048.jpg)
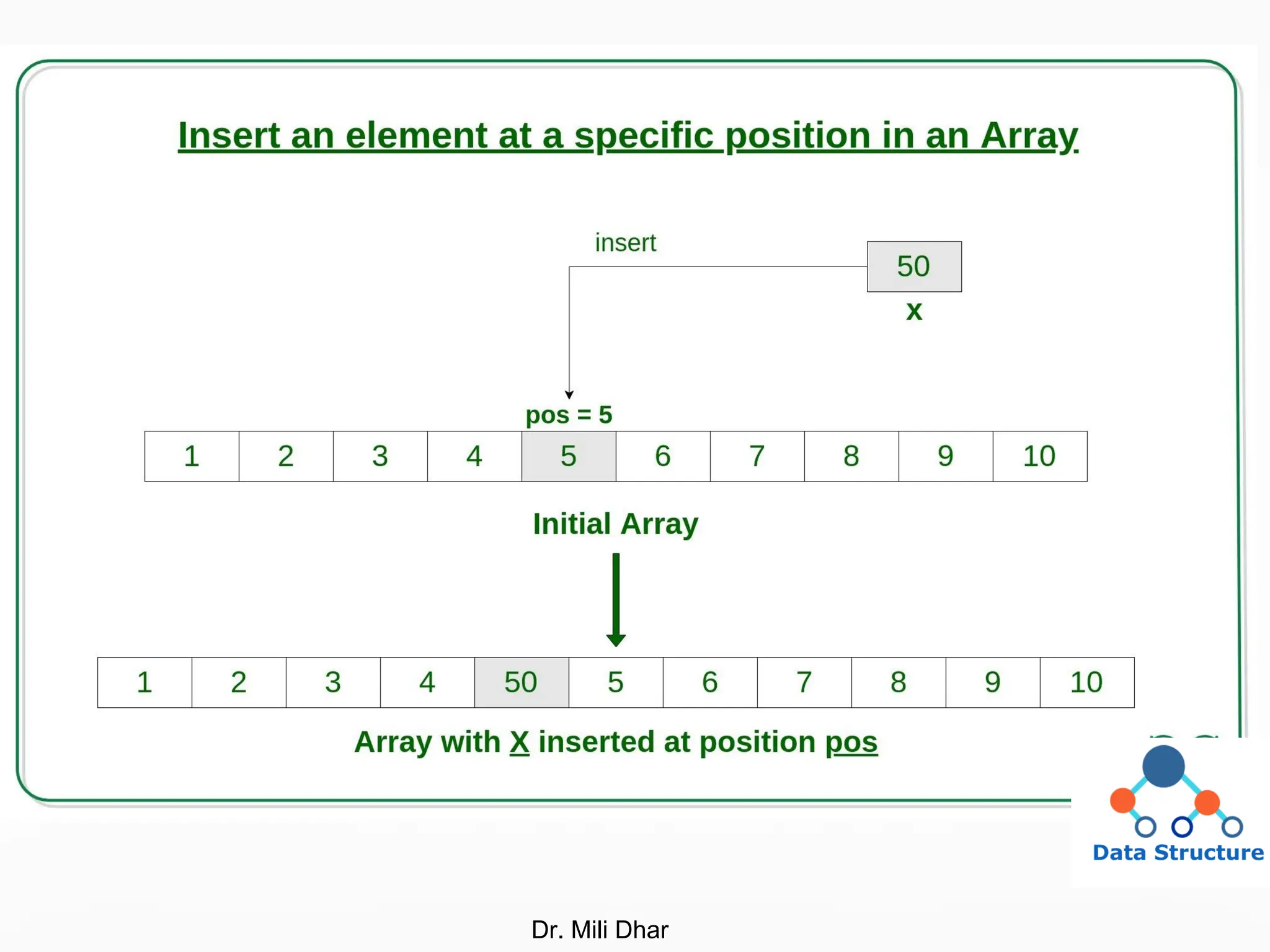
![Write a program to insert an element in ith
position of the array.
import java.io.*;
import java.lang.*;
import java.util.*;
class InsertElement
{
// Function to insert x in arr at position pos
public static int[] insertX(int n, int arr[], int x, int pos)
{
int i;
// create a new array of size n+1
int newarr[] = new int[n + 1];
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-41-2048.jpg)
![Write a program to insert an element in ith
position of the array.
// insert the elements from the old array into the new
// array. insert all elements till pos then insert x at
pos then insert rest of the elements
for (i = 0; i < n + 1; i++) {
if (i < pos - 1)
newarr[i] = arr[i];
else if (i == pos - 1)
newarr[i] = x;
else
newarr[i] = arr[i - 1];
}
return newarr;
}
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-42-2048.jpg)
![Write a program to insert an element in ith
position of the array.
// Main function
public static void main(String[] args)
{
int n = 10;
int i;
// initial array of size 10
int arr[] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };
// print the original array
System.out.println("Initial Array:n" + Arrays.toString(arr));
// element to be inserted
int x = 50;
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-43-2048.jpg)

![Write a program to delete ith element
of the array.
import java.util.Arrays;
class DeleteElement {
// Function to remove the element
public static int[] removeTheElement(int[] arr, int index)
{
// If the array is empty
// or the index is not in array range
// return the original array
if (arr == null || index < 0 || index >= arr.length) {
return arr;
}
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-45-2048.jpg)
![Write a program to delete ith element
of the array.
// Create another array of size one less
int[] anotherArray = new int[arr.length - 1];
// Copy the elements except the index
// from original array to the other array
for (int i = 0, k = 0; i < arr.length; i++) {
// if the index is the removal element index
if (i == index) {
continue;
}
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-46-2048.jpg)
![Write a program to delete ith element
of the array.
// if the index is not the removal element index
anotherArray[k++] = arr[i];
}
// return the resultant array
return anotherArray;
}
// Driver Code
public static void main(String[] args)
{
// Get the array
int[] arr = { 1, 2, 3, 4, 5 };
// Print the resultant array
System.out.println("Original Array: " + Arrays.toString(arr));
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-47-2048.jpg)

![Write a program to reverse the element
of the array.
import java.util.Scanner;
public class ArrayReverser {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("Enter the size of the array:");
int size = scanner.nextInt();
int[] array = new int[size];
System.out.println("Enter " + size + " elements:");
for (int i = 0; i < size; i++) {
array[i] = scanner.nextInt();
}
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-49-2048.jpg)

![Write a program to delete ith element
of the array.
public static void reverseArray(int[] array) {
int startIndex = 0;
int endIndex = array.length - 1;
while (startIndex < endIndex) {
int temp = array[startIndex];
array[startIndex] = array[endIndex];
array[endIndex] = temp;
startIndex++;
endIndex--;
}
}
}
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-51-2048.jpg)



![Tree Recursion
class tree
{
static void fun(int n)
{
if (n > 0) {
System.out.print(" "+ n);
fun(n - 1);
fun(n - 1);
}
}
public static void main(String[] args)
{
fun(3);
}
}
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-56-2048.jpg)

![Tree Recursion
public static void main(String []args)
{
// Initialize variable n.
int n = 5;
System.out.print("Fibonacci series of 5 numbers is: ");
// for loop to print the fibonacci series.
for (int i = 0; i < n; i++)
{
System.out.print(fib(i)+" ");
}
}
}
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-58-2048.jpg)
![Nested Recursion
Nested Recursion: In this recursion, a recursive function
will pass the parameter as a recursive call. That means
“recursion inside recursion”.
import java.util.*;
class NestedRecursion {
static int fun(int n)
{
if (n > 100)
return n - 10;
return fun(fun(n + 11));
}
public static void main(String
args[])
{
int r;
r = fun(95);
System.out.print(" "+ r);
} }
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-59-2048.jpg)
![Write a recursive program to print an
array in reverse order.
import java.util.Scanner;
public class PrintArrayReverseOrder {
static void ReverseArray(int arr[], int n)
{
int i;
if(n>0)
{
i=n-1;
System.out.print(arr[i]+" ");
ReverseArray(arr,i);
}
}
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-60-2048.jpg)
![Write a recursive program to print an
array in reverse order.
public static void main(String[] args) {
Scanner cs=new Scanner(System.in);
int n,i;
System.out.println("Enter your Array Size:");
n=cs.nextInt();
int arr[]=new int[n];
System.out.println("Enter the Array Element:");
for(i=0;i<n;i++)
{
arr[i]=cs.nextInt();
}
System.out.print("After reversing Array Element Are:");
ReverseArray(arr,n);
cs.close();
}
}
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-61-2048.jpg)
![Write a recursion Program to find a^b
class Power {
public static void main(String[] args) {
int base = 3, powerRaised = 4;
int result = power(base, powerRaised);
System.out.println(base + "^" + powerRaised + "=" + result);
}
public static int power(int base, int powerRaised)
{
if (powerRaised != 0) {
return (base * power(base, powerRaised - 1));
}
else {
return 1;
}
}
}
Dr. Mili Dhar](https://image.slidesharecdn.com/datastructurelecturearrayandrecursion-250116142140-7ffe515b/75/Data-Structure-Lecture-Array-and-Recursion-pdf-62-2048.jpg)