data structure on bca.

1Ruli Manurung (Fasilkom UI) IKI10100: Lecture 27th
Mar 2007
AVL Tree
 Definition
 Properties
 Operations
Outline

2Ruli Manurung (Fasilkom UI) IKI10100: Lecture
Balanced binary tree
The disadvantage of a binary search tree is that its
height can be as large as N-1
This means that the time needed to perform insertion
and deletion and many other operations can be O(N)
in the worst case
We want a tree with small height
A binary tree with N node has height at least Θ(log
N)
Thus, our goal is to keep the height of a binary
search tree O(log N)
Such trees are called balanced binary search trees.
Examples are AVL tree, red-black tree.

3Ruli Manurung (Fasilkom UI) IKI10100: Lecture
AVL tree
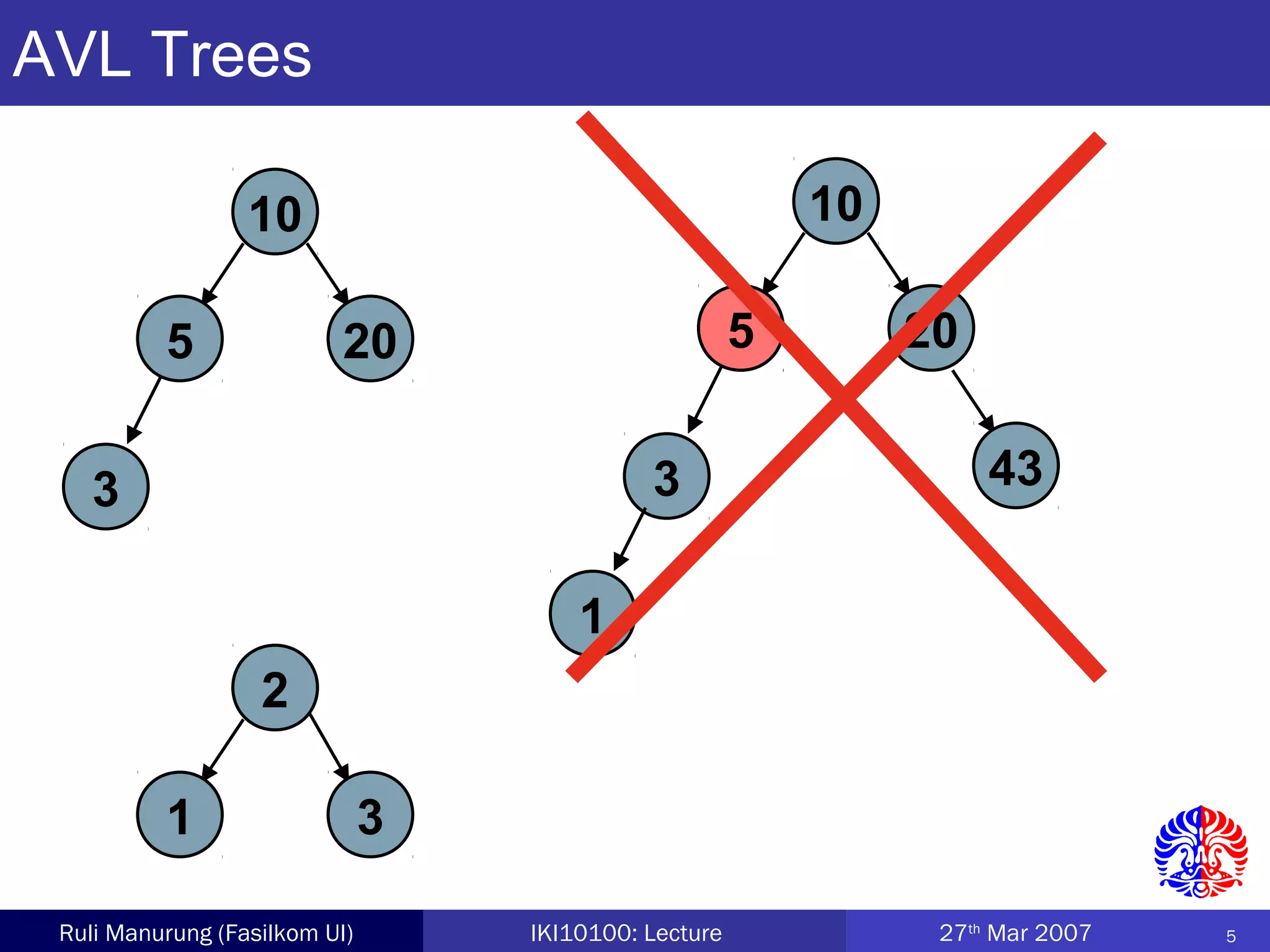
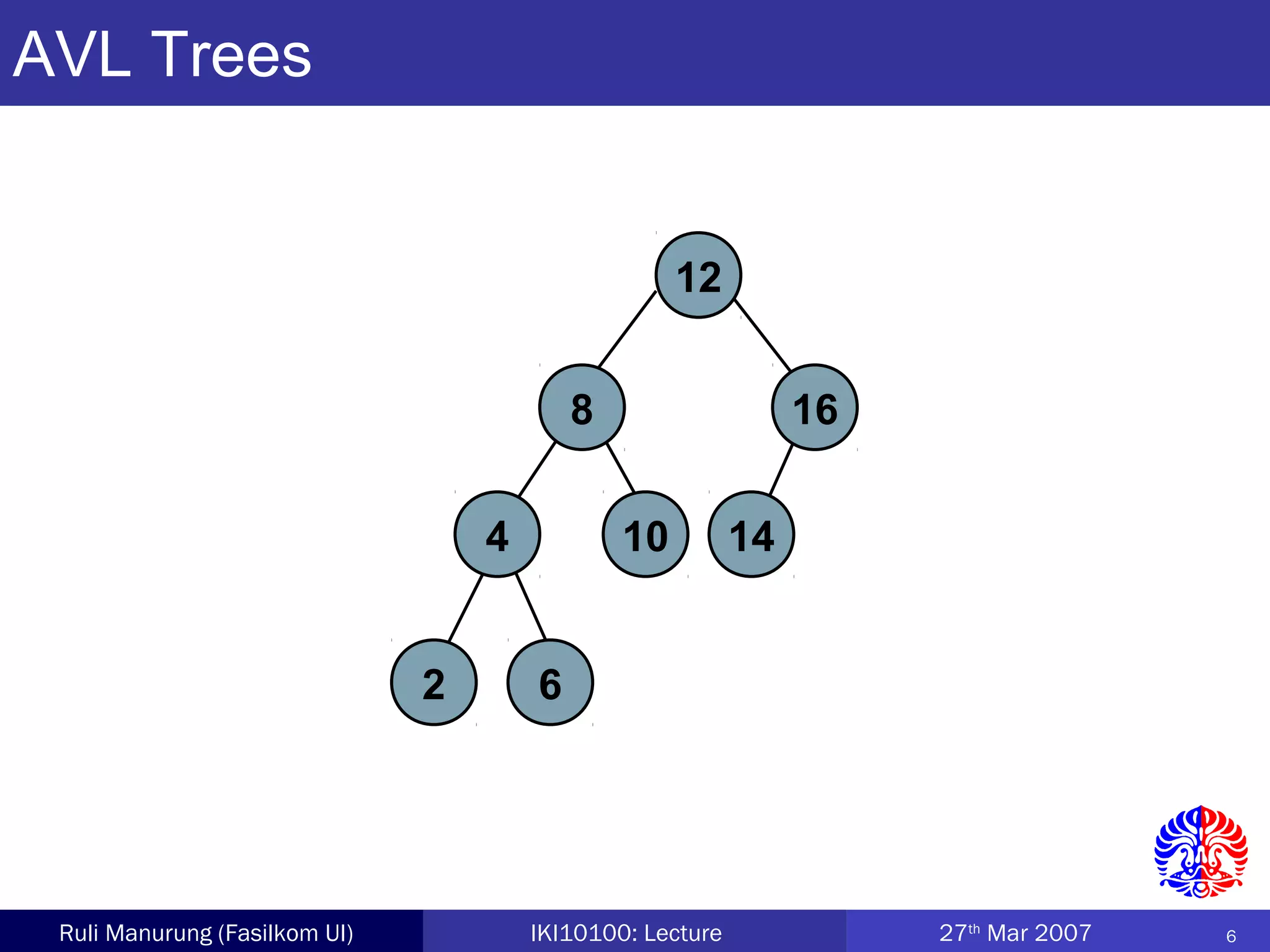
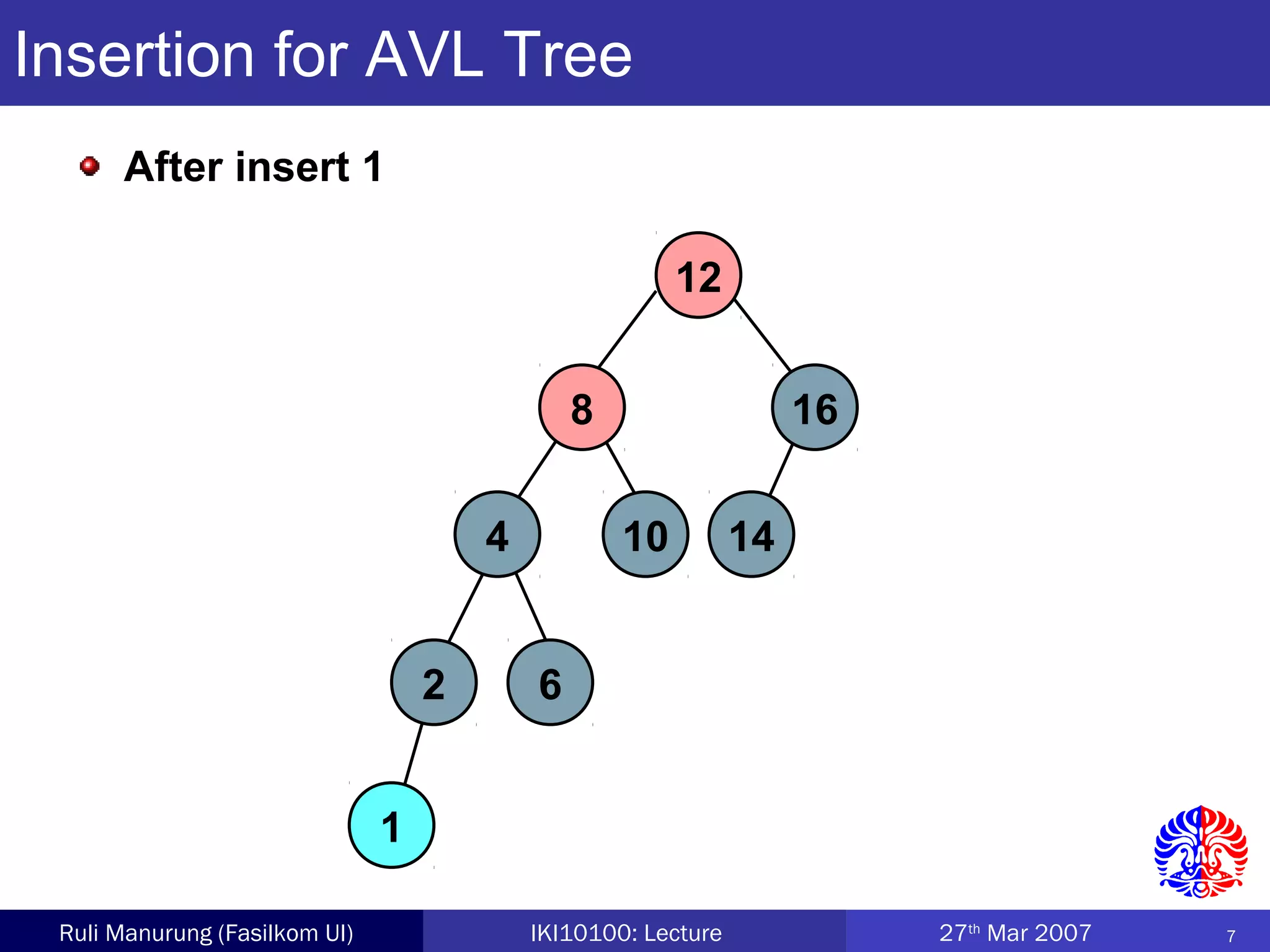
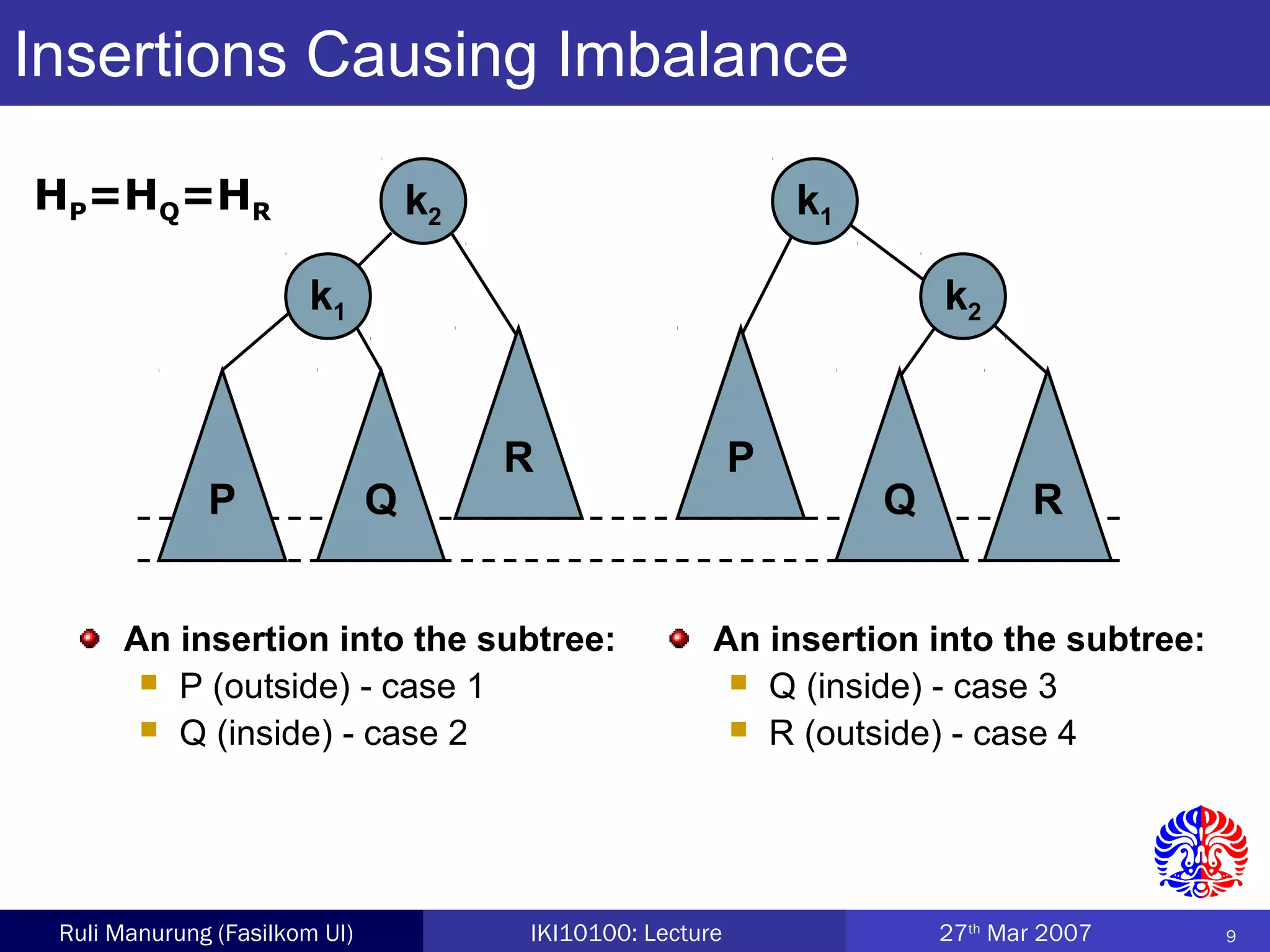
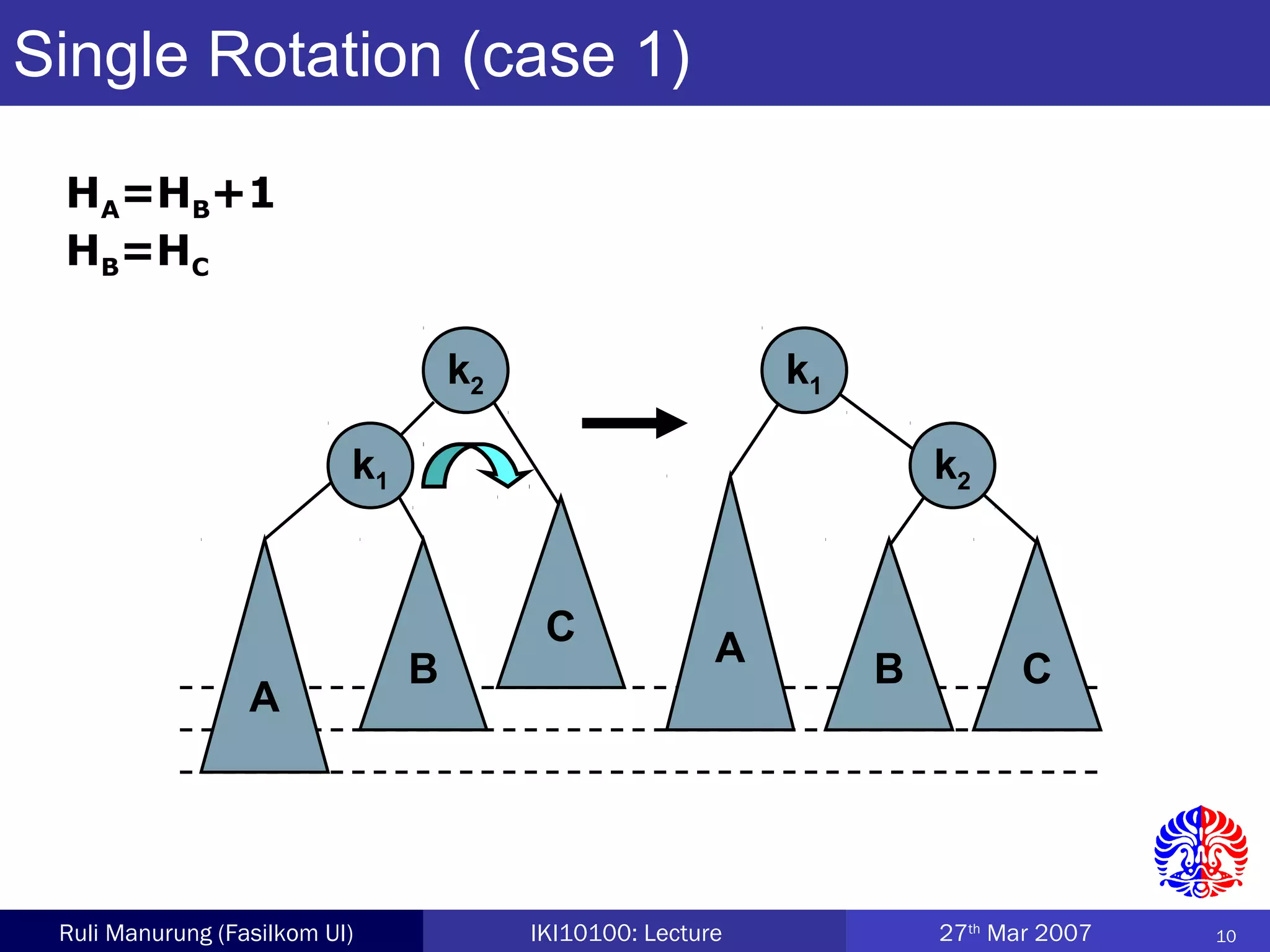
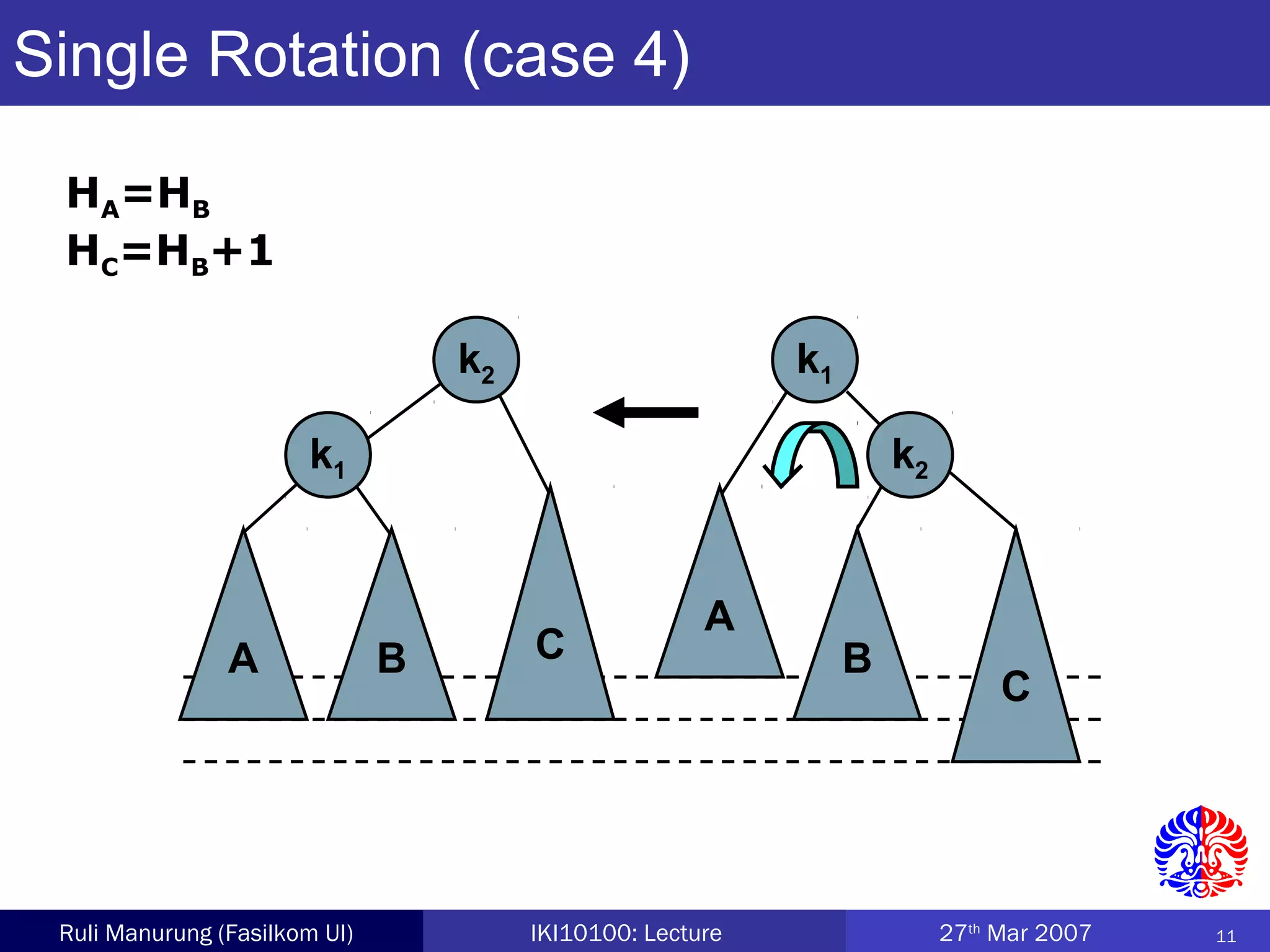
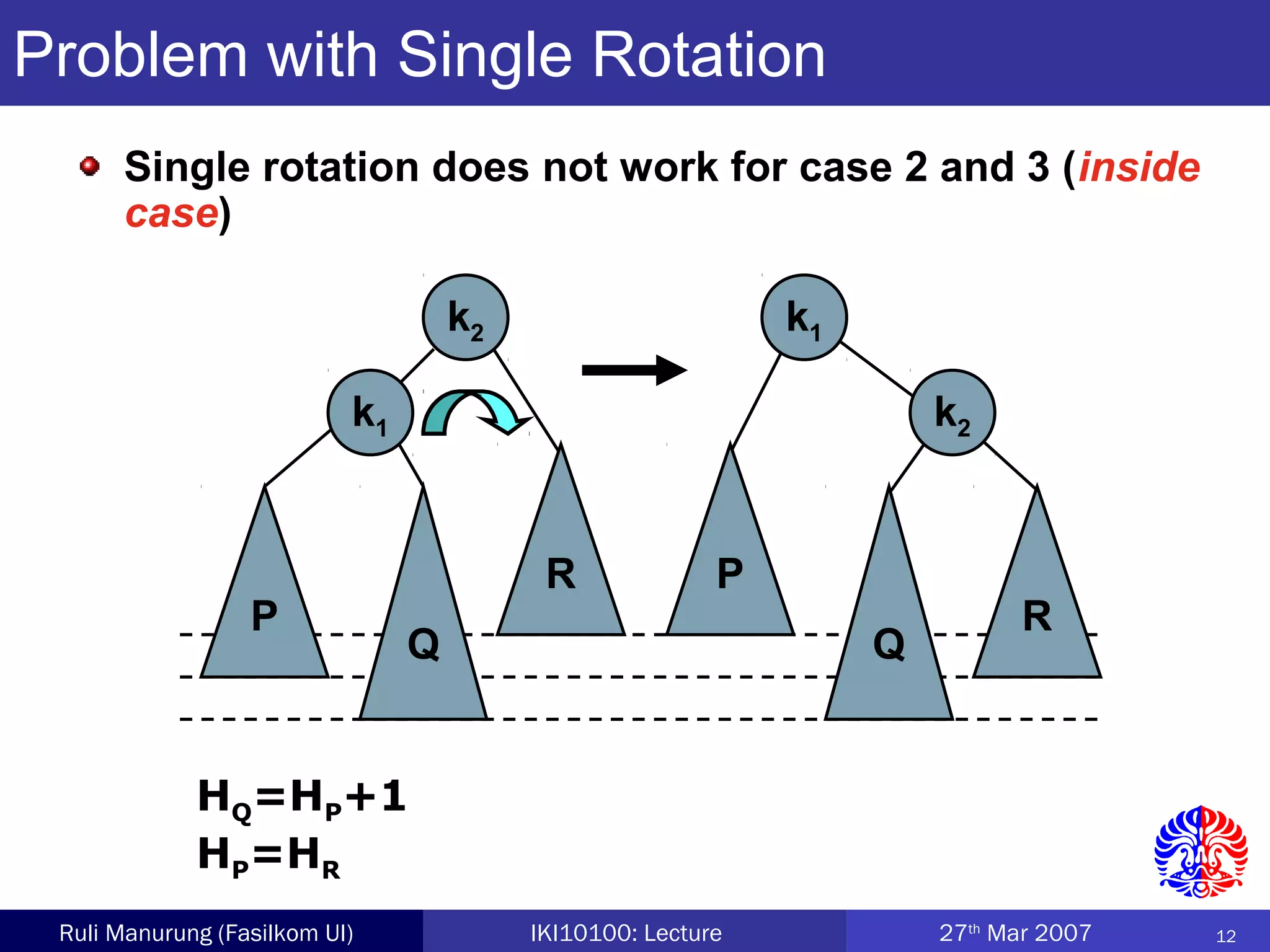
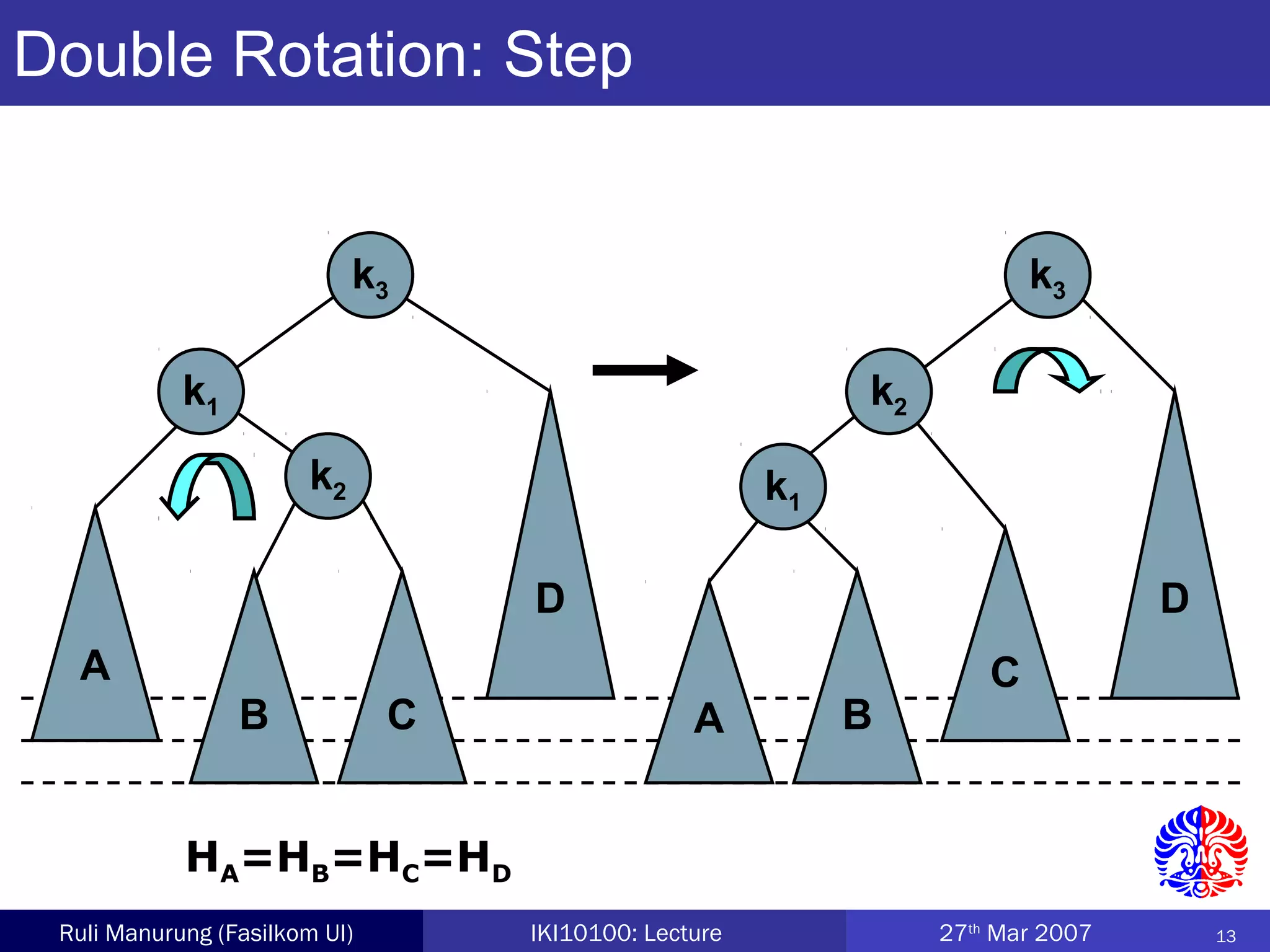
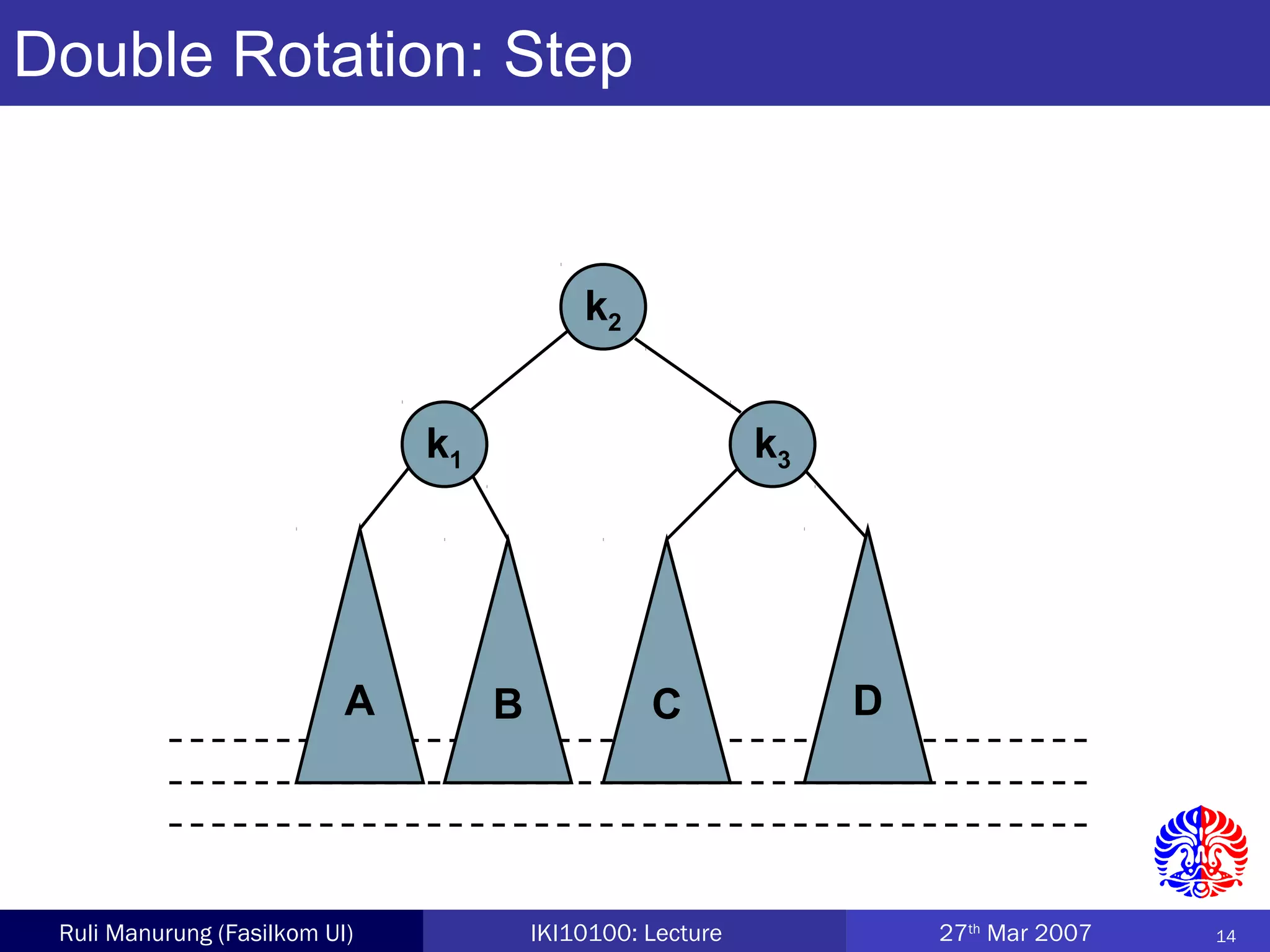
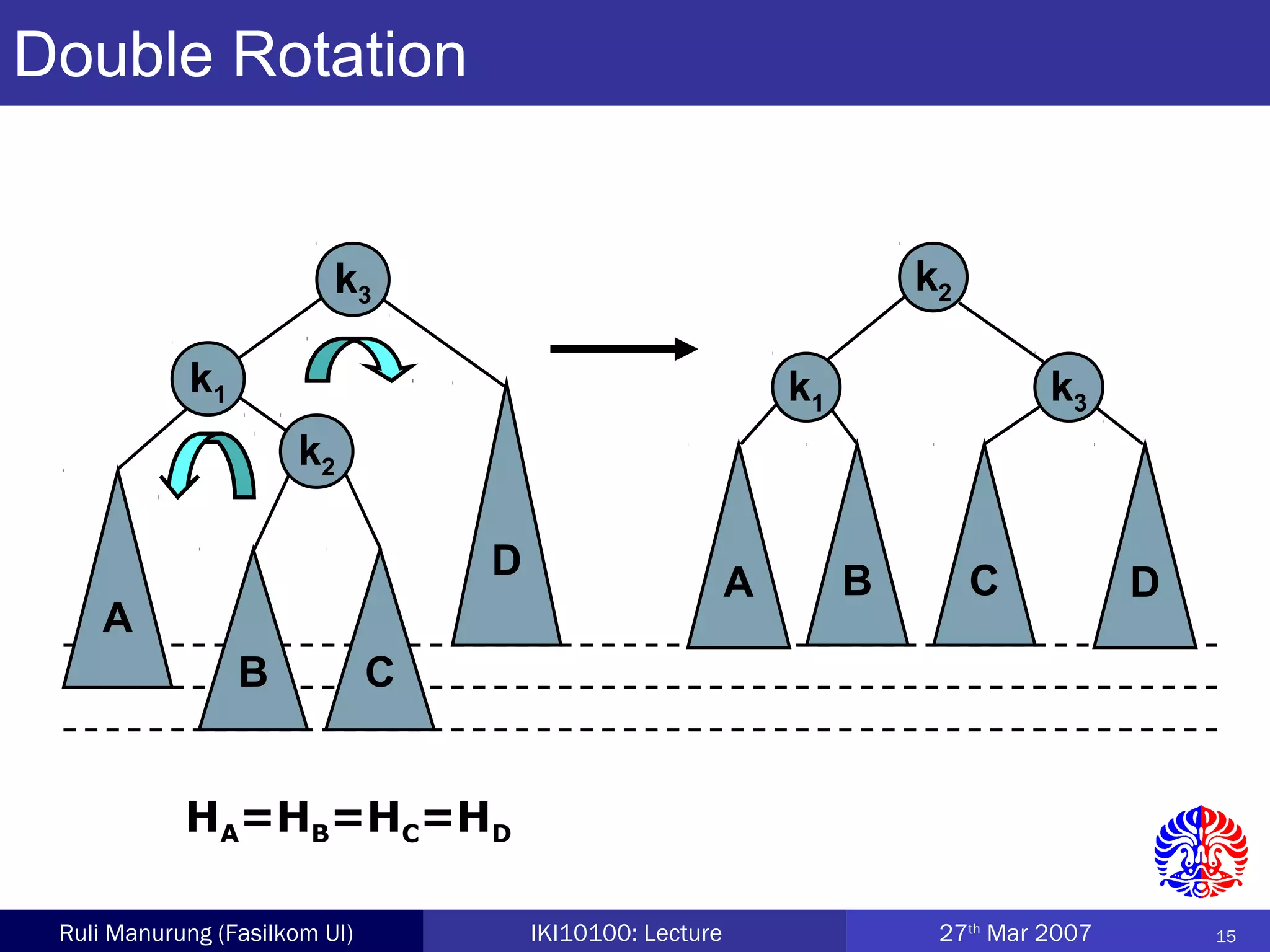
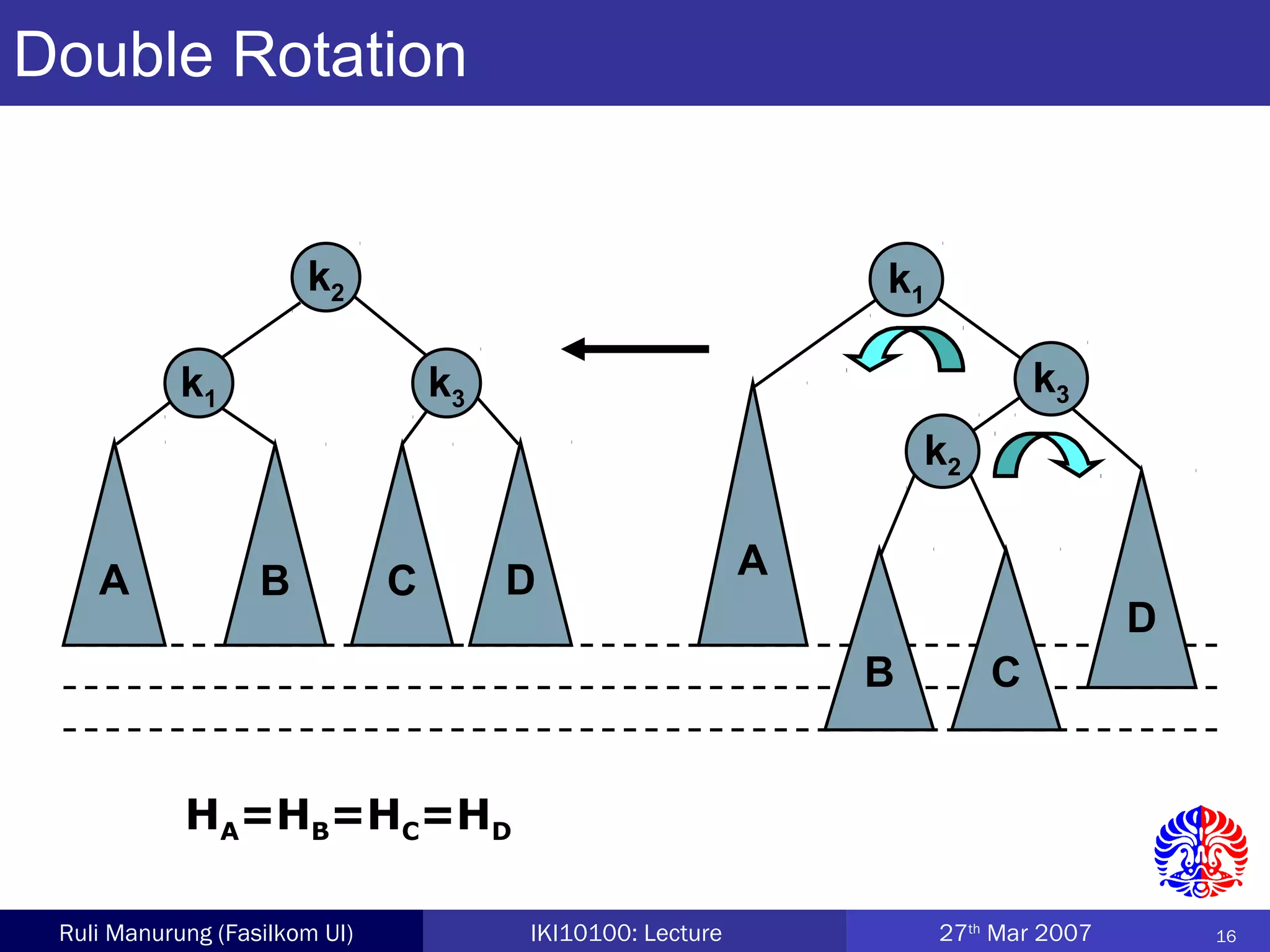
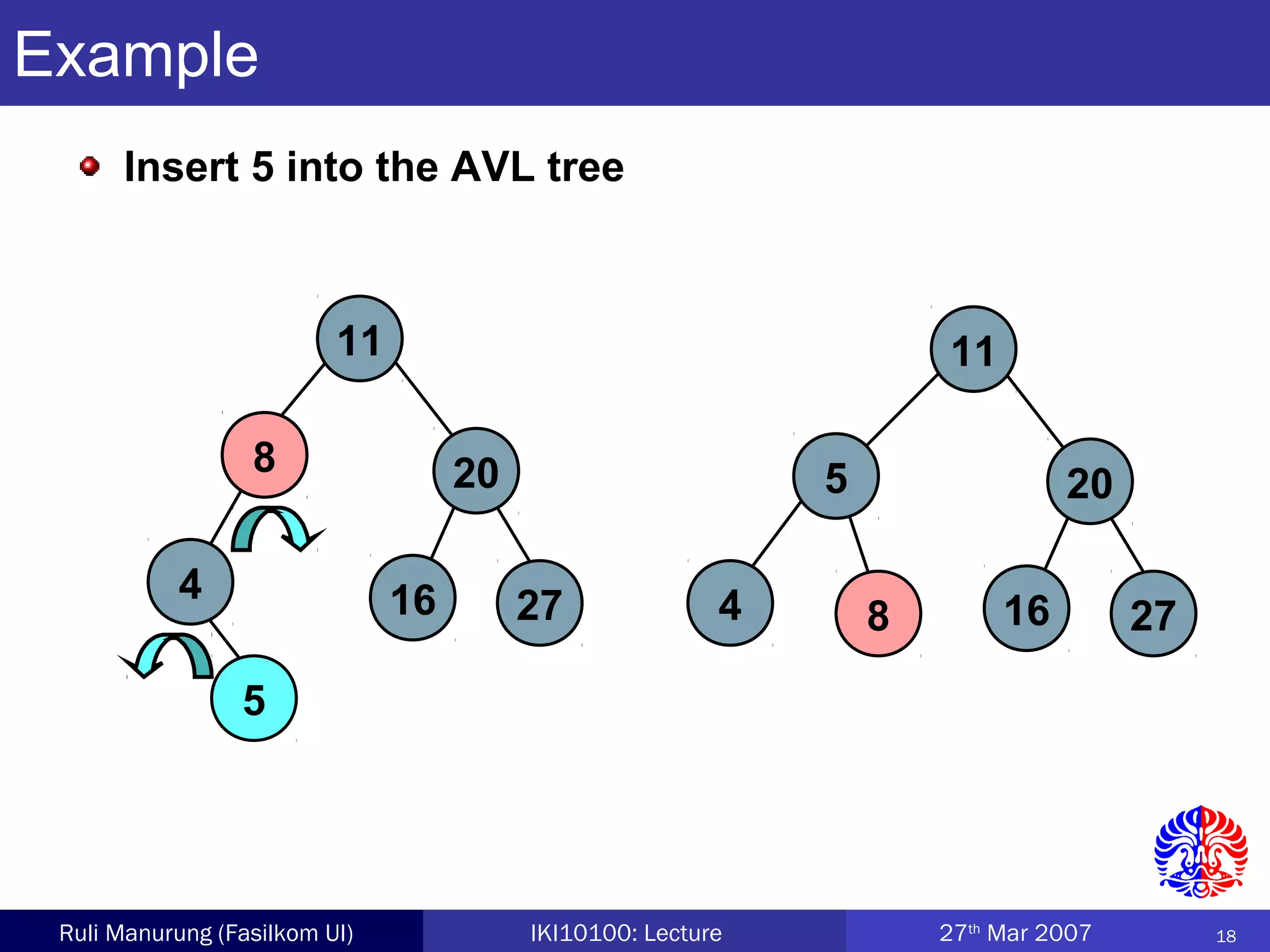
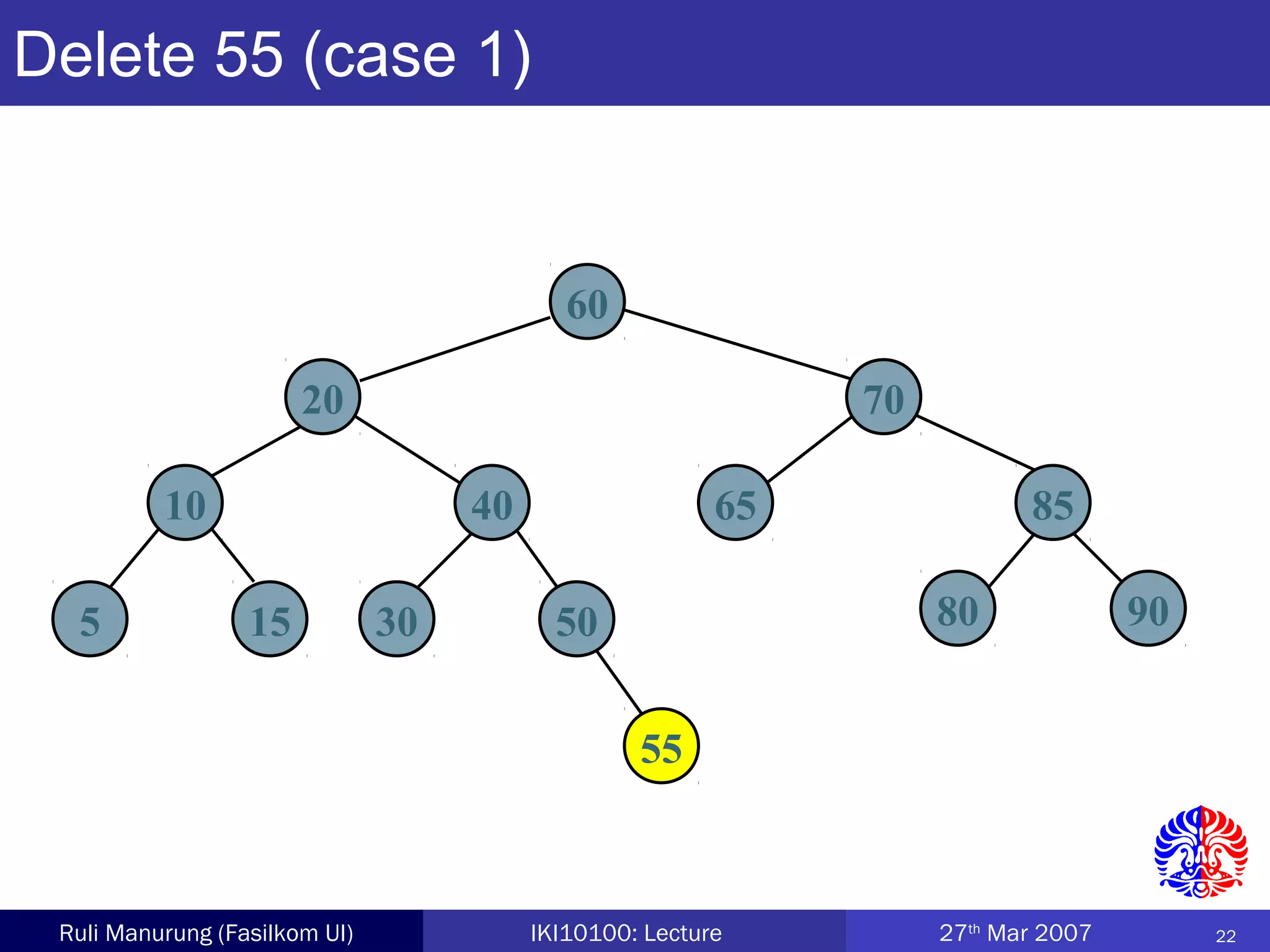
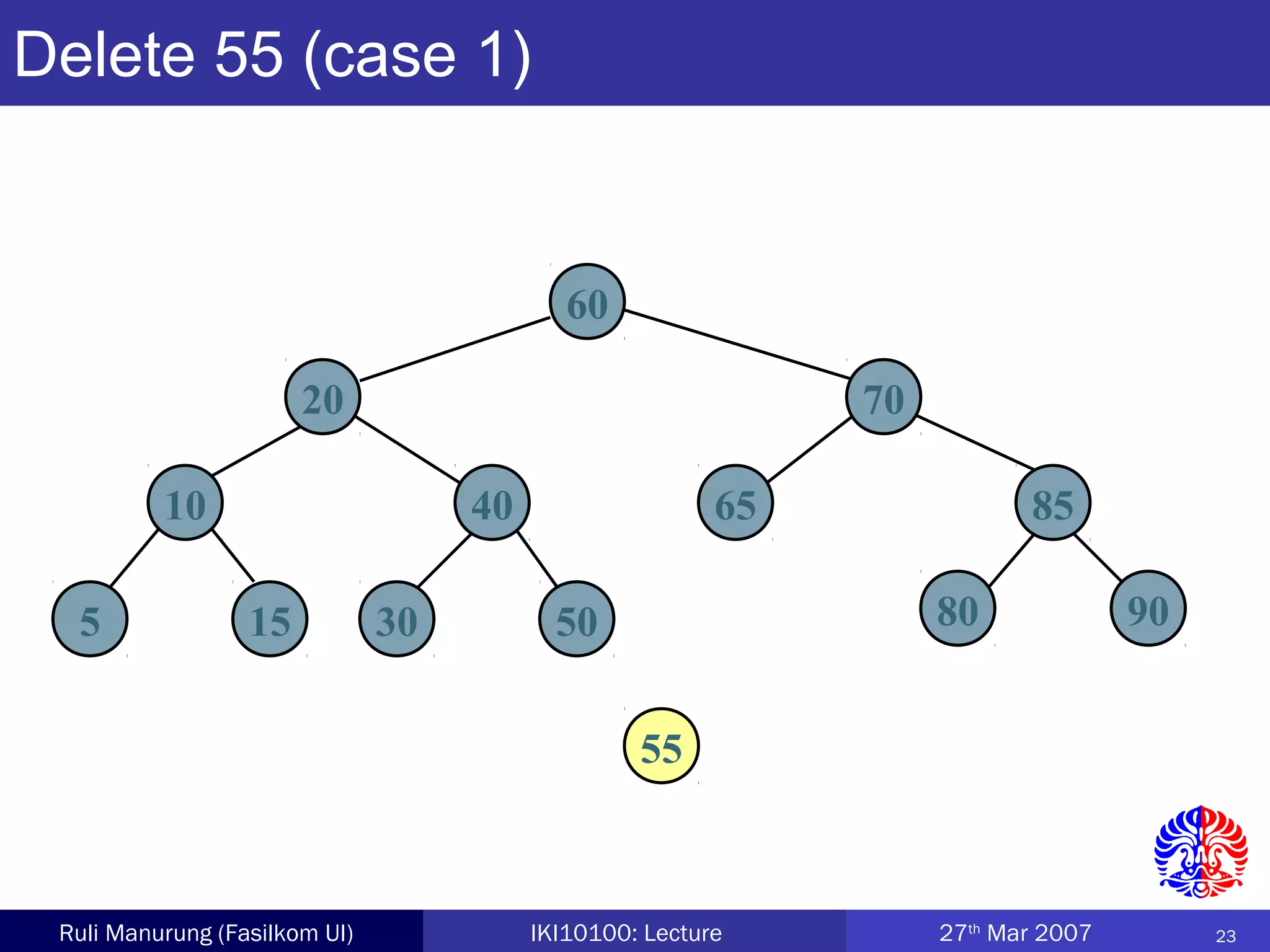
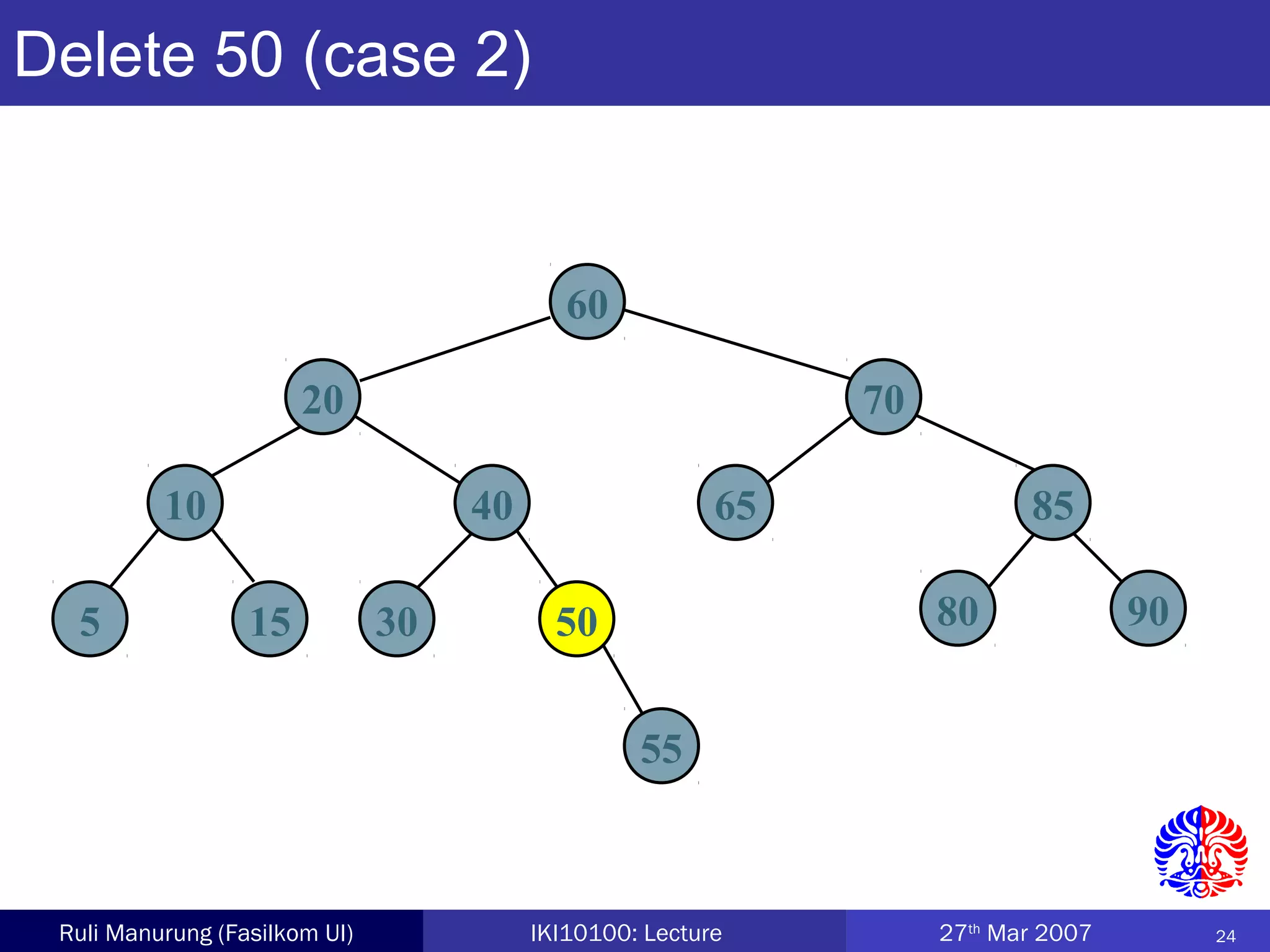
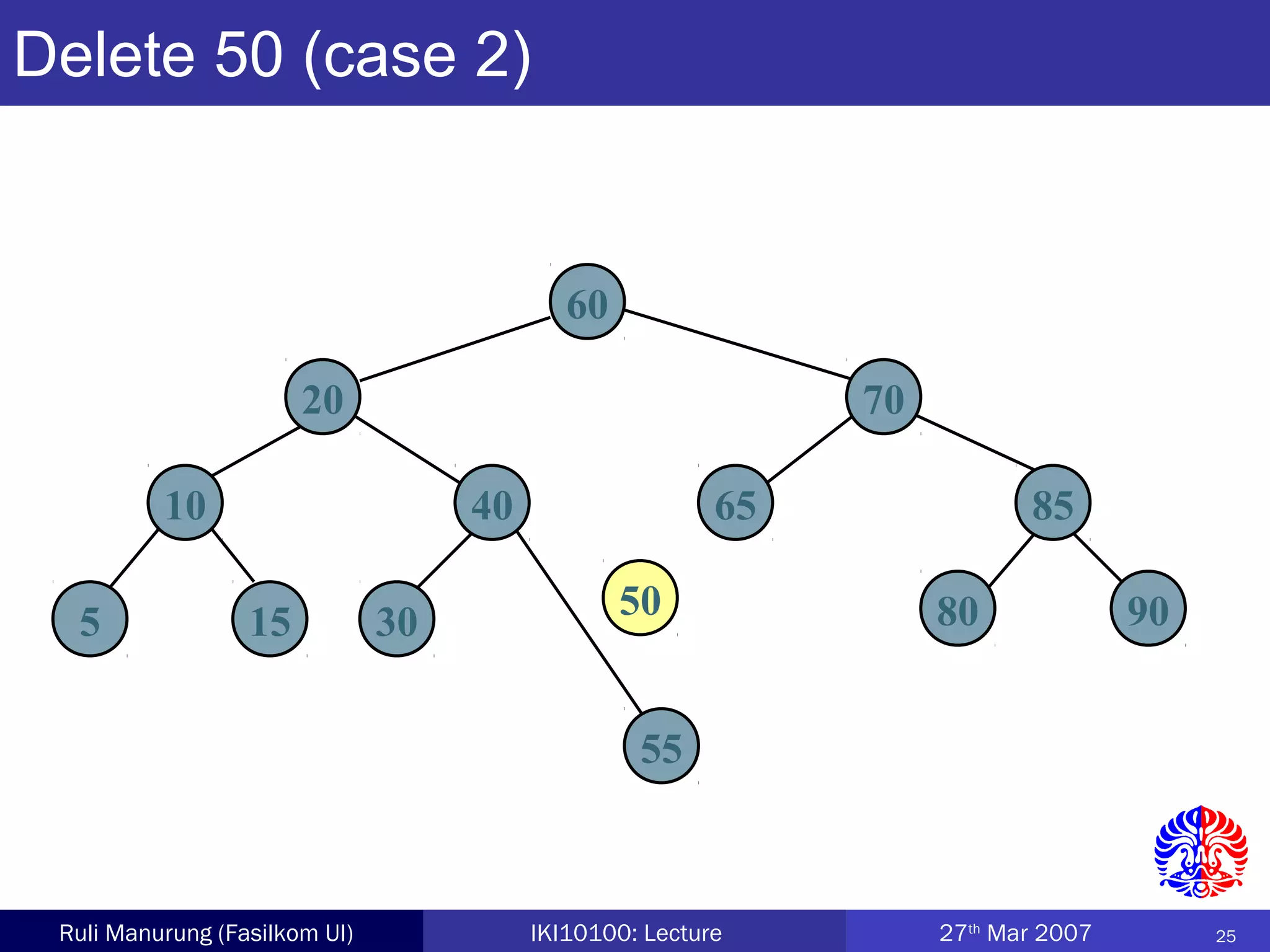
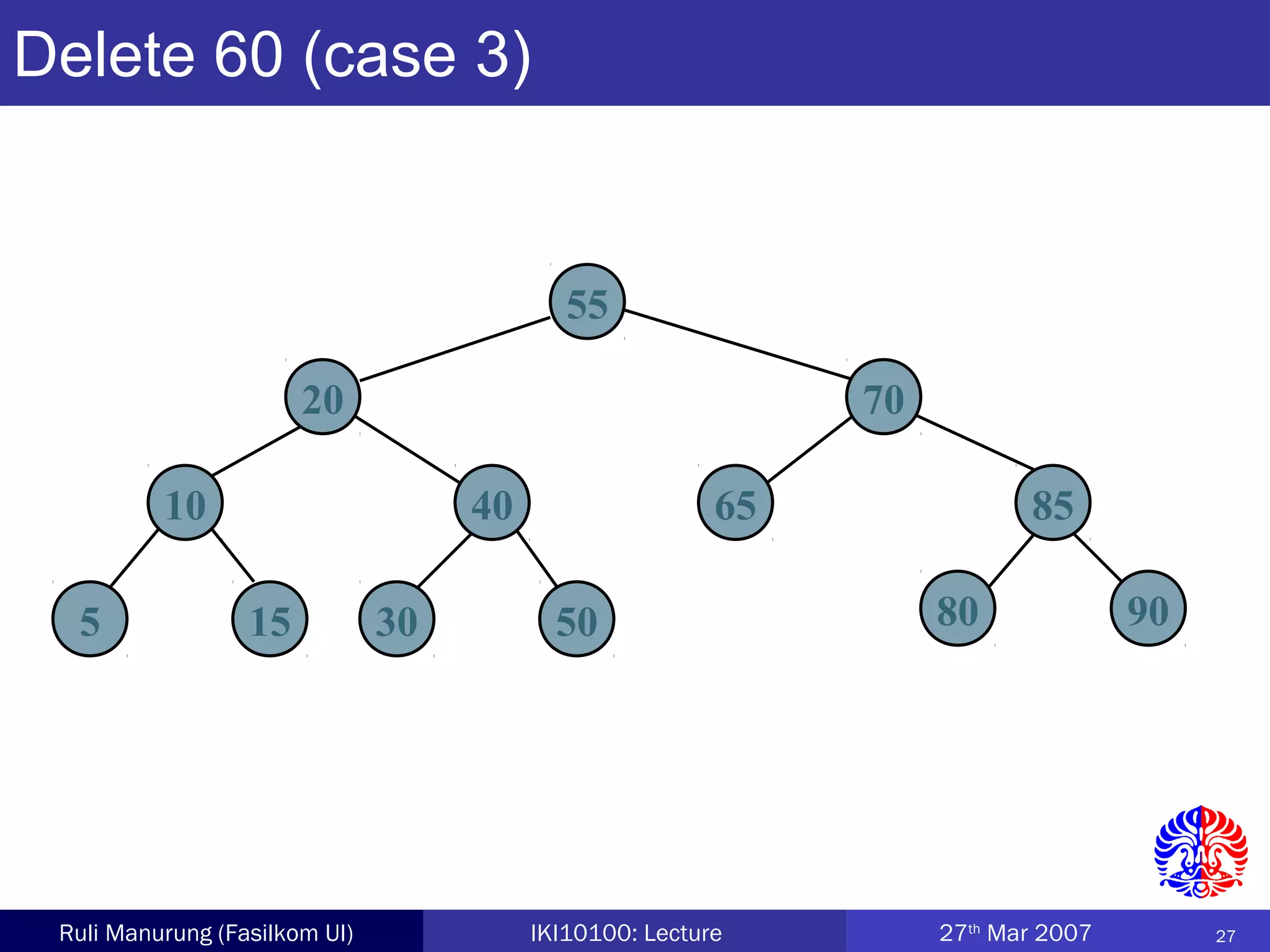
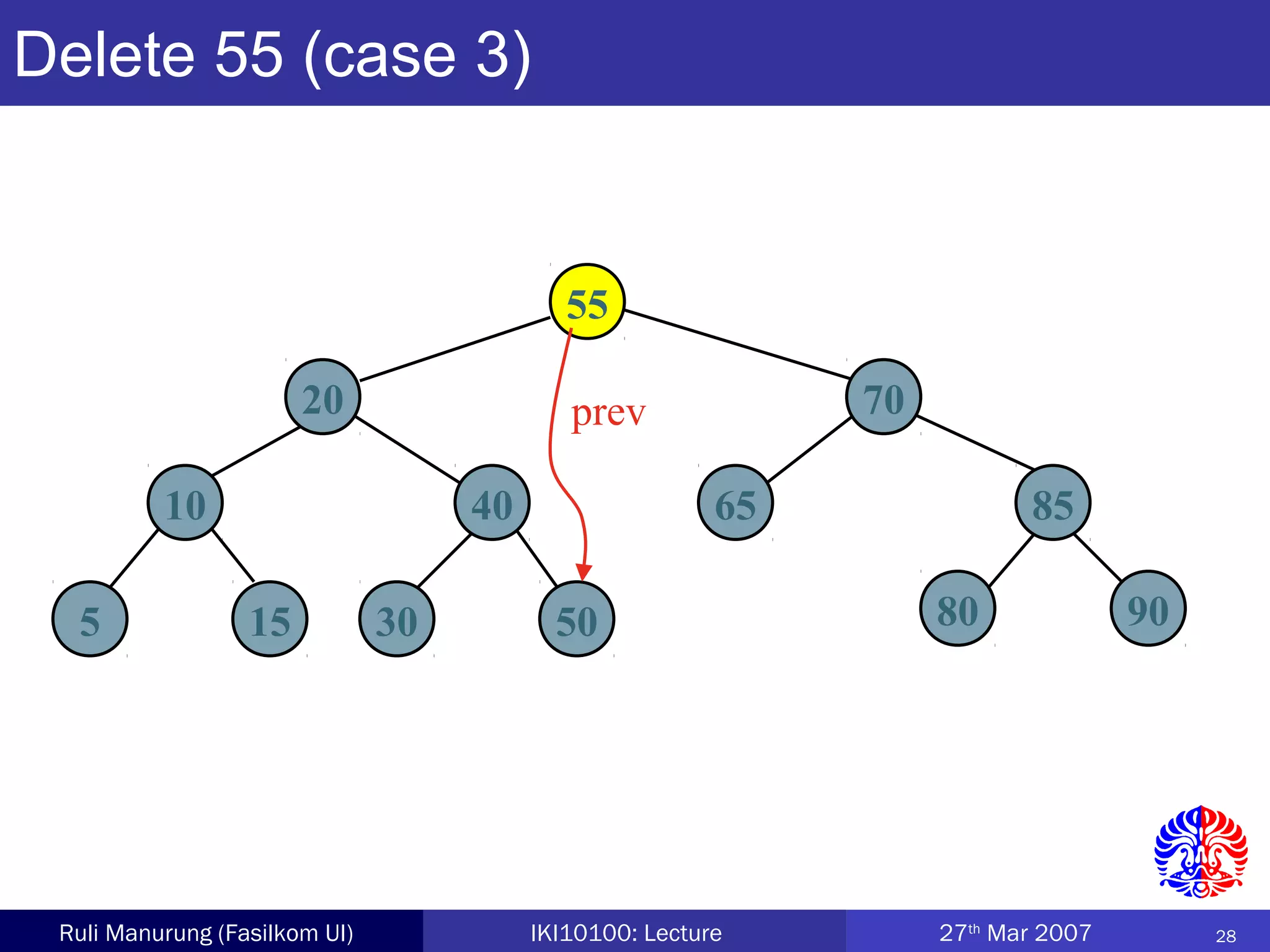
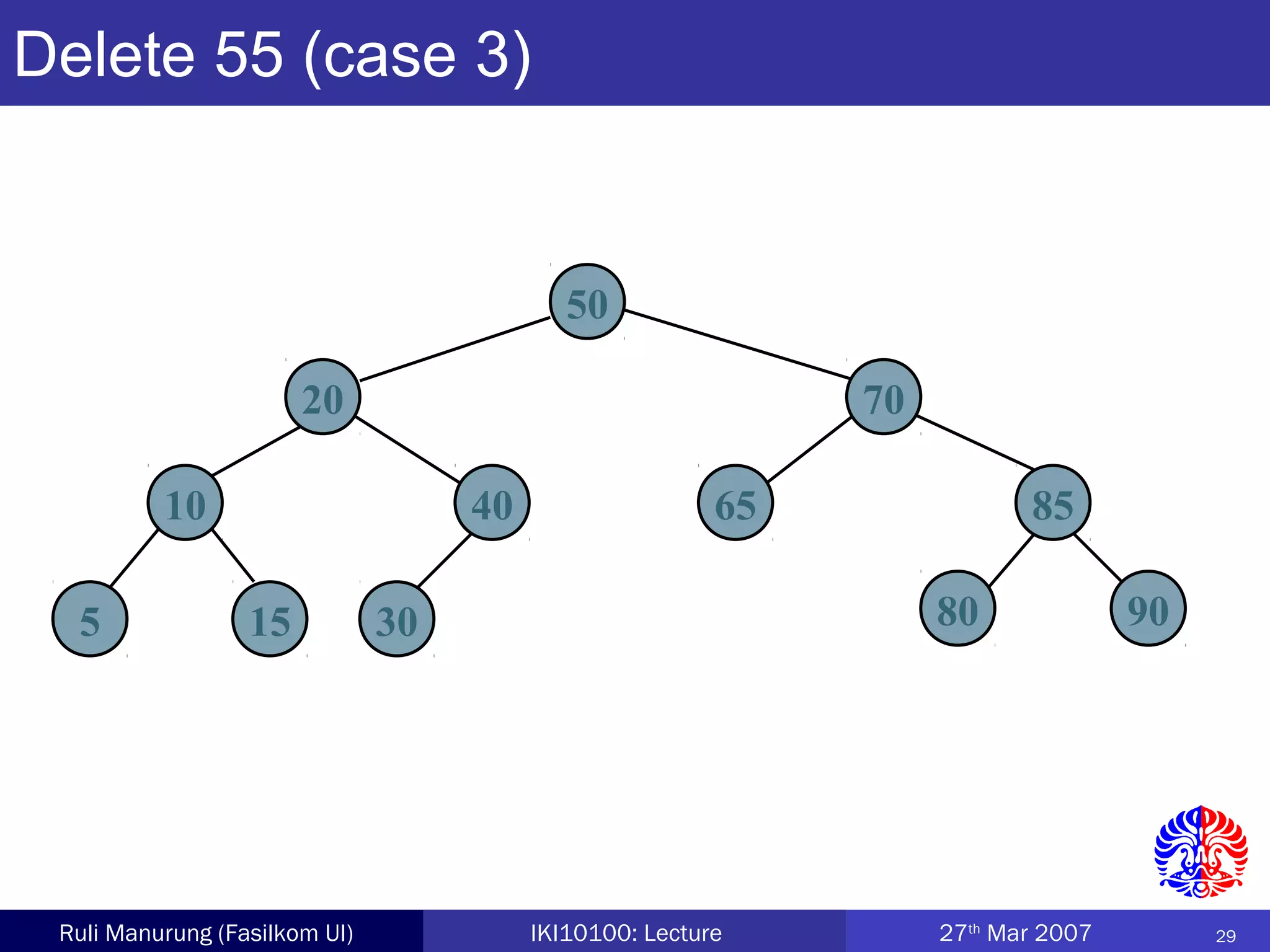
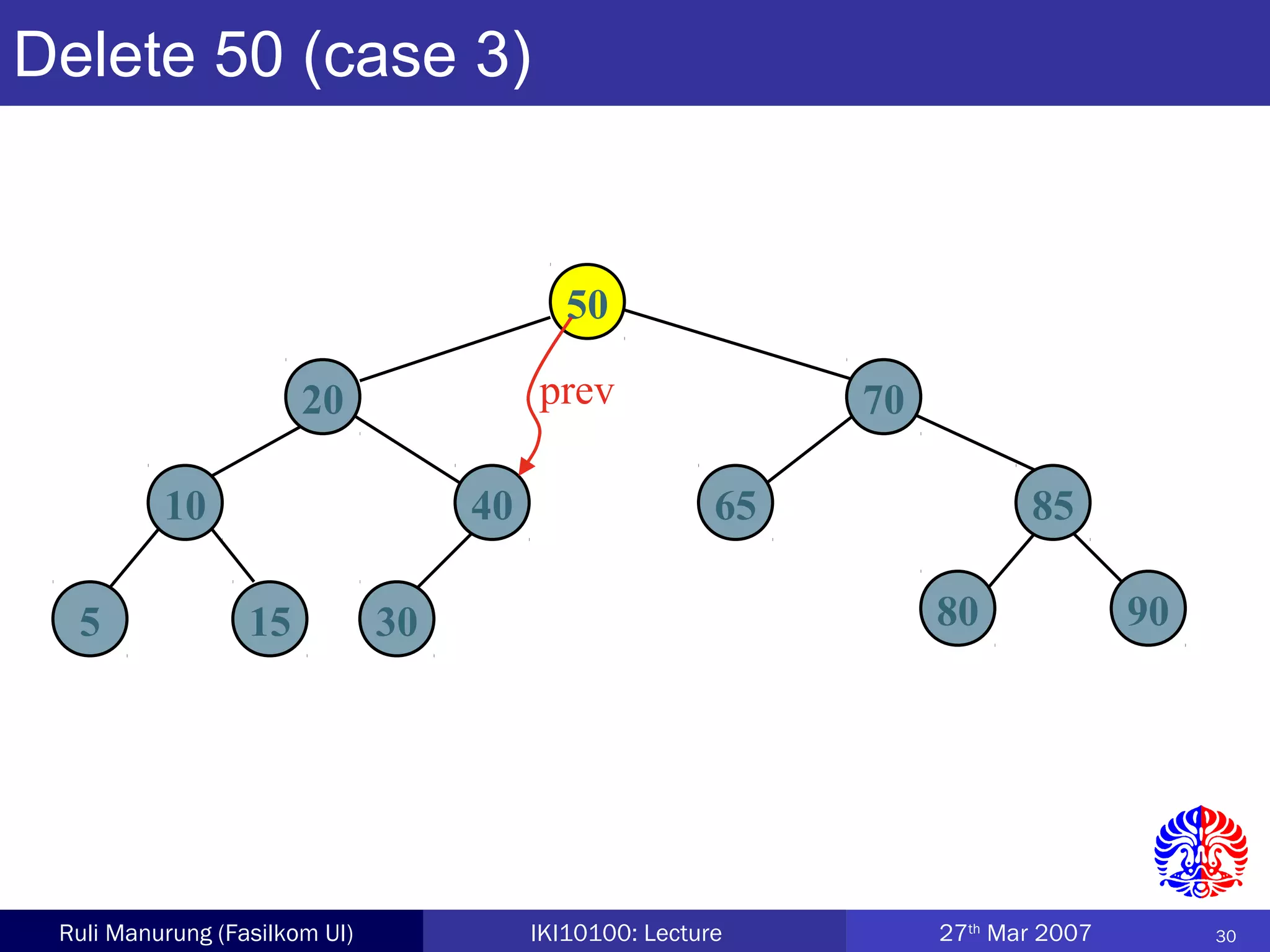
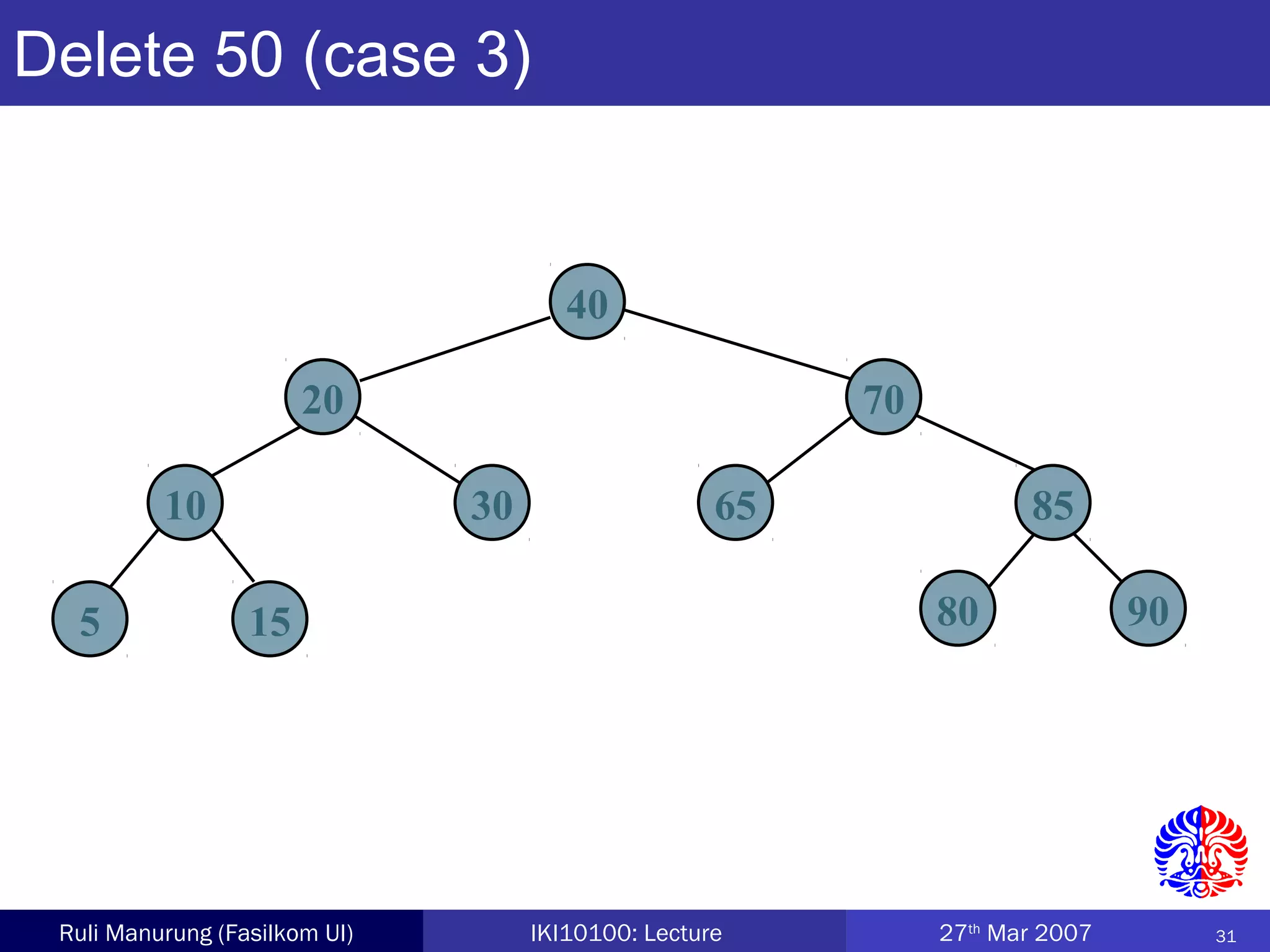
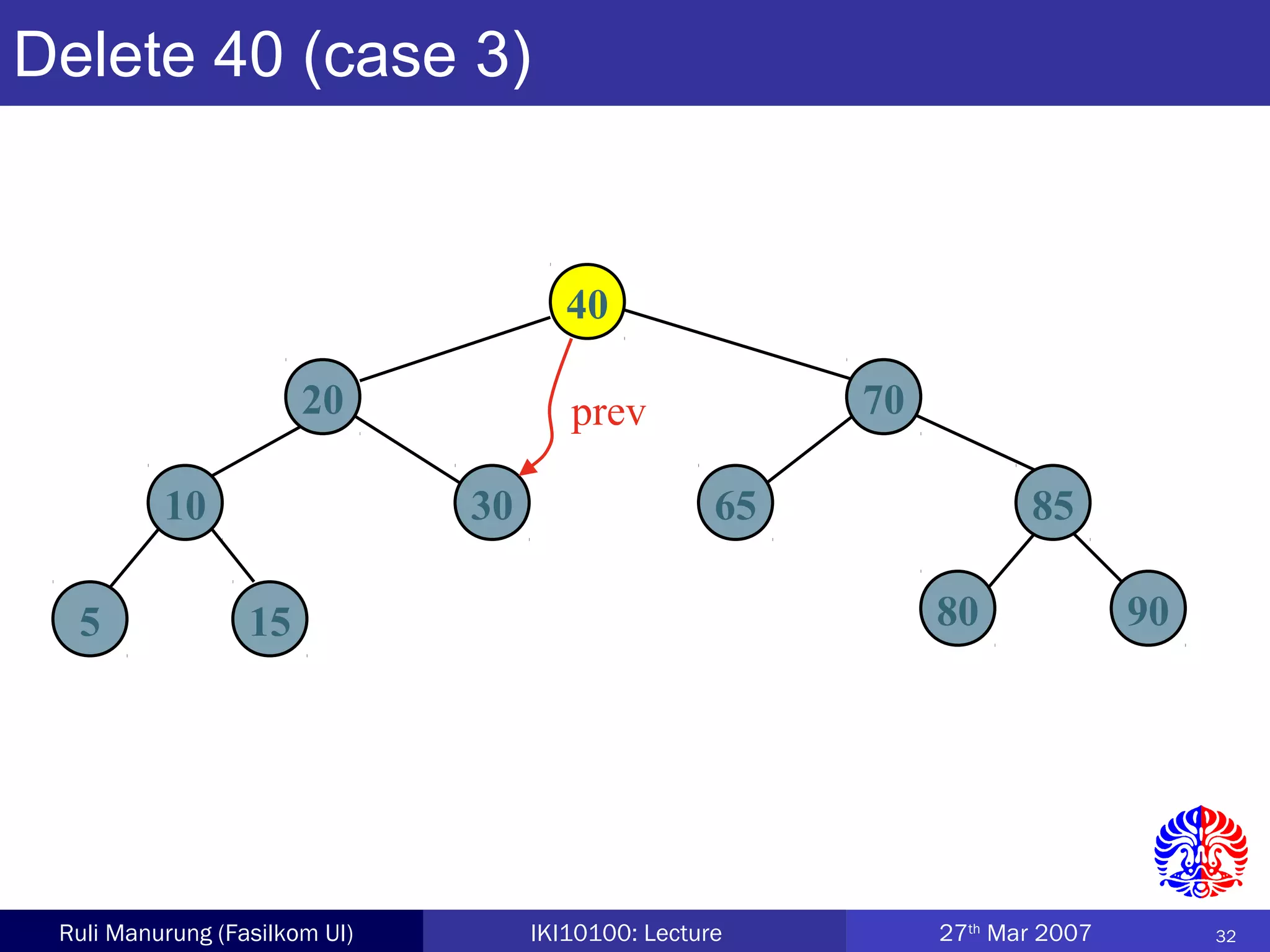
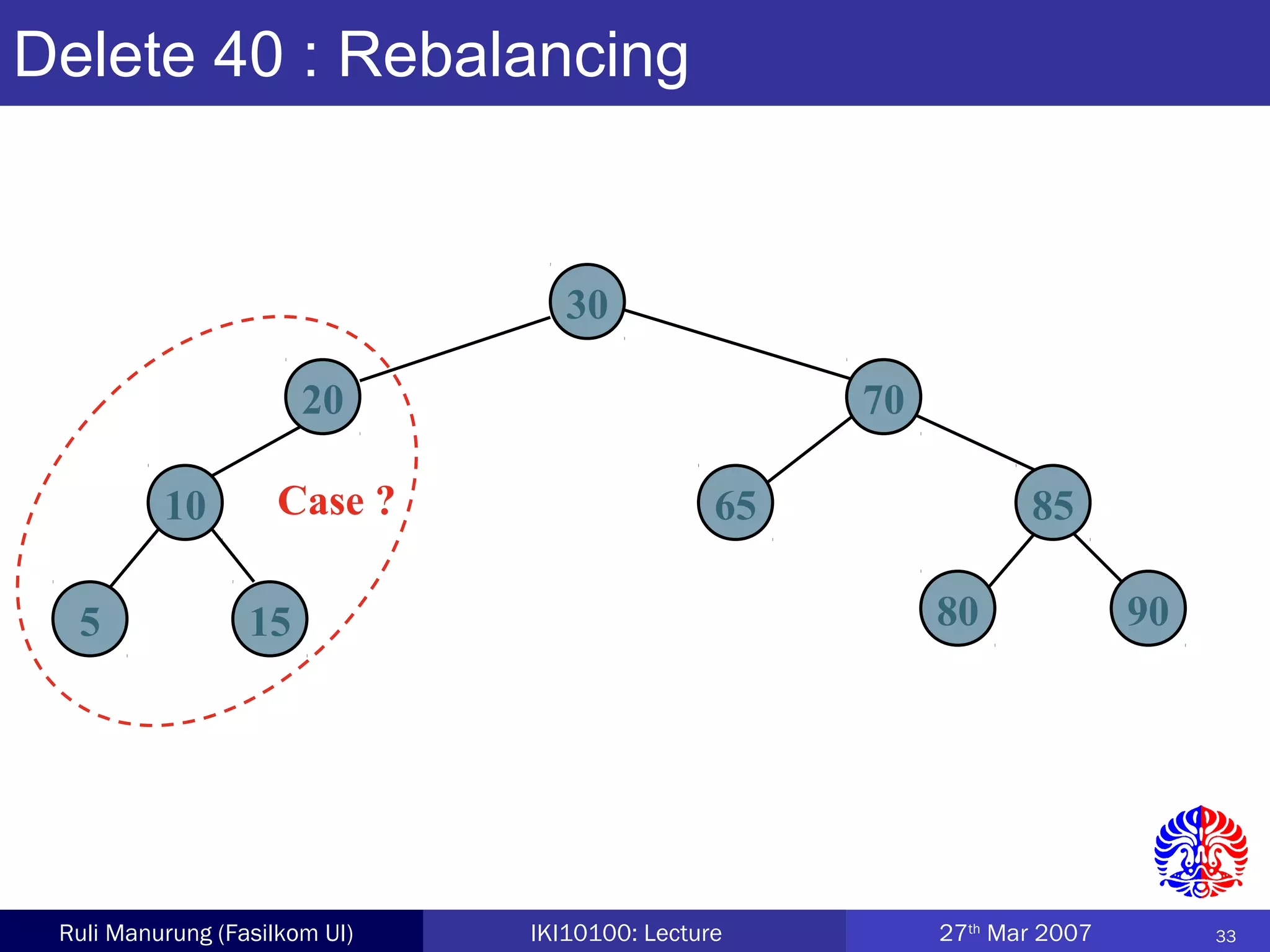
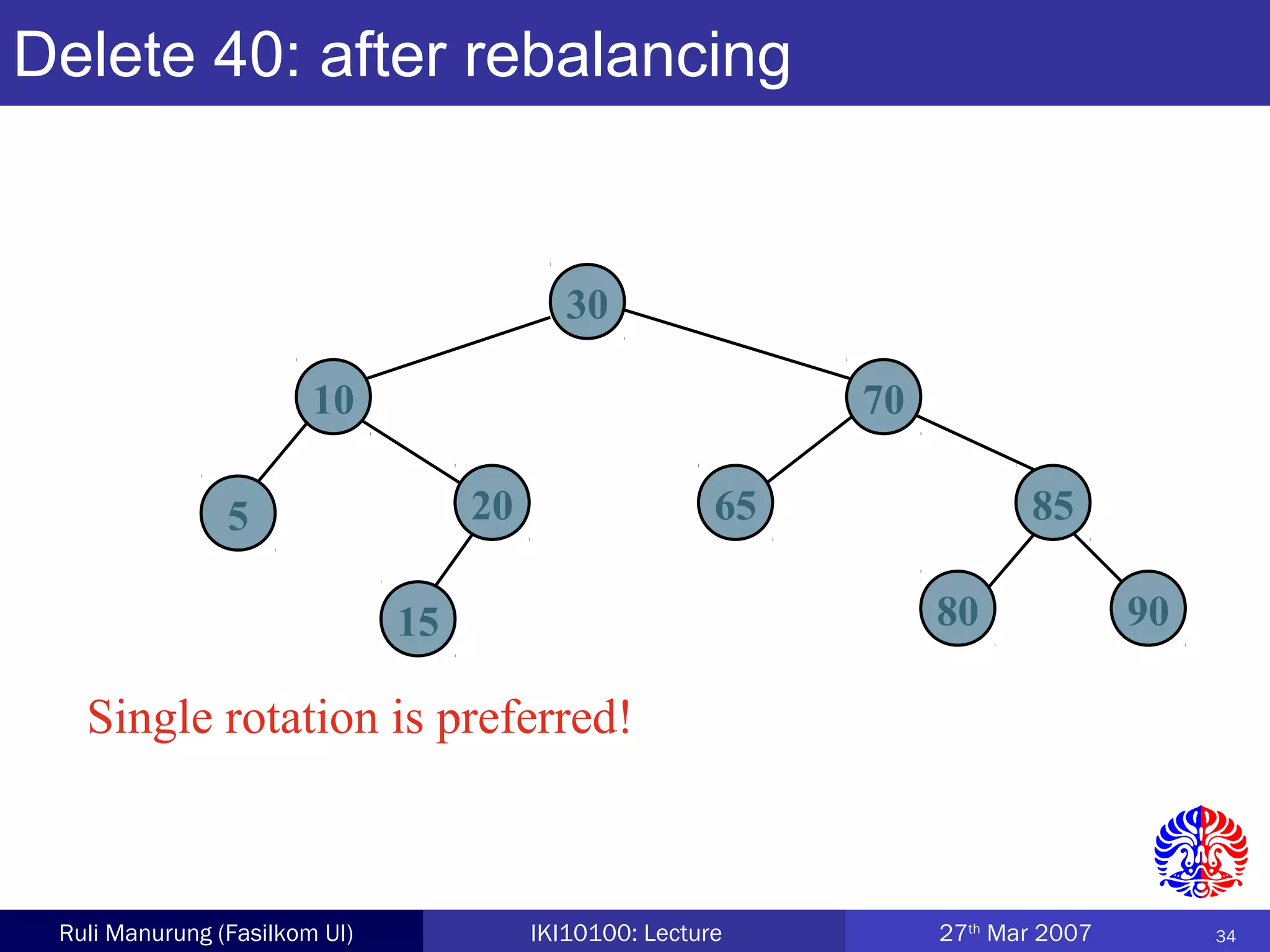
An AVL tree is a binary search tree in which
 for every node in the tree, the height of the left and
right subtrees differ by at most 1.
AVL property
violated here

Mar 2007
X X
AVL Trees
Unbalanced Binary Search Trees are bad. Worst
case: operations take O(n).
AVL (Adelson-Velskii & Landis) trees maintain
balance.
For each node in tree, height of left subtree and
height of right subtree differ by a maximum of 1.
H
H-1
H-2

Mar 2007
AVL Trees
10
5
3
20
2
1 3
10
5
3
20
1
43
5

Mar 2007
AVL Trees
12
8 16
4 10
2 6
14

Mar 2007
12
8 16
4 10
2 6
14
1
Insertion for AVL Tree
After insert 1

Mar 2007
Insertion for AVL Tree
To ensure balance condition for AVL-tree, after
insertion of a new node, we back up the path from the
inserted node to root and check the balance
condition for each node.
If after insertion, the balance condition does not hold
in a certain node, we do one of the following
rotations:
 Single rotation
 Double rotation

Mar 2007
Insertions Causing Imbalance
R
P
Q
k1
k2
Q
k2
P
k1
R
An insertion into the subtree:
 P (outside) - case 1
 Q (inside) - case 2
An insertion into the subtree:
 Q (inside) - case 3
 R (outside) - case 4
HP=HQ=HR

Mar 2007
A
k2
B
k1
C
CB
A
k1
k2
Single Rotation (case 1)
HA=HB+1
HB=HC

Mar 2007
Single Rotation (case 4)
C
k1
B
k2
A
A B C
k2
k1
HA=HB
HC=HB+1

Mar 2007
Q
k2
P
k1
R
R
P
Q
k1
k2
Problem with Single Rotation
Single rotation does not work for case 2 and 3 (inside
case)
HQ=HP+1
HP=HR

Mar 2007
C
k3
A
k1
D
B
k2
Double Rotation: Step
C
k3
A
k1
D
B
k2
HA=HB=HC=HD

Mar 2007
C
k3
A
k1
DB
k2
Double Rotation: Step

Mar 2007
C
k3
A
k1
D
B
k2
C
k3
A
k1
DB
k2
Double Rotation
HA=HB=HC=HD

Mar 2007
B
k1
D
k3
A
C
k2
B
k1
D
k3
A C
k2
Double Rotation
HA=HB=HC=HD

Mar 2007
3
Example
Insert 3 into the AVL tree
11
8 20
4 16 27
8
8
11
4 20
3 16 27

Mar 2007
Example
Insert 5 into the AVL tree
5
11
8 20
4 16 27 8
11
5 20
4 16 27
8

Mar 2007
AVL Trees: Exercise
Insertion order:
 10, 85, 15, 70, 20, 60, 30, 50, 65, 80, 90, 40, 5, 55

Mar 2007
Remove Operation in AVL Tree
Removing a node from an AVL Tree is the same as
removing from a binary search tree. However, it may
unbalance the tree.
Similar to insertion, starting from the removed node
we check all the nodes in the path up to the root for
the first unbalance node.
Use the appropriate single or double rotation to
balance the tree.
May need to continue searching for unbalanced
nodes all the way to the root.

Mar 2007
Deletion X in AVL Trees
Deletion:
 Case 1: if X is a leaf, delete X
 Case 2: if X has 1 child, use it to replace X
 Case 3: if X has 2 children, replace X with its inorder
predecessor (and recursively delete it)
Rebalancing

Mar 2007
Delete 55 (case 1)
60
20 70
10 40 65 85
5 15 30 50 80 90
55

Mar 2007
Delete 50 (case 2)
60
20 70
10 40 65 85
5 15 30 50 80 90
55

Mar 2007
Delete 50 (case 2)
60
20 70
10 40 65 85
5 15 30
50 80 90
55

Mar 2007
Delete 60 (case 3)
60
20 70
10 40 65 85
5 15 30 50 80 90
55
prev

Mar 2007
Delete 60 (case 3)
55
20 70
10 40 65 85
5 15 30 50 80 90

Mar 2007
Delete 55 (case 3)
55
20 70
10 40 65 85
5 15 30 50 80 90
prev

Mar 2007
Delete 55 (case 3)
50
20 70
10 40 65 85
5 15 30 80 90

Mar 2007
Delete 50 (case 3)
50
20 70
10 40 65 85
5 15 30 80 90
prev

Mar 2007
Delete 50 (case 3)
40
20 70
10 30 65 85
5 15 80 90

Mar 2007
Delete 40 (case 3)
40
20 70
10 30 65 85
5 15 80 90
prev

Mar 2007
Delete 40 : Rebalancing
30
20 70
10 65 85
5 15 80 90
Case ?

Mar 2007
Delete 40: after rebalancing
30
7010
20 65 855
15 80 90
Single rotation is preferred!

Mar 2007
AVL Tree:
The depth of AVL Trees is at most logarithmic.
So, all of the operations on AVL trees are also
logarithmic.
Find element, insert element, and remove element
operations all have complexity O(log n) for worst
case
The worst-case height is at most 44 percent more
than the minimum possible for binary trees.

data structure on bca.

More Related Content

Similar to data structure on bca.

More from invertis university

Recently uploaded

data structure on bca.