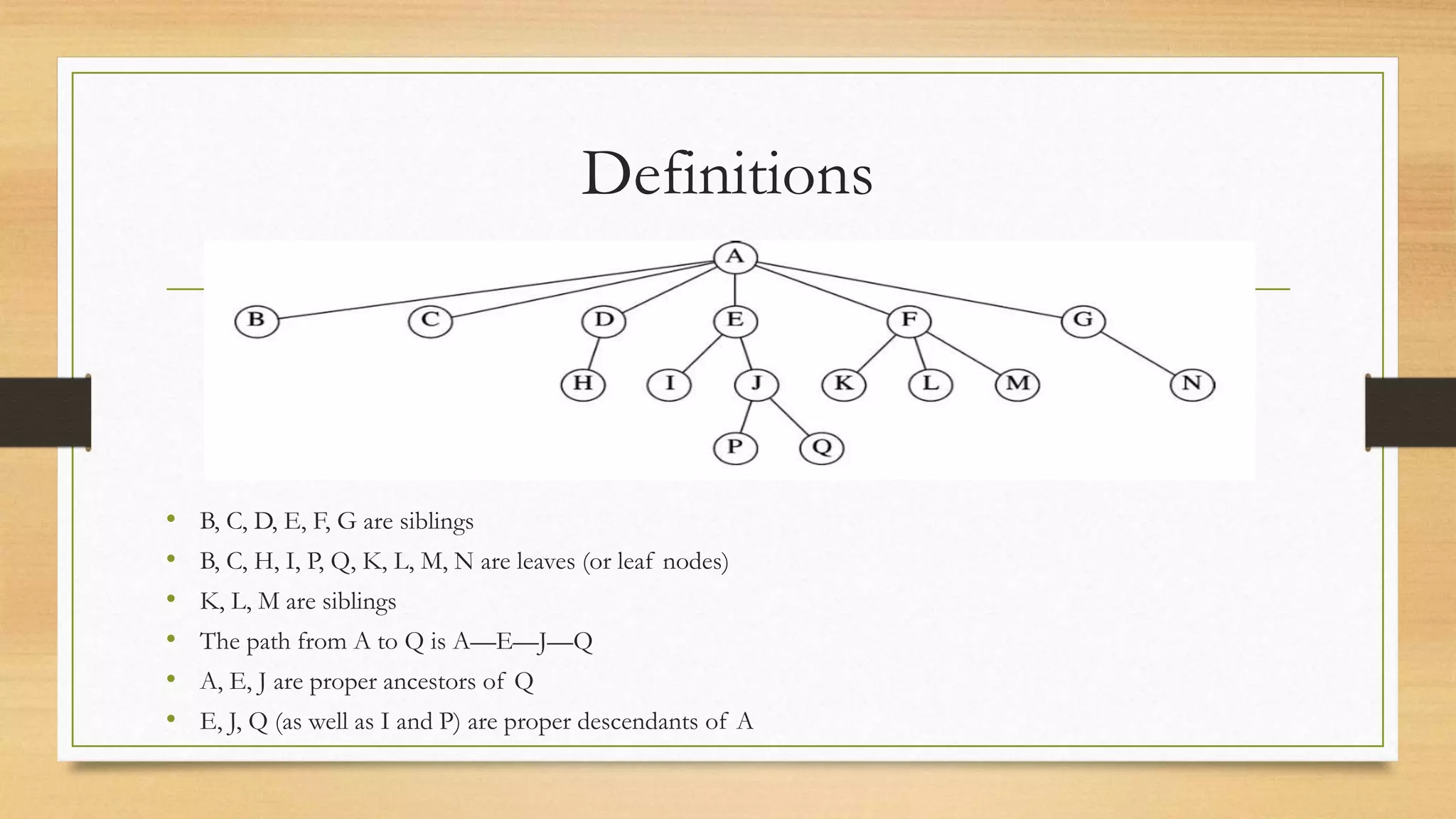
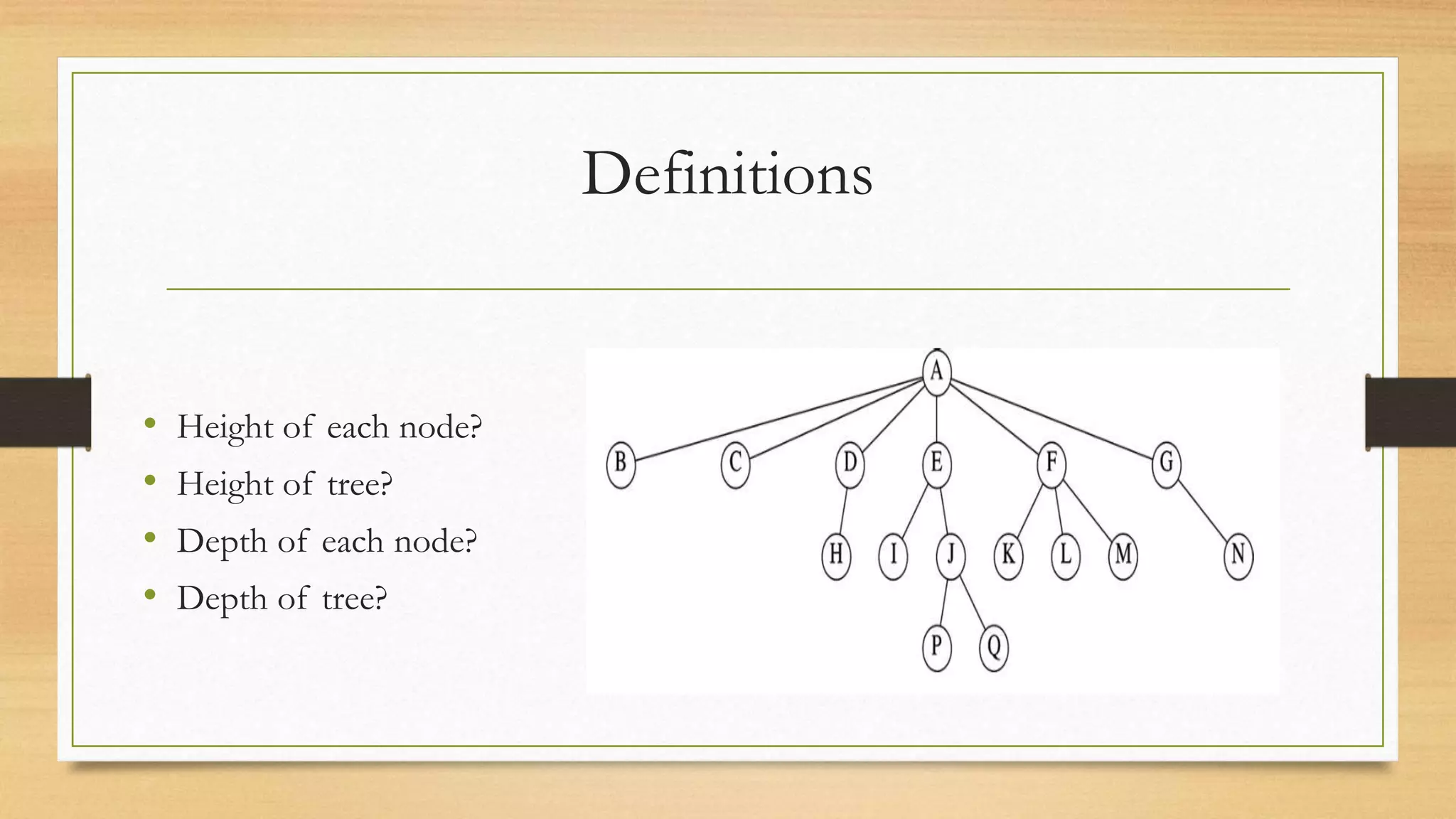
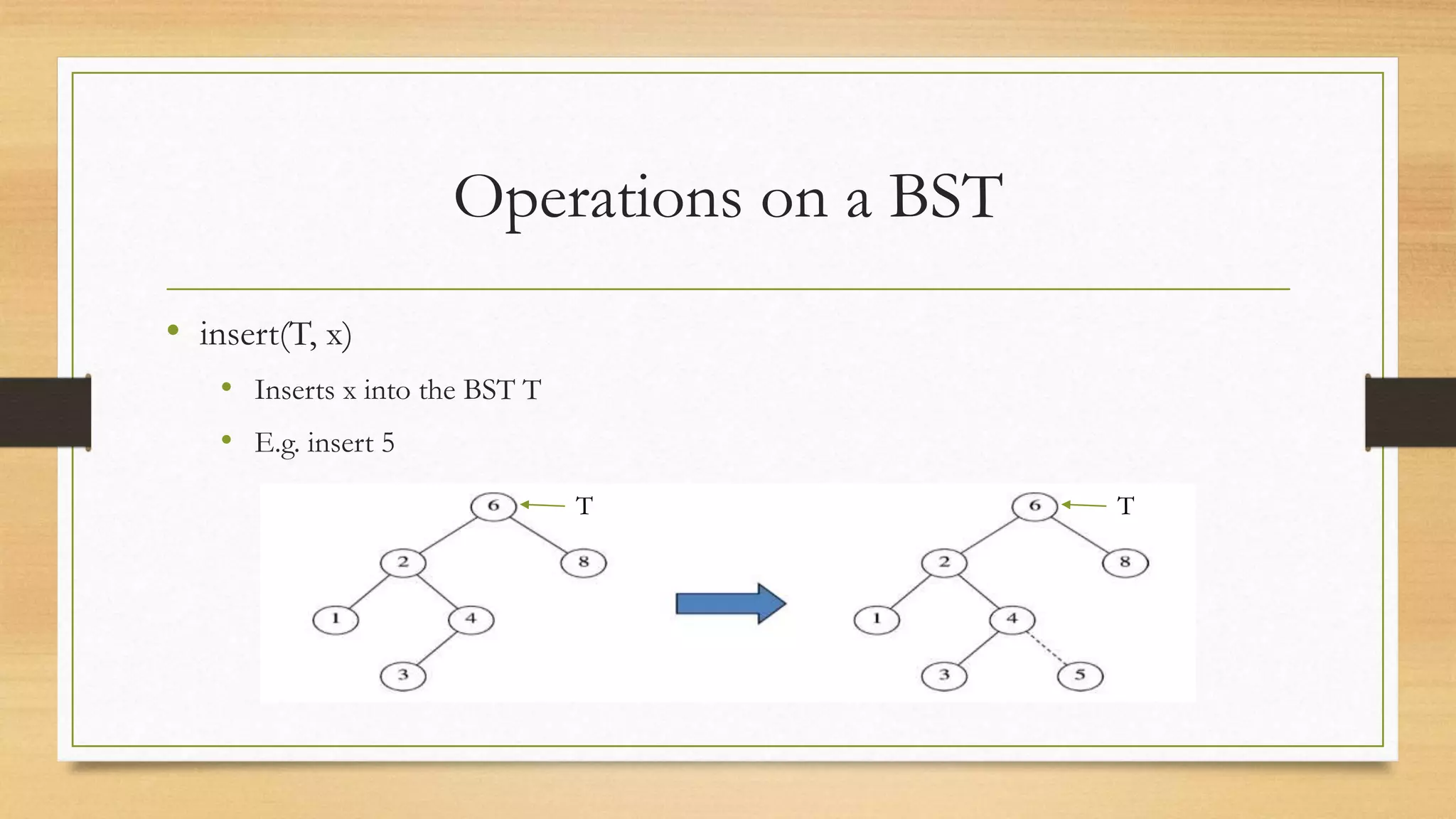
This document defines and explains binary search trees (BSTs). It defines key BST terms like root, leaf nodes, and height. It also outlines common BST operations like search, insertion, deletion, finding the minimum/maximum elements, and tree traversals. Search, minimum/maximum, and traversal operations have linear time complexity based on tree height, while insertion and deletion are O(h) where h is the tree height. The document uses examples to illustrate BST concepts and operations.