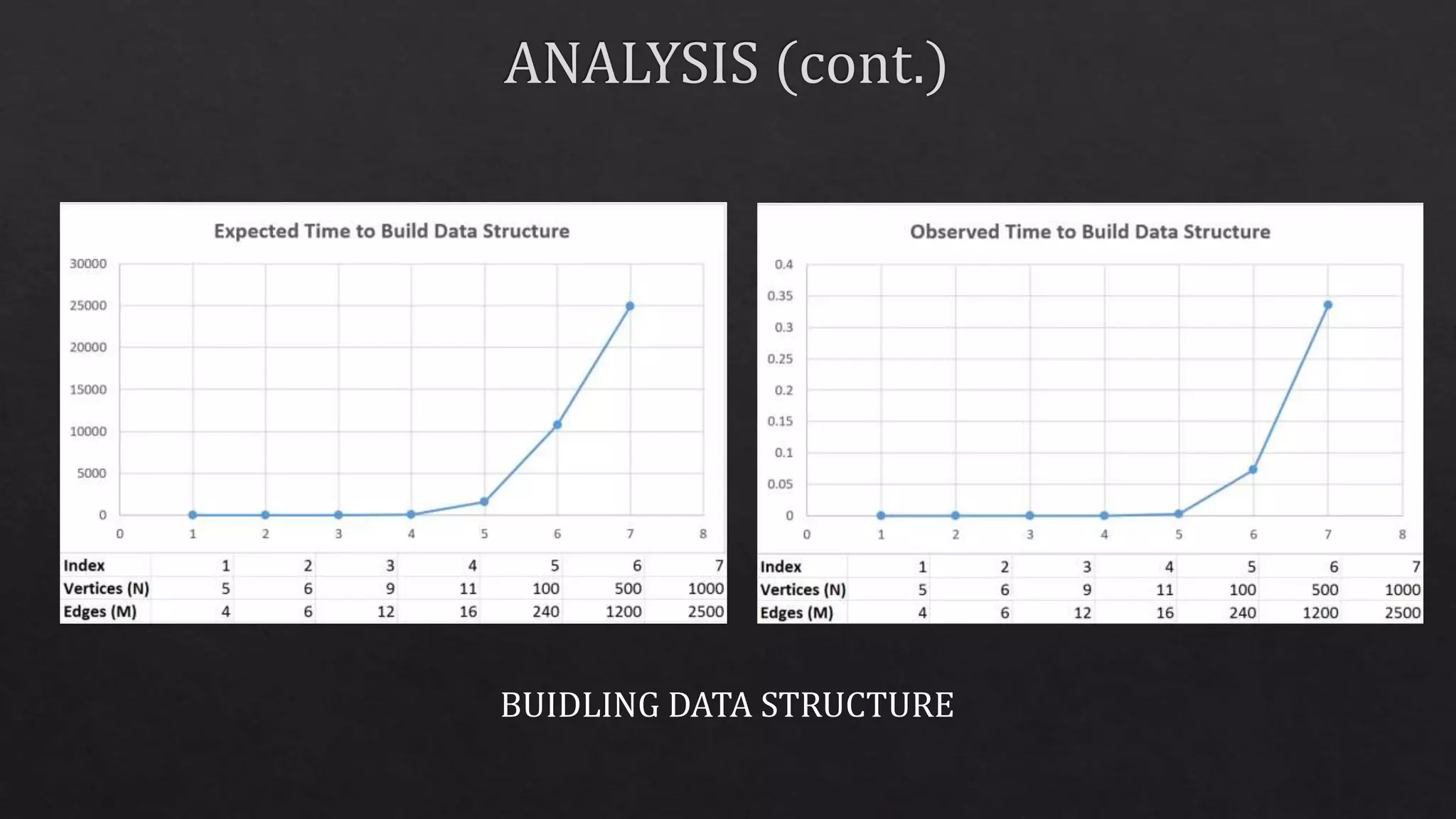
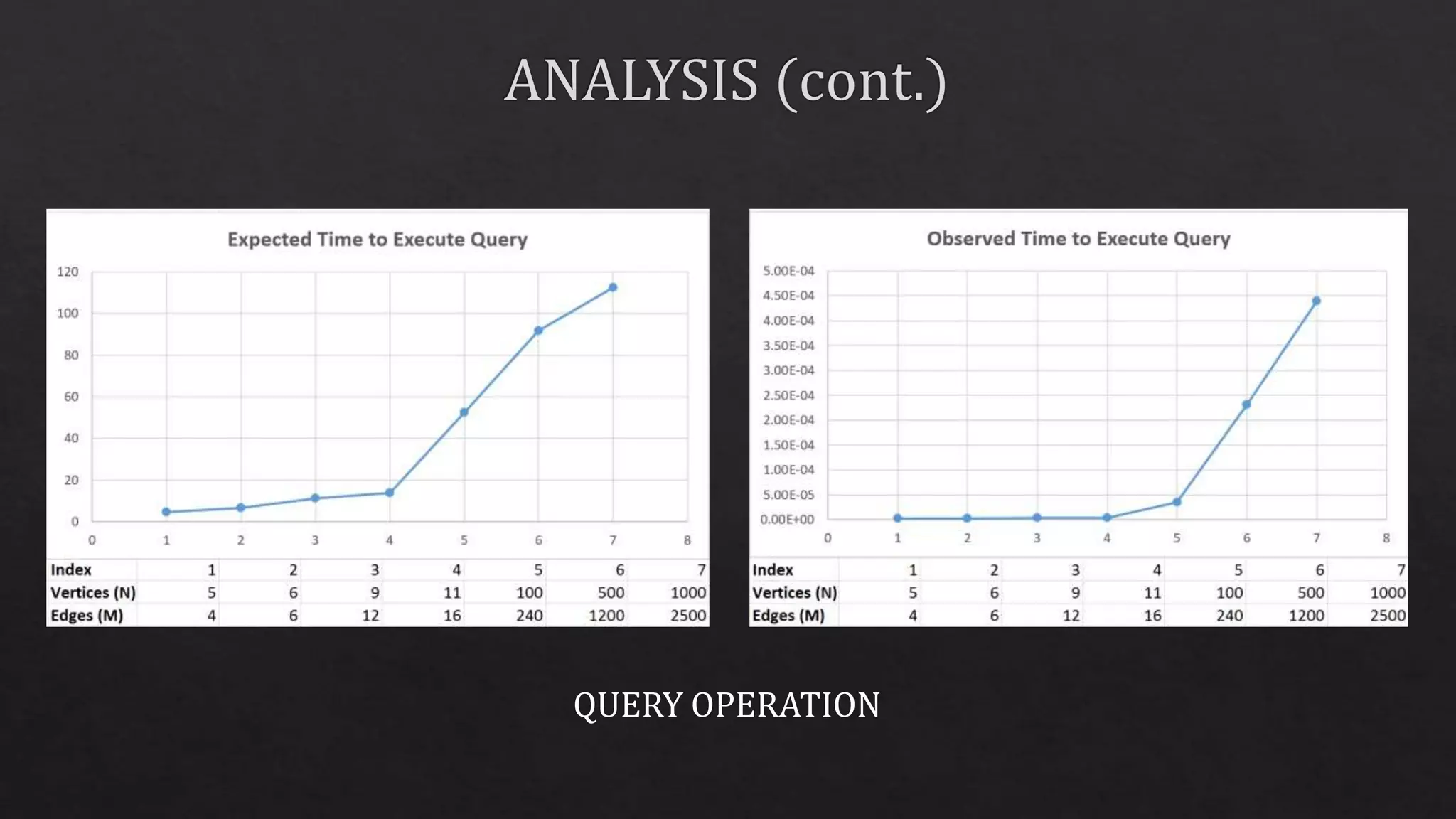
The document discusses a research project on dynamic depth-first search (DFS) in undirected graphs, presenting methods to break the O(m) complexity barrier. It introduces new data structures and algorithms to improve efficiency in handling graph queries. Key findings and the overall complexity of the approach are highlighted, demonstrating significant advancements in the field.




![5
2 5
1 2 5 6
0 1 2 3 4 5
18 17 13 19 15 11 20
[0,6]
[4,6]
[4,5]
[6,6]
[0,0] [1,1] [2,2] [3,3] [4,4] [5,5]
[0,3]
[0,1] [2,3]
0 1 2 3 4 5 6
Array](https://image.slidesharecdn.com/finalpresentatonteam10641-160508002110/75/Dynamic-DFS-in-Undirected-Graph-using-Segment-Tree-5-2048.jpg)
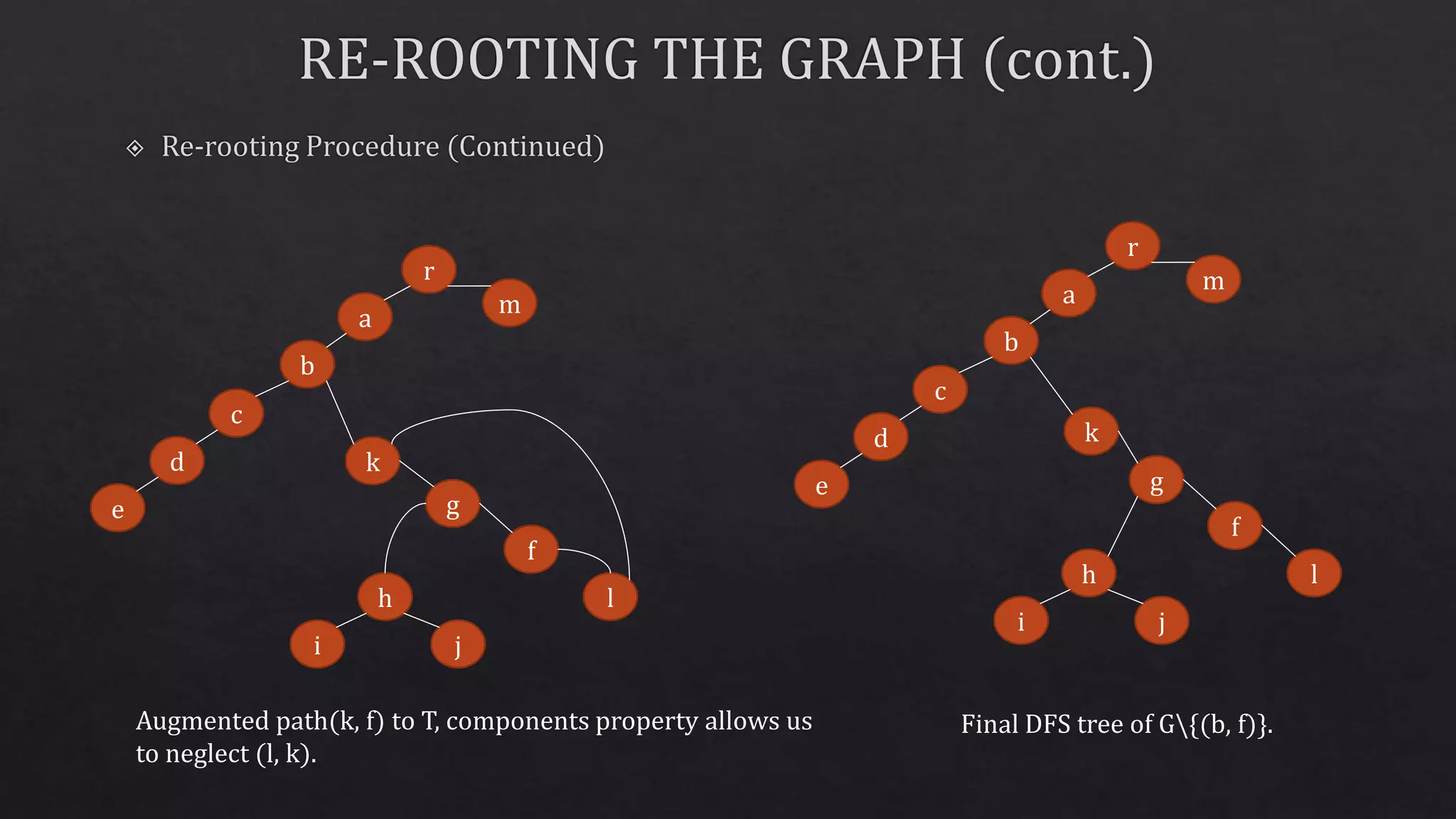
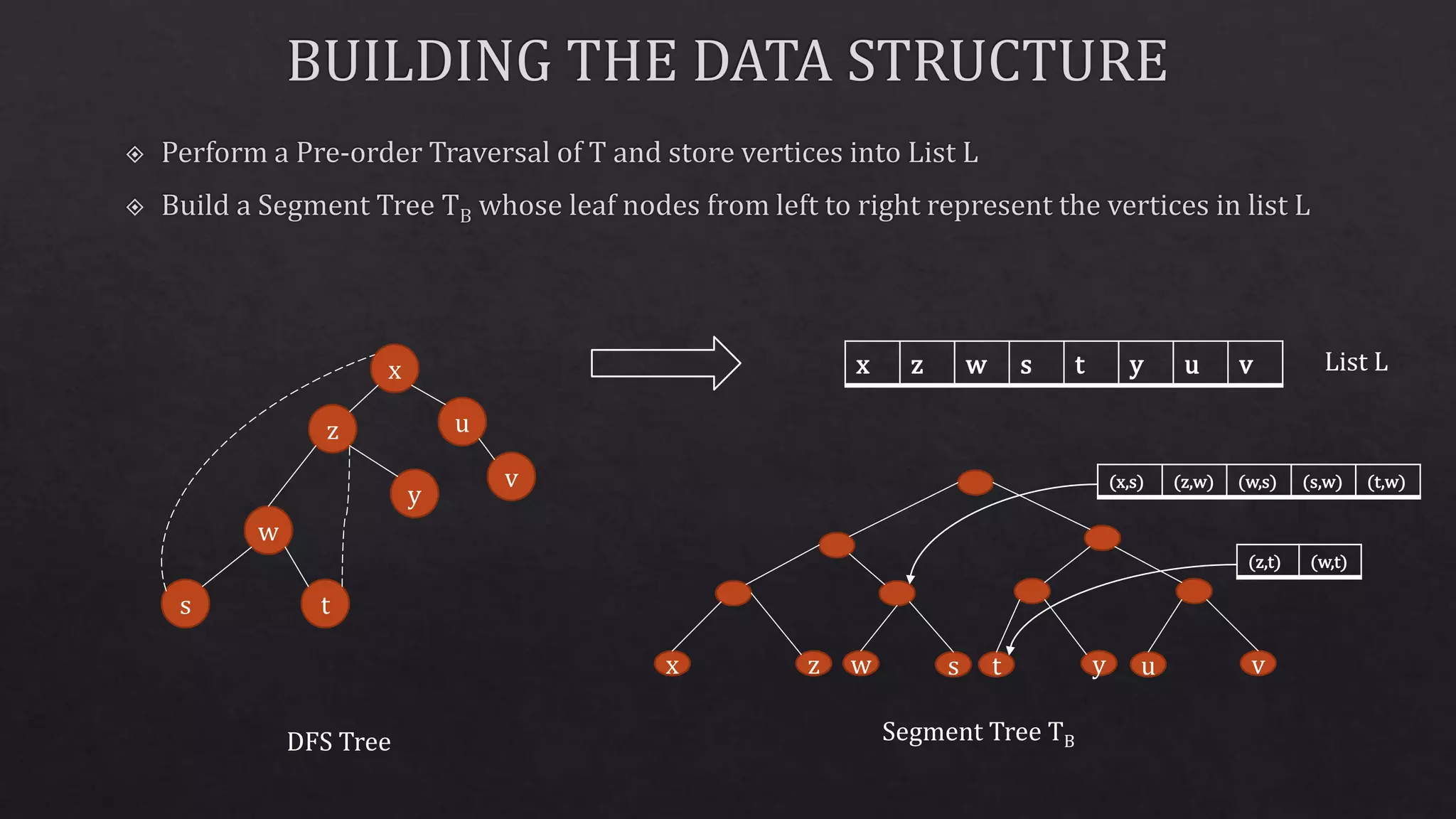
![x z w s t y u v
Segment Tree TB
[w-s]
(s,w)
(t,w)(w,s)
(z,w)
(x,s)
BST stored at segment tree node [w-s]
(x,s) (z,w) (w,s) (s,w) (t,w)
Edge-list sorted according to List L
x z w s t y u v List L](https://image.slidesharecdn.com/finalpresentatonteam10641-160508002110/75/Dynamic-DFS-in-Undirected-Graph-using-Segment-Tree-10-2048.jpg)