Dynamic programming (dp) in Algorithm

Topic
Dynamic Programming (DP)

Dynamic Programming is a general algorithm design technique for solving
problems defined by recurrences with overlapping subproblems
•Invented by American mathematician Richard Bellman in the 1950s to solve
optimization problems and later assimilated by CS
•“Programming” here means “planning”
•Main idea:
- set up a recurrence relating a solution to a larger instance to solutions of some
smaller instances
- solve smaller instances once
- record solutions in a table
- extract solution to the initial instance from that table
Dynamic Programming (DP)

• Two key ingredients for an optimization problem
to be suitable for a dynamic-programming
solution:
Each substructure is
optimal.
(Principle of optimality)
1. optimal substructures 2. overlapping subproblems
Subproblems are dependent.
(otherwise, a divide-and-
conquer approach is the
choice.)

– The recurrence relation (for defining the value of an
optimal solution);
– The tabular computation (for computing the value of an
optimal solution);
– The traceback (for delivering an optimal solution).
The development of a dynamic-programming algorithm has three
basic components:

Some exemple for DP
• Coin Change
• 0/1 Knapsack
• LCS , Etc.

Problem
Set Of Coins = { 8 , 5 , 1}
Make Change Of Taka, n =10
Exemple for Coin Change

T[i]=min[T[i],1+T[i-coin[j]]]
Solution
j c o i n [ j ]
0 8
1 5
2 1
1 2 3 4 5 6 7 8 9 10
1 2 3 4 1 2 3 1 2 2
1 2 3 4 5 6 7 8 9 10
2 2 2 2 1 2 2 0 2 1
10 - 5 = 5 - 5 = 0 5+5=10

Problem :
n = 4
S = 5
Elements (size,value)= {(2,3),(3,4),(4,5),(5,6
Need = 7
Exemple for 0/1 Knapsack

is 0 1 2 3 4 5
0
1
2
3
4
Here ,
max item = 4
max size = 5
Solution

is 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0
2 0
3 0
4 0
For s = 0 to s For i = 0
to n
V[0,s] = 0 V[i,0] =
0

is 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0
2 0
3 0
4 0
Item (Si,Vi
)
1 (2,3)
2 (3,4)
3 (4,5)
4 (5,6)
If Si<=S
if Vi+V[i-1,S-Si]>V[i-1,S]
V[I,s]=Vi+V[i-1,S-Si]
else
V[I,s]=V[i-1,S]
Else V[I,S]=V[i-1,S]

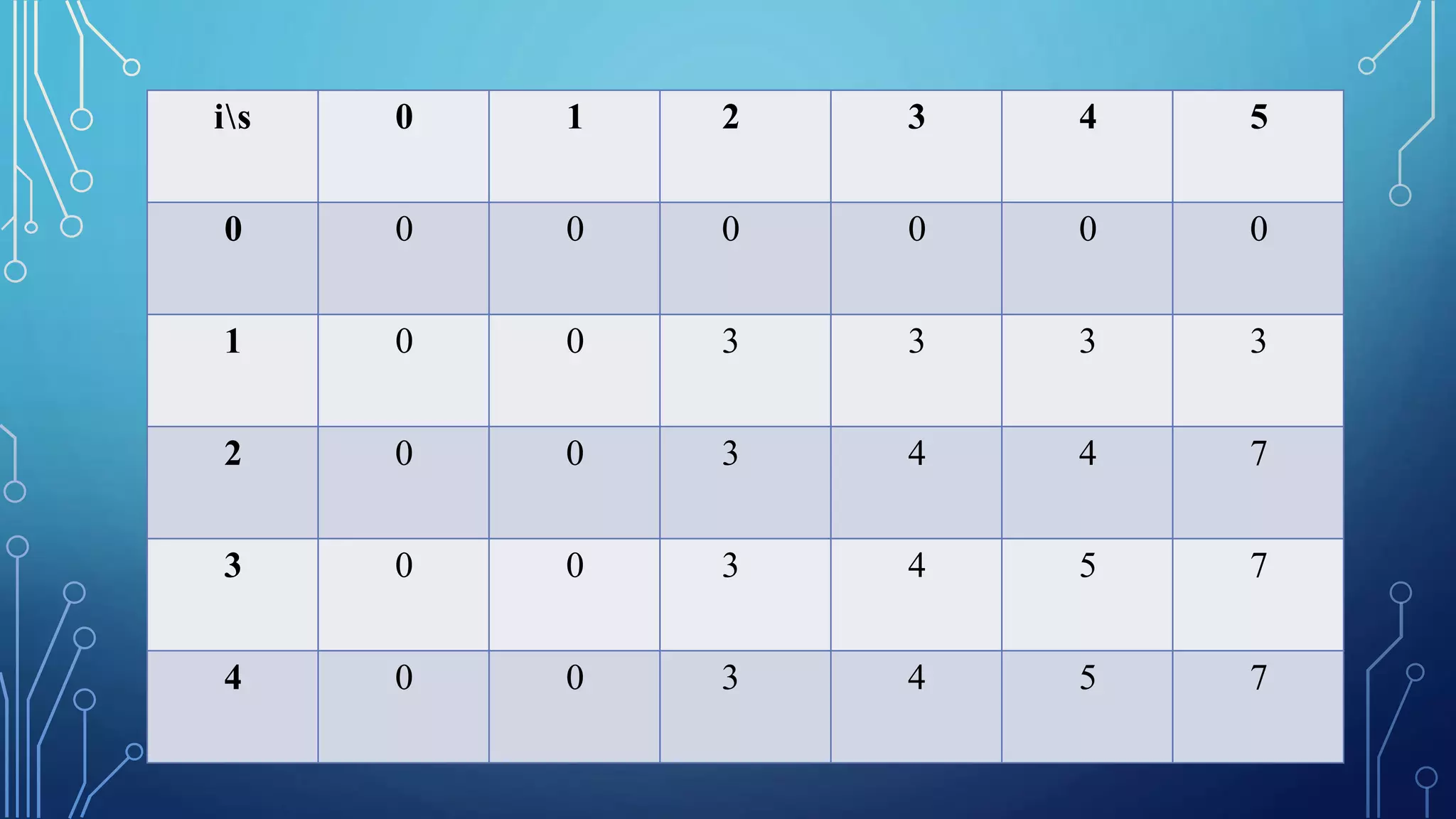
is 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3 3 3 3
2 0 0 3 4 4 7
3 0 0 3 4 5 7
4 0 0 3 4 5 7

is 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 0 3 3 3 3
2 0 0 3 4 4 7
3 0 0 3 4 5 7
4 0 0 3 4 5 7
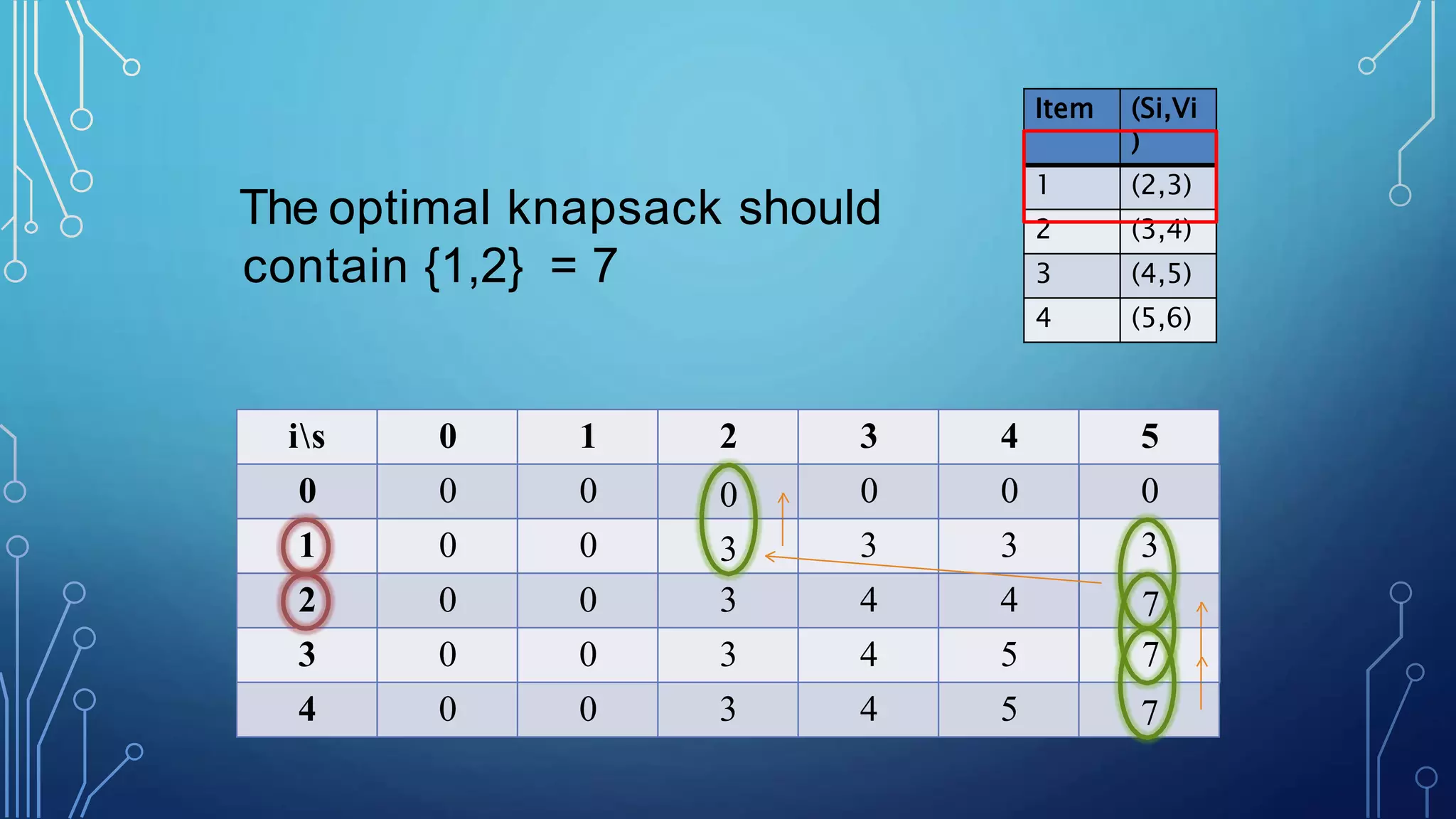
Item (Si,Vi
)
1 (2,3)
2 (3,4)
3 (4,5)
4 (5,6)
i=n,k=S
while i,k > 0
if V[I,k]=V[1-i,k]
I = i-1, k = k-Si
else
i = i-1

is 0 1 2 3 4 5
0 0 0 0 0 00
1 0 0 3 3 33
2 0 0 3 4 4 7
3 0 0 3 4 5 7
4 0 0 3 4 5 7
The optimal knapsack should
contain {1,2} = 7
Item (Si,Vi
)
1 (2,3)
2 (3,4)
3 (4,5)
4 (5,6)

Problem
X = {A, B, C, B, D, A, B}
Y = {B, D, C, A, B, A}
Exemple for LCS

SOLUTION
0 if i = 0 or j = 0
c[i-1, j-1] + 1 if xi = yj
max(c[i, j-1], c[i-1, j]) if xi  yj
0 1 2 3 4 5 6
yj B D C A B A
0 0 0 0 0 0 0
0

0

0

0 1 1 1
0 1 1 1

1 2 2
0

1

1 2 2

2

2
0 1

1

2

2 3 3
0

1 2

2

2

3

3
0

1

2

2 3

3 4
0 1

2

2

3 4

4
If xi = yj
b[i, j] = “ ”
Else if
1 xi
2 A
c[i - 1, j] ≥ c[i, j-1] 2 B
3 C
4 B
5 D
6 A
7 B
b[i, j] = “  ”
else
b[i, j] = “  ”
c[i, j] =

• Start at b[m, n] and follow the arrows
• When we encounter a “ “ in b[i, j]  xi = yj is an element
of the LCS
1 xi
2 A
3 B
4 C
5 B
6 D
7 A
8 B
0 1 2 3 4 5 6
yj B D C A B A
0 0 0 0 0 0 0
0
0
0
0
0
0
0

0
1

1
1

1

1
1

0
1

1

1
2

2

2

0
1
2

2

2

2

2
1

1
2

2

2
3

3
1
2

2
3

3

3
4
1
2

2
3

3
4

4
Longest common subsequence is {A,B,C,B}

Dynamic programming (dp) in Algorithm

Dynamic programming (dp) in Algorithm

More Related Content

What's hot

Similar to Dynamic programming (dp) in Algorithm

Recently uploaded

Dynamic programming (dp) in Algorithm