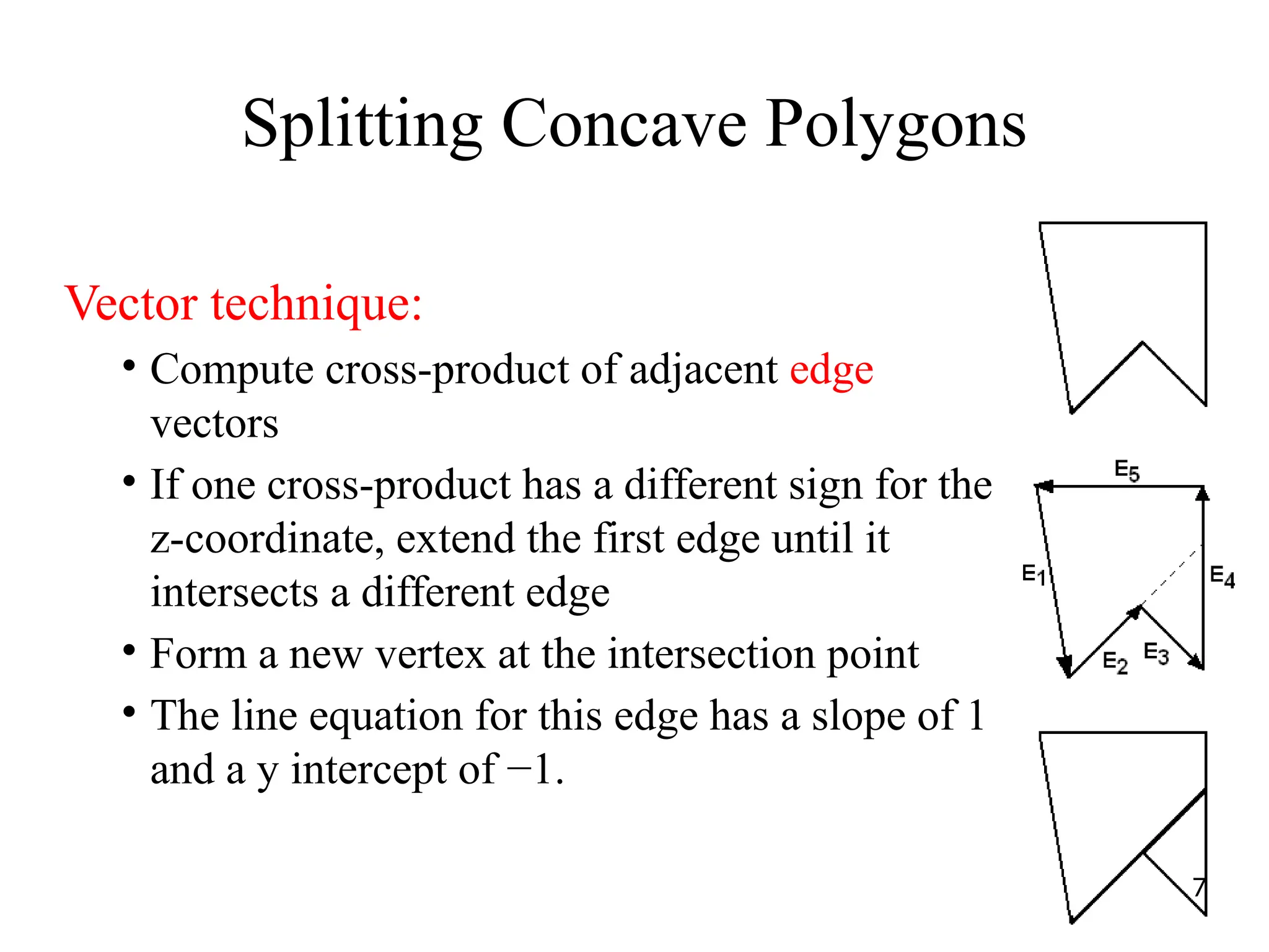
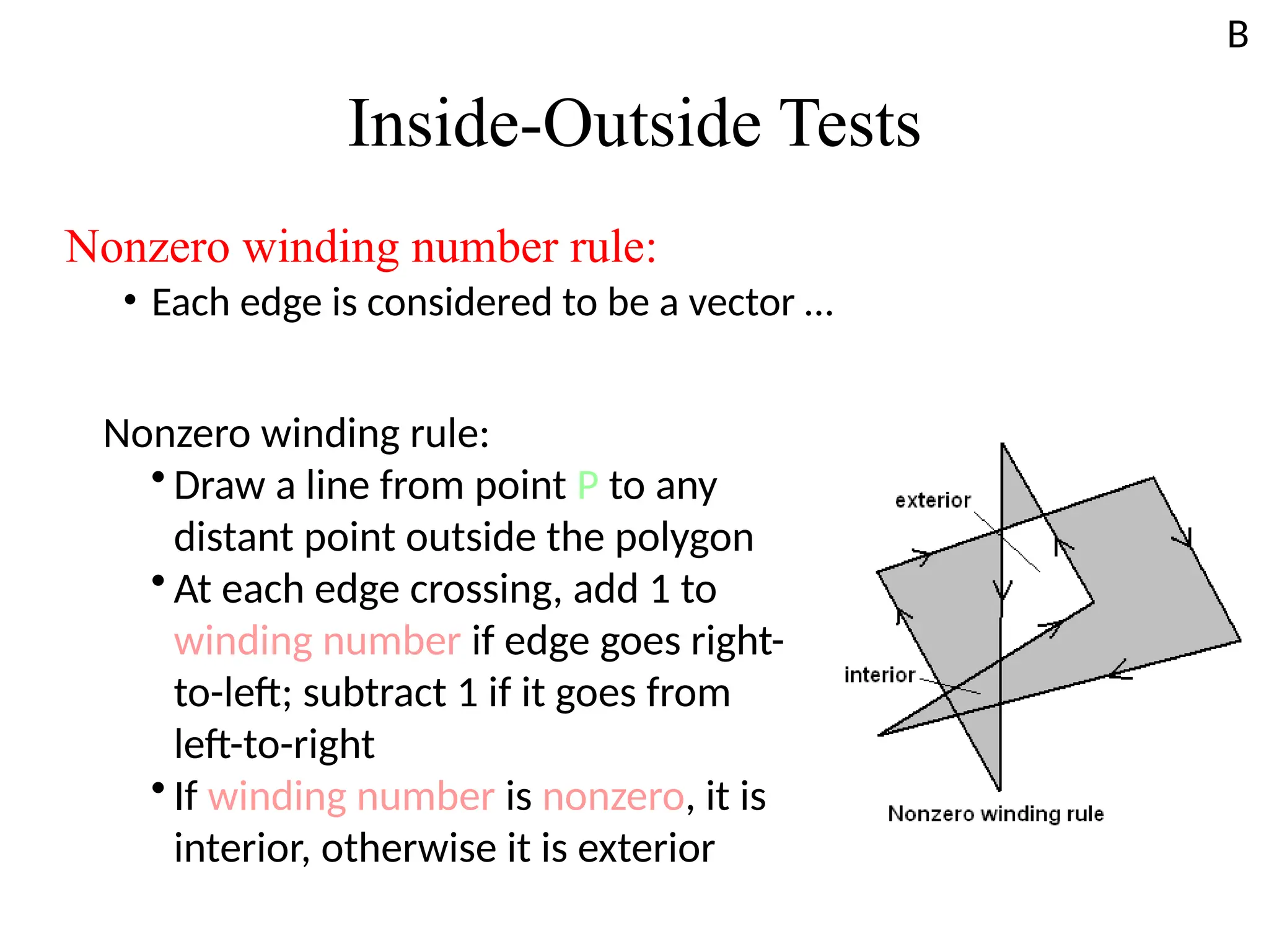
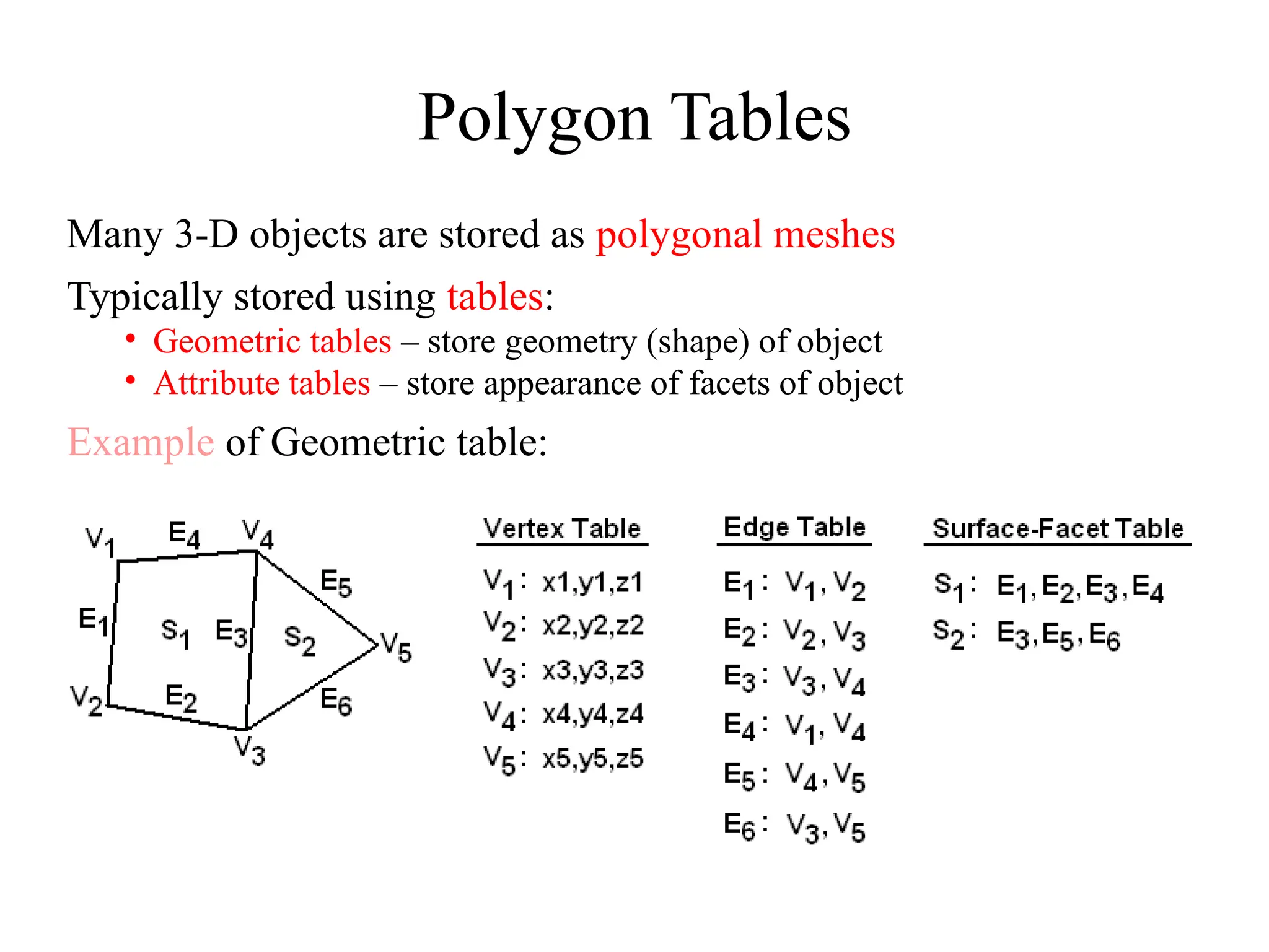
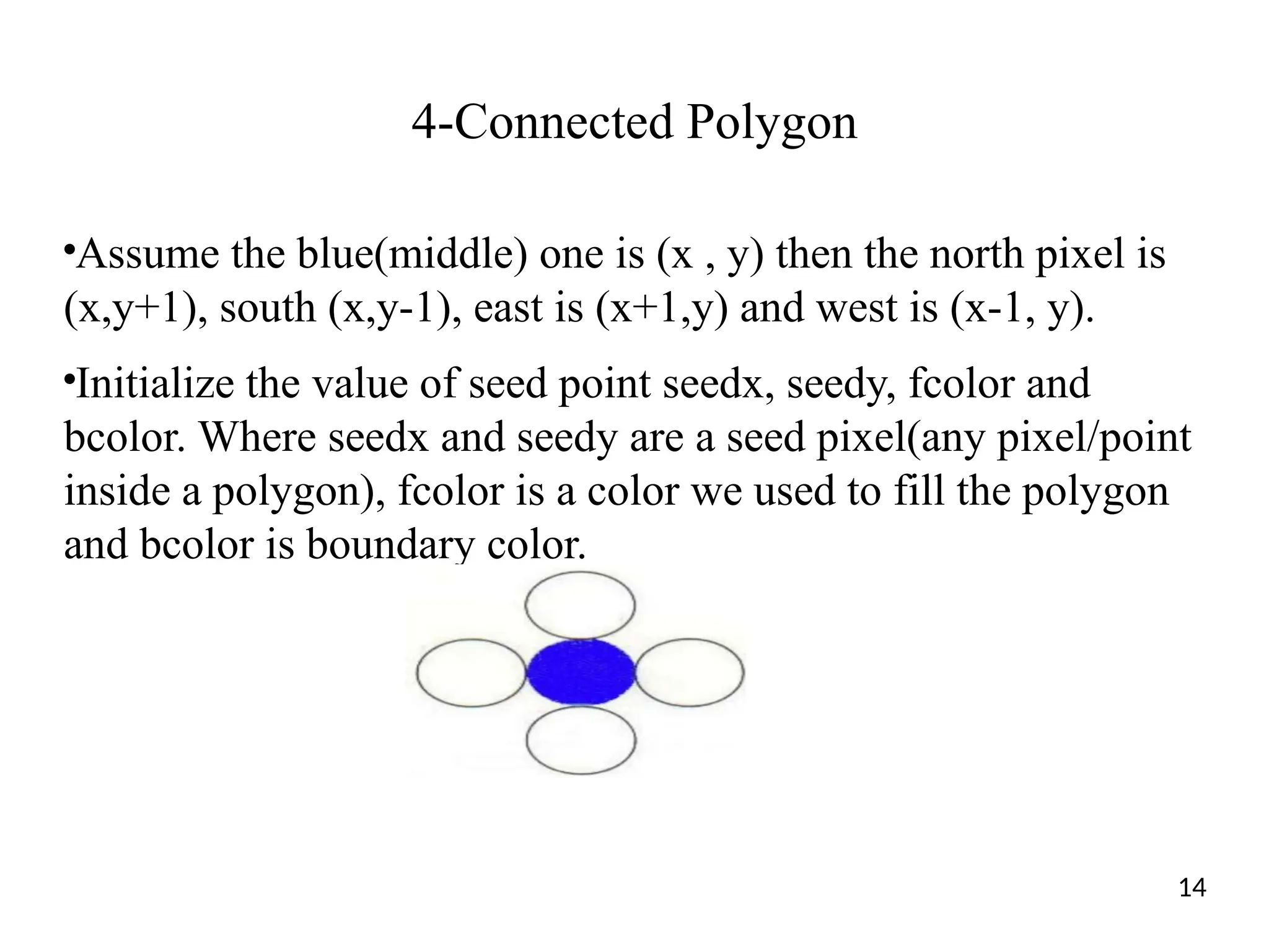
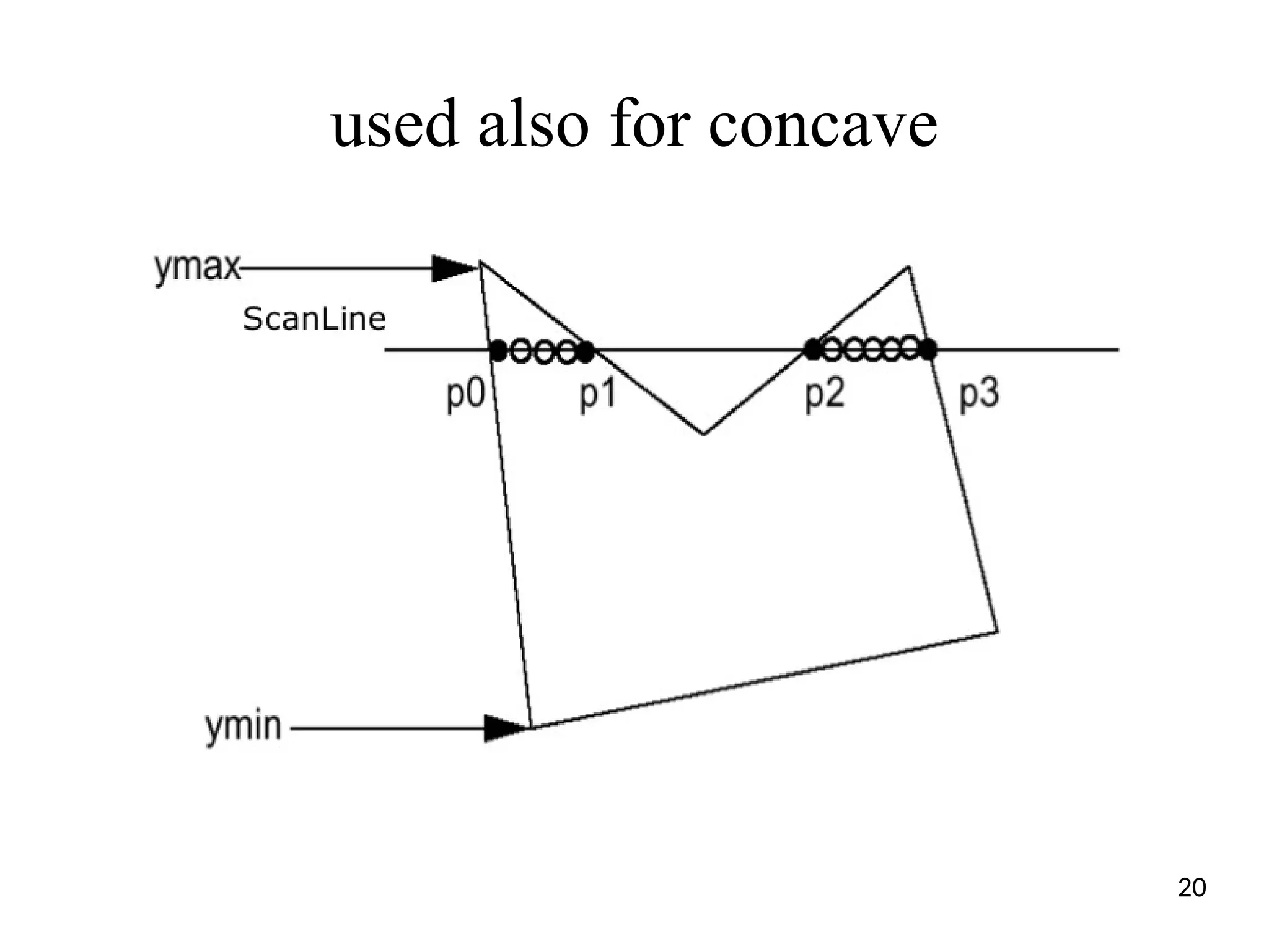
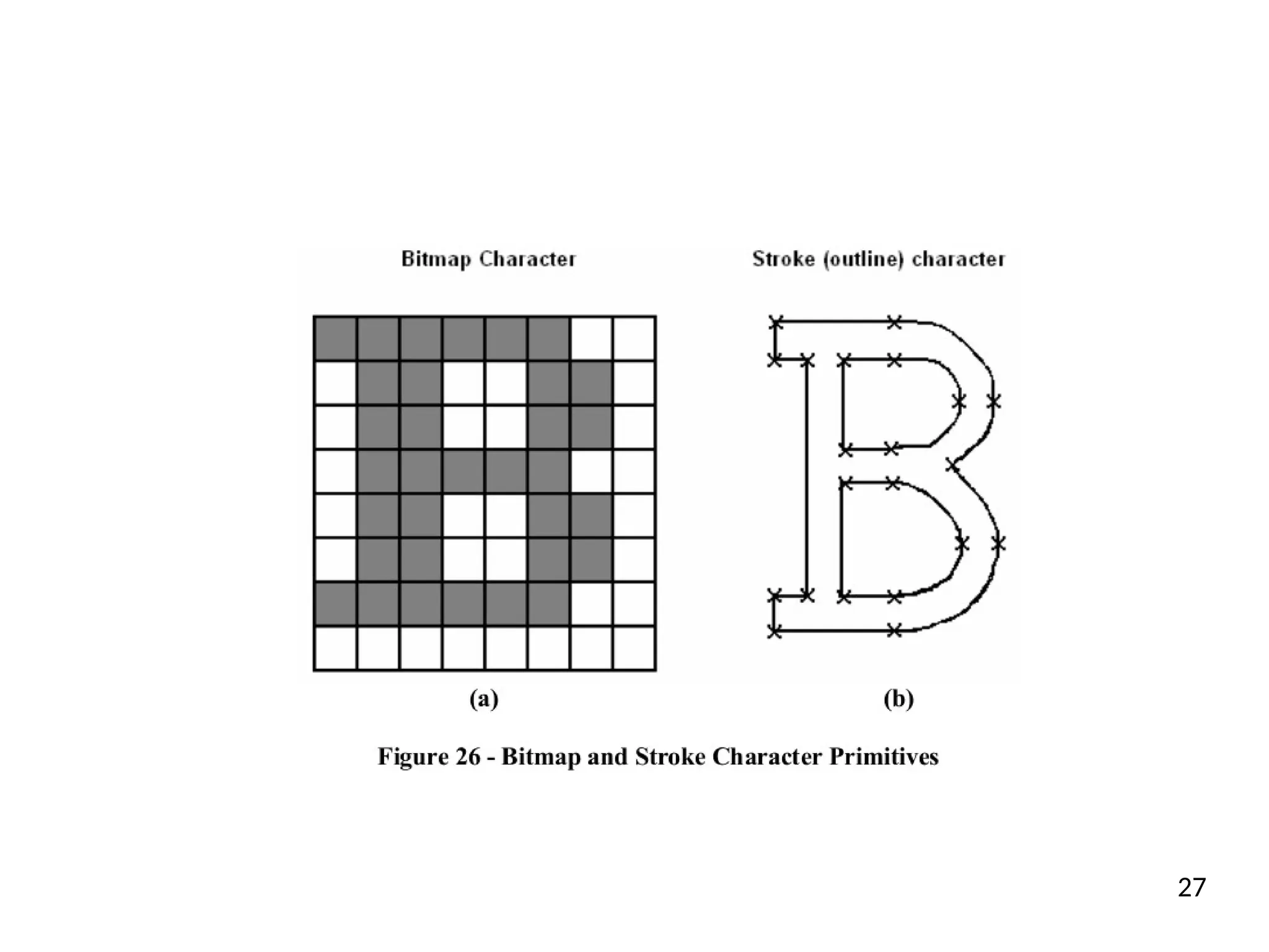
The document discusses the generation of geometric shapes and text representation in computer graphics, focusing on fill area primitives, polygon representation, and character drawing. It covers algorithms for filling polygons, including seed fill and scan line methods, as well as the differences between bitmap and stroke representations for text characters. Additionally, it highlights the importance of managing convex and concave polygons for efficient graphical processing.