From NumPy to PyTorch

From NumPy to PyTorch
Mike Ruberry
software engineer @ Facebook

Outline
- NumPy and working with tensors
- PyTorch and hardware accelerators, autograd, and computational graphs
- Adding NumPy operators to Pytorch
- When PyTorch is Different from NumPy
- Lessons learned and future work

NumPy and working
with tensors

1 >> import numpy as np
2 >> a = np.array(((1, 2), (3, 4)))
array([[1, 2],
[3, 4]])
3 >> b = np.array(((-1, -2), (-3, -4)))
4 >> np.add(a, b)
array([[0, 0],
[0, 0]])
5 >> np.matmul(a, b)
array([[ -7, -10],
[-15, -22]])
Simple NumPy Snippets

2 >> a = np.array(((1, 2), (3, 4)))
array([[1, 2],
[3, 4]])
3 >> b = np.array(((-1, -2), (-3, -4)))
4 >> np.add(a, b)
array([[0, 0],
[0, 0]])
array([[ -7, -10],
[-15, -22]])
Tensor creation

2 >> a = np.array(((1, 2), (3, 4)))
array([[1, 2],
[3, 4]])
3 >> b = np.array(((-1, -2), (-3, -4)))
4 >> np.add(a, b)
array([[0, 0],
[0, 0]])
array([[ -7, -10],
[-15, -22]])
Addition

2 >> a = np.array(((1, 2), (3, 4)))
array([[1, 2],
[3, 4]])
3 >> b = np.array(((-1, -2), (-3, -4)))
4 >> np.add(a, b)
array([[0, 0],
[0, 0]])
array([[ -7, -10],
[-15, -22]])
Matrix multiplication

1 >> np.fft.fft(np.exp(2j * np.pi * np.arange(8) / 8))
array([-3.44509285e-16 +1.14423775e-17 j,
8.00000000e+00 -8.11483250e-16 j,
2.33486982e-16 +1.22464680e-16 j,
0.00000000e+00 +1.22464680e-16 j,
9.95799250e-17 +2.33486982e-16 j,
0.00000000e+00 +7.66951701e-17 j,
1.14423775e-17 +1.22464680e-16 j,
0.00000000e+00 +1.22464680e-16 j])
2 >> A = np.array([[1,-2j],[2j,5]])
3 >> np.linalg.cholesky(A)
array([[1.+0.j, 0.+0.j],
[0.+2.j, 1.+0.j]])
More Complicated NumPy Snippets

NumPy
Operators
Composites Primitives

Composites Primitives
1 def sinc(x):
2 x = np.asanyarray(x)
3 y = pi * where(x == 0, 1.0e-20, x)
4 return sin(y)/y
1 double npy_copysign(
double x,
double y)
2 {
3 npy_uint32 hx , hy;
4 GET_HIGH_WORD(hx, x);
5 GET_HIGH_WORD(hy, y);
6 SET_HIGH_WORD(x,
(hx & 0x7fffffff) |
(hy & 0x80000000));
7 return x;
8 }

PyTorch and
hardware accelerators,
autograd, and computational
graphs

2 >> a = np.array(((1, 2), (3, 4)))
array([[1, 2],
[3, 4]])
3 >> b = np.array(((-1, -2), (-3, -4)))
4 >> np.add(a, b)
array([[0, 0],
[0, 0]])
array([[ -7, -10],
[-15, -22]])
Simple NumPy Snippets (Again)

1 >> import torch
2 >> a = torch.tensor(((1, 2), (3, 4)))
tensor([[1, 2],
[3, 4]])
3 >> b = np.array(((-1, -2), (-3, -4)))
4 >> np.add(a, b)
array([[0, 0],
[0, 0]])
array([[ -7, -10],
[-15, -22]])
Simple NumPy Snippets to PyTorch Snippets
Tensor creation

1 >> import torch
2 >> a = torch.tensor(((1, 2), (3, 4)))
tensor([[1, 2],
[3, 4]])
3 >> b = torch.tensor(((-1, -2), (-3, -4)))
4 >> torch.add(a, b)
tensor([[0, 0],
[0, 0]])
array([[ -7, -10],
[-15, -22]])
Addition

1 >> import torch
2 >> a = torch.tensor(((1, 2), (3, 4)))
tensor([[1, 2],
[3, 4]])
3 >> b = torch.tensor(((-1, -2), (-3, -4)))
tensor([[0, 0],
[0, 0]])
5 >> torch.matmul(a, b)
tensor([[ -7, -10],
[-15, -22]])
Matrix multiplication

1 >> import torch
2 >> a = torch.tensor(((1, 2), (3, 4)))
tensor([[1, 2],
[3, 4]])
3 >> b = torch.tensor(((-1, -2), (-3, -4)))
tensor([[0, 0],
[0, 0]])
5 >> torch.matmul(a, b)
tensor([[ -7, -10],
[-15, -22]])
Simple PyTorch Snippets

1 >> np.fft.fft(np.exp(2j * np.pi * np.arange(8) / 8))
array([-3.44509285e-16 +1.14423775e-17 j,
8.00000000e+00 -8.11483250e-16 j,
2.33486982e-16 +1.22464680e-16 j,
0.00000000e+00 +1.22464680e-16 j,
9.95799250e-17 +2.33486982e-16 j,
0.00000000e+00 +7.66951701e-17 j,
1.14423775e-17 +1.22464680e-16 j,
0.00000000e+00 +1.22464680e-16 j])
2 >> A = np.array([[1,-2j],[2j,5]])
3 >> np.linalg.cholesky(A)
array([[1.+0.j, 0.+0.j],
[0.+2.j, 1.+0.j]])
More Complicated NumPy Snippets (Again)

1 >> torch.fft.fft(torch.exp(2j * math.pi * torch.arange(8) / 8))
2 tensor([ 3.2584e-07+3.1787e-08j, 8.0000e+00+4.8023e-07j,
3 -3.2584e-07+3.1787e-08j, -1.6859e-07+3.1787e-08j,
4 -3.8941e-07-2.0663e-07j, 1.3691e-07-1.9412e-07j,
5 3.8941e-07-2.0663e-07j, 1.6859e-07+3.1787e-08j])
1 >> A = torch.tensor([[1,-2j],[2j,5]])
2 >> torch.linalg.cholesky(A)
3 tensor([[1.+0.j, 0.+0.j],
4 [0.+2.j, 1.+0.j]])
More Complicated PyTorch Snippets

1 >> t = torch.tensor((1, 2, 3))
2 >> a = t.numpy()
3 array([1, 2, 3])
3 >> b = np.array((-1, -2, -3))
4 >> result = a + b
array([0, 0, 0])
5 >> torch.from_numpy(result)
tensor([0, 0, 0])
PyTorch and NumPy Interoperability

Does PyTorch have EVERY NumPy operator?
- No!
- NumPy has a lot of operators: A LOT
- Many of them are rarely used, niche, deprecated, or in need of deprecation
- But PyTorch does have hundreds of NumPy operators

1 >> import torch
2 >> a = torch.tensor(((1., 2), (3, 4)), device='cuda')
tensor([[1, 2],
[3, 4]], device='cuda:0')
3 >> b = torch.tensor(((-1, -2), (-3, -4)), device='cuda')
tensor([[0, 0],
[0, 0]], device='cuda:0')
5 >> torch.matmul(a.float(), b.float())
tensor([[ -7., -10.],
[-15., -22.]], device='cuda:0')
Simple PyTorch Snippets on CUDA

1 >> a = torch.tensor((1., 2.), requires_grad=True)
2 >> b = torch.tensor((3., 4.))
3 >> result = (a * b).sum()
4 >> result.backward()
5 >> a.grad
tensor([3., 4.])
Autograd in PyTorch

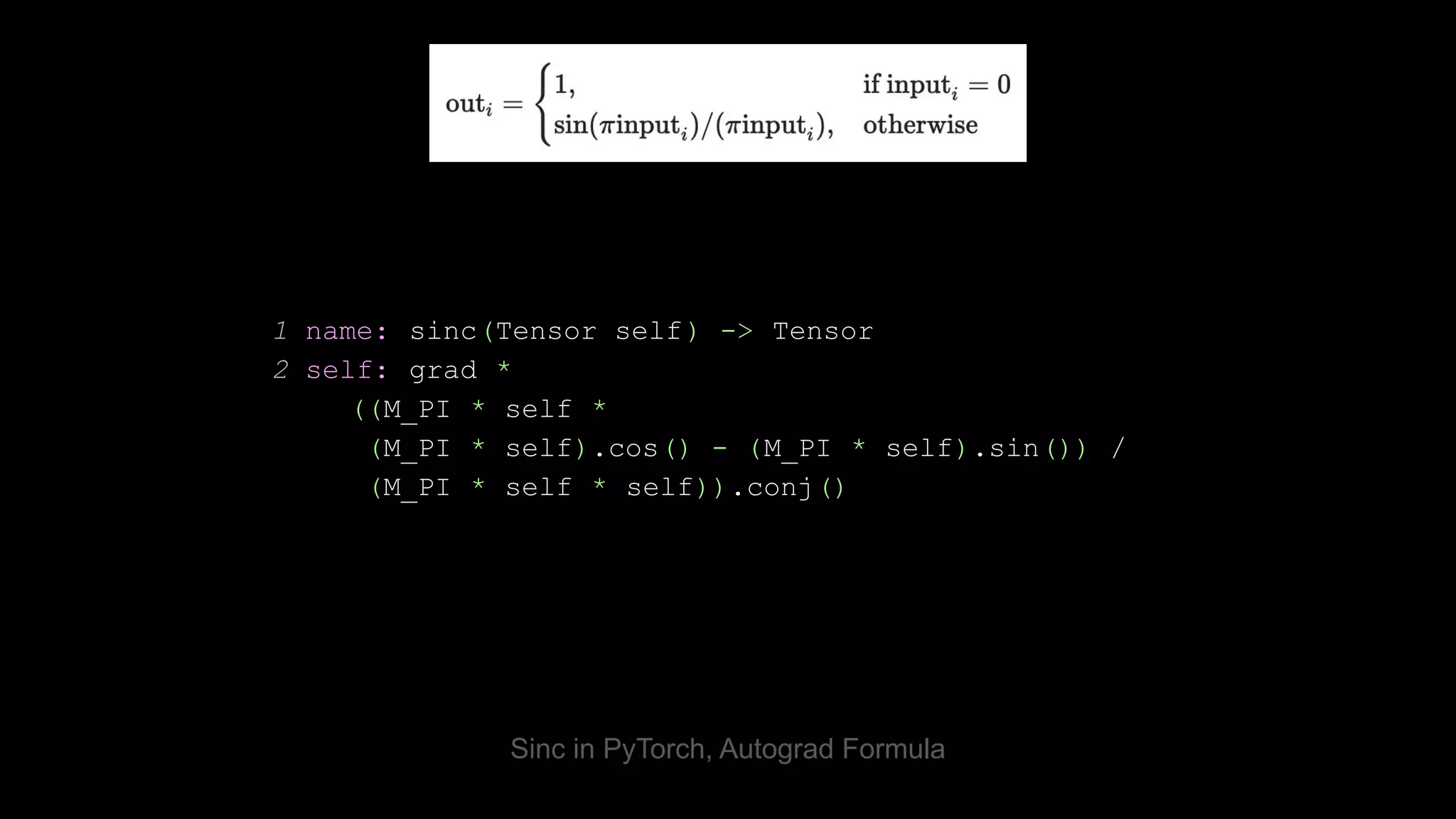
1 def sinc(x):
2 y = math.pi * torch.where(x == 0, 1.0e-20, x)
3 return torch.sin(y)/y
4
5 scripted_sinc = torch.jit.script(sinc)
graph(%x.1 : Tensor):
%1 : float = prim::Constant[value=3.1415926535897931 ]
%3 : int = prim::Constant[value=0]
%5 : float = prim::Constant[value=9.9999999999999995e-21 ]
%4 : Tensor = aten::eq(%x.1, %3)
%7 : Tensor = aten::where(%4, %5, %x.1)
%y.1 : Tensor = aten::mul(%7, %1)
%10 : Tensor = aten::sin(%y.1)
%12 : Tensor = aten::div(%10, %y.1)
return (%12)
Computational Graphs in PyTorch

1 >> t = torch.randn(10)
2 >> linear_layer = torch.nn.Linear(10, 5)
3 >> linear_layer(t)
tensor([ 0.0066, 0.2467, -0.0137, -0.4091, -1.1756],
grad_fn=<AddBackward0>)
Deep Learning in PyTorch

PyTorch as NumPy+
- While PyTorch doesn’t have every NumPy operator, for those it supports we
can think of it as NumPy PLUS:
- Support for hardware accelerators, like GPUs and TPUs
- Support for autograd
- Support computational graphs
- Support for deep learning
- A C++ API
- … and many additional features (visualization, distributed training, …)
- PyTorch also has additional operators that NumPy does not

PyTorch Behind the Scenes
- To recap, NumPy had…
- Composite operators (typically implemented in Python)
- Primitive operators (implemented in C++)
- And PyTorch has...
- Composite operators (implemented in C++)
- Primitive operators (implemented in C++, CPU intrinsics, and CUDA)
- Computational graphs (executed by torchscript or XLA)
- Plus autograd formulas for differentiable operations

1 def sinc(x):
2 x = np.asanyarray(x)
3 y = pi * where(x == 0, 1.0e-20, x)
4 return sin(y)/y
Sinc in NumPy (reminder)

1 static void sinc_kernel(TensorIteratorBase& iter) {
2 AT_DISPATCH_FLOATING_AND_COMPLEX_TYPES_AND1(
kBFloat16, iter.common_dtype(), "sinc_cpu", [&]() {
3 cpu_kernel(
4 iter,
5 [=](scalar_t a) -> scalar_t {
6 if (a == scalar_t(0)) {
7 return scalar_t(1);
8 } else {
9 scalar_t product = c10::pi<scalar_t> * a;
10 return std::sin(product) / product;
11 }
12 });
13 });
14 }
Sinc in PyTorch, CPU kernel

Sinc in PyTorch, Autograd Formula
1 name: sinc(Tensor self) -> Tensor
2 self: grad *
((M_PI * self *
(M_PI * self).cos() - (M_PI * self).sin()) /
(M_PI * self * self)).conj()

Adding NumPy Operators to
PyTorch

Porting an operator from NumPy
- Need to write a C++ implementation
- Possibly a CPU kernel or a CUDA kernel
- Need to write an autograd formula (if the op is differentiable)
- Need to write comprehensive tests (more on this in a moment)
… why do we bother?

Porting an operator from NumPy
- Need to write a C++ implementation
- Possibly a CPU kernel or a CUDA kernel
- Made easier with the C++ “TensorIterator” architecture
- Need to write an autograd formula (if the op is differentiable)
- Simplified by allowing users to write Pythonic YAML formulas
- Need to write comprehensive tests (more on this in a moment)
- Significant coverage automated with PyTorch’s OpInfo metadata and test generation
framework

PyTorch’s test matrix
- Tensor properties:
- Datatype (long, float, complexfloat, etc.)
- Device (CPU, CUDA, TPU, etc.)
- Differentiable operations support autograd
- Operations need to work in computational graphs
- Operations have “function,” “method” and “inplace” variants

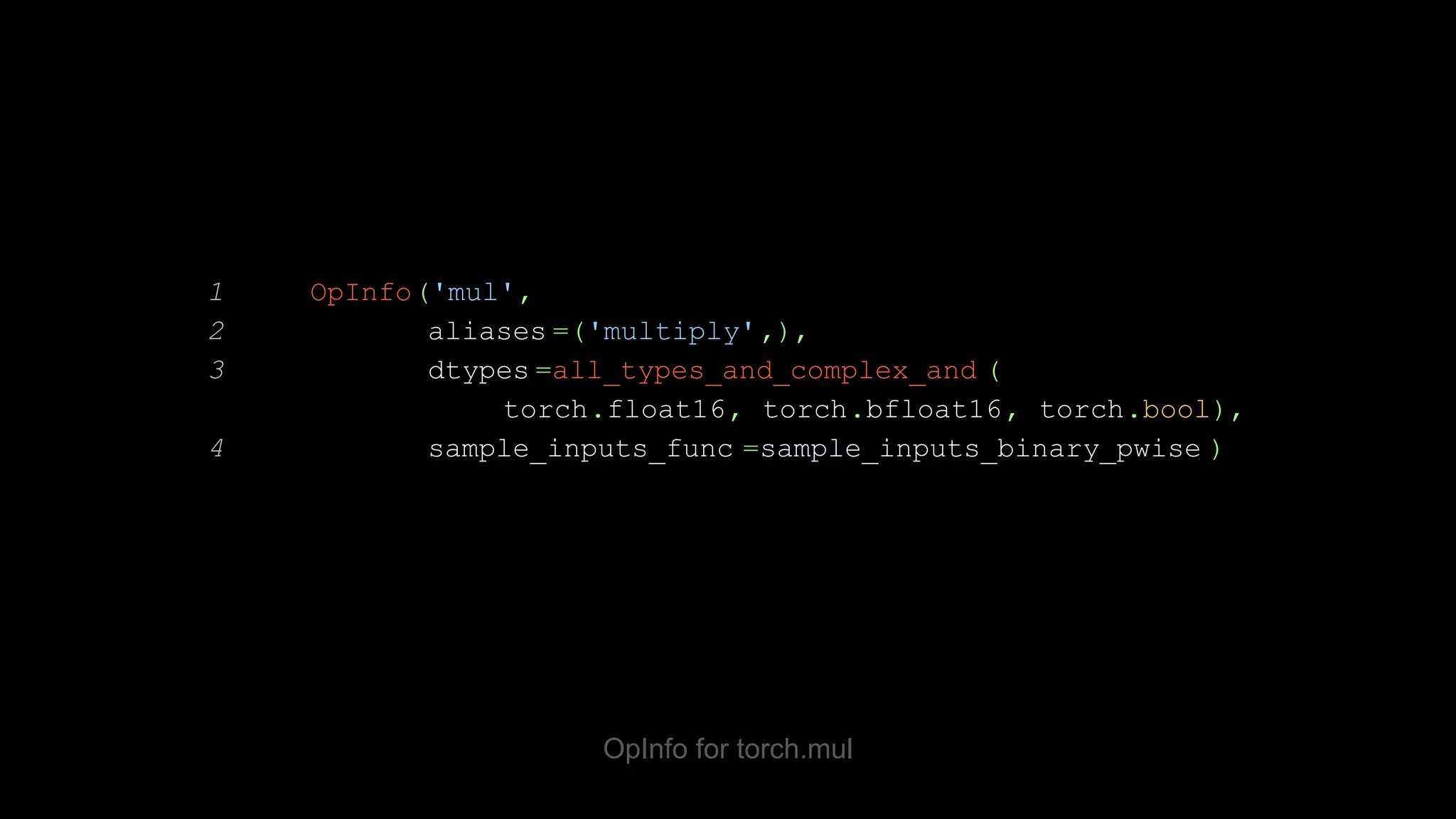
OpInfo for torch.mul
1 OpInfo('mul',
2 aliases =('multiply',),
3 dtypes =all_types_and_complex_and (
torch.float16, torch.bfloat16, torch.bool),
4 sample_inputs_func =sample_inputs_binary_pwise )

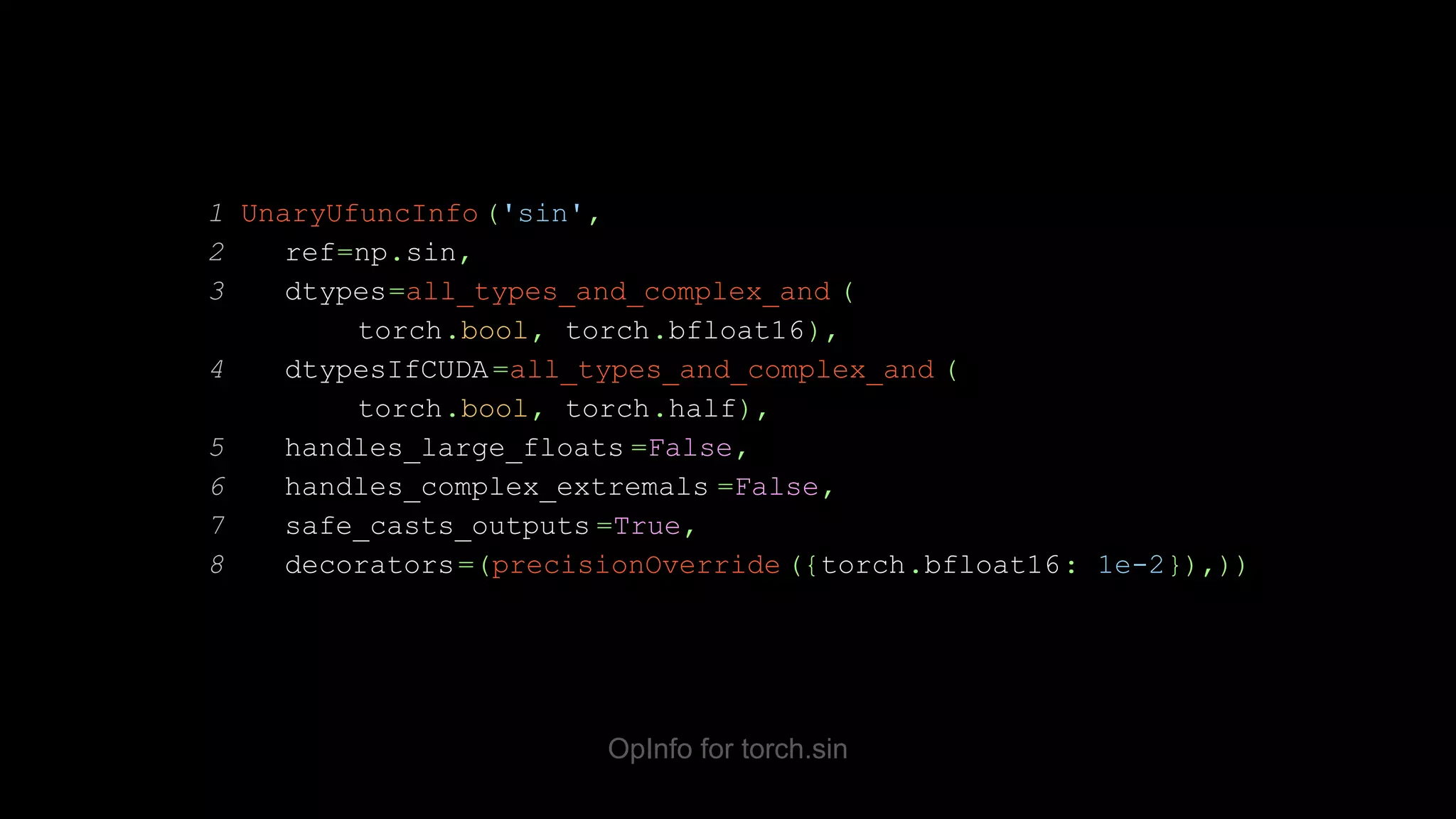
OpInfo for torch.sin
1 UnaryUfuncInfo ('sin',
2 ref=np.sin,
3 dtypes=all_types_and_complex_and (
torch.bool, torch.bfloat16),
4 dtypesIfCUDA=all_types_and_complex_and (
torch.bool, torch.half),
5 handles_large_floats =False,
6 handles_complex_extremals =False,
7 safe_casts_outputs =True,
8 decorators=(precisionOverride ({torch.bfloat16: 1e-2}),))

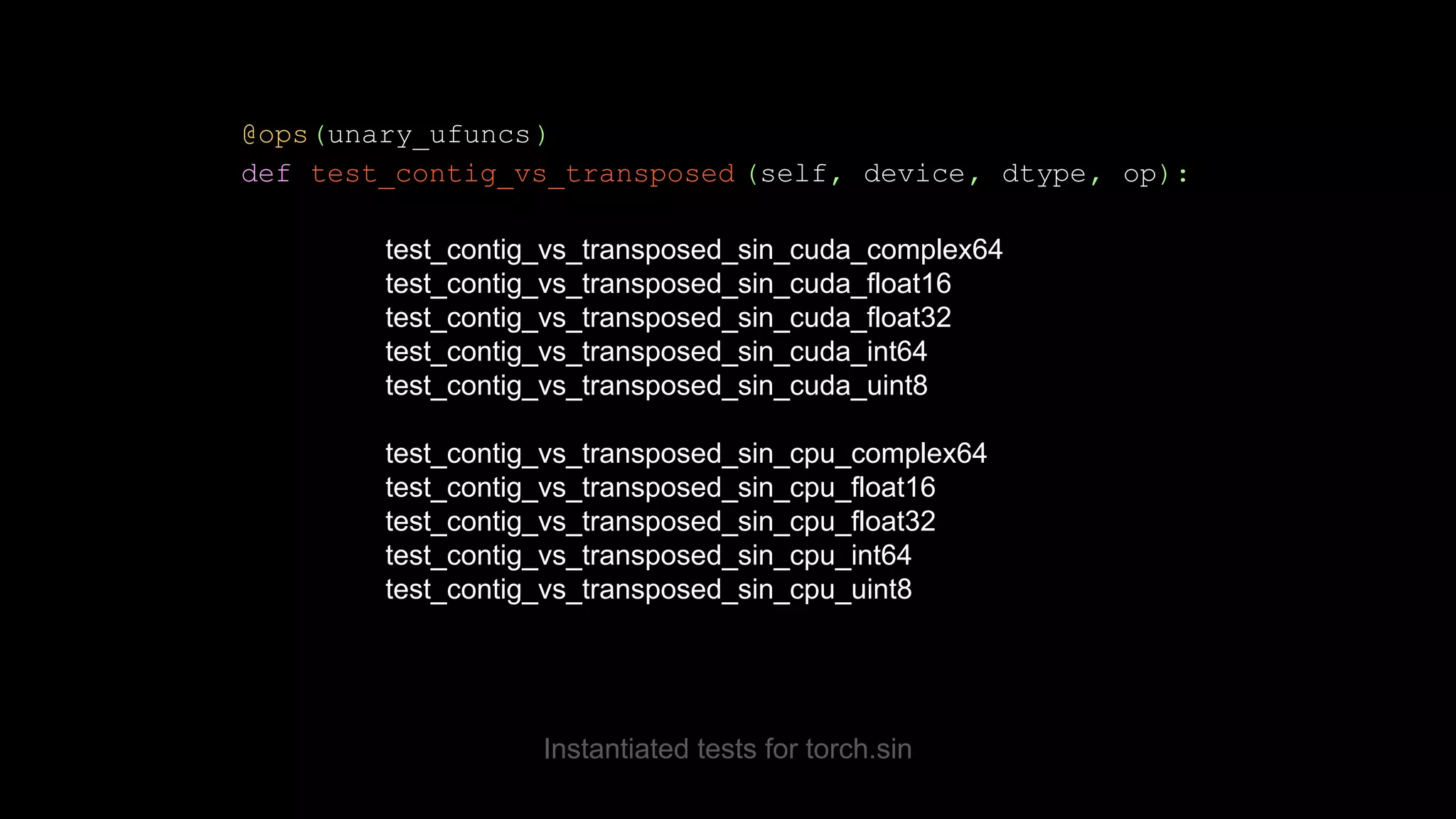
OpInfo test template
1 @ops(unary_ufuncs)
2 def test_contig_vs_transposed (self, device, dtype, op):
3 contig = make_tensor((789, 357),
device=device, dtype=dtype,
low=op.domain[0], high=op.domain[1])
4 non_contig = contig.T
5 self.assertTrue(contig.is_contiguous())
6 self.assertFalse(non_contig.is_contiguous())
7 torch_kwargs, _ = op.sample_kwargs(device, dtype, contig)
8 self.assertEqual(
op(contig, **torch_kwargs).T,
op(non_contig, **torch_kwargs))

Instantiated tests for torch.sin
@ops(unary_ufuncs)
def test_contig_vs_transposed (self, device, dtype, op):
test_contig_vs_transposed_sin_cuda_complex64
test_contig_vs_transposed_sin_cuda_float16
test_contig_vs_transposed_sin_cuda_float32
test_contig_vs_transposed_sin_cuda_int64
test_contig_vs_transposed_sin_cuda_uint8
test_contig_vs_transposed_sin_cpu_complex64
test_contig_vs_transposed_sin_cpu_float16
test_contig_vs_transposed_sin_cpu_float32
test_contig_vs_transposed_sin_cpu_int64
test_contig_vs_transposed_sin_cpu_uint8

Example properties validated for every operator
- Autograd is implemented correctly
- Tested using finite differences
- The operation works with torchscript and torch.fx
- The operation’s function, method, and inplace variants all compute the same
operation
- One big caveat: can’t automatically test correctness except for special
classes of operators (like unary ufuncs)

Features of PyTorch’s test generator
- Works with pytest and unittest
- Dynamically identifies available device types
- Allows for device type-specific logic for setup and teardown
- Extensible by other packages adding new device types (like PyTorch/XLA)
- Provides a central “source of truth” for operator’s functionality
- Makes it easy to test new features with every PyTorch operator

When PyTorch is Different
from NumPy

NumPy PyTorch
1 >> a = np.array((1, 2, 3))
2 >> np.reciprocal(a)
array([1, 0, 0])
np.reciprocal vs torch.reciprocal
1 >> t = torch.tensor((1, 2, 3))
2 >> torch.reciprocal(t)
tensor([
1.0000,
0.5000,
0.3333])

NumPy PyTorch
1 >> a = np.diag(
np.array((1., 2, 3)))
2 >> w, v = np.linalg.eig(a)
array([1., 2., 3.]),
array([
[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]]))
np.linalg.eig vs torch.linalg.eig
1 >> t = torch.diag(
torch.tensor((1., 2, 3)))
2 >> w, v = torch.linalg.eig(t)
torch.return_types.linalg_eig(
eigenvalues=tensor(
[1.+0.j, 2.+0.j, 3.+0.j]),
eigenvectors=tensor(
[[1.+0.j, 0.+0.j, 0.+0.j],
[0.+0.j, 1.+0.j, 0.+0.j],
[0.+0.j, 0.+0.j, 1.+0.j]]))

NumPy PyTorch
1 >> a = np.array(
(complex(1, 2),
complex(2, 1)))
2 >> np.amax(a)
(2+1j)
3 >> np.sort(a)
array([1.+2.j, 2.+1.j],
dtype=complex64)
Ordering complex numbers in NumPy vs. PyTorch
1 >> t = torch.tensor(
(complex(1, 2),
complex(2, 1)))
2 >> torch.amax(t)
RUNTIME ERROR
3 >> torch.sort(t)
RUNTIME ERROR

Principled discrepancies
- The PyTorch community seems OK with these principled discrepancies
- Different behavior must be very similar to NumPy’s behavior
- It’s OK to not support some things, as long as there are other mechanisms to do them
- PyTorch also has systematic discrepancies with NumPy that pass without
comment
- Type promotion
- Functions vs. method variants
- Returning scalars vs tensors

Lessons Learned
and Future Work

Recap
- NumPy and PyTorch are popular Python packages with operators that manipulate
tensors
- PyTorch implements many of NumPy’s operators, and extends them with support for
hardware accelerators, autograd, and other systems that support modern scientific
computing and deep learning
- The PyTorch community wants both the functionality and familiarity these operators
provide
- But it’s OK with principled differences
- To make implementing all these operators tractable, PyTorch has had to develop
architecture supporting C++ and CUDA implementations, autograd formulas and
testing

Lessons Learned
- Do the work to engage your community and listen carefully to their feedback
- At first it wasn’t clear whether people just wanted the functionality of NumPy operators, but our
community has clarified they also want fidelity
- Focus on developer efficiency
- Be clear about your own principles when implementing operators from
another project

Future Work
- Prioritize deprecating and updating the few PyTorch operators with
significantly different behavior than their NumPy counterparts
- Make success criteria clearer: implementing every NumPy operator is
impractical and inadvisable
- The new Python Array API may solve this problem
- More focus on SciPy functionality, including SciPy’s special module, linear
algebra module, and optimizers

From NumPy to PyTorch

More Related Content

What's hot

Similar to From NumPy to PyTorch

Recently uploaded

From NumPy to PyTorch