Downloaded 39 times
Uploaded byDaffodil International University
Graph & Heap in Data Structure (Basic Information)
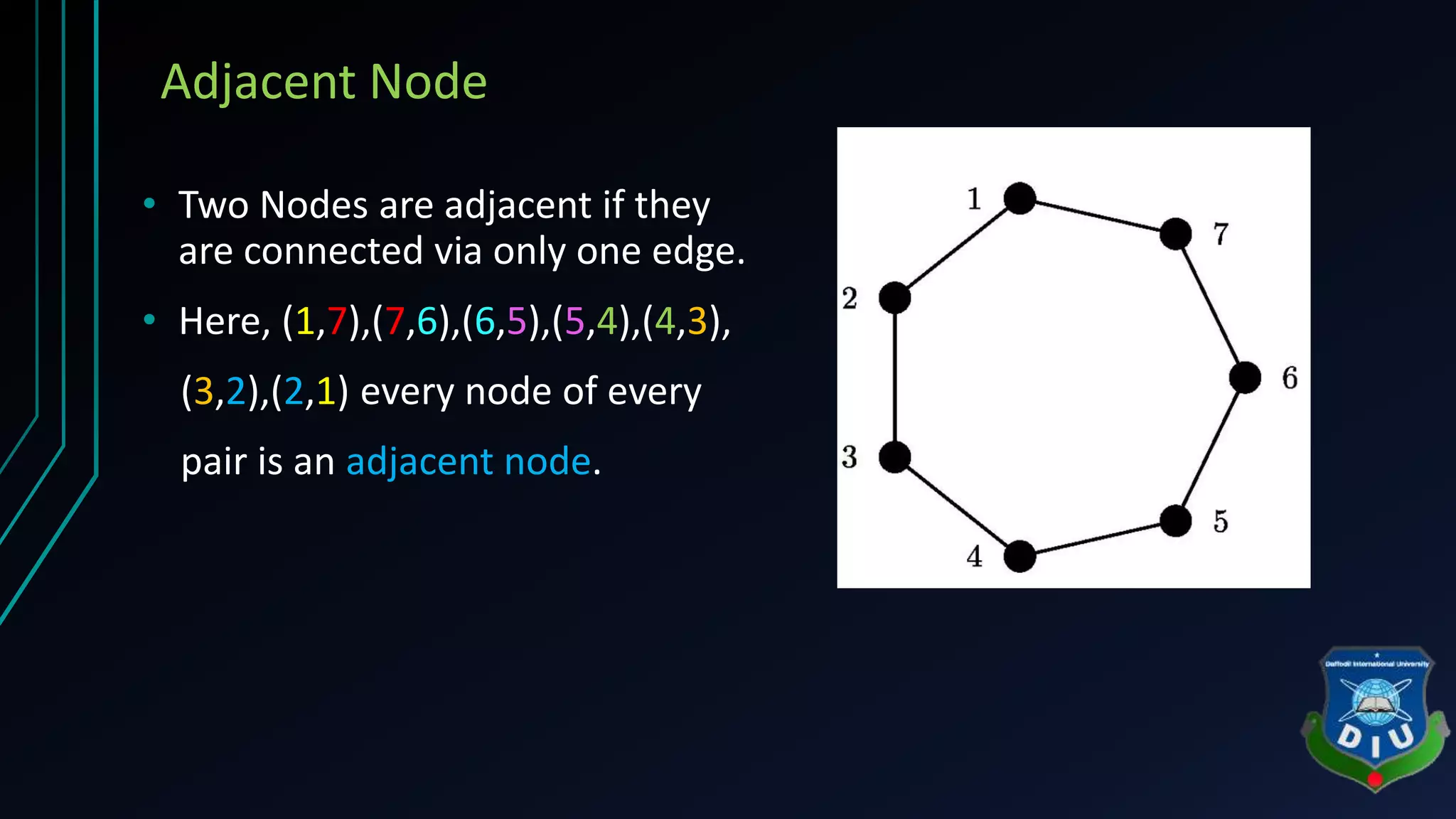
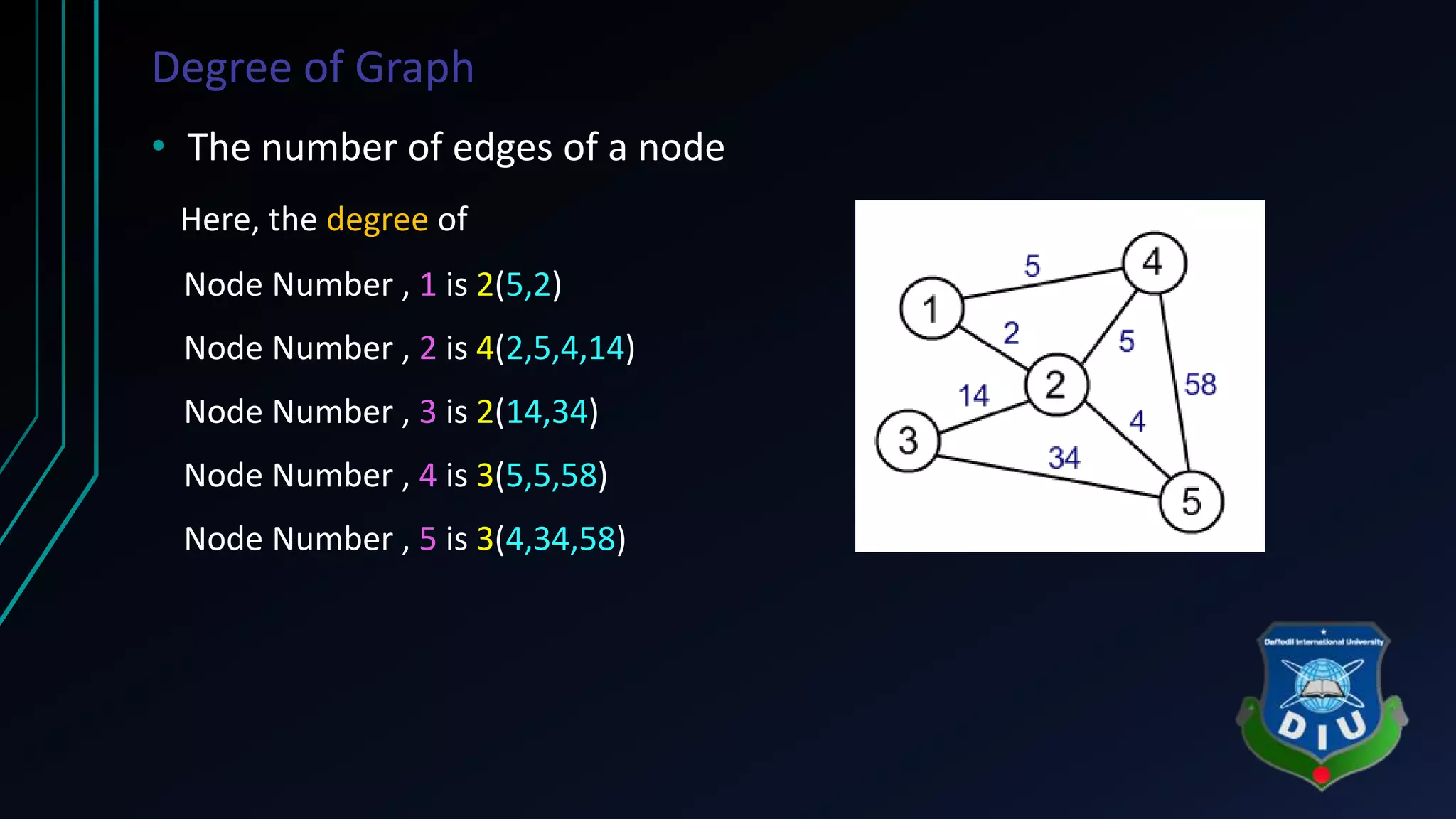
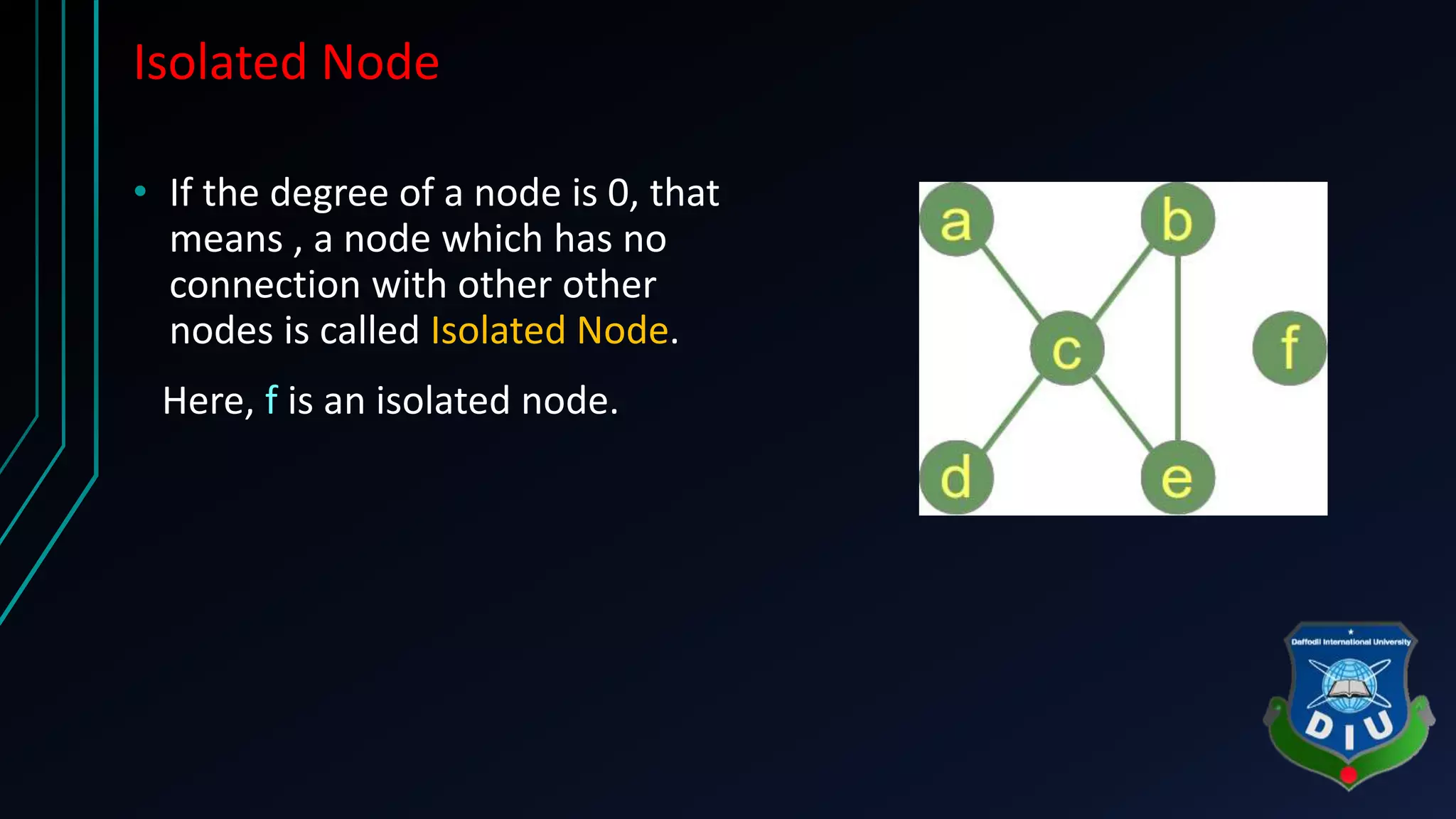
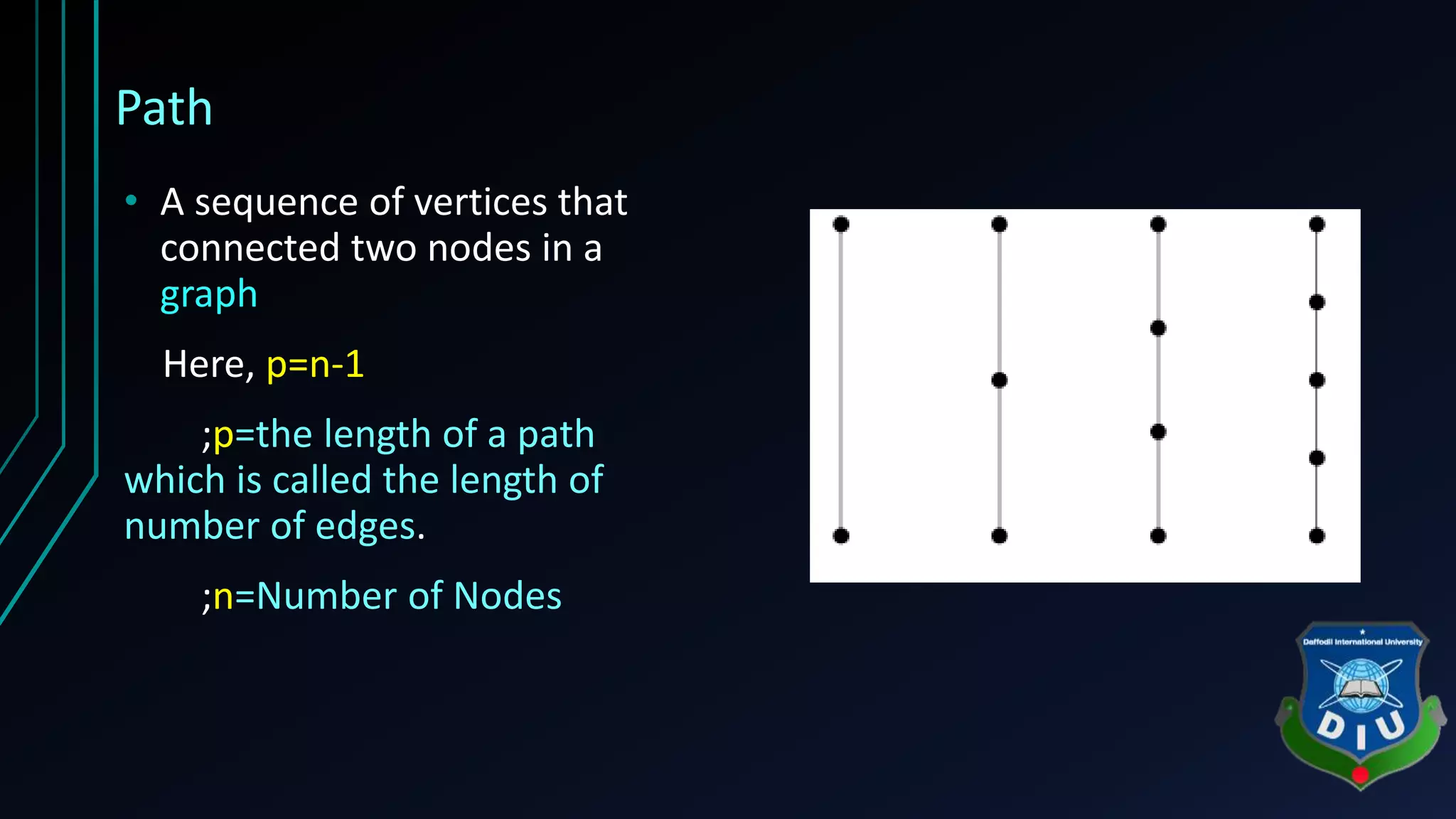
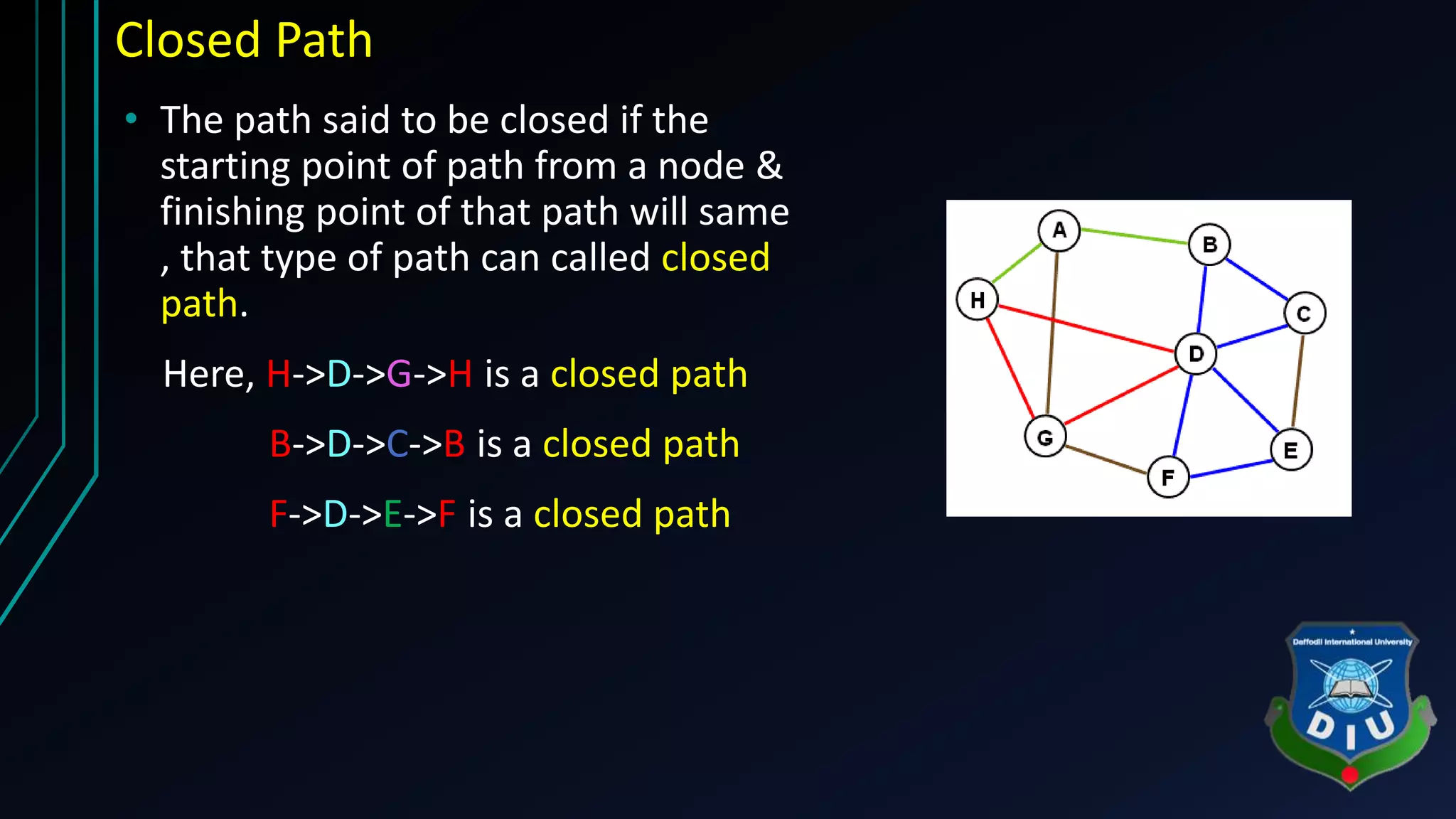
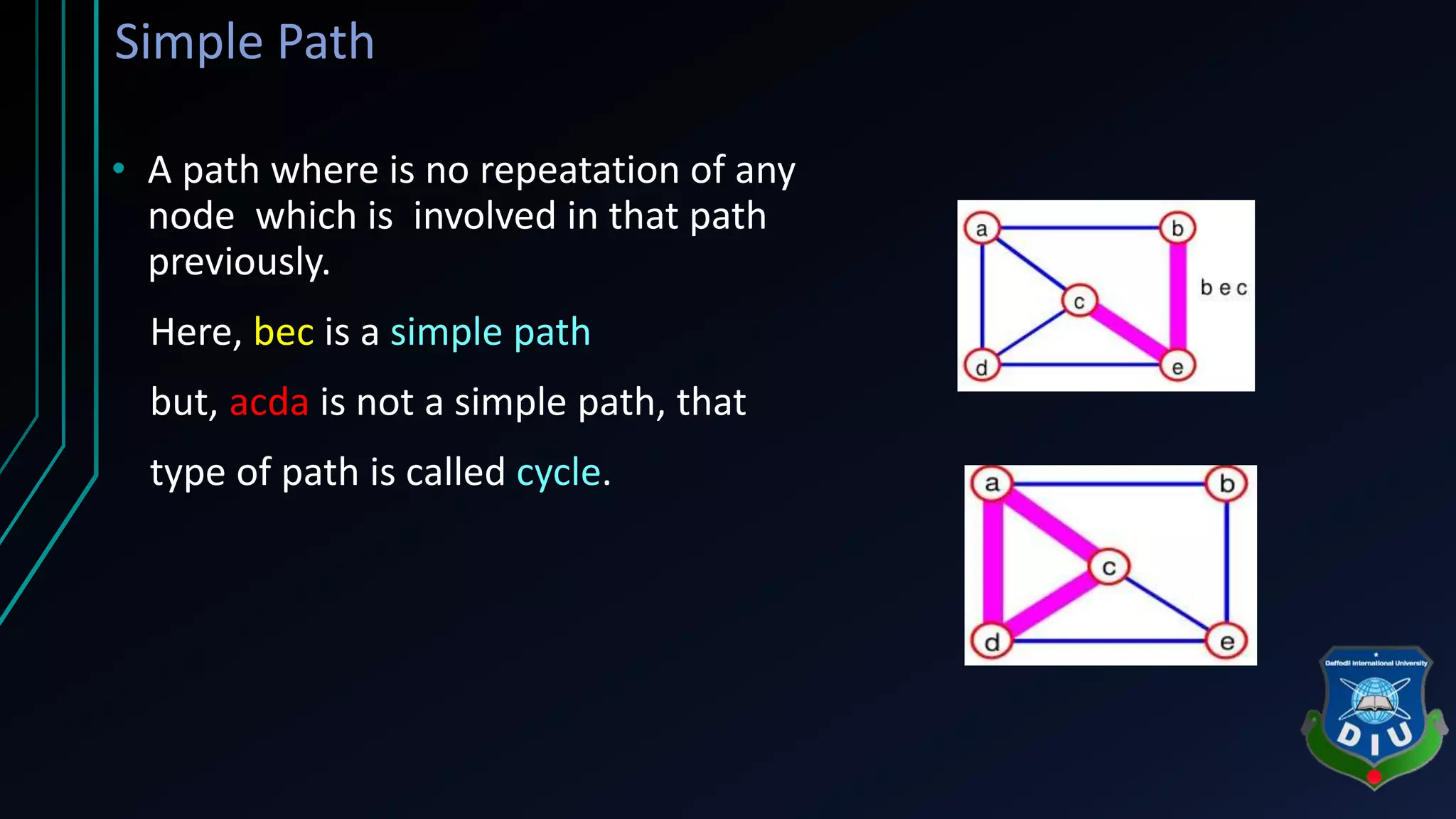
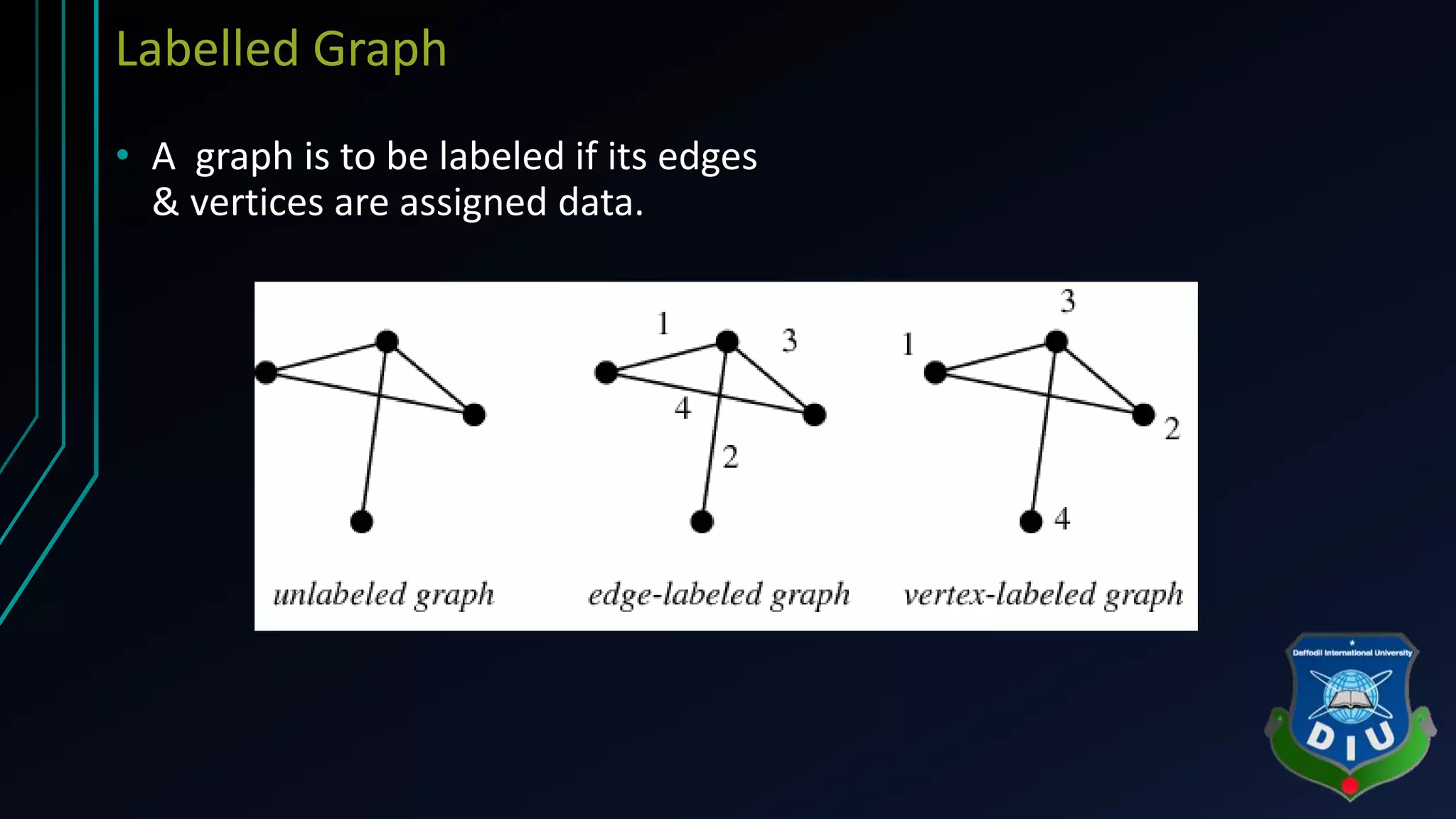
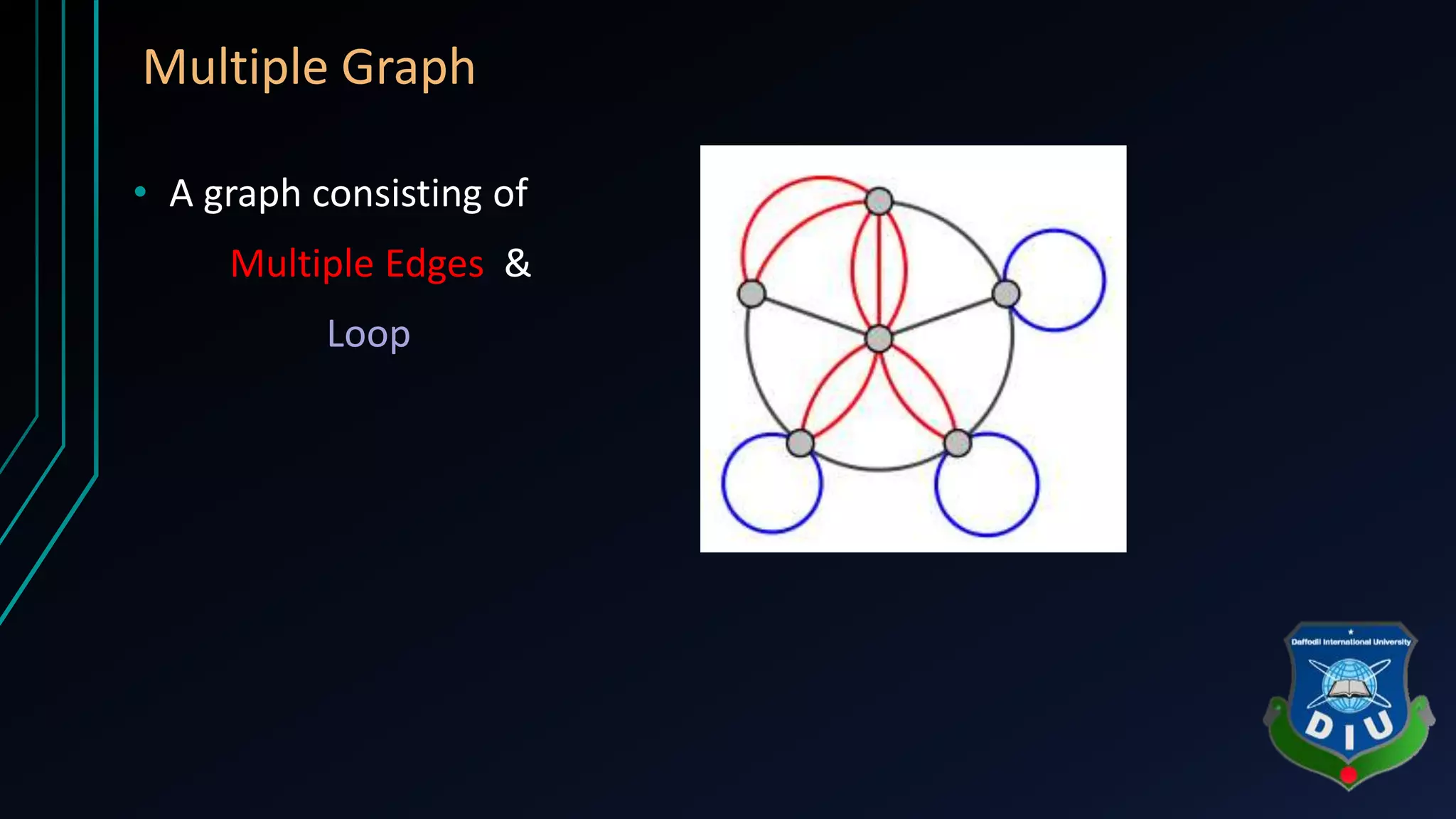
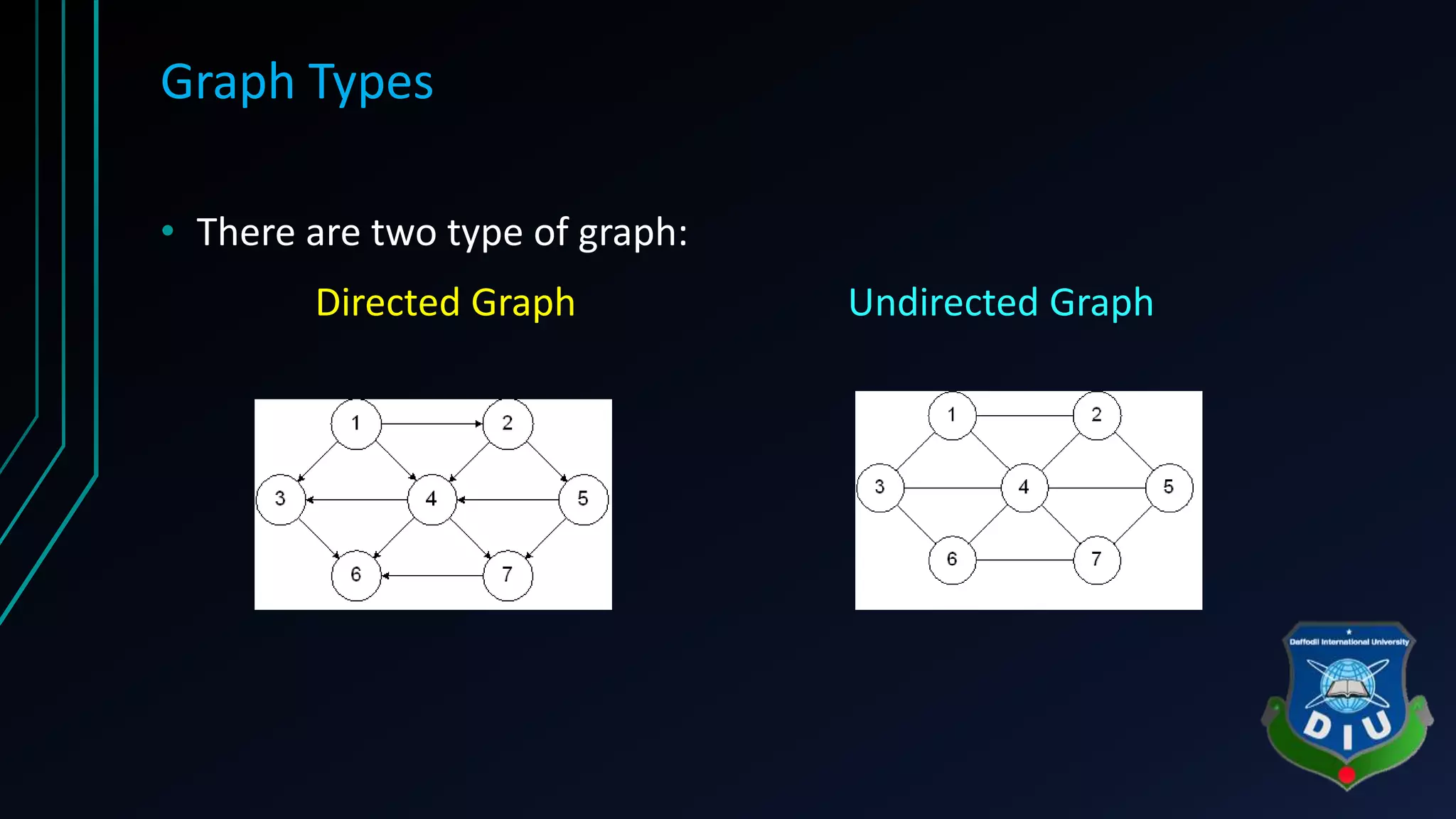
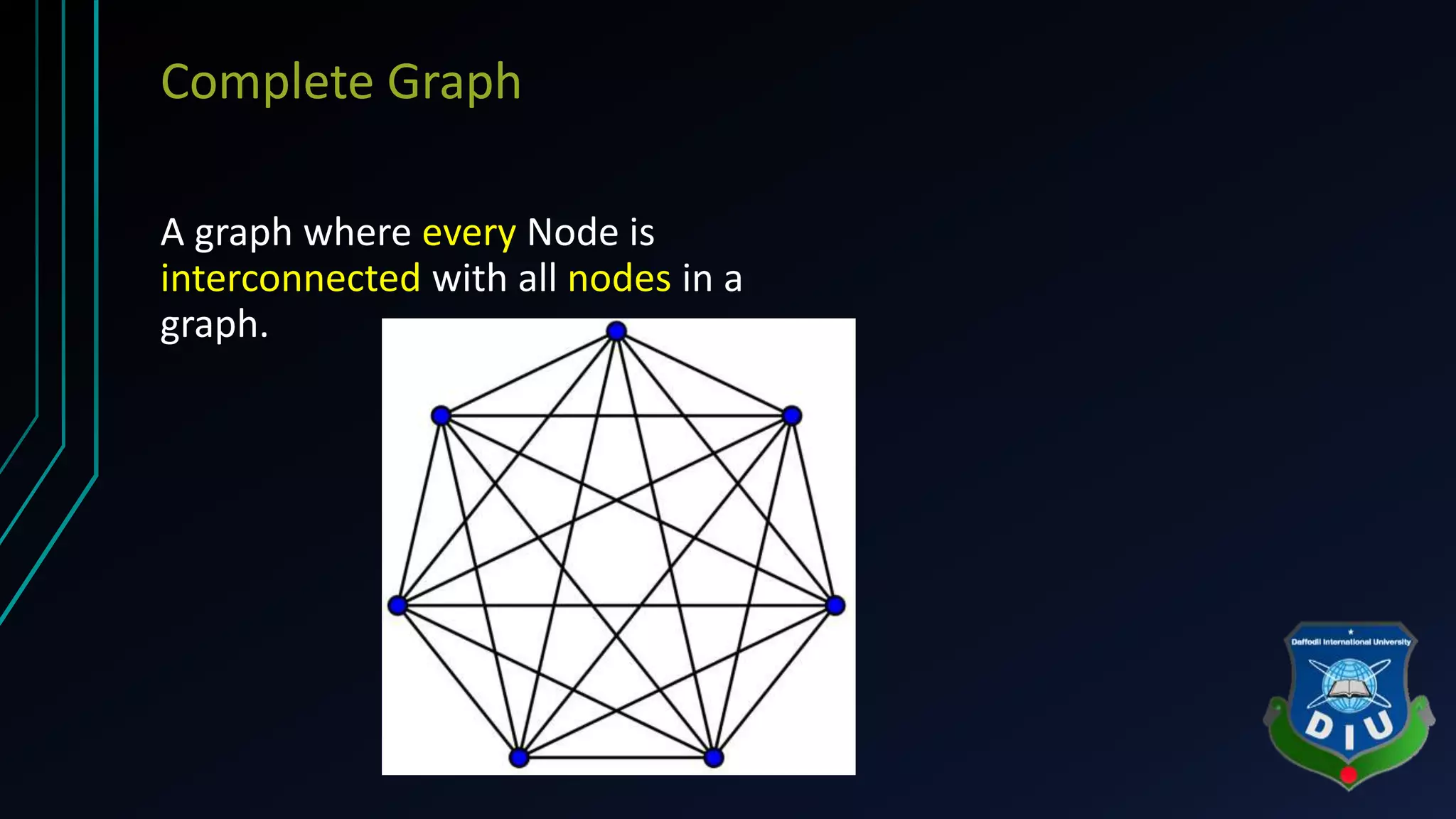
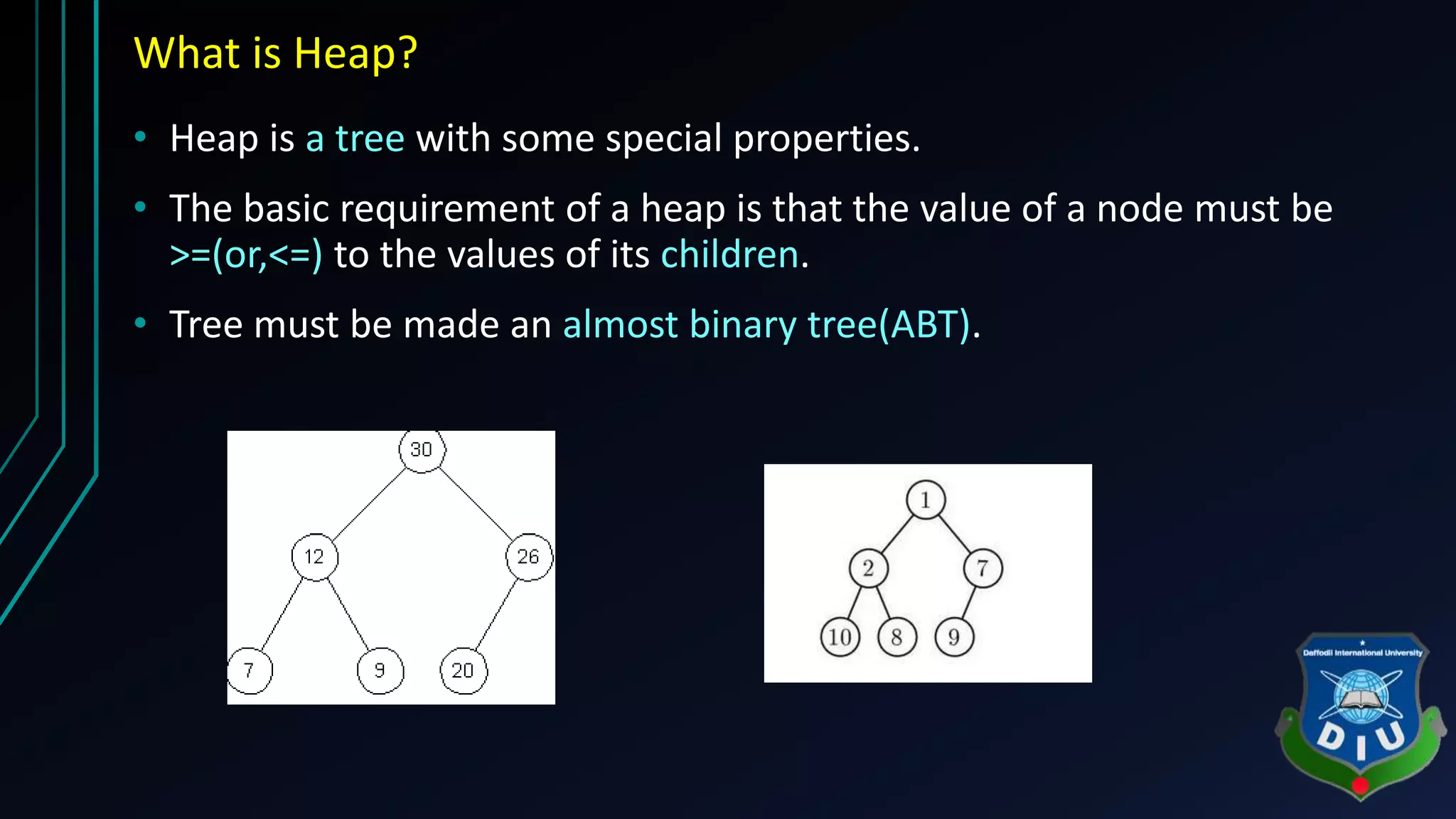
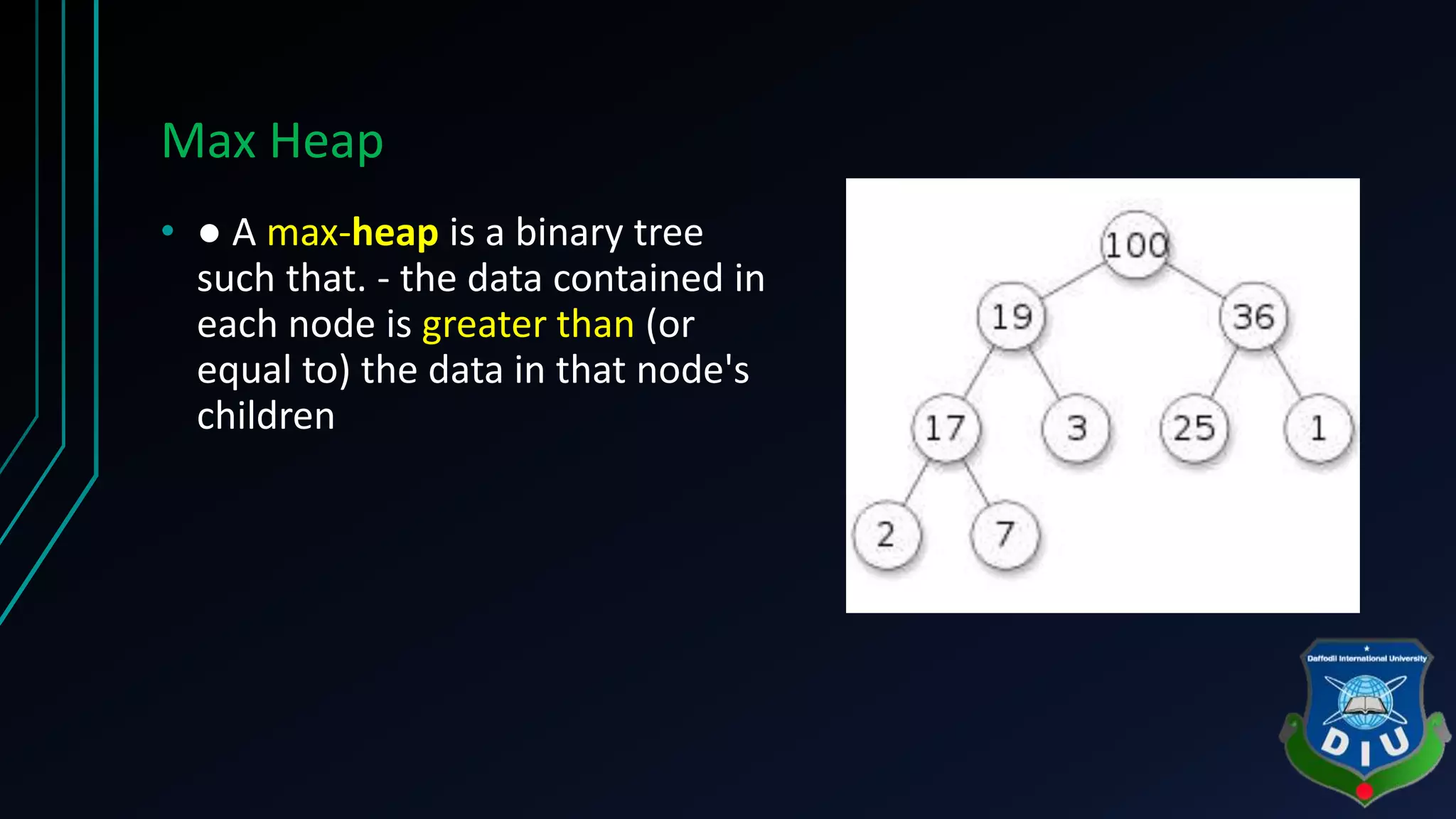
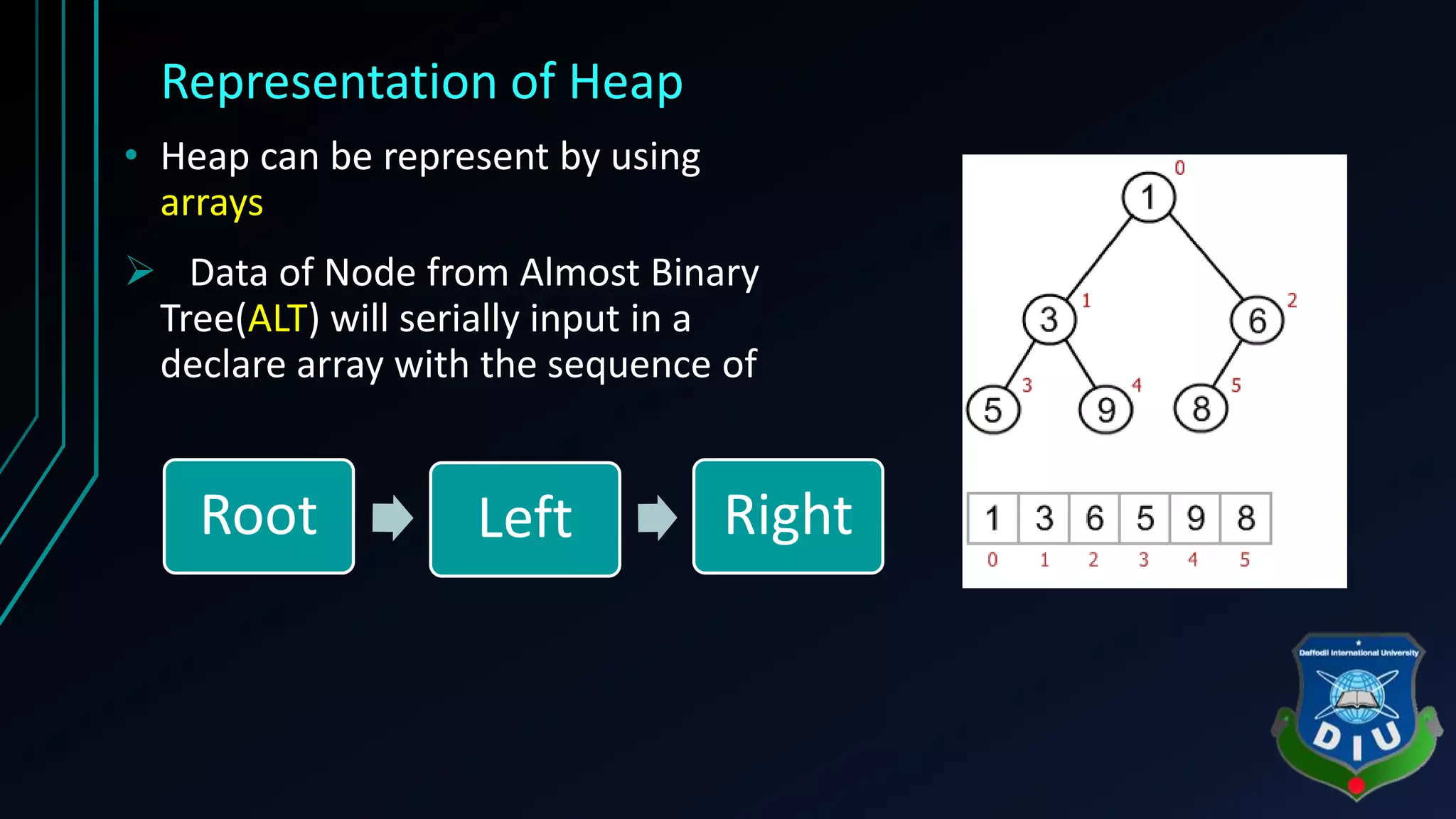
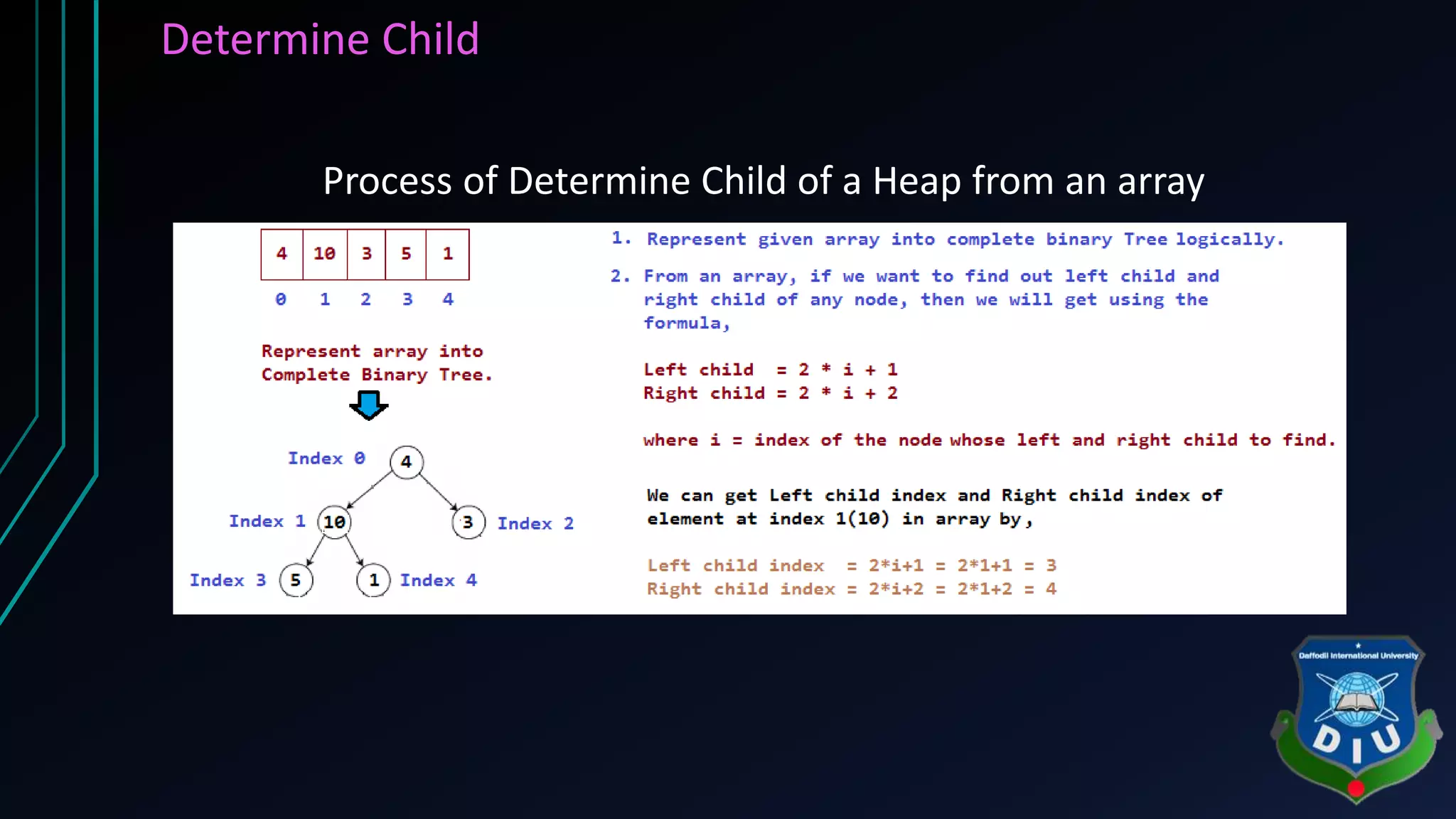
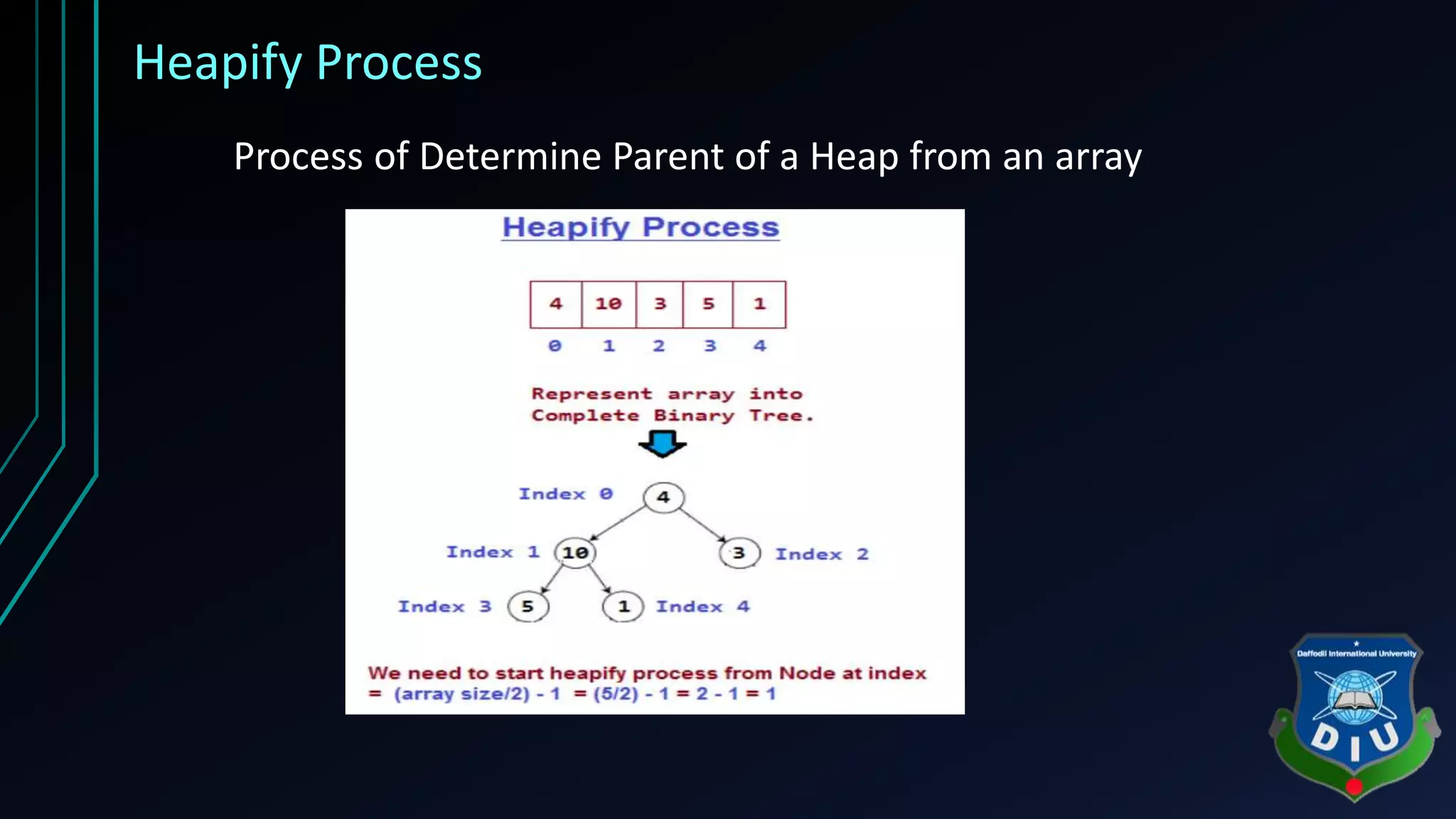
The document covers fundamental concepts of graphs and heaps in data structures for a CSE134 course. It explains definitions, types, and properties of graphs, such as adjacent nodes, degrees, paths, and various graph types, as well as heap structures, including min and max heaps, and their representations. The material serves as a comprehensive introduction to these essential data structures in computer science.
More Related Content
![Data Structures - Lecture 10 [Graphs]](https://cdn.slidesharecdn.com/ss_thumbnails/datastructures-lecture10graphs-150305004608-conversion-gate01-thumbnail.jpg?width=600ounds&width=560&fit=bounds)
Similar to Graph & Heap in Data Structure (Basic Information)
More from Daffodil International University
Graph & Heap in Data Structure (Basic Information)
- 1.
- 2. Course: CSE134 (DataStructure) Course Teacher: Mr. A. S. M. Farhan Al Haque (ASMFH) Section: P Group: A Depertment: CSE(43 Batch) Group Members: 01. Md. Ashaf Uddaula (161-15-7473) 02. Alamin Hossain (161-15-7483) 03. Md. Khasrur Rahman (161-15-7214) 04. Md. Eram Talukder (161-15-7485) 05. Ijaz Ahmed Utsa (161-15-7180)
- 3. Going to tellabout……. Graph • Definition of Graph • Adjacent Node • Degree of Graph • Isolated Node • Path • Closed Path • Simple Path • Connected Graph • Labelled Graph • Multiple Edges & Loop • Multi Graph • Graph Types • Directed Graph • Complete Graph • Null Graph • Sub-Graph Heap • Definition of Heap • Type of heap • Min Heap • Max Heap • Representation of Heap • Determine Child • Heapify Process
- 4. What is Graph? •A collection of Nodes(v1,v2,v3,v4,v5,v6) & connected by Edges(e1,e2,e3,e4,e5,e6). • Abstract Data Type. • In Mathematically, A graph G is composed by a set V of vertices or node connected through a set E of edges or links. Here, V={v1,v2,v3,v4,v5,v6} & E={e1,e2,e3,e4,e5,e6} Then , Graph G will be the sets of V & E, Graph, G = {V,E}
- 5. Adjacent Node • TwoNodes are adjacent if they are connected via only one edge. • Here, (1,7),(7,6),(6,5),(5,4),(4,3), (3,2),(2,1) every node of every pair is an adjacent node.
- 6. Degree of Graph •The number of edges of a node Here, the degree of Node Number , 1 is 2(5,2) Node Number , 2 is 4(2,5,4,14) Node Number , 3 is 2(14,34) Node Number , 4 is 3(5,5,58) Node Number , 5 is 3(4,34,58)
- 7. Isolated Node • Ifthe degree of a node is 0, that means , a node which has no connection with other other nodes is called Isolated Node. Here, f is an isolated node.
- 8. Path • A sequenceof vertices that connected two nodes in a graph Here, p=n-1 ;p=the length of a path which is called the length of number of edges. ;n=Number of Nodes
- 9. Closed Path • Thepath said to be closed if the starting point of path from a node & finishing point of that path will same , that type of path can called closed path. Here, H->D->G->H is a closed path B->D->C->B is a closed path F->D->E->F is a closed path
- 10. Simple Path • Apath where is no repeatation of any node which is involved in that path previously. Here, bec is a simple path but, acda is not a simple path, that type of path is called cycle.
- 11. Connected Graph • Agraph is connected when there is a path between every pair of vertices.
- 12. Labelled Graph • Agraph is to be labeled if its edges & vertices are assigned data.
- 13. Multiple Edges &Loop • MULTIPLE EDGES: Edges have the same pair of end points. • LOOP: An edge whose end points are equal.
- 14. Multiple Graph • Agraph consisting of Multiple Edges & Loop
- 15. Graph Types • Thereare two type of graph: Directed Graph Undirected Graph
- 16. Directed Graph • Agraph where every node has a direction by using edges of that node. Here , A -> B , A->C & B->C are directed .
- 17. Complete Graph A graphwhere every Node is interconnected with all nodes in a graph.
- 18. Null Graph • Agraph which has no edges between nodes
- 19. Sub-Graph • All theedges and vertices of (a) might not be present in M1,M2,M3,M4; but if a vertex is present in M1,M2,M3,M4, it has a corresponding vertex in (a) and any edge that connects two vertices in M1,M2,M3,M4 will also connect the corresponding vertices in (a).
- 20. What is Heap? •Heap is a tree with some special properties. • The basic requirement of a heap is that the value of a node must be >=(or,<=) to the values of its children. • Tree must be made an almost binary tree(ABT).
- 21. Type of heap •Heap is two type basically. 1. Min Heap 2. Max Heap
- 22. Min Heap • Amin-heap is a binary tree such that. - the data contained in each node is less than (or equal to) the data in that node's children. - the binary tree is complete.
- 23. Max Heap • ●A max-heap is a binary tree such that. - the data contained in each node is greater than (or equal to) the data in that node's children
- 24. Representation of Heap •Heap can be represent by using arrays Data of Node from Almost Binary Tree(ALT) will serially input in a declare array with the sequence of Root Left Right
- 25. Determine Child Process ofDetermine Child of a Heap from an array
- 26. Heapify Process Process ofDetermine Parent of a Heap from an array