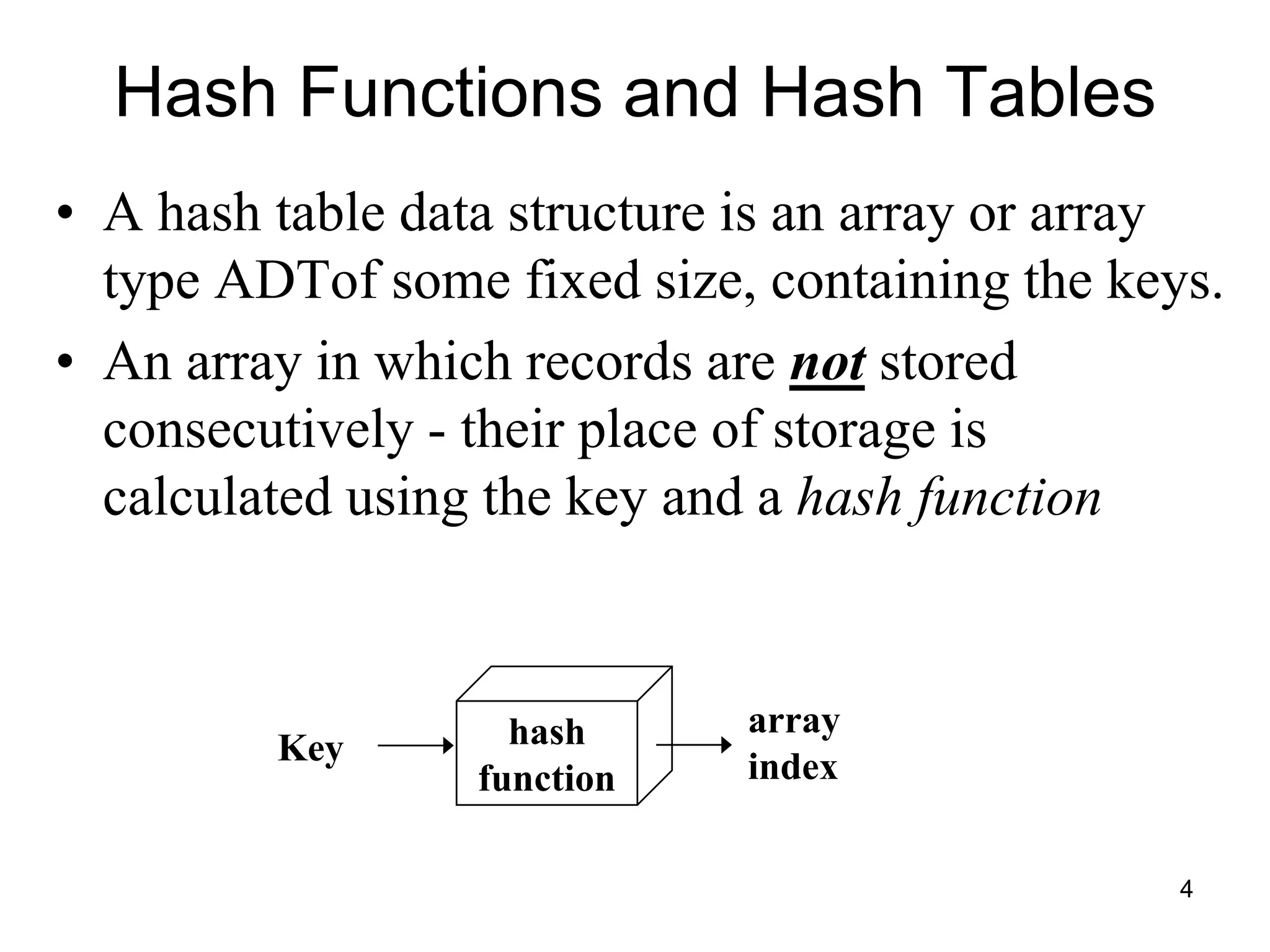
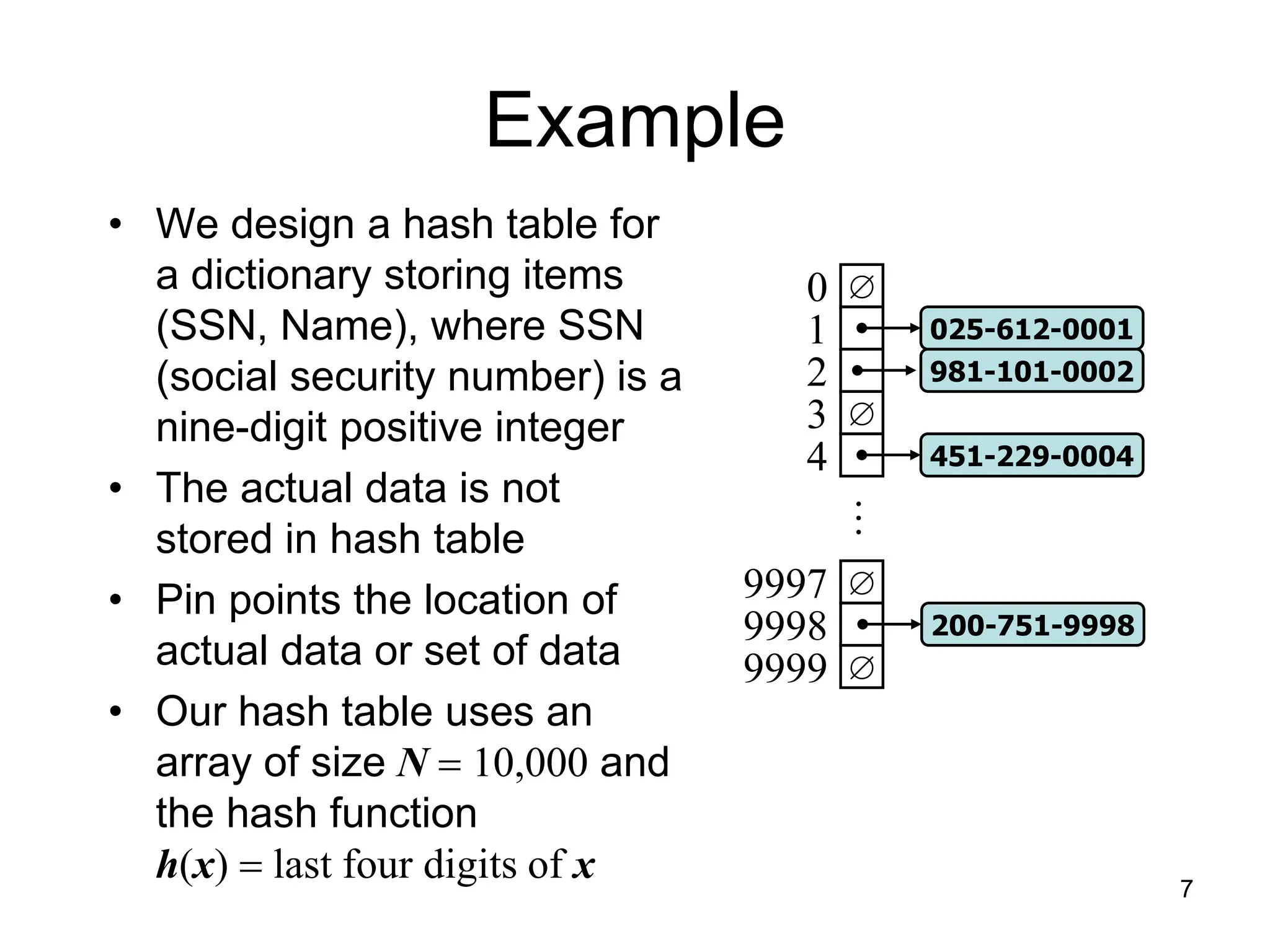
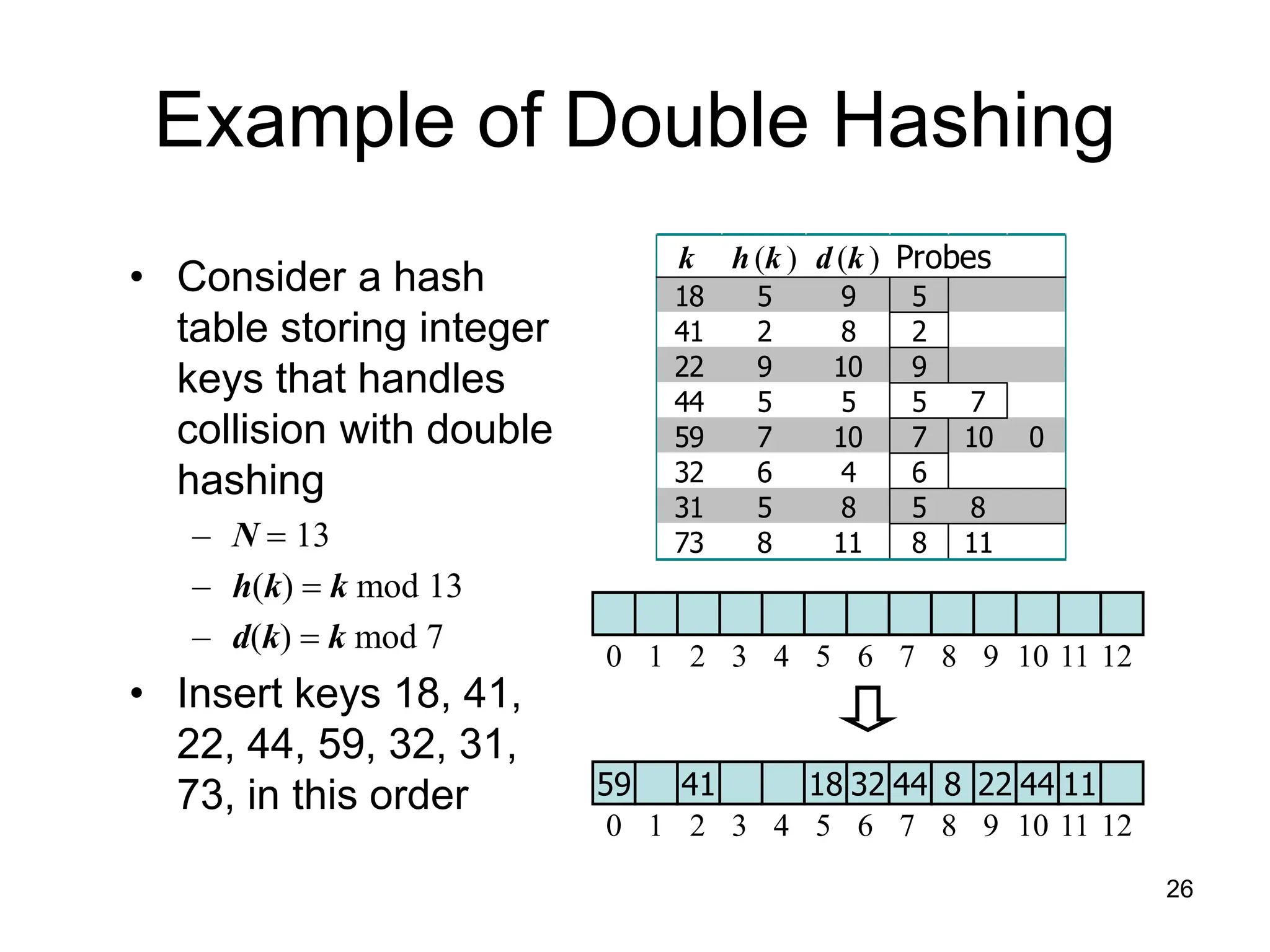
The document explains hashing as a mathematical concept used extensively in discrete mathematics, focusing on hash functions and hash tables for efficient data storage and retrieval. It details the components of hashing, methods for defining hash functions, and strategies for collision resolution, including separate chaining and open addressing techniques. Additionally, the document outlines various applications of hashing, such as in compilers and online spelling checkers.