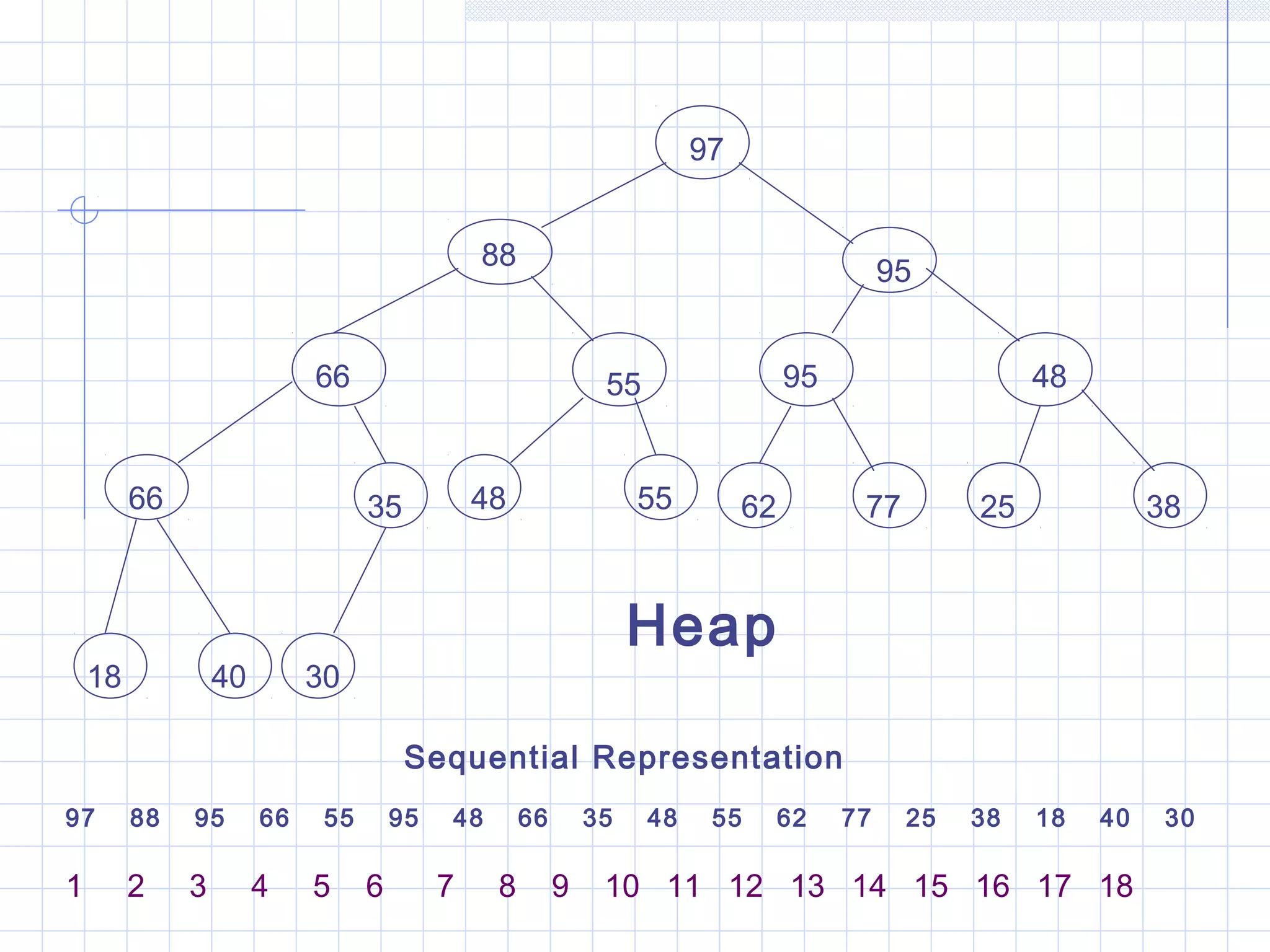
The document discusses heap sort, which is a sorting algorithm that uses a heap data structure. It works in two phases: first, it transforms the input array into a max heap using the insert heap procedure; second, it repeatedly extracts the maximum element from the heap and places it at the end of the sorted array, reheapifying the remaining elements. The key steps are building the heap, processing the heap by removing the root element and allowing the heap to reorder, and doing this repeatedly until the array is fully sorted.



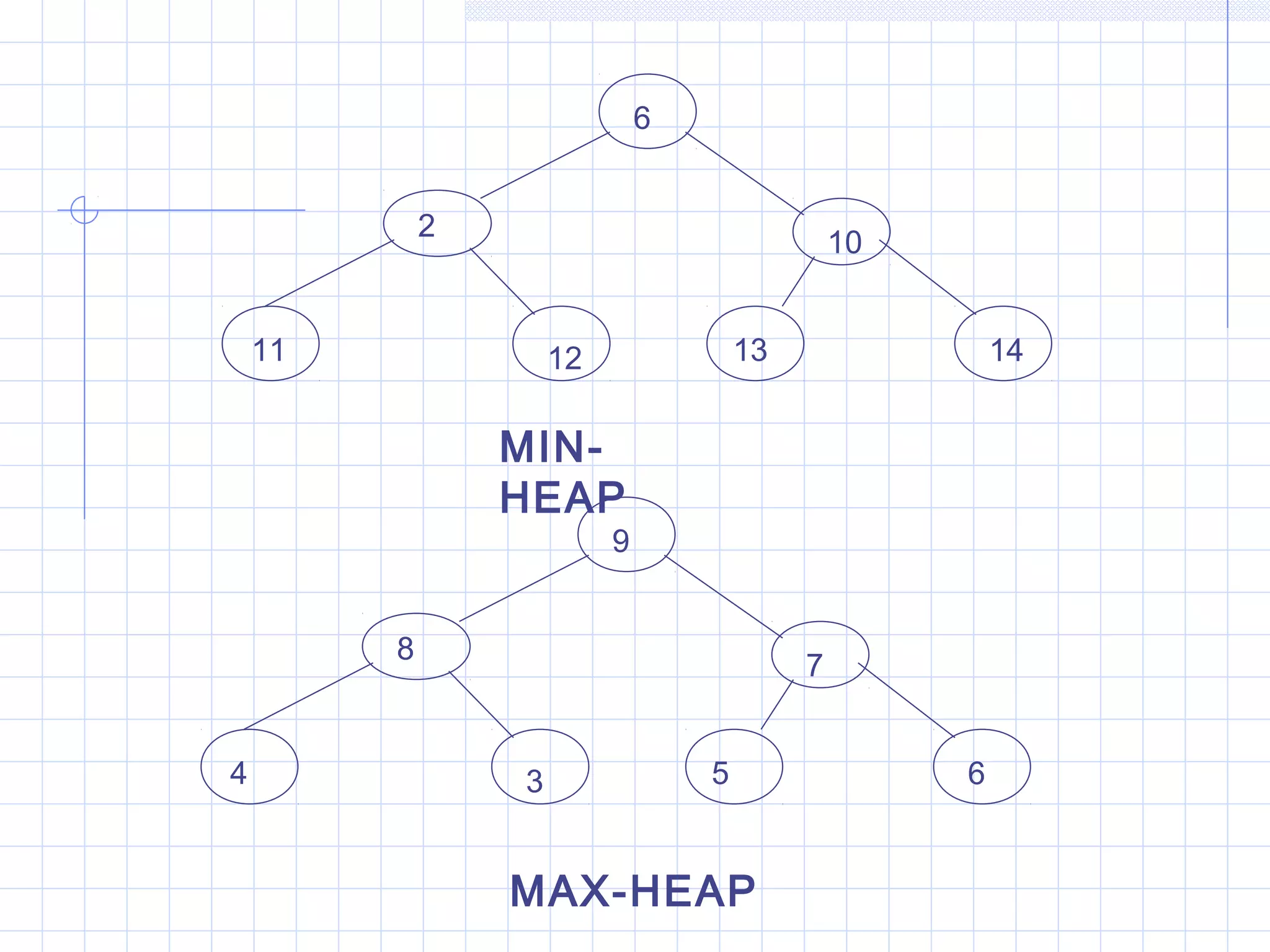
![Types Of Heap
Min Heap :- If the value at the node
N, is less than or equal to the value at
each of the children of N, then Heap is
called a MIN-HEAP.
In General, a Heap represents a
table of N elements or records
satisfying the following property;
Nj ≥ Ni for i≤j≤n & i = [j/2]](https://image.slidesharecdn.com/heapsort-130409104315-phpapp02/75/Heap-sort-5-2048.jpg)
![Max Heap :- If the value at the node
N, is greater than or equal to the value
at each of the children of N, then Heap
is called a MAX-HEAP.
In General, a Heap represents a
table of N elements or records
satisfying the following property;
Nj ≤ Ni for i≤j≤n & i = [j/2]](https://image.slidesharecdn.com/heapsort-130409104315-phpapp02/75/Heap-sort-6-2048.jpg)



![Algo for Creation of Heap
INSHEAP(TREE, N, ITEM)
Heap H with N elements is stored in the array Tree,
and an ITEM of information is given. This procedure
inserts ITEM as a new element of H. PTR gives the
location of ITEM as it rise in the tree, and PAR
denotes the location of parents of ITEM.
1. [Add new node to H and initialize PTR]
Set N := N+1 and PTR := N
2. [Find location to insert ITEM]
Repeat steps 3 to 6 while PTR < 1](https://image.slidesharecdn.com/heapsort-130409104315-phpapp02/75/Heap-sort-11-2048.jpg)
![3. Set PAR := [PTR/2]. [Location of parent node]
4. If ITEM <= TREE[PAR], then:
Set TREE[PTR] := ITEM, and Return.
[END of IF structure]
5. Set TREE[PTR] := TREE[PAR]. [Moves node
down]
6. Set PTR := PAR. [Updates PTR].
[End of step 2 loop]
7. [Assign ITEM as the root of H.]
8. Set TREE[1] := ITEM.
9. Return.](https://image.slidesharecdn.com/heapsort-130409104315-phpapp02/75/Heap-sort-12-2048.jpg)
![Algo for Processing of Heap
DELHEAP(TREE, N, ITEM)
A Heap H with N elements is stored in the array
TREE. This procedure assigns the root TREE[1] of H
to the variable ITEM and then reheaps the remaining
elements. The variables LAST saves the value of the
original Last node of H. The pointers PTR, LEFT and
RIGHT give the locations of LAST and its left and
right children as LAST sinks in the tree.
1. Set ITEM := TREE[1]. [Removes root of H.]
2. Set LAST := TREE[N] and N := N-1
[Removes last node of H.]](https://image.slidesharecdn.com/heapsort-130409104315-phpapp02/75/Heap-sort-13-2048.jpg)
![3. Set PTR := 1, LEFT := 2
and RIGHT := 3. [Initializes pointers.]
4. Repeat Steps 5 to 7 while RIGHT <= N:
5. If LAST >= TREE[LEFT] and
LAST >= TREE[RIGHT], then:
Set TREE[PTR] := LAST and Return.
[End of IF Structure.]
6. If TREE[RIGHT] <= TREE[LEFT], then:
Set TREE[PTR] := TREE[LEFT] and
PTR := LEFT.
Else:
Set TREE[PTR] := TREE[RIGHT] and
PTR := RIGHT.
[End of IF structure.]](https://image.slidesharecdn.com/heapsort-130409104315-phpapp02/75/Heap-sort-14-2048.jpg)
![7. Set LEFT := 2 * PTR and
RIGHT := LEFT+1.
[End of Step 4 loop.]
8. If LEFT = N and
If LAST < TREE[LEFT], then:
Set PTR := LEFT.
9. Set TREE[PTR] := LAST.
10. Return.](https://image.slidesharecdn.com/heapsort-130409104315-phpapp02/75/Heap-sort-15-2048.jpg)
![Algo for HEAP SORT
HEAPSORT(A, N)
An array A with N elements is given. This algorithm sorts the
elements of A.
1. [Build a Heap H, using Procedure INSHEAP(TREE, N,
ITEM) ]
Repeat for J = 1 to N-1:
Call INSHEAP(A, J, A[J+1]).
[End of loop]
2. [Sort A by repeatedly deleting the root of H, using procedure
DELHEAP(TREE, N, ITEM) ]
Repeat while N > 1:
(a) Call DELHEAP(A, N, ITEM).
(b) Set A[N+1] := ITEM.
[End of loop.]
3. Exit.](https://image.slidesharecdn.com/heapsort-130409104315-phpapp02/75/Heap-sort-16-2048.jpg)