This document provides an overview of quadratic functions including:
- The graph of a quadratic function is a parabola.
- The general form of a quadratic function is f(x) = ax2 + bx + c.
- Key aspects that must be identified before sketching the graph are the nature of the turning point, y-intercept, x-intercepts, and axis of symmetry.
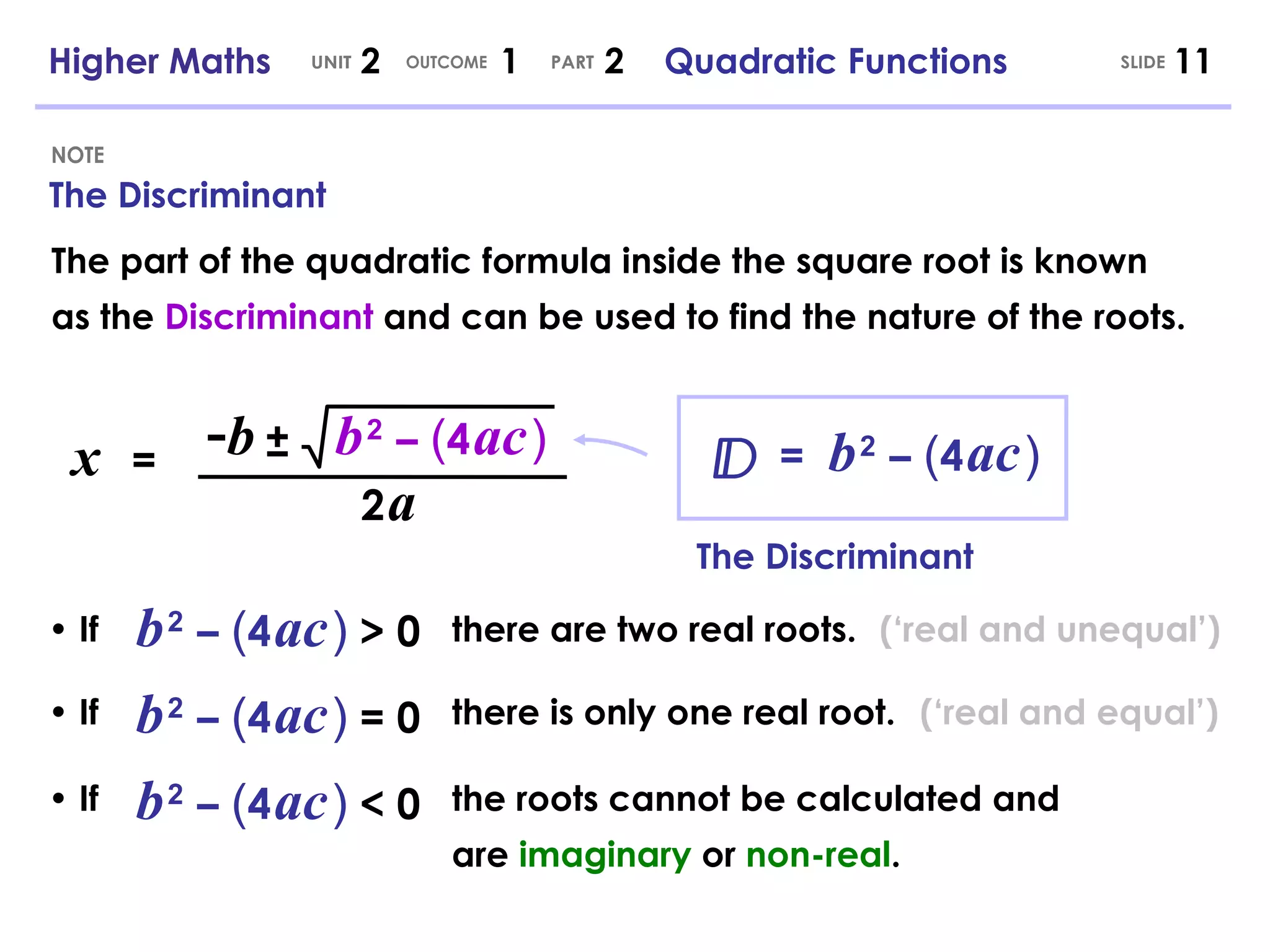
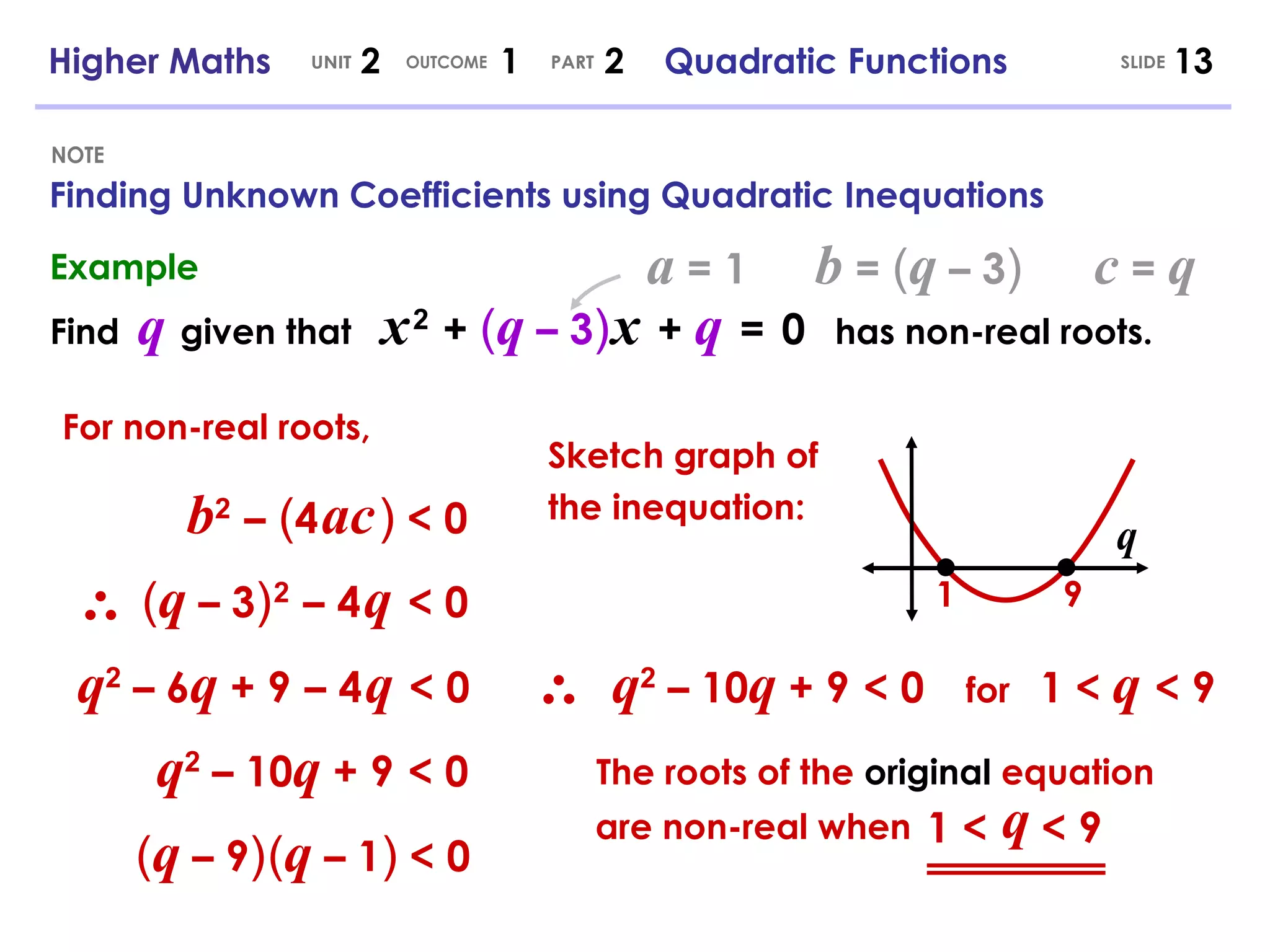
- Quadratic equations can be solved by factorizing, completing the square, or using the quadratic formula. The discriminant determines the nature of the roots.