Downloaded 102 times
Uploaded byClement Tay
How to plot a good graph
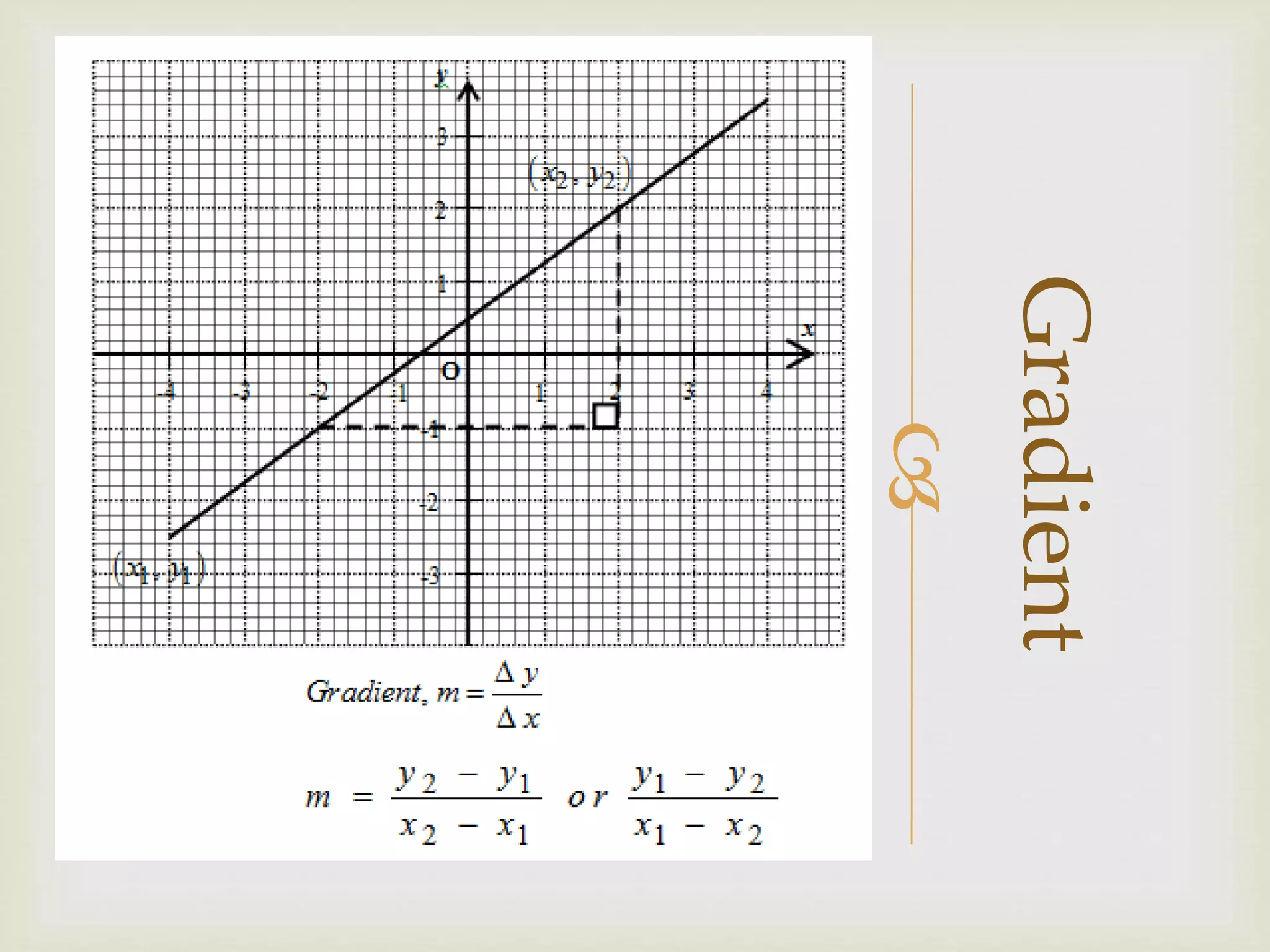
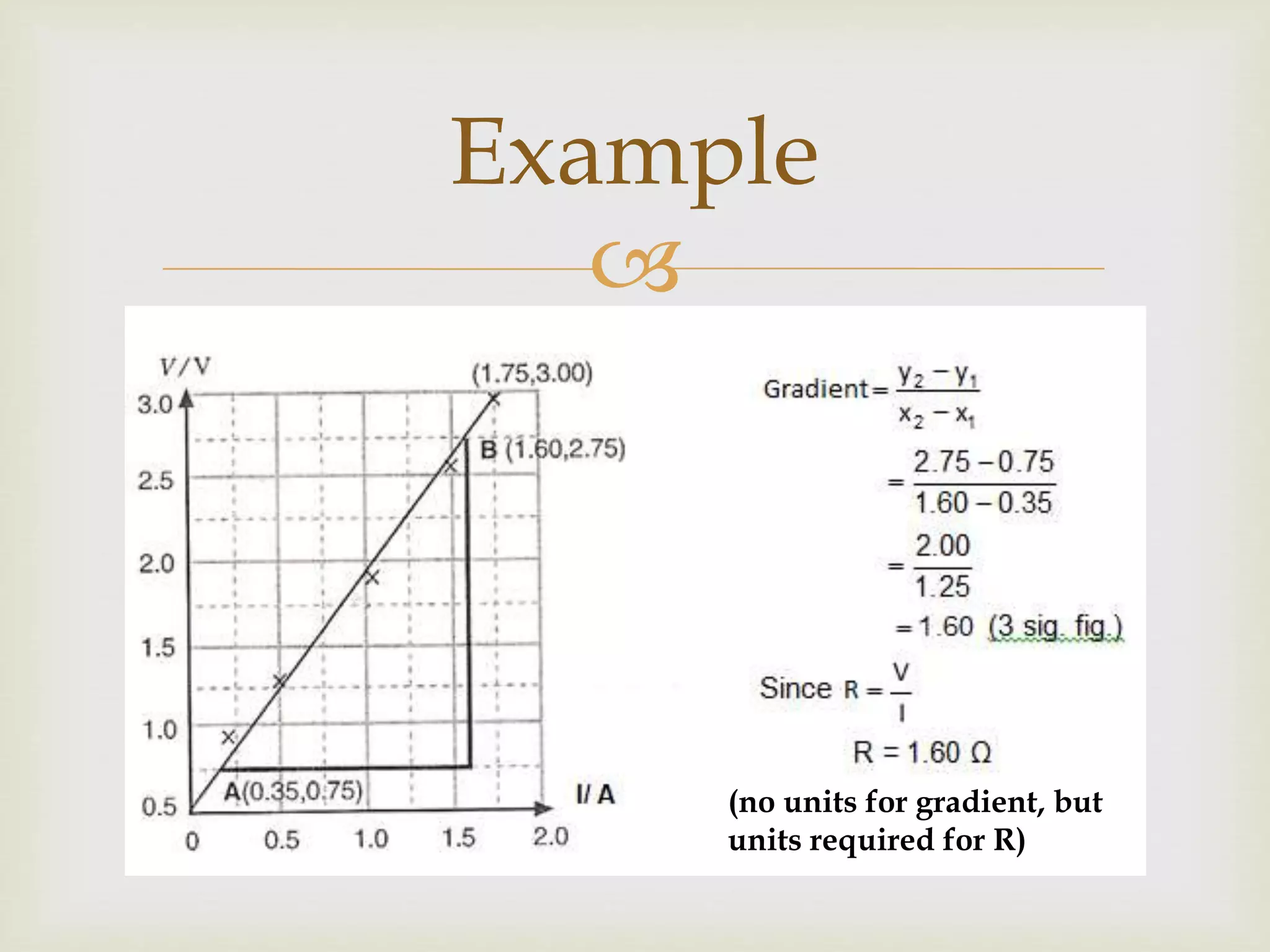
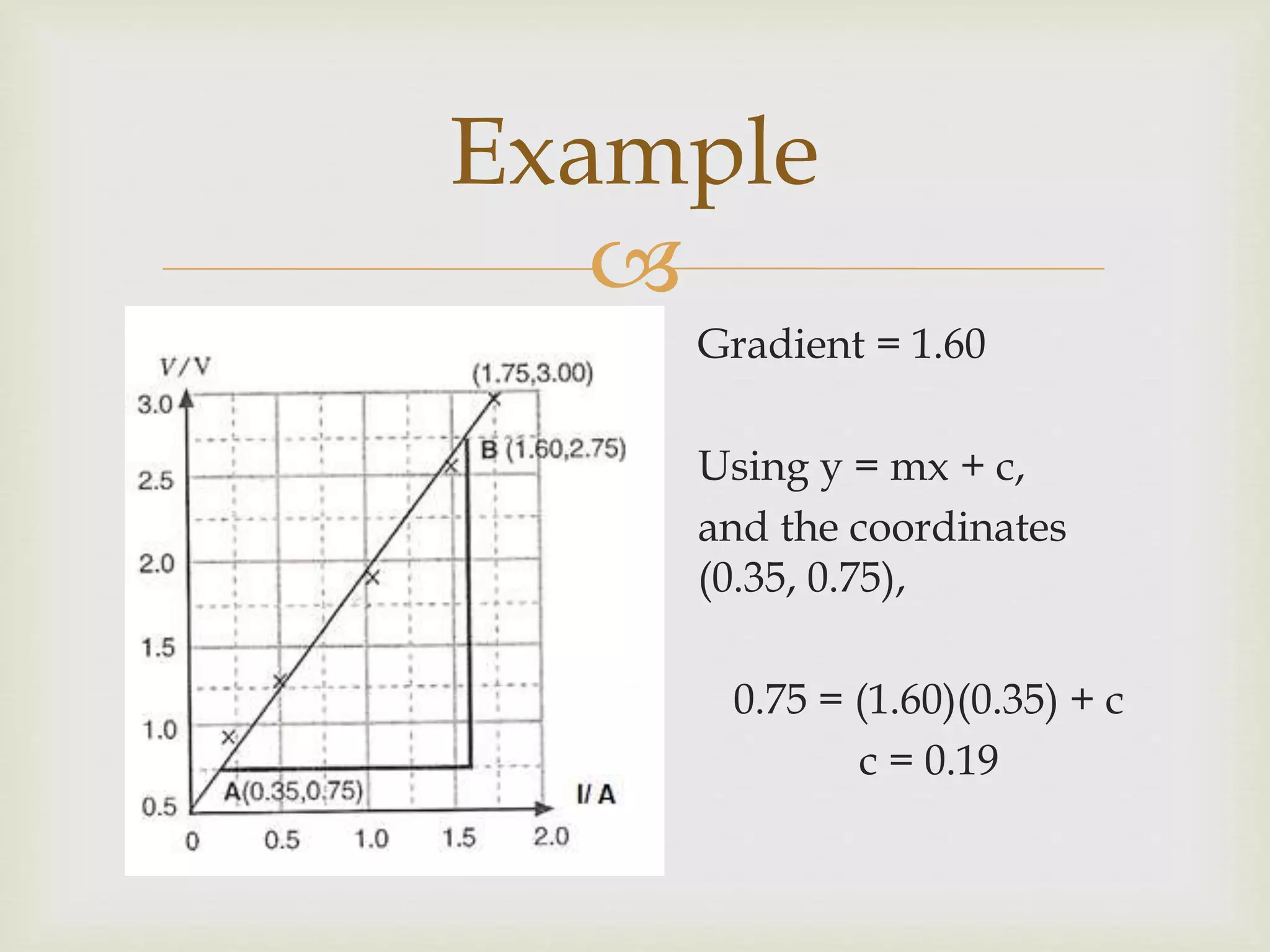
This document provides guidance on creating high-quality graphs with proper scaling, labeling, plotting of points, and calculating gradients. Key steps include using a scale where each small unit on the graph represents 1-5 units of the variable, labeling the axes with the variables and units, plotting points according to the values in the table, drawing a best-fit smooth line passing through most points, and using a triangle that covers half the line to calculate the gradient without using actual plotted points. Following these techniques will result in clear, accurate graphs.
More Related Content
Similar to How to plot a good graph
![Checklist for practicals[1]](https://cdn.slidesharecdn.com/ss_thumbnails/checklistforpracticals1-110206102018-phpapp02-thumbnail.jpg?width=600ounds&width=560&fit=bounds)
How to plot a good graph
- 1.
- 2. Characteristics Rememberthe acronym SLAP Scale Line Axis Points
- 3. Scale First and last points to cover more than half the graph paper in both directions unless prevented by certain conditions specified in the question Avoid awkward scales e.g. 2 cm is used to represent 3 units making it impossible to read each small square accurately. Recommended scale – 2 cm to represent 1, 2, 5 units of the variable (or 0.1, 20, 500 etc). show the area covered by 1st and last points and indicate at least 6 squares vertically and at least 5 squares horizontally
- 4.
- 5. Line Usesharp pencil to draw thin, neat and smooth line or curve. Best fit straight line or curve means Passing through as many points as possible. Equal points are on either side of line, for points that do not pass through the line. No point is too far from line or curve. (Except anomalous points)
- 6. Line Extendline beyond first and last points and the line should be as long as possible. Use a 30-cm long ruler for practical to draw straight line.
- 7. Axis Axesare correctly labelled with correct physical quantities and units (in solidus notation). Use more markings to prevent wrong reading of scale. Plot a graph of Variable 1 (Vertical Axis) against Variable 2 (Horizontal Axis)
- 8. Points Markthe data points clearly with neat thin small crosses. Points must be plotted according to the values in the table. Read the scales carefully.
- 9.
- 10.
- 11. Gradient Thetriangle used should cover at least half of the line drawn. The triangle should be drawn in dotted line and do not mark the points used with crosses. Indicate the coordinates to be used. The coordinates must be on the line.
- 12. Gradient Donot use plotted/ data points to calculate gradient. Use other coordinates. Show complete working as to how gradient is obtained. Values read from graph should be according to the number of decimal places of the scales used.
- 13. Example (nounits for gradient, but units required for R)
- 14. Example Gradient= 1.60 Using y = mx + c, and the coordinates (0.35, 0.75), 0.75 = (1.60)(0.35) + c c = 0.19