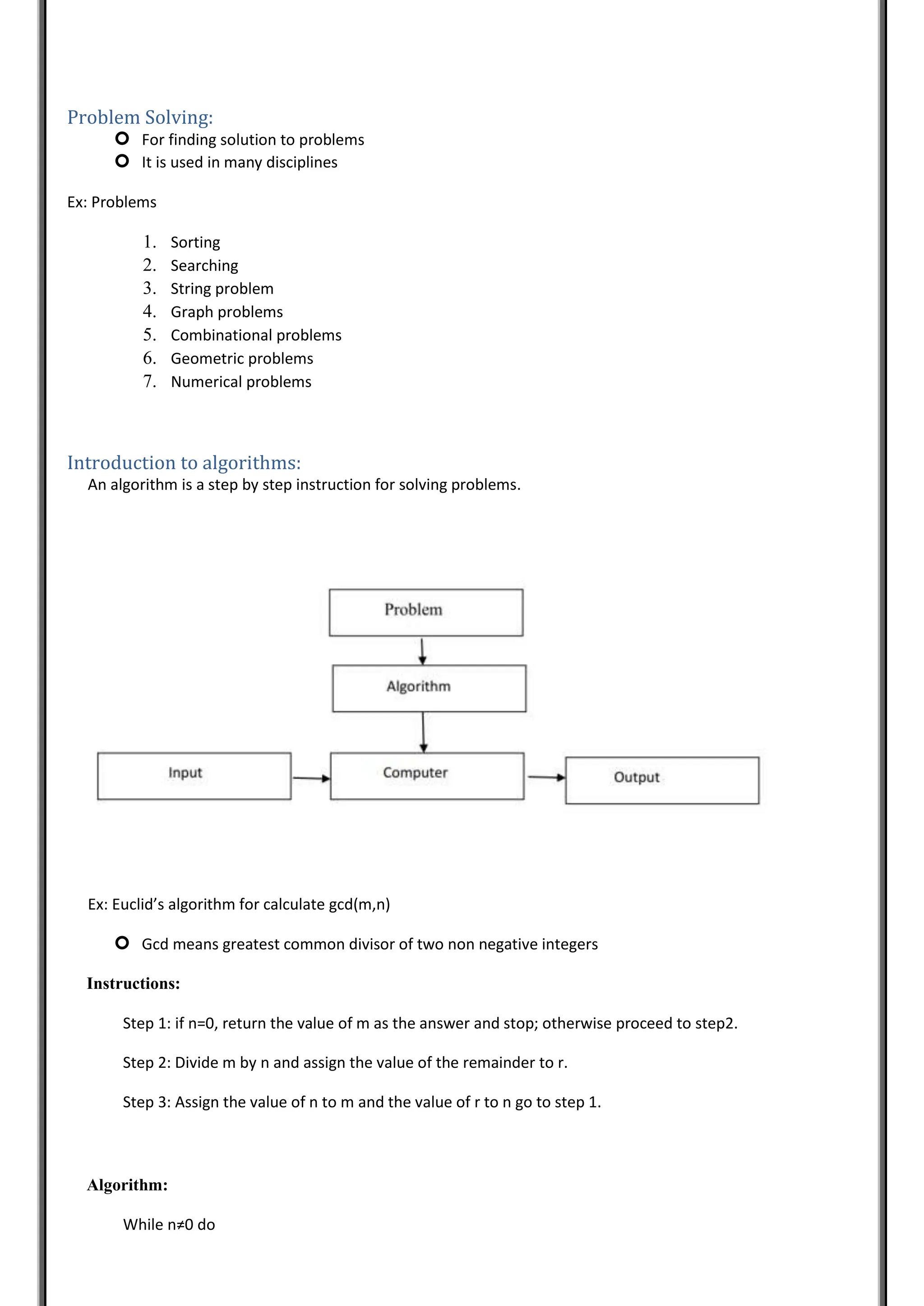
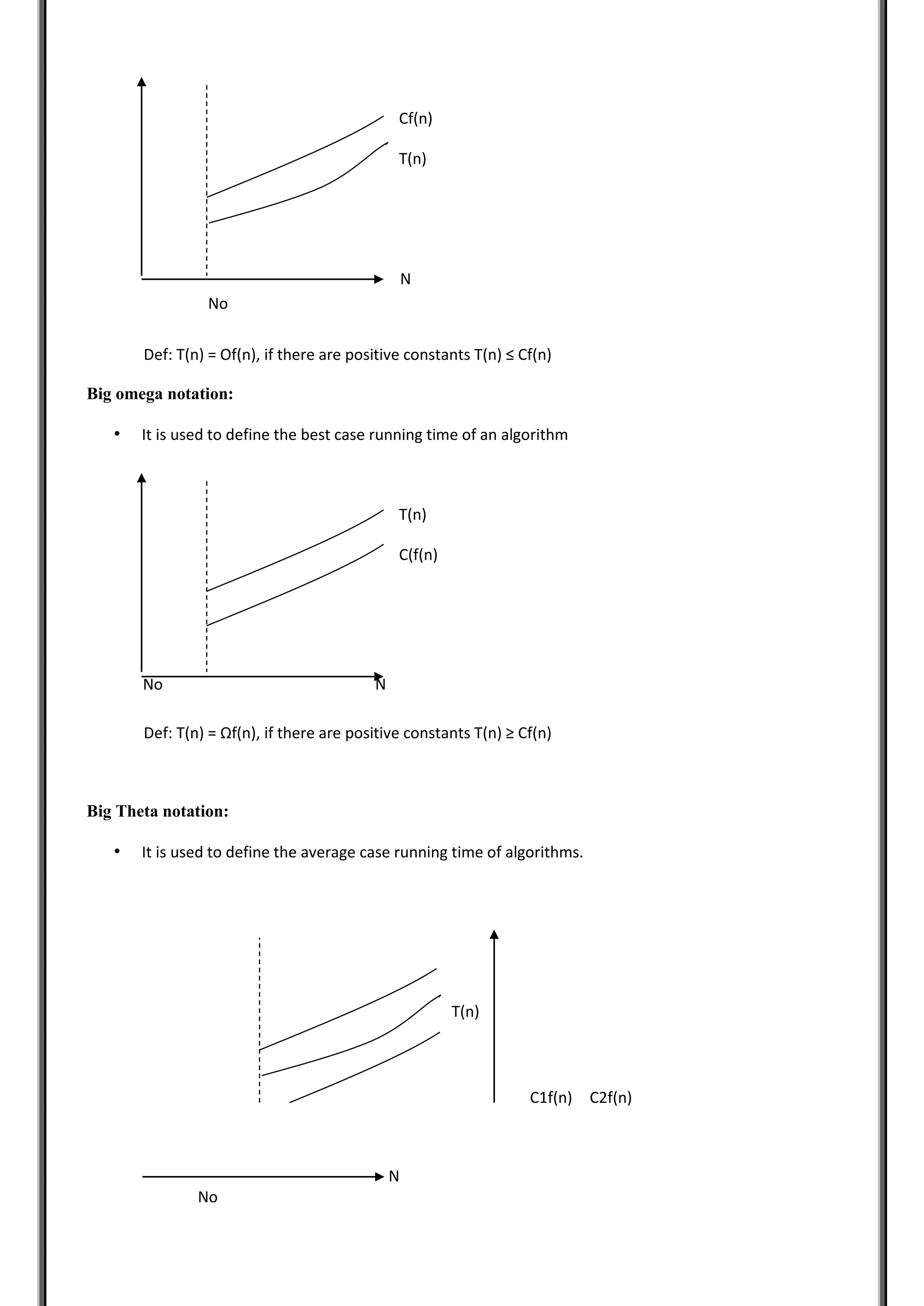
The document provides comprehensive notes on data structures and algorithms, covering essential topics such as algorithm characteristics, time and space complexity, and various algorithm design strategies like divide and conquer and greedy methods. It also discusses different types of data structures, including primitive and non-primitive, linear and non-linear structures, and the concepts of static, dynamic, persistent, and ephemeral data. Furthermore, the notes include explanations of recurrence relations and techniques for solving them.