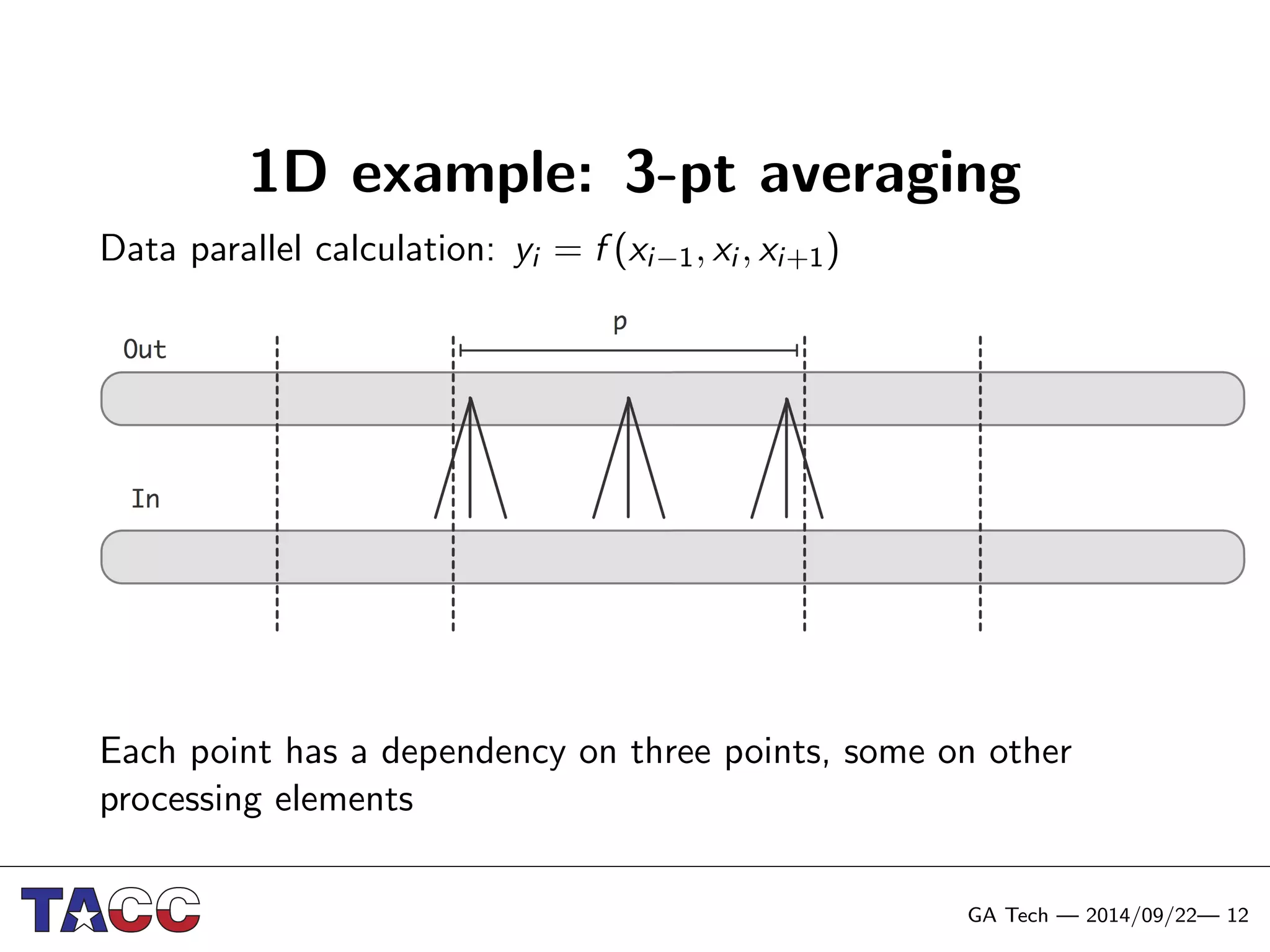
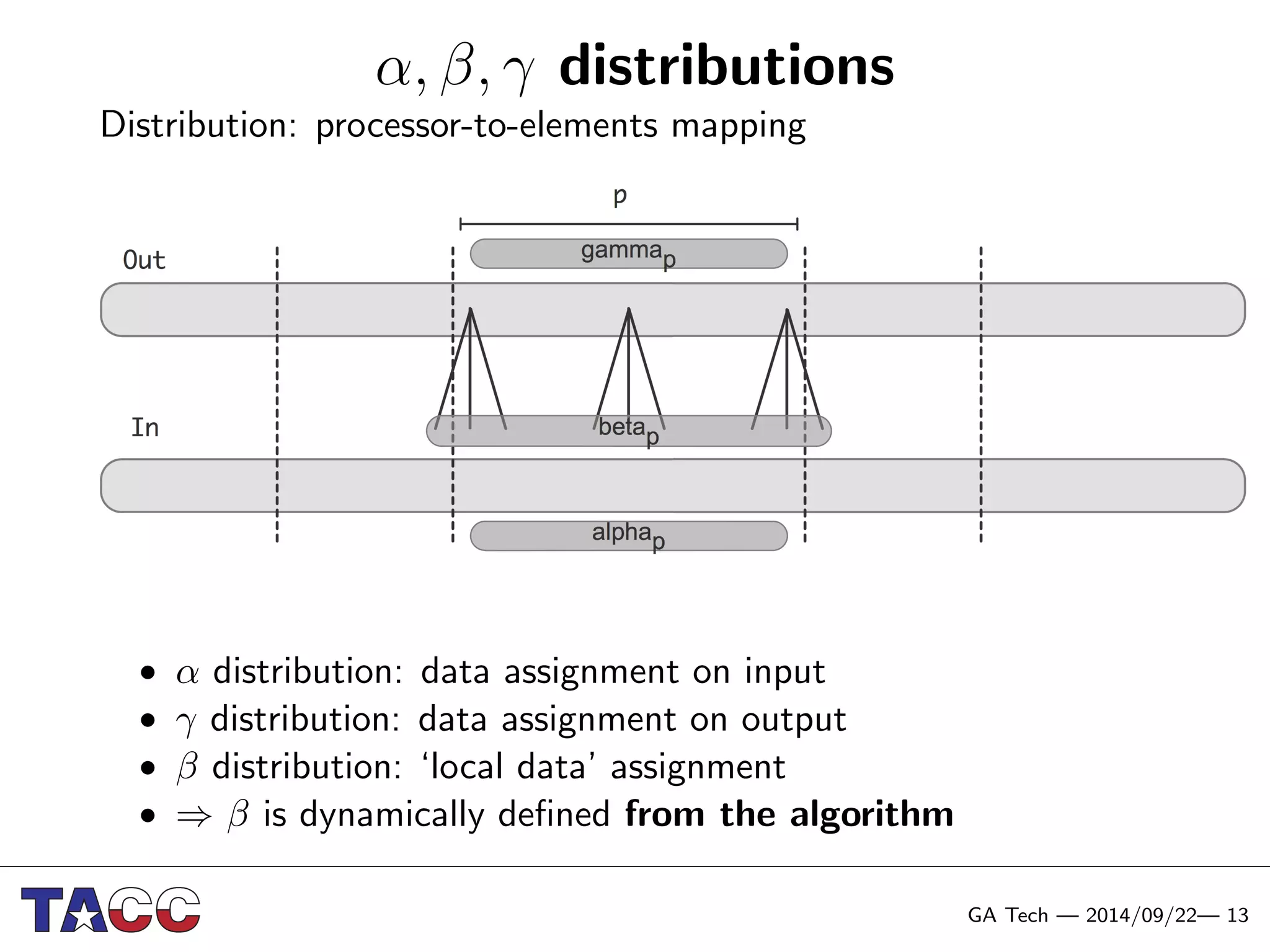
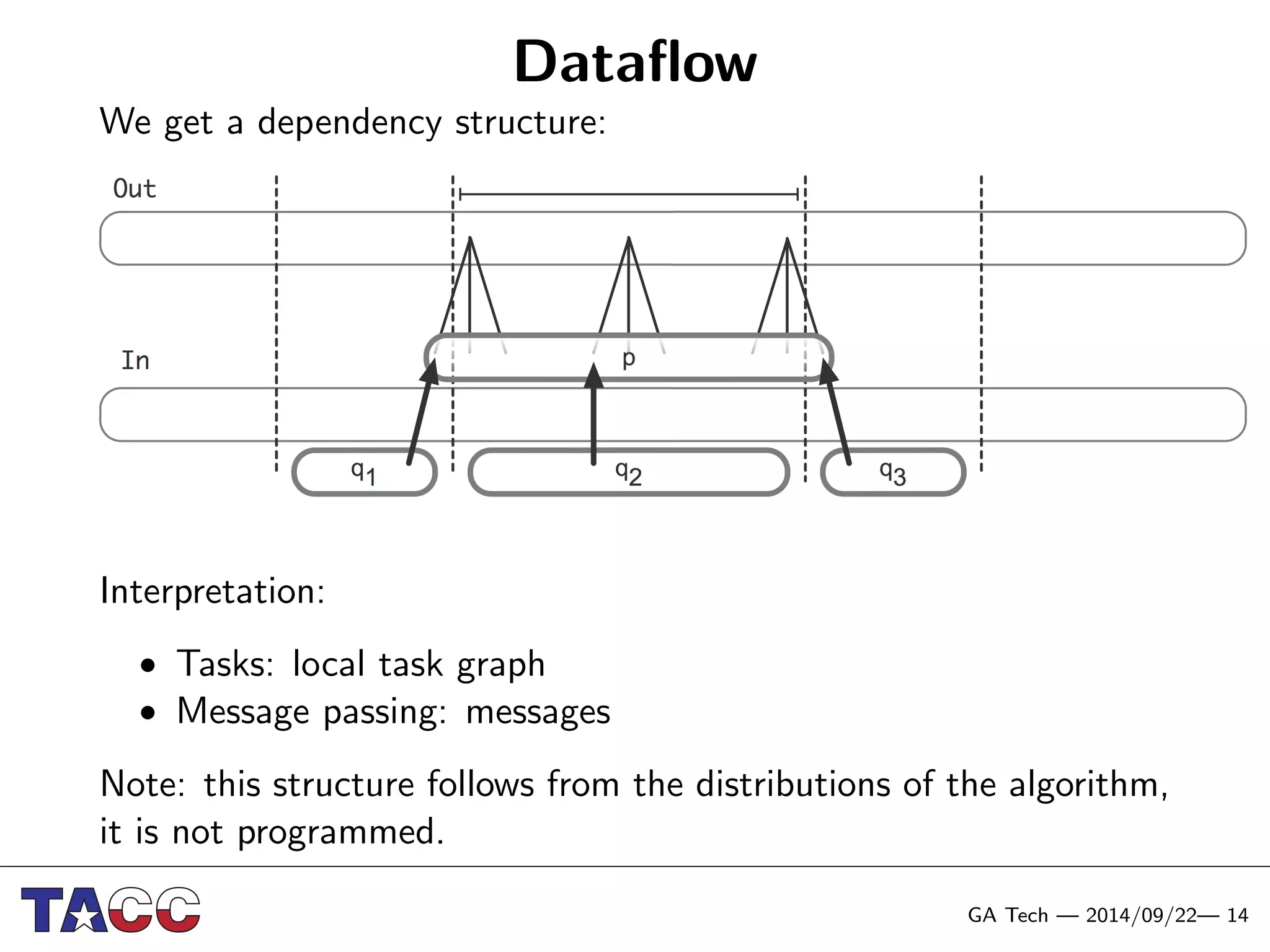
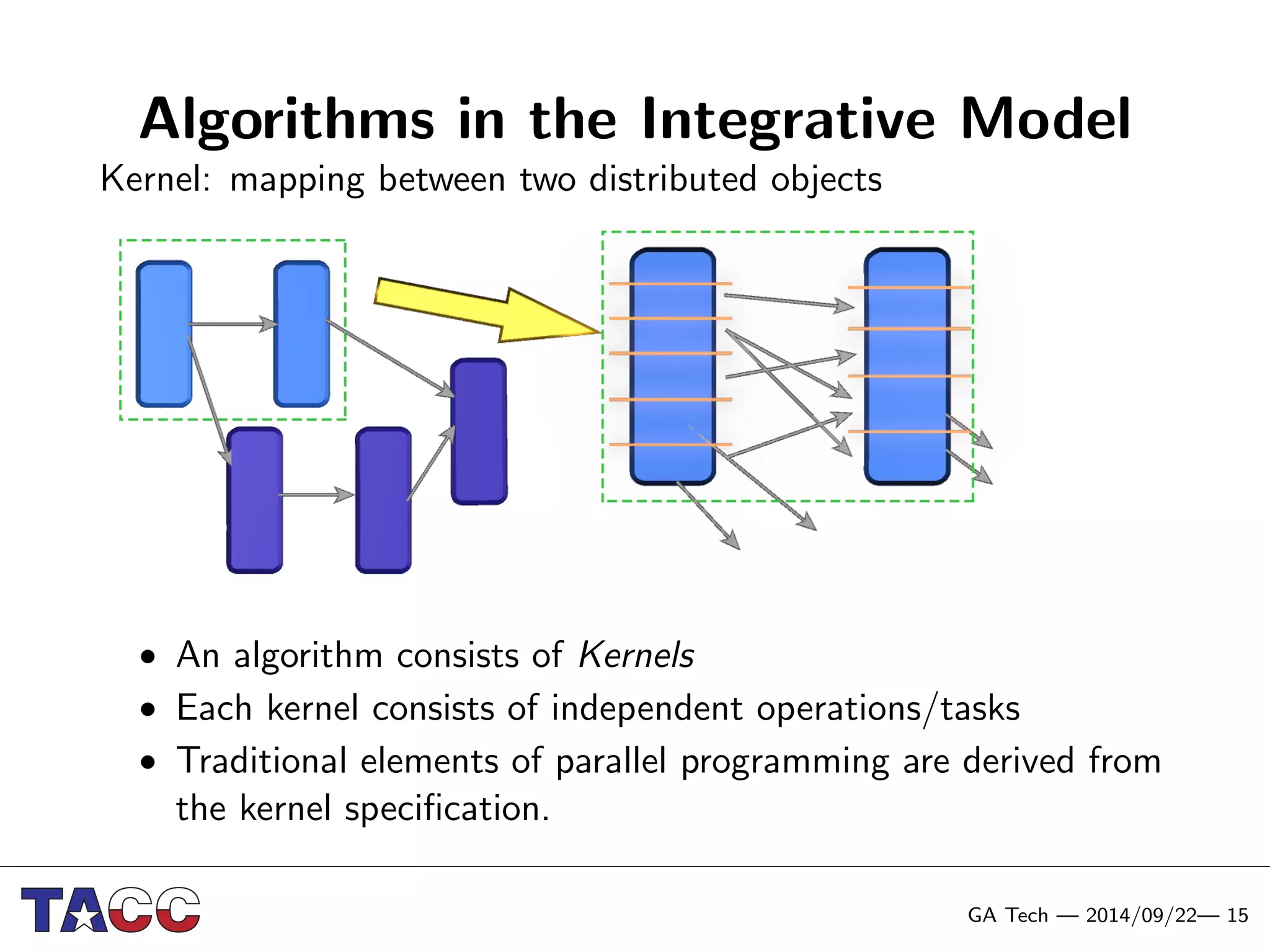
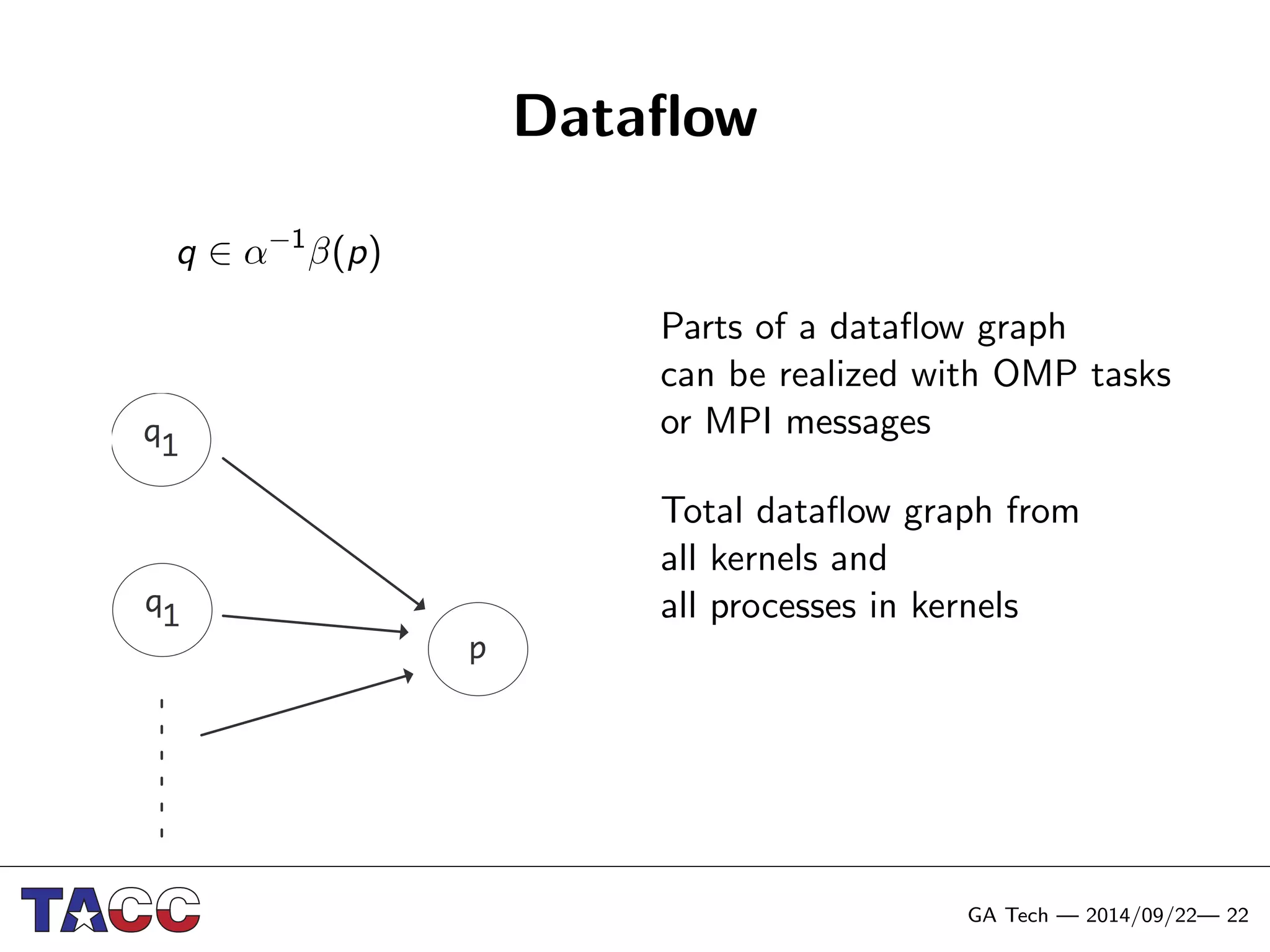
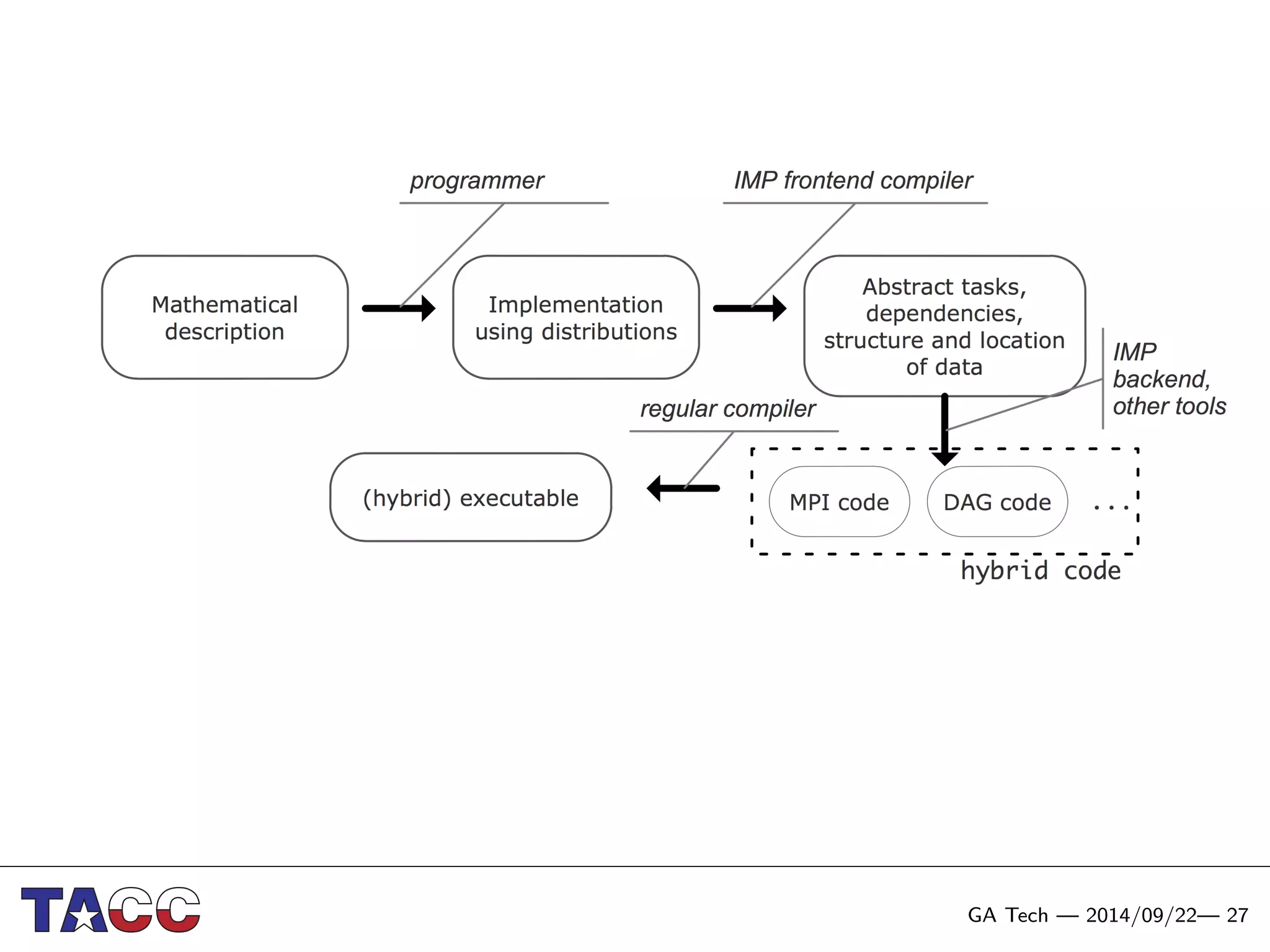
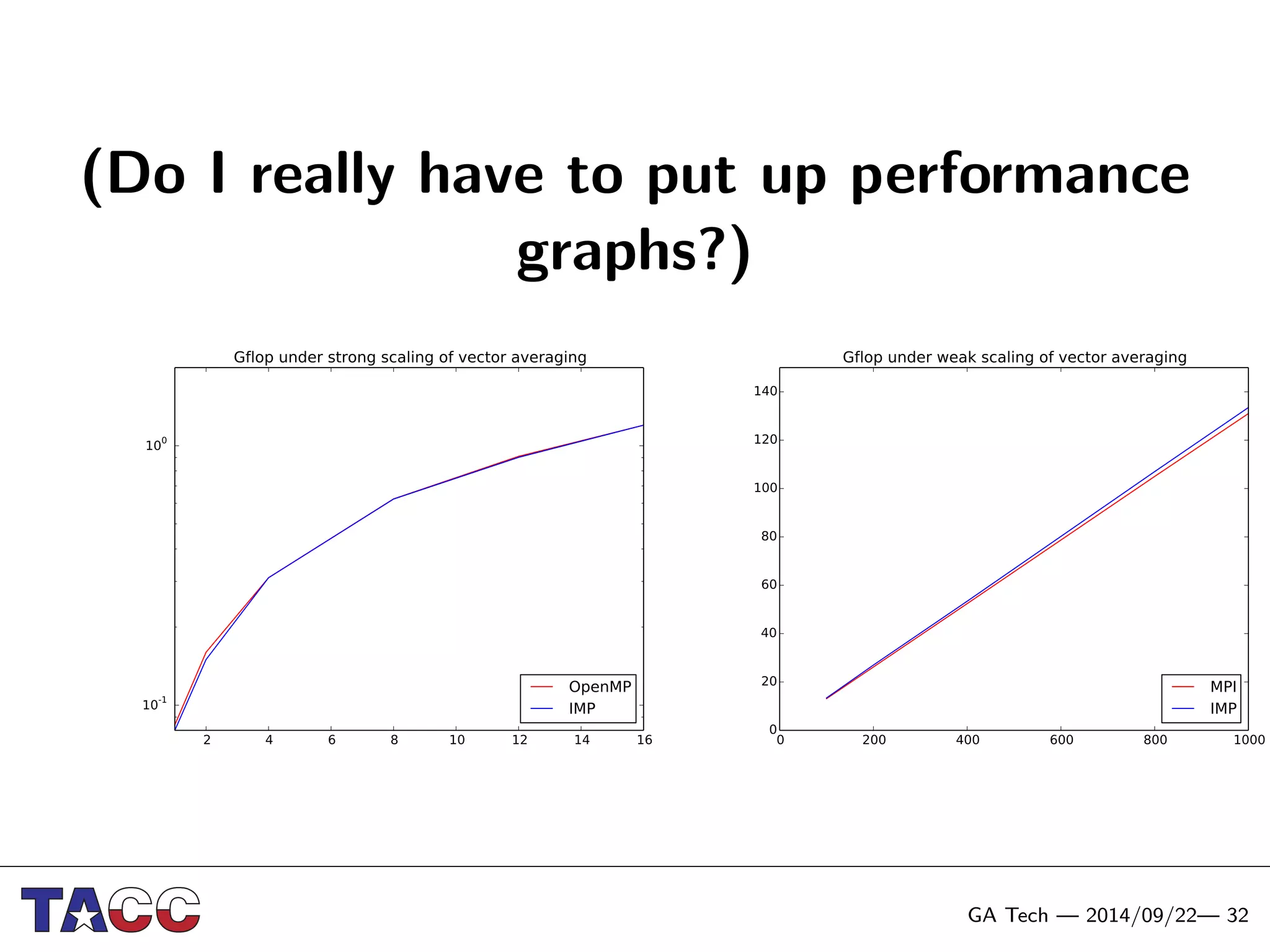
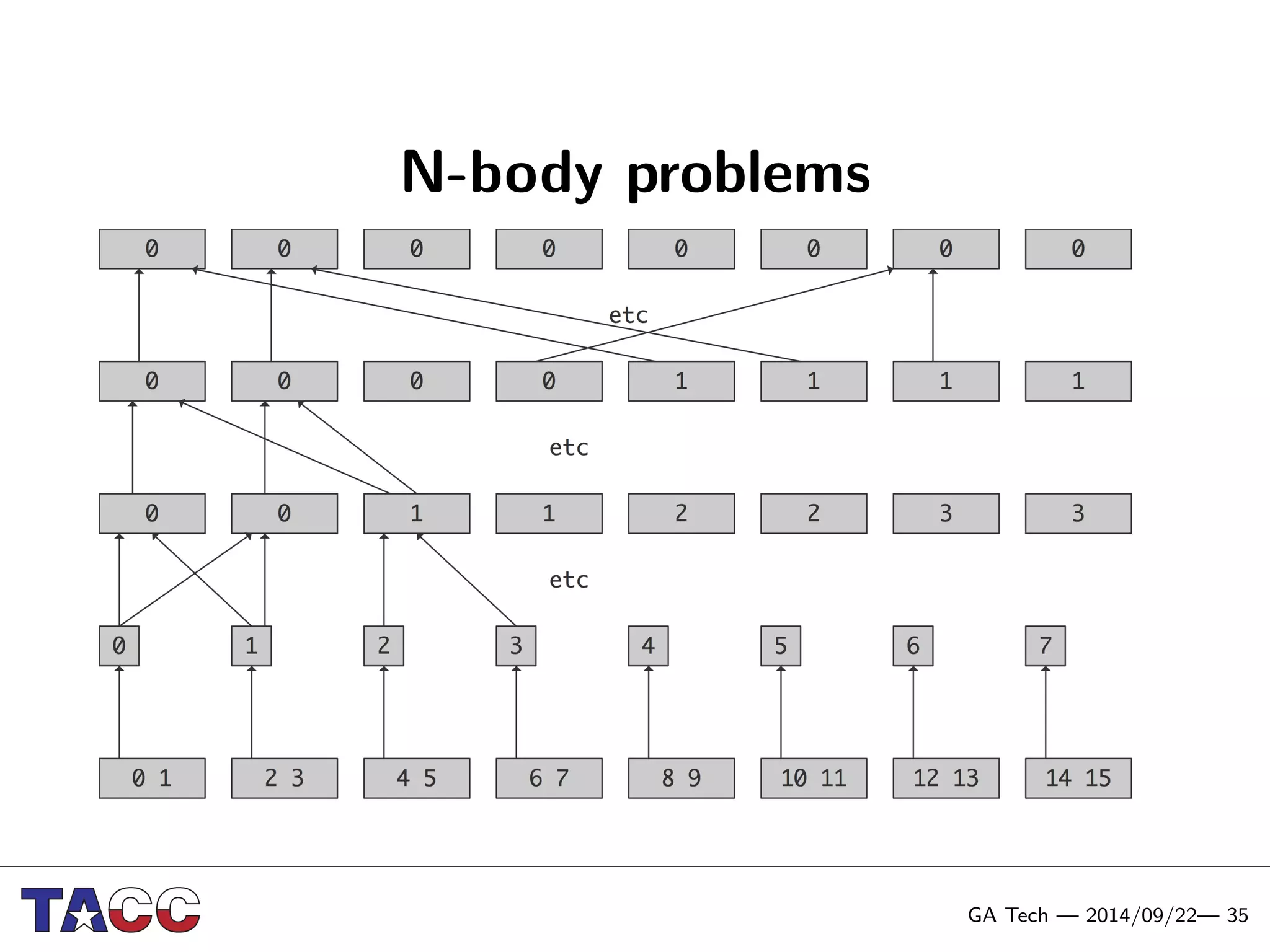
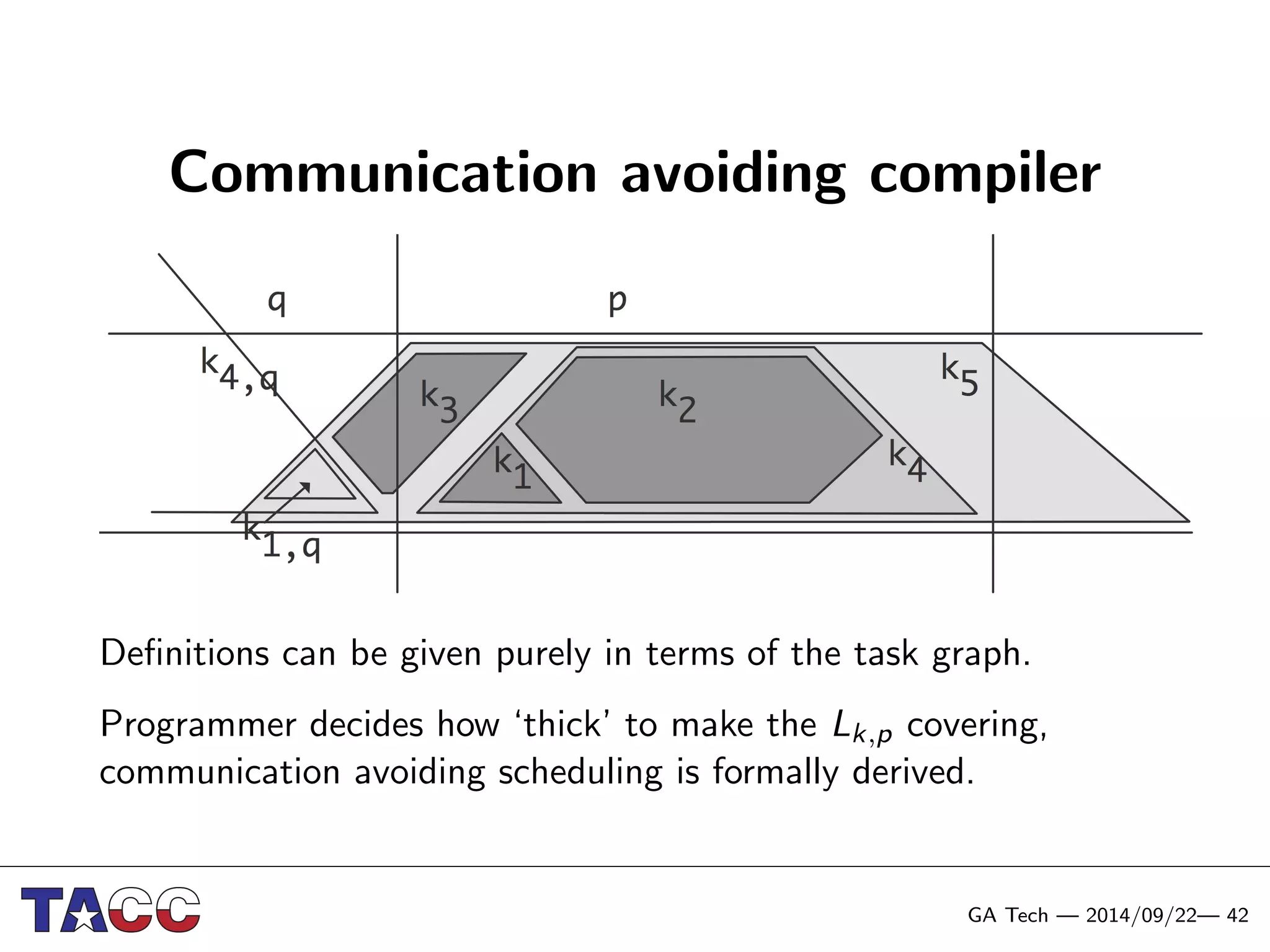
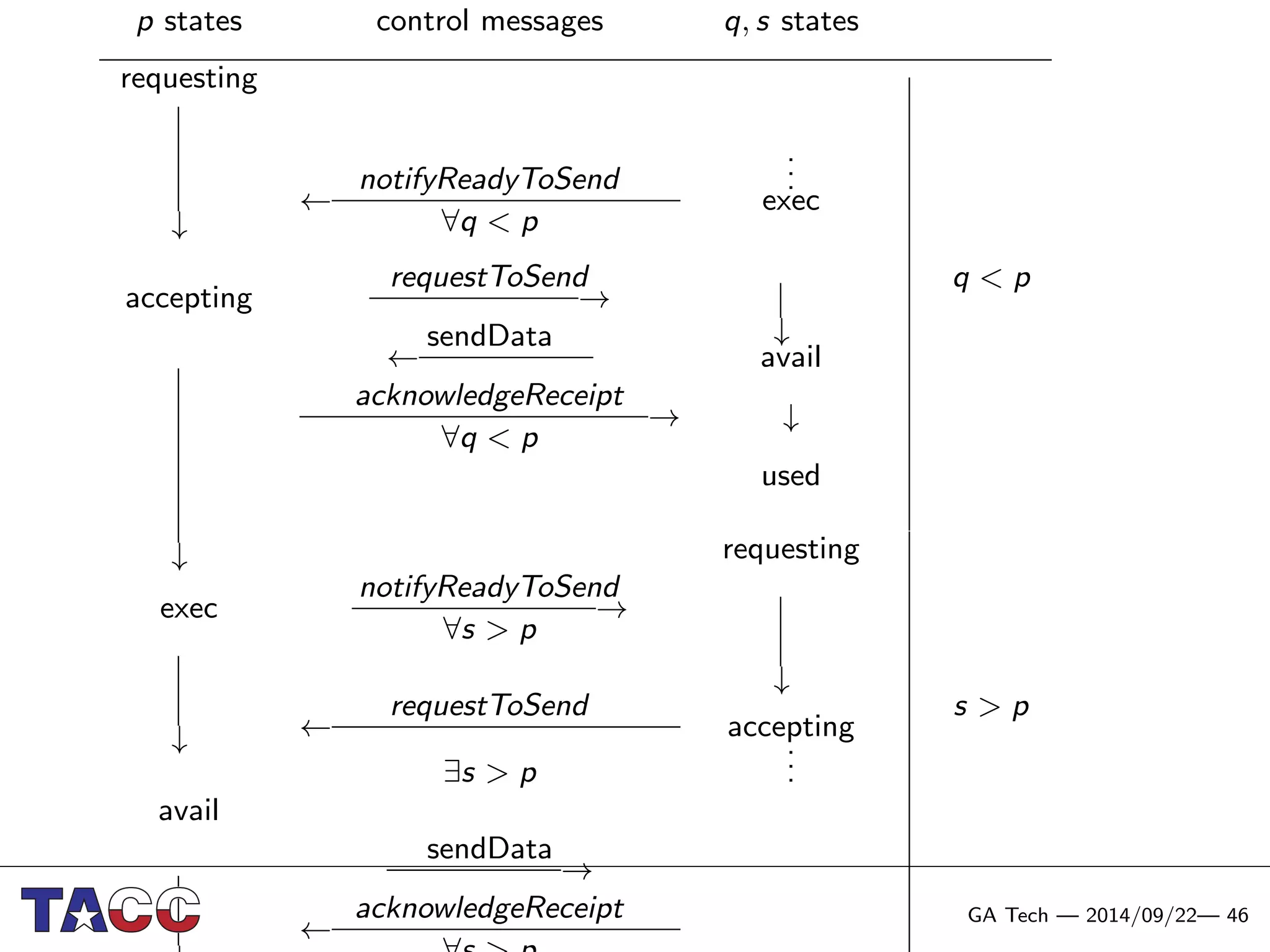
This document presents an Integrative Model for Parallelism (IMP) that aims to provide a unified treatment of different types of parallelism. It describes the key concepts of the IMP including the programming model using sequential semantics, the execution model using a data flow virtual machine, and the data model using distributions to describe data placement. It demonstrates the IMP concepts using a motivating example of 3-point averaging and discusses tasks, processes, and research opportunities around the IMP approach.





![Programming model
Sequential semantics
[A]n HPF program may be understood (and debugged)
using sequential semantics, a deterministic world that we are
comfortable with. Once again, as in traditional programming,
the programmer works with a single address space, treating an
array as a single, monolithic object, regardless of how it may
be distributed across the memories of a parallel machine.
(Nikhil 1993)
As opposed to
[H]umans are quickly overwhelmed by concurrency and](https://image.slidesharecdn.com/wolfhpc2014-140921132915-phpapp01/75/Integrative-Parallel-Programming-in-HPC-6-2048.jpg)