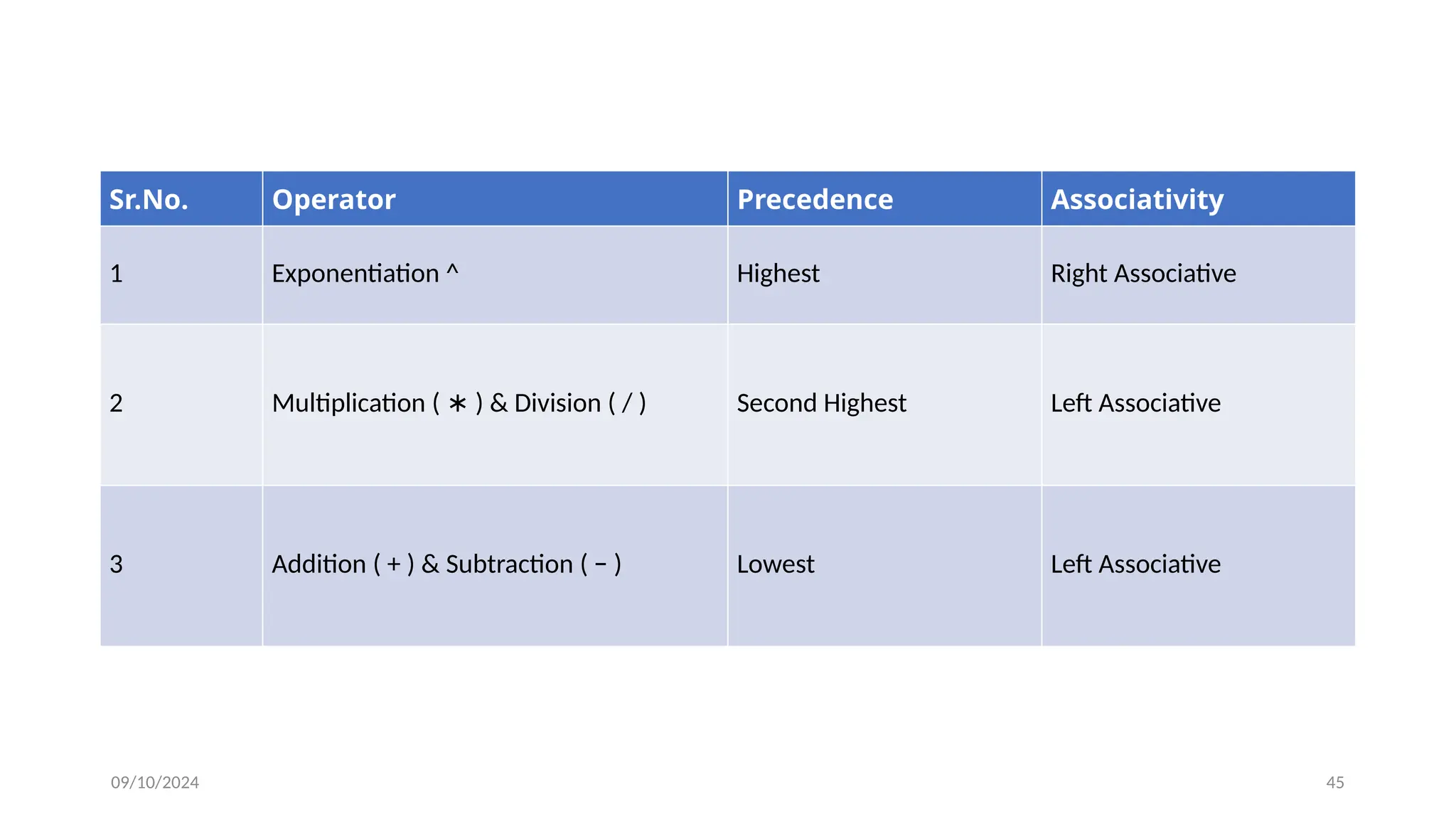
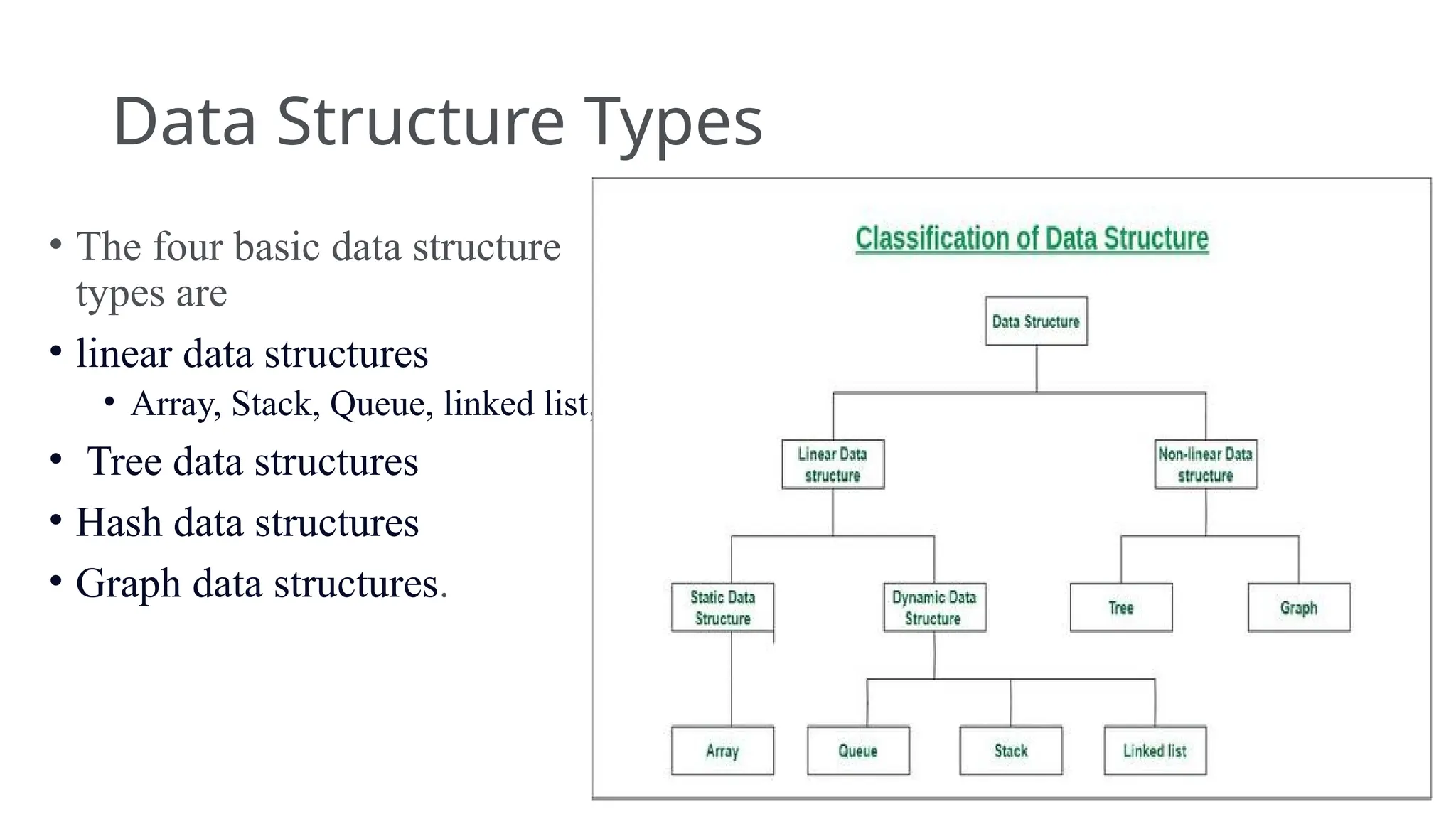
The document provides an extensive overview of data structures, detailing their definitions, types, and applications. It discusses fundamental concepts including arrays, stacks, their operations, advantages, and disadvantages, while emphasizing the importance of choosing appropriate data structures based on specific requirements. Additionally, practical applications in computer programming and real-life scenarios are presented to demonstrate the utility of these structures.











![Syntax
• Creating an array in C and C++ programming languages −
• data_type array_name[array_size] = {elements separated using
commas}
• Int arr[5]={23,20,13,26,7}
• or,
• data_type array_name[array_size];
• Int arr[5];](https://image.slidesharecdn.com/damocs-240910100911-9f710312/75/introduction-of-Data-strutter-and-algirithm-pptx-13-2048.jpg)
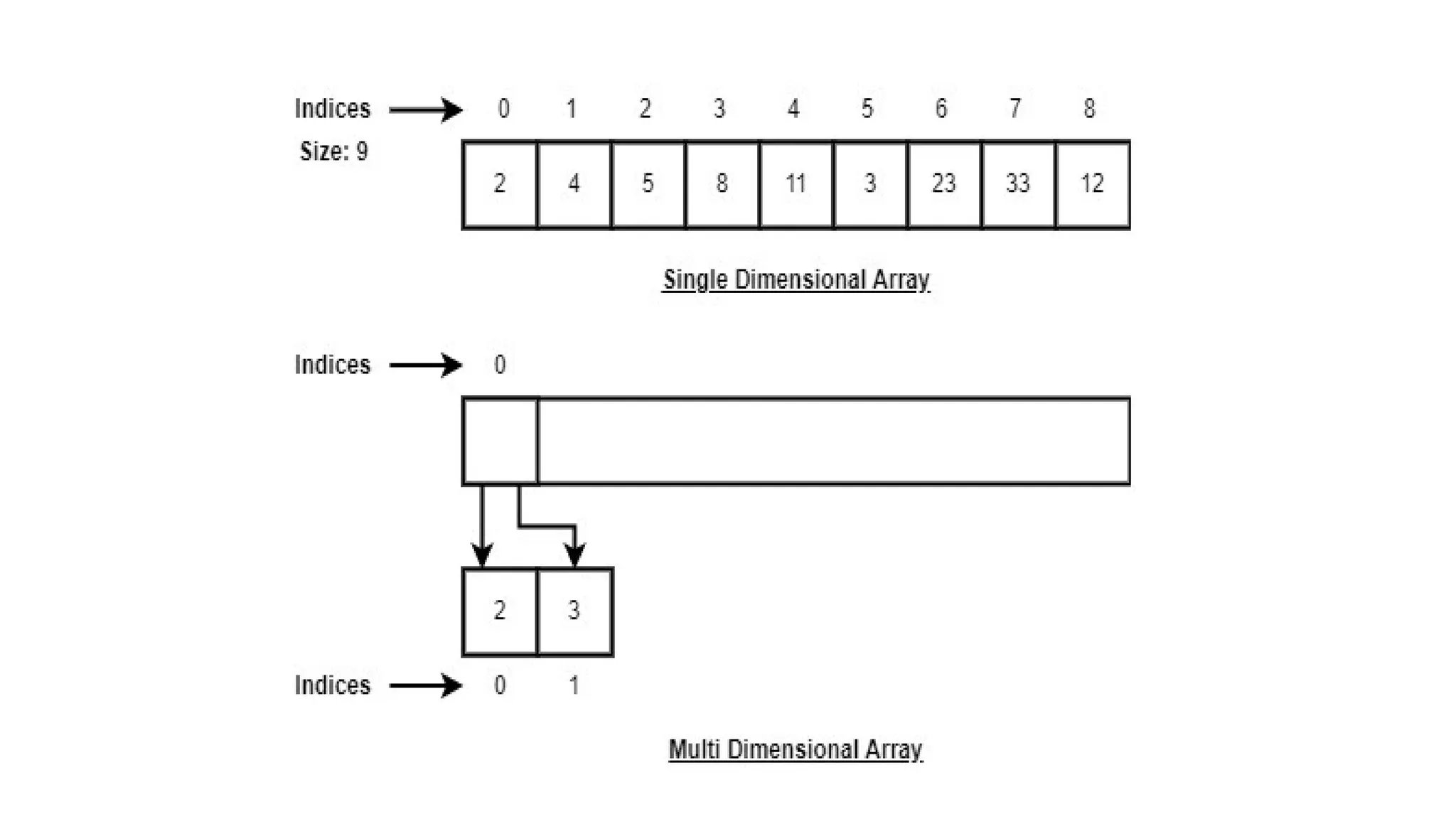
![Array Representation
• Arrays are represented as a collection of buckets where each
bucket stores one element.
• These buckets are indexed from ‘0’ to ‘n-1’, where n is the size
of that particular array.
• For example, an array with size 10 will have buckets indexed
from 0 to 9.
• This indexing will be similar for the multidimensional arrays as
well.
• If it is a 2-dimensional array, it will have sub-buckets in each
bucket.
• Then it will be indexed as array_name[m][n], where m and n
are the sizes of each level in the array.](https://image.slidesharecdn.com/damocs-240910100911-9f710312/75/introduction-of-Data-strutter-and-algirithm-pptx-14-2048.jpg)






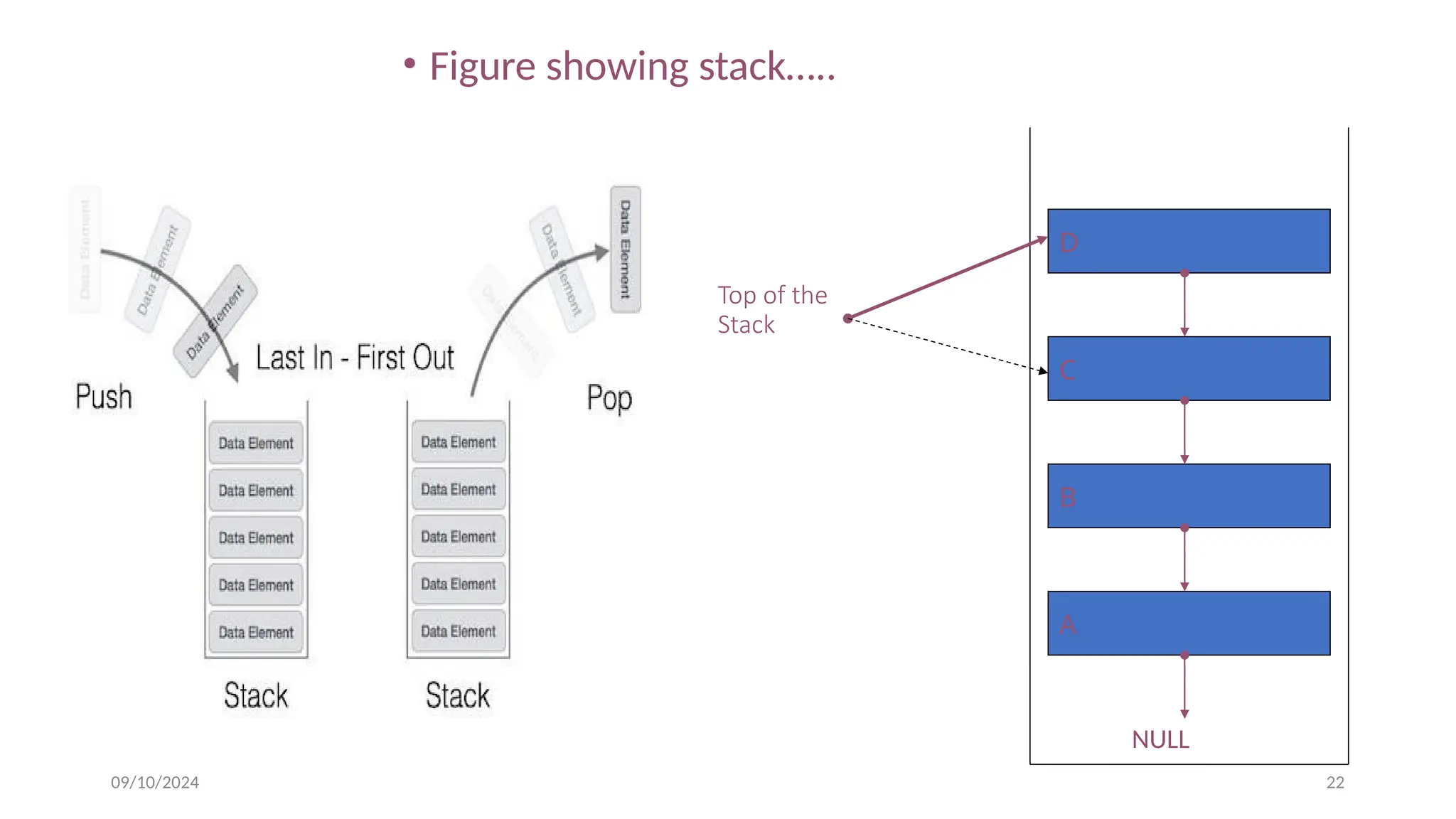




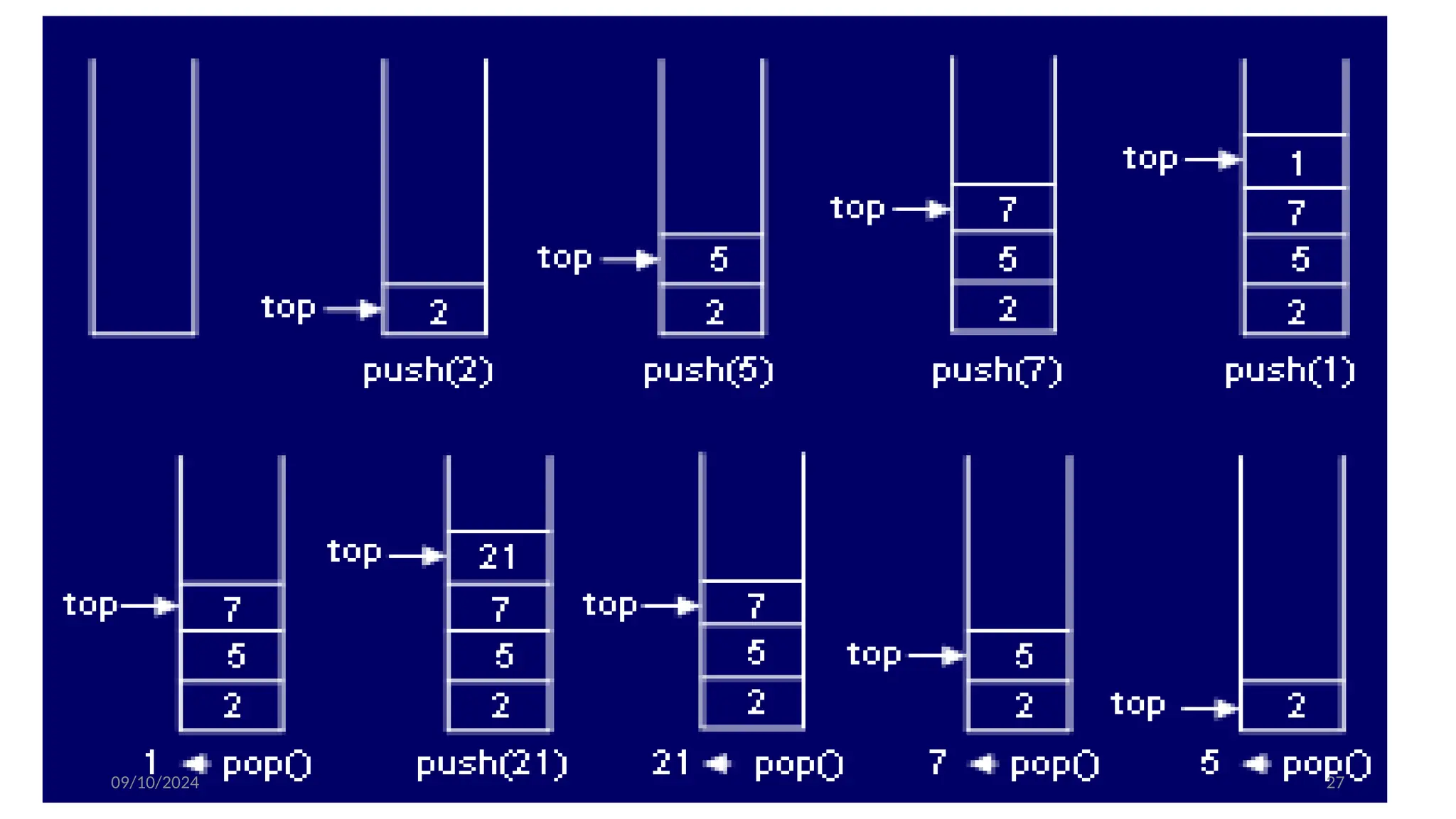



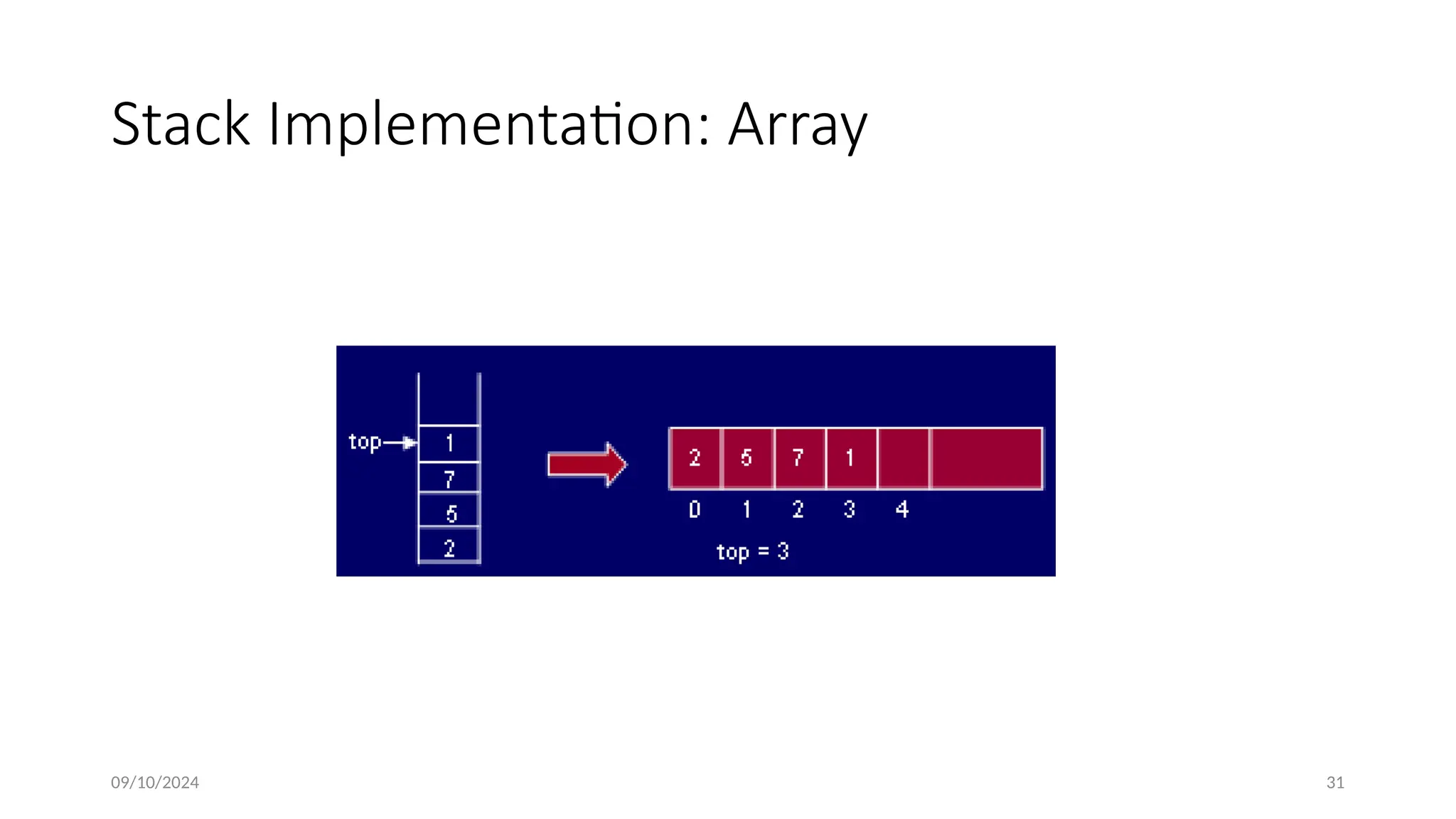

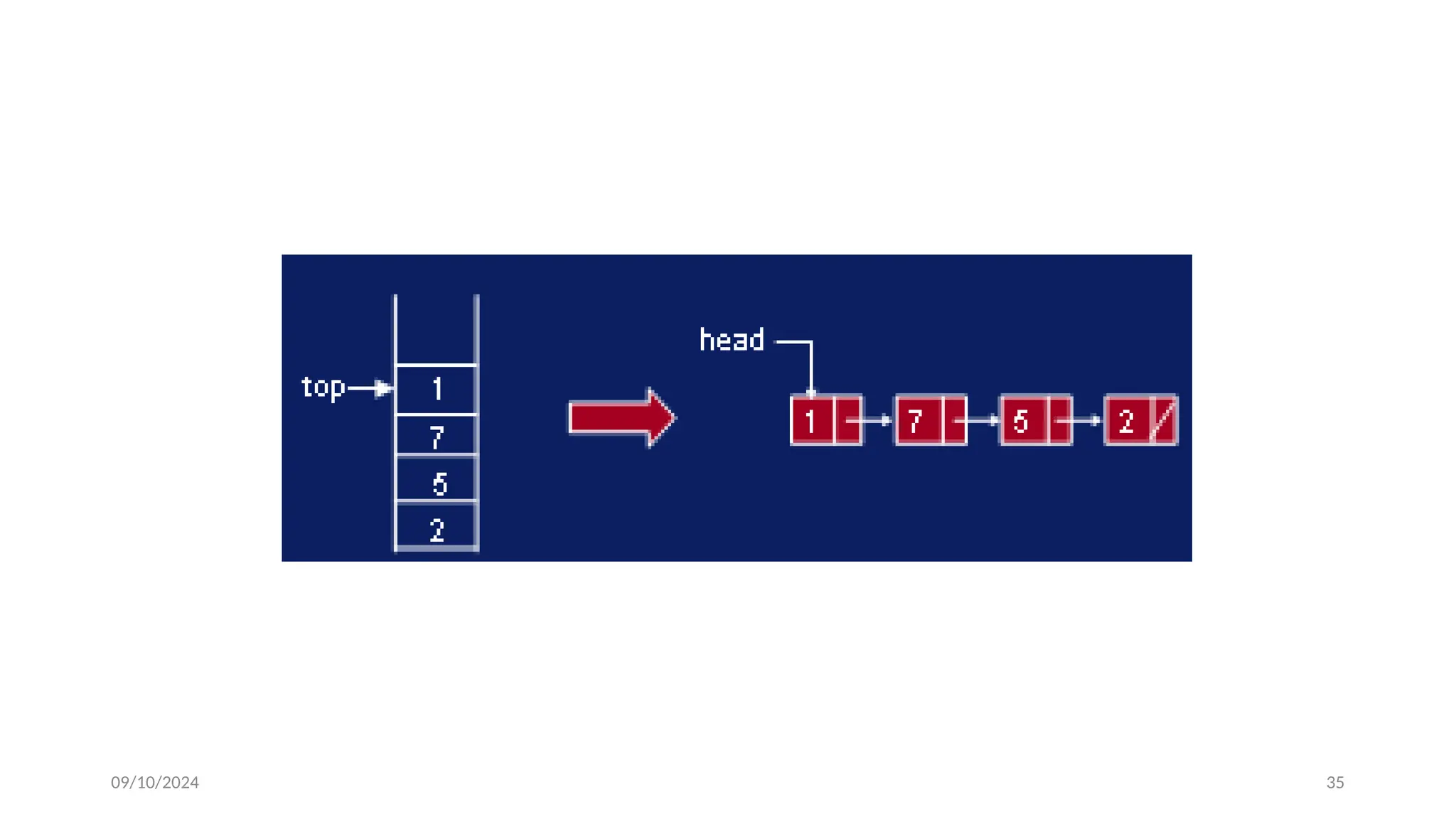
![09/10/2024 33
• Advantages of array implementation:
• Easy to implement.
• Memory is saved as pointers are not involved.
• Disadvantages of array implementation:
• It is not dynamic i.e., it doesn’t grow and shrink depending on
needs at runtime. [But in case of dynamic sized arrays like vector
in C++, list in Python, ArrayList in Java, stacks can grow and shrink
with array implementation as well].
• The total size of the stack must be defined beforehand.](https://image.slidesharecdn.com/damocs-240910100911-9f710312/75/introduction-of-Data-strutter-and-algirithm-pptx-33-2048.jpg)





![09/10/2024 41
• The sequence [()] is legal, but [(]) is wrong.
• Obviously, it is not worthwhile writing a huge program for this, but it
turns out that it is easy to check these things.
• For simplicity, we will just check for balancing of parentheses, brackets,
and braces and ignore any other character that appears.
The simple algorithm uses a stack and is as follows:
• Make an empty stack. Read characters until end of file.
• If the character is an opening symbol, push it onto the stack.
• If it is a closing symbol and the stack is empty, report an error.
• Otherwise, pop the stack.
• If the symbol popped is not the corresponding opening symbol, then
report an error.
• At end of file, if the stack is not empty, report an error.](https://image.slidesharecdn.com/damocs-240910100911-9f710312/75/introduction-of-Data-strutter-and-algirithm-pptx-41-2048.jpg)