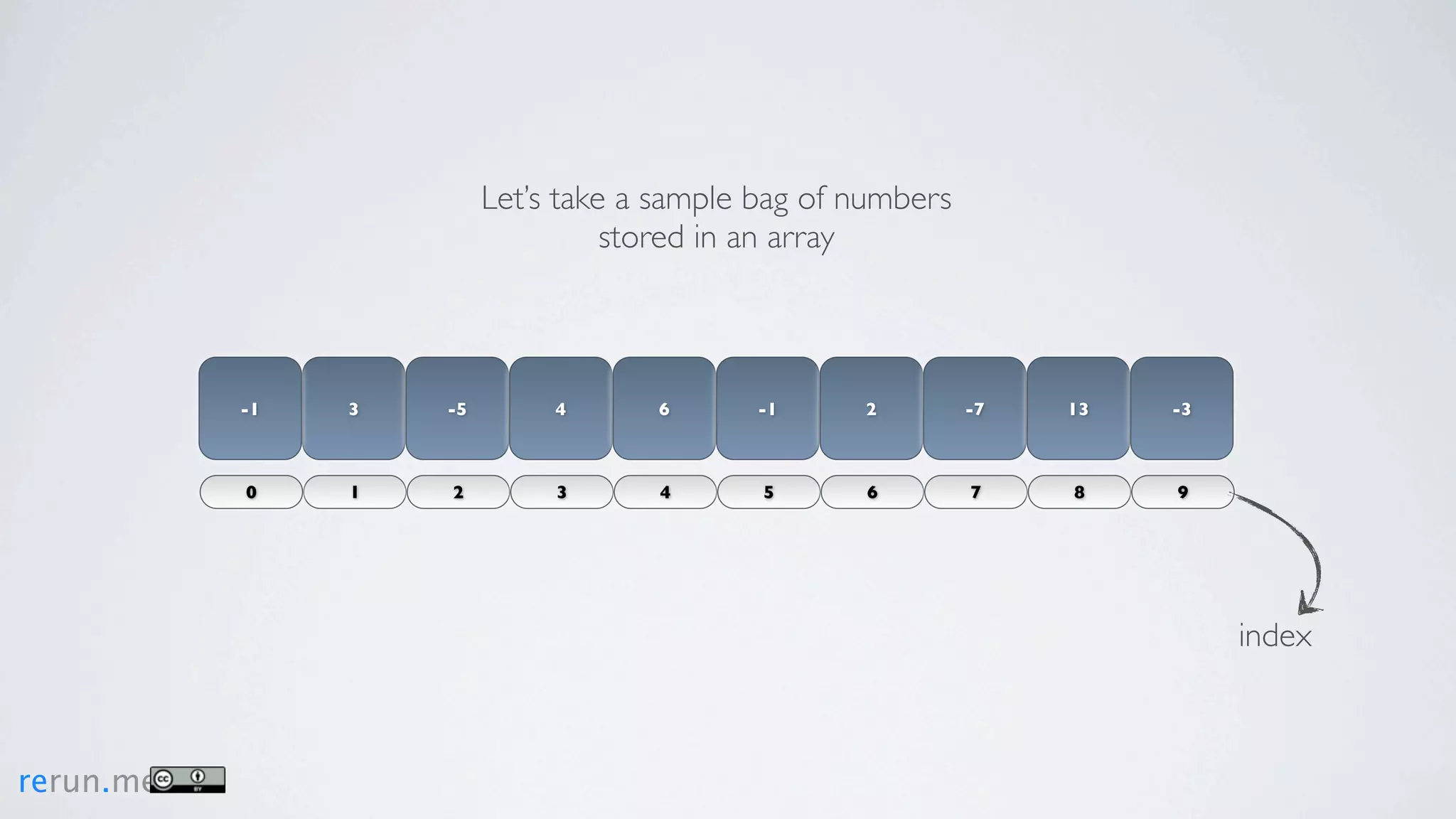
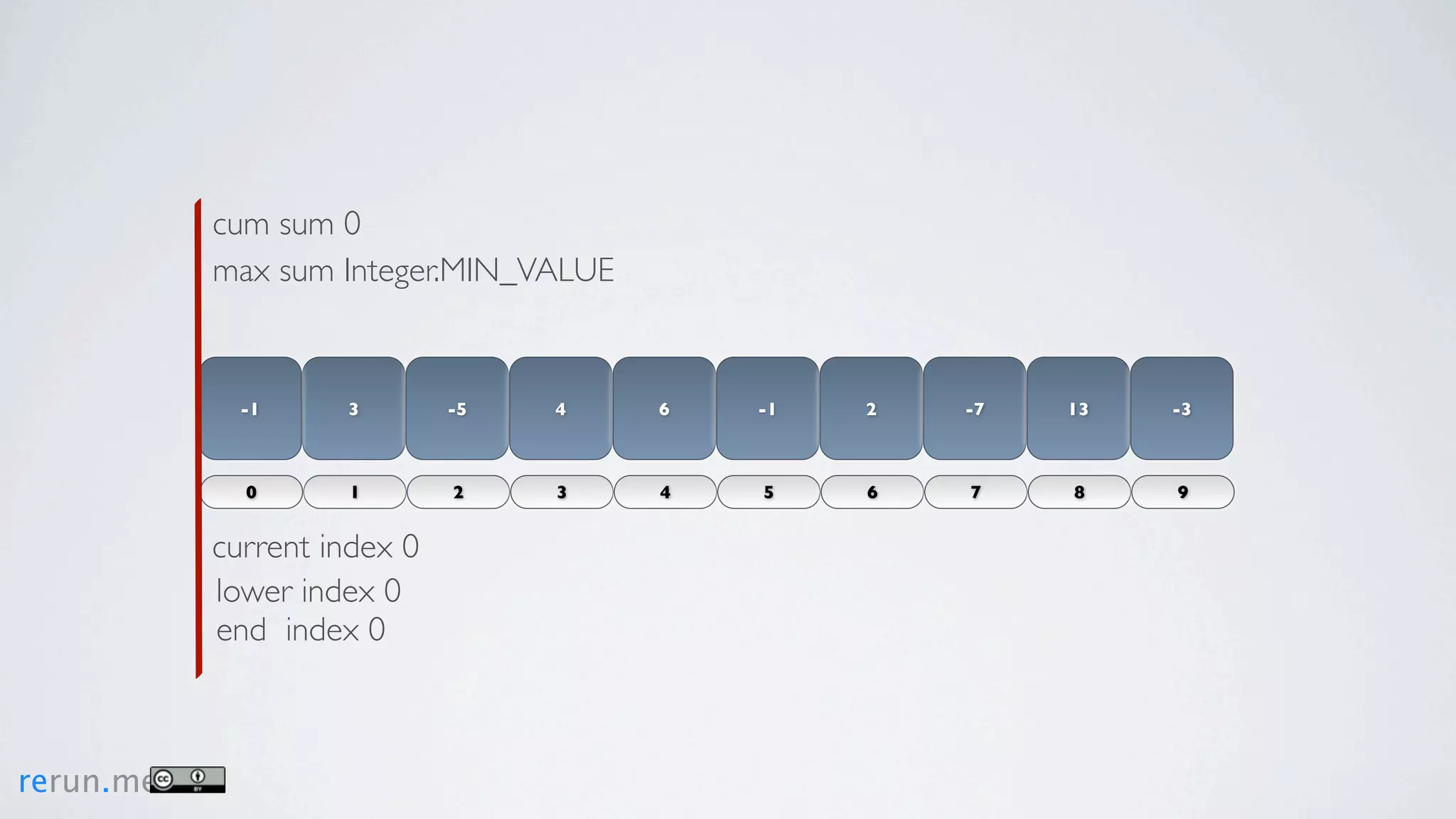
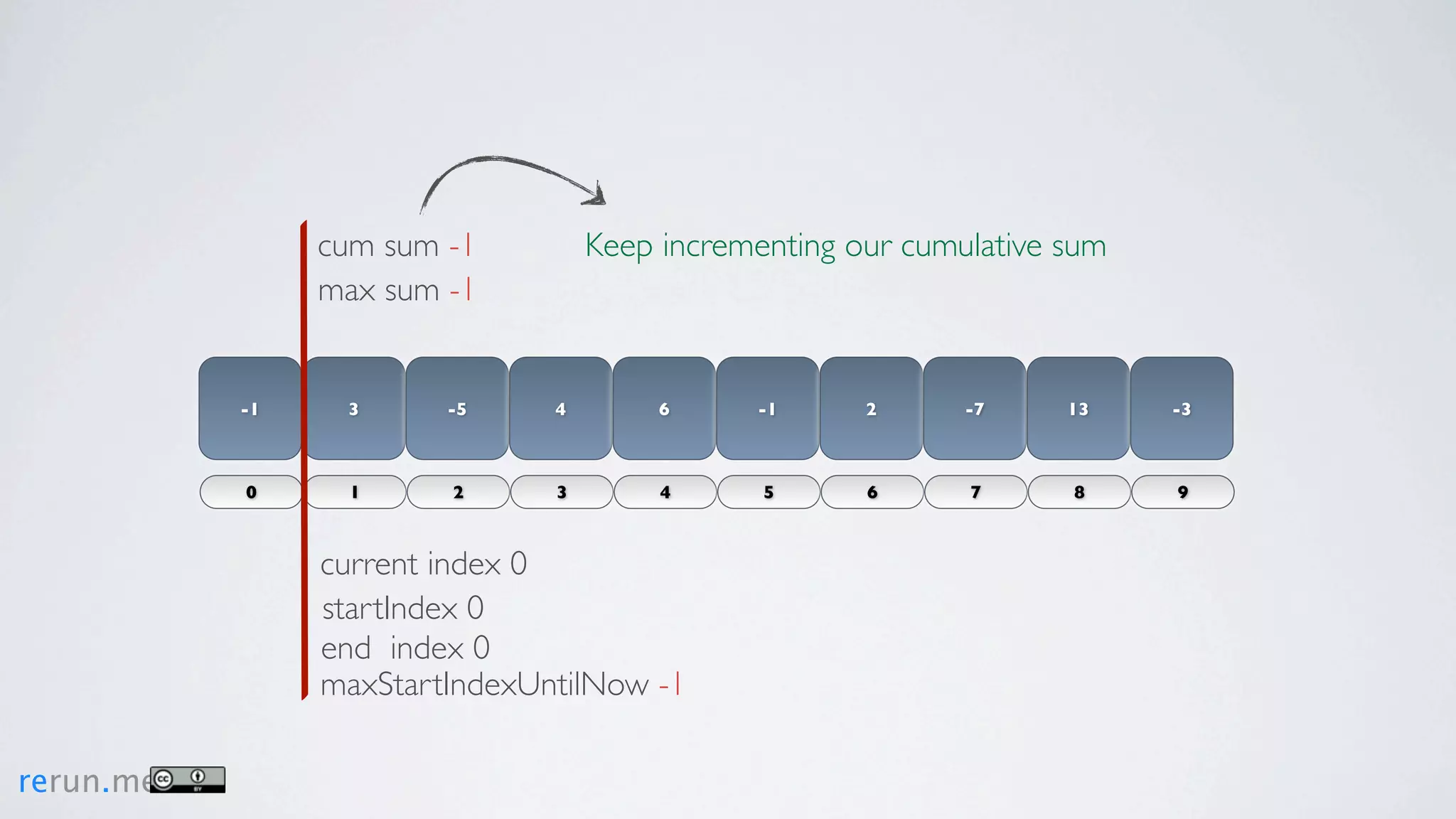
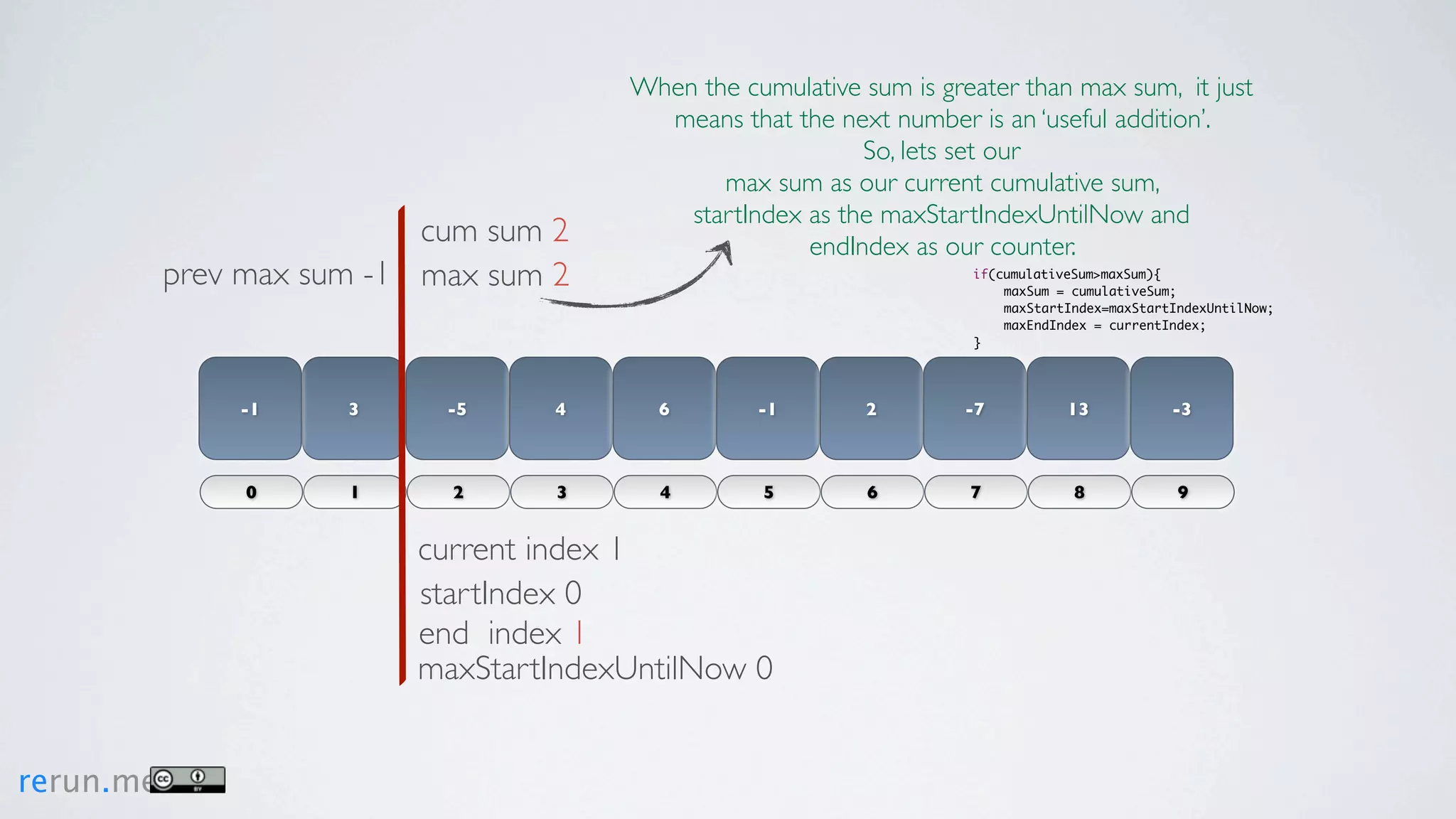
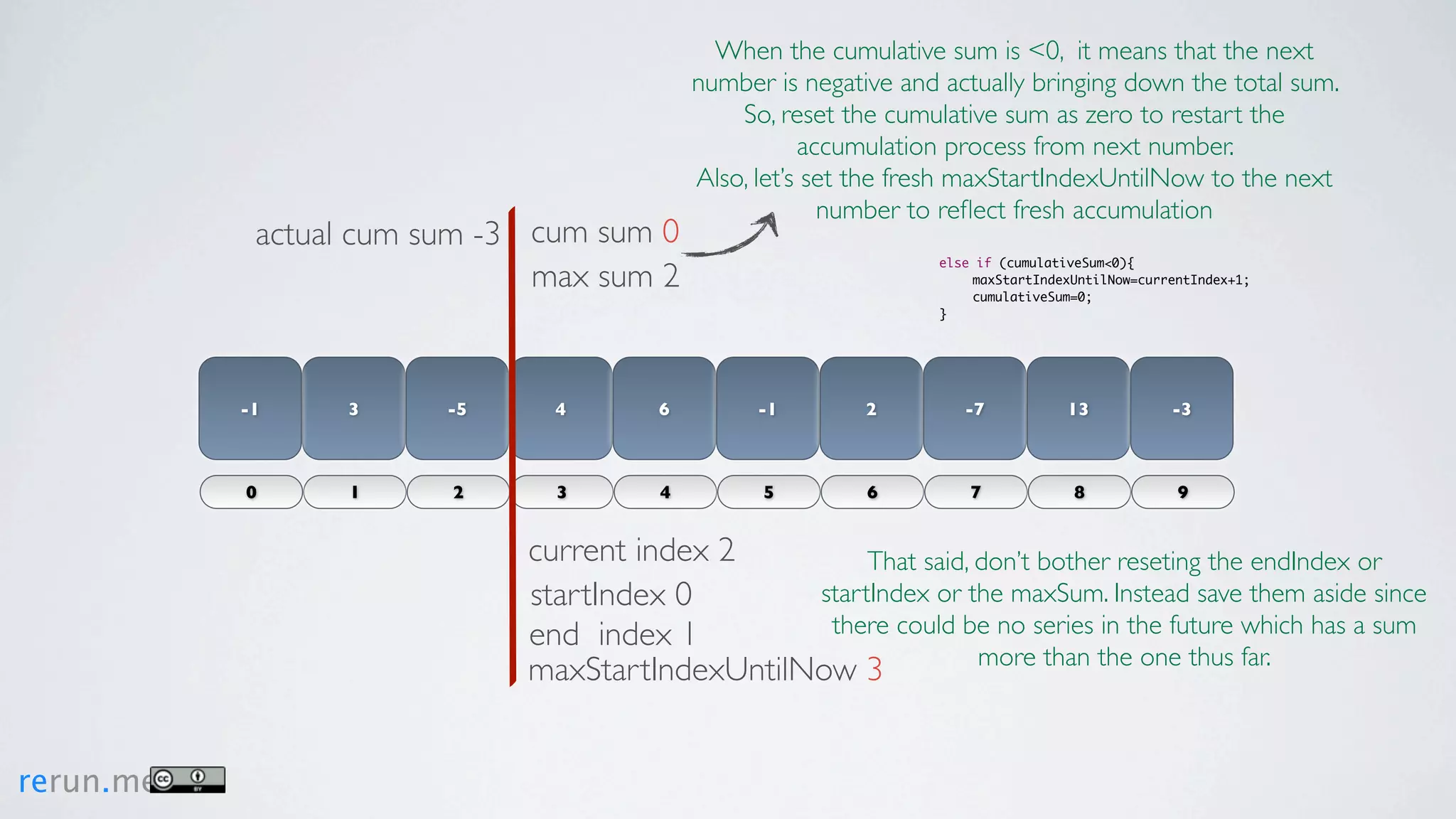
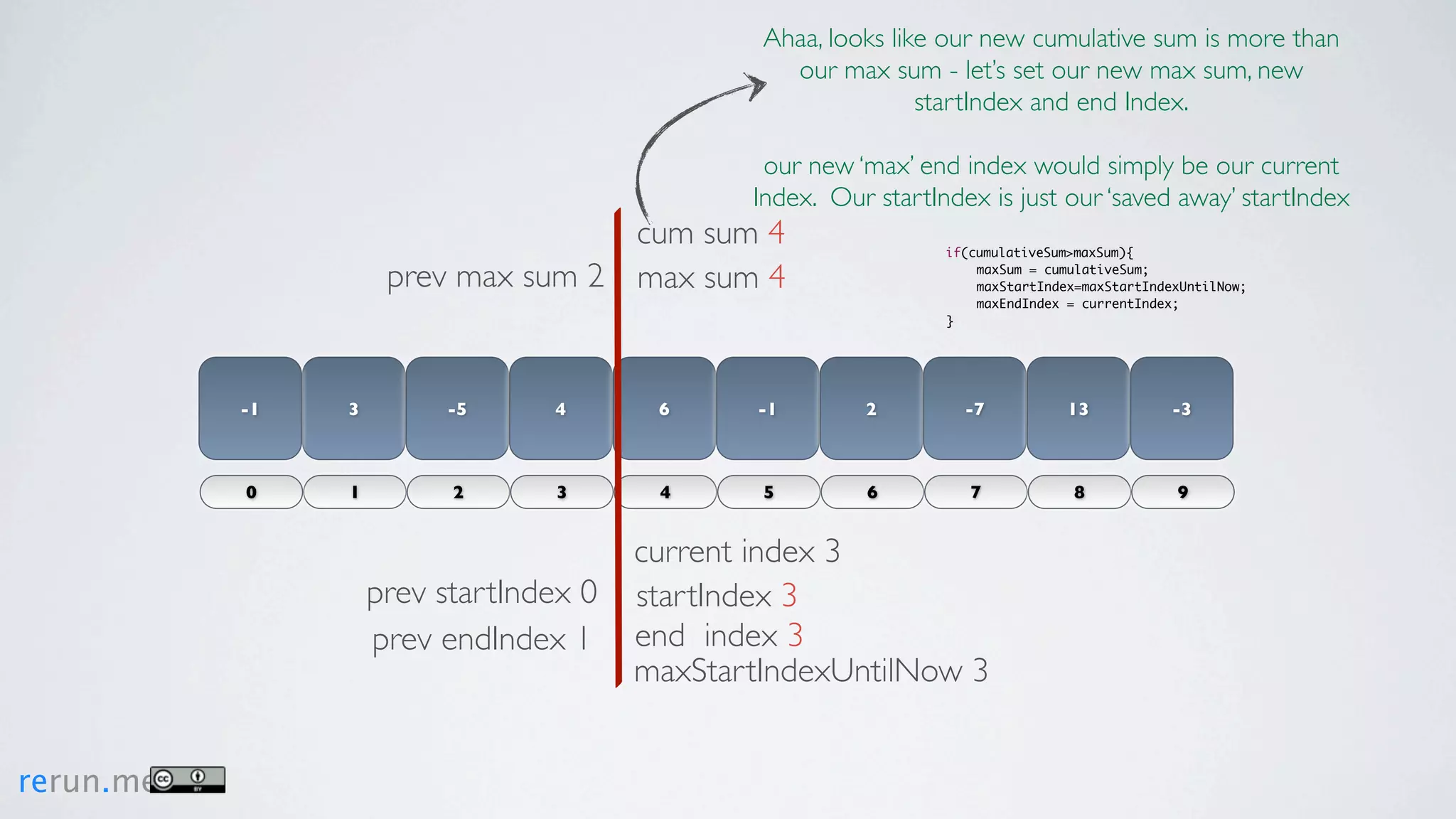
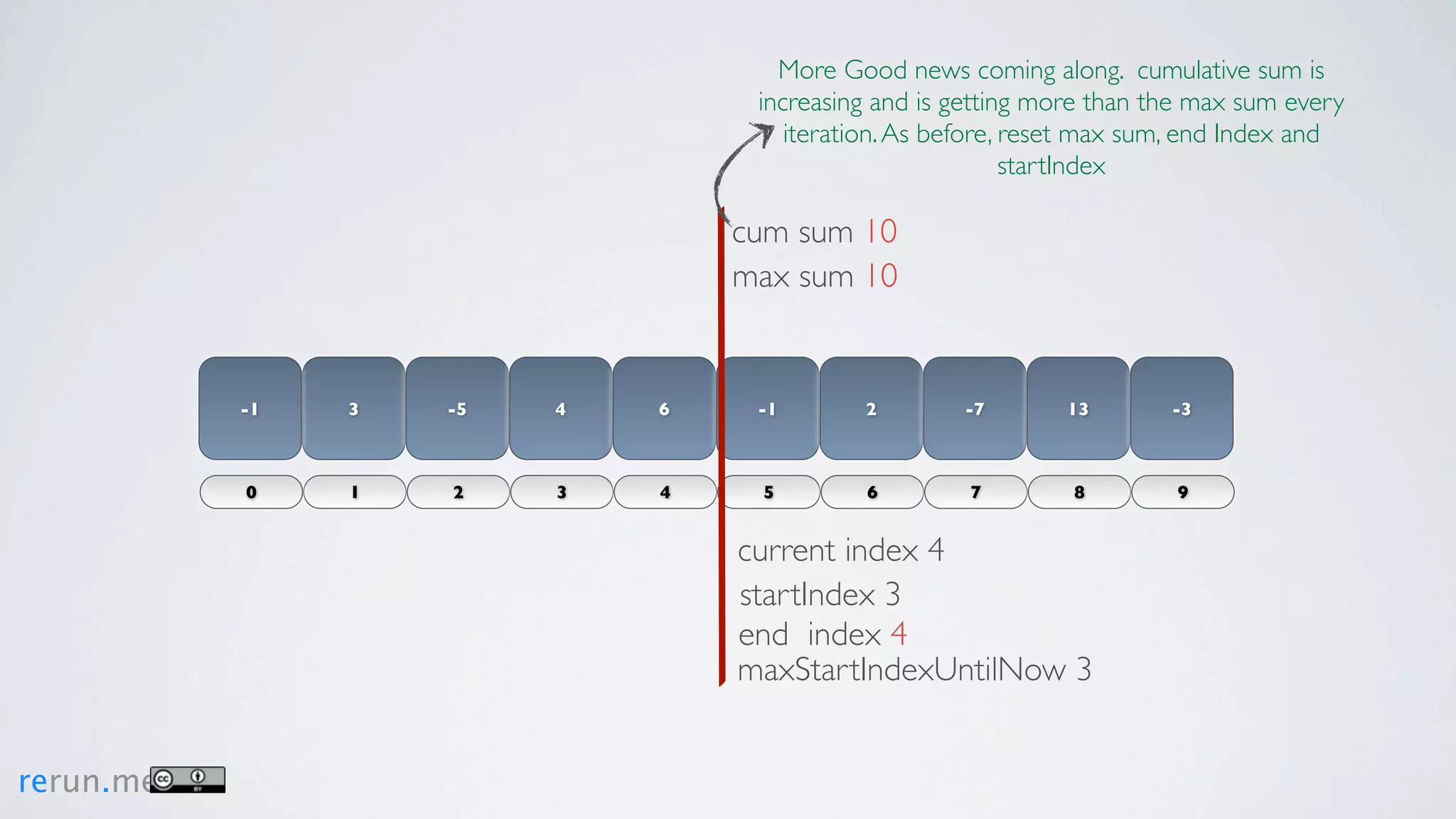
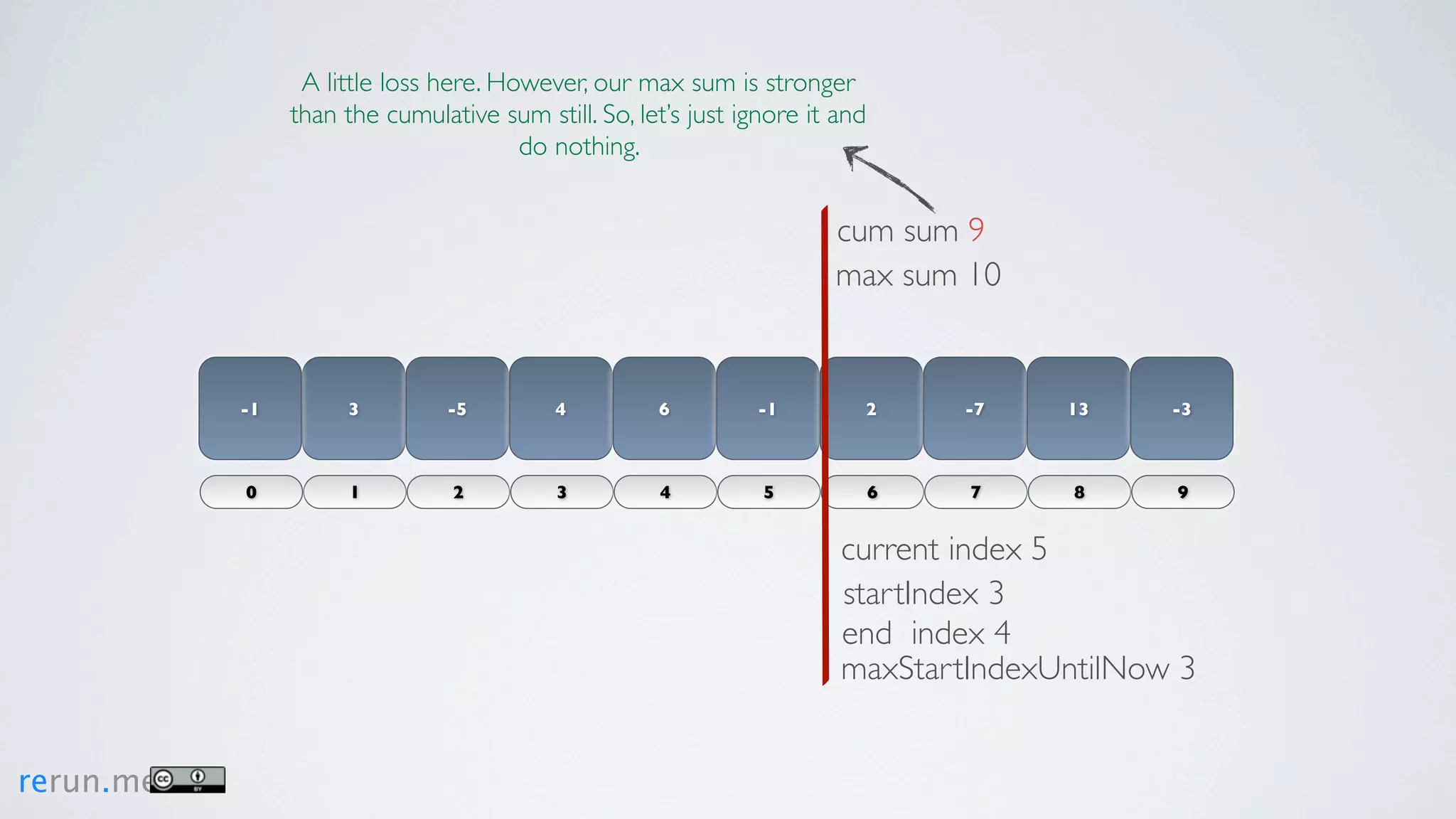
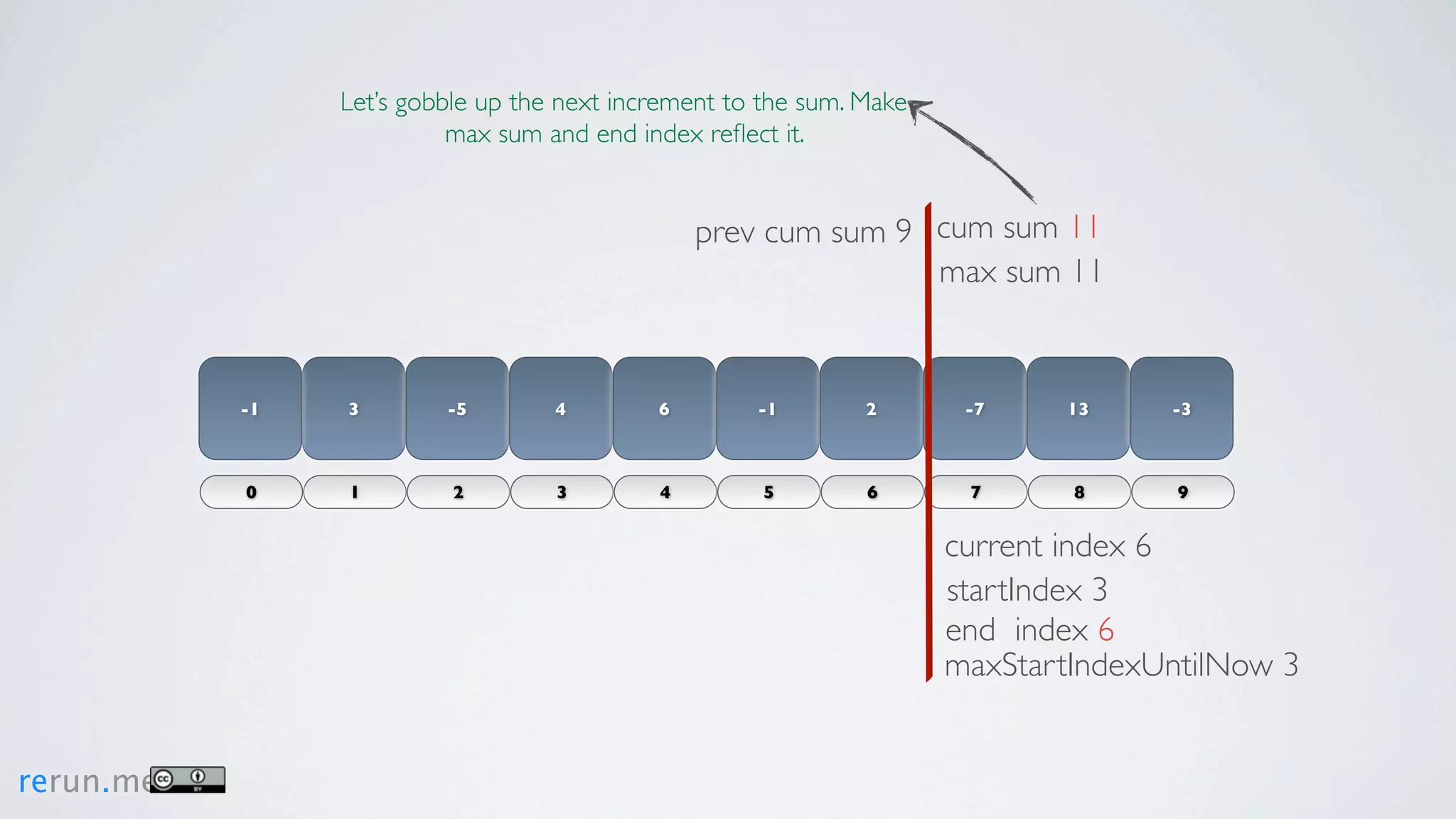
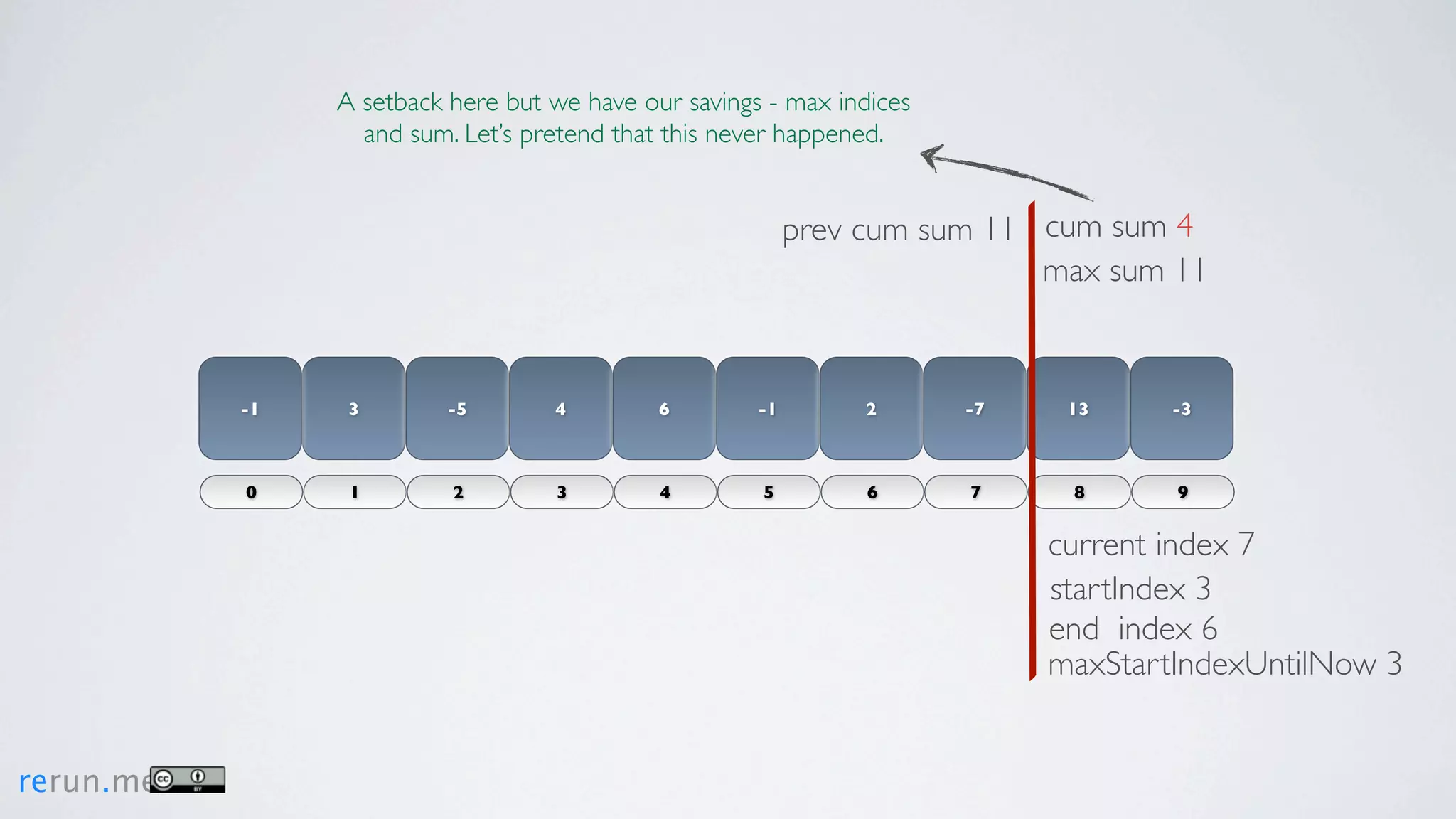
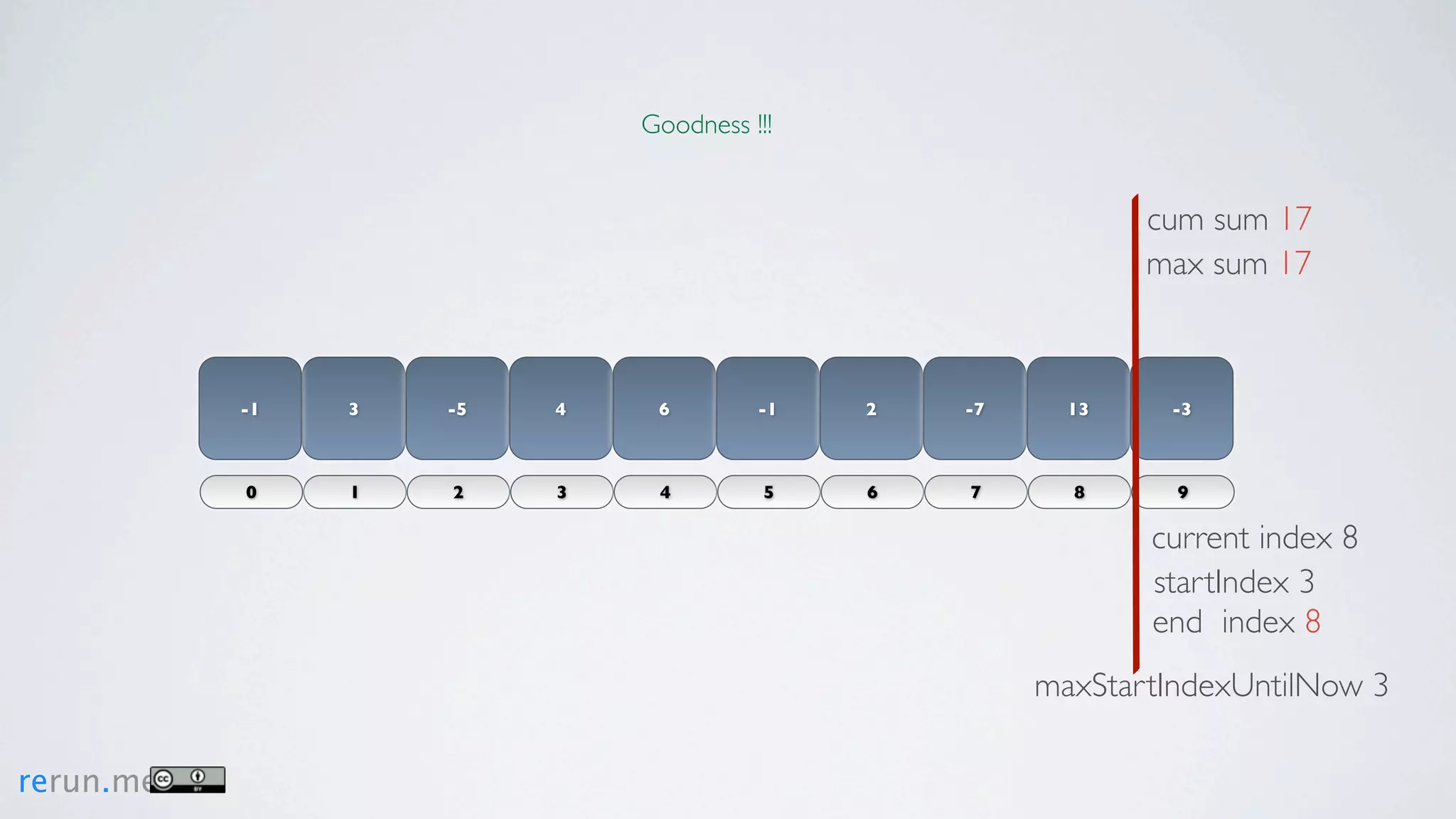
Kadane's algorithm finds the maximum sum subarray in an array by tracking the cumulative sum and updating the maximum sum, start index, and end index as it iterates through the array. It resets the cumulative sum if it drops below 0 to avoid including negative numbers in the running total. The algorithm tracks these values to return the subarray with the true maximum sum.