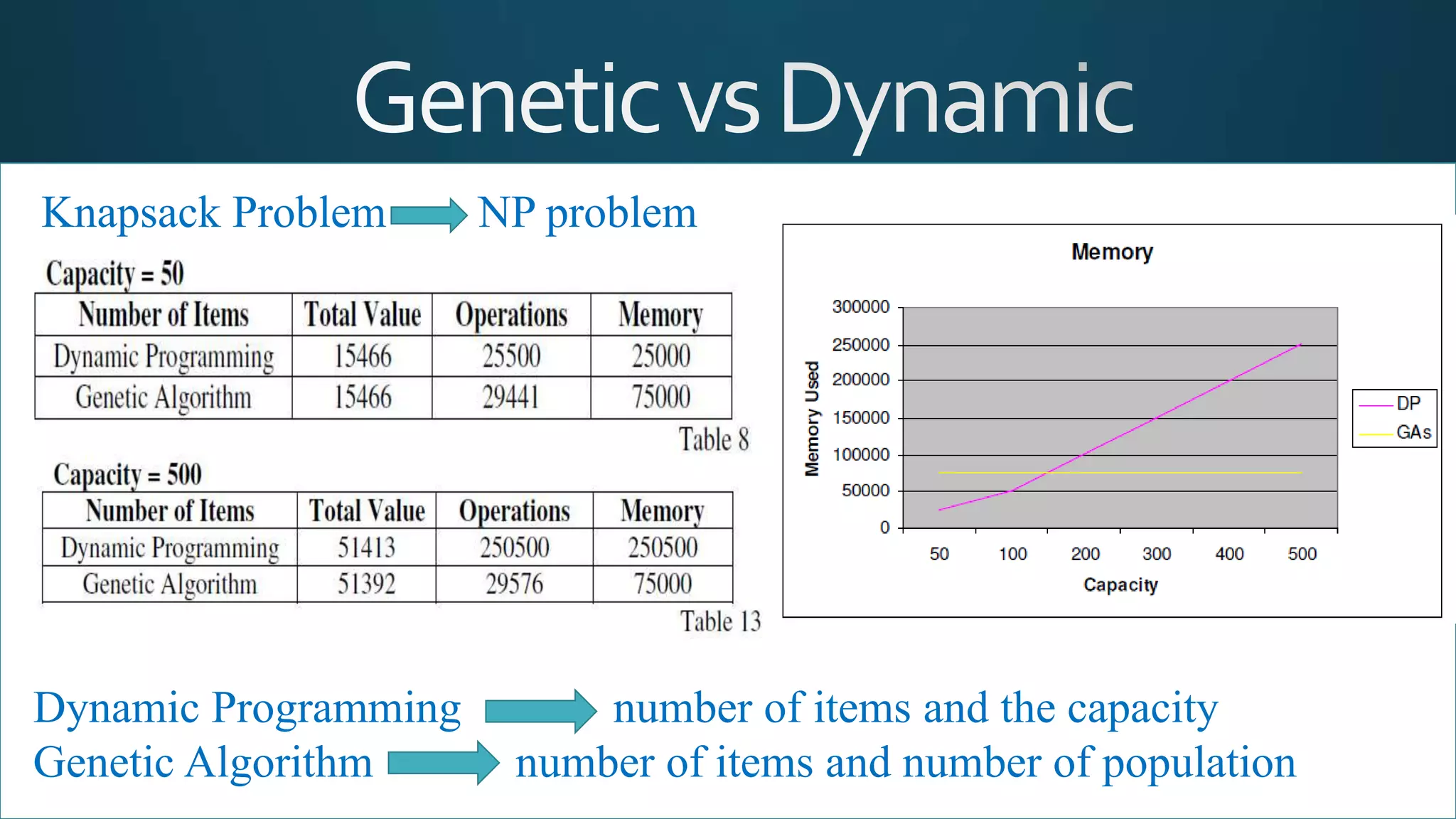
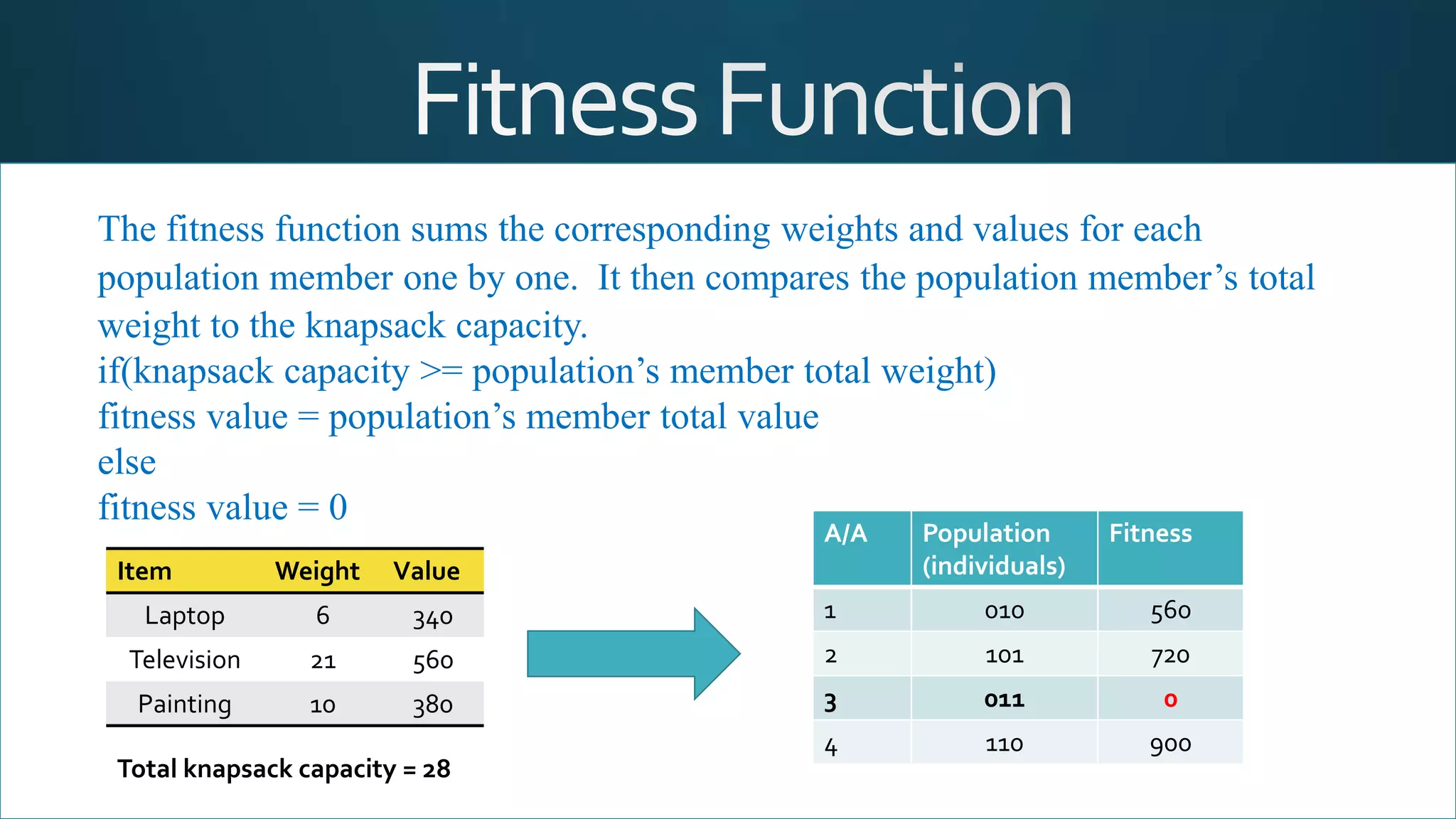
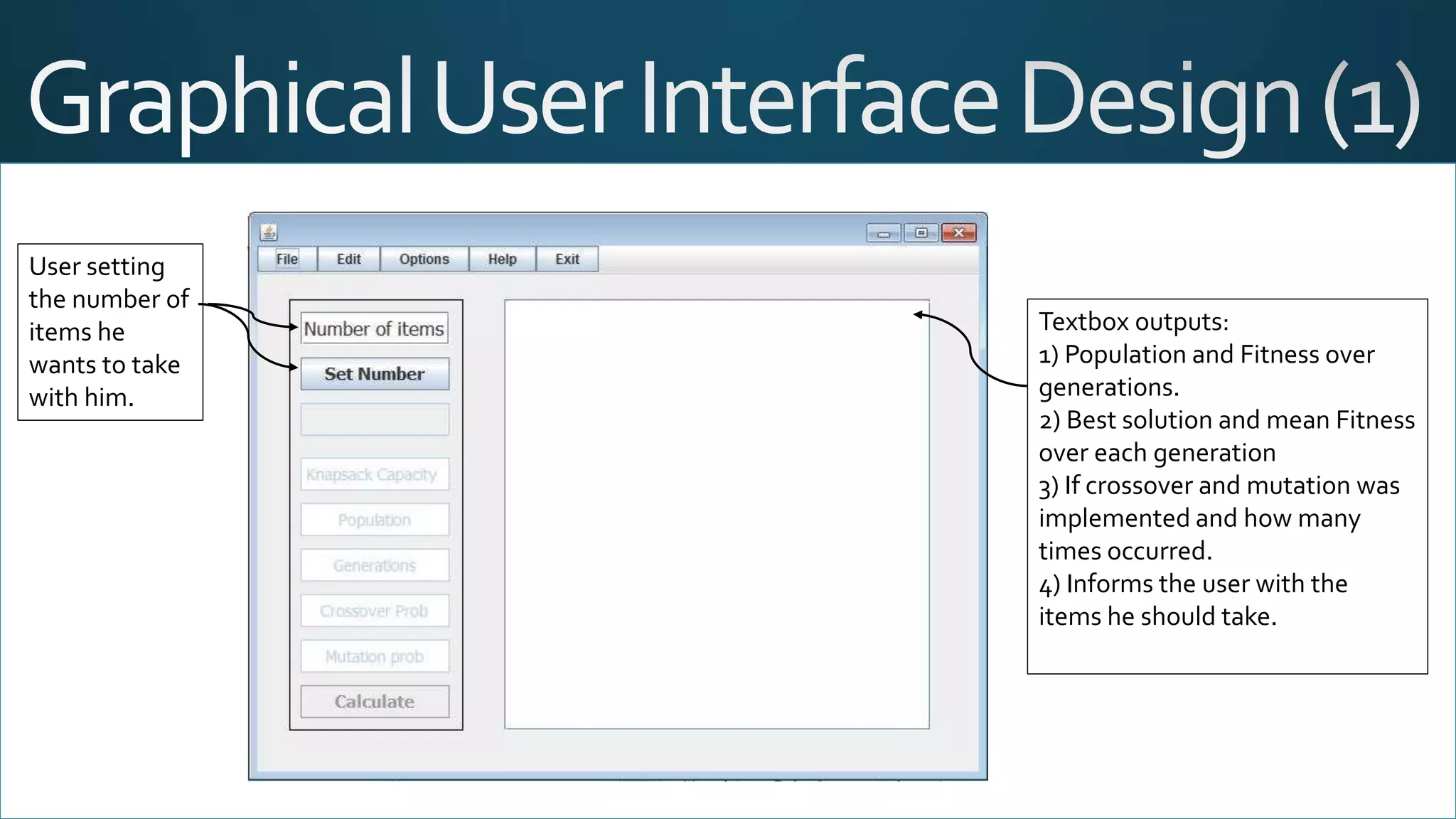
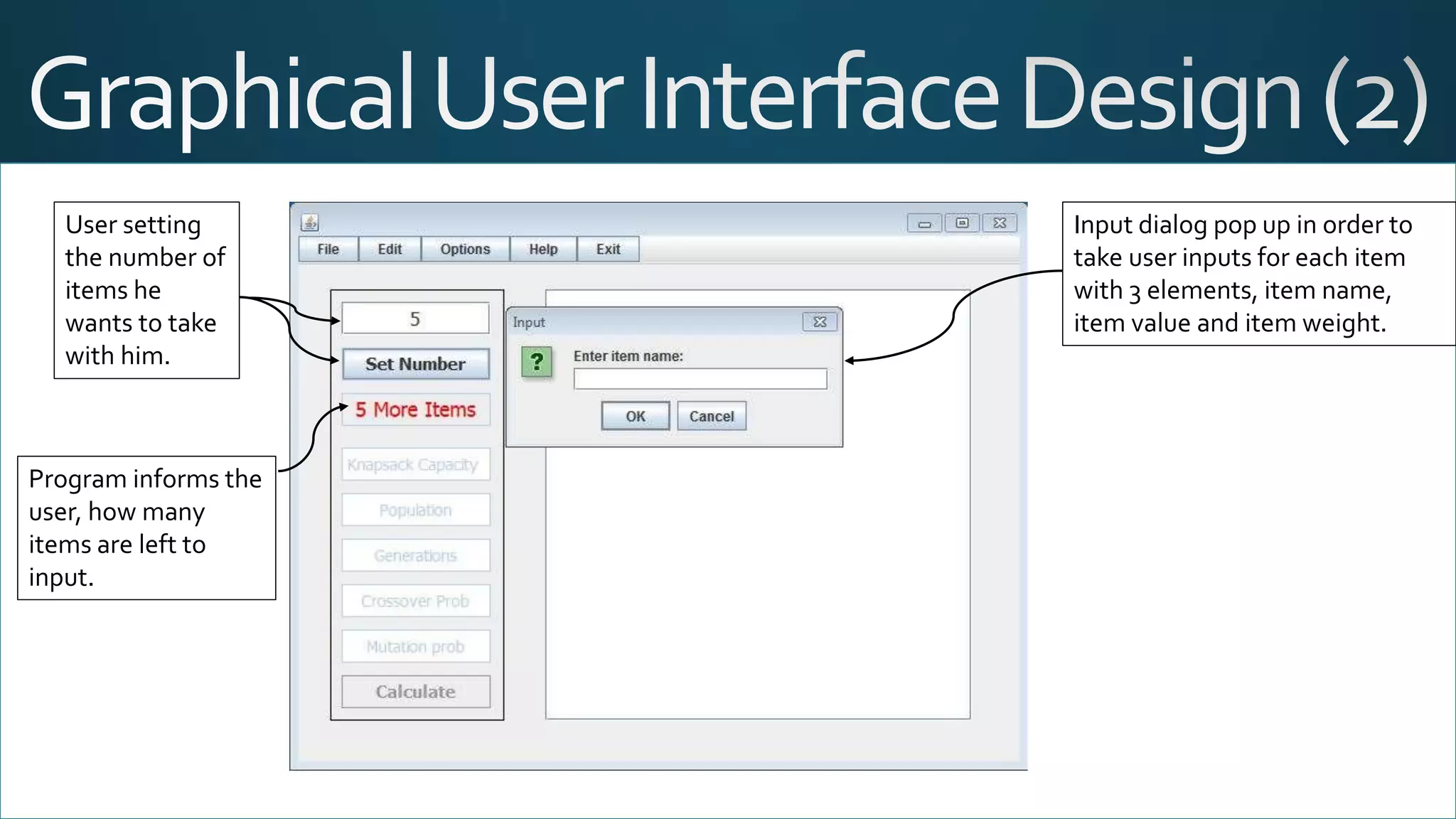
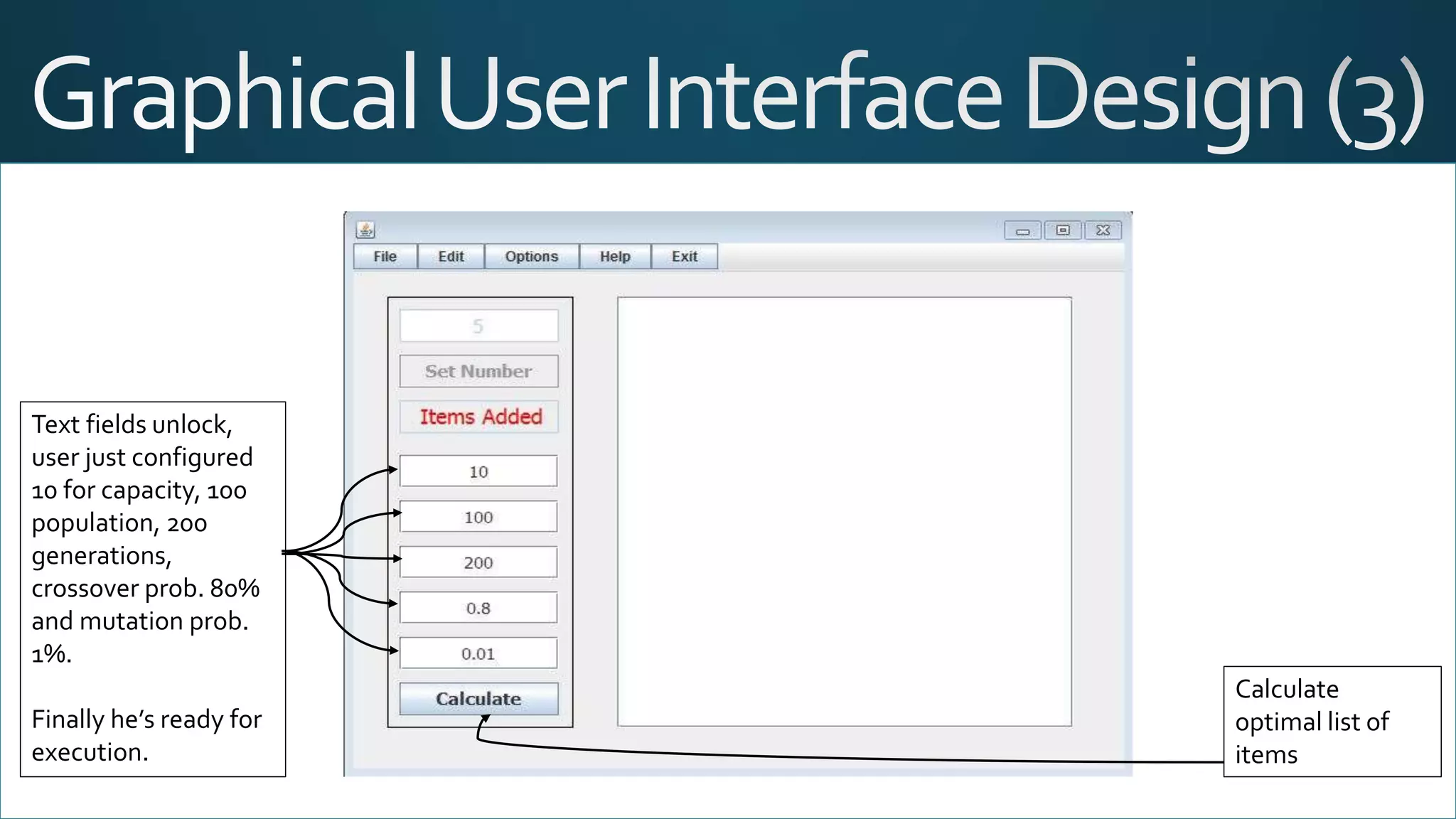
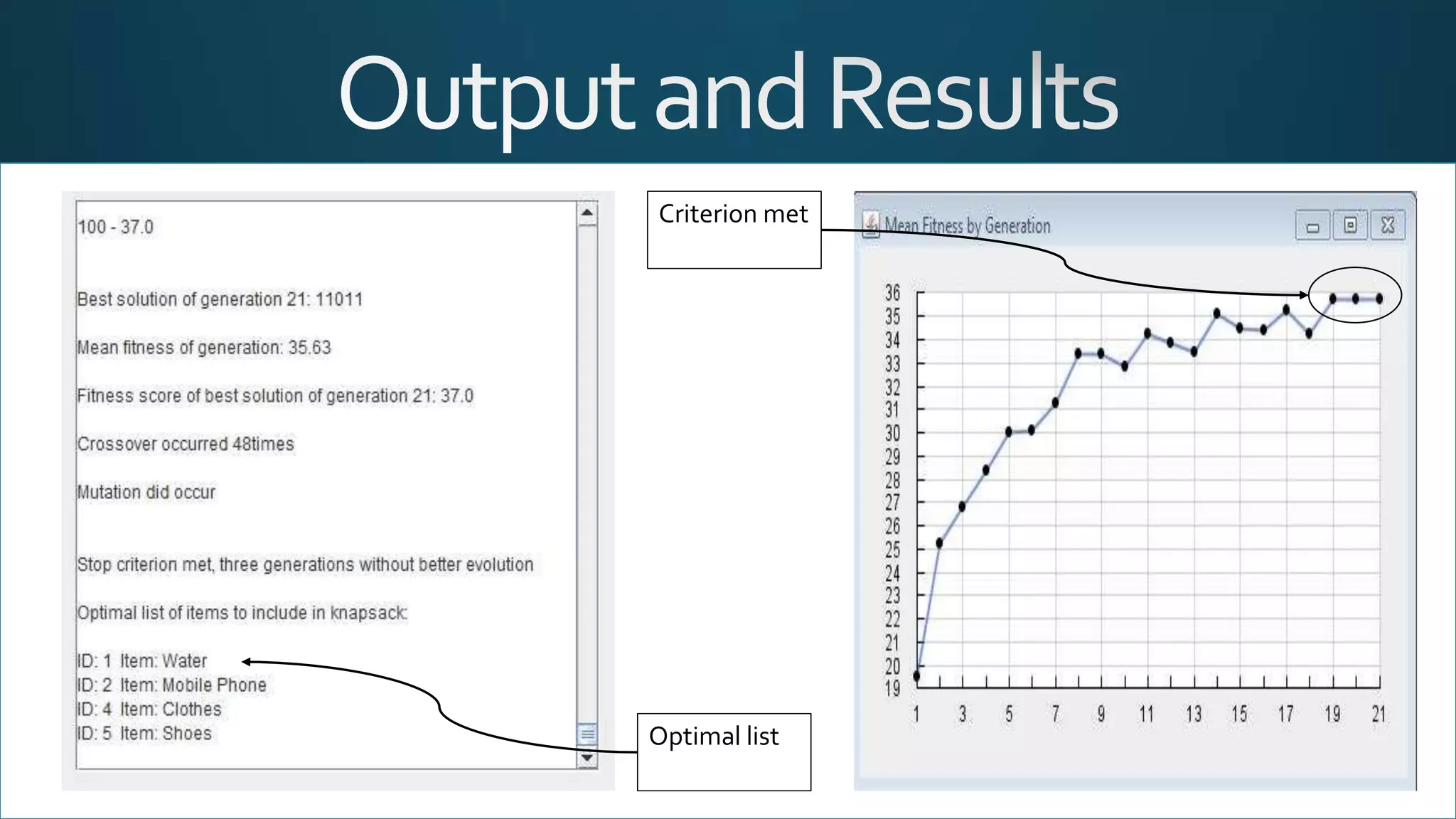
The document discusses the knapsack problem, a combinatorial optimization issue regarding the selection of items based on weight and value constraints. It outlines historical developments in solving the problem, particularly focusing on genetic algorithms as a solution method. A Java-based program is detailed, enabling users to input item parameters and run simulations to determine the optimal set of items for maximizing value within a weight limit.











![[1] M. Lagoudakis, “The 0-1 knapsack problem—An introductory survey,” Citeseer.
Nj. Nec. Com/151553. Html, 1996.
[2] M. Hristakeva and D. Shrestha, “Solving the 0-1 knapsack problem with genetic
algorithms,” Midwest Instr. Comput. …, 2004.
[3] M. Hristakeva and D. Shrestha, “Different Approaches to Solve the 0/1
Knapsack Problem,” Retrieved Novemb., pp. 0–14, 2004.
[4] J. J. Bartholdi, “Building Intuition,” vol. 115, 2008.
[5] http://www.nils-haldenwang.de/computer-science/computational-
intelligence/genetic-algorithm-vs-0-1-knapsack
[6] https://github.com/mmmayo13/knapsack-problem-ga](https://image.slidesharecdn.com/1computationalfinal-151208203322-lva1-app6891/75/Knapsack-problem-solved-by-Genetic-Algorithms-18-2048.jpg)
![[7] L. S. - and M. L. -, “Comparative Study on the Knapsack problem based on PAR
Method and other Methods,” Int. J. Digit. Content Technol. its Appl., vol. 6, no.
18, pp. 211–218, 2012.
[8] C. H. Papadimitriou, “On the Complexity of Integer Programming,” vol. 28, no.
4, pp. 765–768, 1981.
[9] R. C. Eberhart and Y. Shi, Computational Intelligence: Concepts to
Implementations, no. March. 2007.
[10] M. Melanie, “An introduction to genetic algorithms,” Cambridge, Massachusetts
London, England, …, p. 162, 1996.
[11] L. S. - and M. L. -, “Comparative Study on the Knapsack problem based on PAR
Method and other Methods,” Int. J. Digit. Content Technol. its Appl., vol. 6, no.
18, pp. 211–218, 2012.](https://image.slidesharecdn.com/1computationalfinal-151208203322-lva1-app6891/75/Knapsack-problem-solved-by-Genetic-Algorithms-19-2048.jpg)
