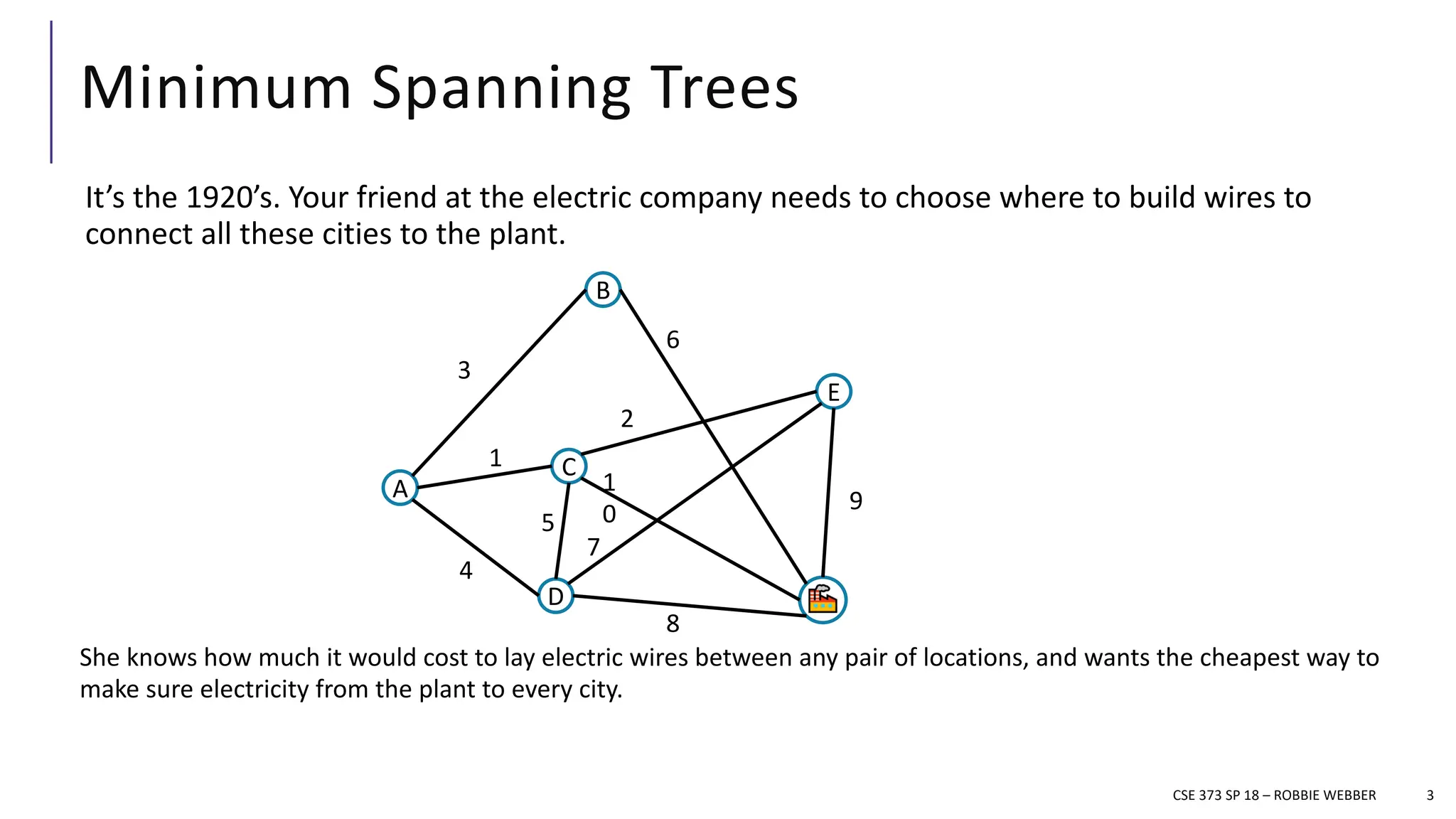
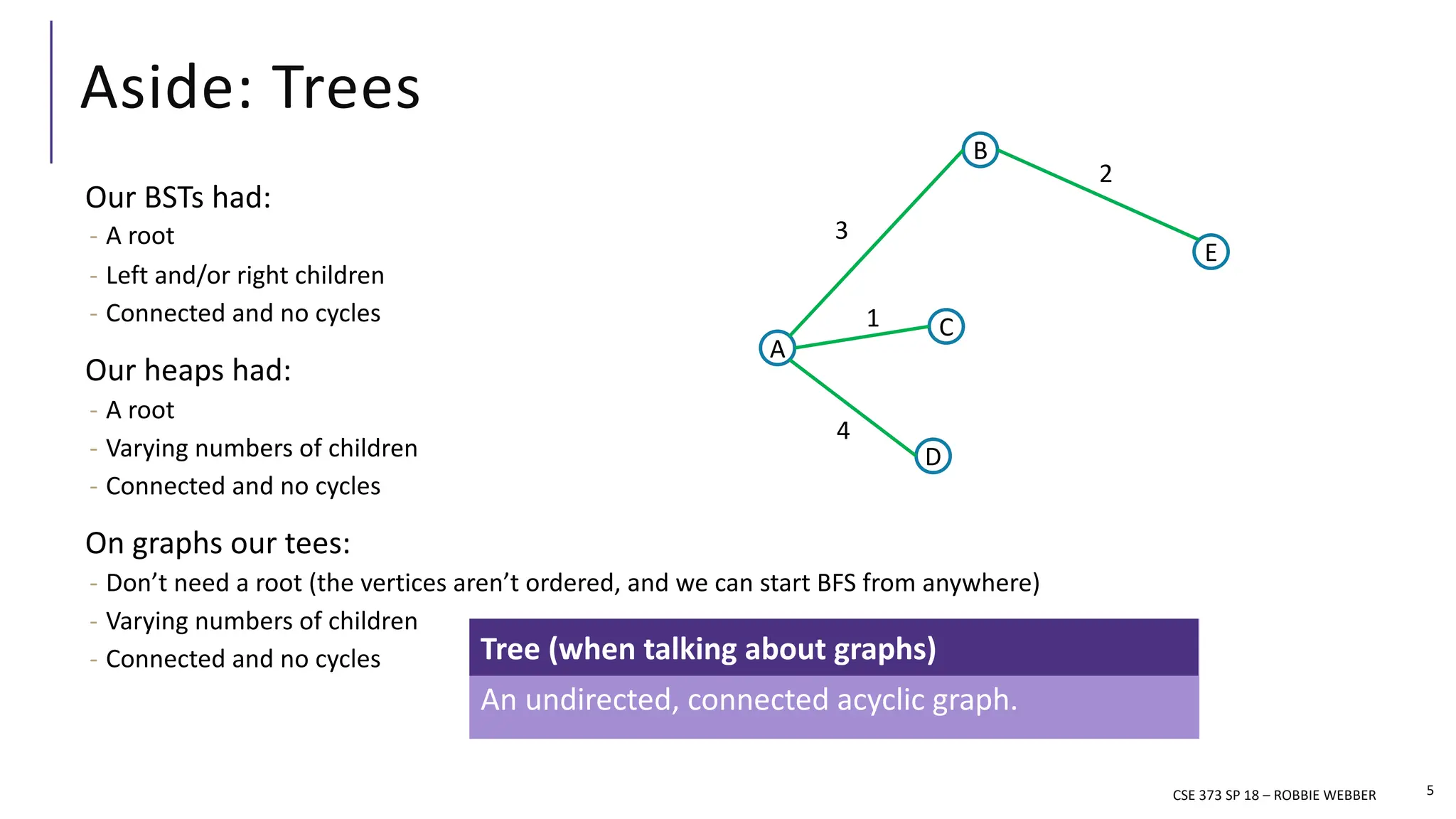
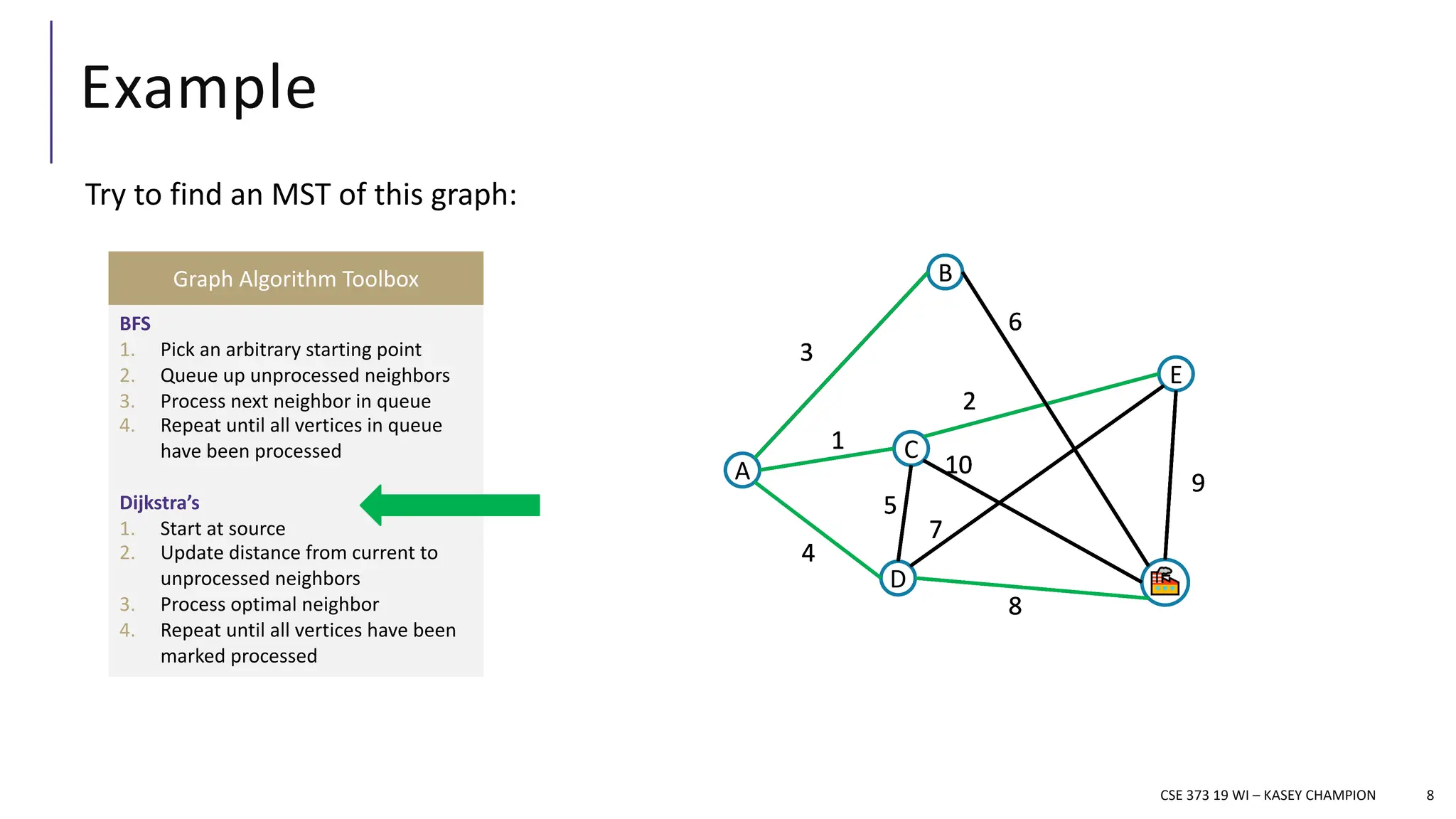
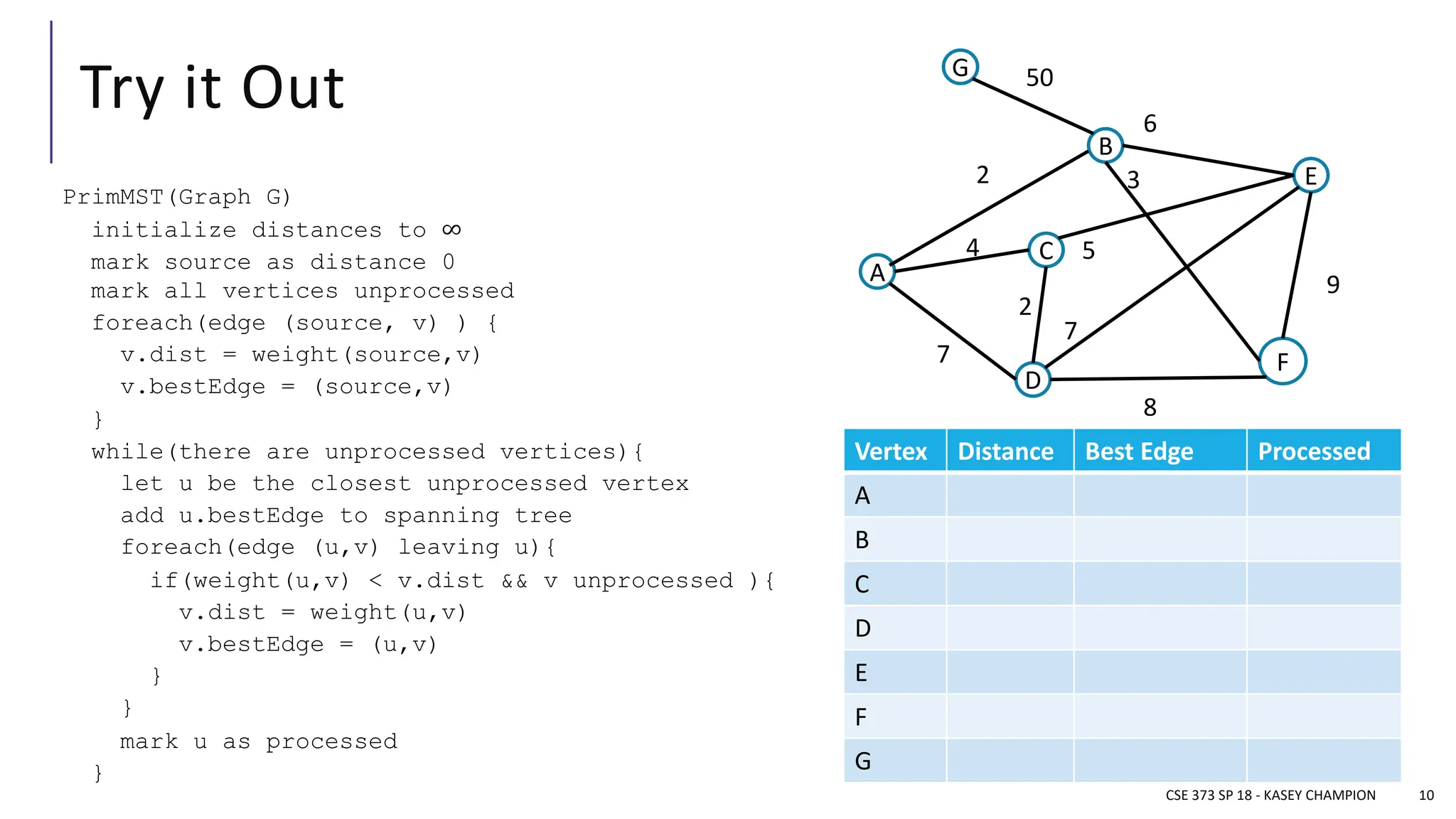
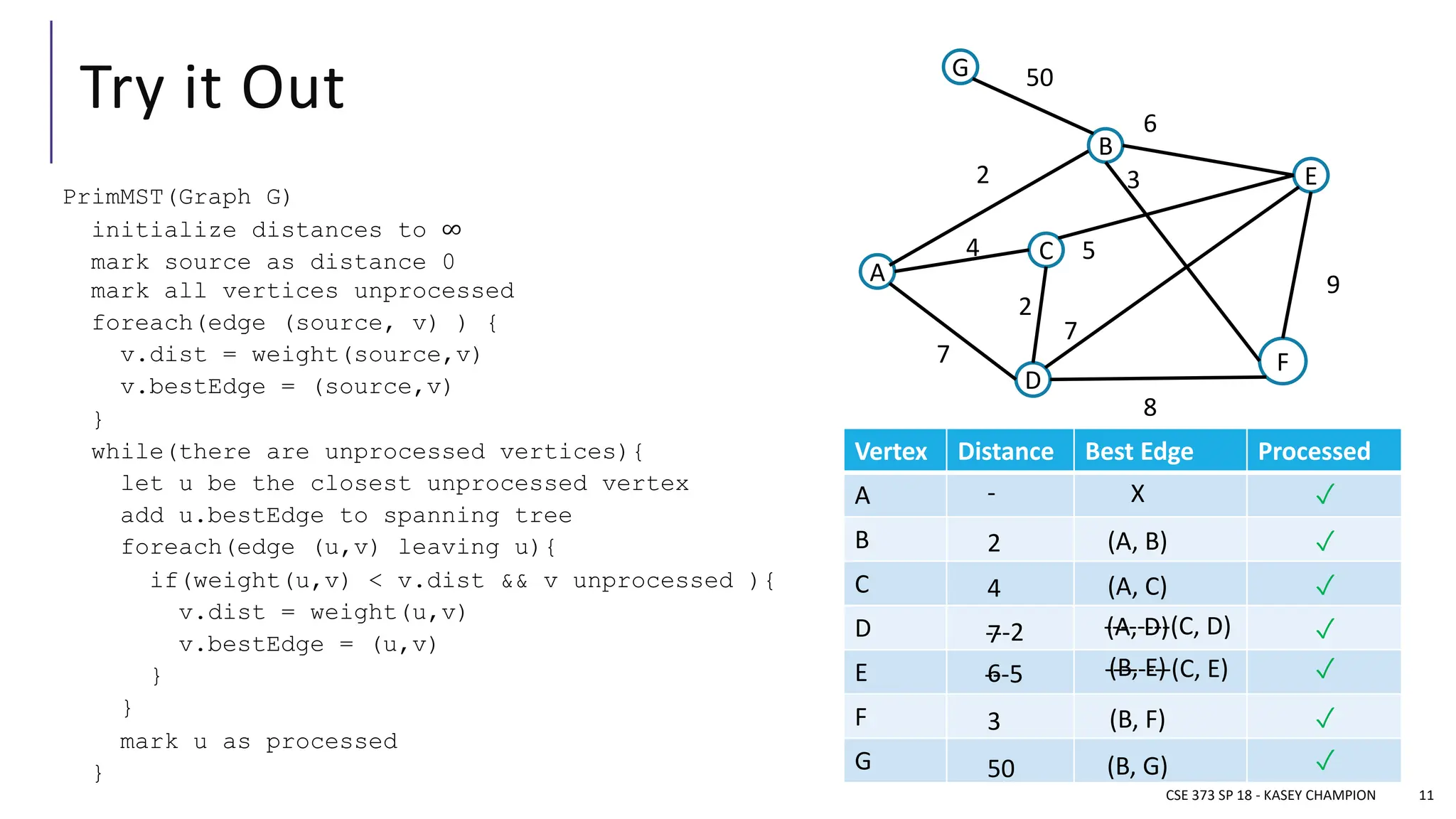
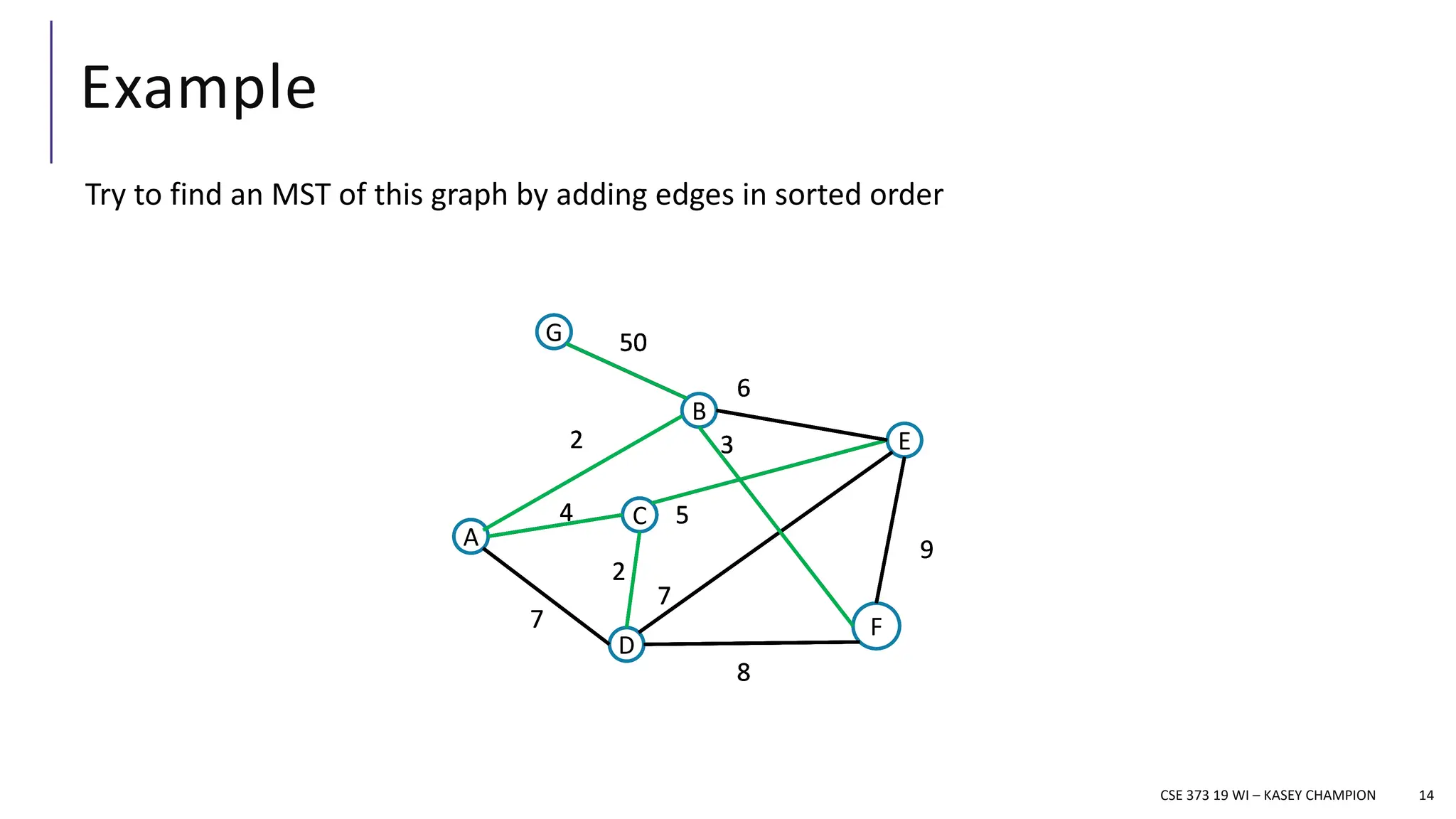
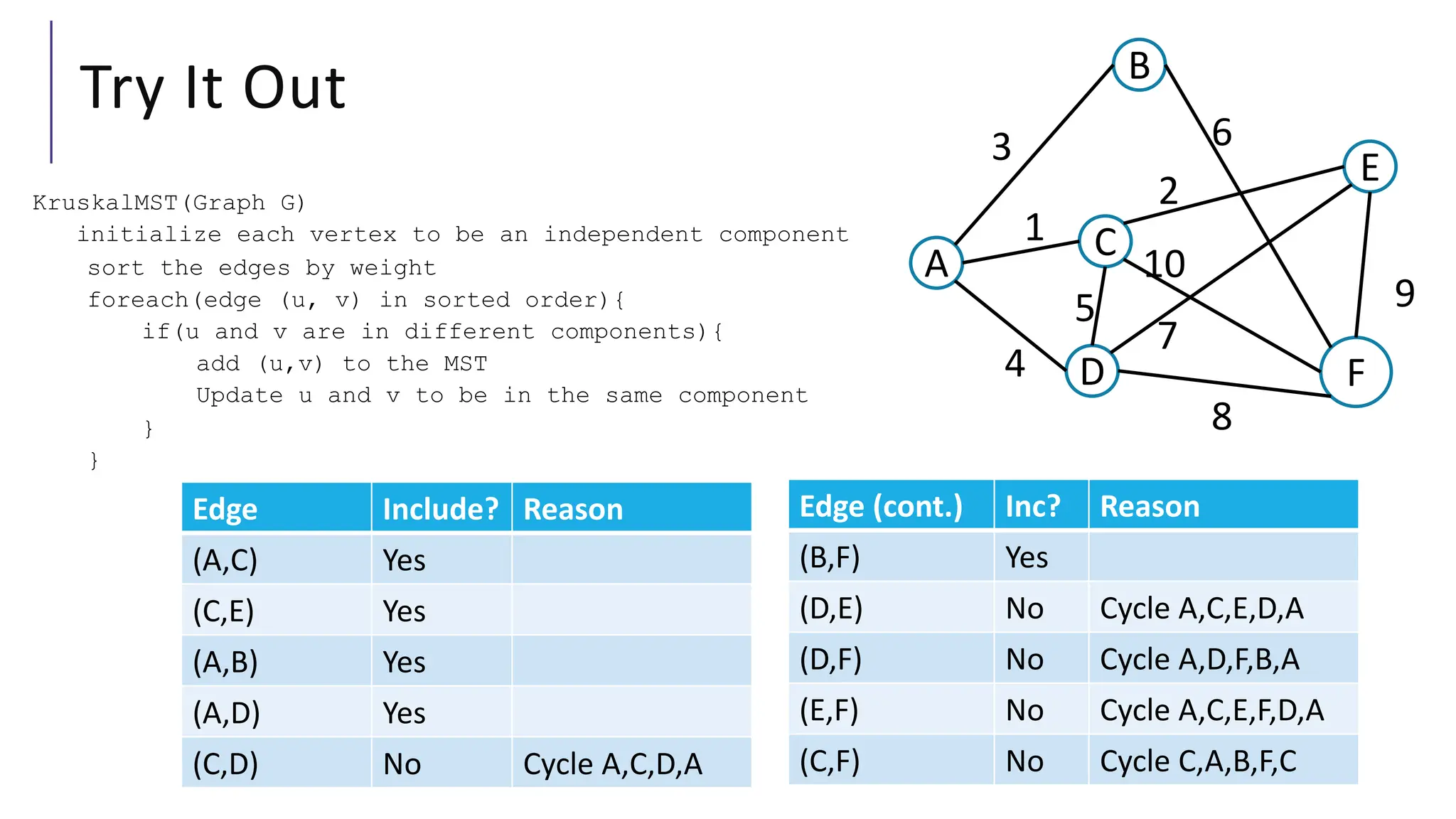
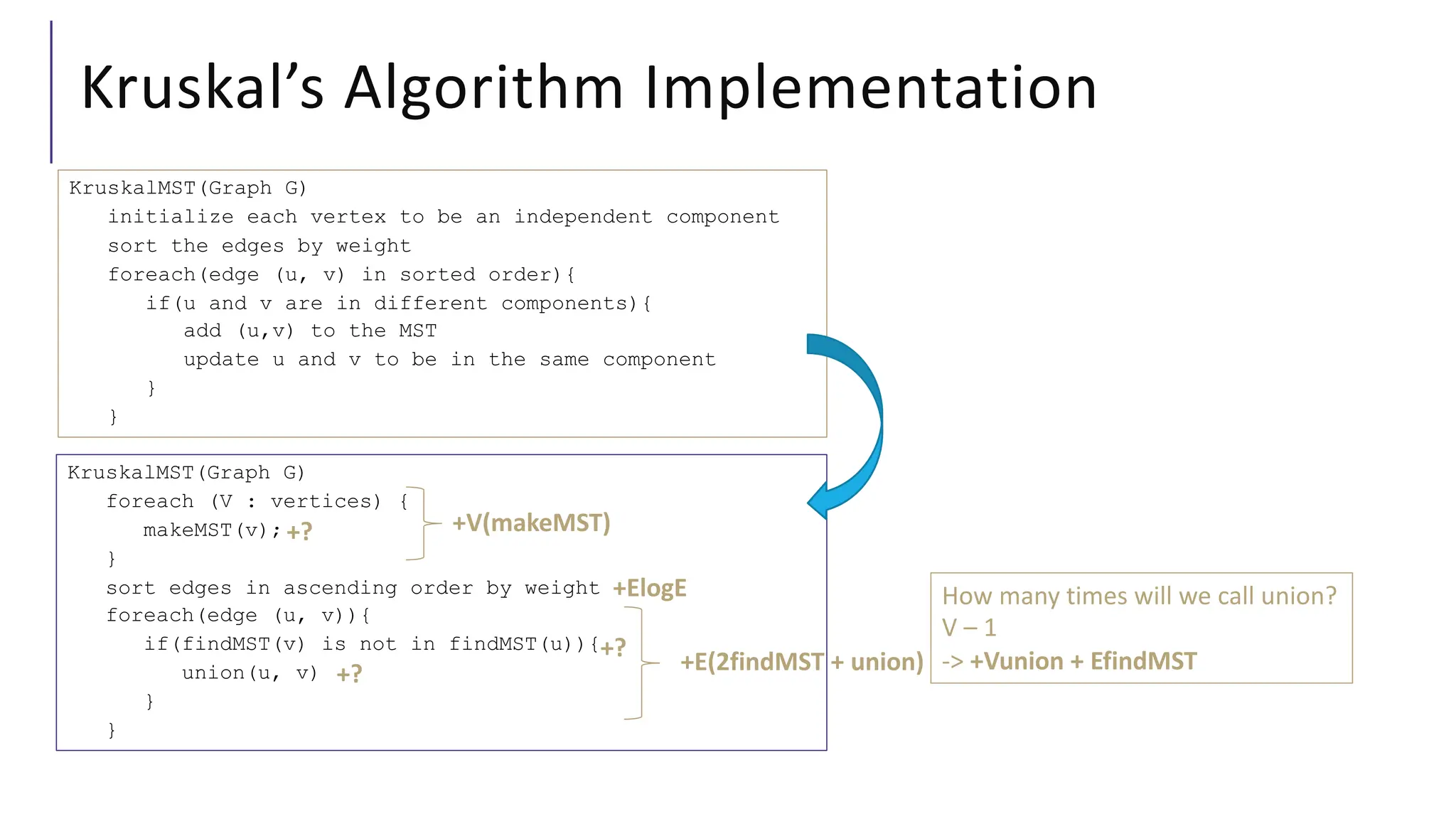
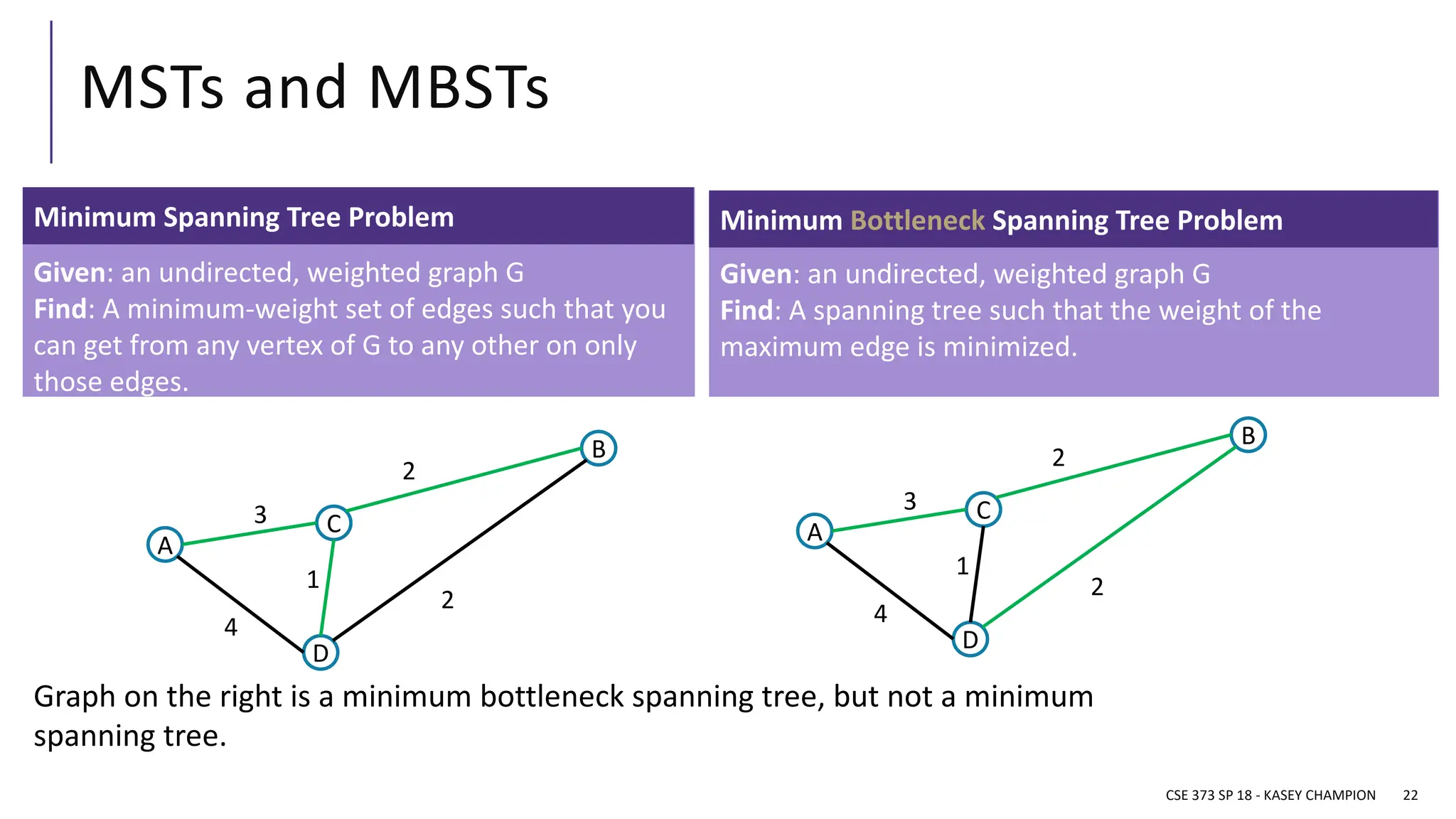
The document discusses minimum spanning trees (MSTs) in the context of algorithms used to connect vertices in a weighted, undirected graph with the least total edge cost. It outlines Prim's and Kruskal's algorithms for finding MSTs, explaining their workings, properties, and applications. The lecture emphasizes the properties of MSTs, such as the cycle and cut properties, and their importance in practical problems like optimizing construction connections.