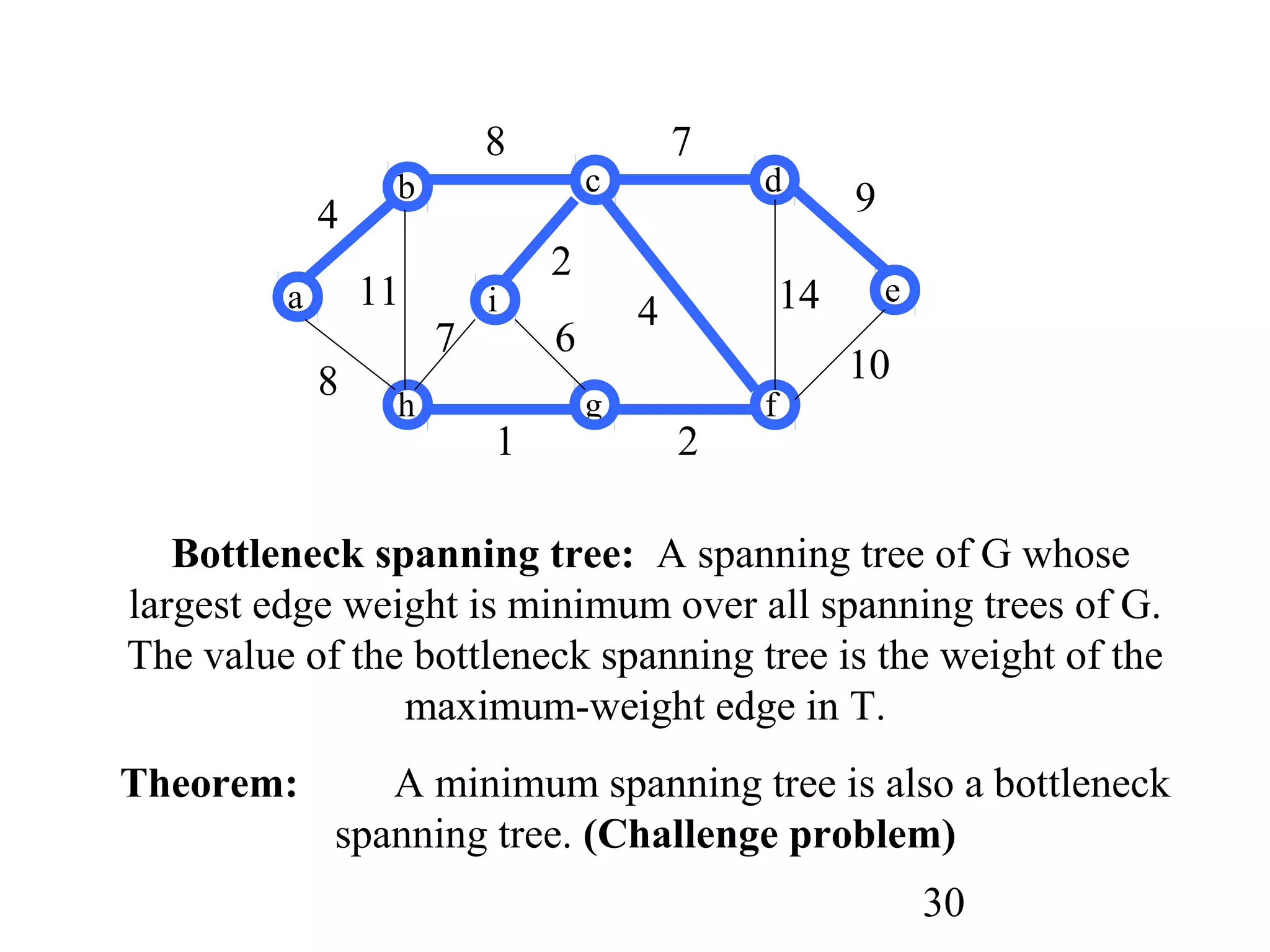
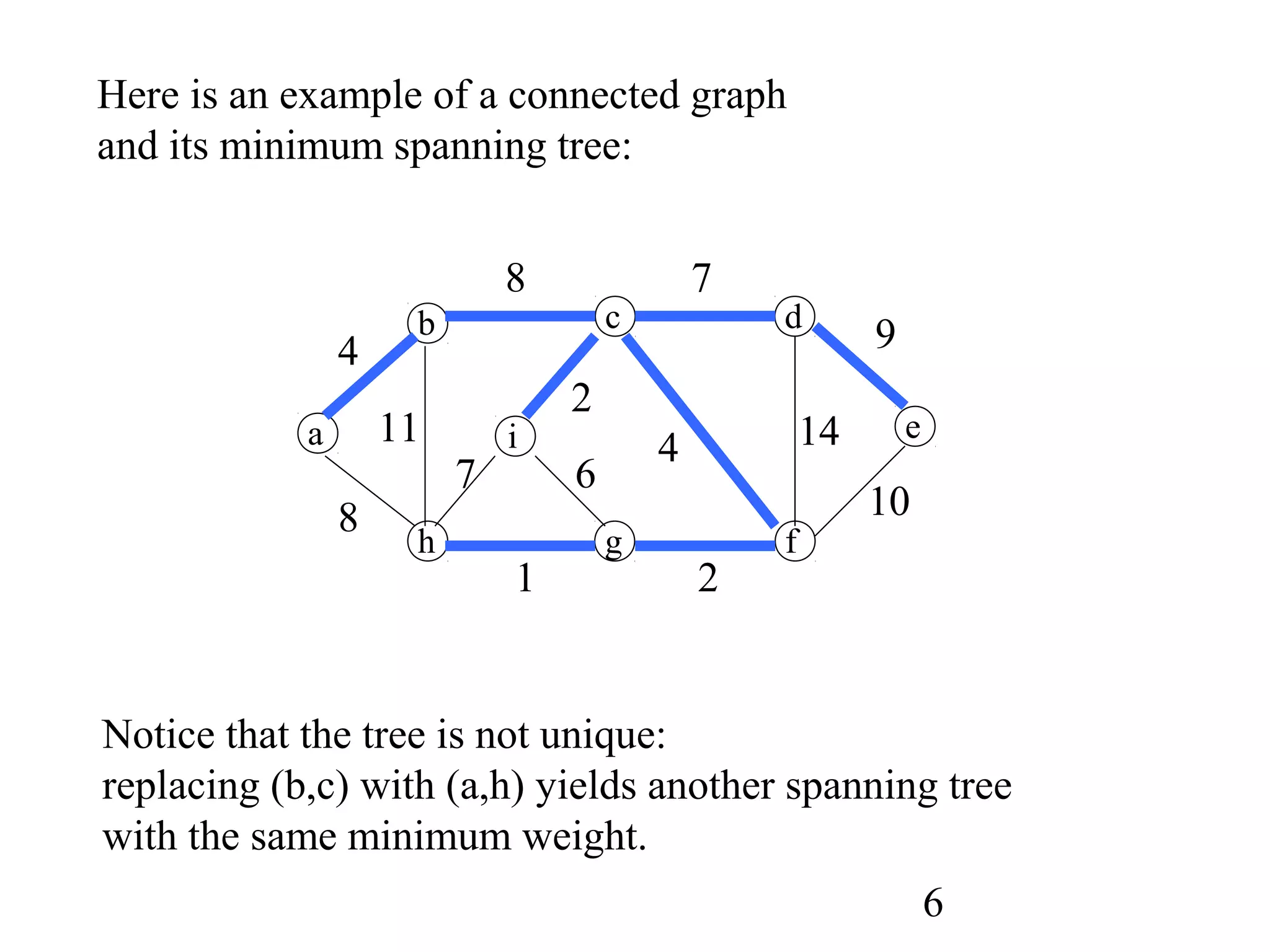
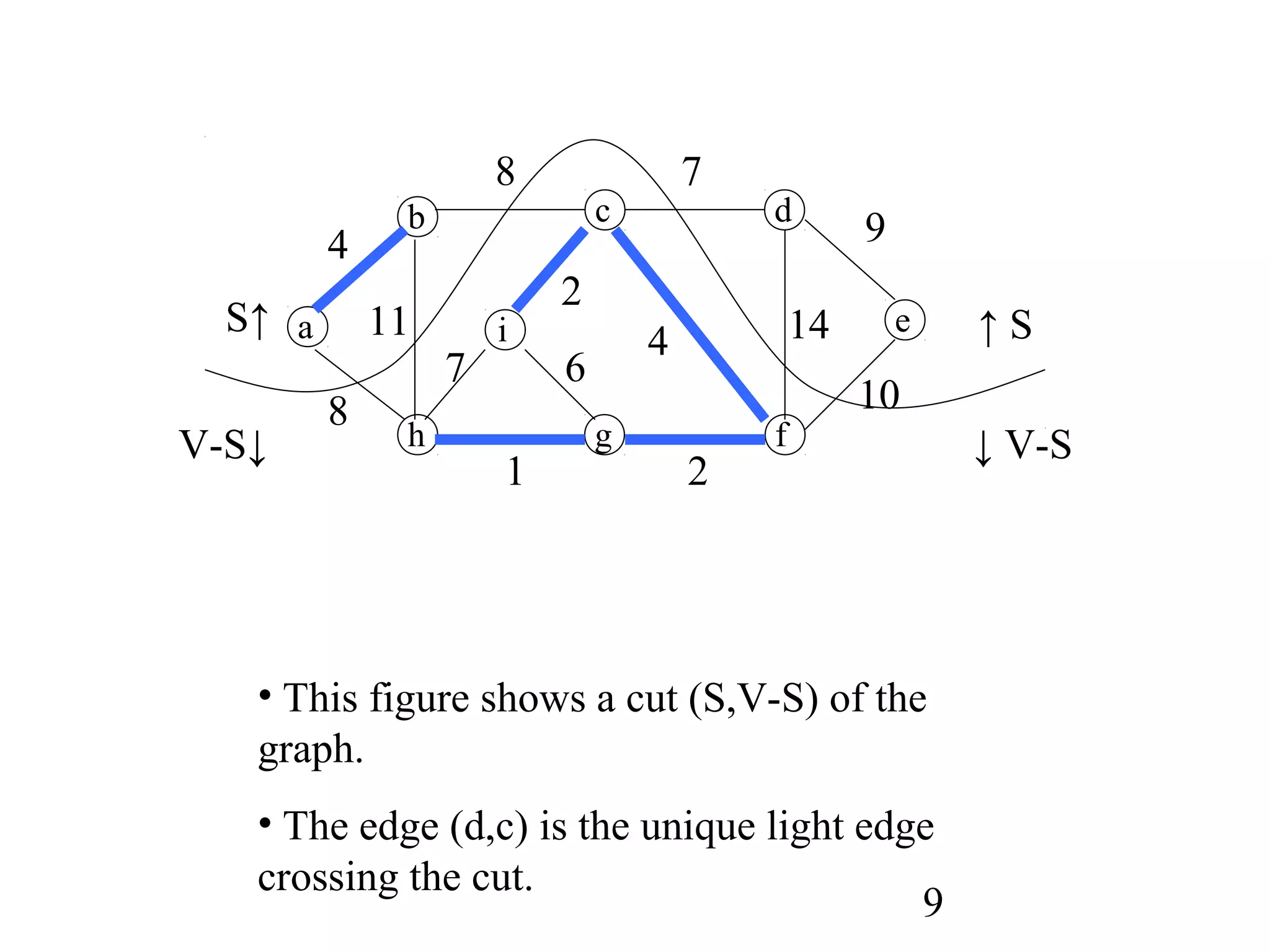
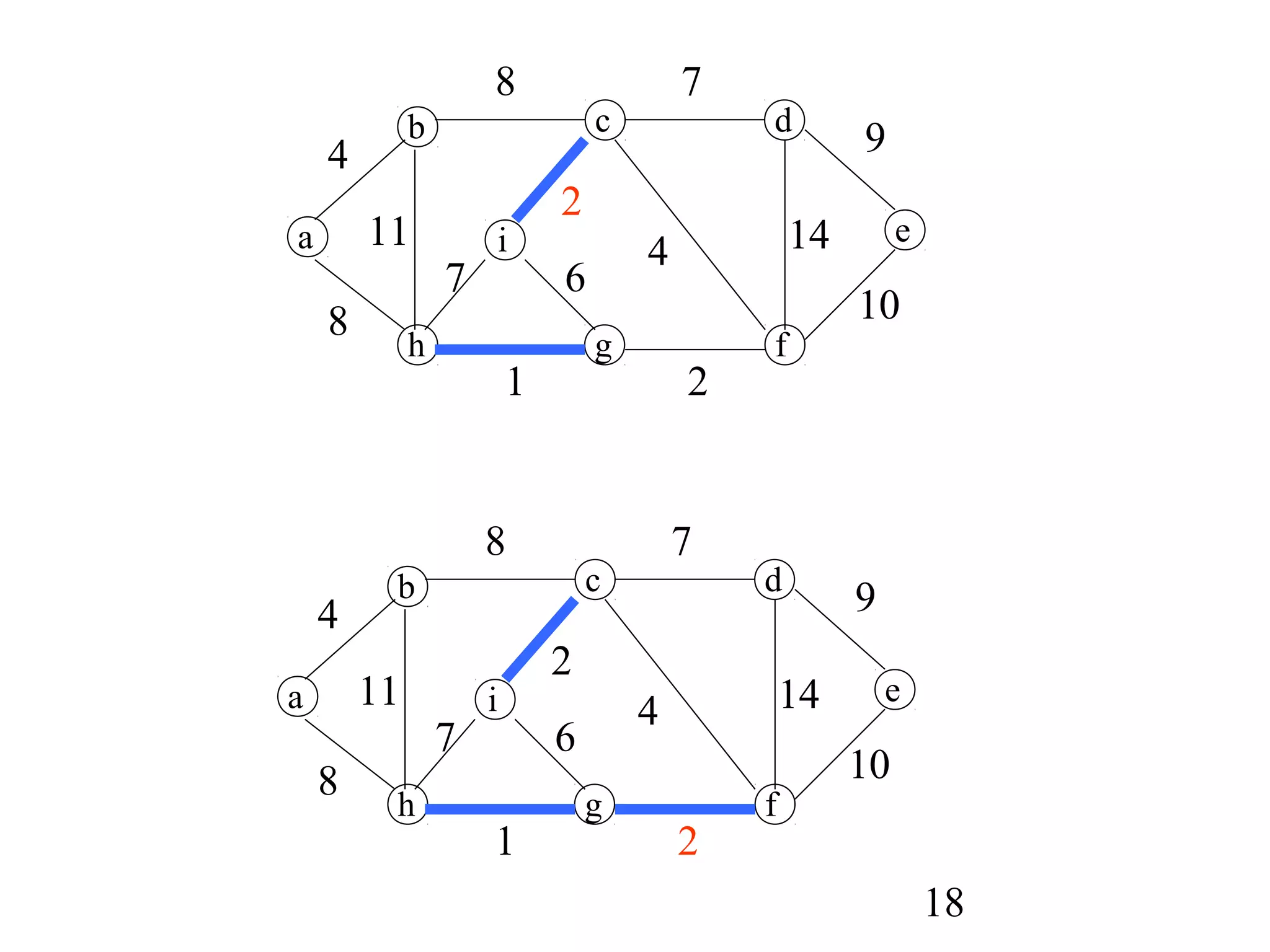
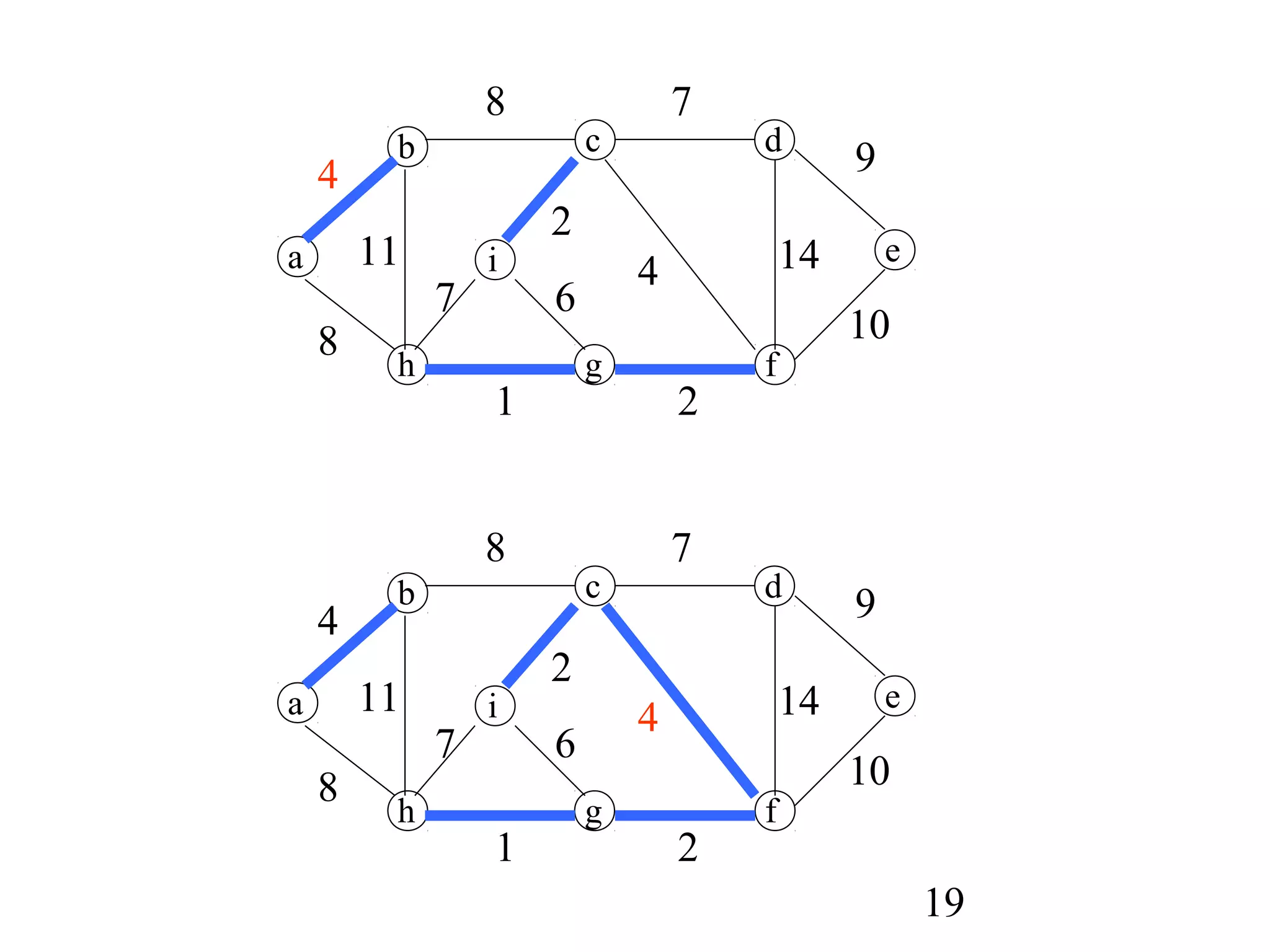
The document discusses minimum spanning trees (MSTs). It defines MSTs and provides examples of applications like wiring electronic circuits. It then describes two common algorithms for finding MSTs: Kruskal's algorithm and Prim's algorithm. Kruskal's algorithm finds MSTs by sorting edges by weight and adding edges that connect different components without creating cycles. Prim's algorithm grows an MST from a single vertex by always adding the lowest-weight edge connecting a vertex to the growing tree.











![14
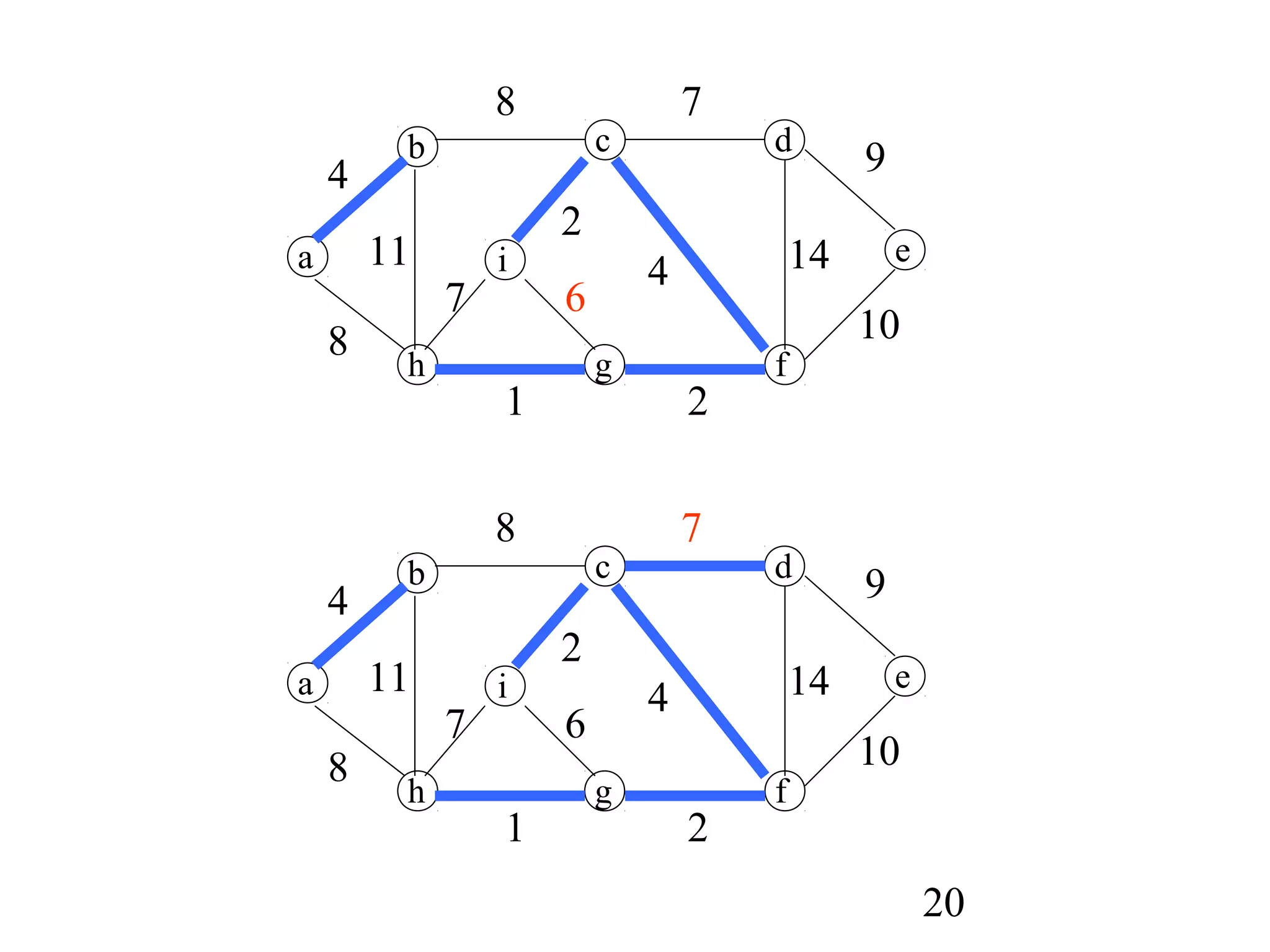
Kruskal's algorithm (Fun Part, not required)
MST_KRUSKAL(G,w)
1 A:={}
2 for each vertex v in V[G]
3 do MAKE_SET(v)
4 sort the edges of E by nondecreasing weight w
5 for each edge (u,v) in E, in order by
nondecreasing weight
6 do if FIND_SET(u) != FIND_SET(v)
7 then A:=A {(u,v)}∪
8 UNION(u,v)
9 return A
(Disjoint set is discussed in Chapter 21, Page 498)](https://image.slidesharecdn.com/algorithm1620416129-170221161937/75/minimum-spanning-trees-Algorithm-14-2048.jpg)





![24
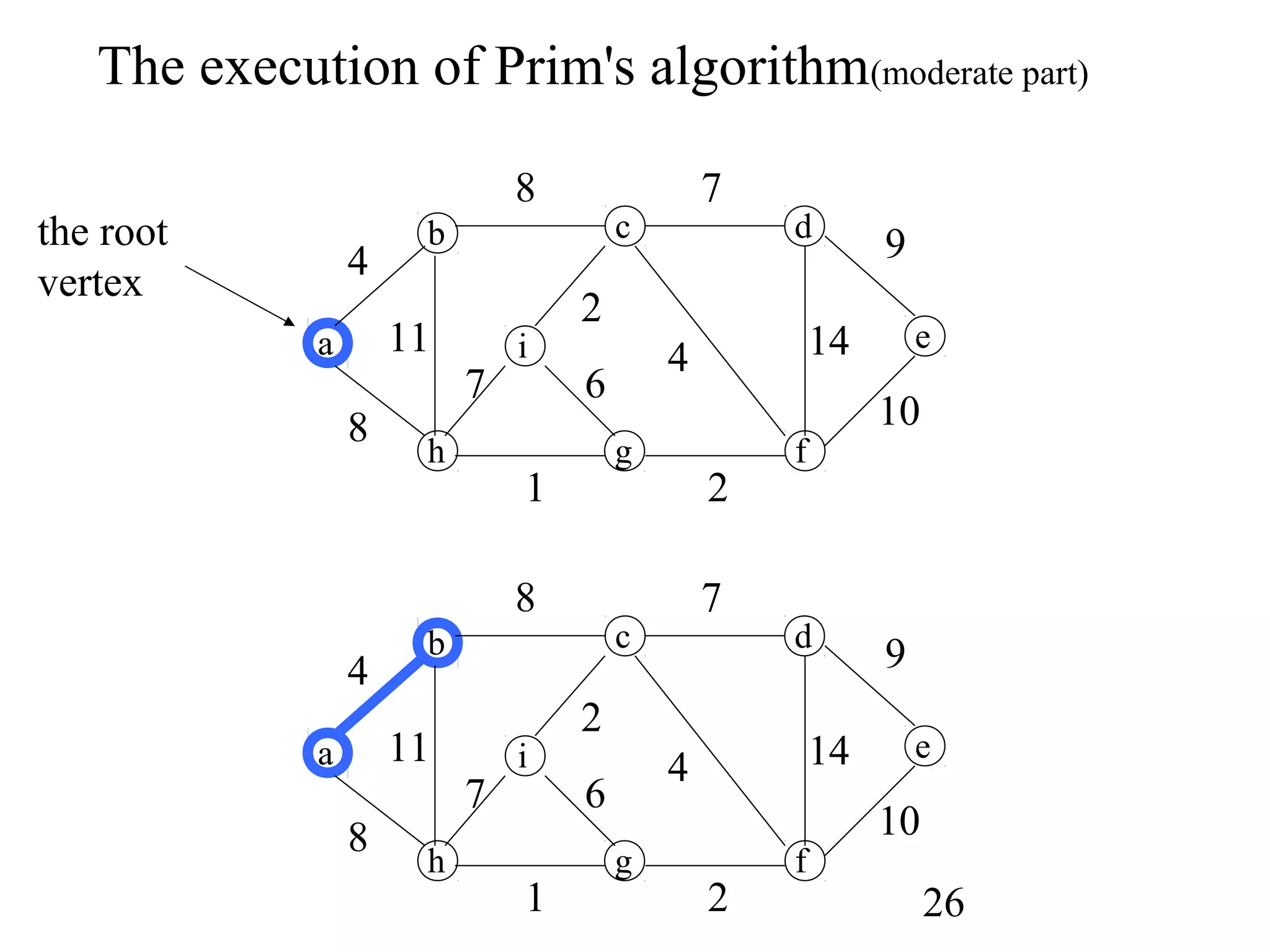
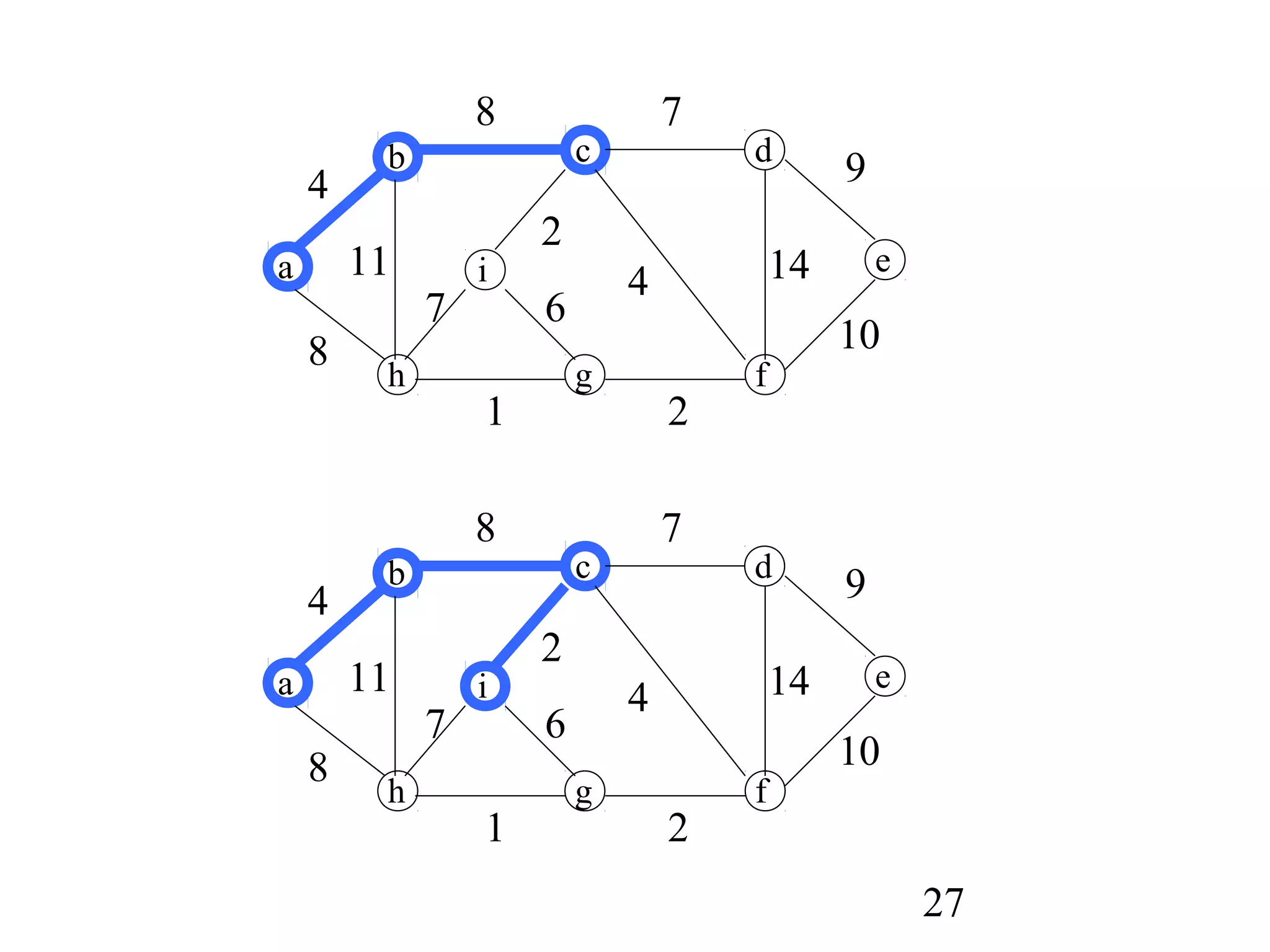
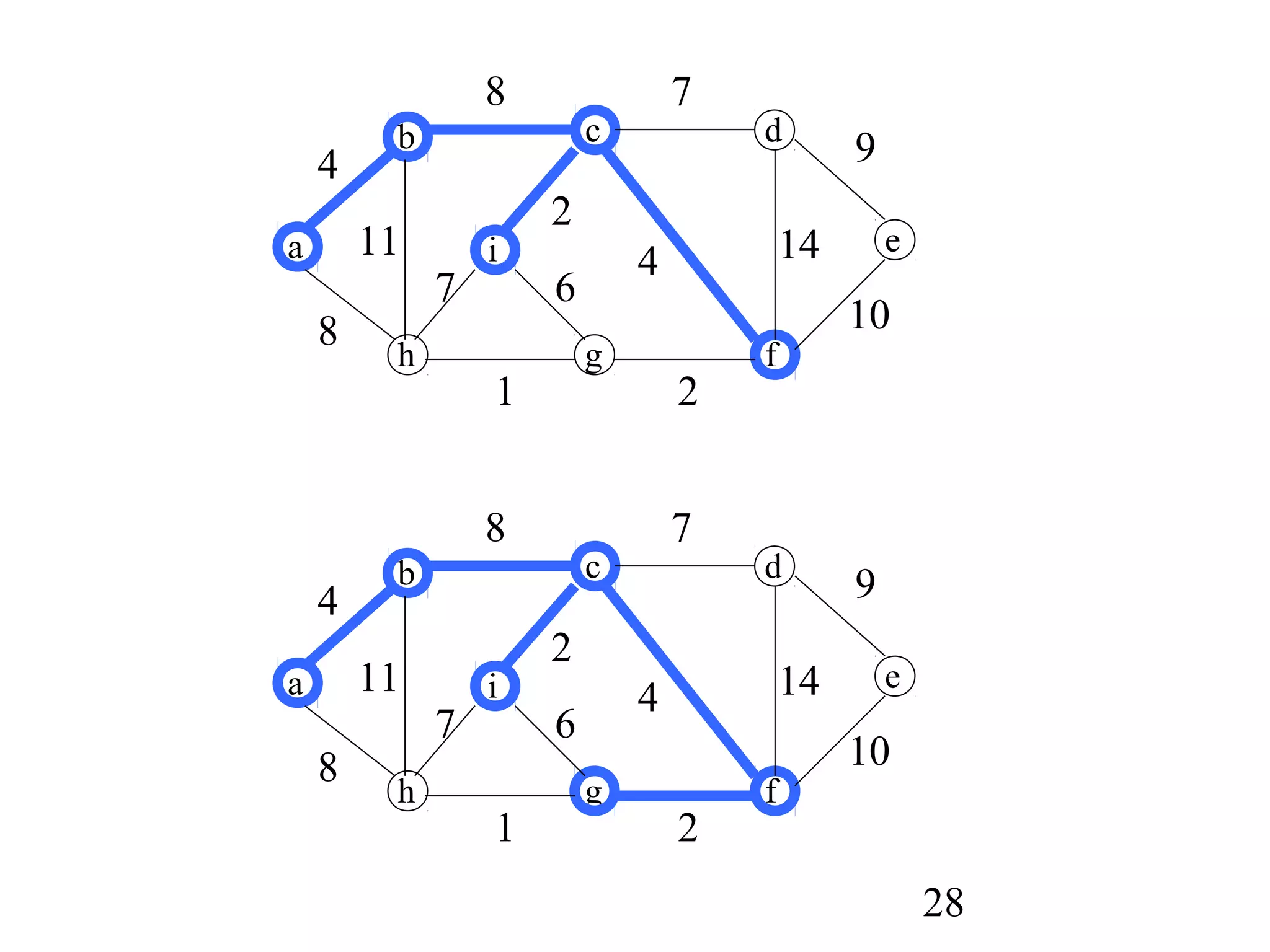
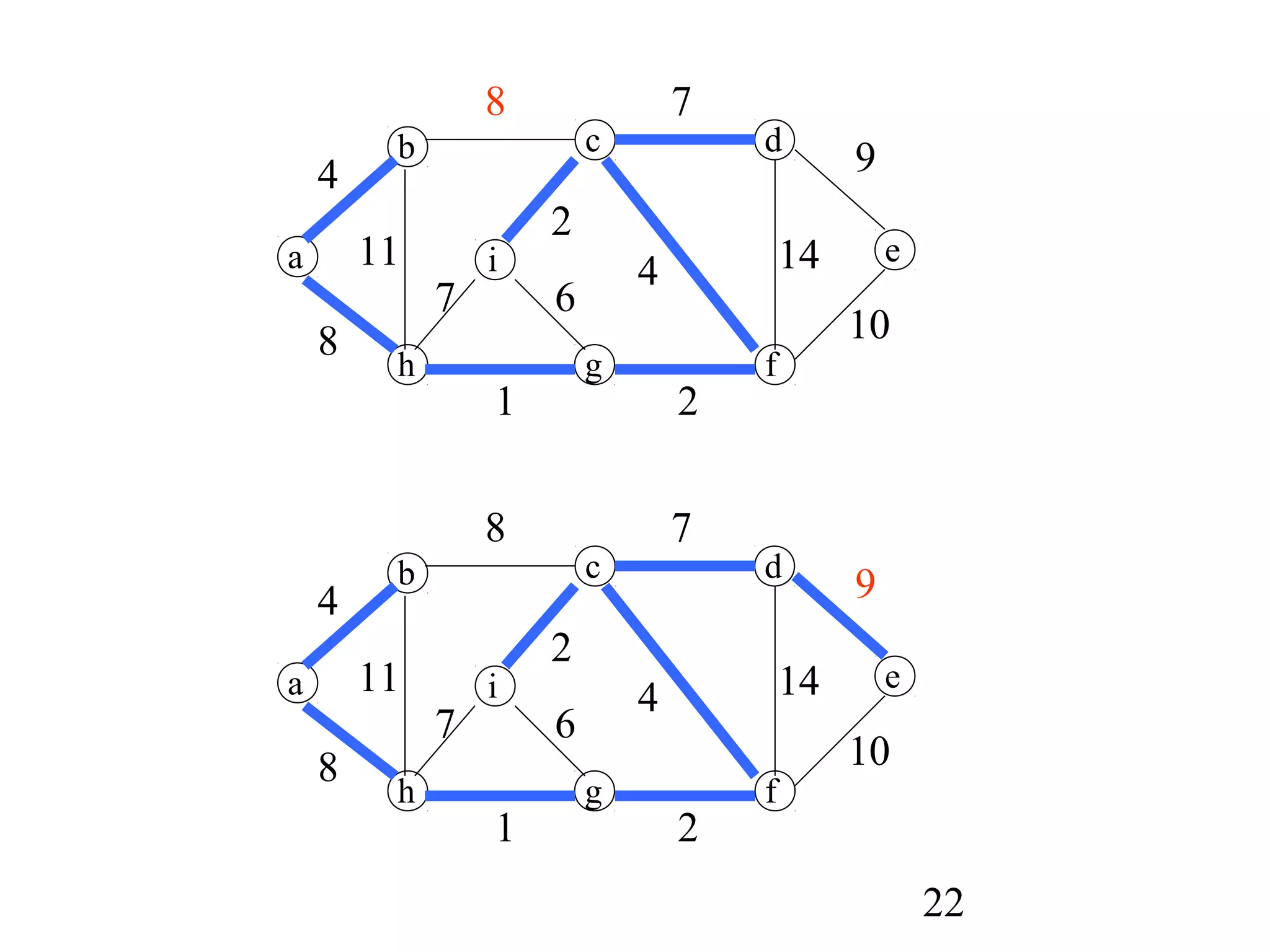
Prim's algorithm
MST_PRIM(G,w,r)
1 for each u in Q do
2 key[u]:=∞
3 parent[u]:=NIL
4 key[r]:=0; parent[r]=NIL;
5 Q←V[Q]
6 while Q!={} do
7 u:=EXTRACT_MIN(Q); if parent[u]≠Nil print (u, parent[u])
8 for each v in Adj[u] do
9 if v in Q and w(u,v)<key[v]
10 then parent[v]:=u
11 key[v]:=w(u,v)](https://image.slidesharecdn.com/algorithm1620416129-170221161937/75/minimum-spanning-trees-Algorithm-24-2048.jpg)
![25
• Grow the minimum spanning tree from the root
vertex r.
• Q is a priority queue, holding all vertices that are
not in the tree now.
• key[v] is the minimum weight of any edge
connecting v to a vertex in the tree.
• parent[v] names the parent of v in the tree.
• When the algorithm terminates, Q is empty; the
minimum spanning tree A for G is thus
A={(v,parent[v]):v∈V-{r}}.
• Running time: O(||E||lg |V|).](https://image.slidesharecdn.com/algorithm1620416129-170221161937/75/minimum-spanning-trees-Algorithm-25-2048.jpg)