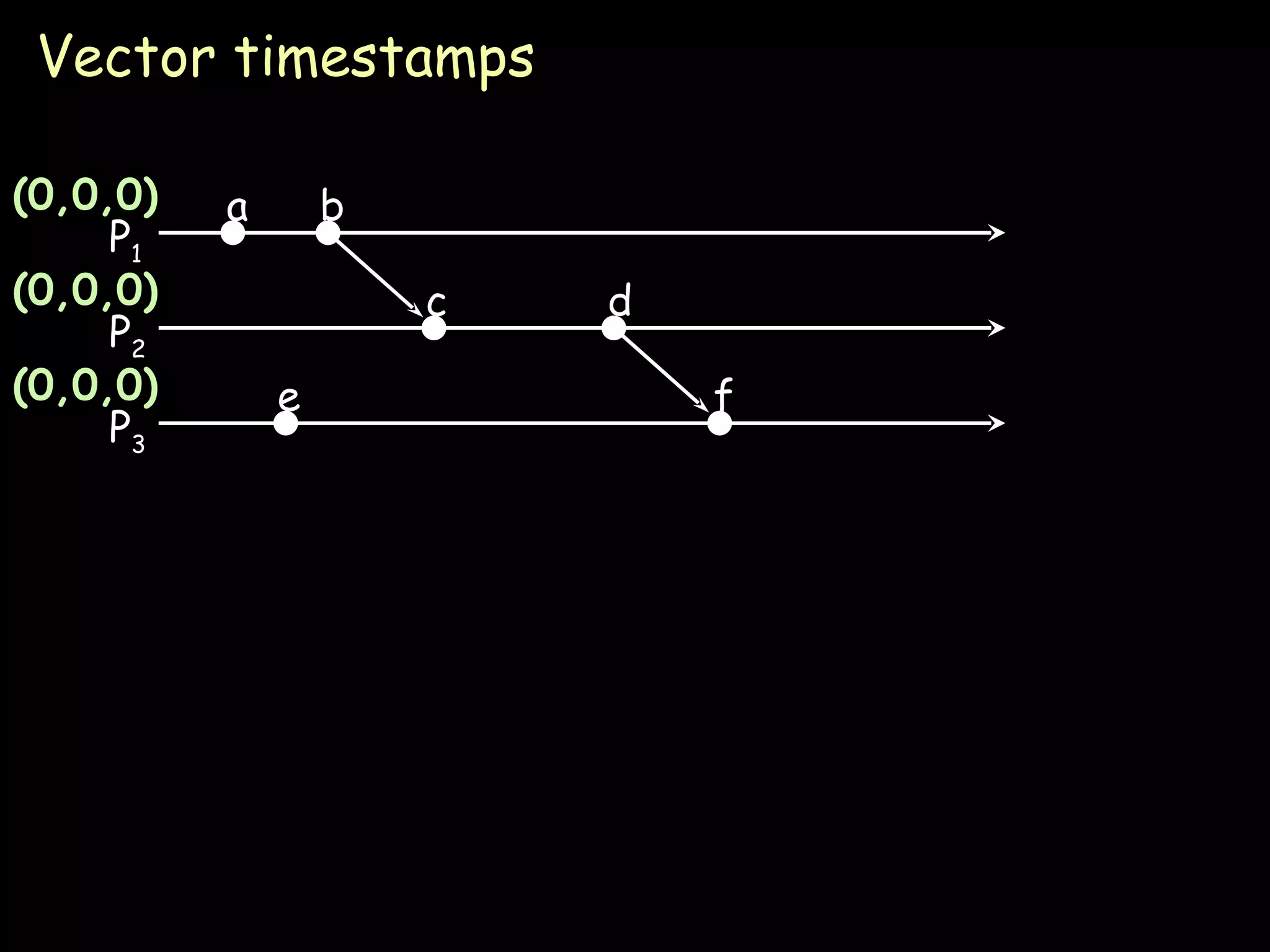
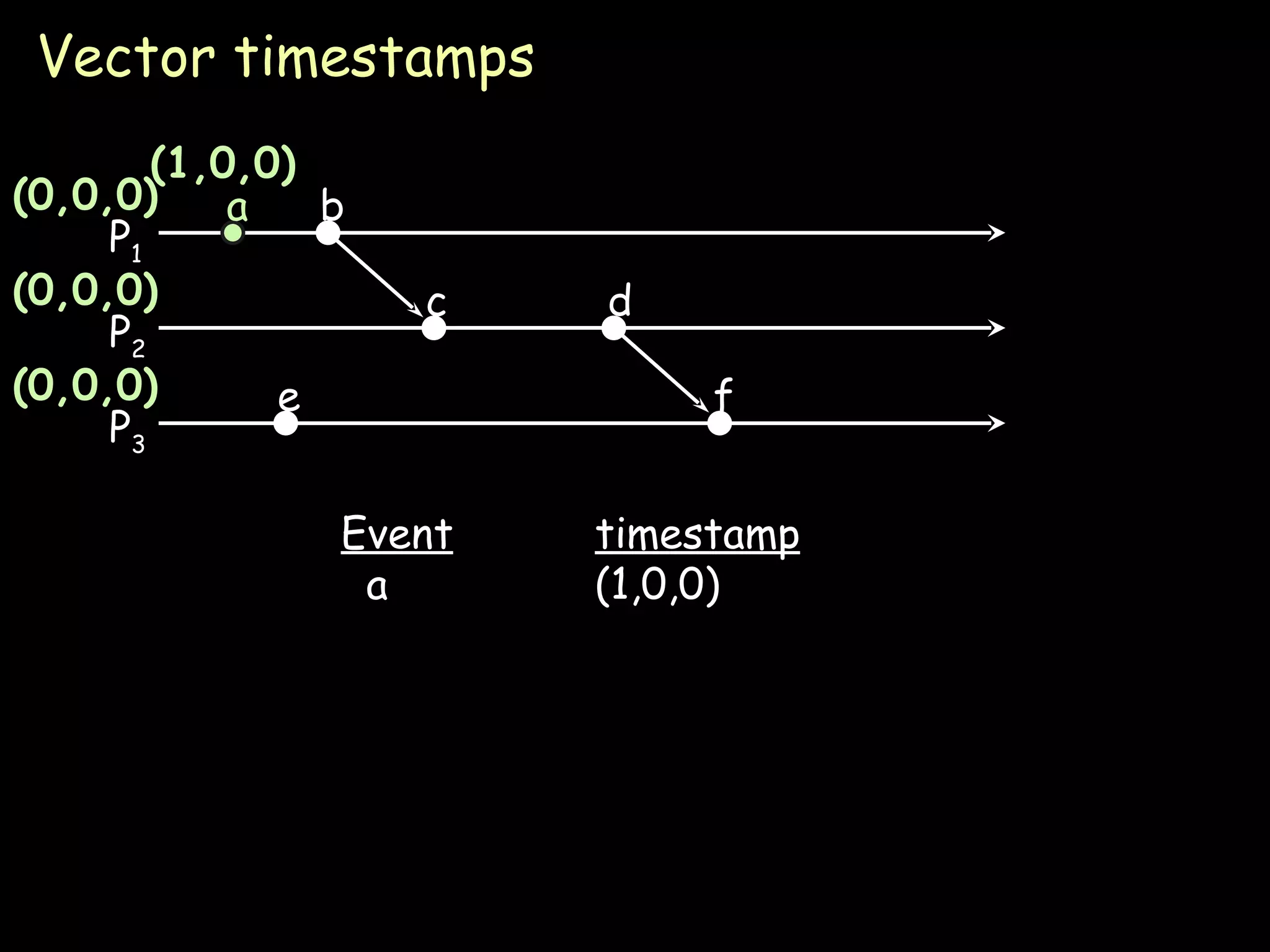
Logical clocks assign sequence numbers to distributed system events to determine causality without a global clock. Lamport's algorithm uses logical clocks to impose a partial ordering on events. Vector clocks extend this to also detect concurrent events that are not causally related, providing a full happened-before relation between all events. Each process maintains a vector clock that is incremented after local events and updated when receiving messages from other processes.
![Logical Clocks Paul Krzyzanowski [email_address] [email_address] Distributed Systems Except as otherwise noted, the content of this presentation is licensed under the Creative Commons Attribution 2.5 License.](https://image.slidesharecdn.com/10-logicalclocks-090902071053-phpapp01/75/Logical-Clocks-Distributed-computing-1-2048.jpg)













![Vector clocks Rules: Vector initialized to 0 at each process V i [ j ] = 0 for i, j =1, …, N Process increments its element of the vector in local vector before timestamping event: V i [ i ] = V i [ i ] +1 Message is sent from process P i with V i attached to it When P j receives message, compares vectors element by element and sets local vector to higher of two values V j [ i ] = max(V i [ i ], V j [ i ]) for i=1, …, N](https://image.slidesharecdn.com/10-logicalclocks-090902071053-phpapp01/75/Logical-Clocks-Distributed-computing-16-2048.jpg)
![Comparing vector timestamps Define V = V’ iff V [ i ] = V’[ i ] for i = 1 … N V V’ iff V [ i ] V’[ i ] for i = 1 … N For any two events e, e’ if e e’ then V(e) < V(e’) Just like Lamport’s algorithm if V(e) < V(e’) then e e’ Two events are concurrent if neither V(e) V(e’) nor V(e’) V(e)](https://image.slidesharecdn.com/10-logicalclocks-090902071053-phpapp01/75/Logical-Clocks-Distributed-computing-17-2048.jpg)