Downloaded 44 times
Uploaded bygarishma bhatia
MATCHING GRAPH THEORY
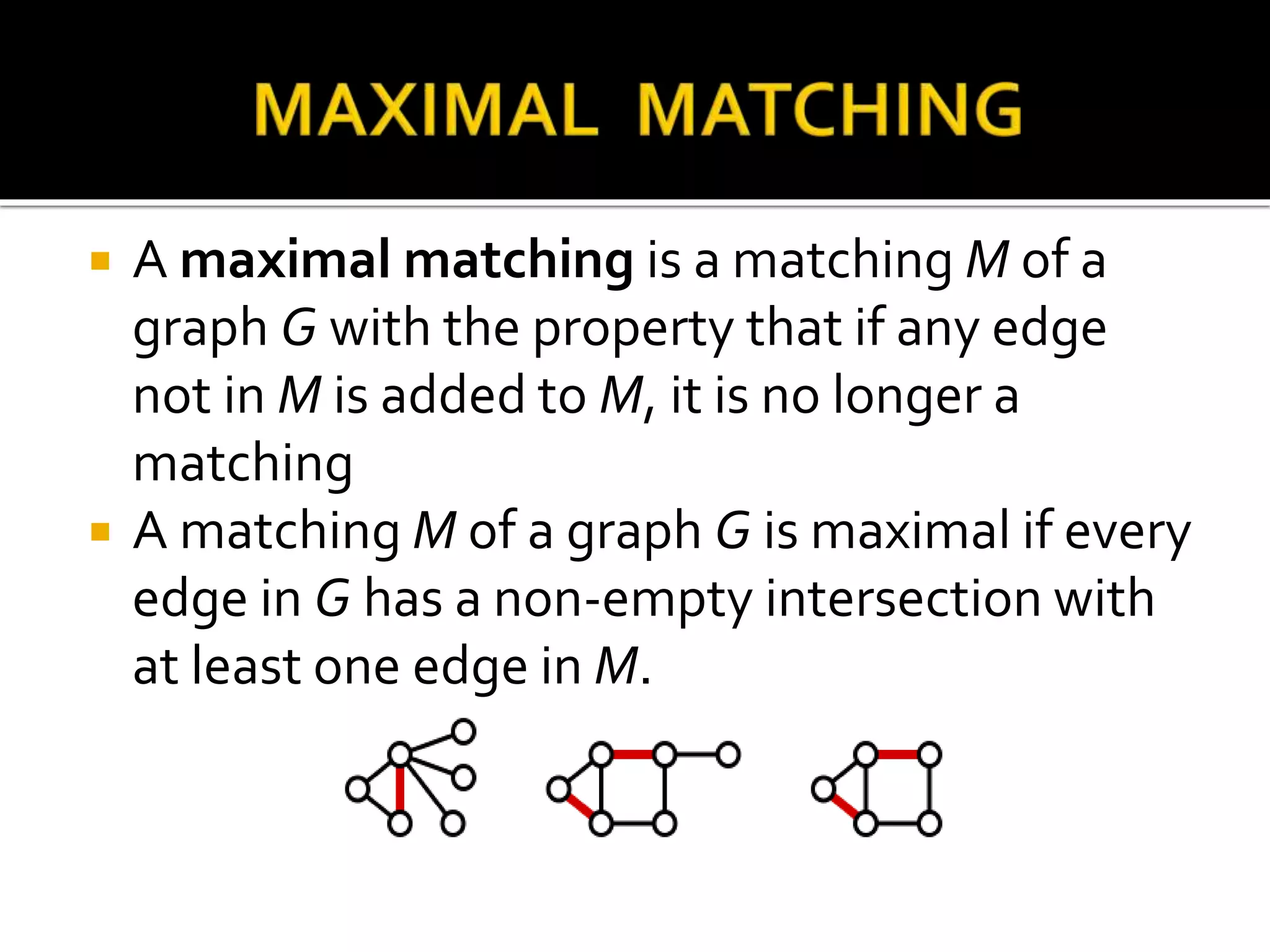
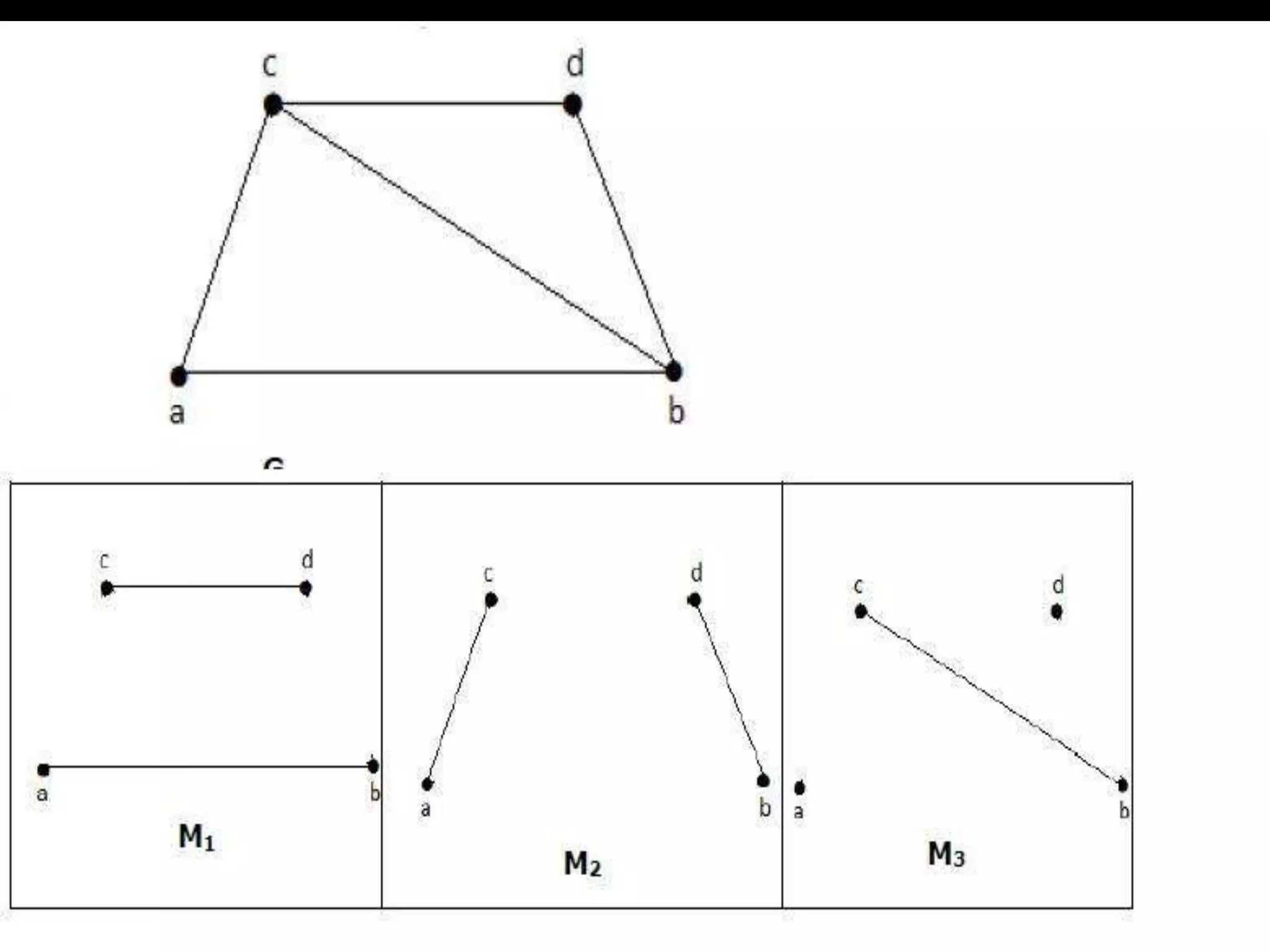
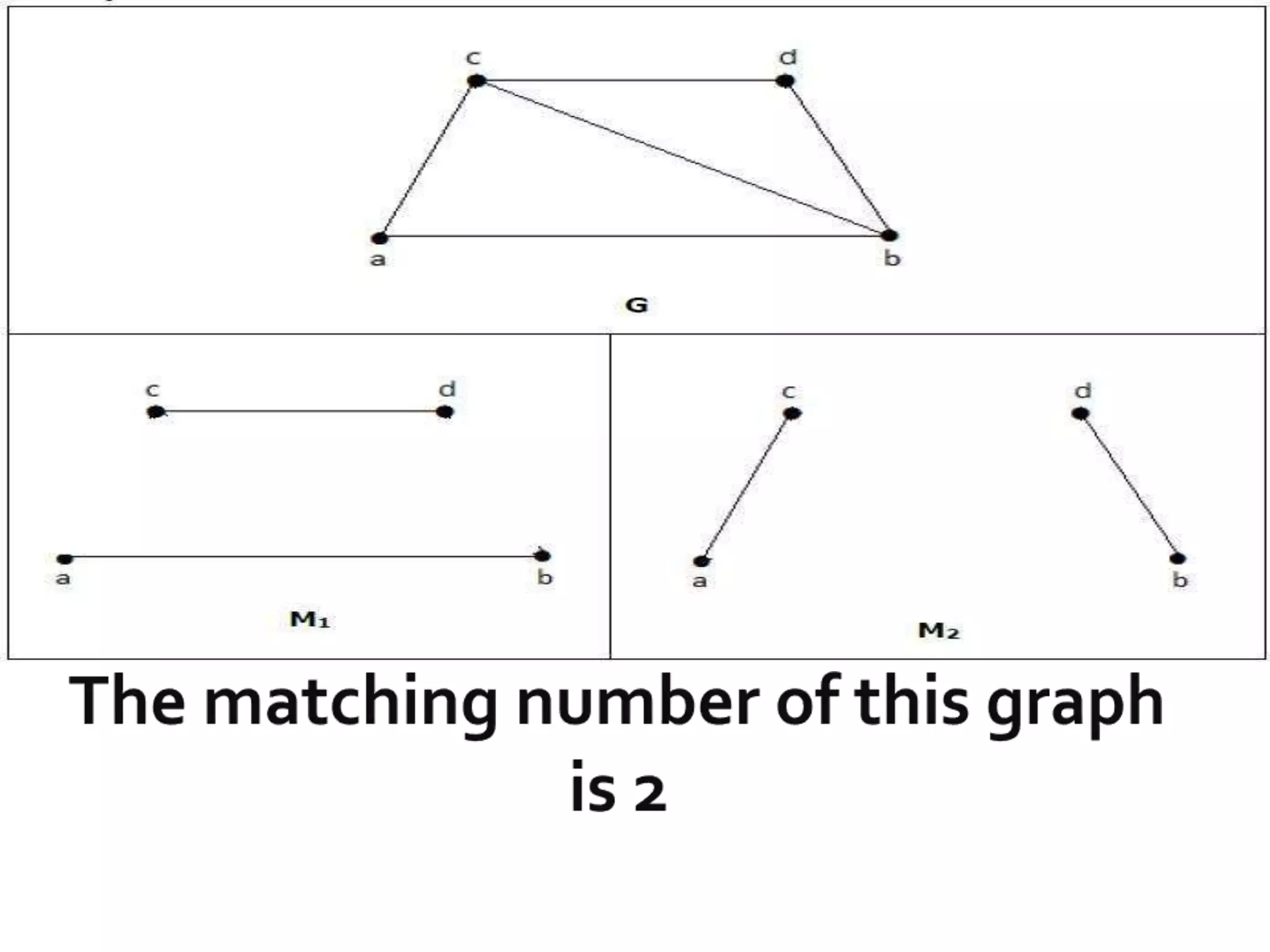
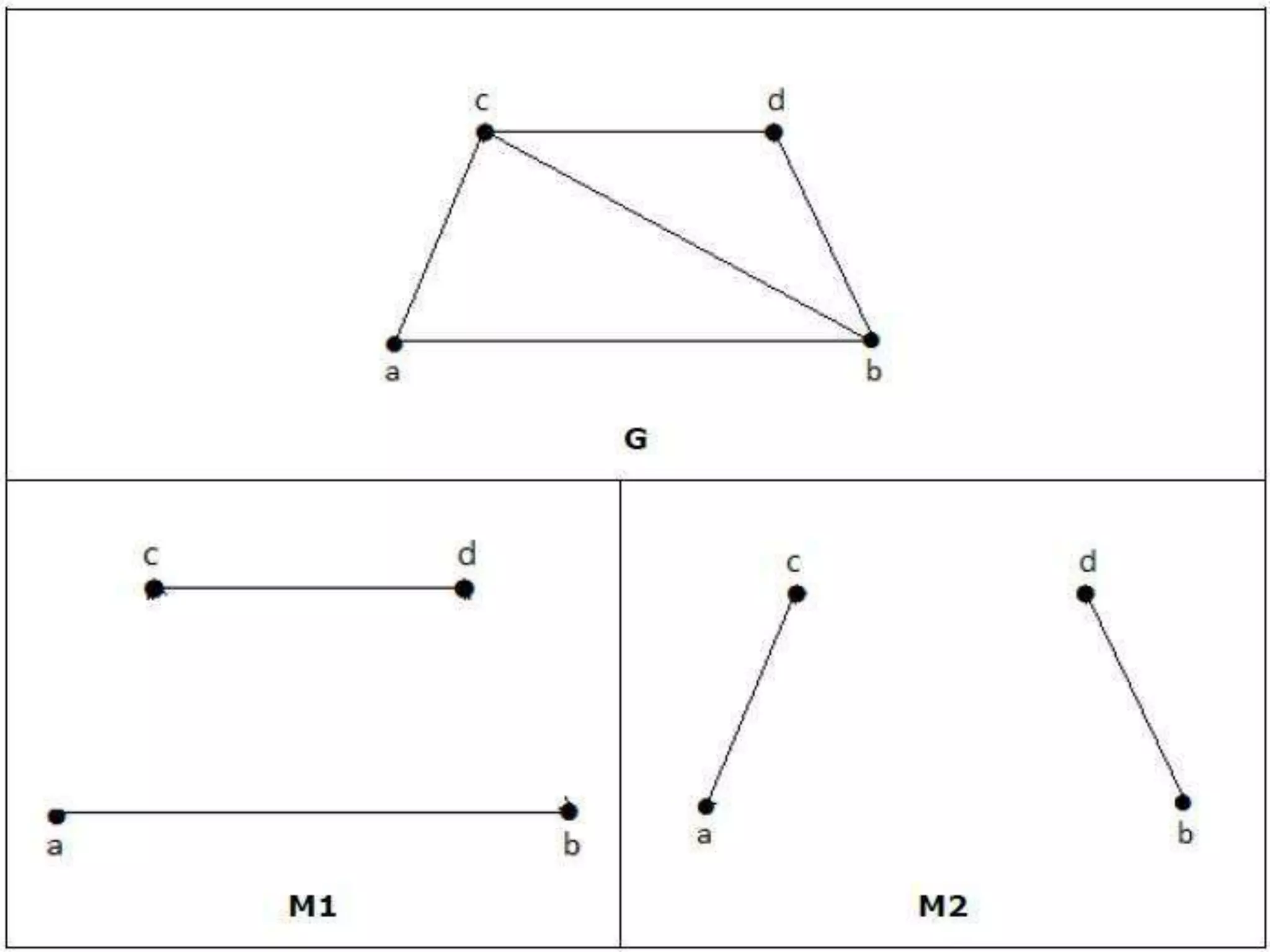
This document discusses different types of matchings in graphs. A matching is a set of edges without common vertices. A maximum matching contains the largest possible number of edges. A maximal matching is one where no additional edges can be added without violating the matching property. A perfect matching is where every vertex is incident to exactly one edge, making it both maximum and maximal. The document provides definitions and properties of different matchings in graphs.
More Related Content
More from garishma bhatia
MATCHING GRAPH THEORY
- 1.
- 2. A matchingor independent edge set in a graph is a set of edges without common vertices. A vertex is said to be a matched if it is incident to an edge otherwise unmatched. A matching ‘m’ that contains largest possible number of edges is called maximum matching.
- 3. A maximalmatching is a matching M of a graph G with the property that if any edge not in M is added to M, it is no longer a matching A matching M of a graph G is maximal if every edge in G has a non-empty intersection with at least one edge in M.
- 5. It isalso known as maximum cardinality matching. It is a matching that contains the largest possible number of edges. The number of edges in the maximum matching of ‘G’ is called its matching number.
- 7. A matching(M) of graph (G) is said to be a perfect match, if every vertex of graph g (G) is incident to exactly one edge of the matching (M), i.e., deg(V) = 1 ∀V Every perfect matching of graph is also a maximum matching of graph, because there is no chance of adding one more edge in a perfect matching graph.
- 9.
Editor's Notes
- #2 Am