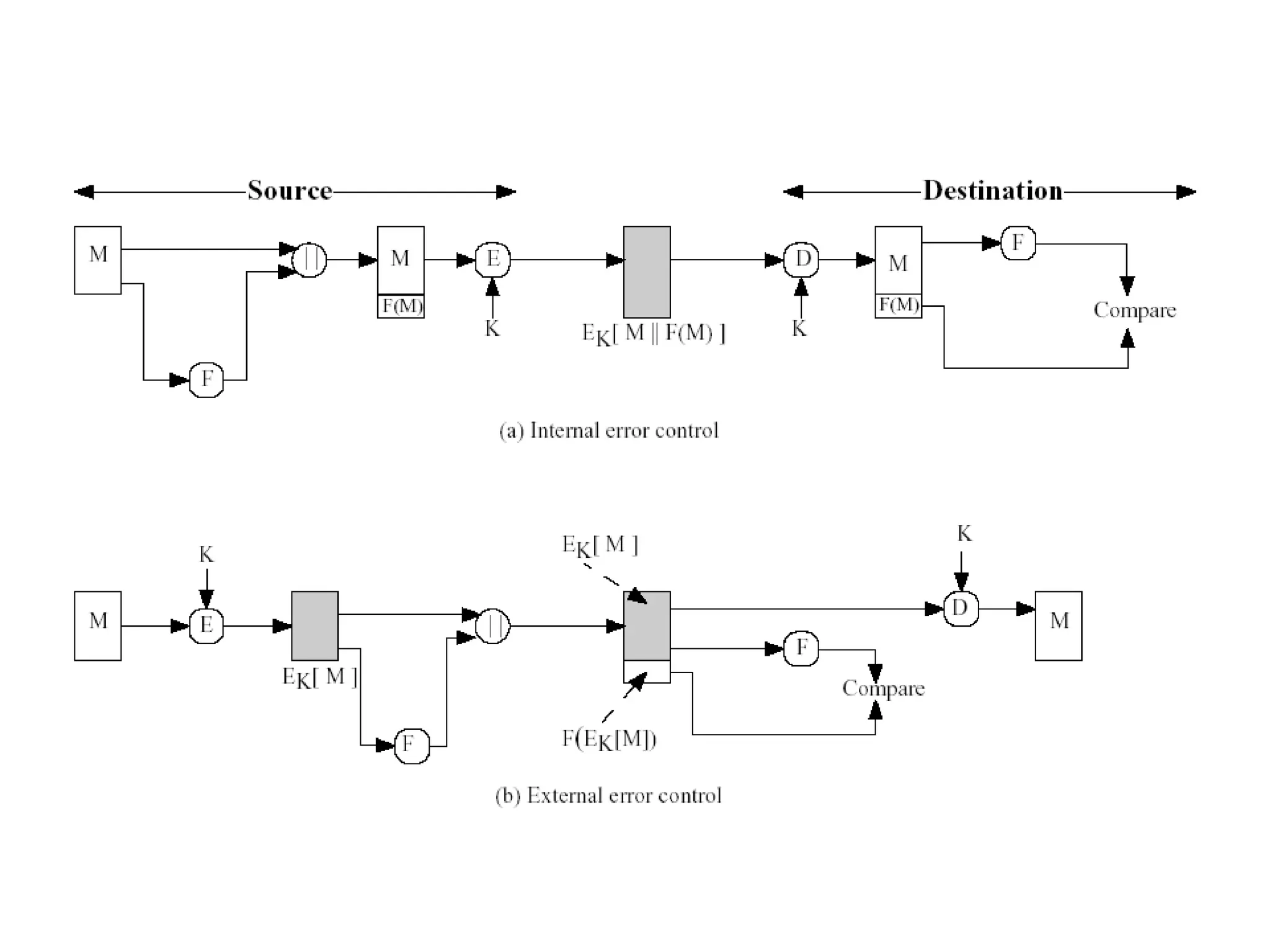
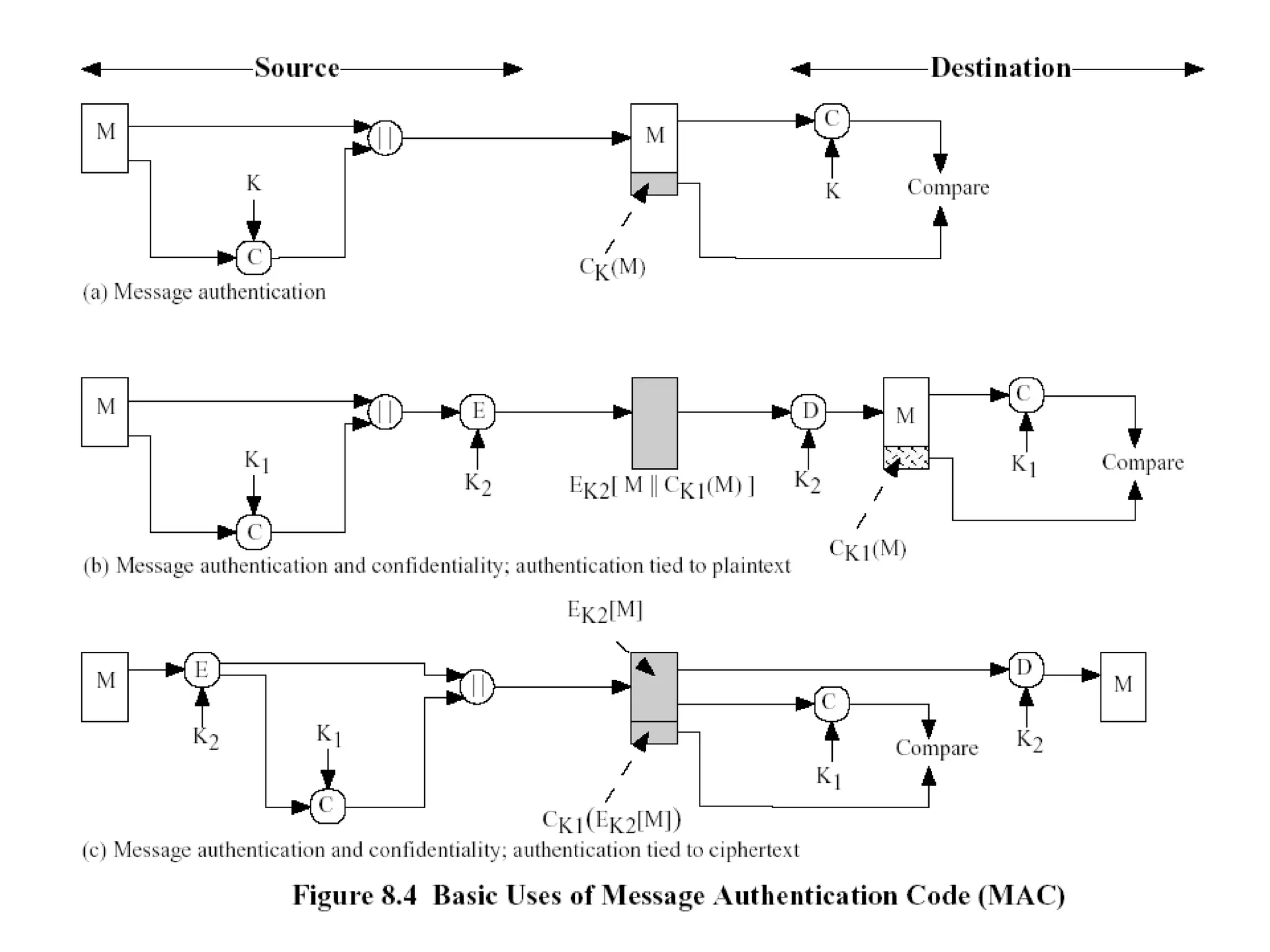
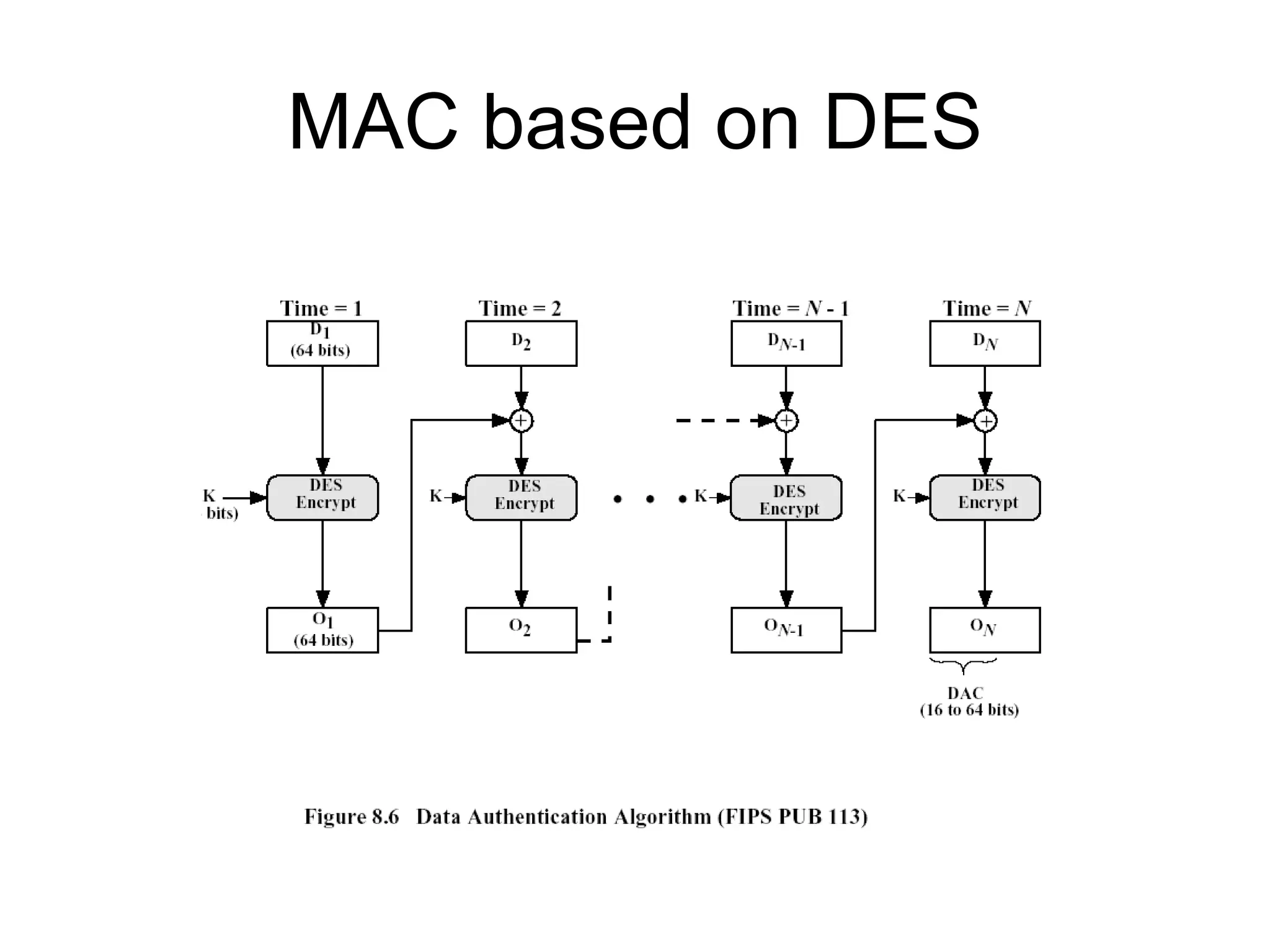
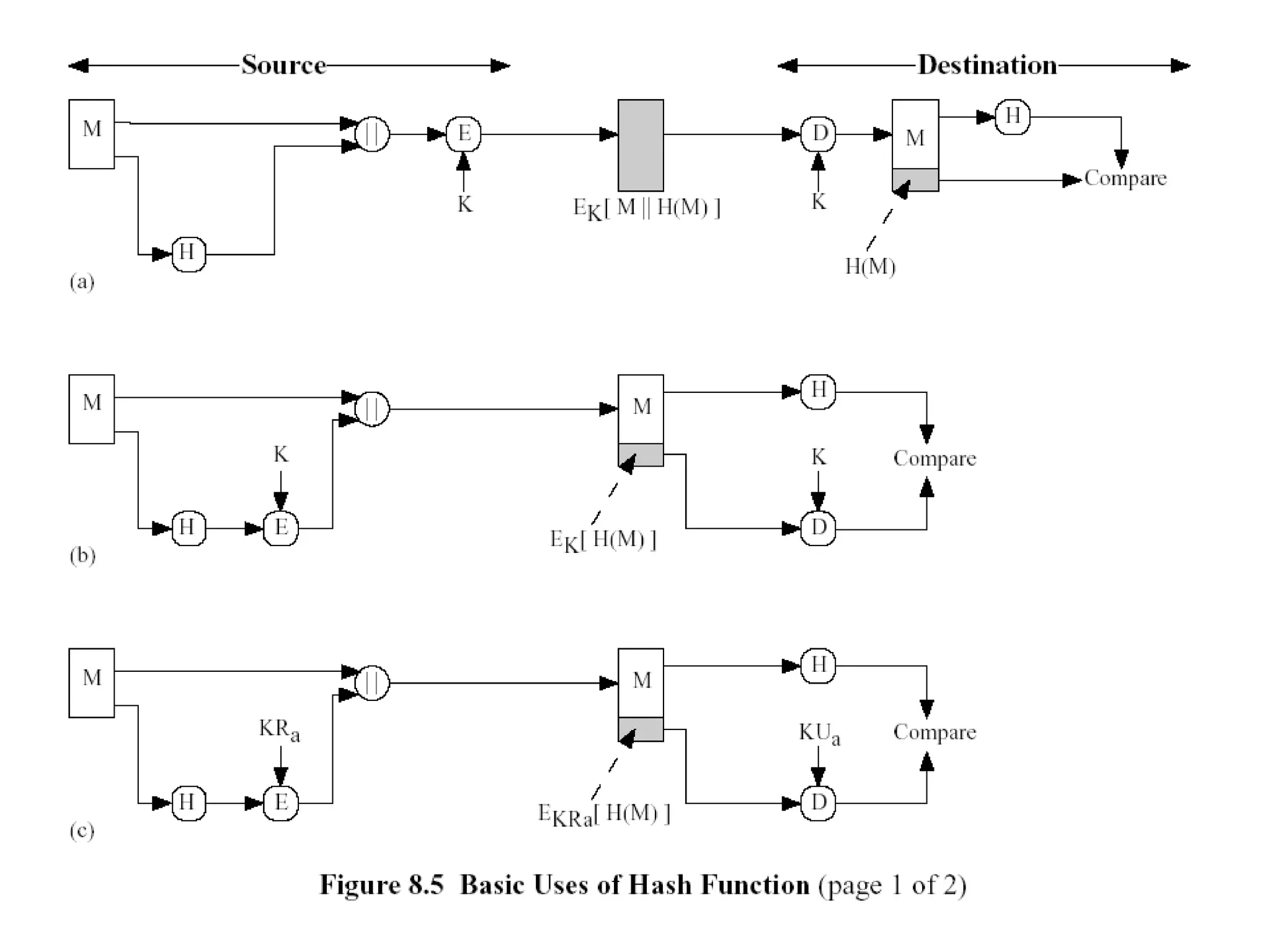
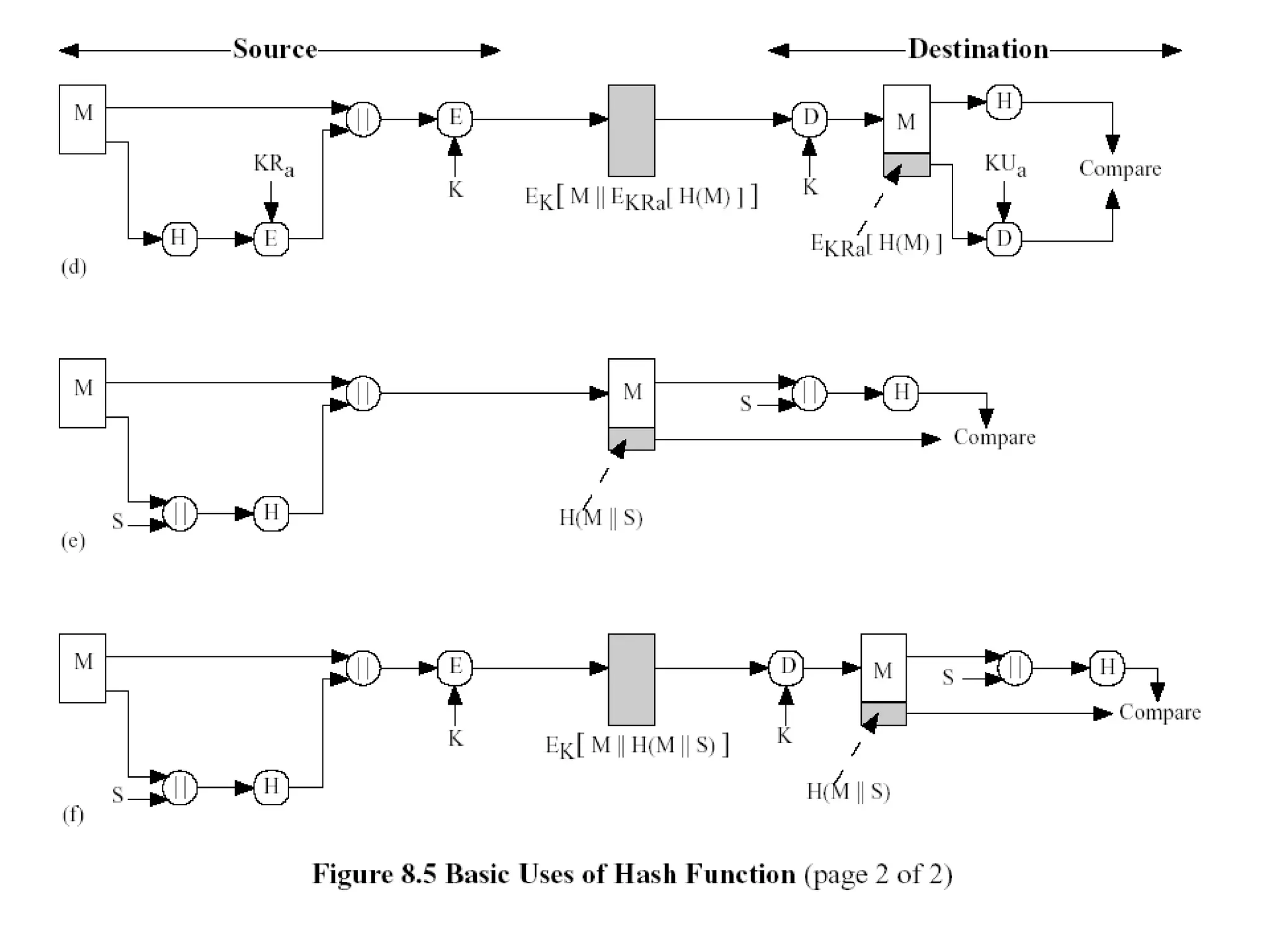
Message Authentication

Message authentication Procedure to verify that Recvd message is from alleged source Message has not been altered There is no change in message sequence message is not delayed or a replay Includes mechanism for non-repudiation by source

Authentication functions Lower level function Authenticator or value Higher level function Use authenticator to verify authenticity of message Functions to produce authenticator Message encryption cirhertext Message authentication code ( MAC) F(K,M) -> fixed length value Hash Function Mapping of message -> fixed length value

Message Authentication codes ( MAC) MAC also known as cryptographic checksum MAC = C k (M) M : variable length message K : Shared key between sender and receiver C k (M) : Fixed length authenticator MAC is appended to the message at src Receiver verifies by re-computing MAC

MAC attacks In encryption security depends on length of key brute force attack requires 2 k-1 combinations of k bit key Mac is many to one function Known M1 and MAC1 If k > n ( length of MAC) Brute force attack can result in 2 k-n matches ==  C k-n (M1) = MAC1

MAC attack to find Key Round 1: given M1, MAC1 = C k (M1) Compute MAC i = Ck i (M i ) for all 2 k keys Number of matches ~ 2 k-n Round 2: given M2, MAC2 = C k (M2) Compute MAC i = Ck i (M i ) for all 2 k-n keys Number of matches ~ 2 k-2n And so on……. Brute force over many rounds

Mac attack without finding key Mac algo M = X1||X2||…||Xm --  Xi = 64 bit blocks  M = X1  X2  ….  Xm C k (M) = E k (  M) encryption by DES ECB Attack Replace X1..Xm-1 by Y1..Ym-1 Ym = Y1  Y2  ….  Ym-1  M Attacker inserts new message which will be authenticated correctly by receiver

MAC requirements Knowing M and Ck(M) it should not be possible to make M’-> Ck(M’) = Ck(M) For any random M, M’; Pr[Ck(M) =Ck(M’)] should be 2 -n for n MAC bits If M’ = f(M); Pr[Ck(M) =Ck(M’)] should be 2 -n

HASH functions h = H(M) M = variable length message H(M) is fixed length hash value Hash is appended to M by sender Receiver re-computes hash to verify M

Requirements of Hash function Applied on any length of block of data Output fixed length H(x) easy to compute H(x) should exhibit one way property For given x, infeasible to find y!=x with H(y) = H(x): weak collision resistance Infeasible to find any pair (x,y) such that H(y) = H(x)

What is Birthday attack? Derived from "birthday paradox“ A lthough there are 365 days in a year T he probability is greater than 1/2 that T wo of more people share the same birthday in any randomly chosen group of 23 people.

Birthday Attack A class of attacks against cryptographic functions including both encryption functions and hash functions. The attacks take advantage of a statistical property: Given a cryptographic function having an N-bit output for 2 N/2 randomly chosen inputs the function will produce at least two outputs that are identical With a probability greater than1/2

More on Birthday attacker Birthday attacks enable an attacker to find two inputs for which a cryptographic /hash function produces the same cipher text M uch faster than a brute-force attack can N o birthday attack can enable an a ttacker T o decrypt a given cipher text or find a hash input that results in a given hash result any faster than a brute-force attack can.

MD5 processing steps Step 1: Appending padding bits To ensure each block size is 512 bit Min 1 bit to max 512 bit padding Padding bits : 10000….. (Msg + pad bits + 64 bit for length) = n x 512 Step 2: Append length 64 bit long filed for length of message Step 3: Initialize MD buffer A,B,C,D buffers of 32 bit size each Step 4: Process message in 512-bit blocks 16 words of 32 bit each Step 5: output 128 bit ( also fed back to input)

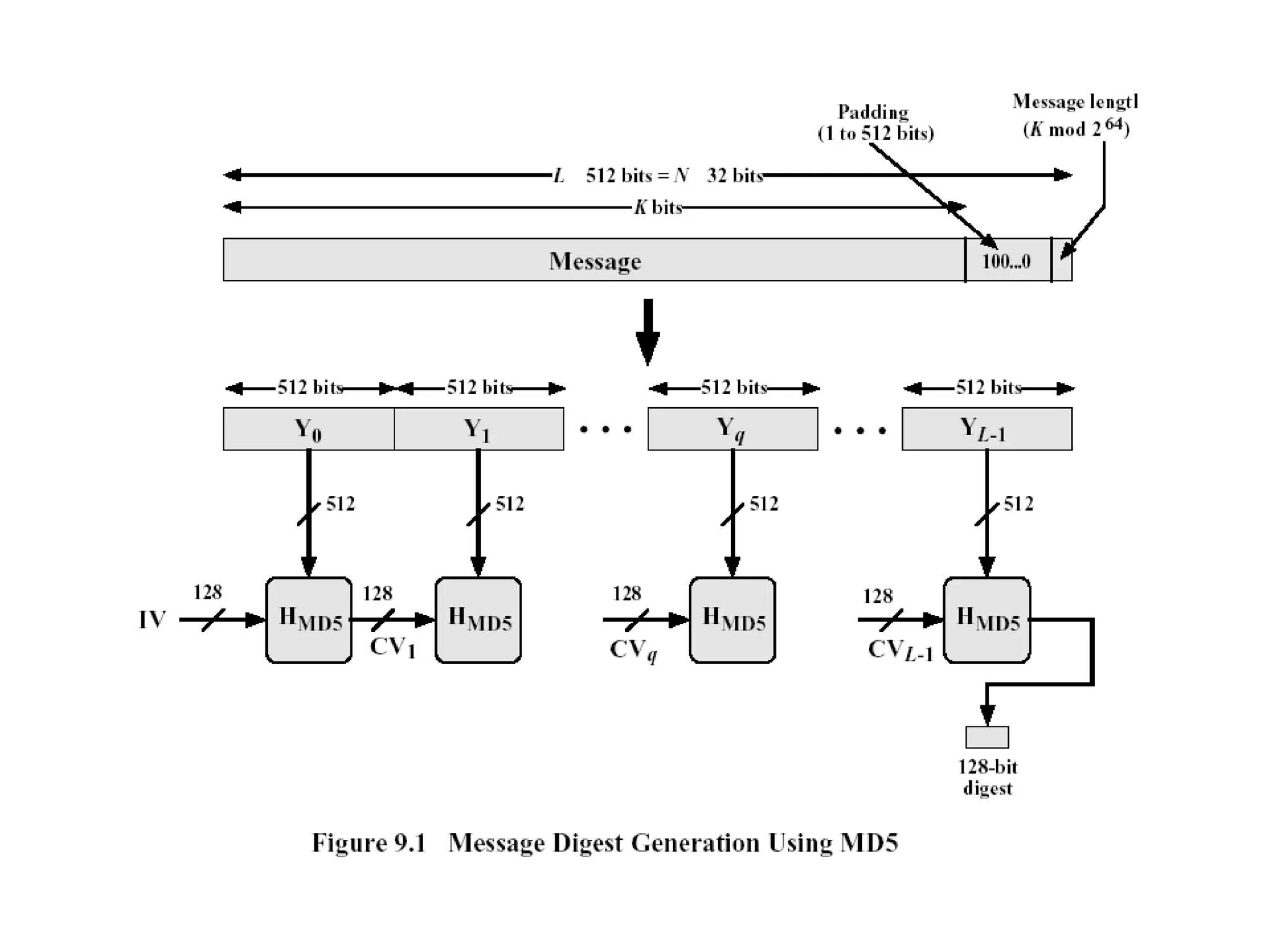
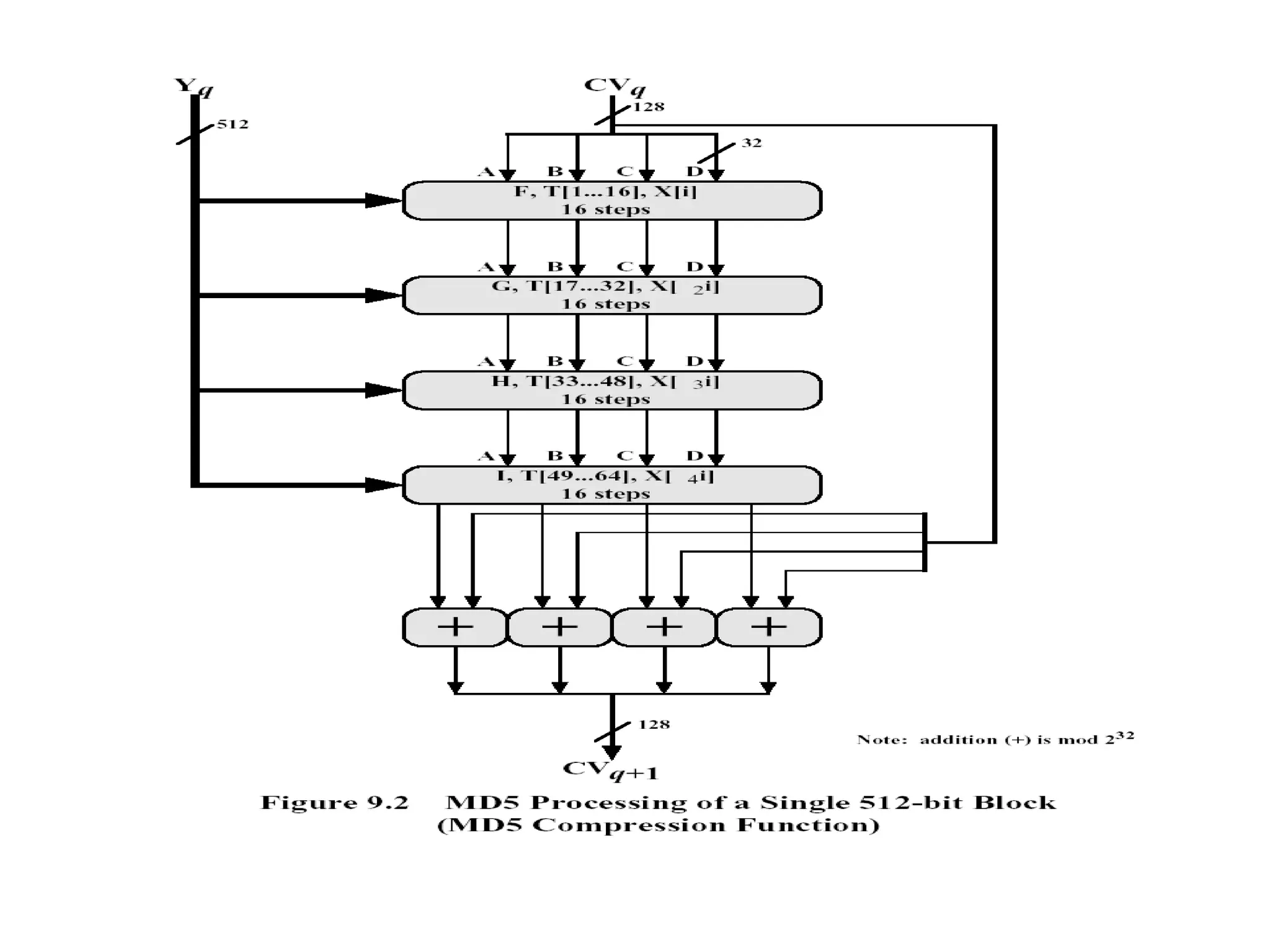
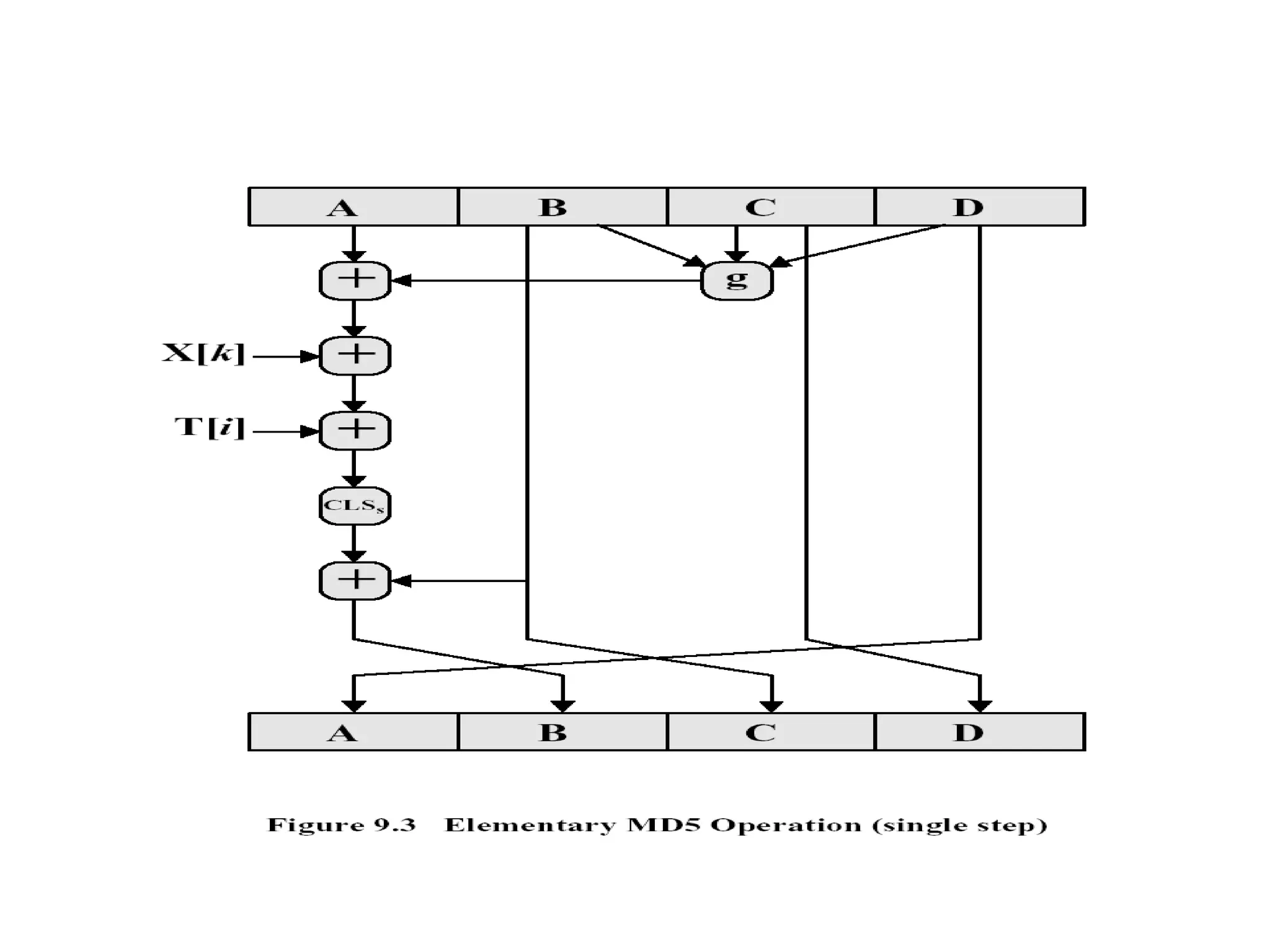
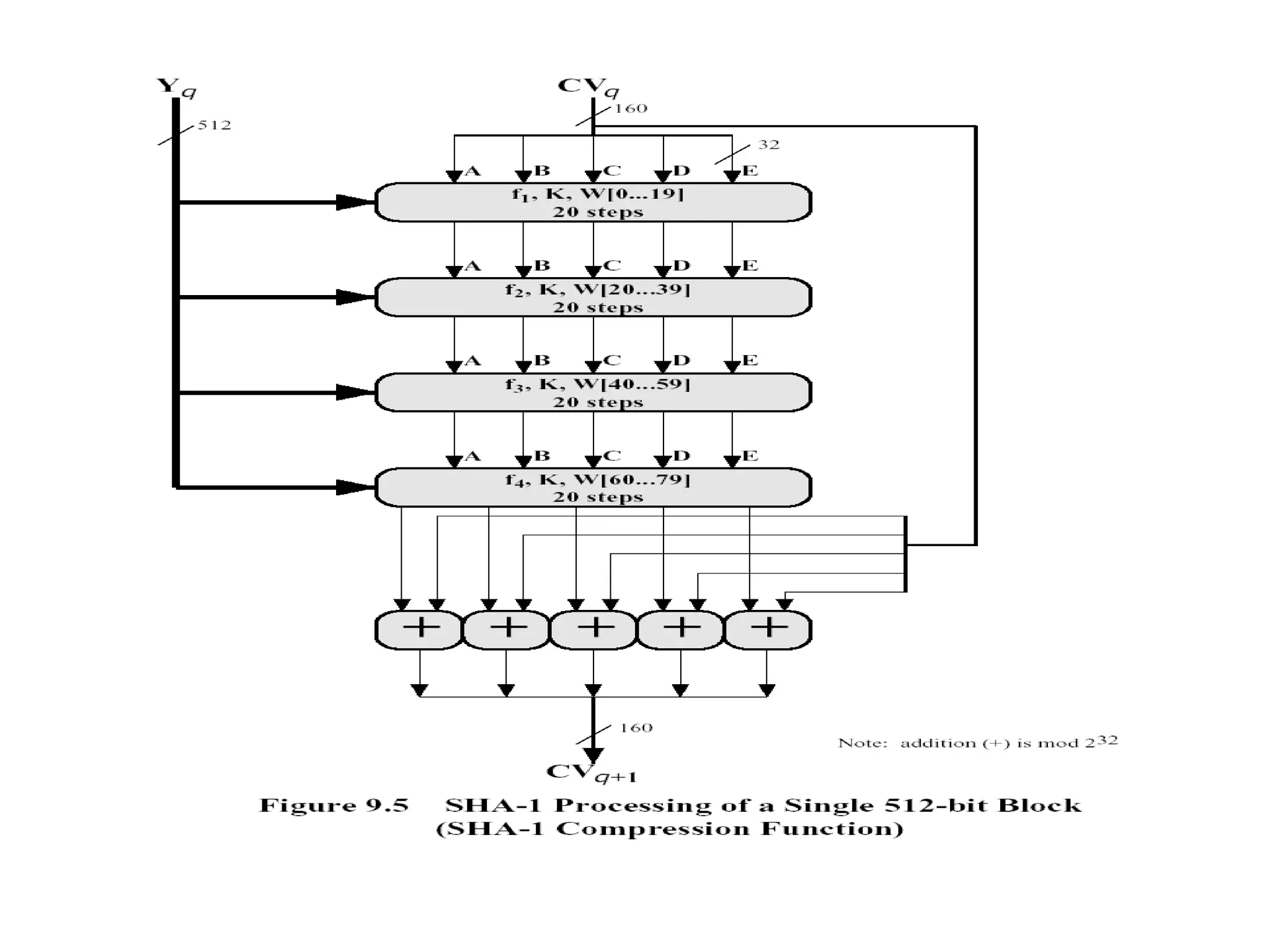
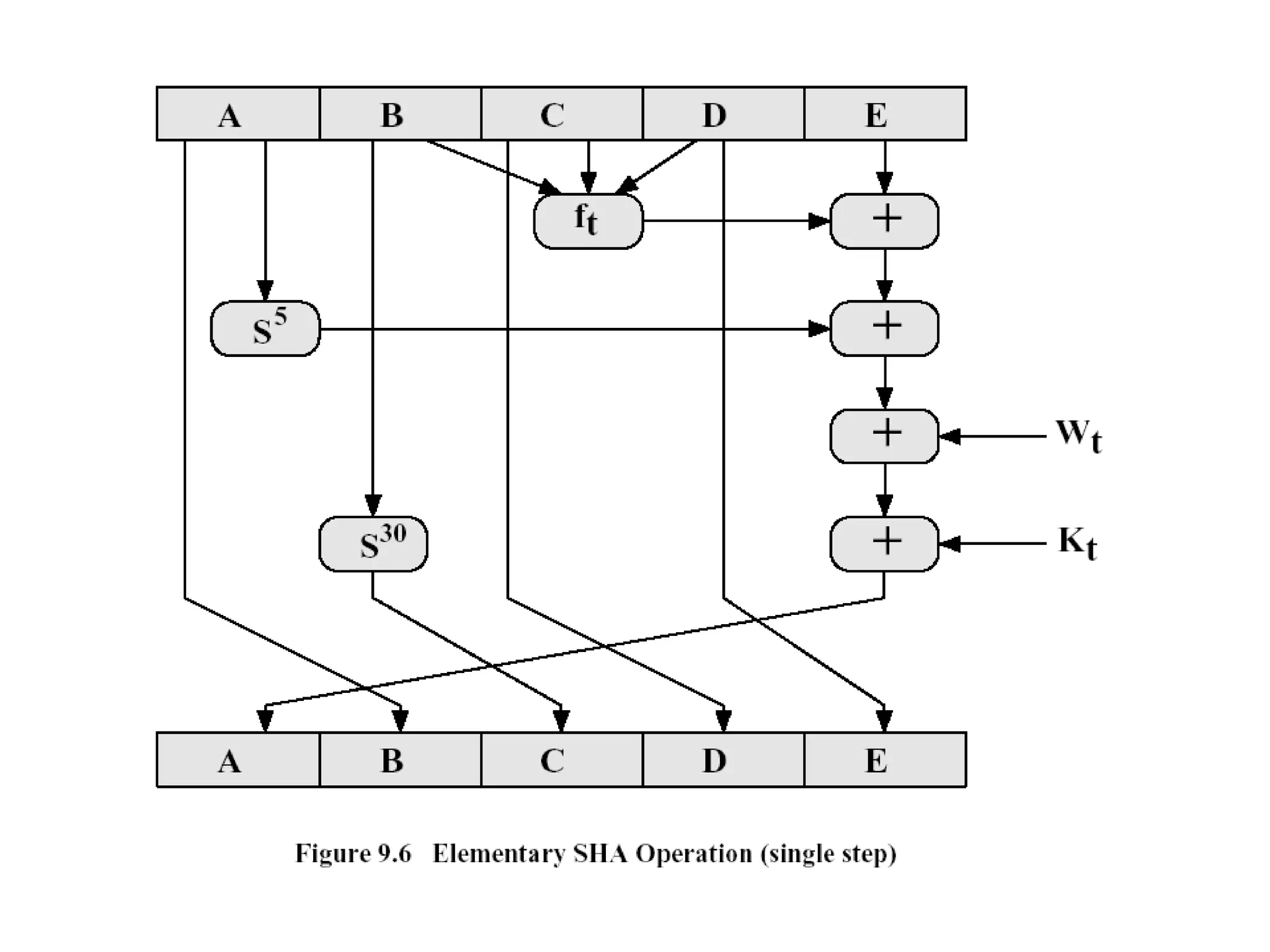
Step 4 Four rounds 16 steps in each round Details of each round Inputs A,B,C,D ( 32 bits each) 512 bit block Message ( 16 x 32) T[ i ] 32 bit array of cont from sin value Processing F,G,H &I functions in each round Output A,B,C,D

SHA-1 processing steps Step 1: Appending padding bits To ensure each block size is 512 bit Min 1 bit to max 512 bit padding Padding bits : 10000….. (Msg + pad bits + 64 bit for length) = n x 512 Step 2: Append length 64 bit long filed for length of message Step 3: Initialize MD buffer A,B,C,D,E buffers of 32 bit size each Step 4: Process message in 512-bit blocks 20 words of 32 bit each Step 5: output 128 bit ( also fed back to input)

Message Authentication

More Related Content

What's hot

Similar to Message Authentication

More from Ram Dutt Shukla

Recently uploaded

Message Authentication