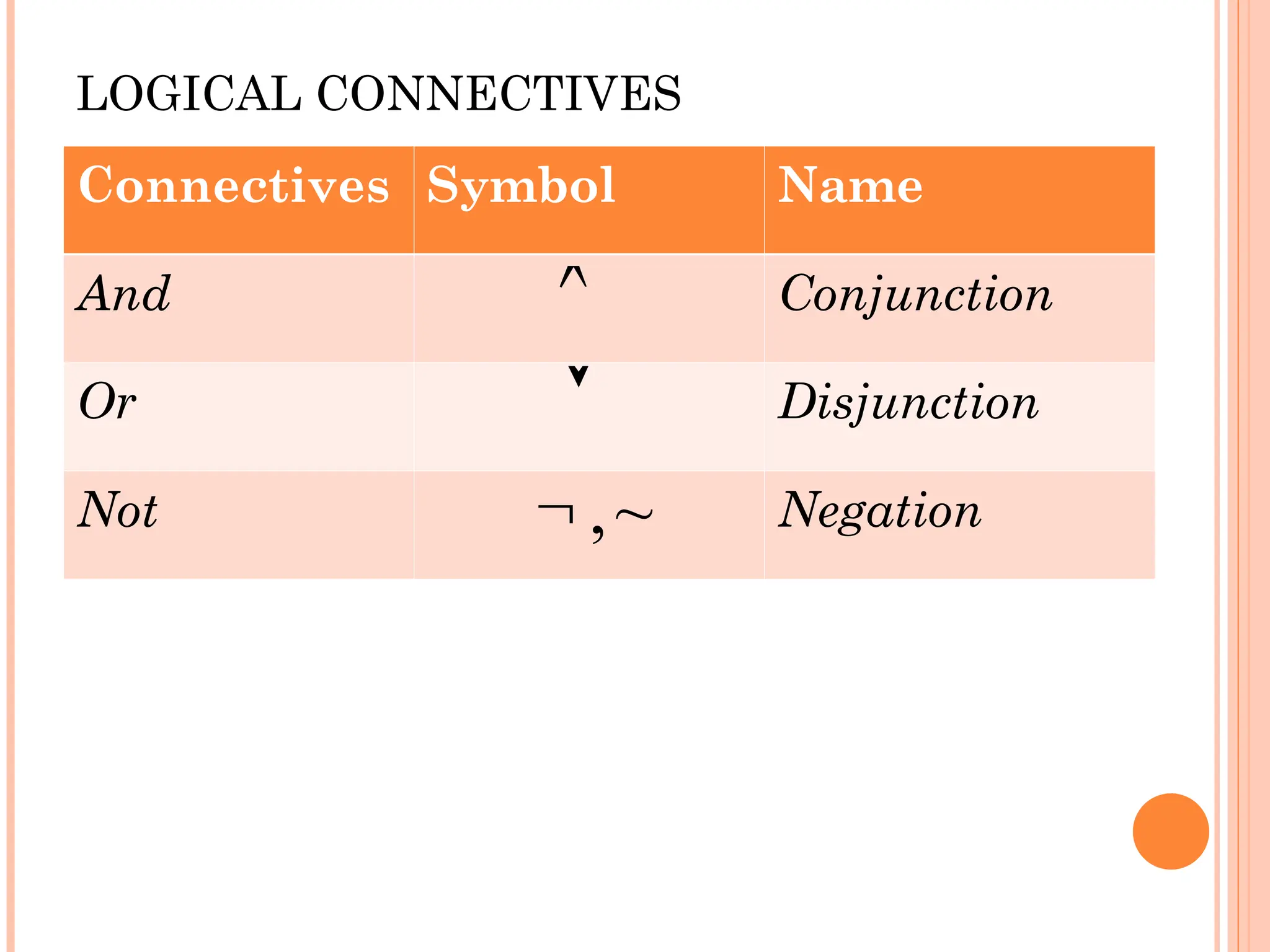
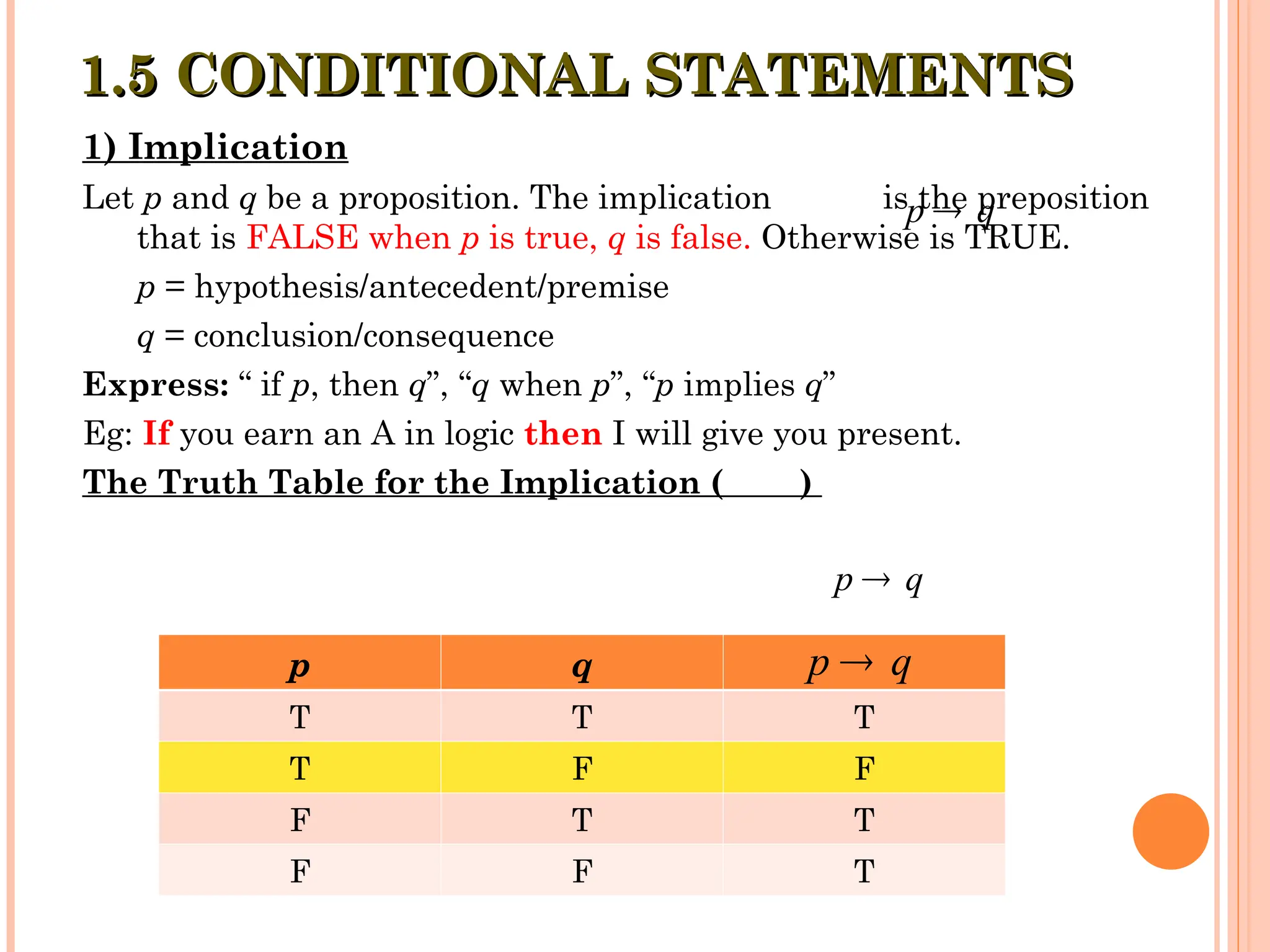
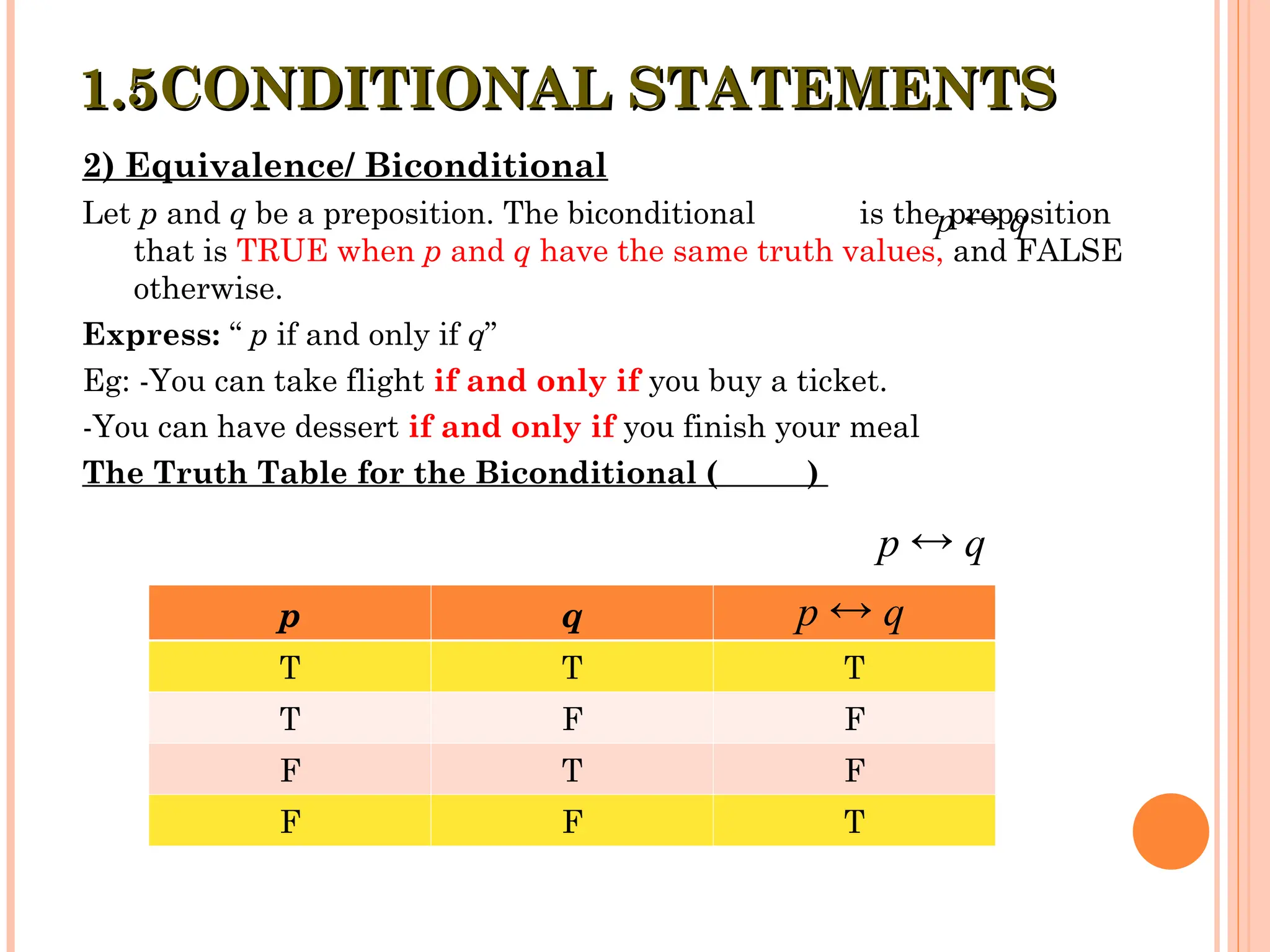
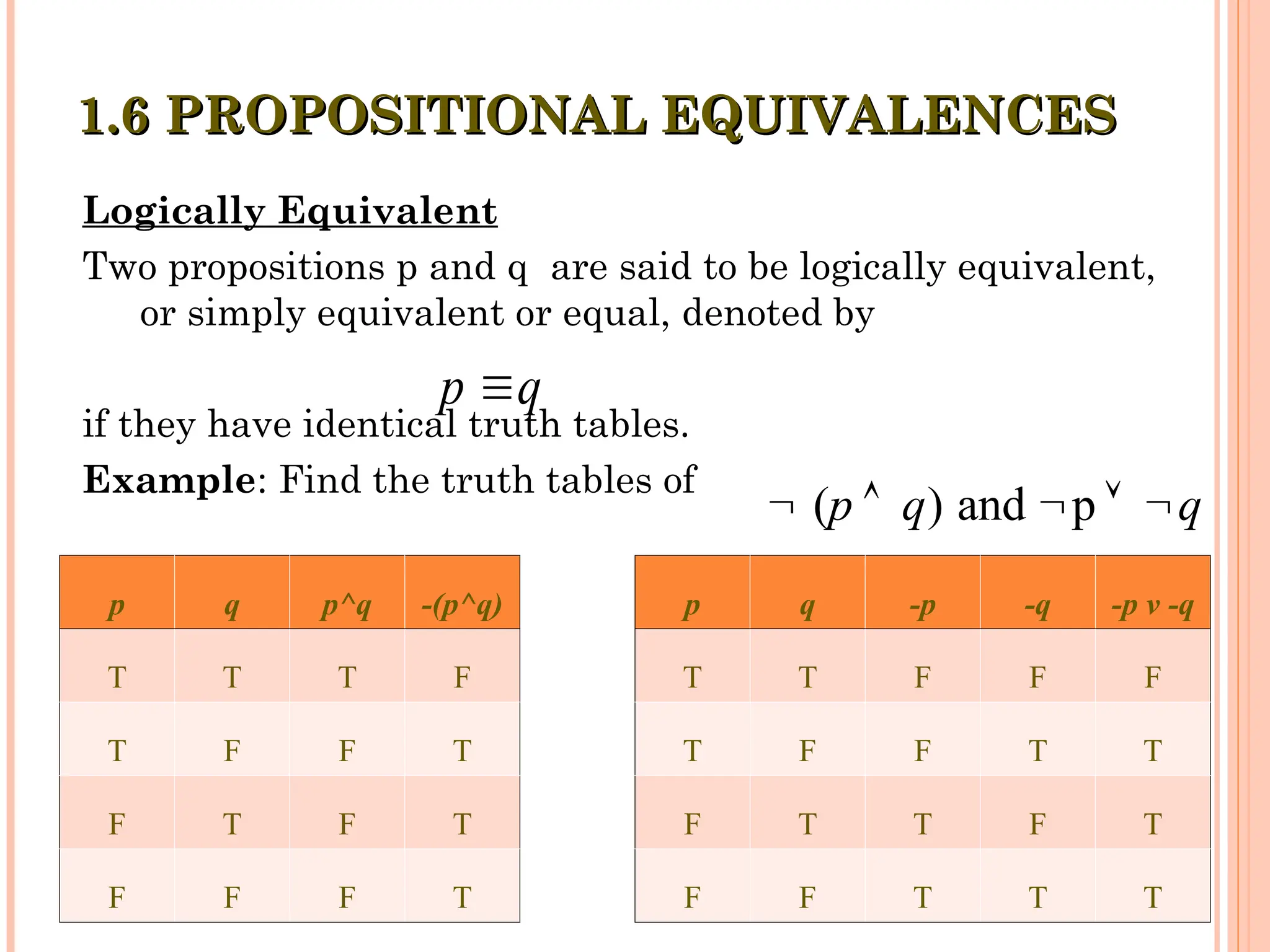
The document covers propositional logic, introducing key concepts such as propositions, compound statements, and logical connectives. It discusses the construction and evaluation of propositions through truth tables, conditional statements, and equivalences. Practical examples illustrate how to apply logical notation and identify the truth values of various statements.