Download as PDF, PPTX
Uploaded byFellowBuddy.com
Ratio and Proportion, Indices and Logarithm Part 1
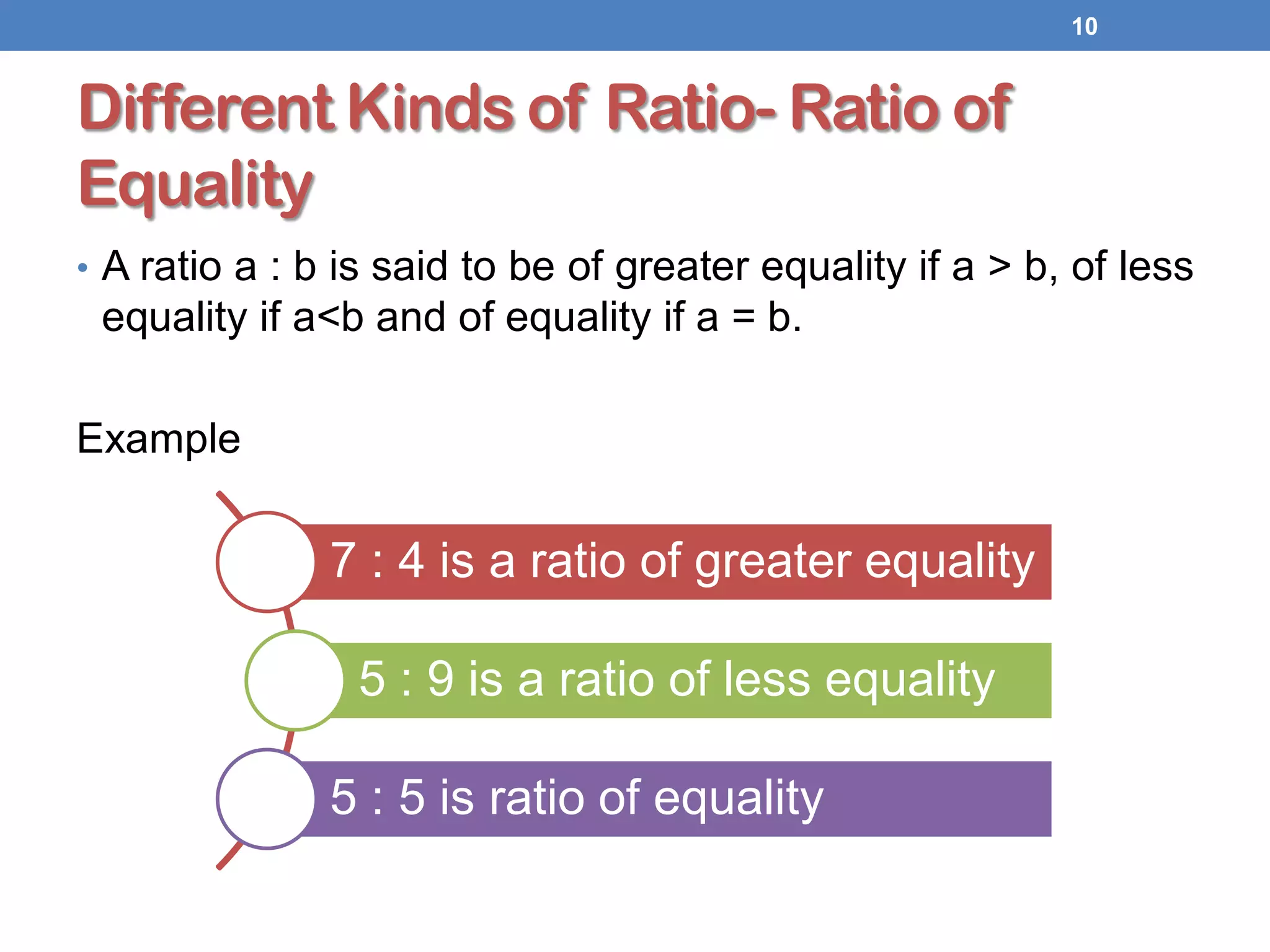
The document covers the topic of ratios and proportions, outlining their definitions, properties, and various types such as compound, duplicate, and triplicate ratios. It provides examples and methods for computing ratios, including solving practical problems related to weight and currency. Key points emphasize that ratios compare quantities of the same kind and the importance of maintaining the correct order of terms.
More Related Content
Similar to Ratio and Proportion, Indices and Logarithm Part 1
Ratio and Proportion, Indices and Logarithm Part 1
- 1. Ratio and Proportion, Indicesand Logarithm Paper 4: Quantitative Aptitude Chapter 1 Part I: Ratio & Proportion Ms. Ritu Gupta, MA (Maths.)
- 2.
- 3. Learning Objectives How to compute and compare tworatios Effect of increase or decrease of a quantity on the ratio The concept and application of different kinds of ratio 3
- 4. Ratio A ratio isa comparison of the sizes of two or more quantities of the same kind (in same units) by methods of division. If a and b are two quantities of the same kind then the fraction a/b is called the ratio of a to b. It is written as a : b or a/b The quantities a and b are called the terms of the ratio, a is called the first term or antecedent and b is called the second term or consequent. 4
- 5. Points to Remember 1 •Both terms of a ratio can be multiplied or divided by the same (non – zero) number. Usually a ratio is expressed in the lowest form or the simplest form. Example:- 10 : 15 = 10/15 = (5×2)/ (5×3) = 2/3 = 2:3 2 • Ratio exists only between quantities of the same kind. For Example: There is no ratio between the height of a child and the salary of a teacher. 3 • The order of the terms in a ratio is important. For example - 4:5 ≠ 5:4 4 • If a quantity increases or decreases in the ratio a : b, then new quantity = b of the original quantity / a 5
- 6. Points to Remember- 2 Raju’s weight is 48.8 kg. If he reduces his weight in the ratio of 8:7, find his new weight. Solution: Original weight of Raju = 48.8 kg He reduces his weight in the ratio 8:7 His new weight = (7 × 48.8) / 8 = 42.7 kg 6 5 • The fraction by which the original quantity is multiplied to get a new quantity is called the factor multiplying ratio.
- 7. Points to Remember- 3 Example Ratio between 1 hour and 20 minutes = Ratio between (1x60) min. and 20 min. = 60 / 20 = 3/1 = 3:1 7 6 • Quantities to be compared (by division) must be in the same units.
- 8. Points to Remember- 4 8 7 • To compare two ratios, convert them into equivalent like fractions.
- 9. Different Kinds ofRatio- Inverse Ratio 9
- 10. Different Kinds ofRatio- Ratio of Equality • A ratio a : b is said to be of greater equality if a > b, of less equality if a<b and of equality if a = b. Example 10 7 : 4 is a ratio of greater equality 5 : 9 is a ratio of less equality 5 : 5 is ratio of equality
- 11. Different Kinds ofRatio- Compounded Ratio 11
- 12. Different Kinds ofRatio- Duplicate Ratio • A ratio compounded to itself is called its duplicate ratio. Thus a² : b² is the duplicate ratio of a : b. Example Duplicate ratio of 5 : 7 is 52 : 72 = 25 : 49 12
- 13. Different Kinds ofRatio- Triplicate Ratio • The compounded ratio of a ratio with its duplicate ratio is called its triplicate ratio. Thus a³ : b³ is the triplicate ratio of a : b Example Triplicate ratio of 2 : 3 is 23 : 33 = 8 : 27 13
- 14. Different Kinds ofRatio- Sub – Duplicate Ratio 14
- 15. Different Kinds ofRatio- Sub – Triplicate ratio 15
- 16. Different Kinds ofRatio - Continued Ratio • Continued Ratio is the relation (comparison) between the magnitudes of three or more quantities of the same kind. The continued ratio of three similar quantities a, b, c is written as a : b : c Example The continued ratio of 200, 400 and 600 is 200 : 400 : 600 = 1 : 2 : 3 16
- 17. Different Kinds ofRatio - Commensurable Ratio • If the ratio of two similar quantities can be expressed as a ratio of two integers then the quantities are called commensurable e.g. 3:4 17
- 18. Different Kinds ofRatio - Incommensurable Ratio 18
- 19.
- 20. Illustration 2 The ratiocompounded of duplicate ratio of 4:5, triplicate ratio of 1:3. sub duplicate ratio of 81:256 and sub triplicate ratio of 125:512 is (a) 4 : 512 (b) 3 : 32 (c) 1 : 120 (d) None of these Solution The duplicate of ratio of 4 : 5 is 42 : 52 = 16 : 25 The triplicate ratio of 1 : 3 is 13 : 33 = 1 : 27 20
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29. Illustration- 8 A bagcontains Rs. 187 in the form of 1 Rupee, 50 paise and 10 paise coins in the ratio of 3 : 4 : 5. Find the number of each type of coins. (a) 102, 136, 170 (b) 136, 102, 170 (c) 170, 102, 136 (d) None of these Solution Let the number of 1 Rupee, 50 paise and 10 paise coins be 3x, 4x and 5x respectively. Then, 29
- 30.
- 31.
- 32.
- 33. Illustration - 11 Findin what ratio will the wages of the employees in a workshop be increased or decreased if there is a reduction in the number of employees in the ratio 7 : 4 and an increment in their wages in the ratio 16 : 21. (a) 2 : 7 (b) 4 : 3 (c) 4 : 1 (d) 7 : 3 Solution Let the original number of employees be x. Therefore the number of employees after reduction will be 4x/7. Let the (average) wages per worker be y 33
- 34. Illustration – 11-Continued 34
- 35. Illustration – 11-Continued 35
- 36. Illustration - 12 Theratio of the number of boys to the number of girls in a dance school of 360 students is 3 : 5. If 15 new girls are admitted to the dance school, find how many new boys should be admitted so that the ratio of the number of boys to the number of girls becomes 4 : 5. (a) 75 (b) 57 (c) 55 (d) 45 Solution Let the number of boys and number of girls be 3x and 5x Therefore 3x+5x = 360 36
- 37. Illustration – 12-Continued 37
- 38. Illustration – 12-Continued 38
- 39. Thank You Please seenext part for e-Lecture on Proportion