Downloaded 376 times
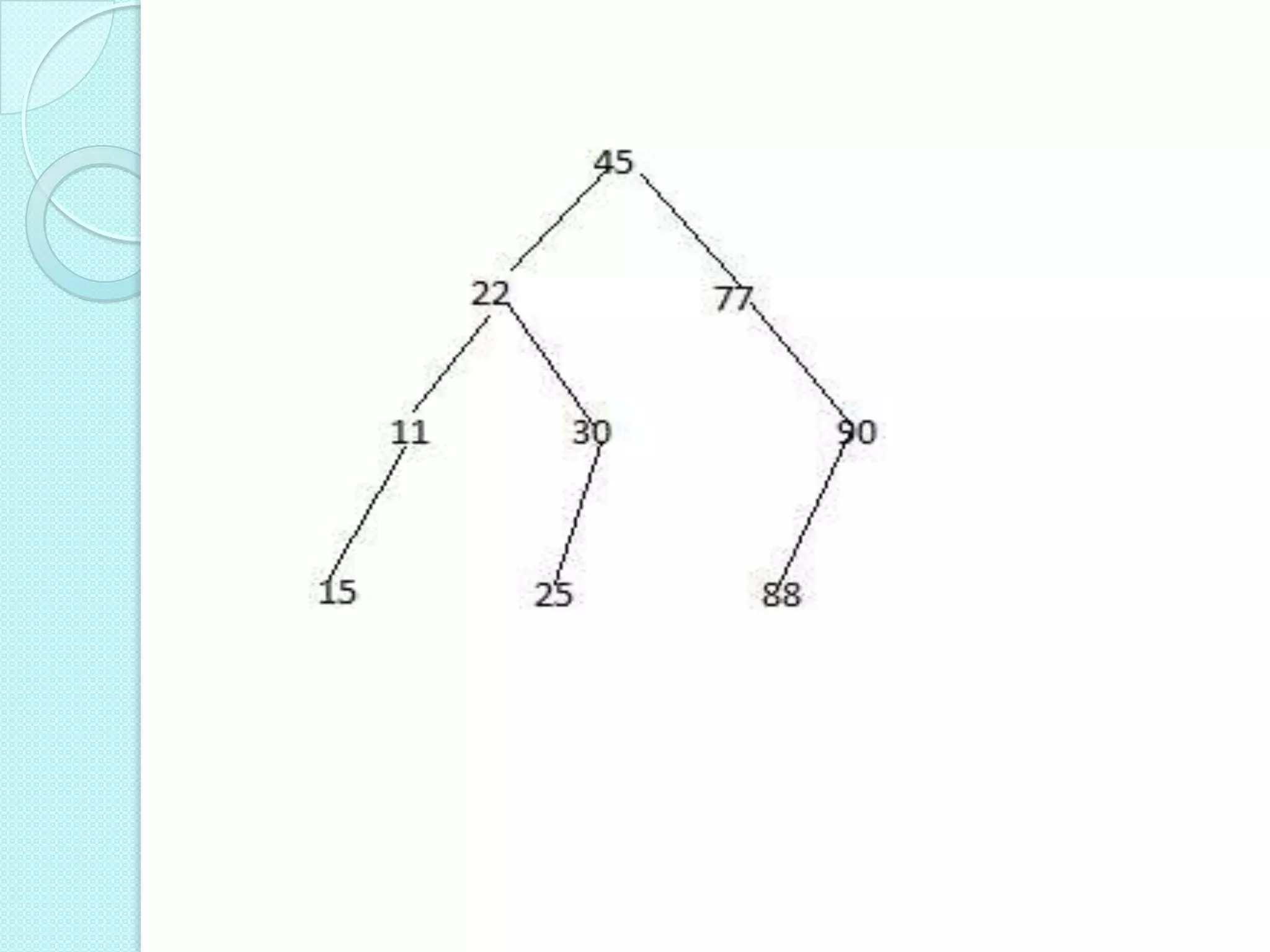
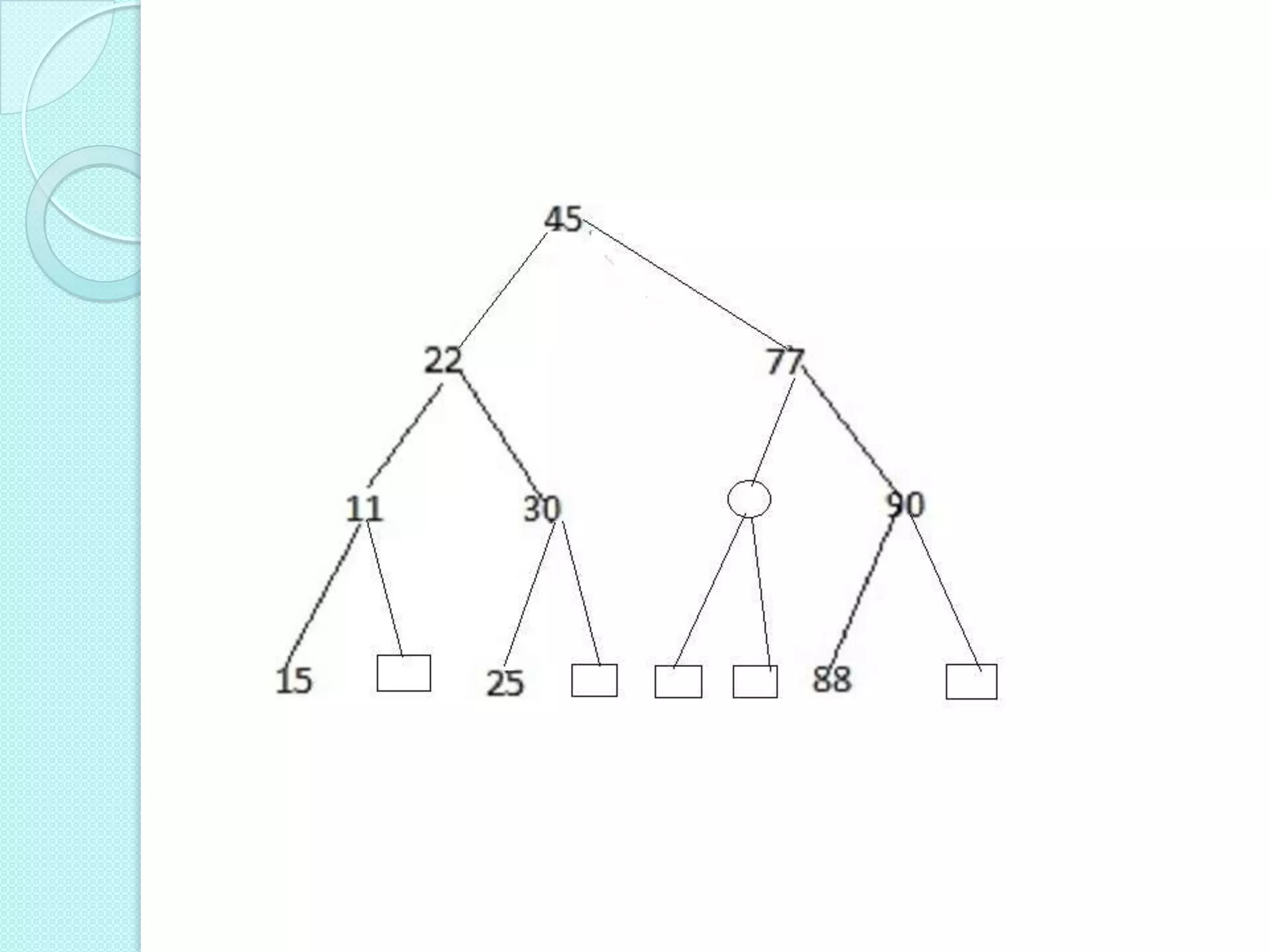
![ The root R is stored in TREE[0].
If a node n occupies TREE[K],
then its left child in TREE[2*K]
& right child TREE [2*K+1].
If TREE[1]=NULL then it is empty
tree.](https://image.slidesharecdn.com/representationofbinarytreeinmemory-130215094958-phpapp01/85/Representation-of-binary-tree-in-memory-3-320.jpg)
![Linked Representation
The linked representation uses three parallel
arrays,INFO,LEFT & RIGHT & a pointer variable
ROOT.Each node N of Y will correspond to a location K
such that:
1) INFO[K] contains the data at node N.
2) LEFT[K] contains the location of left child of node N.
3) RIGHT[K] contains the location of right child of node
N.
ROOT will contain location of root R of T.](https://image.slidesharecdn.com/representationofbinarytreeinmemory-130215094958-phpapp01/85/Representation-of-binary-tree-in-memory-7-320.jpg)
![ The root R is stored in TREE[0].
If a node n occupies TREE[K],
then its left child in TREE[2*K]
& right child TREE [2*K+1].
If TREE[1]=NULL then it is empty
tree.](https://image.slidesharecdn.com/representationofbinarytreeinmemory-130215094958-phpapp01/75/Representation-of-binary-tree-in-memory-3-2048.jpg)
![Linked Representation
The linked representation uses three parallel
arrays,INFO,LEFT & RIGHT & a pointer variable
ROOT.Each node N of Y will correspond to a location K
such that:
1) INFO[K] contains the data at node N.
2) LEFT[K] contains the location of left child of node N.
3) RIGHT[K] contains the location of right child of node
N.
ROOT will contain location of root R of T.](https://image.slidesharecdn.com/representationofbinarytreeinmemory-130215094958-phpapp01/75/Representation-of-binary-tree-in-memory-7-2048.jpg)
Uploaded byRohini Shinde
Representation of binary tree in memory
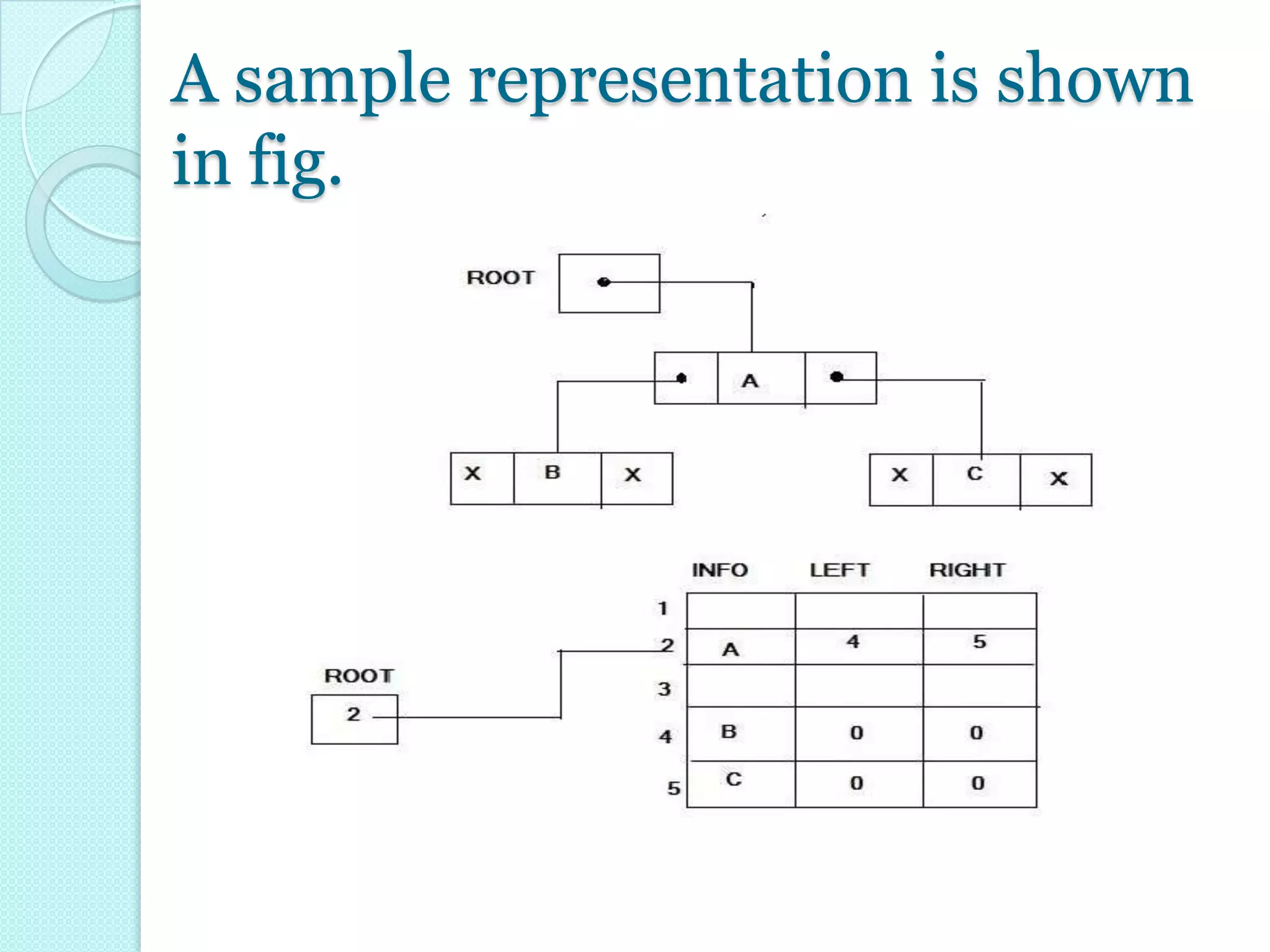
There are two ways to represent a binary tree in memory: sequential representation which uses a single linear array to store the tree, and linked representation which uses three parallel arrays (INFO, LEFT, and RIGHT) along with a ROOT pointer to link nodes. The sequential representation stores the root at index 0 of the array and children at calculated indices, while the linked representation stores the data, left child index, and right child index of each node in the parallel arrays.
More Related Content
Representation of binary tree in memory
- 1. Representation of Binarytree in memory Let T be a binary. There are two ways for representing binary tree in memory. Sequential Representation Linked Representation
- 2. Sequential Representation Suppose T is a complete binary tree. Then only single linear array TREE is used as follows.
- 3. The root R is stored in TREE[0]. If a node n occupies TREE[K], then its left child in TREE[2*K] & right child TREE [2*K+1]. If TREE[1]=NULL then it is empty tree.
- 7. Linked Representation The linked representation uses three parallel arrays,INFO,LEFT & RIGHT & a pointer variable ROOT.Each node N of Y will correspond to a location K such that: 1) INFO[K] contains the data at node N. 2) LEFT[K] contains the location of left child of node N. 3) RIGHT[K] contains the location of right child of node N. ROOT will contain location of root R of T.
- 8. A sample representationis shown in fig.