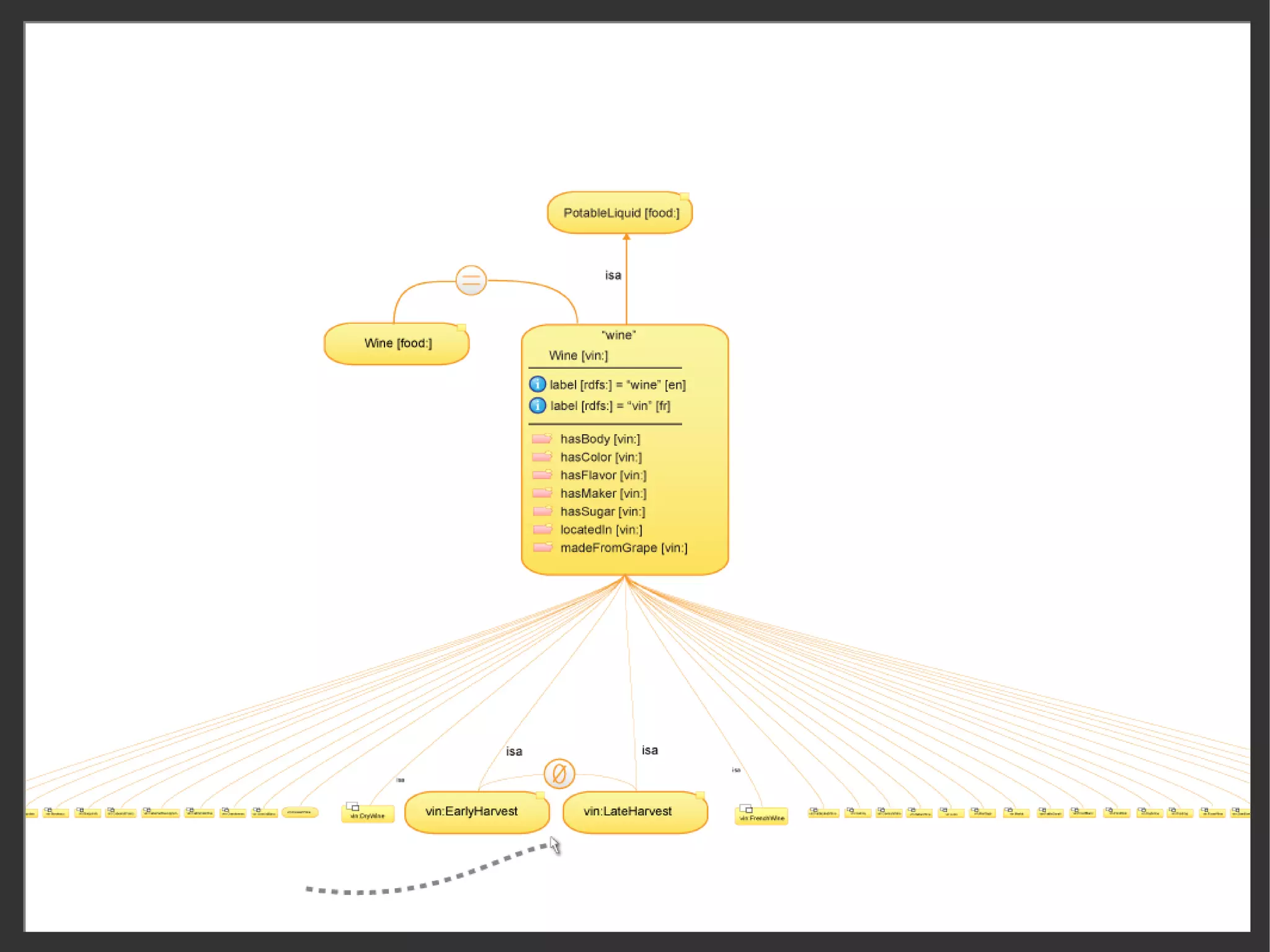
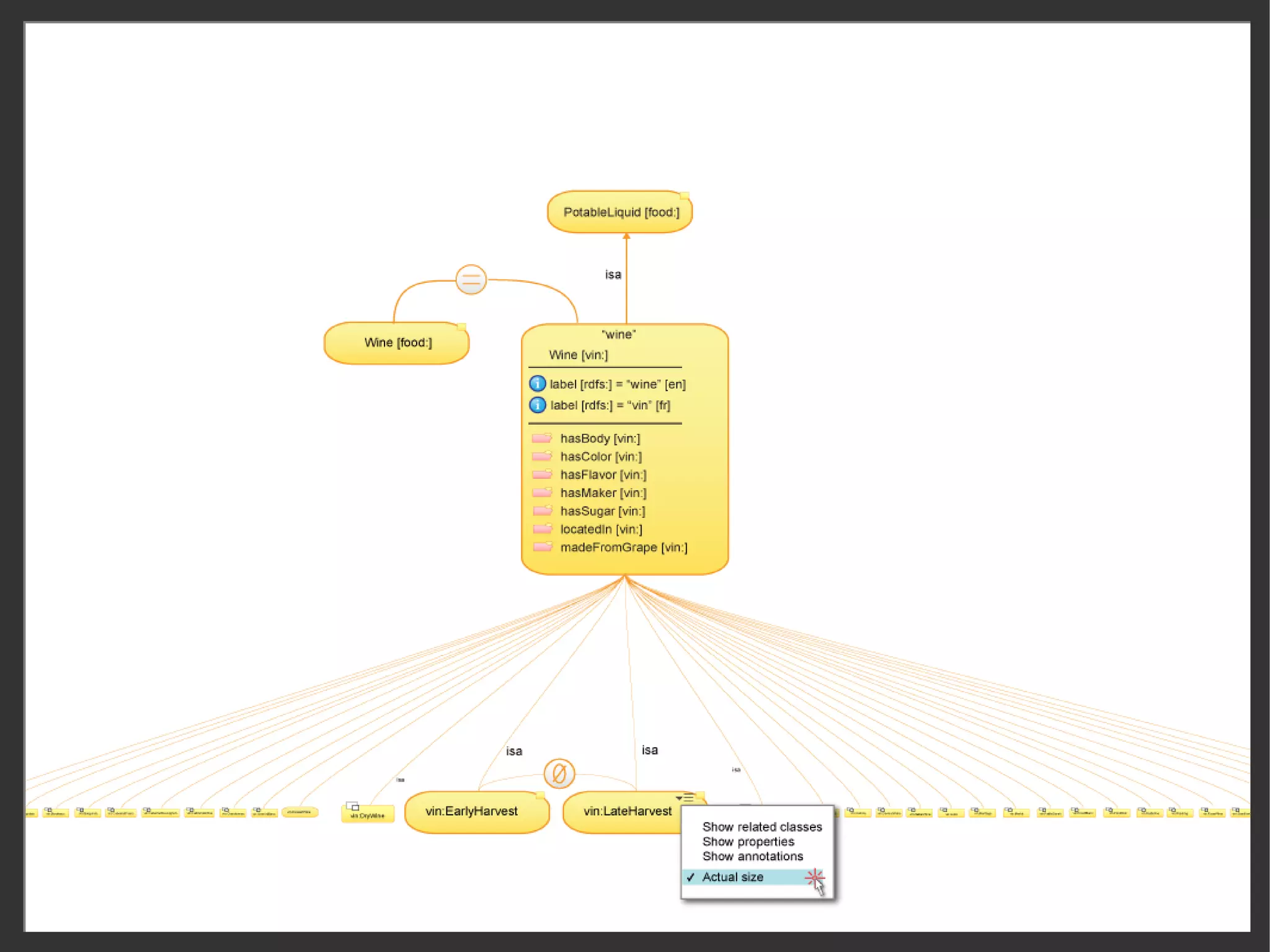
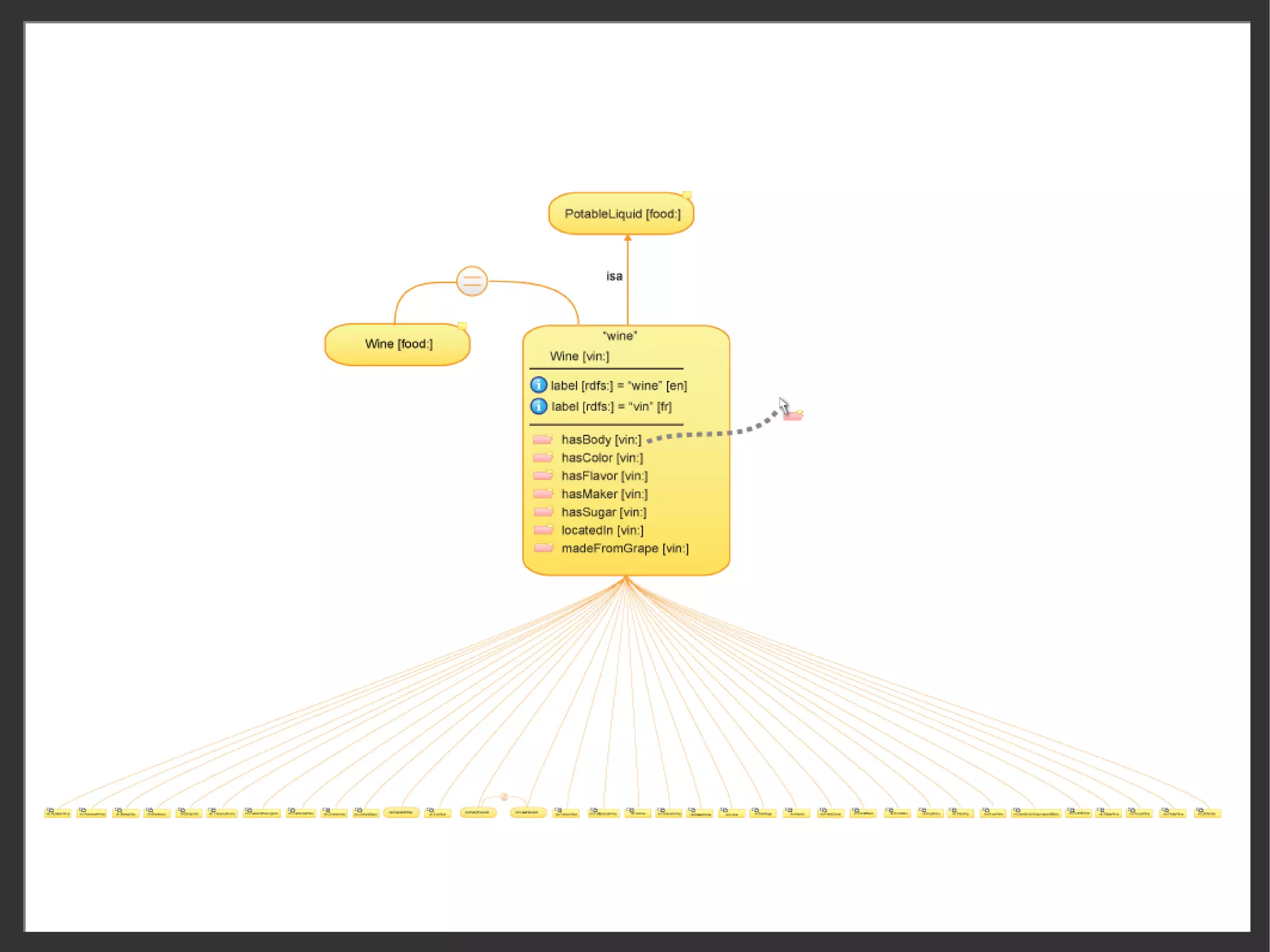
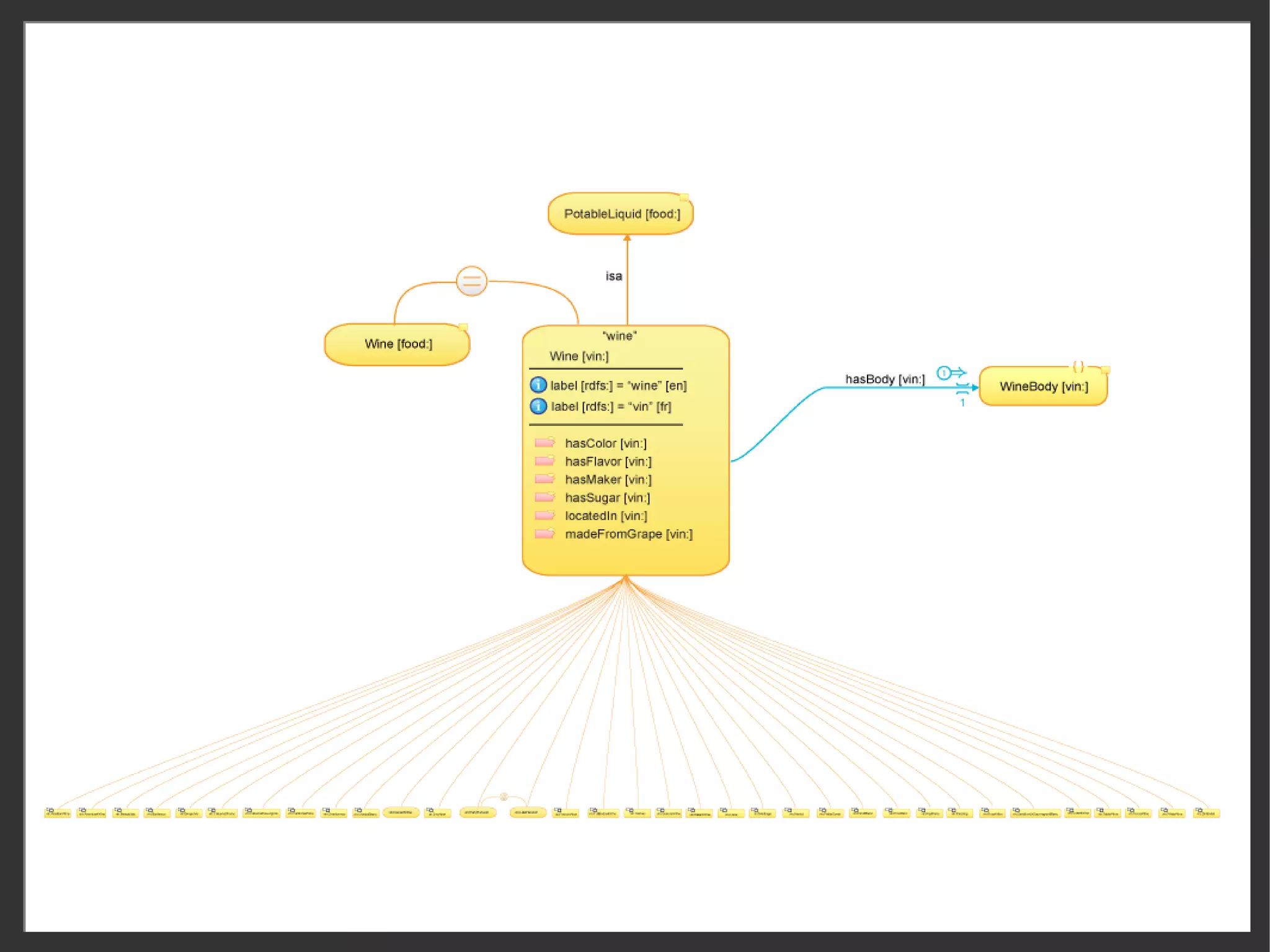
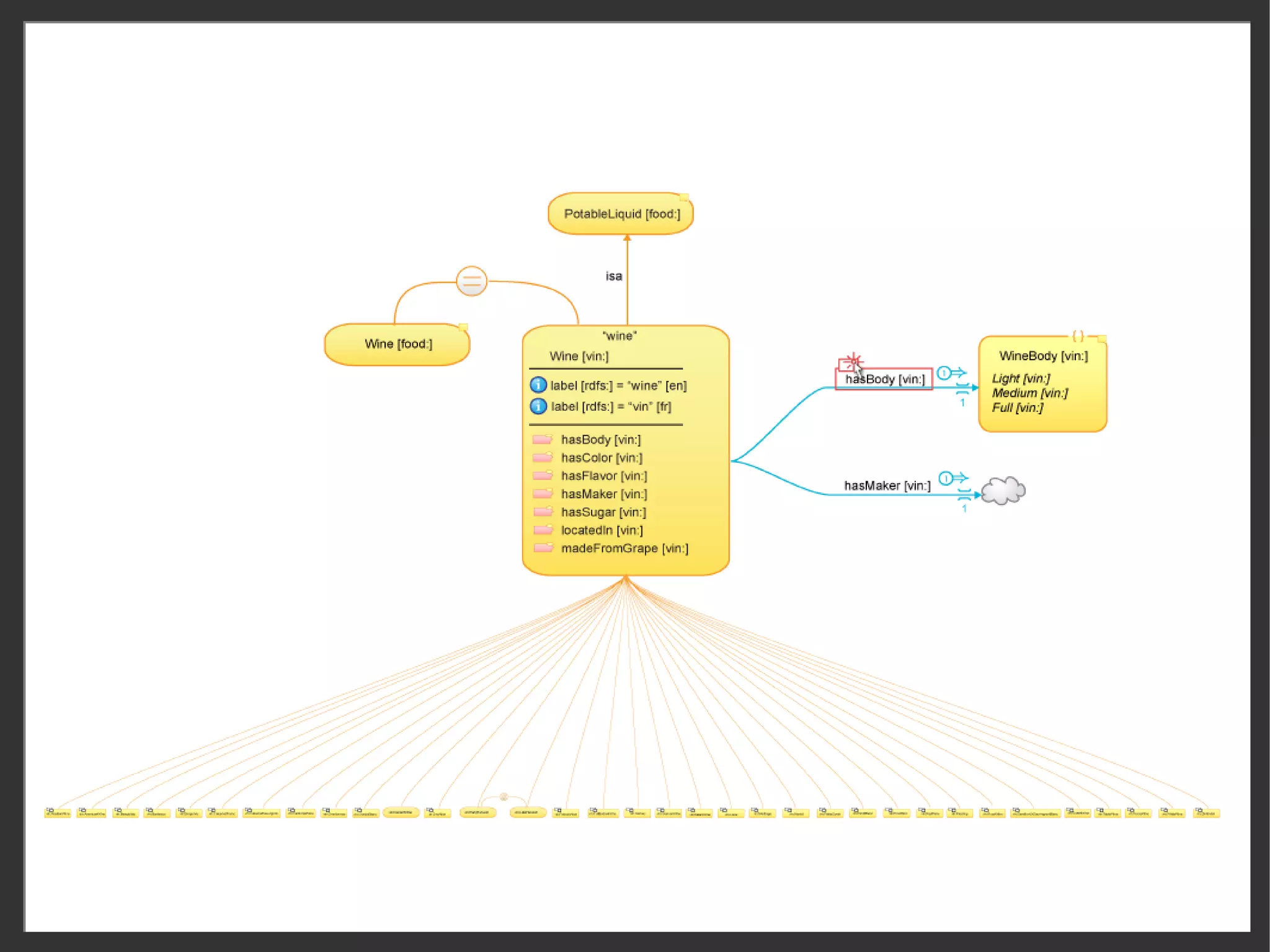
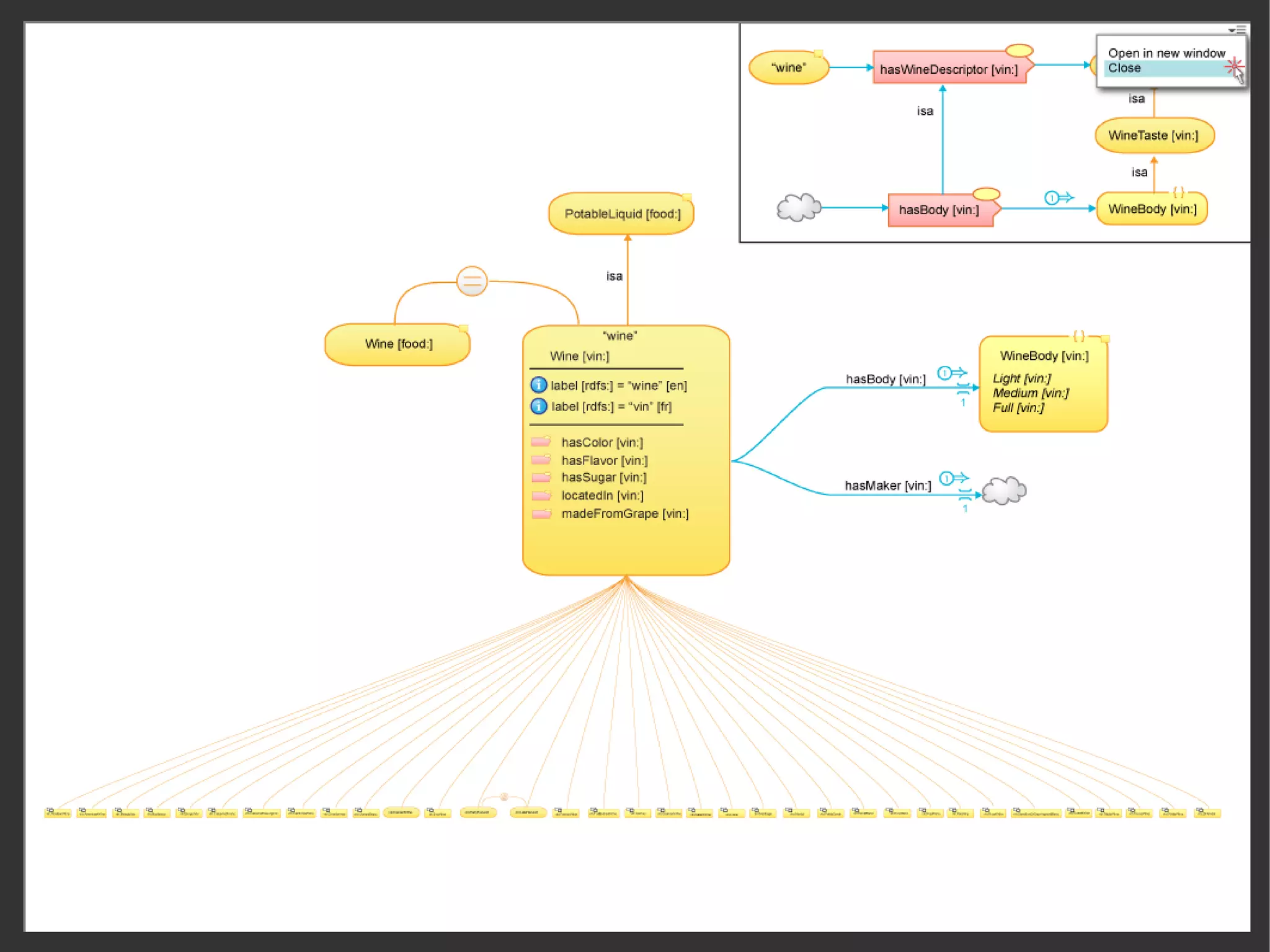
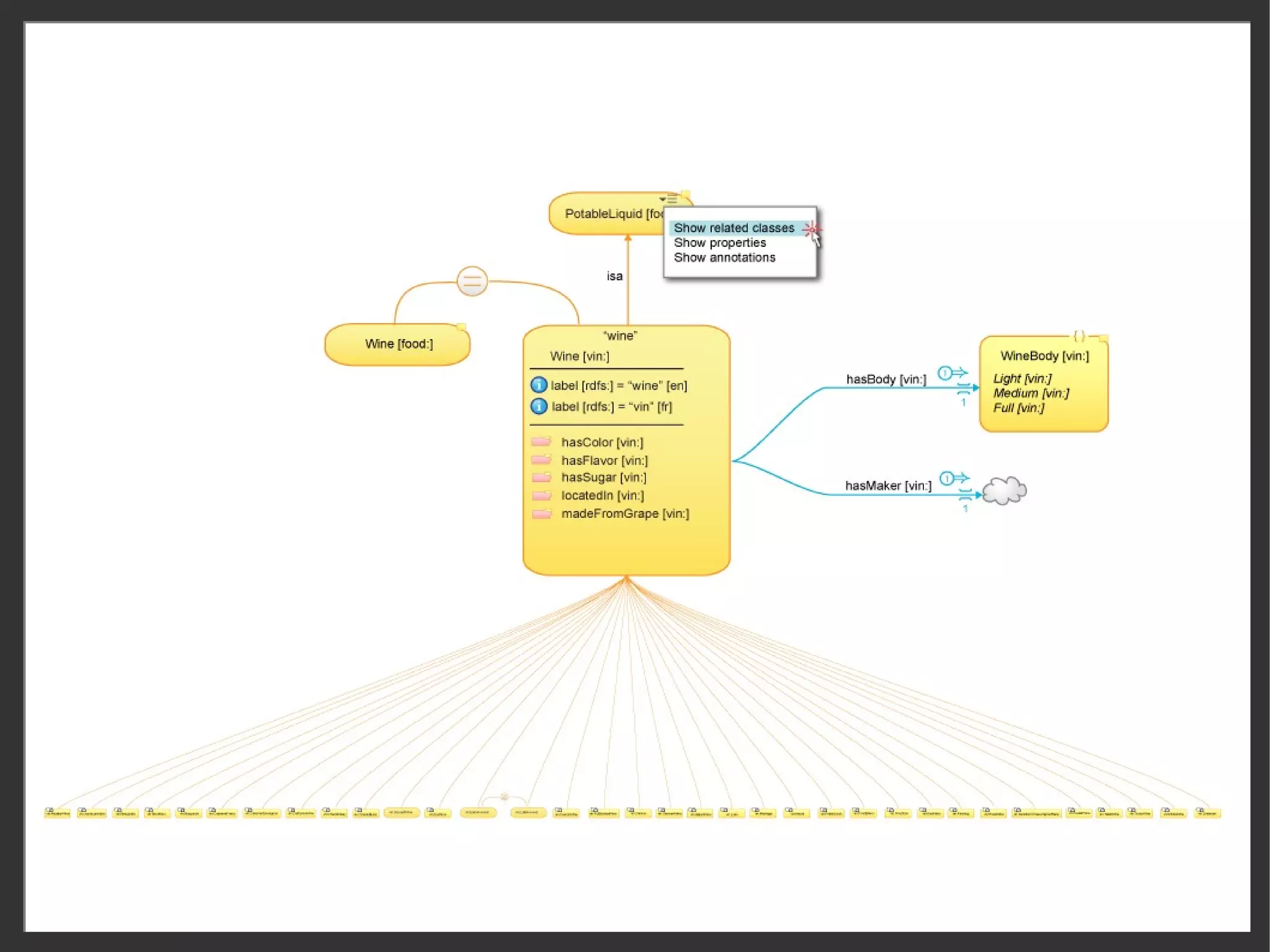
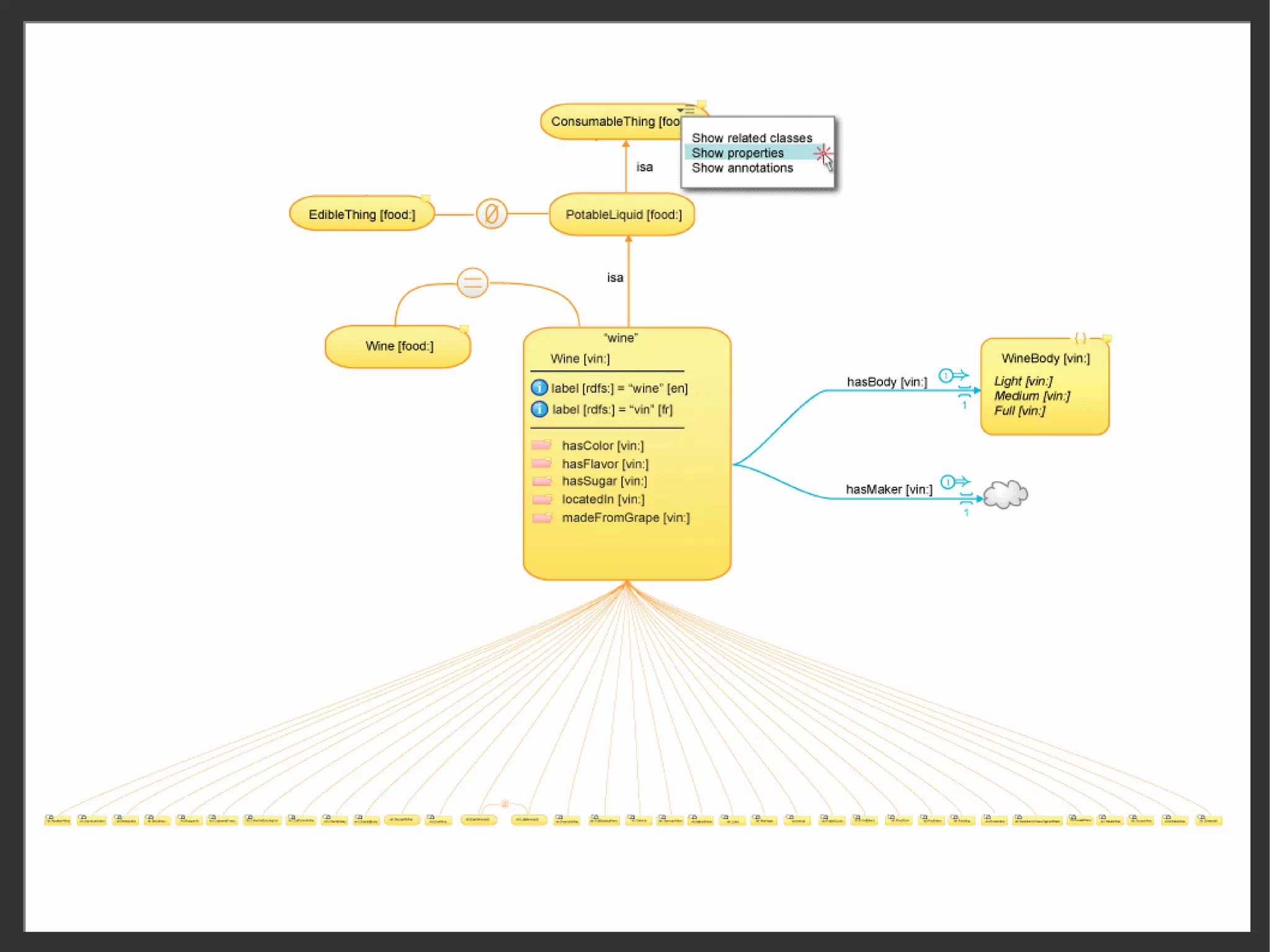
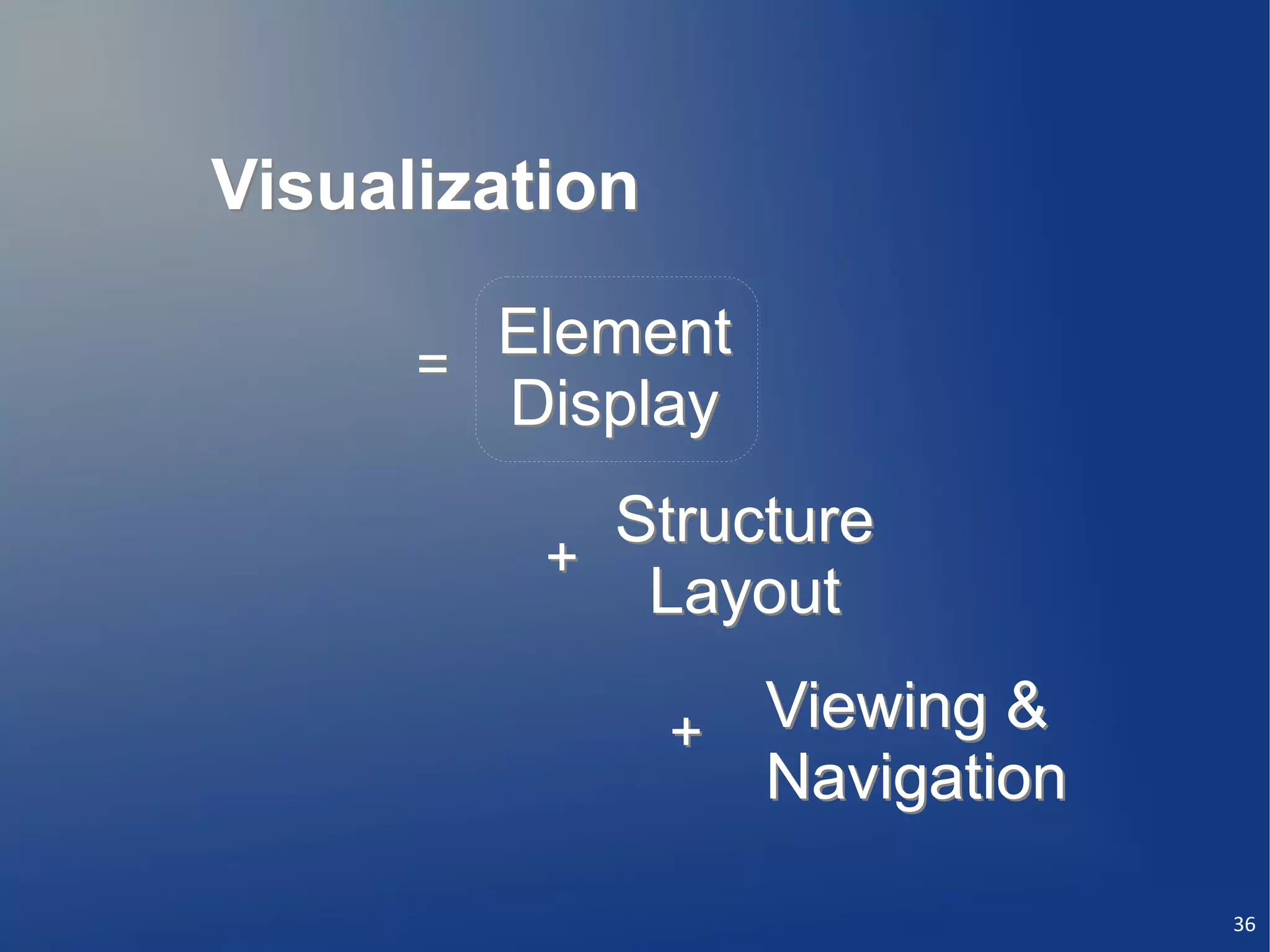
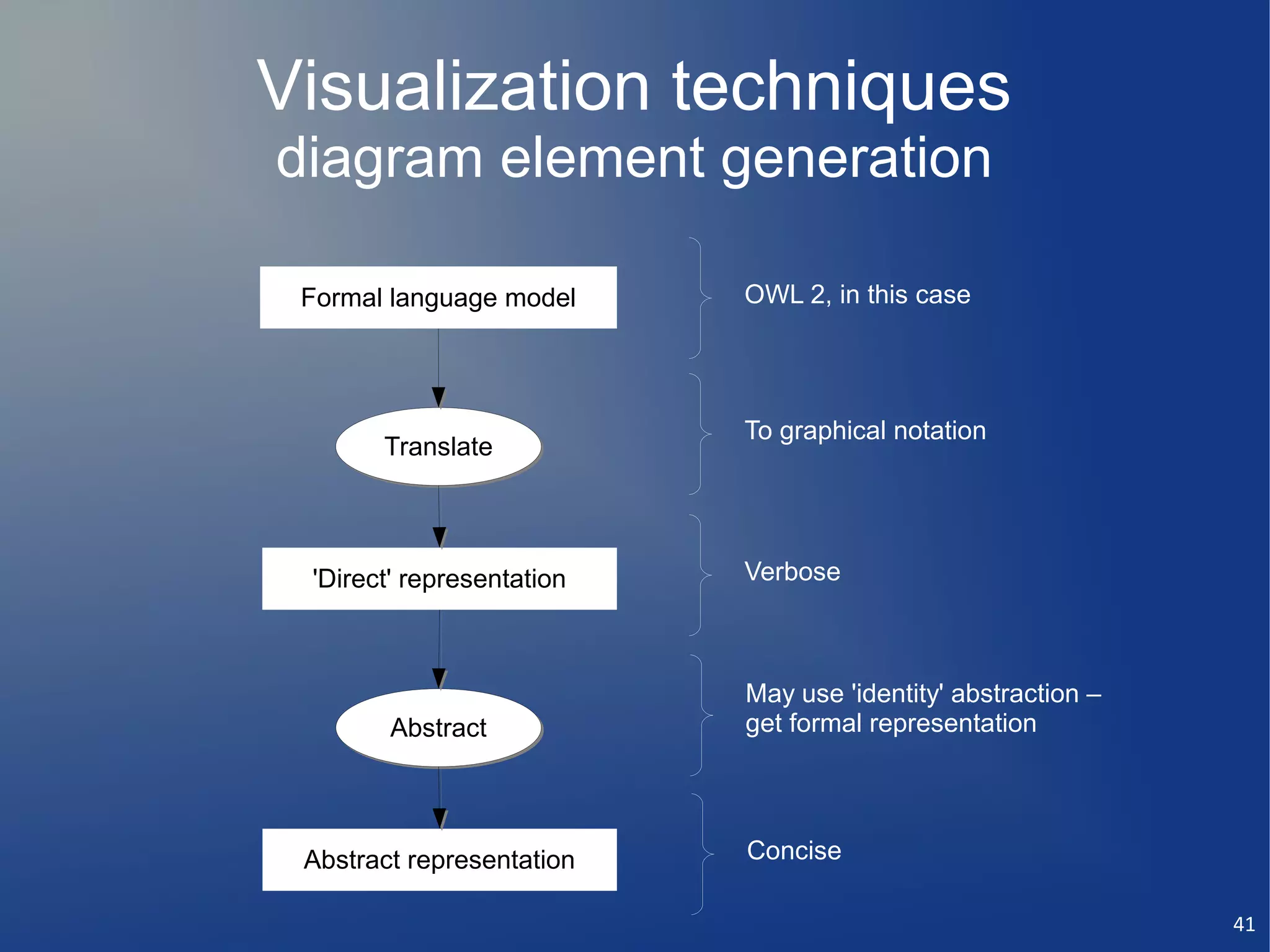
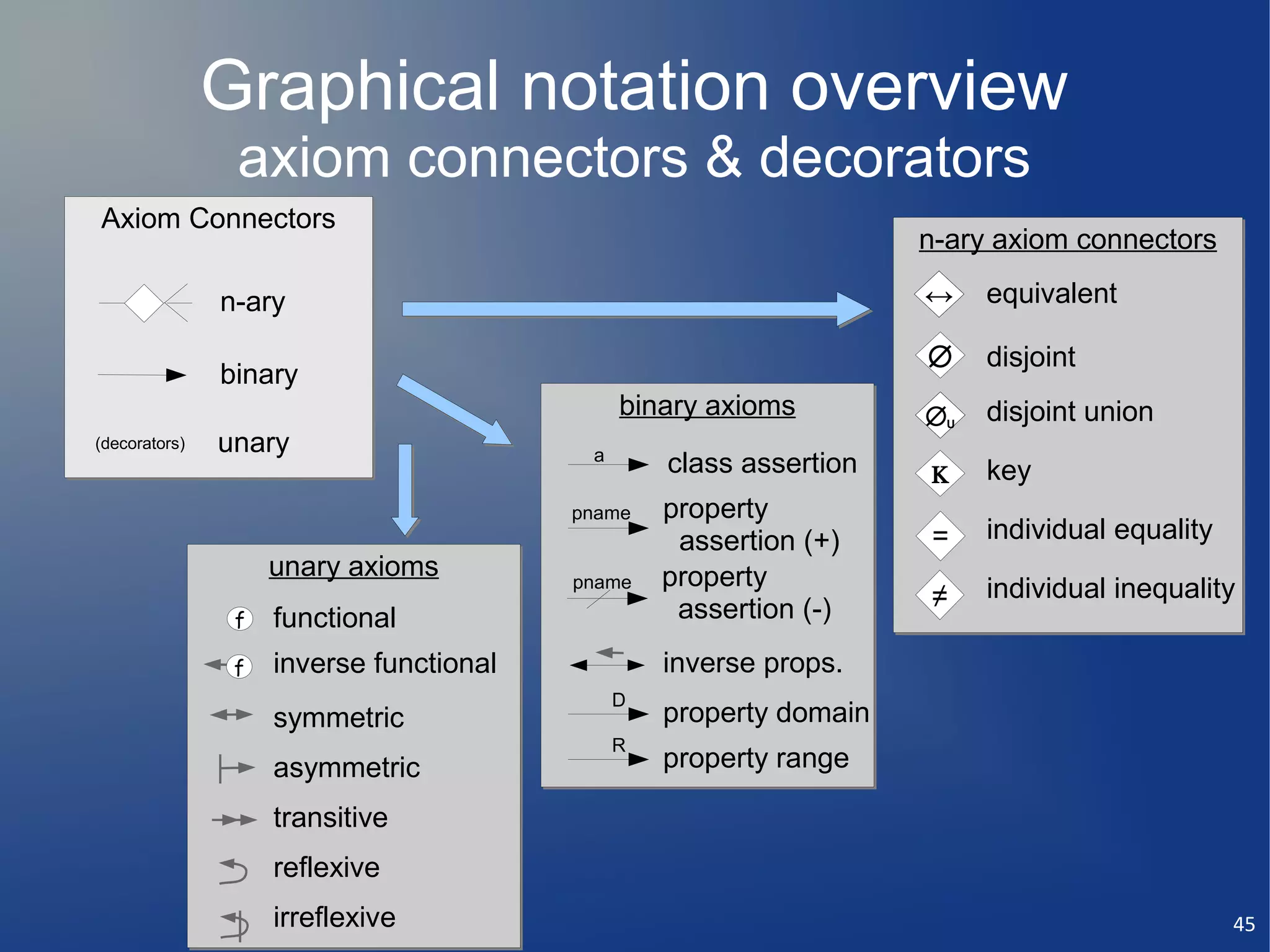
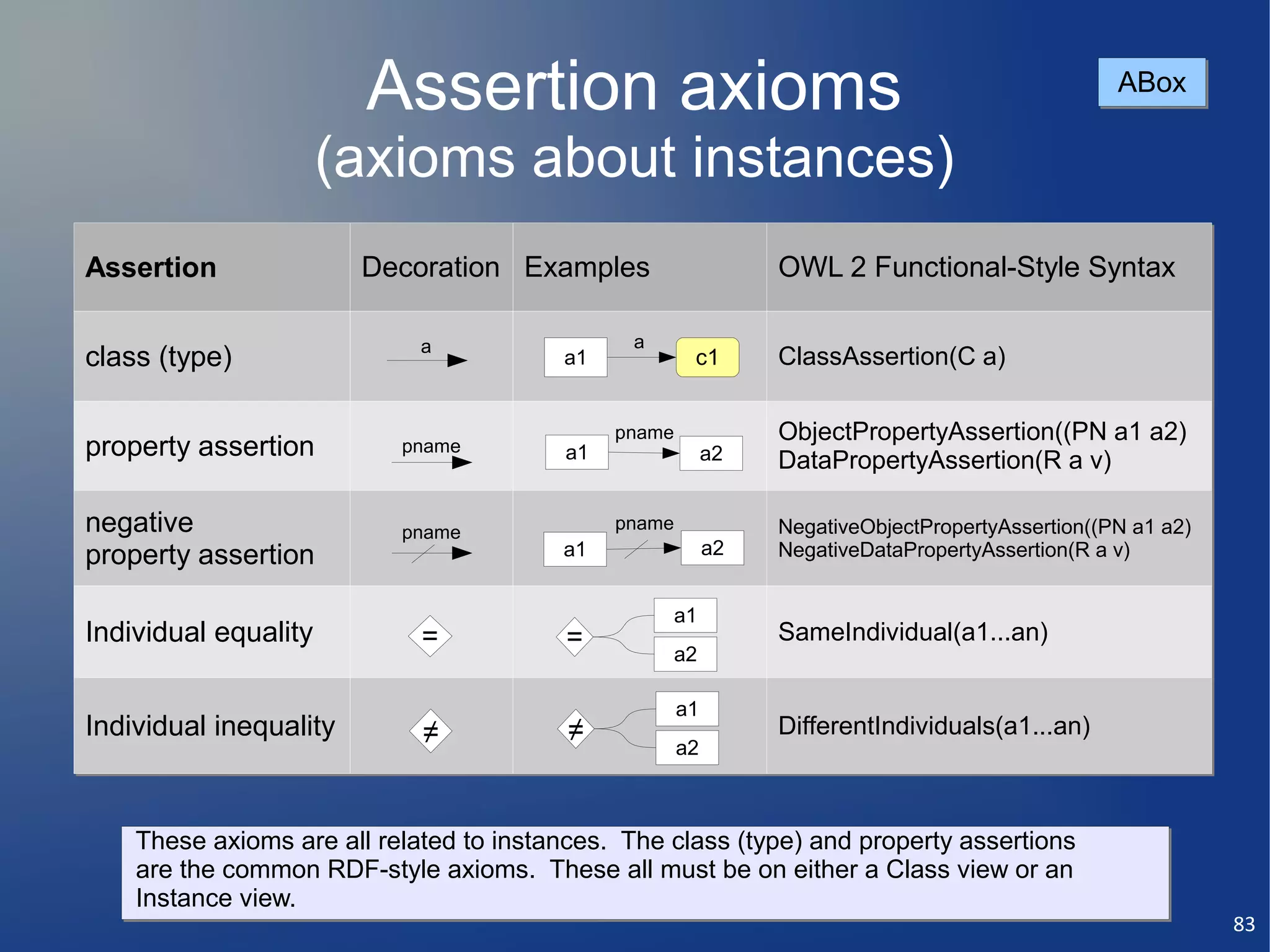
This document discusses the importance of semantic modeling and visualization techniques for ontologies, particularly in making them accessible to both technical and non-technical users. It emphasizes the need for standardized visualization notations to enhance understanding and collaboration, especially in projects involving complex data integration and analytics. It also outlines key requirements for effective graphical notation, including conciseness, completeness, and intuitiveness.







![Visualization research
2
OWL2UML/OWLGrEd,
DLG [2005]
2
OntoTrack [2005] Protege [2010]
OntoVis, Protege [2007] OWLVis, Protege [2005] OWLPropViz, Protege [2008]
Growl [~2006] EzOWL [2006] Jambalaya, Protege [2009]
27](https://image.slidesharecdn.com/revelytixsemanticmodelingnotationscanlonsemtech2010-110104144941-phpapp01/75/Semantic-Modeling-Notation-Scanlon-SemTech-2010-27-2048.jpg)










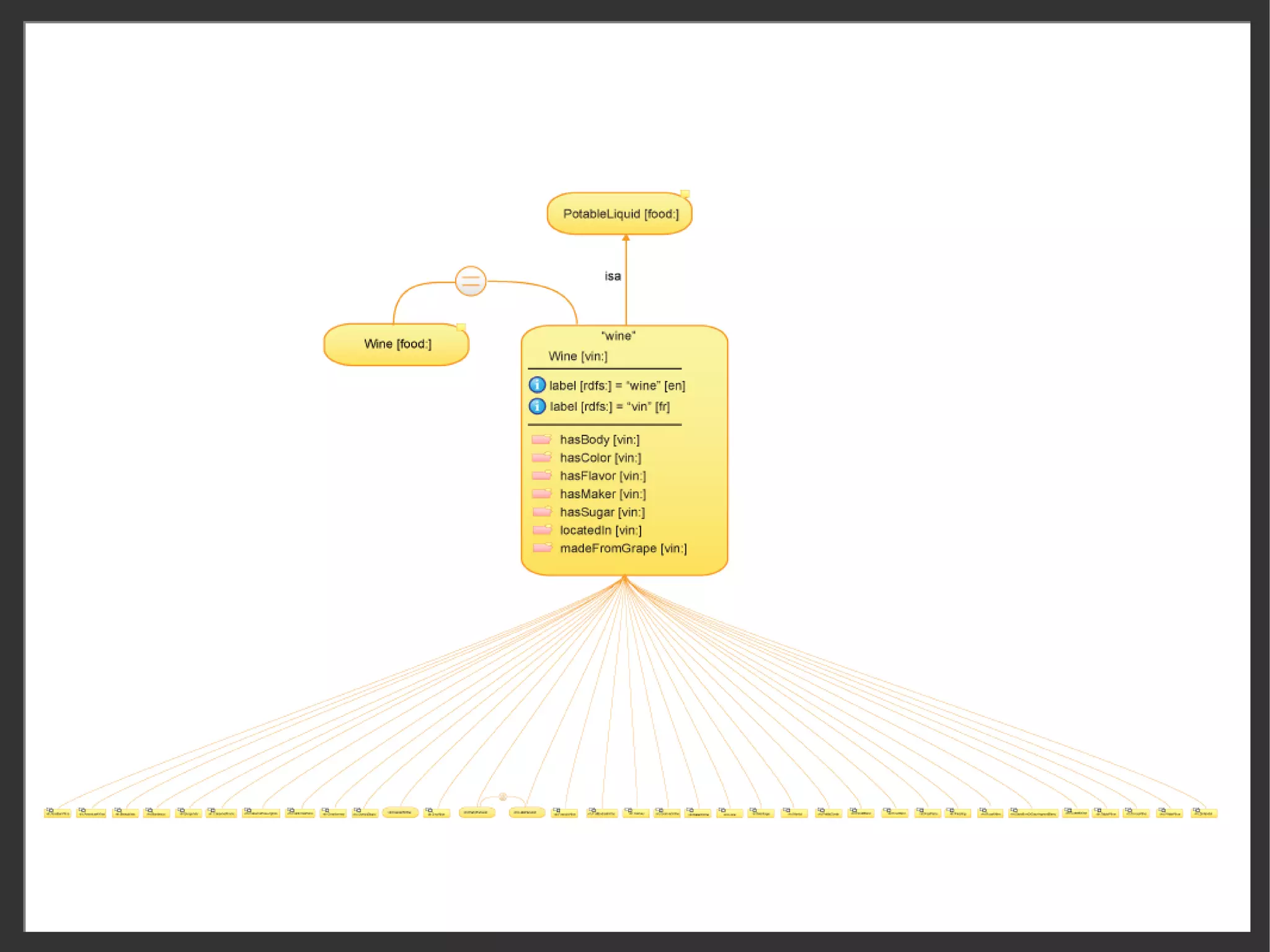
![Map of the (owl 2) universe
Concepts/Categories Roles/Relations Instances Data types
(individuals, (data ranges,
(classes) (properties)
literals) datatypes)
Simple named class
named class named object property
named object property named individual
named named datatype
named datatype
Expressions named data property
named data property anonymous individual
anonymous individual
(defined via declarations)
(defined via declarations) literal value
value
enumeration
enumeration inverse (anonymous)
inverse (anonymous) enumeration
enumeration
Boolean compositions
Boolean compositions Boolean compositions
Boolean compositions
Complex - intersection
- intersection - intersection
- intersection
Expressions - union
- union - union
- union
- complement
- complement - complement
- complement
(defined via Restrictions (obj,data)
Restrictions Restrictions
Restrictions
constructors) - universal, existential
- universal, existential - datatype restriction
- datatype restriction
- value, local reflexivity
- value, reflexivity
- cardinality (qualified)
- cardinality (qualified)
TBox RBox ABox TBox ?
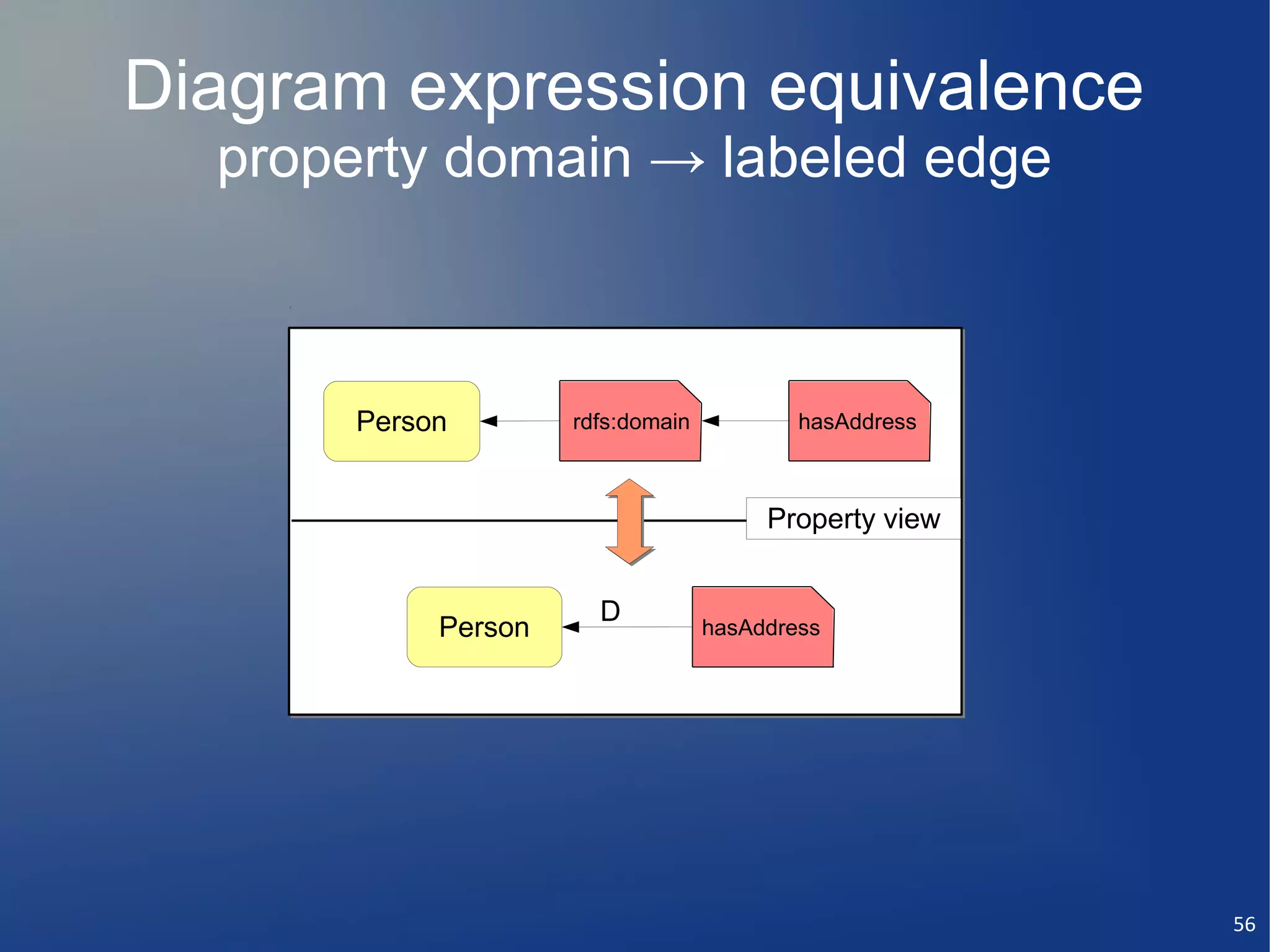
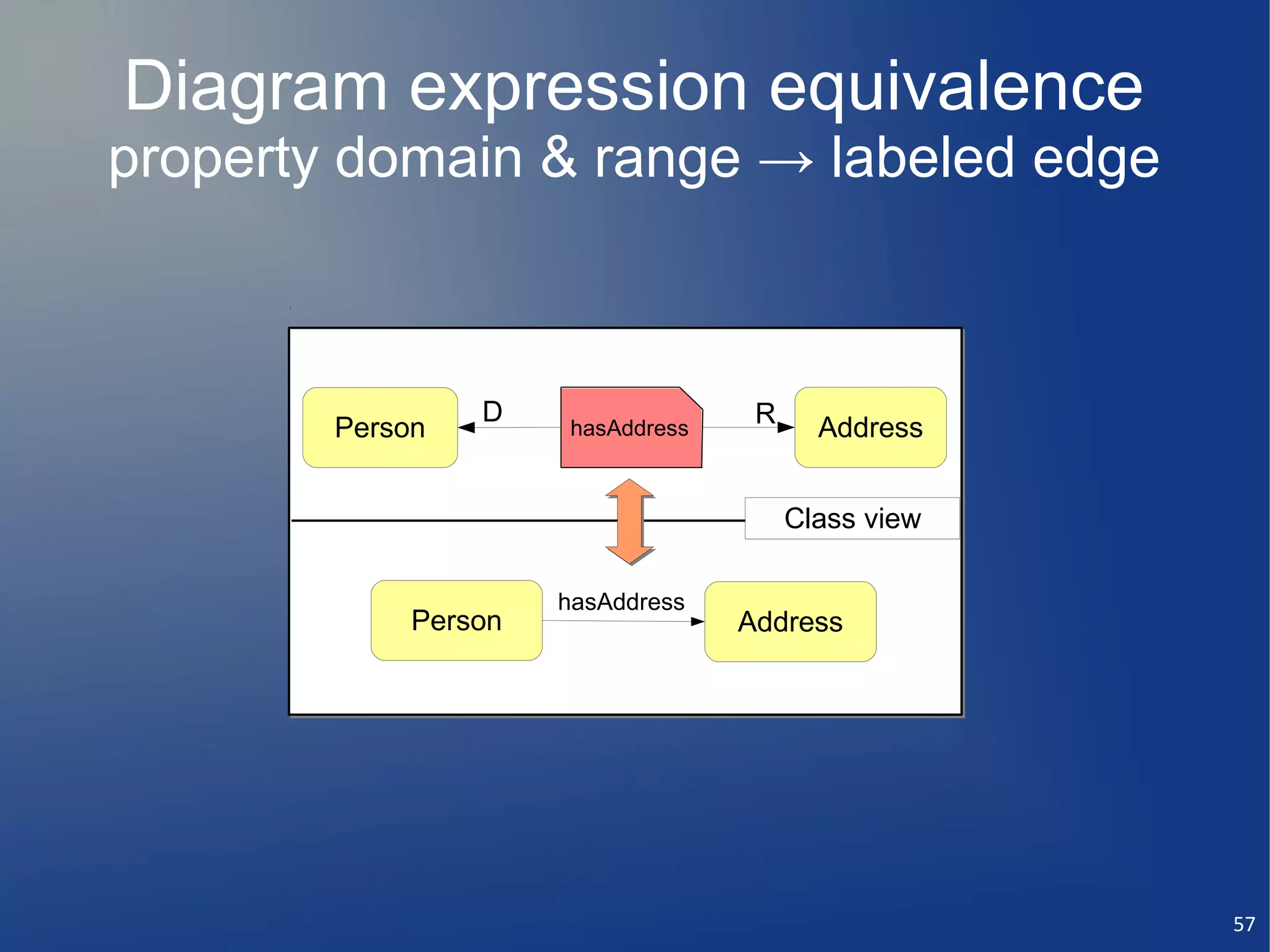
Class relationships
Class relationships domain, range
domain, range class (rdf:type)
class datatype definition
datatype
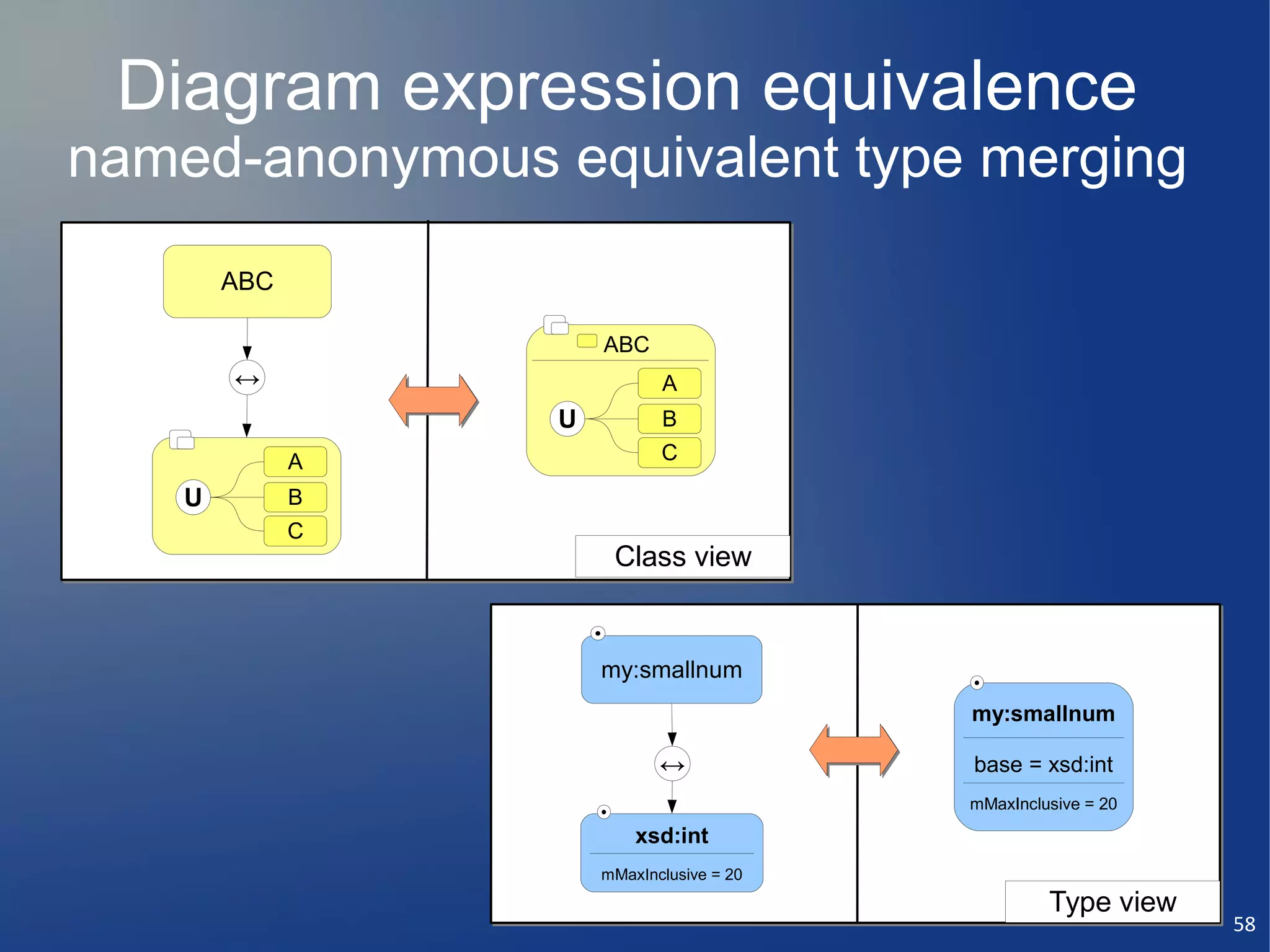
- subclass
subclass Property relationships
Property relationships Instance equality
Instance equality
- equivalent classes
equivalent classes - subproperty [chained]
- subproperty [chained] - same individuals
same individuals
Axioms - disjoint classes - equivalent properties - different individuals
disjoint classes - equivalent properties different individuals
- disjoint union
disjoint union - disjoint properties
- disjoint properties Property assertions
Property
(defined via key - inverse (obj only)
- inverse (obj only) - object property, pos
object property, pos
statements) Object property char.
Object property char. - data property, pos
data property, pos
- functional, inverse func. - object property, neg
- functional, inverse func. object property, neg
- symmetric, asymmetric - data property, neg
- symmetric, asymmetric data property, neg
- reflexive, irreflexive
- reflexive, irreflexive
- transitive
- transitive
40](https://image.slidesharecdn.com/revelytixsemanticmodelingnotationscanlonsemtech2010-110104144941-phpapp01/75/Semantic-Modeling-Notation-Scanlon-SemTech-2010-40-2048.jpg)





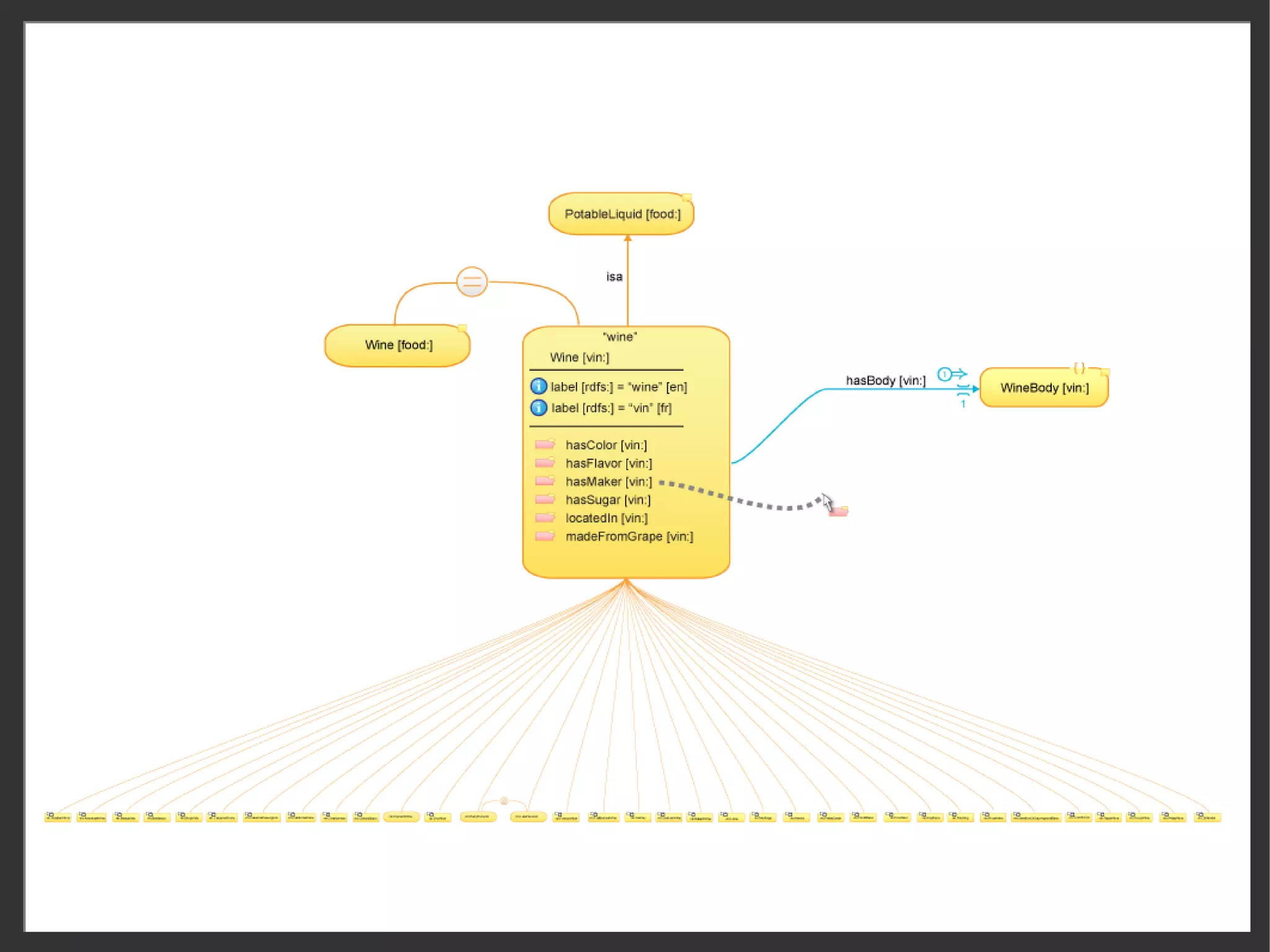
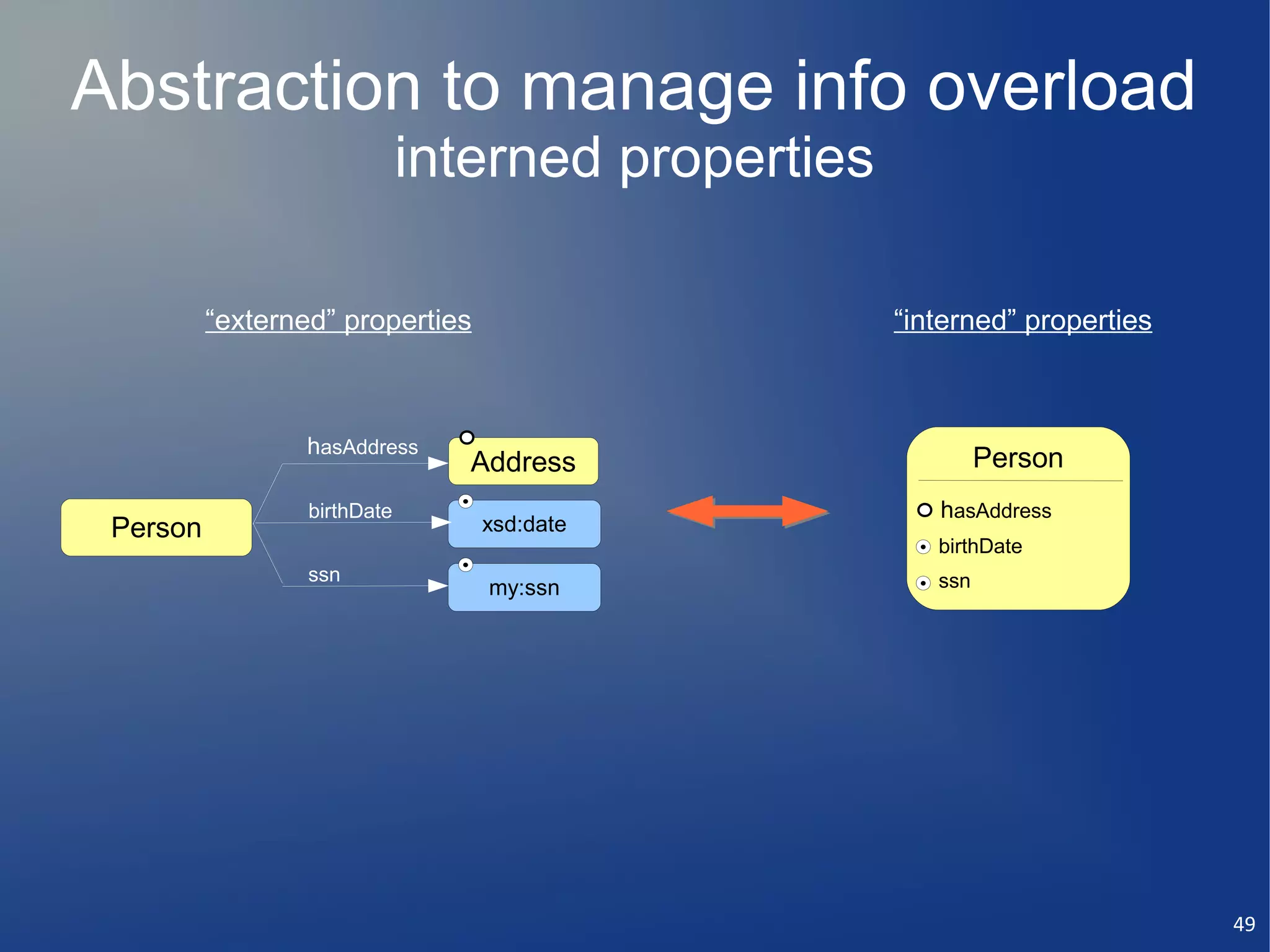
![Multiple forms to manage info overload
class details
Decorators to expand and contract
to expand and contract
shown only on-screen, on mouse
over.
over.
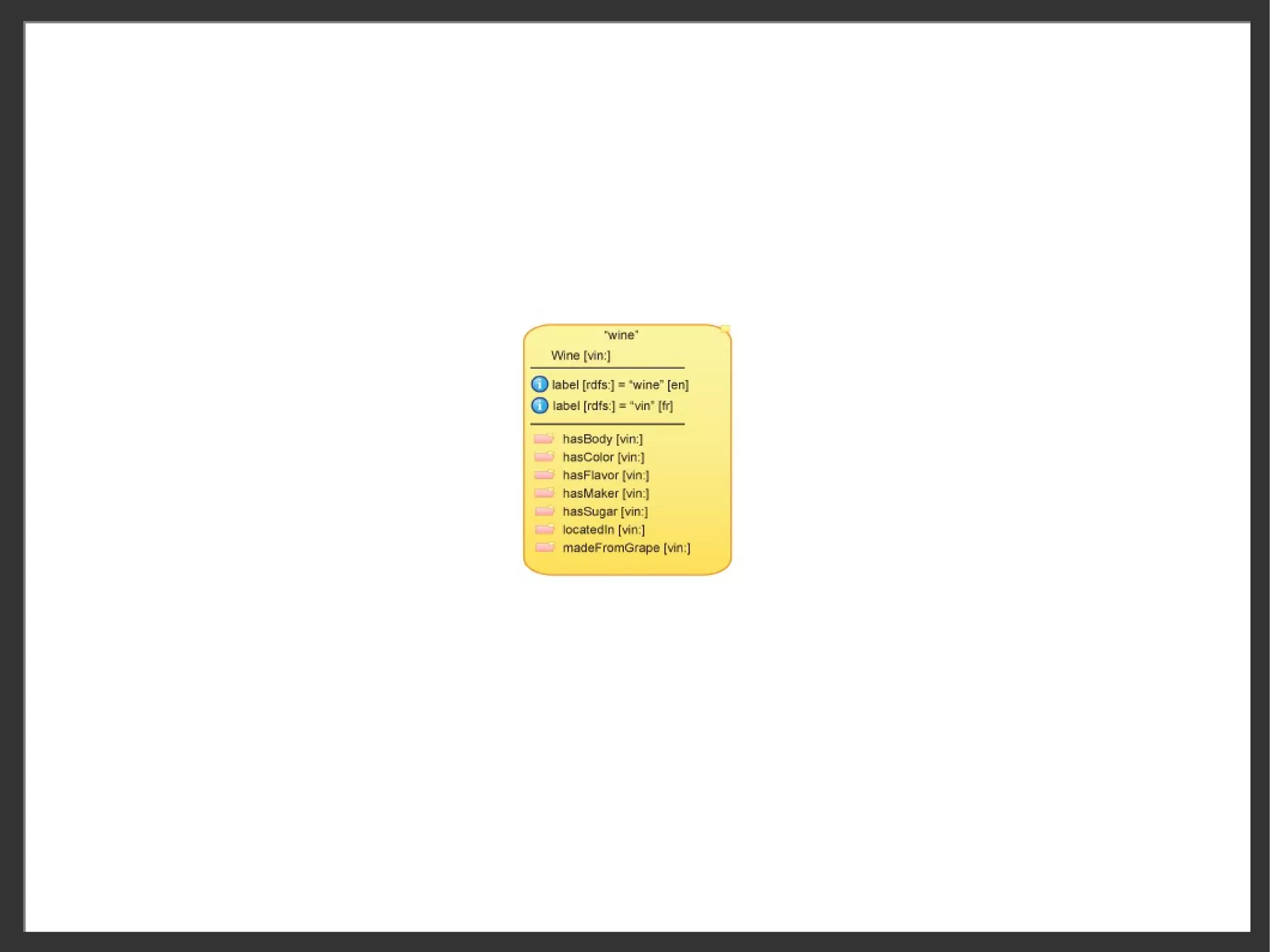
Person Person label and/or IRI
i label “Person” [en]
metadata (annotations)
i label “Persona” [sp]
asAddress
birthDate 'interned' properties
ssn
collapsed expanded
48](https://image.slidesharecdn.com/revelytixsemanticmodelingnotationscanlonsemtech2010-110104144941-phpapp01/75/Semantic-Modeling-Notation-Scanlon-SemTech-2010-48-2048.jpg)
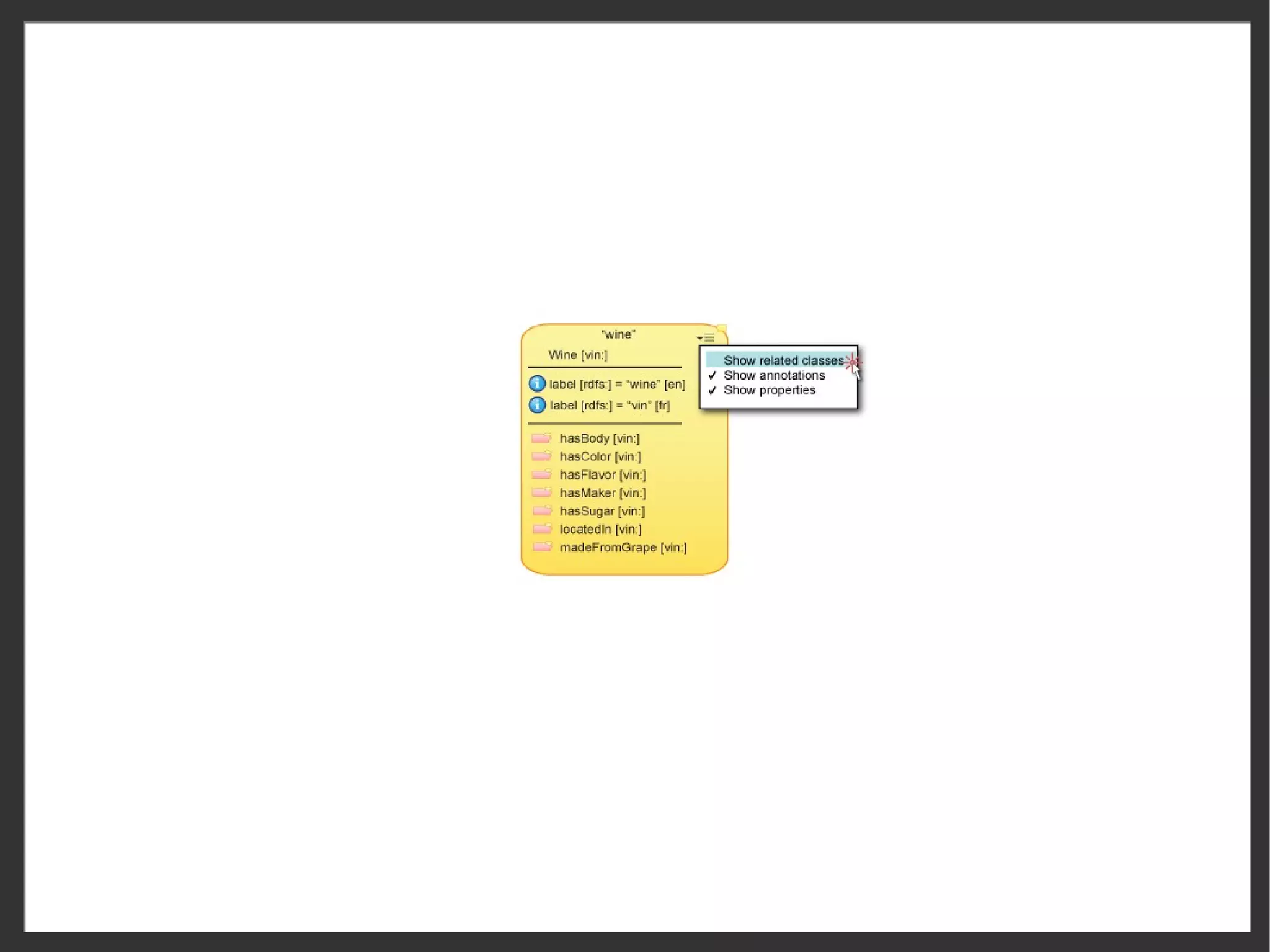
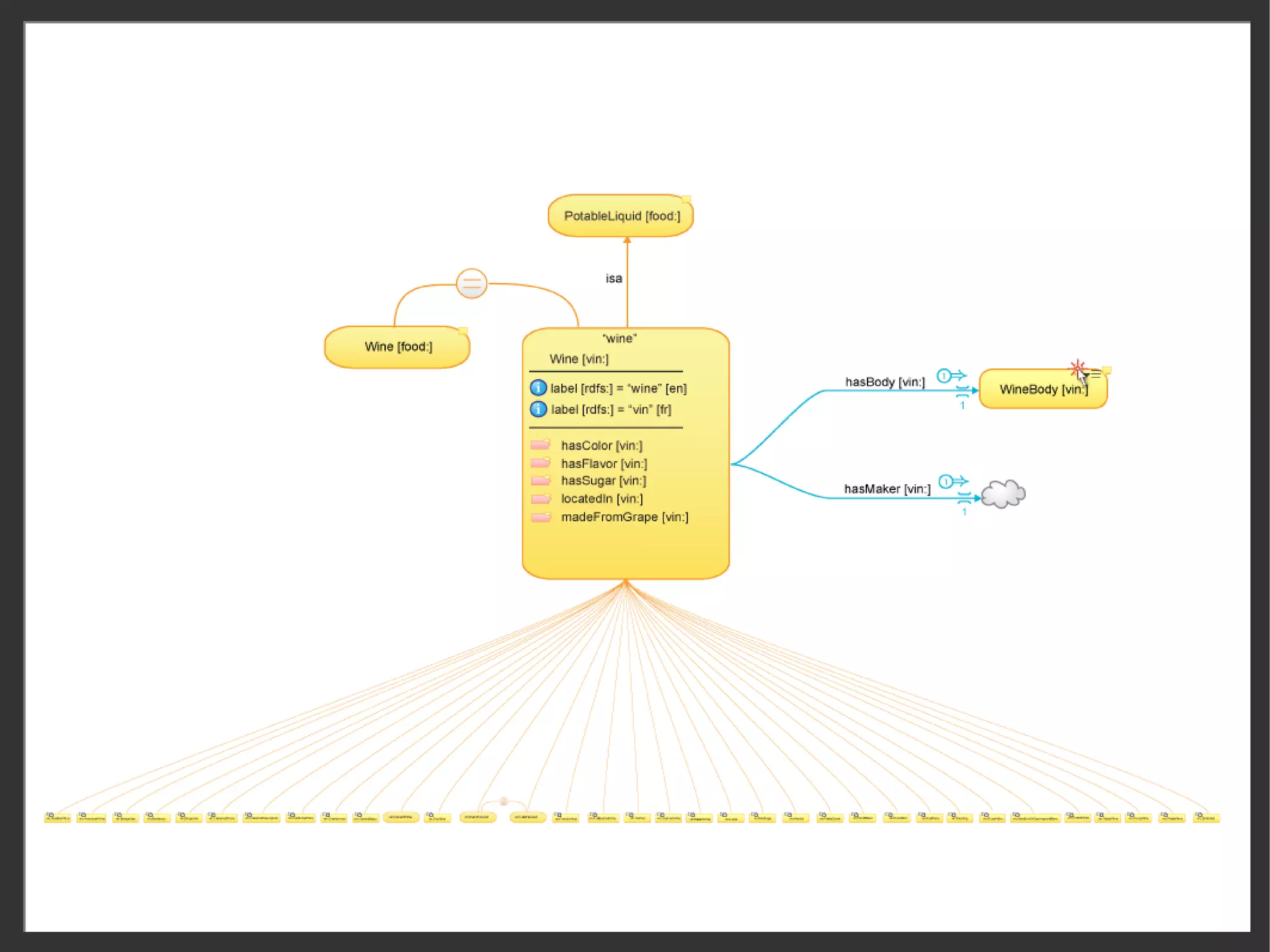
![User interaction to manage info overload
interning/externing of properties
Person Person
i label “Person” [en] i label “Person” [en]
hasAddress
i label “Persona” [sp] i label “Persona” [sp]
Address
hasAddress birthDate
birthDate ssn drag property in
(“intern”)
ssn
Person Person
i label “Person” [en] i label “Person” [en]
hasAddress
i label “Persona” [sp] i label “Persona” [sp]
Address
hasAddress birthDate
birthDate drag property out ssn
ssn (“extern”)
50](https://image.slidesharecdn.com/revelytixsemanticmodelingnotationscanlonsemtech2010-110104144941-phpapp01/75/Semantic-Modeling-Notation-Scanlon-SemTech-2010-50-2048.jpg)











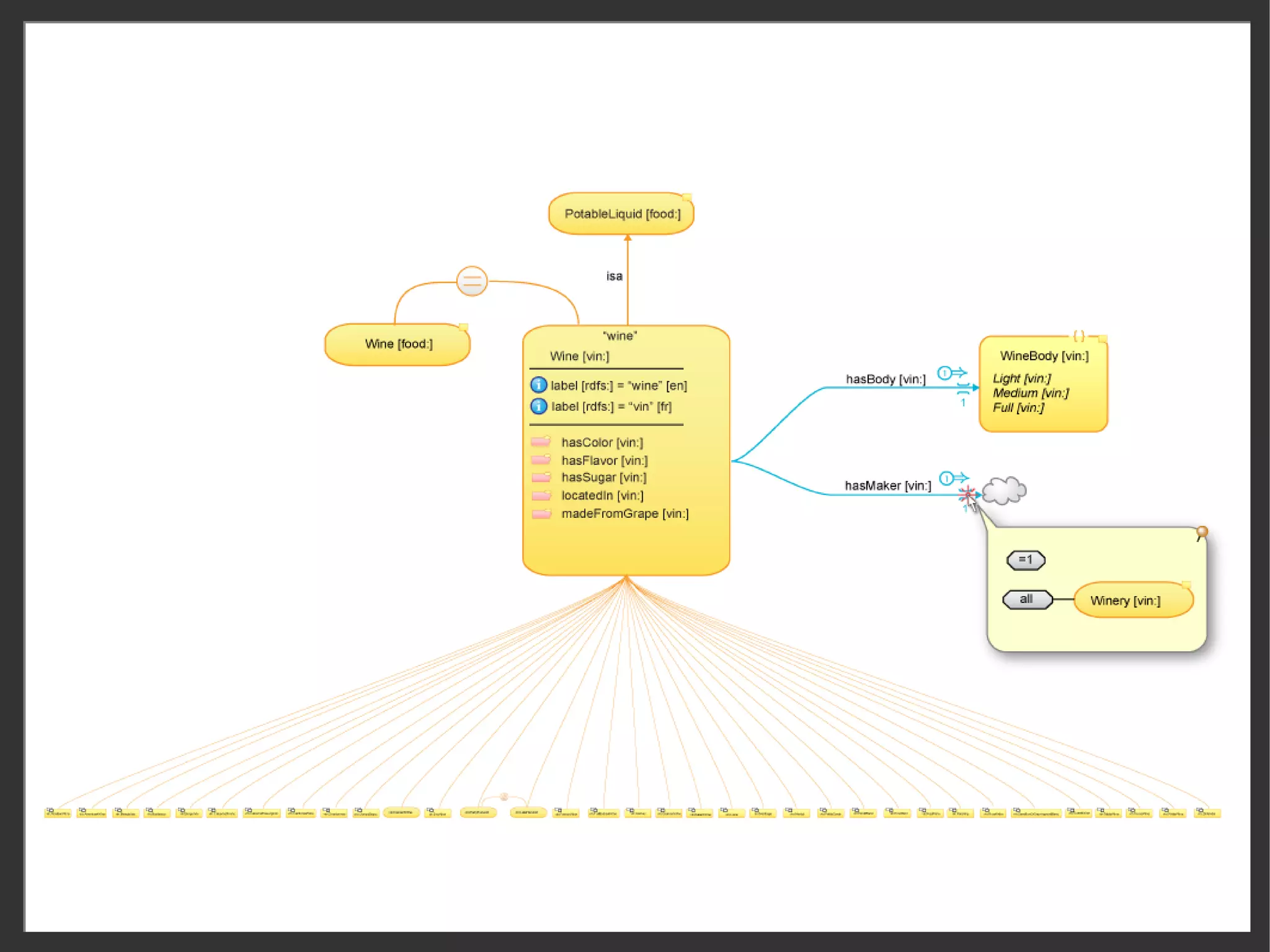
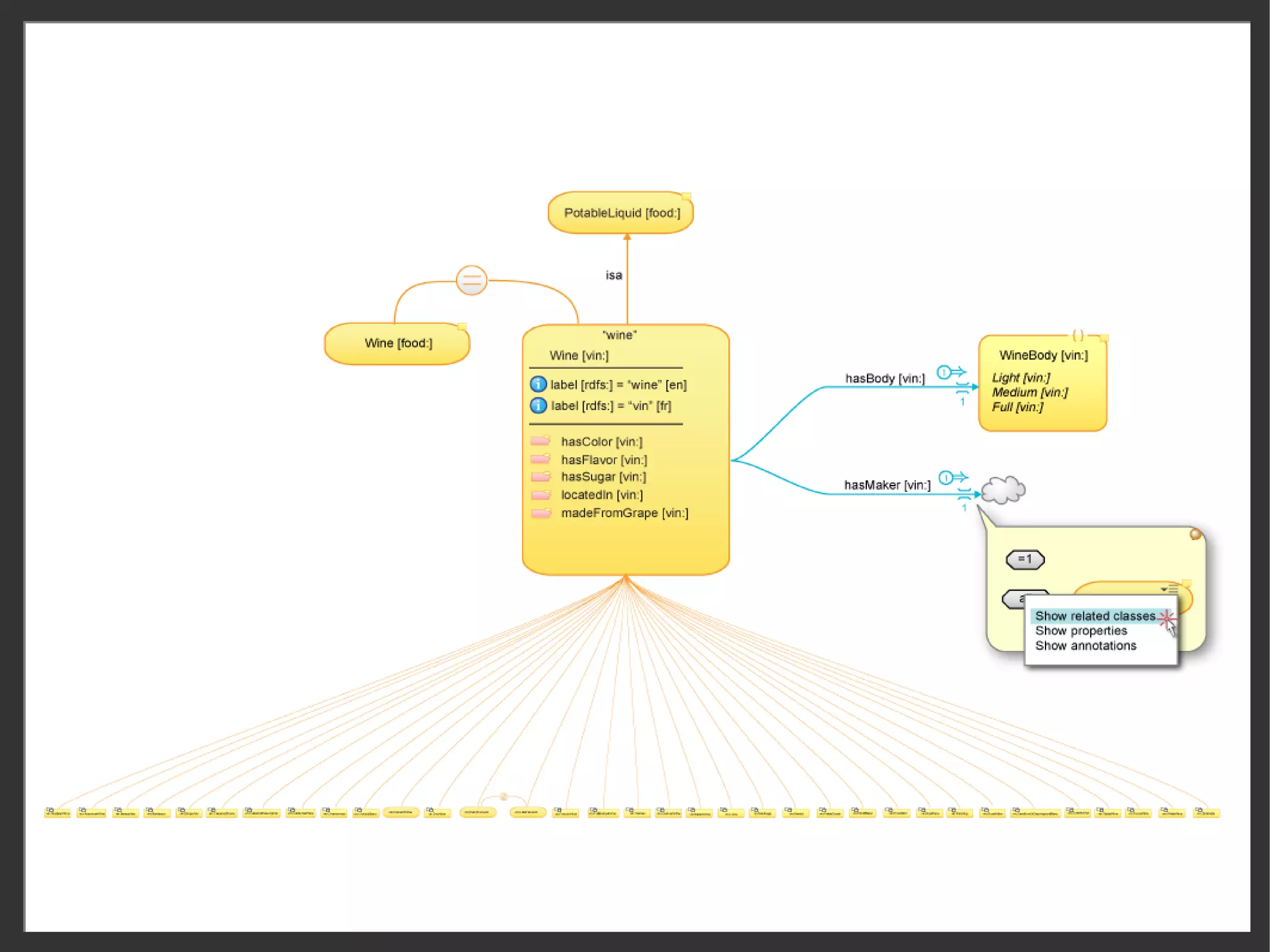
![Property expressions
object property expressions
Property
Decoration Examples OWL 2 Functional-Style Syntax
Expression
inverse [p]
[ ] c1 c2 ObjectInverseOf(P)
(anonymous)
There is only a single property expression, for defining an anonymous property as an
inverse of an existing property. This must be on a Class Representation View.
75](https://image.slidesharecdn.com/revelytixsemanticmodelingnotationscanlonsemtech2010-110104144941-phpapp01/75/Semantic-Modeling-Notation-Scanlon-SemTech-2010-75-2048.jpg)










![Semantic Modeling
Notation
Bob Scanlon
[ svp development, rscanlon @ revelytix.com ]
Jim Irwin
[ svp development, jirwin @ revelytix.com ]
SemTech, 25 June 2010
90](https://image.slidesharecdn.com/revelytixsemanticmodelingnotationscanlonsemtech2010-110104144941-phpapp01/75/Semantic-Modeling-Notation-Scanlon-SemTech-2010-90-2048.jpg)